Hier rechts zie je de balans uit het filmpje. Links van de steen zie je 2 zakken en 1 losse knikker. Rechts van de steen zie je 7 losse knikkers.
Wanneer we een vergelijking oplossen willen we de onbekende uitrekenen. We willen dus weten hoeveel 1 zak waard is.
Noteer de vergelijking die bij de balans hoort.
... + 2 zakken = ....
Wanneer we aan beide kanten 1 losse weg halen dan krijg je de volgende vergelijking:
2 zakken = ....
We willen niet weten wat 2 zakken waard is, maar we willen weten wat 1 zak waard is.
daarom delen we beide kanten van de steen door 2. De oplossing is dan:
1 zak = ...
2
Balans
In plaats van een wipwap (de steen uit het filmpje) kun je ook een ouderwetse weegschaal gebruiken om de balansmethode voor je te zien.
Op de balans hiernaast zie je uitgebeeld:
2 + 4x = 12
Neem de vergelijking over in je schrift.
2 + 4x = 12
Haal aan beide kanten losse blokjes weg
*let op: bewaar het evenwicht. Noteer je stappen.
Als je het goed gedaan hebt, heb je links de x-jes over en recht de losse blokjes
Controleer dit met wat er in je schrift staan. Fout? doe vraag a en b opnieuw.
Bereken wat één x waard is. Noteer de stap in je schrift en schrijf je antwoord op.
3
Balans
Hiernaast zie je een balans getekend.
Noteer de vergelijking die bij de balans hoort in je schrift.
Los de vergelijking op.
Welke waarde van x heb je gevonden?
4
Waar zit de fout?
Hierboven zie je de balans getekend die hoort bij de vergelijking
2x + 1 = 9
Hieronder zie je de uitwerking van de vergelijking. Ergens gaat het fout.
2x + 1
=
9
-1x
-1x
1x + 1
=
8
-1
-1
1x
=
7
Bij welke stap zit de fout?
Welke fout wordt er gemaakt?
Neem de vergelijking over en los hem netjes op (verbeter de opgaven!)
Begrijp je nog niet helemaal wat we aan het doen zijn? Bekijk dan dit nog even voordat je verder gaat met vraag vijf.
5
Balans
Vul in: De balans hiernaast is in evenwicht.
Neem over en vul in. Aan de linkerkant van de balans liggen:
... losse en ... x-en
Aan de rechterkant van de balans liggen:
... losse en ... x-en
De vergelijking die bij de balans hoort is: 4 + ...x = ... + 3x
Los de vergelijking op.
4 + 5x
=
10 + 3x
...
...
5x
=
6 + 3x
...
...
...
=
6
...
...
x
=
.....
Het op deze manier oplossen van een vergelijking noem je de .........
Lukt het je niet om de balans op te lossen? Bekijk dan even dit
6
Teken zelf de balans
Teken zelf een balans bij:
8x + 6 = 2x + 24
Los de vergelijking op:
8x + 6
=
2x + 24
...
...
..... + 6
=
24
...
...
.....
=
.....
...
...
x
=
.....
7
Twee vergelijkingen
Los deze vergelijkingen op met de balansmethode.
5x + 6 = 2x + 24
8x + 36 = x + 1
8
Taxibedrijf
Een taxibedrijf gebruikt bij het berekenen van de ritprijs de volgende formule:
prijs = 2 + 3 × afstand of korter genoteerd: p = 2 + 3a
De prijs is in euro’s en de afstand in kilometers.
Meneer Harmsen heeft een rit gemaakt met dit taxibedrijf.
Hij moet € 17,- afrekenen.
Meneer Harmsen wil weten hoeveel kilometer de rit was.
Hij moet de vergelijking: 2 + 3a = 17 oplossen.
Los de vergelijking op met een (terug-)rekenschema
Los de vergelijking op met de balansmethode
Welke manier heeft jouw voorkeur?
9
Kaarsen
Twee kaarsen worden tegelijk aangestoken. De eerste kaars is 20 cm lang per branduur wordt de kaars 2 cm korter. De tweede kaars is 30 cm lang wordt per branduur 4 cm korter.
Neem je t voor brandtijd in uren en L voor de lengte van de kaars, wat zijn dan de twee formules die bij de lengtes van deze kaarsen horen?
Je wilt weten na hoeveel uur branden beide kaarsen even lang zijn.
Met welke vergelijking kun je dit berekenen? Noteer de vergelijking in je schrift
Los die vergelijking op.
Na hoeveel uren branden zijn beide kaarsen even lang?
Hoe lang zijn de kaarsen dan?
10
Vergelijkingen oplossen
Los de volgende vergelijkingen op met behulp van de balansmethode:
4x = 16 + 2x
14a + 9 = 7a + 86
8 - 6y = 3y - 28
11
Omtrek
Bekijk deze twee figuren.
Wat kun je schrijven voor de omtrek van het linker figuur?
Wat kun je schrijven voor de omtrek van het rechter figuur?
Welke vergelijking moet je oplossen om uit te zoeken voor welke a de omtrek van beide figuren gelijk is?
Los die vergelijking ook op.
12
Toetscijfer
Voor een toets kun je maximaal 36 punten halen. De docent berekent bij deze toets het cijfer door bij het behaalde aantal punten vier op te tellen en dan de uitkomst daarvan te delen door vier.
Stel het behaalde aantal punten voor door p en het cijfer door c .
Maak het rekenschema dat de docent hierbij gebruikt.
Stel een bijpassende formule op: c = .....
Je wilt weten hoeveel punten je moet halen voor een 7,5.
Stel de vergelijking op die hier bij hoort en bepaal de oplossing.
13
Oplossen met de balansmethode
Los de volgende vergelijkingen op met behulp van de balansmethode:
Wanneer we aan beide kanten 1 losse weg halen dan krijg je de volgende vergelijking:
2 zakken = 6
De oplossing is dan:
1 zak = 3
2
2 + 4x = 12
2 + 4X = 12 -2 -2
4x = 10
Als je het goed gedaan hebt, heb je links de x-jes over en recht de losse blokjes
Controleer dit met wat er in je schrift staan. Fout? doe vraag a en b opnieuw.
4x = 10 :4 :4
x = 2,5
3
3x + 8
=
26
-8
-8
3x
=
18
:3
:3
x
=
6
Je vindt: x = 6
4
De fout zit bij de eerste stap: 9 - 1x geeft niet 8 !
Er wordt van 1x van 9 afgehaald, maar dat kan niet.
2x + 1
=
9
-1
-1
2x
=
8
:2
:2
x
=
4
5
Aan de linkerkant van de balans liggen: 4 losse en 5 x-en
Aan de rechterkant van de balans liggen: 10 losse en 3 x-en
De vergelijking die bij de balans hoort is: 4 + 5x = 10 + 3x
Los de vergelijking op.
4 + 5x
=
10 + 3x
-4
-4
5x
=
6 + 3x
-3x
-3x
2x
=
6
:2
:2
x
=
3
Het op deze manier oplossen van een vergelijking noem je de balansmethode
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Vergelijkingen oplossen
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
Test jezelf
2H04.4T Test jezelf .......................................................................................................
Je sluit de paragraaf Balansmethode af met een toets.
Na het maken van de vragen krijg je een score en kun je de gegeven antwoorden vergelijken met de goede antwoorden.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Het arrangement 2H05 §4 Balansmethode is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 3.0 Nederlands licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Hier rechts zie je de balans uit het filmpje.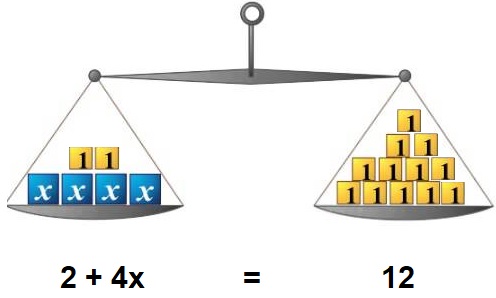
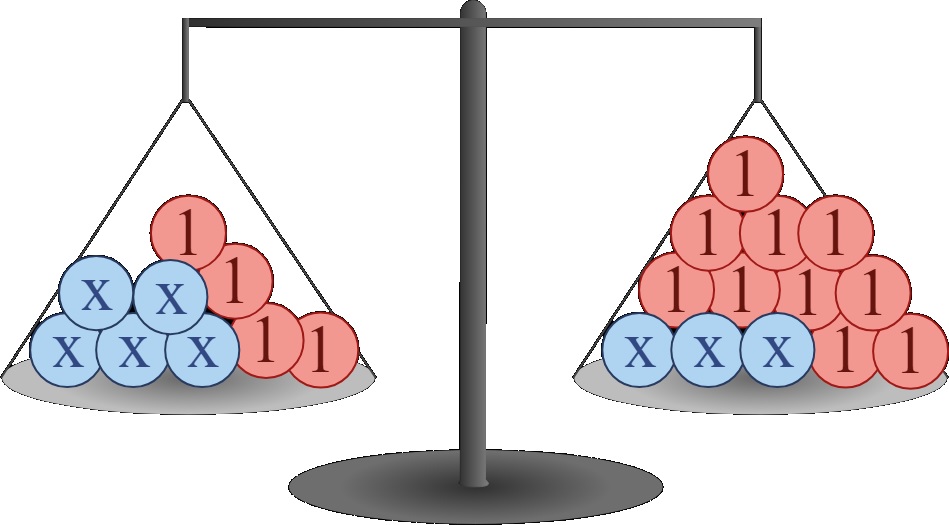
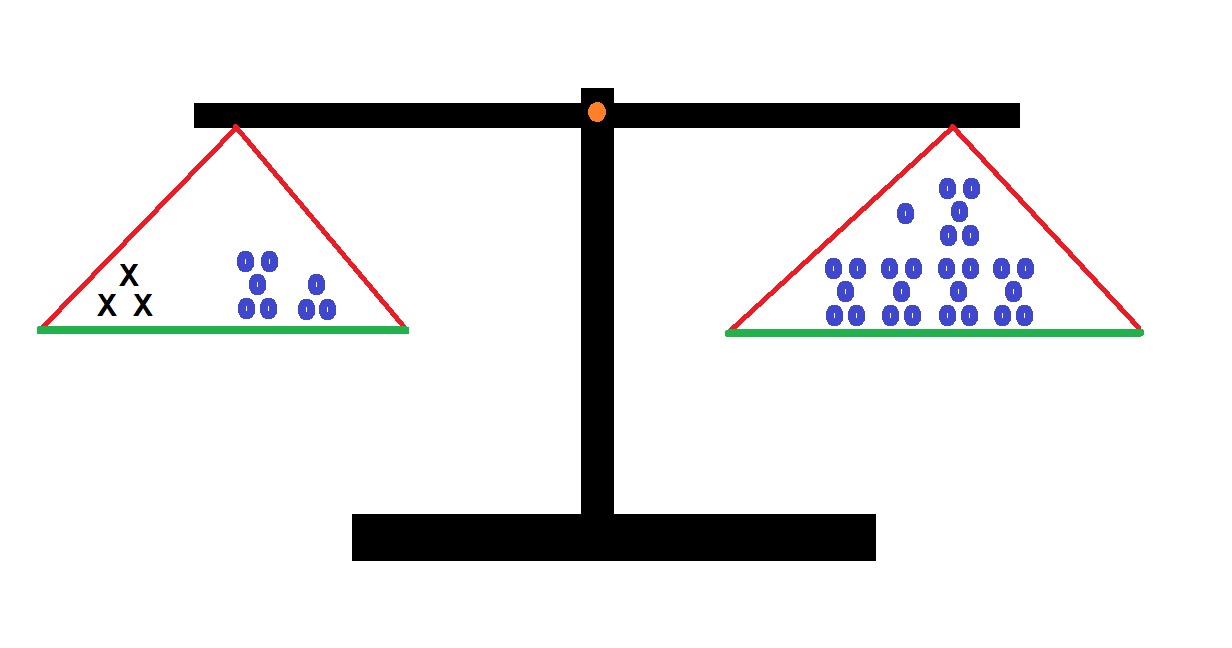Hiernaast zie je een balans getekend.
c
7,5 dus p = 26
