Het arrangement 2H01 Kijkmeetkunde is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 08-09-2020 15:26:33
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Rearrangeerbare versie. Dit thema heeft als titel kijkmeetkunde. Aan het eind van dit thema: - weet je wat inhoud van een ruimtelijk figuur is; - weet je wat een kijklijn en een kijkhoek is; - weet je wat een aanzicht is.
- Leerniveau
- VMBO gemengde leerweg, 2; VMBO kaderberoepsgerichte leerweg, 2; VMBO theoretische leerweg, 2;
- Leerinhoud en doelen
- Lengte, omtrek, oppervlakte en inhoud; Rekenen/wiskunde; Rekenen in de meetkunde; Meten en meetkunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- 2 mavo, leerlijn, rearrangeerbare, vo-content, wiskunde
Gebruikte Wikiwijs Arrangementen
VO-content Wiskunde. (2025).
Thema 14 Kijkmeetkunde vmbo-kgt12
https://maken.wikiwijs.nl/57102/Thema_14_Kijkmeetkunde_vmbo_kgt12
Wiskundesectie Juliana. (2018).
Alle uitleg bij elkaar
Wiskundesectie Juliana. (z.d.).
§1 Voorkennis (opgaven)

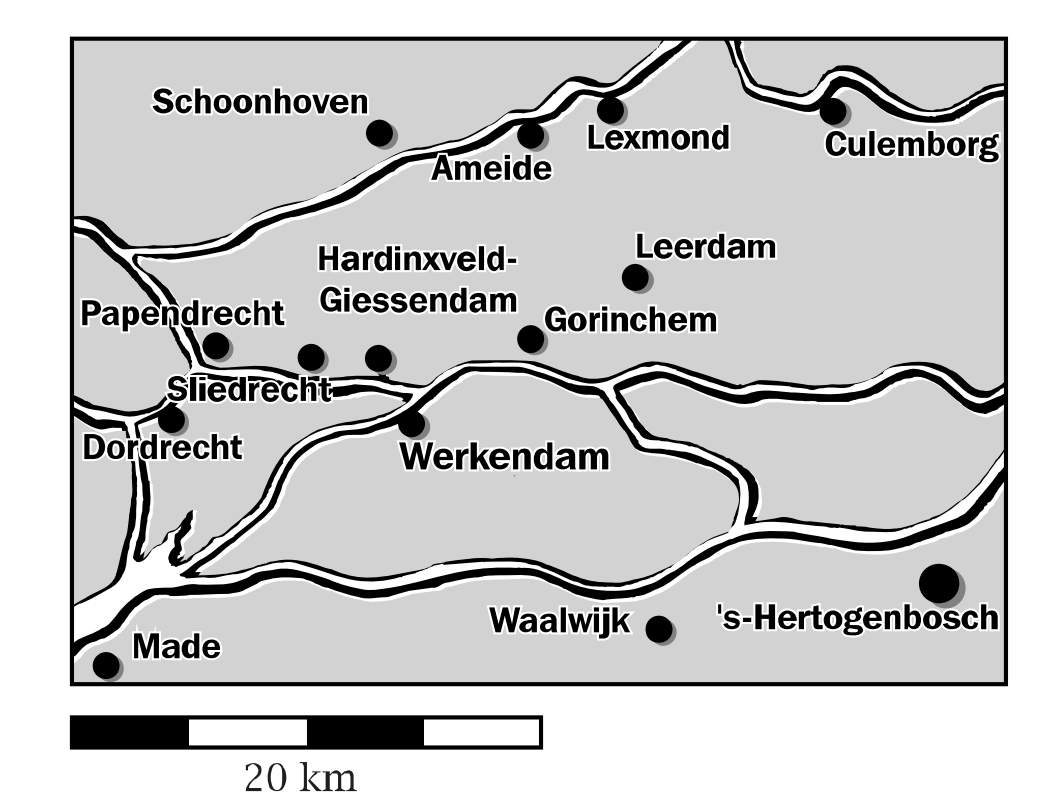
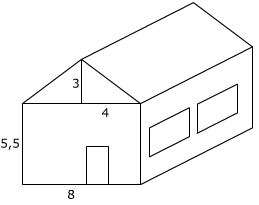
 Een bouwbedrijf wil een vakantiepark met vakantiehuisjes aanleggen. Het park komt bij het plaatsje Opperdam. De naam van het park wordt “Heideheuvel”. De vakantiehuisjes gaan ze verkopen. Het bouwbedrijf heeft een folder nodig. In de folder staat informatie over het park en informatie over de omgeving.
Een bouwbedrijf wil een vakantiepark met vakantiehuisjes aanleggen. Het park komt bij het plaatsje Opperdam. De naam van het park wordt “Heideheuvel”. De vakantiehuisjes gaan ze verkopen. Het bouwbedrijf heeft een folder nodig. In de folder staat informatie over het park en informatie over de omgeving.




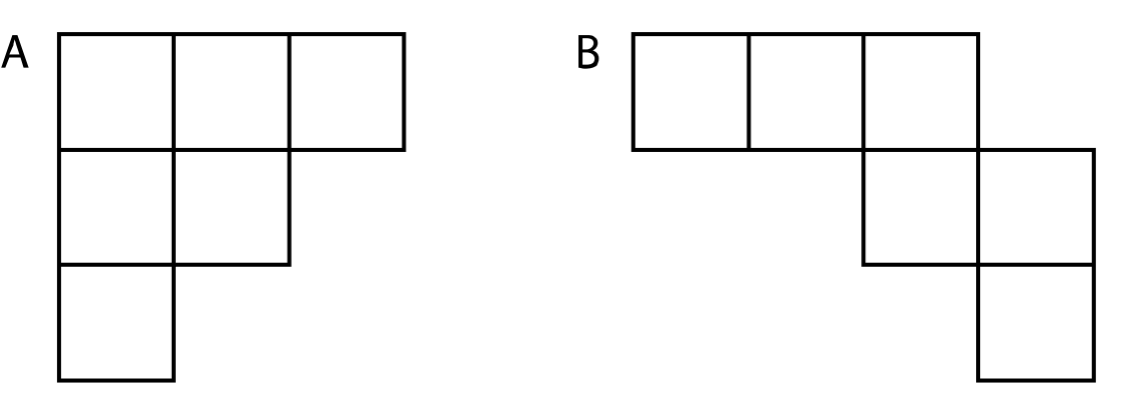
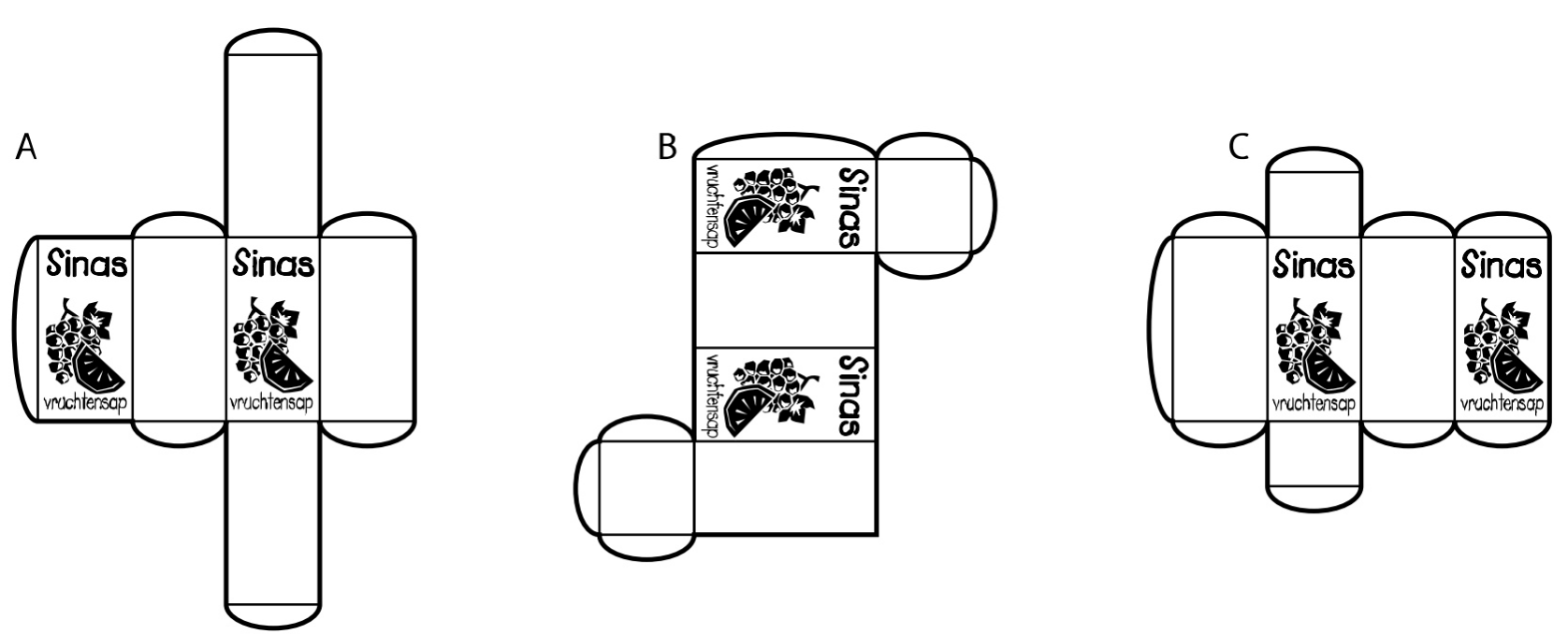
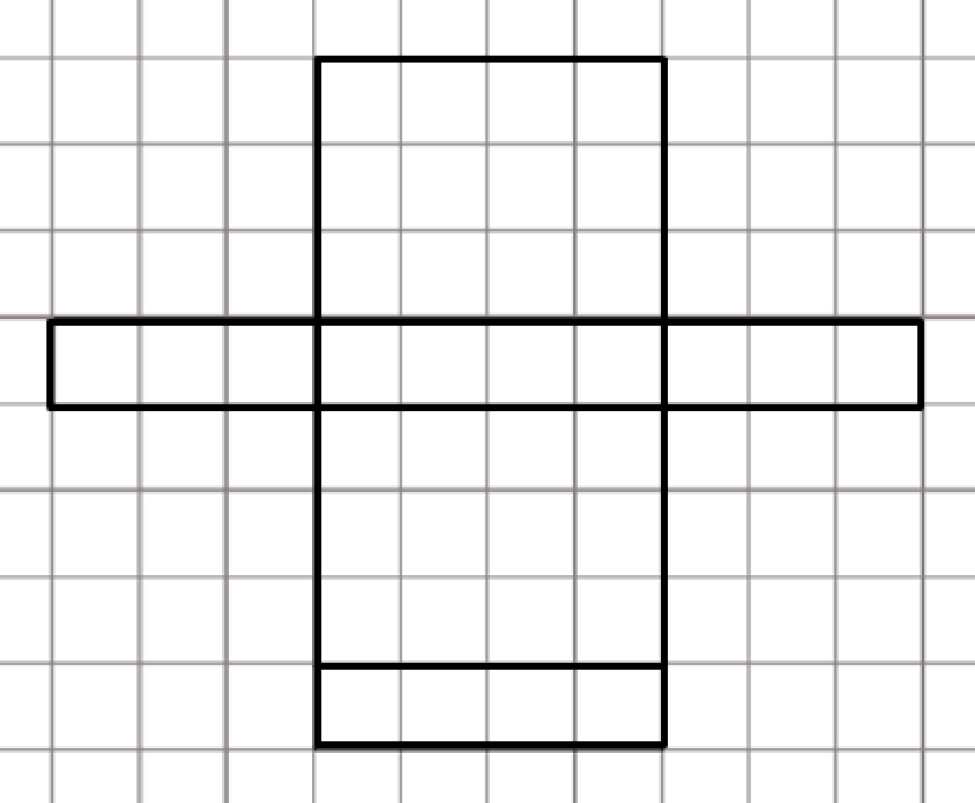
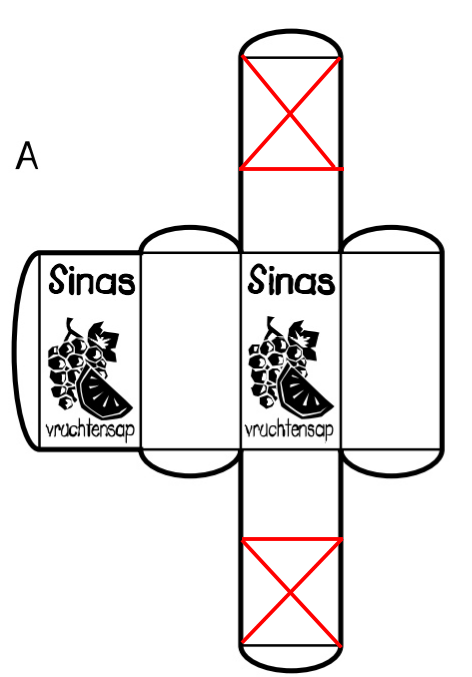








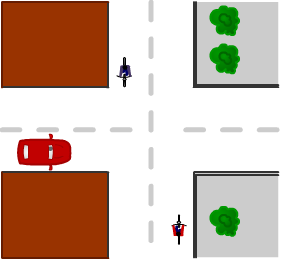

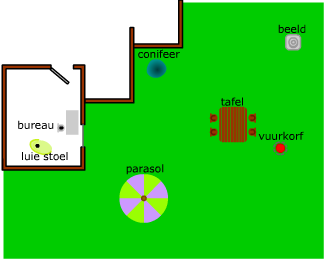
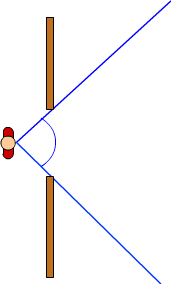
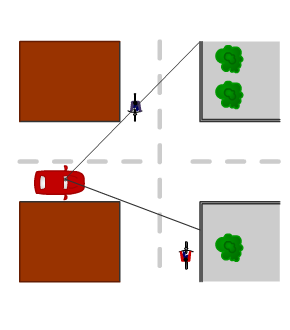



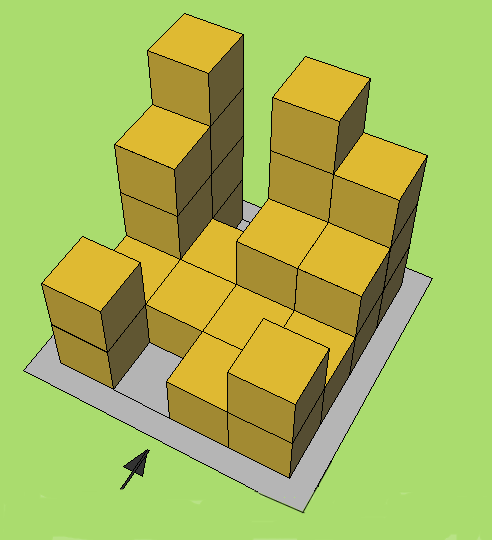
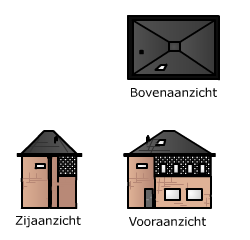

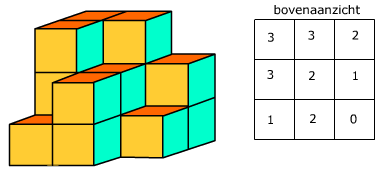
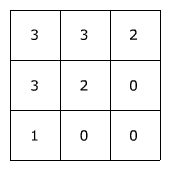


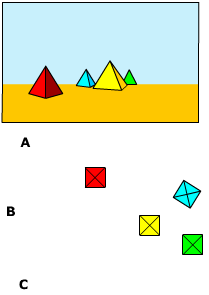
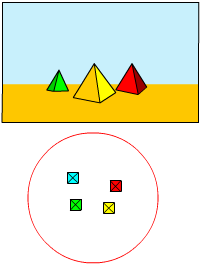
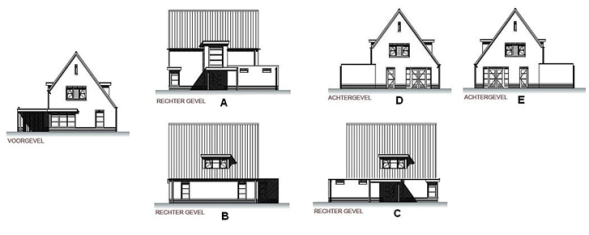

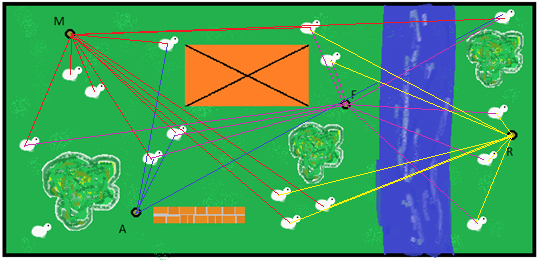
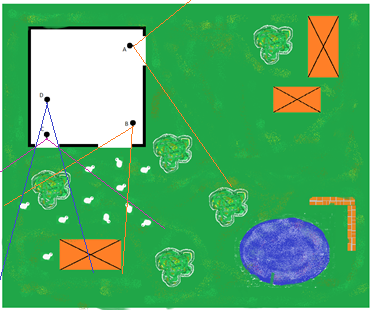 Bekijk het plaatje hiernaast.
Bekijk het plaatje hiernaast.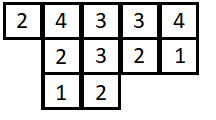
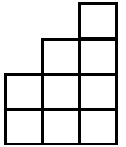





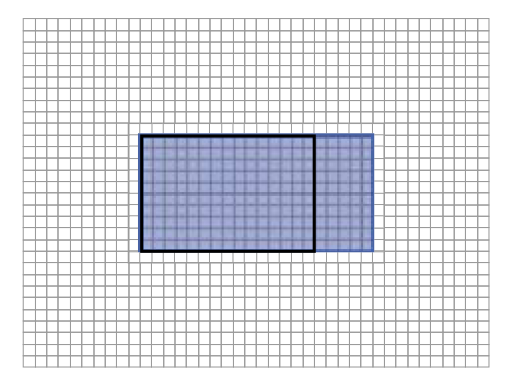
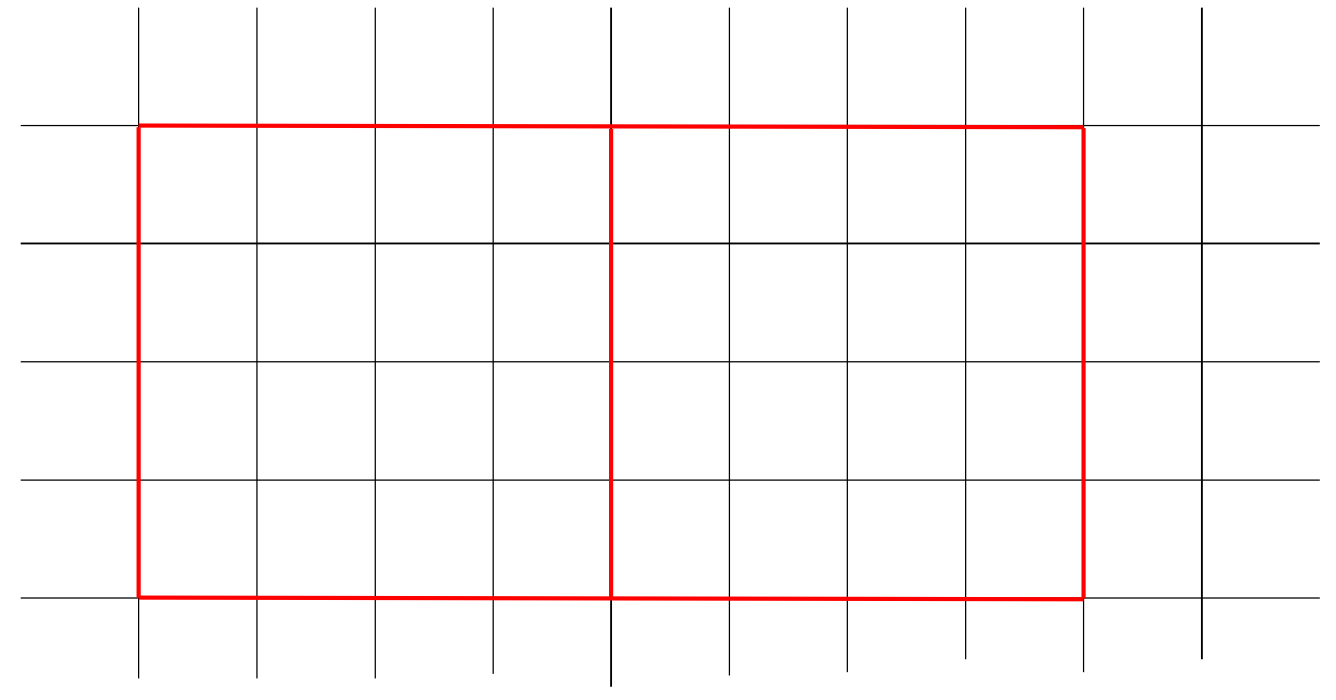
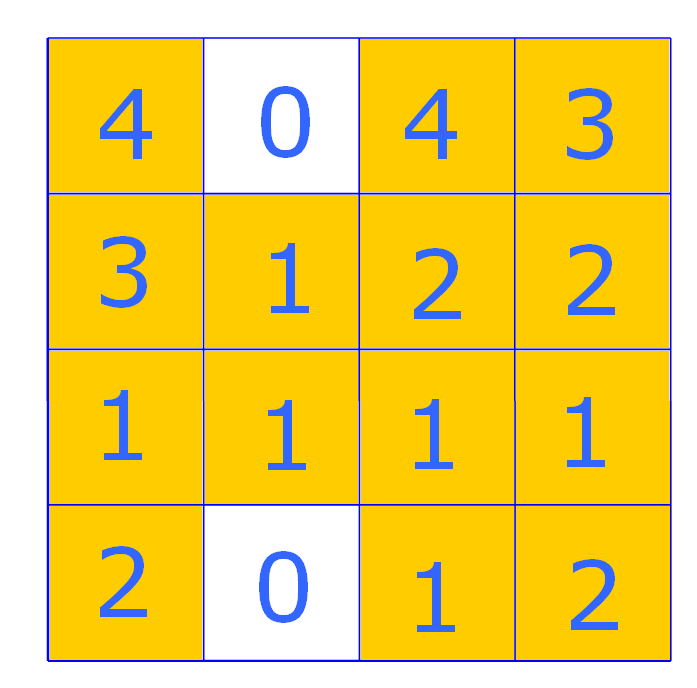
 Hiernaast zie je een handbalveld getekend.
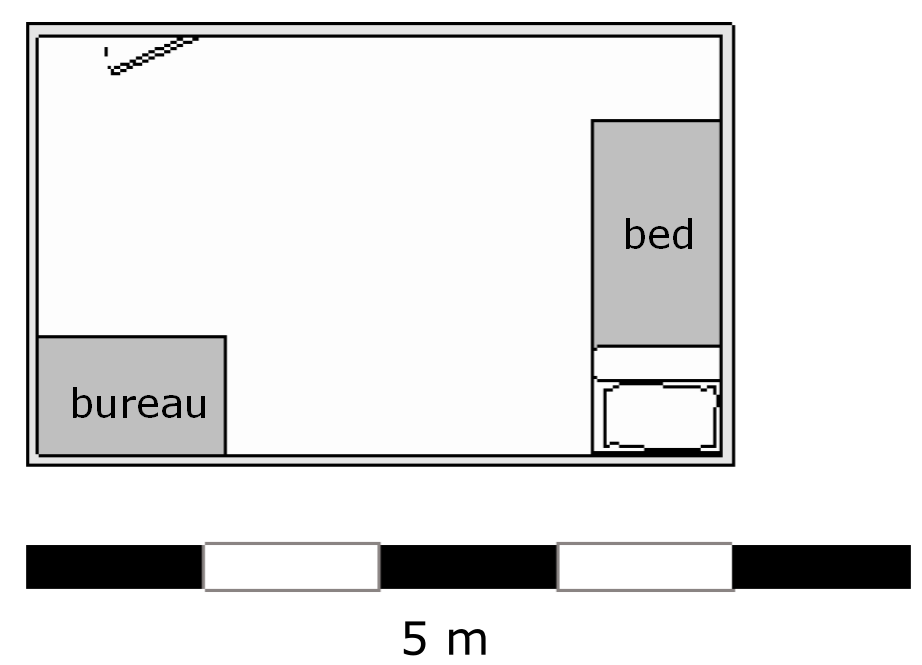
Hiernaast zie je een handbalveld getekend. Elk hokje is in werkelijkheid 5 m bij 5 m.
Elk hokje is in werkelijkheid 5 m bij 5 m.

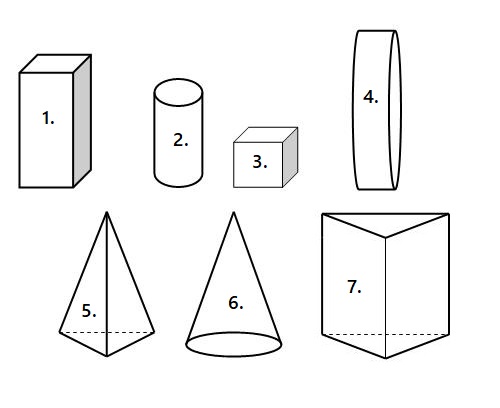
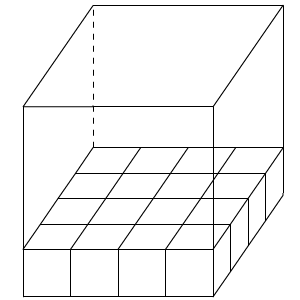
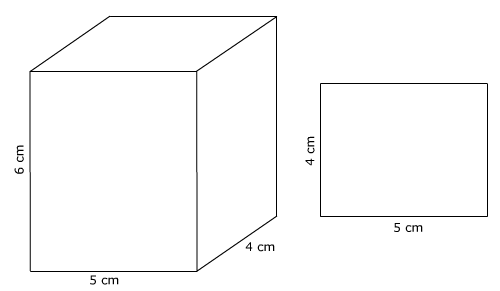
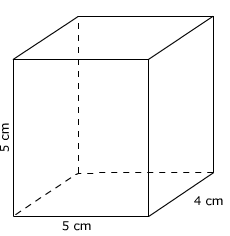
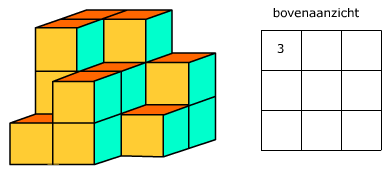
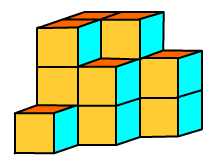
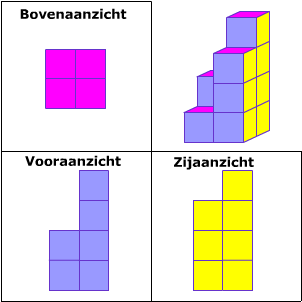
 De inhoud van deze balk bepaal je door te tellen hoeveel kubusjes van 1 cm3 er in passen.
De inhoud van deze balk bepaal je door te tellen hoeveel kubusjes van 1 cm3 er in passen.






















