Niet alleen in het examen maar ook in je latere carriere zul je opdrachten moeten uitvoeren. Vaak staan deze onder tijdsdruk. Dan is het van groot belang dat je dan niet alleen over je kennis (wat je weet), maar ook over belangrijke vaardigheden (wat je kunt) paraat hebt.
Bij die vaardigheden horen bijvoorbeeld: proefopstellingen bouwen, meetgegevens verzamelen, berekeningen uitvoeren, grafieken lezen en tekenen, verslag maken enzovoort. In deze WikiWijs gaan enkele van deze vaardigheden behandeld worden. Bij een goede voorbereiding zul je hier weinig nieuwe zaken tegen komen, maar misschien kunnen de verschillende tips je toch nog net even meer 'op scherp' zetten.
Examenopgave maken
Voorbeeld: Het centraal examen natuur- en scheikunde 1 bestaat uit ongeveer 40 opgaven.
Dit is een goede manier om die opgaven aan te pakken:
Kijk Wat het onderwerp is.
In het examen/opdrachten komen verschillende onderwerpen aan de orde. Meestal worden er over één onderwerp verschillende vragen gesteld. Aan de koppen die in het examen/opdrachten staan, zie je wanneer er een nieuw onderwerp aan de orde komt.
Ga na hoe de opgave is opgebouwd.
Veel opgaven zitten als de afbeelding hieronder in elkaar:
- een leestekst en/of een illustratie;
- een inleiding;
- de eigenlijke vraag of opdracht.
Een examenopgave bestaat uit verschillende onderdelen
Lees de opgave zorgvuldig door.
Lees de hele tekst, van begin tot einde. Bekijk foto's, tekeningen en grafieken nauwkeurig.
Stel vast wat je precies moet doen.
Sommige opgaven zijn vragen die je gewoon moet beantwoorden. Als er staat: Wat is de functie van de transformator bij een deurbel?
schrijf je natuurlijk op wat de functie van zo'n transformator is.
Andere opgaven zijn opdrachten. Zoek in zo’n opgave eerst het opdrachtwoord op. Dat vertelt je wat je precies moet doen.
Opdrachtwoorden en hun betekenis
Bedenk Wat het antwoord moet zijn.
Twee tips, voor als je hierbij vastloopt.
Tip 1 Weet je niet welke formule je moet gebruiken?
- Kijk wetke grootheid je moet berekenen, en vertaal die in een letter.
- Zoek in Binas of Polytechnisch zakboek (tabellenboekjes) alle formules op waarin die letter voorkomt.
- Kijk welke van die formules het beste past bij de gegevens.
Tip 2
Mis je een gegeven datje voor de opgave nodig hebt?
In dat geval kunnen er drie dingen aan de hand zijn:
Je kunt het ontbrekende gegeven opzoeken in Binas.
Let op: dit wordt er niet bij gezegd. Je moet dat zelf bedenken.
Je kunt het ontbrekende gegeven aflezen uit een grafiek, een tekening of een foto.
In de opgave zit een extra gegeven ’verstopt’. Dat is bijvoorbeeld zo als je de remweg van een auto moet berekenen. Uit het woord ’remweg’ kun je zelf de conclusie trekken dat de auto aan het einde van de beweging stilstaat. Je hebt dus één gegeven meer dan je misschien dacht: de eindsnelheid (ve = 0 m/s).
Schrijf het antwoord op.
Schrijf bij elke opgave iets op, ook al ben je niet zeker van je zaak. Voor een gedeeltelijk goed antwoord krijg je attijd nog een deel van de punten. Een meerkeuzevraag kun je, ook als je gokt, toch helemaal goed maken.
Controleer het antwoord.
Lees de vraag nog eens en controleer:
Geeft jouw uitwerking (volledig) antwoord op de vraag?
Heb je de gegevens goed (af)gelezen en opgeschreven?
Kloppen je berekeningen als je die nog eens narekent?
Onderzoek doen
Tijdens de opleiding zijn er een aantal ideeën voor onderzoek. Bij het uitvoeren van zo'n onderzoek kun je het beste stap voor stap te werk gaan.
Bedenk een onderzoeksvraag.
Soms staat de onderzoeksvraag al in de opdracht vermeld. Dan hoef je er alleen over na te denken hoe je die vraag kunt beantwoorden. Soms mag of moet je zelf een onderzoeksvraag bedenken. Wees daarbij niet te gauw tevreden; denk er goed over na of je vraag wel geschikt is.
Je moet al een idee hebben hoe je aan het antwoord kunt komen.
Maak een werkplan.
In je werkplan schrijf je op:
welke grootheden je gaat meten;
welke materialen en apparatuurje nodig hebt;
welke opstelling je gaat bouwen (maak een tekening);
welke metingen je gaat uitvoeren;
(eventueel) welke formules je gaat gebruiken.
Voorbeeld: Jermaine heeft als onderzoeksvraag gekozen: Welk deel van de energie van een stuiterende bal gaat tijdens het stuiteren verloren?
Jermaine wil de zwaarte-energie van de bal berekenen, voor en na het stuiteren. Hij weet dat hij de beweging van de bal kan vastleggen met een videocamera.
Hij heeft bedacht dat hij een meetlat op de achtergrond mee kan filmen. Z0 kan hij de beginhoogte en de terugstuithoogte straks nauwkeurig bepalen. Verder heeft hij ook de massa van de bal nodig, maar die kan hij eenvoudig meten met een weegschaal of een balans.
Conclusies trekken
Als alles goed gegaan is, kun je nu conclusies trekken. Probeer een antwoord te geven op je onderzoeksvraag. Vraag je ook af wat er in je onderzoek beter had gekund.
Een verslag maken
Tot slot maak je een verslag van je onderzoek.
Wil je nog meer weten over het opzetten van je onderzoek, kijk dan op de site van de onderzoekspraktijk.net. In 8 simpele stappen, met onderwerpen als: Verkennen, Opsporen, Bepalen, Formuleren, Verzinnen, Gegevens, Analyseren en Presenteren wordt je door het gehele proces geleid.
Formules
Bij natuur- en scheikunde moet je af en toe berekeningen maken. Dit is een goede aanpak:
Lees de opgave
Lees de opgave en schat in welke buurt de uitkomst zal liggen. In het voorbeeld hieronder moet je de tijd berekenen waarin een waterkoker een liter water opwarmt. Je verwacht dan een tijd van enkele minuten. Een paar seconden is duidelijk te weinig en een paar uur duidelijk te veel.
Noteer de gegevens
Vertaal alle gegevens in letters en cijfers, en noteer ze.
Een gegeven zoals '336 kJ warmte' noteer je bijvoorbeeld als: Q = E = 336 kJ.
Schrijf de formule(s) op
Sommige formules kun je op verschillende manieren opschrijven. Neem de vorm waarin de te berekenen grootheid voor het is-teken (=) staat. Je schrijft dus:
Het ombouwen of omwerken van formules is niet altijd even eenvoudig. Daarom nog een extra uitleg en een handige werkwijze waarmee het ombouwen altijd gaat werken.
Vul de gegevens in
Werk de berekening uit
Noteer de uitkomst
De uitkomst is een getal + een eenheid. De eenheid moet kloppen met de gegevens:
als je het vermogen invult in watt (W) en de tijd in seconden (s), dan vind je de hoeveelheid energie in joule (J).
Controleer de uitkomst
Vergelijk de uitkomst met de schatting die je in het begin maakte. Ga ook na of je geen reken- of overschrijffouten hebt gemaakt.
Voorbeeld
Om een liter water van 20 oC aan de kook brengen, is 336 kJ warmte nodig.
Hoe lang doet een waterkoker van 2000 W erover deze hoeveelheid warmte te leveren?
Machten van 10
Bij natuur- en scheikunde krijg je soms te maken met getallen die erg groot of juist erg klein zijn. Er is een handige manier bedacht om dat soort getallen op te schrijven. Voor grote getallen gebruik je positieve machten van 10. Voor kleine getallen gebruik je negatieve machten van 10.
positieve machten
negatieve machten
101 = 10
10-1 = 1/10 = 0,1
102 = 10 x 10 = 100
10-2 = 1/100 = 0,01
103 = 10 x 10 x 10 = 1000
10-3 = 1/1000 = 0,001
enzovoort
enzovoort
Soms is het handig om een macht van 10 te vervangen door een voorvoegsel. In plaats van "De afstand is 11,3x103 m" kun je ook schrijven: "De afstand is 11,3 km". Het voorvoegsel k (kilo) betekent duizend, net als 103.
Voorbeeld
De kerncentrale in Gravelines (Frankrijk) heeft een elektrisch vermogen van 5460 MW. In de praktijk wordt gemiddeld 75% van dit vermogen gebruikt. De overige 25% is niet beschikbaar. De reactoren van de centrale hebben regelmatig onderhoud nodig en kunnen dus niet altijd energie leveren. Bereken hoeveel kWh elektrische energie de kerncentrale in één jaar levert.
kerncentrale Gravelines in Frankrijk
75% van 5460 MW = 4095 MW
P = 4095 MW = 4095 x 106 W = 4095 x 103 kW
t = 365 x 24 = 8760 h
E = P x t
=> 4095 x 103 x 8760
=> 3,5872 x 109 kWh, en dat is ongeveer 36 x 109 kWh
De centrale produceert elk jaar 36 miljard kWh elektrische energie.
Grootheden en Eenheden
Grootheid
Een grootheid is iets dat je kunt meten met een geschikt meetinstrument. Voorbeelden van grootheden zijn lengte
(afstand), massa en kracht. Meer grootheden zie je in onderstaande tabel.
Eenheid
Om een grootheid te kunnen meten, heb je een afgesproken maat nodig. Zo'n afgesproken maat noem je een eenheid.
Je meet je lengte in meters, je massa in kilogrammen en je spierkracht in newton. De meter is de eenheid van lengte, de kilogram de eenheid van massa en de newton de eenheid van kracht. Elke grootheid heeft een officiële internationale Sl-eenheid (SI staat voor Système International: het in 1960 ingevoerde internationale systeem van eenheden).
Voor het meten van je lengte is de meter heel geschikt. Maar voor de lengte van de spoorlijn van Amsterdam naar Rotterdam kun je beter een grotere eenheid gebruiken: de kilometer. Tijd meten we vaak in uren en niet in seconden. En voor temperatuur gebruiken we veel liever de graad Celsius dan de Kelvin. Het ligt dus aan de situatie welke eenheid wordt gebruikt.
In tabel vind je een overzicht van alle grootheden en hun eenheden die op deze site voorkomen. In de derde en vierde kolom staan de Sl-eenheden. Andere veelgebruikte eenheden staan in de laatste twee kolommen.
Grootheden- en eenheden tabel
Tabellen & Grafieken
Veel onderzoeksvragen gaan over het verband tussen twee grootheden. Over een zonnecel kun je bijvoorbee[d vragen: Hoe hangt de spanning van een zonnecel af van de hoek waaronder het zonlicht op de zonnecel valt?
Om deze vraag te beantwoorden, voer je een serie metingen uit. Je sluit een spanningsmeter aan op een paneel zonnecellen. Daarna zet je het paneel onder verschillende hoeken neer en meet je telkens de spanning. In een tabel noteer je de meetresultaten: links de hoek, rechts de bijbehorende spanning.
meten - noteren - tekenen
Verbanden worden duidelijker als je ze weergeeft in een grafiek. Zo'n grafiek maak je als volgt:
Werk alles uit in potlood. Anders kun je later niets meer verbeteren.
Teken een assenstelsel. In het werkboek op school was dat meestal al voor je gedaan. Helaas zullen je meeste metingen geen kant-en-klare werkbladen meer hebben.
Zet bij elke as een grootheid, met de eenheid waarin je hebt gemeten.
Bijvoorbeeld: temperatuur (oC) en stroomsterkte (A).
Zet langs beide assen een geschikte schaalverdeling. Zorg ervoor dat al je metingen in de grafiek passen en dat je grafiek niet te klein wordt.
Teken de meetresultaten in als punten. Realiseer je daarbij dat er altijd kleine meetfouten in je meetresultaten zitten. Je mag er niet van uitgaan dat elk punt exact juist is.
Trek een rechte lijn als de meetpunten ongeveer op een rechte lijn liggen. Laat die lijn zo goed mogelijk bij de punten aansluiten. Je mag de punten niet een voor een met elkaar verbinden.
Teken een vloeiende kromme als de punten duidelijk niet op één lijn liggen. Laat de kromme zo goed mogelijk bij de punten aansluiten. Je mag de punten niet een voor een met elkaar verbinden.
Het geeft dus niet dat een rechte lijn of een kromme niet precies door alle meetpunten loopt.
Verbanden
Veel onderzoeksvragen gaan over het verband tussen twee grootheden. Neem bijvoorbeeld de onderzoeksvraag: Wat is het verband tussen de kracht en de uitrekking bij een spiraalveer?
Bij deze vraag zijn de grootheden de kracht (op de spiraalveer) en de uitrekking (van de spiraalveer).
Hoe meet je nu zo'n verband? Een paar aanwijzingen:
Maak eerst een tabel waarin je de meetresultaten kunt noteren. Links de kracht, rechts de uitrekking.
Kies voor de grootheid in de linker kolom een serie 'mooie' getallen. Als je gewichtjes van 10 gram aan de spiraalveer hangt, krijgt de kracht bijvoorbeeld de volgende waarden (in N): 0 - 0,1 - 0,2 - 0,3 - 0,4 enzovoort.
Dat maakt het gemakkelijker om straks een grafiek te tekenen.
Meetwaarden noteren en uitwerken
Noteer de meetwaarden in de tabel: links de kracht (in N), rechts de uitrekking (in cm).
Verwerk je metingen tot een grafiek. In Tabellen & Grafieken kun je lezen hoe dat moet.
Zet de kracht langs de horizontale as en de uitrekking langs de verticale as.
Vergelijk jouw grafiek met afbeelding hieronder. Daarin zie je hoe een grafiek eruitziet:
als het verband evenredig is;
als het verband lineair is;
als het verband kwadratisch is;
als het verband omgekeerd evenredig is.
Het (kracht,uitrekking)-diagram van een spiraalveer is een rechte lijn door de oorsprong. Daaraan zie je dat het verband tussen de uitrekking en de kracht bij een spiraalveer evenredig is.
vier soorten verbanden
Verslag
Bij een onderzoek hoort een verslag. In dat verslag leg je uit hoe het onderzoek is verlopen. Iemand die er niet bij geweest is, moet precies kunnen begrijpen Wat er allemaal is gebeurd. Deel je verslag als volgt in:
Titelpagina
Hierop vermeld je: de titel van het onderzoek, de namen van de leerlingen in het onderzoeksgroepje, de naam van je docent, de datum en het jaartal.
§ 1 Onderzoeksvraag
In deze paragraaf leg je uit welke vraag je met je onderzoek wilde beantwoorden.
wat voor opstelling je hebt gemaakt (maak een tekening);
wat je precies hebt gedaan:
Welke metingen heb je uitgevoerd?
Hoe heb je de meetresultaten verwerkt (tekenen/berekenen)?
Welke berekeningen heb je uitgevoerd (inclusief formules)?
§3 Onderzoeksresultaten
Hierin vermeld je wat je hebt waargenomen of gemeten: in de vorm van tekst, tabellen, grafieken, foto's en dergelijke.
§ 4 Conclusies
Hierin staat het antwoord op de onderzoeksvraag. Ook schrijf je op wat er beter had gekund.
Een verslag hoort er goed uit te zien. Het gaat niet alleen om de inhoud van je verslag. Je moet die inhoud ook duidelijk en overzichtelijk presenteren. Een aantal aanwijzingen:
Maak je verslag als het even kan met een tekstverwerker.
Gebruik papier op A4-formaat.
Zorg dat er ruime marges overblijven: onder en boven, links en rechts.
Kies een goed leesbaar lettertype, met een goede lettergrootte.
Zet een vet kopje boven elke paragraaf. Sla daarna een regel over.
Zorg voor nette tekeningen, tabellen en grafieken. Zet er een nummer bij zodat je ernaar kunt verwijzen.
Taal en Rekenkaartje
De Taal en Rekenkaart zijn handige geheugensteuntjes voor elke ‘student die wel eens struikelt over het toepassen van d’s en t’s. Of die de Nederlandse grammatica en spelling nog aan het leren is.
De TaalKaart geeft spellingsregels rond werkwoordvervoegingen op een begrijpelijke en overzichtelijke manier weer aan de hand van uitgewerkte voorbeelden.De Rekenkaart doet dit met rekenen waar het gaat om volgorde van de bewerkingen en de meest gangbare formules voor omtrek, oppervlakte en inhoud van vlakken en diverse ruimtelijke opjecten.
Je kunt deze afbeeldingen afdrukken in kleur, klein afdrukken (ongeveer de grootte van een bankpas) en dan dubbelzijdig 'sealen'. Je hebt dan altijd deze handige kaartjes bij de hand.
Het arrangement Vaardigheden student is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
Patrick Oosterhuis
Laatst gewijzigd
2017-07-07 10:28:47
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 3.0
Nederlands licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of
bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
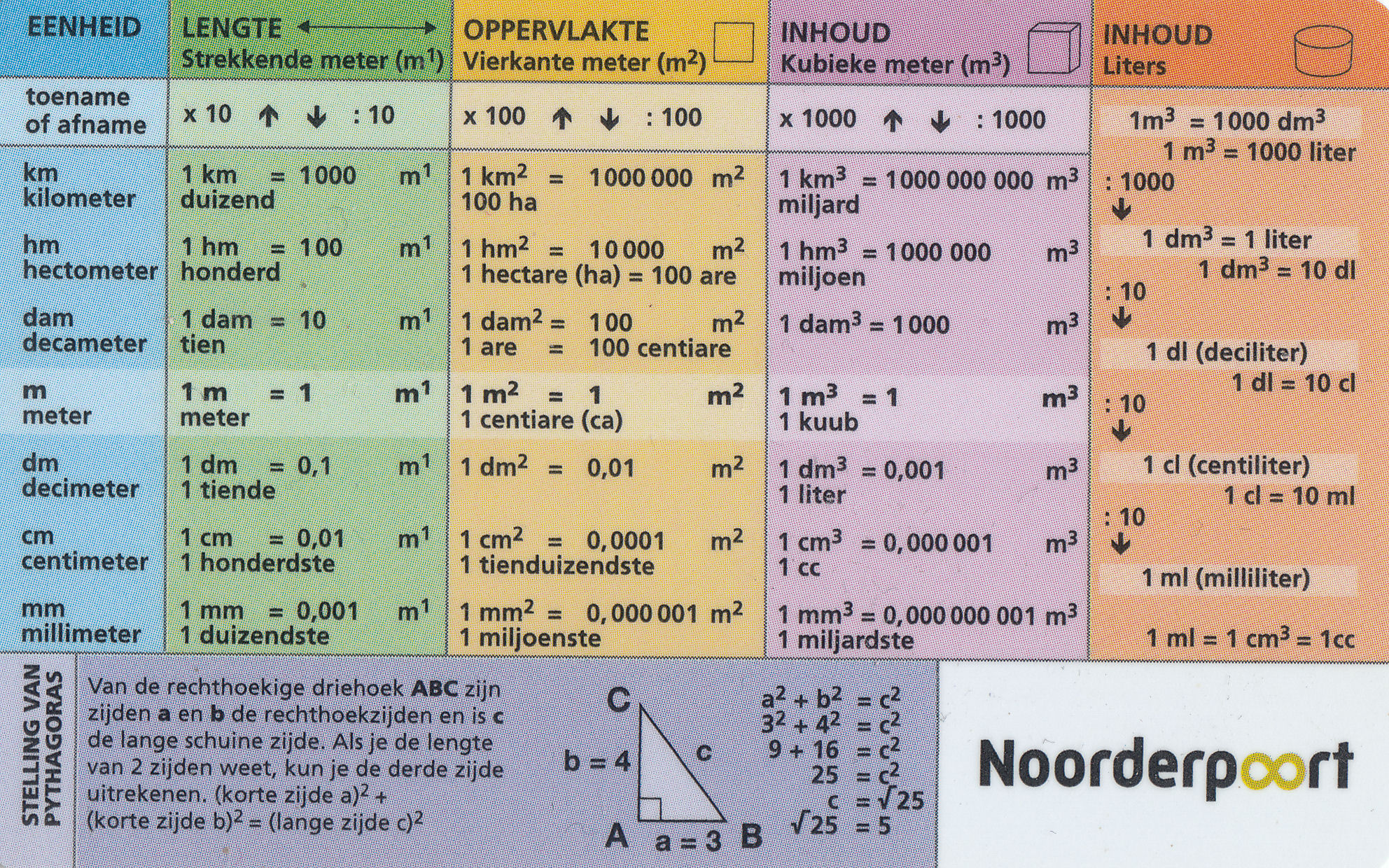
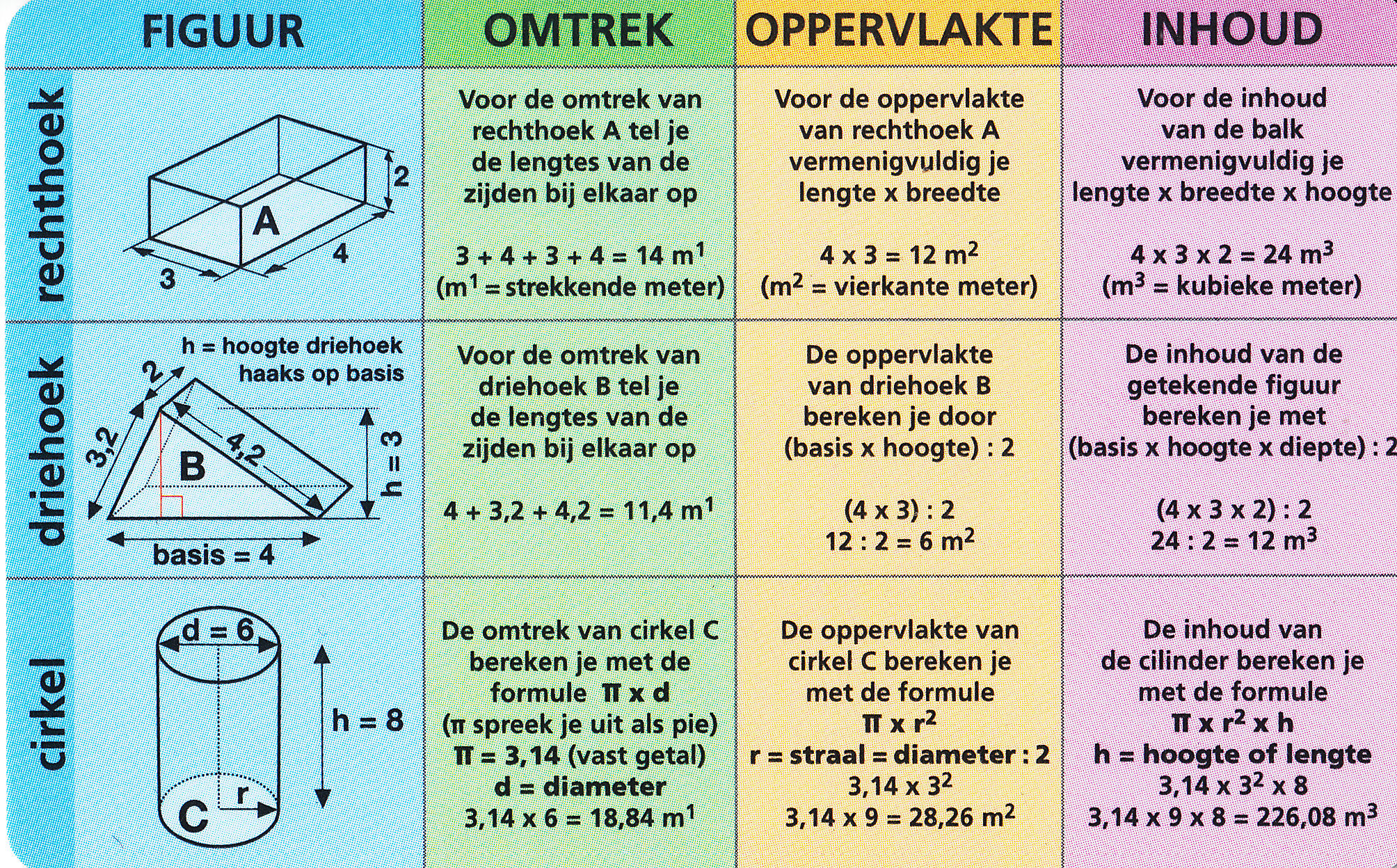
MBO Studenten doen veel kennis op tijdens hun studie op school en in de praktijk. Maar deze kennis moet ook worden toegepast. Daarmee wordt kennis ook omgezet in vaardigheden. Maar omdat te kunnen zijn enkele basisvaardigheden noodzakelijk.
In deze WikiWijs komen enkele onderwerpen aanbod die handig zijn bij het doen van onderzoek of het maken van een verslag. Het omzetten van simpele formules en het rekenen met eenheden en grootheden evenals voorvoegsels zoals kilo en milli komen voorbij.
Deze module is in ontwikkeling en uitbreidingen en suggesties zijn welkom.
Eindgebruiker
leerling/student
Moeilijkheidsgraad
gemiddeld
Trefwoorden
basis vaardigheden, mbo, student
Vaardigheden student
nl
Patrick Oosterhuis
Patrick Oosterhuis
2017-07-07 10:28:47
MBO Studenten doen veel kennis op tijdens hun studie op school en in de praktijk. Maar deze kennis moet ook worden toegepast. Daarmee wordt kennis ook omgezet in vaardigheden. Maar omdat te kunnen zijn enkele basisvaardigheden noodzakelijk.
In deze WikiWijs komen enkele onderwerpen aanbod die handig zijn bij het doen van onderzoek of het maken van een verslag. Het omzetten van simpele formules en het rekenen met eenheden en grootheden evenals voorvoegsels zoals kilo en milli komen voorbij.
Deze module is in ontwikkeling en uitbreidingen en suggesties zijn welkom.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
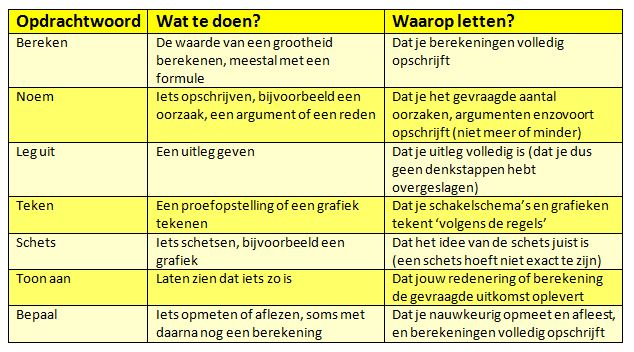
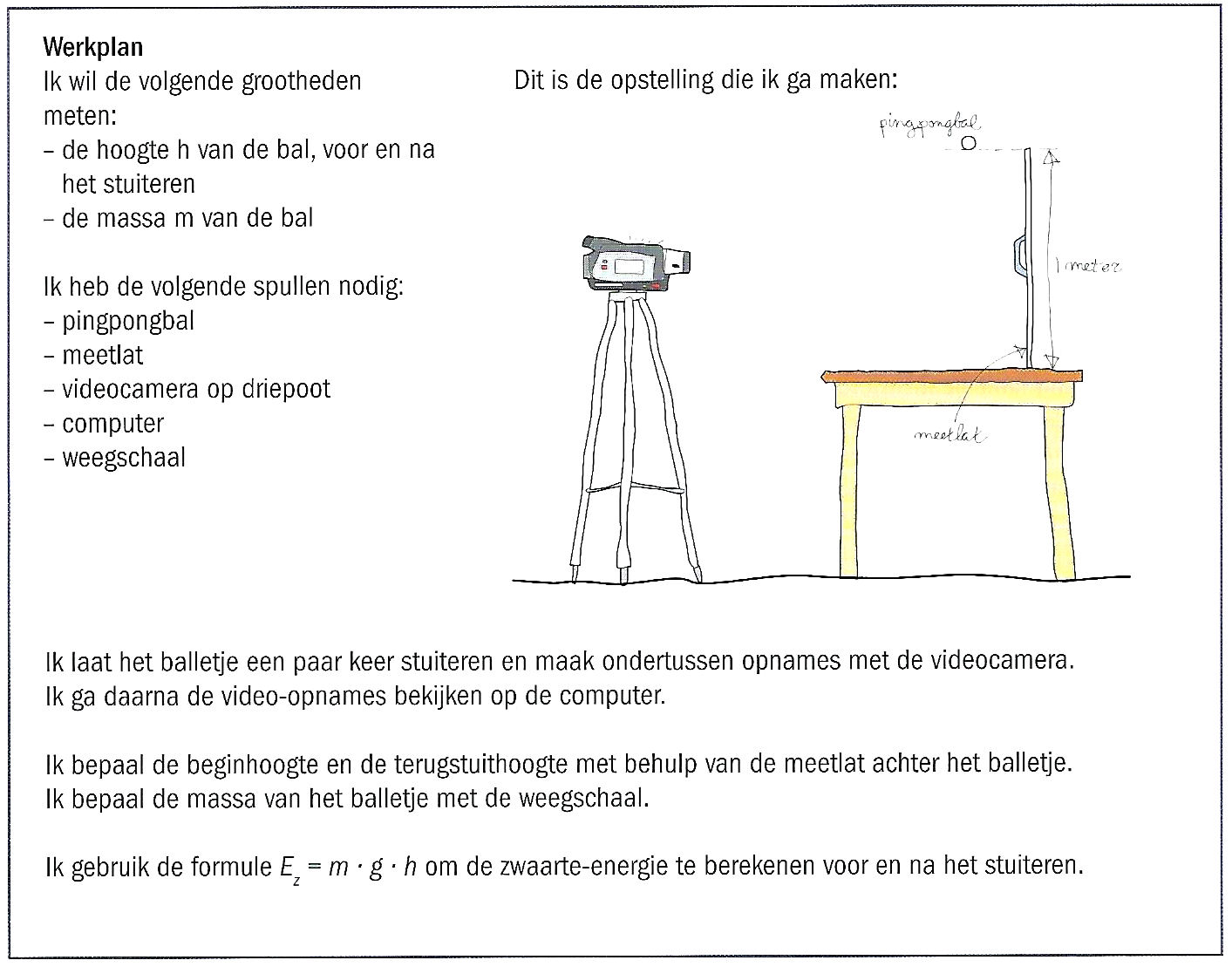
Bij natuur- en scheikunde moet je af en toe berekeningen maken. Dit is een goede aanpak:
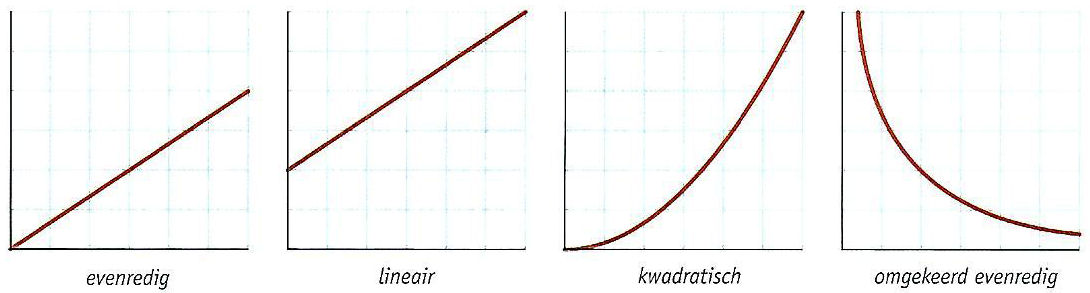
Bij een 
Een aantal aanwijzingen:
