In dit hoofdstuk leer je onder andere hoe je nauwkeurig wiskundige figuren kunt tekenen.
Een timmerman gebruikt allerlei gereedschap: hamer, zaag, waterpas, ... . Een wiskundeleerling heeft ook gereedschap nodig: een passer en een geodriehoek. Hoe je deze twee instrumenten kunt gebruiken, ga je nu leren.
Een passer gebruik je om cirkels te tekenen, een geodriehoek om rechte lijnen te tekenen.
1.2 Passer en geodriehoek
Opgave 2
Opgave 3
Opgave 4
Opgave 5
Opgave 6
Opgave 7
Opgave 8
Opgave 9
Opgave 10
Opgave 11
1.3 Vierhoeken
Van een plank zijn de boven- en onderkant evenwijdig. We zagen met twee rechte zaagsneden een vierhoek uit de plank. Dat kan op allerlei manieren, zoals je ziet.
Omdat boven- en onderkant evenwijdig zijn, krijg je een trapezium.
Als je de zaagsnedes in dezelfde richting maakt, krijg je een parallellogram.
Als je de plank beide keren haaks doorzaagt, krijg je een rechthoek.
Als je de zaagsneden in dezelfde richting maakt en er voor zorgt dat de vier zijden even lang worden, krijg je een ruit.
Als je de plank beide keren haaks doorzaagt en er voor zorgt dat de vier zijden even lang worden, krijg je een vierkant.
In het zesde plaatje is nog een bijzondere vierhoek getekend: een vlieger. Maar die zaag je niet zo gemakkelijk uit een plank. Bij een vlieger zijn twee aan elkaar grenzende zijden even lang en de andere twee aan elkaar grenzende zijden zijn ook even lang.
Opgave 12
Opgave 13
Een vierhoek heeft vier hoekpunten. Vaak geven we die opvolgende hoekpunten namen, bijvoorbeeld \(A\), \(B\), \(C\) en \(D\). Dan kunnen we spreken van vierhoek \(ABCD\). Een vierhoek heeft ook vier zijden (de vier lijnstukken tussen de opvolgende hoekpunten). In het voorbeeld zijn de zijden \(AB\), \(BC\), \(CD\) en \(DA\).
In vierhoek \(ABCD\) kun je ook de overstaande hoekpunten verbinden door een lijnstuk. De verbindingslijnstukken \(AC\) en \(BD\) heten de diagonalen van de vierhoek.
Opgave 14
Opgave 15
Opgave 16
Opgave 17
Origami
Een vierkant vouwen
De figuur laat zien hoe je, zonder te meten, van een rechthoekig stuk papier nauwkeurig een vierkant kunt maken.
Neem een kladblaadje en maak op deze manier een vierkant.
Neem een ander blaadje en scheur er de randen af. Vouw er nu, zonder te meten, precies een vierkant van.
Peper-en-zoutstelletje
Neem een vouwblaadje. Vouw de punten naar binnen, zodat je een kleiner vierkant krijgt.
Keer het kleinere vierkant om en vouw weer de punten naar binnen, zodat je een nog kleiner vierkant krijgt.
Keer het nog kleinere vierkant om en knijp de punten naar beneden, zodat je van boven een + ziet. Nu kun je de hoeken van het oorspronkelijke vierkant naar buiten trekken: je krijgt dan een "peper-en-zoutstelletje". Als je niet goed snapt hoe dit in zijn werk gaat, moet je het aan iemand vragen; er is beslist wel iemand die weet hoe het moet.
In Japan is het papiervouwen tot een kunst verheven: origami.
Geschiedenis
Wiskunde is een typisch Nederlands woord; (wis = zeker). In andere Europese talen heet wiskunde mathematica of iets wat daarop lijkt. Dat Nederland een afwijkend woord heeft, komt door de Vlaming Simon Stevin (1548-1620); die vond dat je aan Nederlandse woorden beter de betekenis kon zien dan aan woorden die aan het Latijn waren ontleend. Door hem spreken we van evenwijdig (in plaats van parallel), van driehoek (in plaats van triangel), van meetkunde (in plaats van geometrie), enzovoort. Stevin noemde een ellips een scheefrondt, maar dat is niet overgenomen.
1.4 Regelmaat
Opgave 18
Opgave 19
Opgave 20
Opgave 21
Opgave 22
Opgave 23
1.5 Ruimtelijke figuren
Opgave 24
Opgave 25
Opgave 26
Opgave 27
De staafjes van een draadmodel heten wel de ribben van de ruimtelijke vorm; de plaatsen waar gesoldeerd moet worden heten de hoekpunten.
Bekijk de tekening van een balk. Anders dan bij een draadmodel, moet je de grensvlakken nu dicht denken, bijvoorbeeld alsof ze van karton zijn. De ribben die aan de achterkant zitten kun je dus niet zien. Daarom zijn ze gestippeld. Op deze manier geef je "diepte" aan de tekening. Als je gewend bent aan deze manier van tekenen, zie je beter hoe de vorm er in werkelijkheid uitziet.
Opgave 28
Opgave 29
Opgave 30
1.6 Volgorde
Opgave 31
Opgave 32
Opgave 33
Opgave 34
Opgave 35
Opgave 36
Opgave 37
1.7 Eindpunt
Passer en geodriehoek
Een passer gebruik je om cirkels te tekenen.
Eencirkelheeft een middelpunt en een straal.
Met een passer kun je ook lengtes afpassen.
Een passer kun je goed gebruiken om een driehoek te tekenen waarvan de zijden gegeven lengtes hebben.
Met een geodriehoek kun je rechte lijnen tekenen, in het bijzonder:
evenwijdige lijnen tekenen,
lijnen loodrecht op elkaar tekenen.
Regelmatig
Als je weet dat een broodje \(€ 1,60\) kost, kun je een tabel maken waarin staat hoeveel verschillende aantallen broodjes kosten. Je kunt de tabel maken door het blokschema te doorlopen.
aantal
\(1\)
\(2\)
\(5\)
\(11\)
\(20\)
\(25\)
prijs ( \(€\) )
\(1,6\)
\(3,2\)
\(8\)
\(17,6\)
\(32\)
\(40\)
\(n\) broodjes kosten dan \(1,6×n\) euro.
Hierin is \(n\) een variabele.
Soorten vierhoeken
Een trapezium heeft een paar evenwijdige zijden.
Een parallellogram heeft twee paar evenwijdige zijden.
Een vlieger heeft twee paar even lange zijden die aan elkaar grenzen.
Een ruit heeft vier even lange zijden.
Een rechthoek heeft vier rechte hoeken.
Een vierkant heeft vier rechte hoeken en vier even lange zijden.
Een balk, kubus, prisma, piramide hebben hoekpunten, ribben en grensvlakken.
Voorbeelden
Een vijfzijdige piramide heeft \(6\) grensvlakken, \(6\) hoekpunten en \(10\) ribben: \(5\) grensvlakken zijn driehoekig, \(1\) grensvlak is een vijfhoek.
Een vijfzijdig prisma heeft \(7\) grensvlakken, \(10\) hoekpunten en \(15\) ribben: \(5\) grensvlakken zijn rechthoekig, \(2\) grensvlakken zijn (gelijke) vijfhoeken.
Voor een goede tekening van een ruimtelijke vorm moet je de ribben aan de achterzijde stippelen (als de grensvlakken tenminste dicht zijn).
Spelregels van rekenen
eerst binnen de (binnenste) haakjes
vermenigvuldigen en delen gaan voor optellen en aftrekken
bij vermenigvuldigen en delen van links naar rechts rekenen: het eerst doen wat je het eerst tegenkomt
bij optellen en aftrekken van links naar rechts rekenen: het eerst doen wat je het eerst tegenkomt
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
Dit thema valt onder de arrangeerbare leerlijn van de Stercollecties voor wiskunde voor havo/vwo leerjaar 1. De volgende onderdelen worden behandeld: passen en geodriehoek, vierhoeken, regelmaat, ruimtelijke figuren, volgorde en eindpunt.
Leerniveau
VWO 2;
HAVO 1;
VWO 1;
HAVO 3;
VWO 3;
HAVO 2;
Leerinhoud en doelen
Vaktaal meetkundige figuren en symbolen;
Rekenen/wiskunde;
Vormen en figuren;
Meten en meetkunde;
Tekenen en construeren;
Vlakke en ruimtelijke figuren herkennen;
Dit thema valt onder de arrangeerbare leerlijn van de Stercollecties voor wiskunde voor havo/vwo leerjaar 1. De volgende onderdelen worden behandeld: passen en geodriehoek, vierhoeken, regelmaat, ruimtelijke figuren, volgorde en eindpunt.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Er is ook een nieuwe, verbeterde versie 2.0 van dit hoofdstuk/thema: 
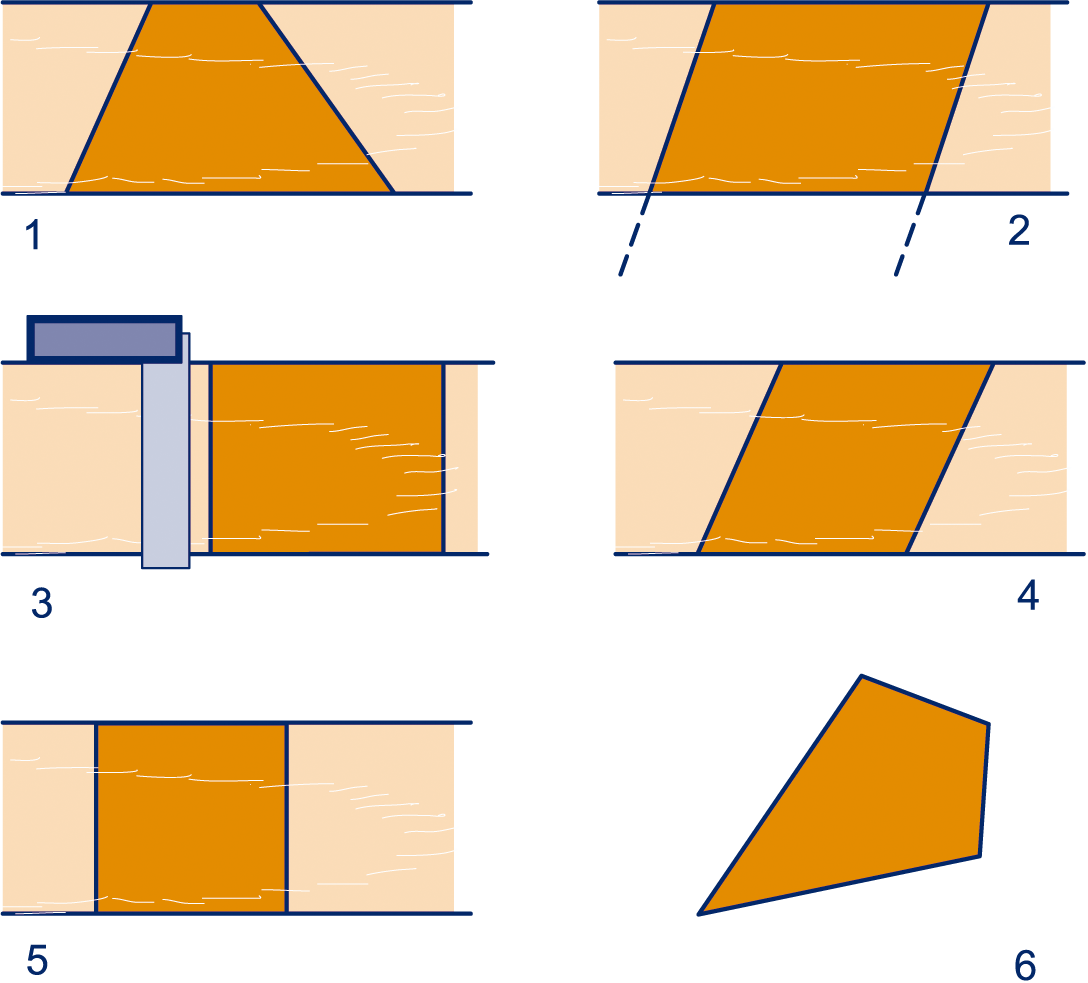
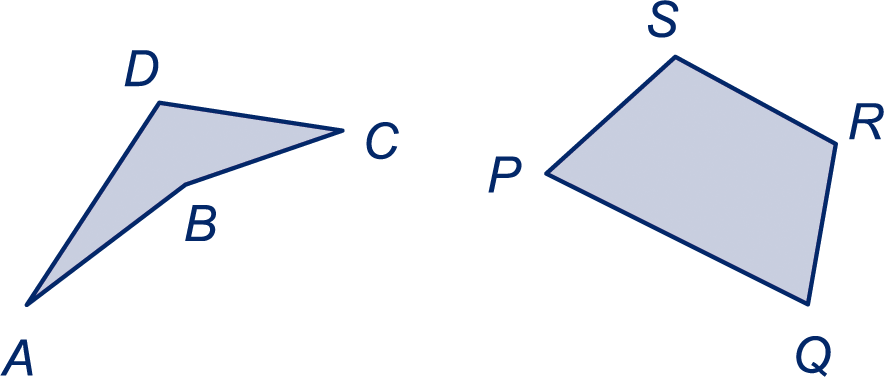Een vierhoek heeft vier hoekpunten. Vaak geven we die opvolgende hoekpunten namen, bijvoorbeeld 
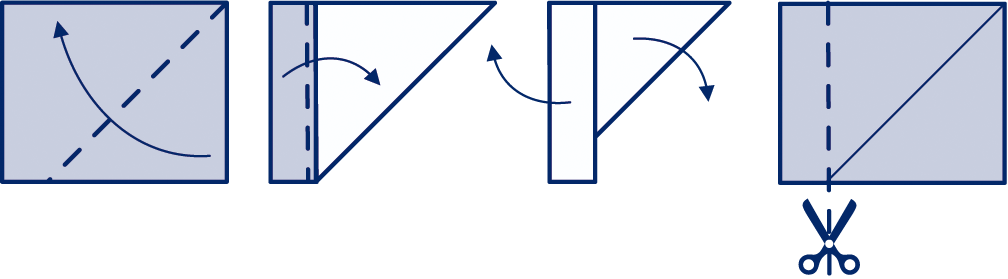
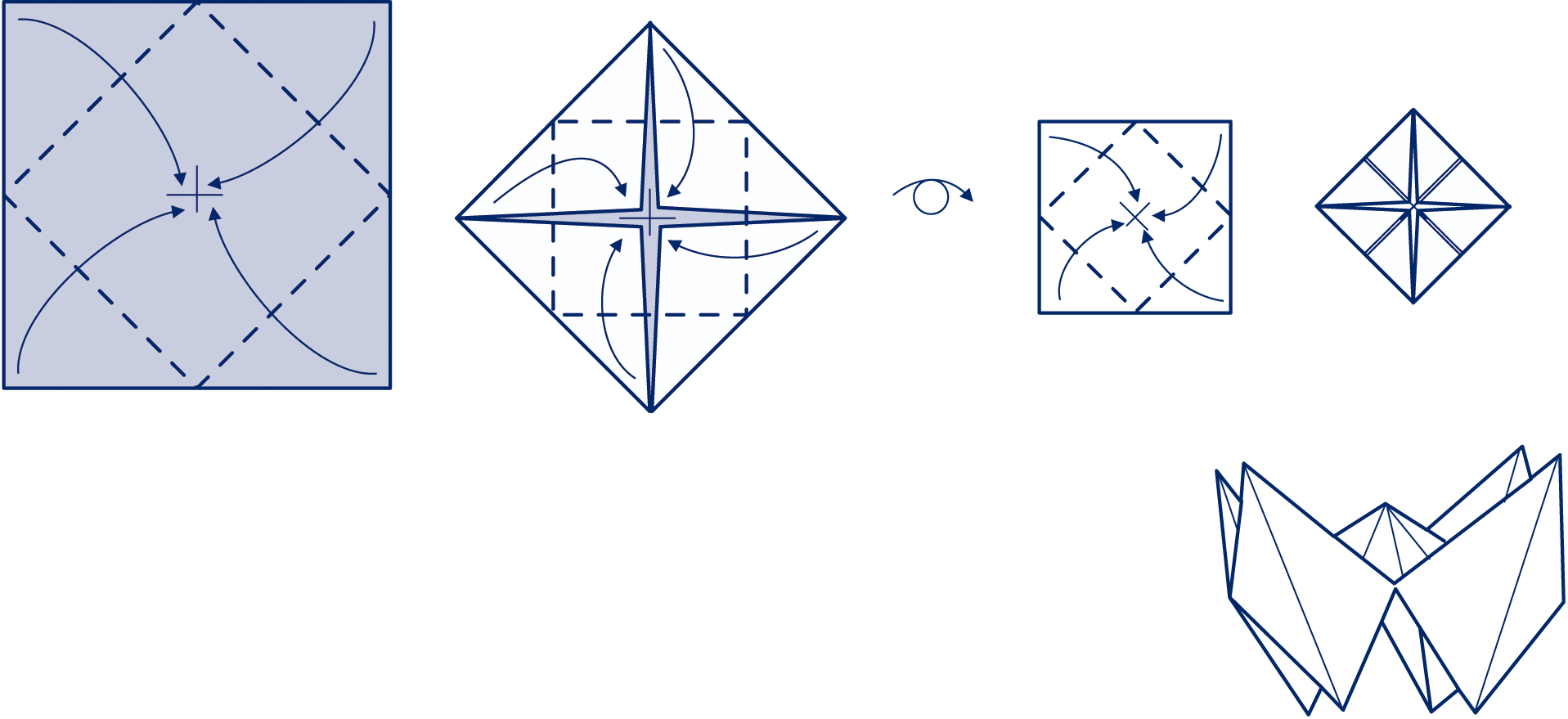
Neem een vouwblaadje. Vouw de punten naar binnen, zodat je een kleiner vierkant krijgt.
Bekijk de tekening van een balk. Anders dan bij een draadmodel, moet je de grensvlakken nu dicht denken, bijvoorbeeld alsof ze van karton zijn. De ribben die aan de achterkant zitten kun je dus niet zien. Daarom zijn ze gestippeld. Op deze manier geef je "diepte" aan de tekening. Als je gewend bent aan deze manier van tekenen, zie je beter hoe de vorm er in werkelijkheid uitziet.
