Het arrangement 2 Basisberoepsgericht is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 27-08-2021 17:12:06
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Wiskunde voor leerjaar 2 VMBO Basis van 't R@velijn Steenbergen. De methode is samengesteld door docenten van 't R@velijn en is gebaseerd op de rearrangeerbare stercollectie van VO-content. Deze zijn ontwikkeld op basis van de kerndoelen basisvorming en de door de SLO ontwikkelde inhoud- en leerdoelspecificaties voor het vak wiskunde. Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO.
- Leerniveau
- VMBO basisberoepsgerichte leerweg, 1; VMBO basisberoepsgerichte leerweg, 2;
- Leerinhoud en doelen
- Rekenen/wiskunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 100 uur 0 minuten
Gebruikte Wikiwijs Arrangementen
VO-content - Leerlijnen. (2025).
Wiskunde vmbo-b12















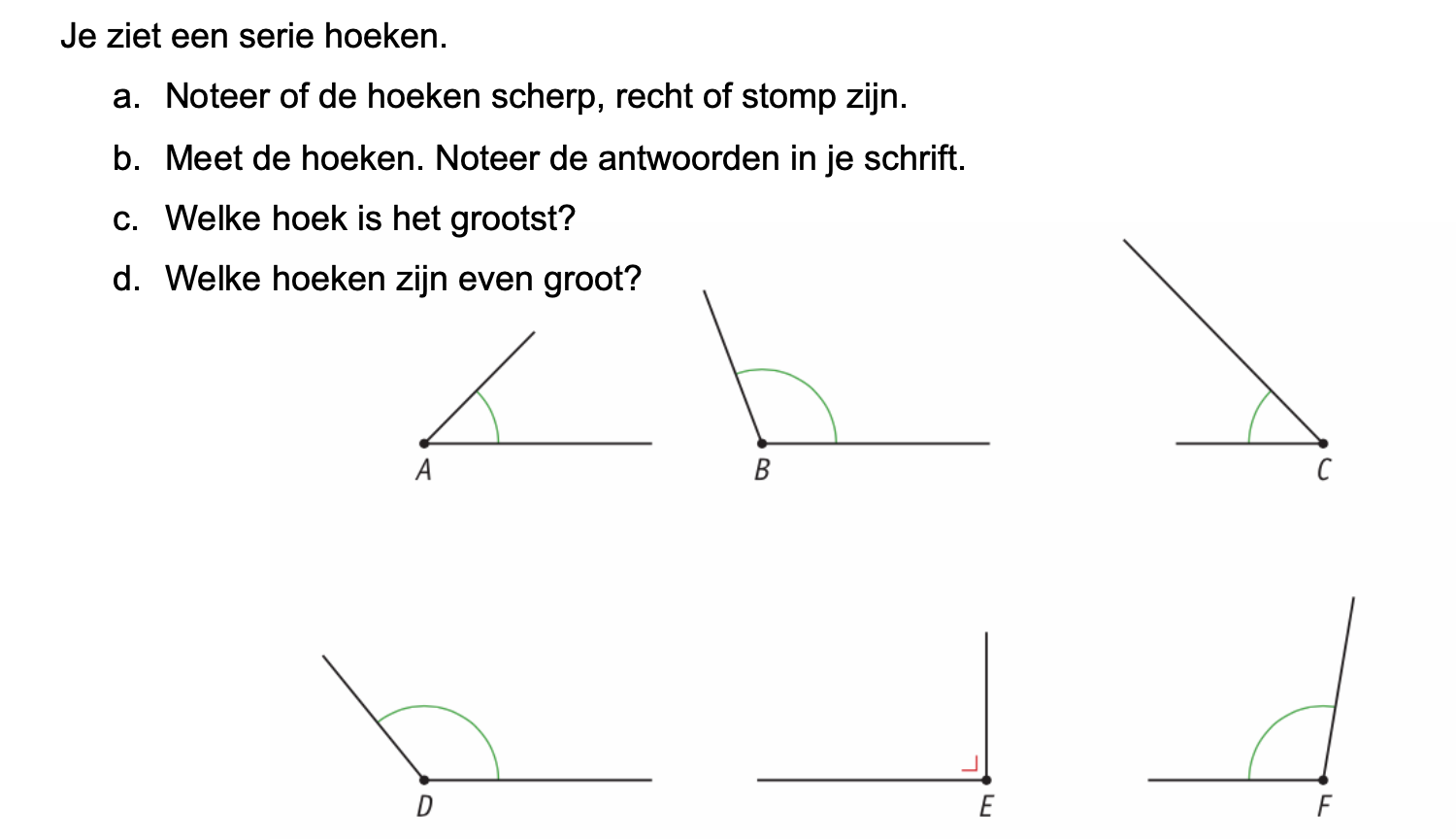
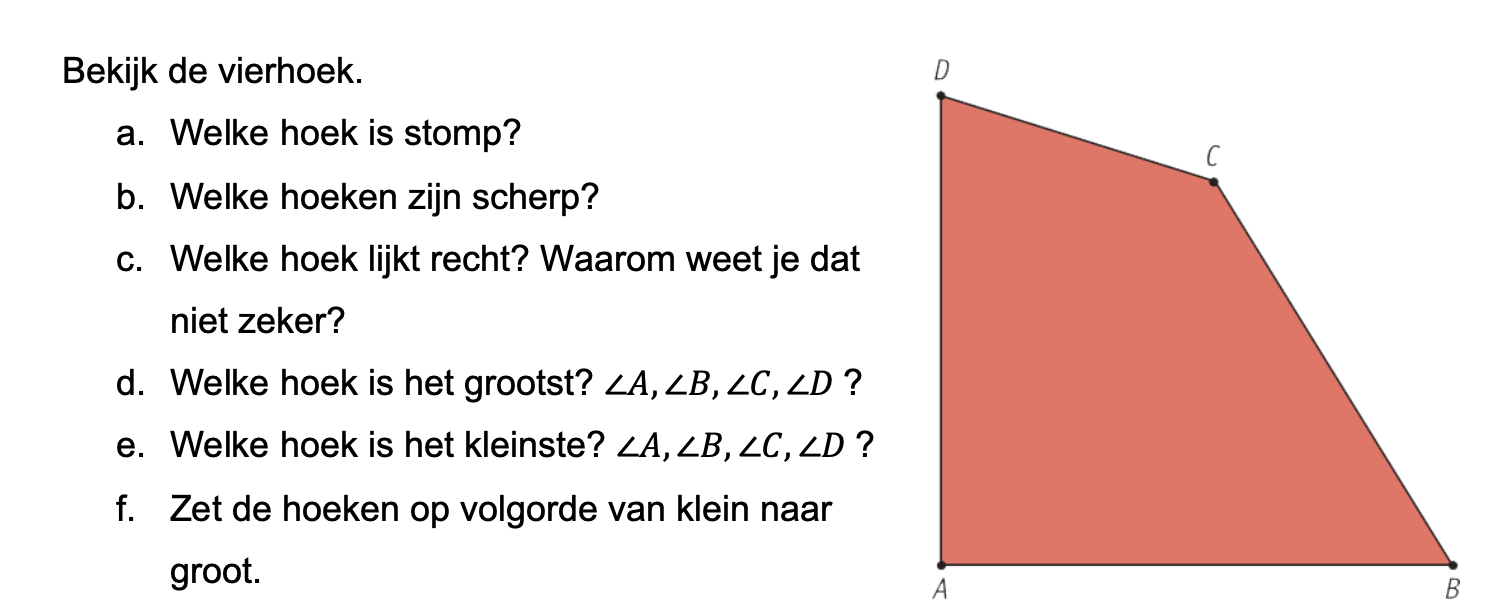
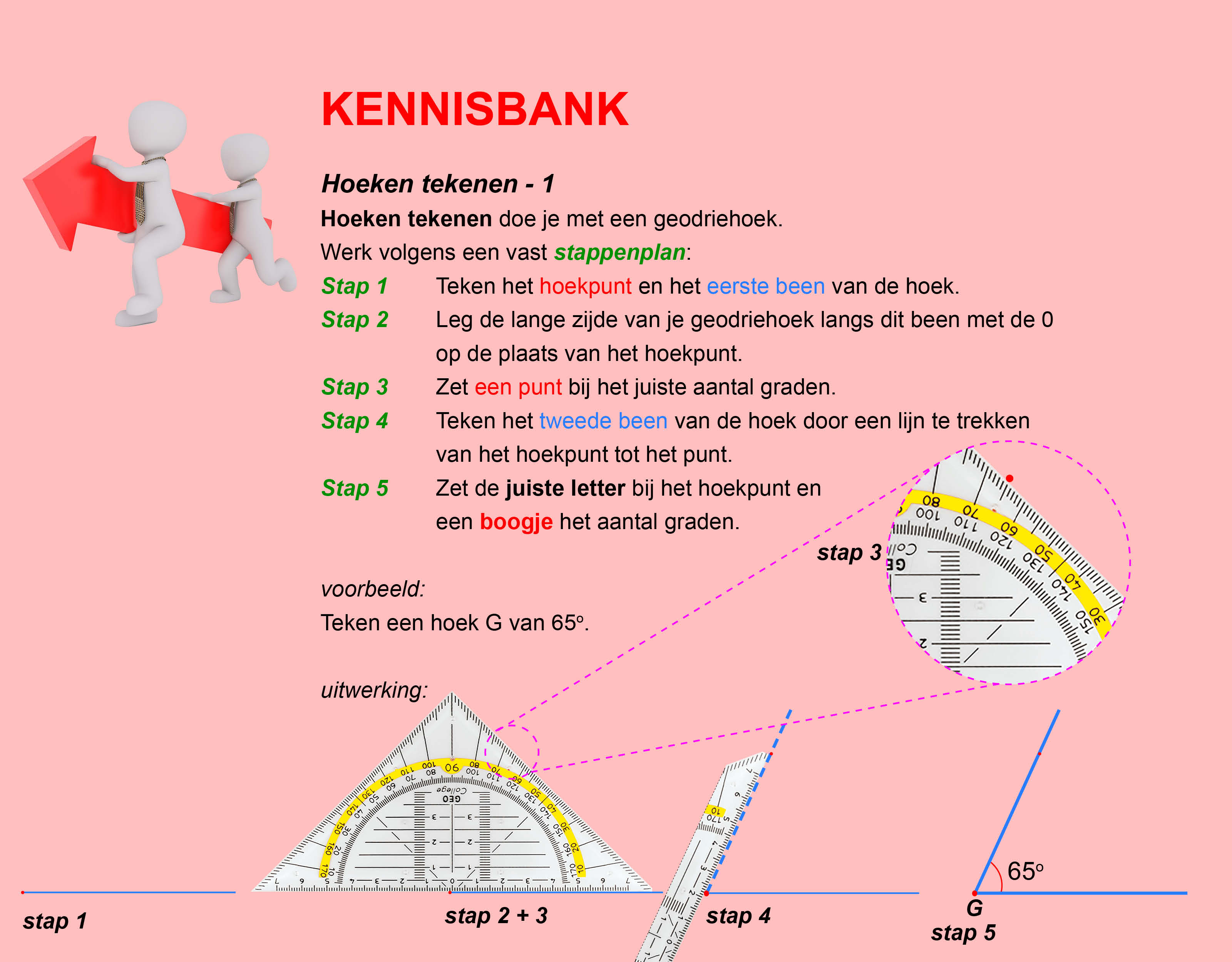

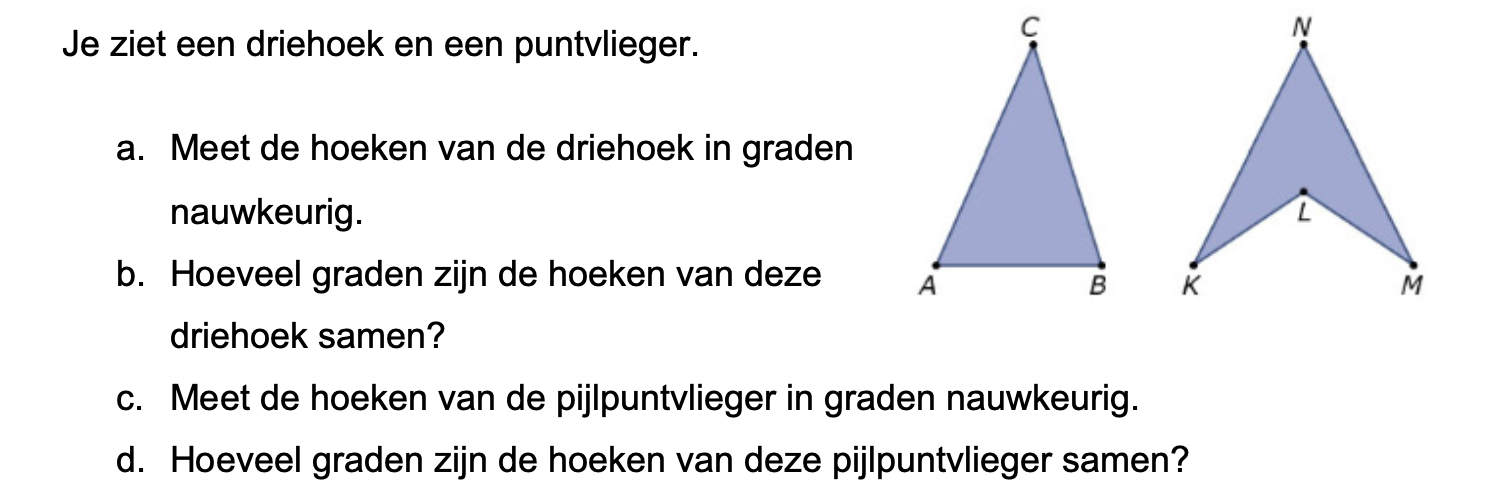




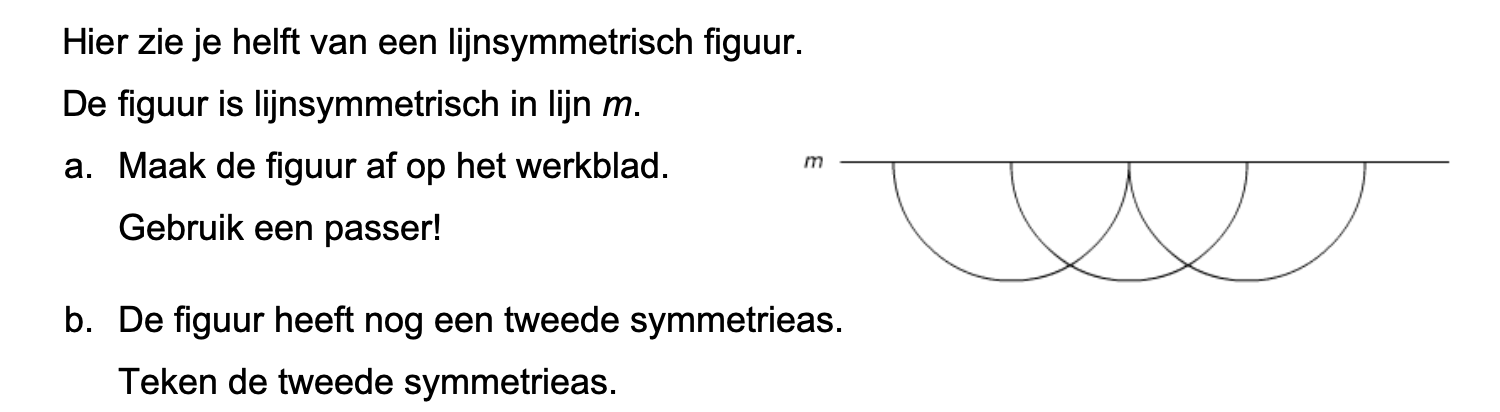
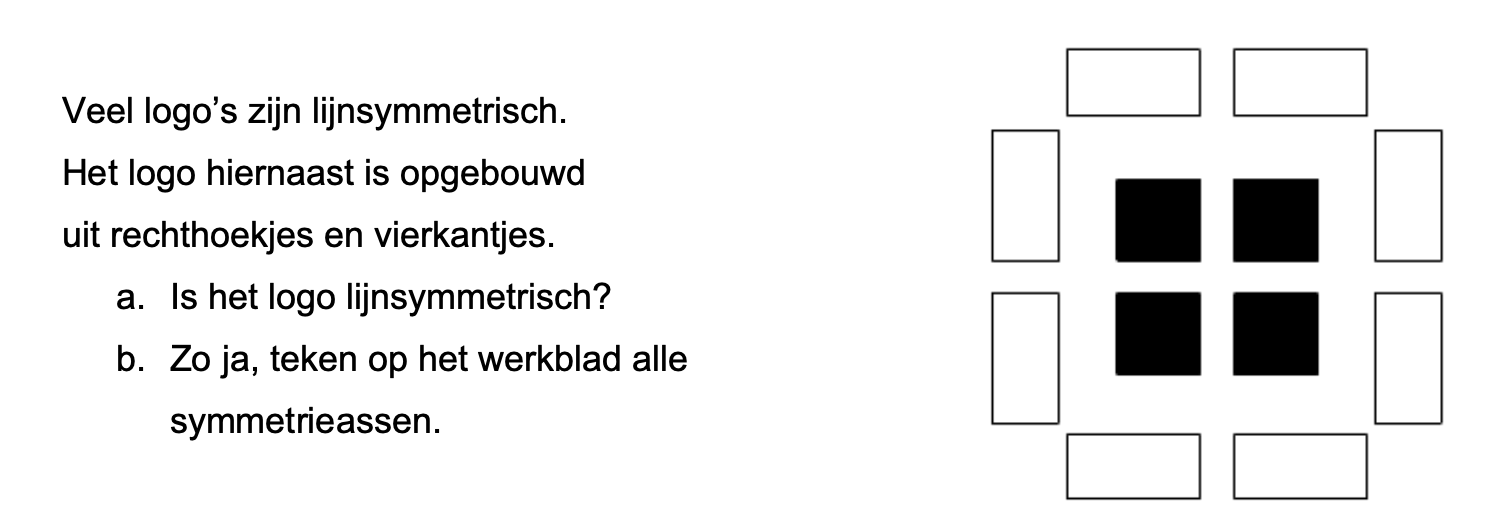



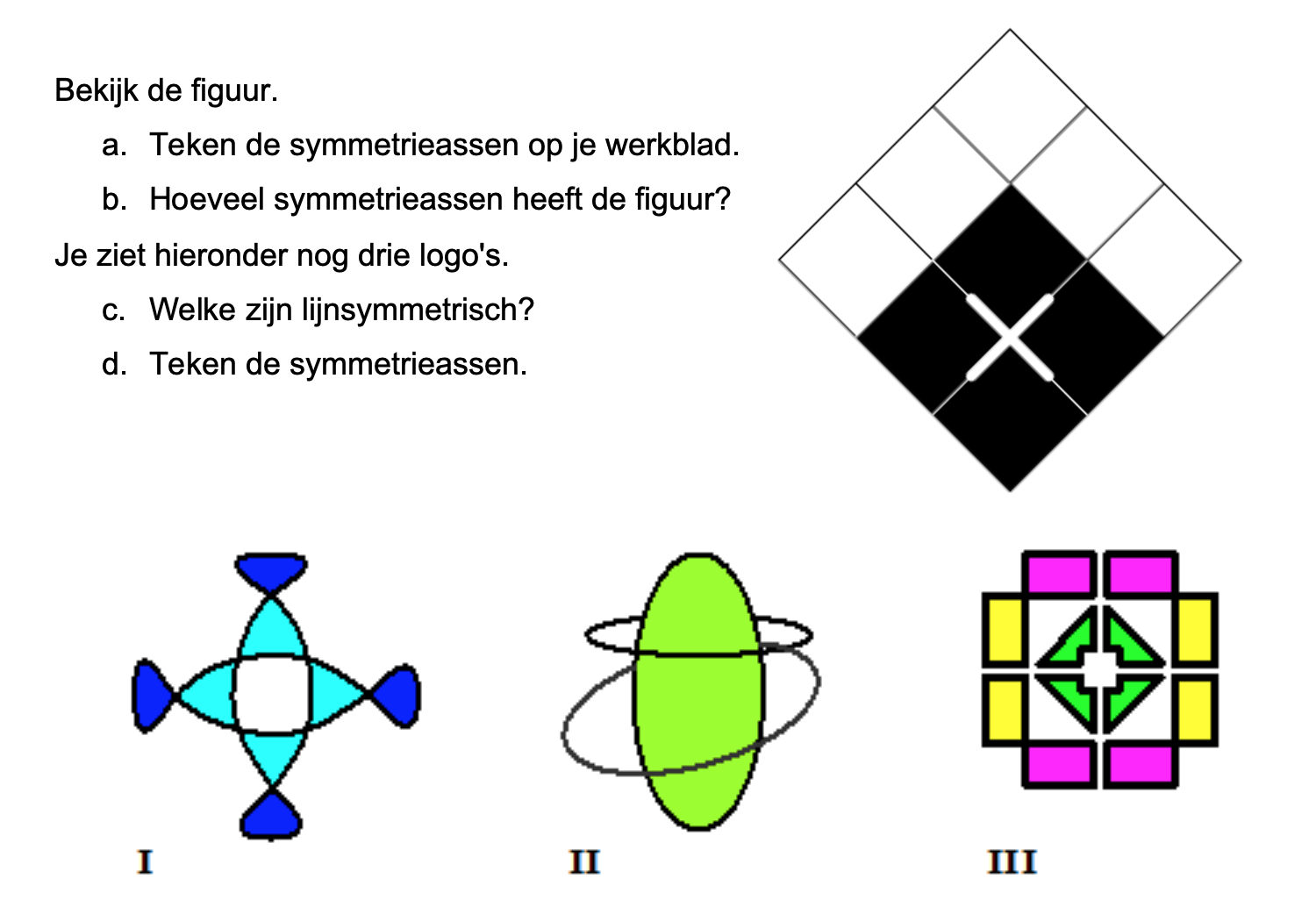


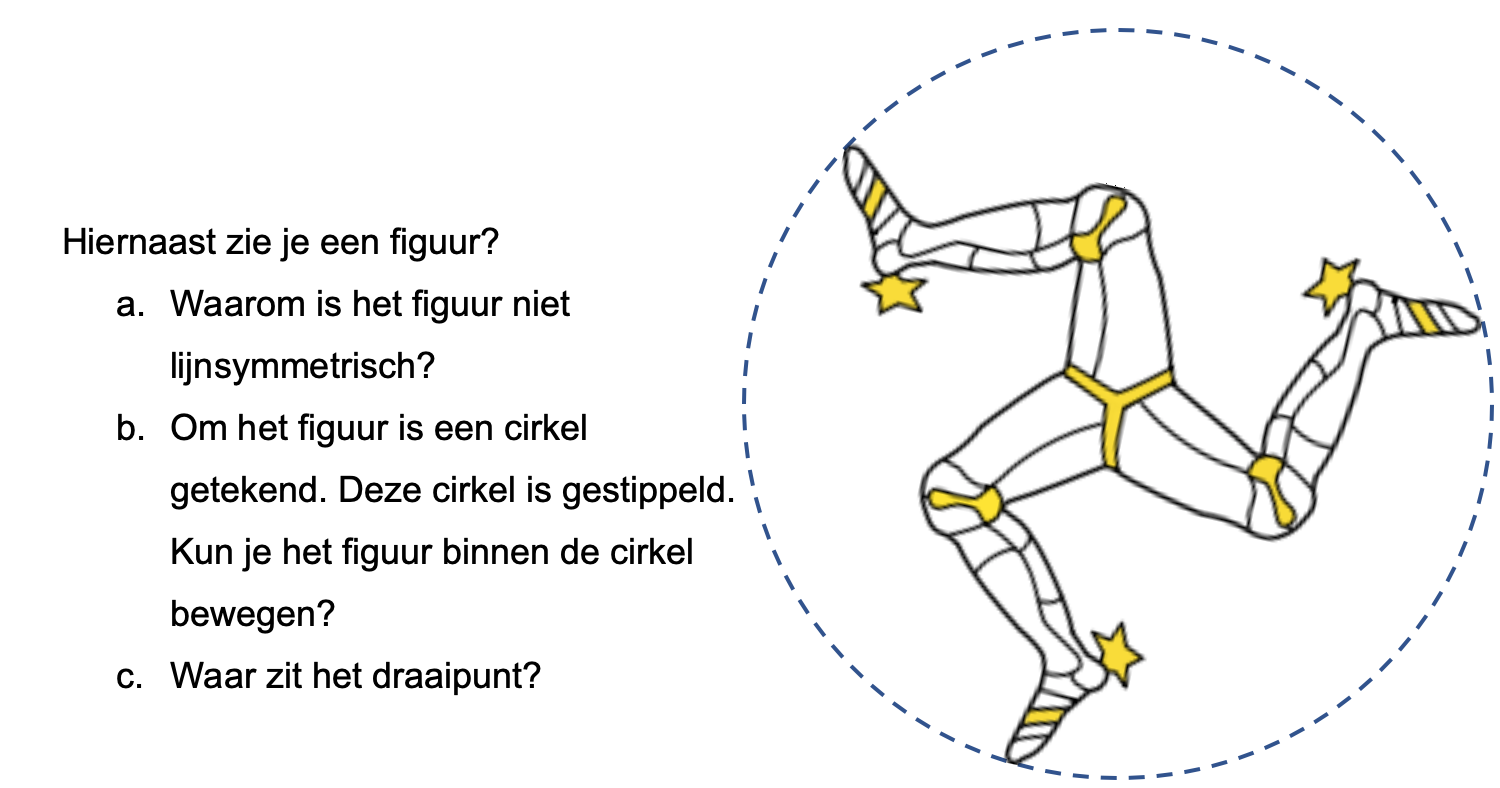

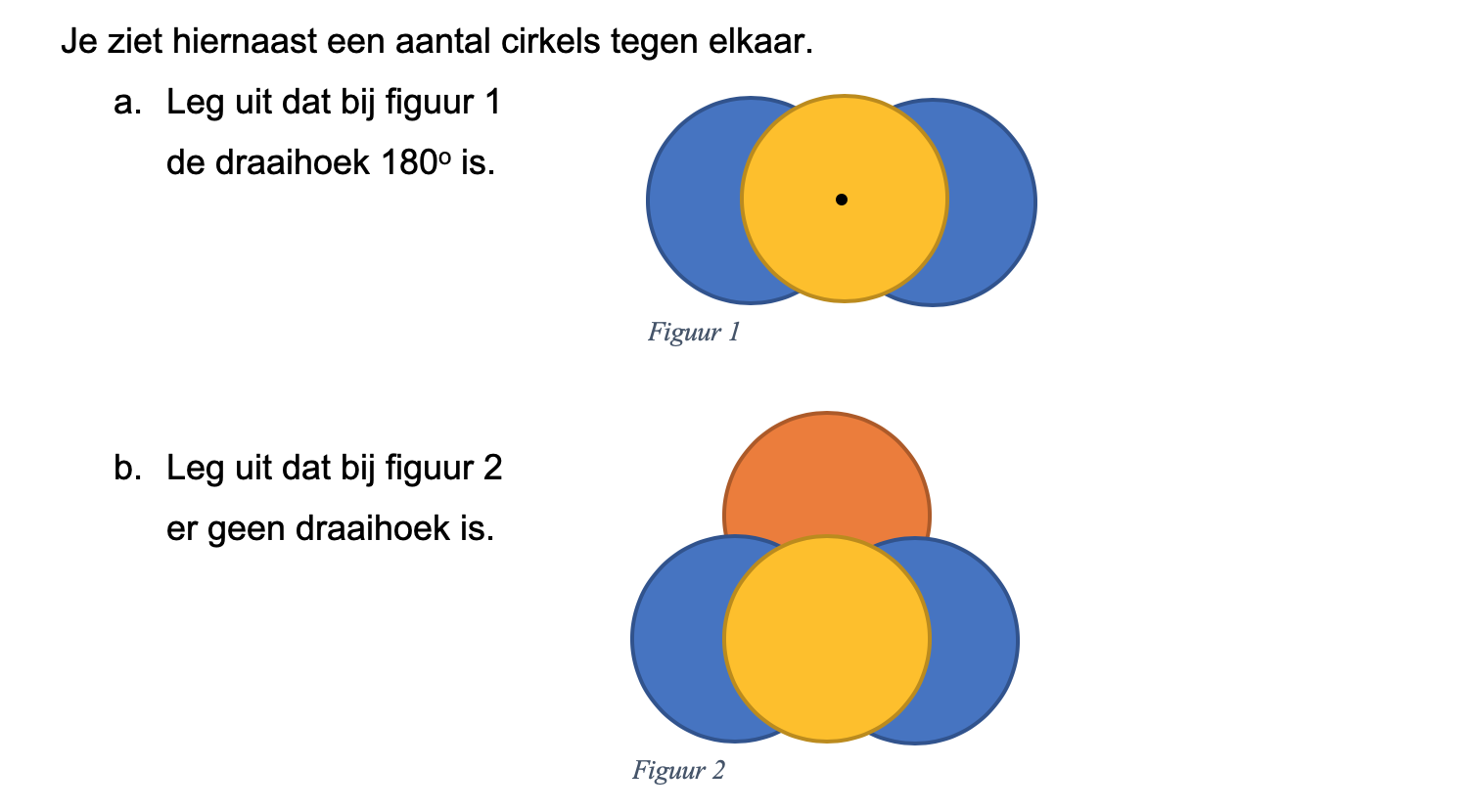



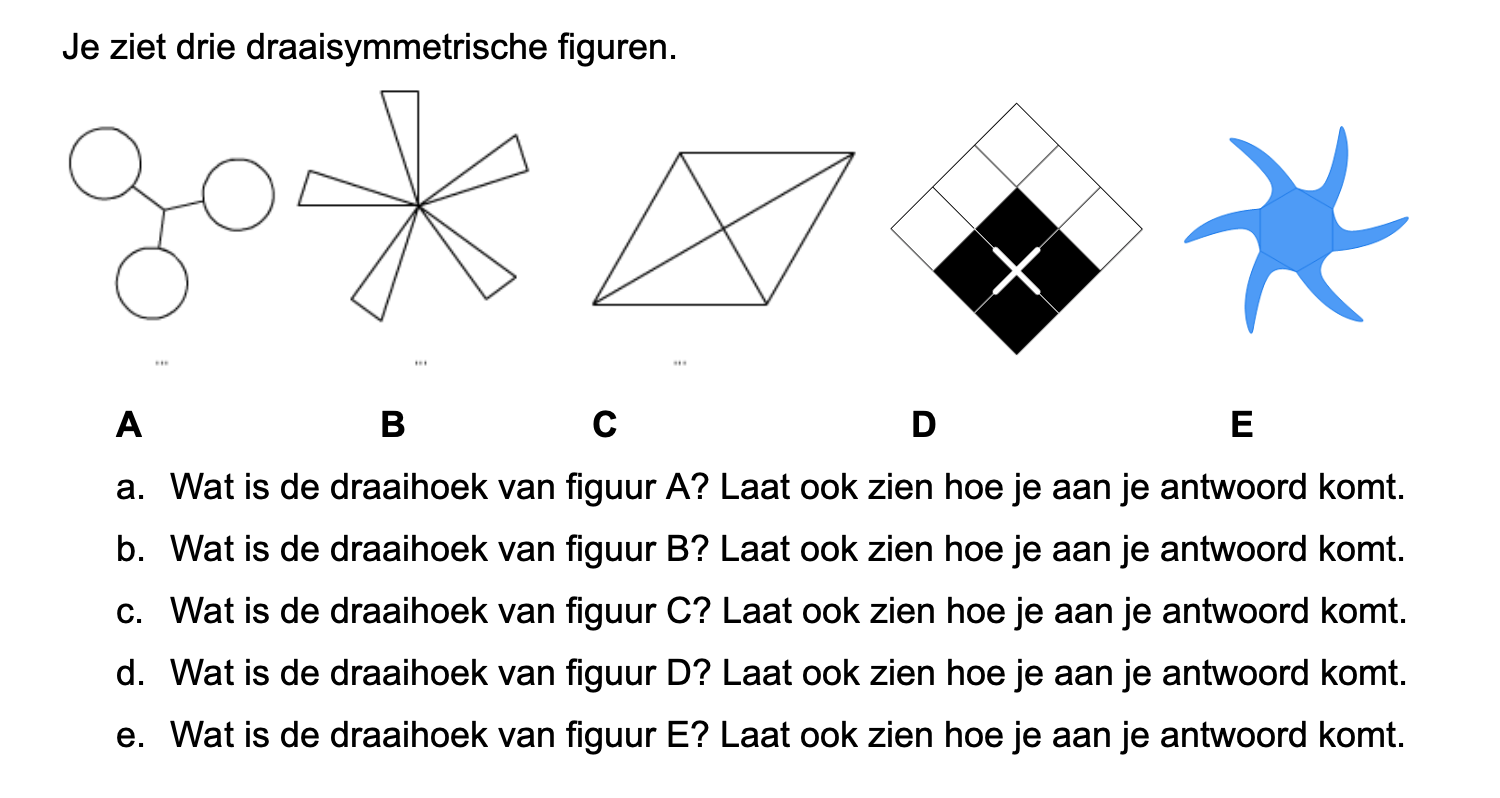
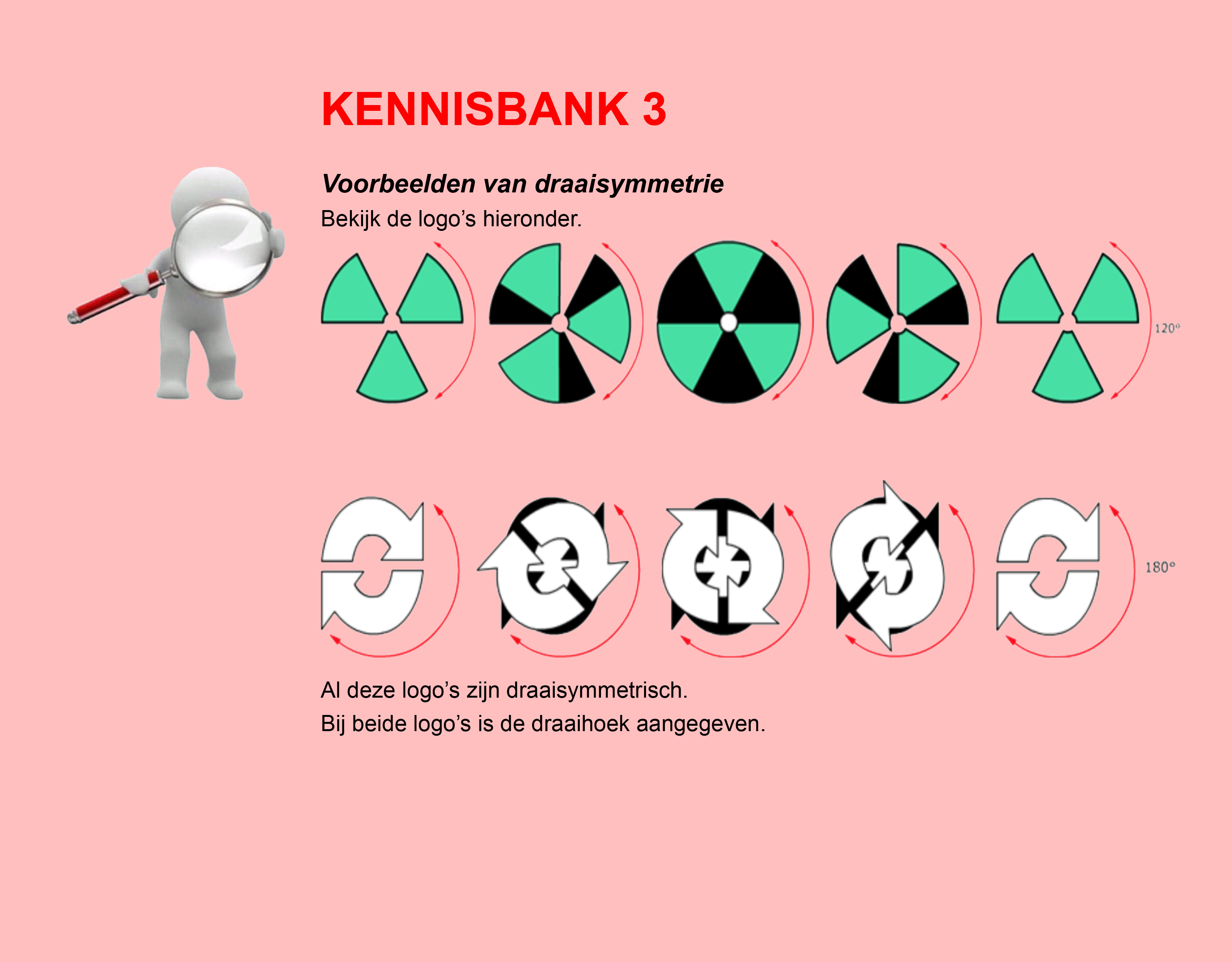

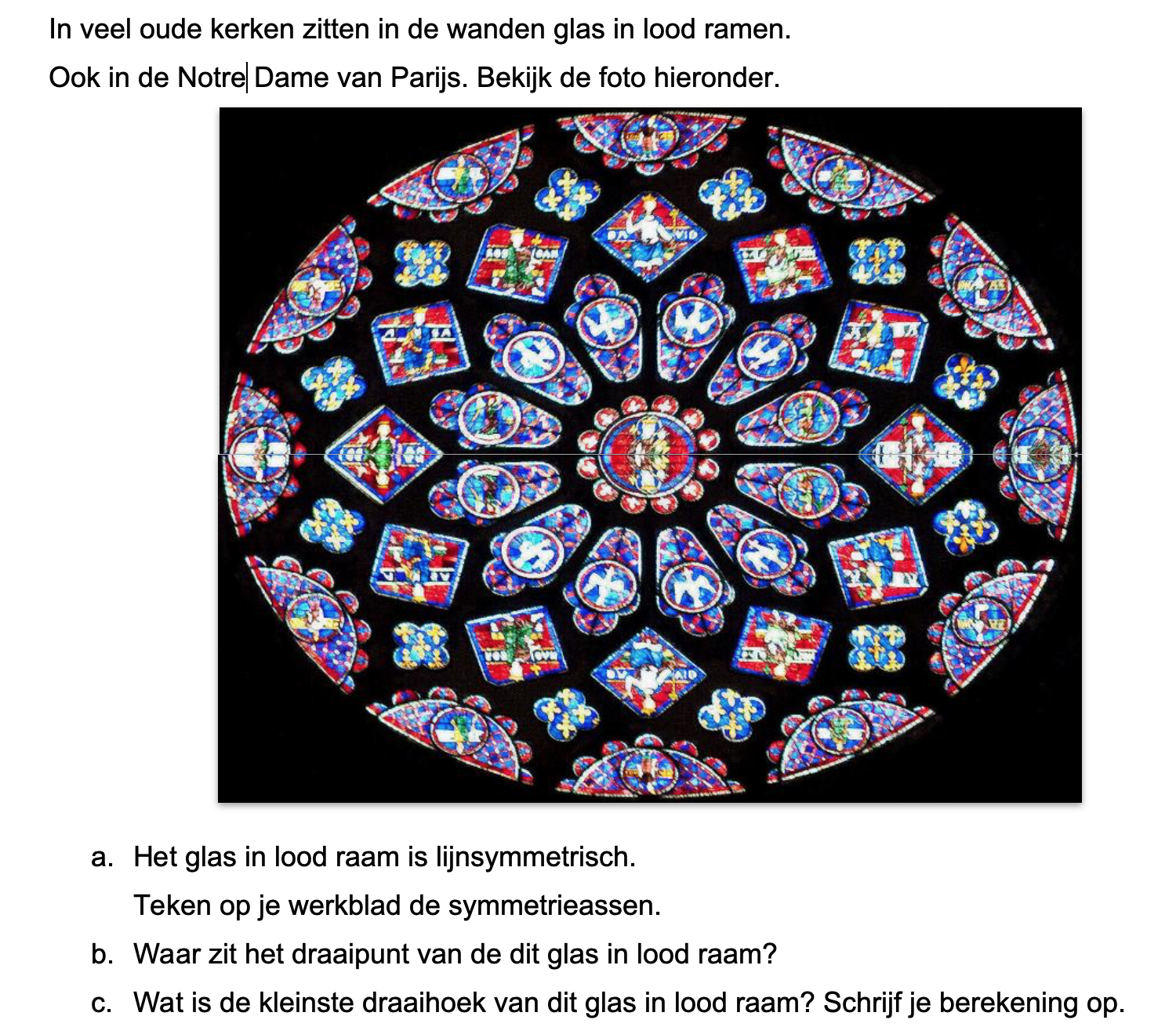


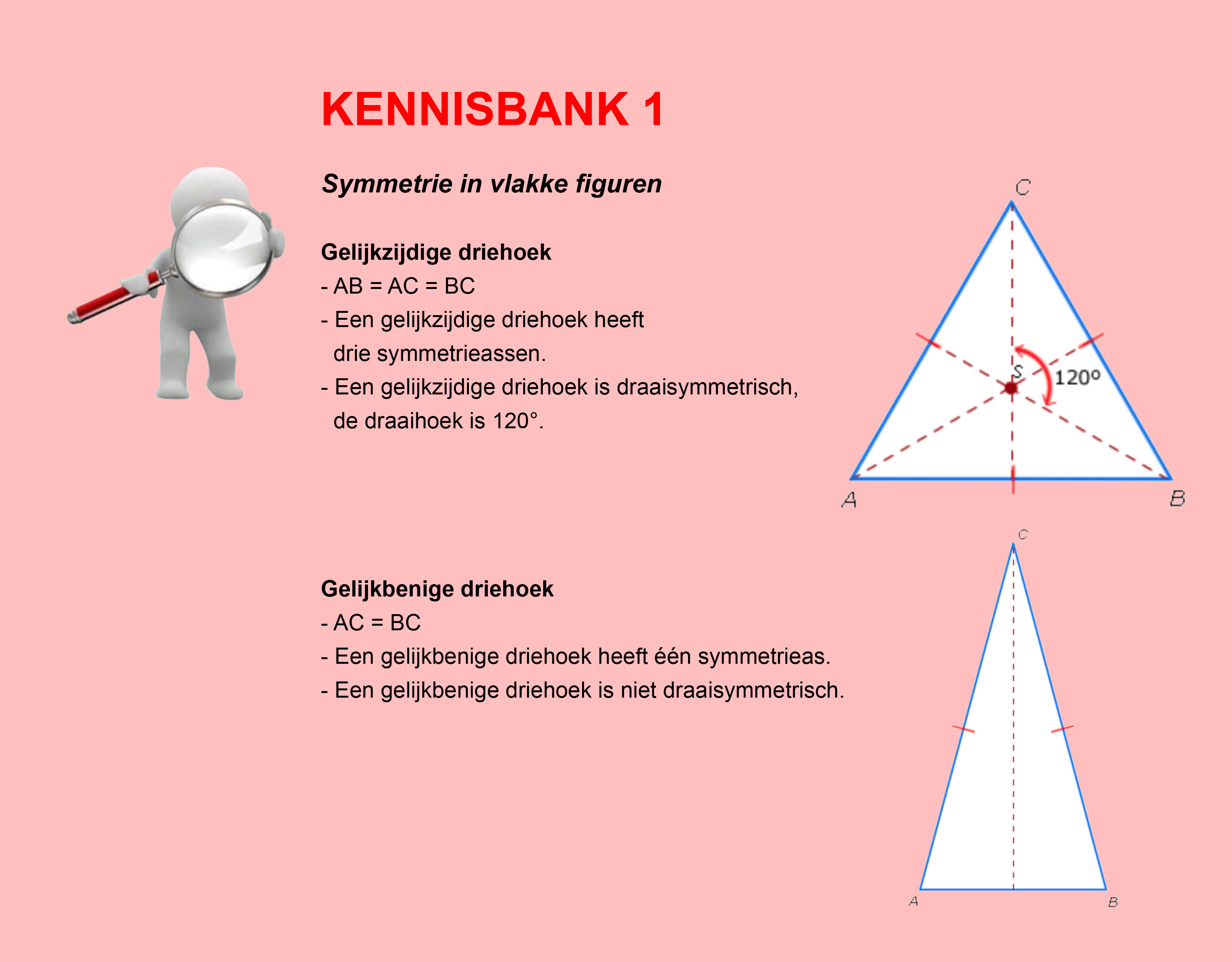
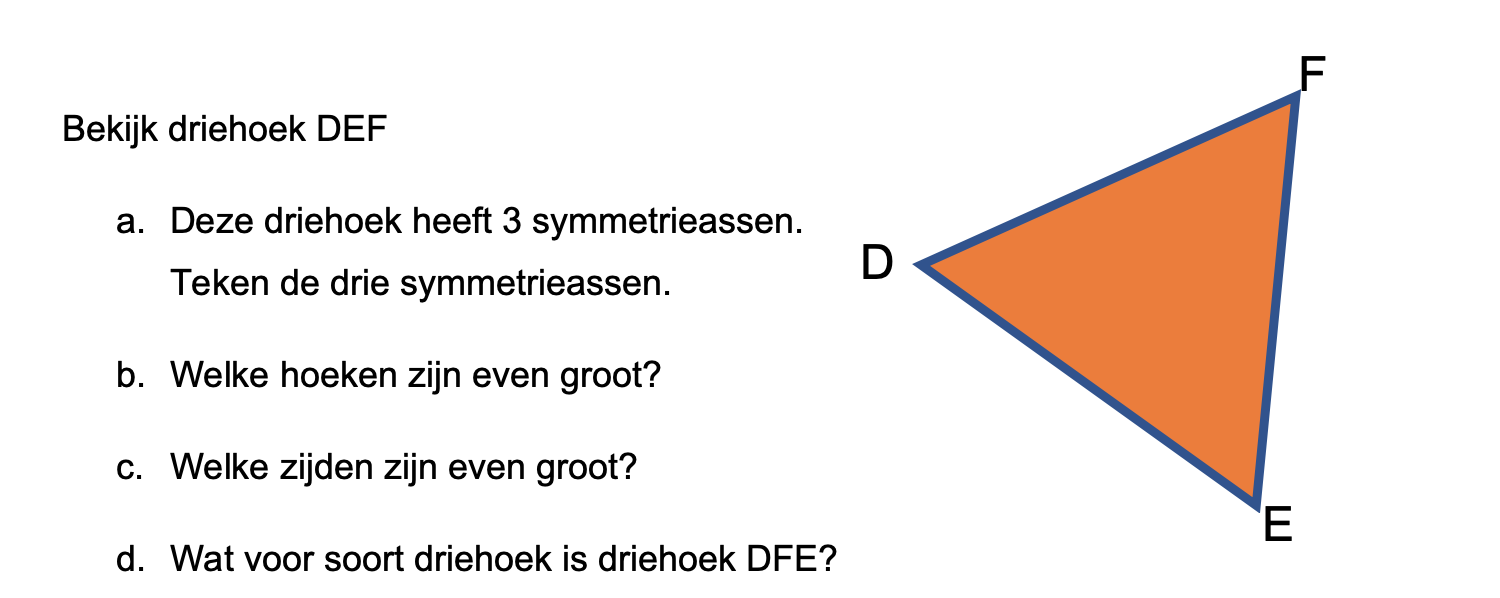

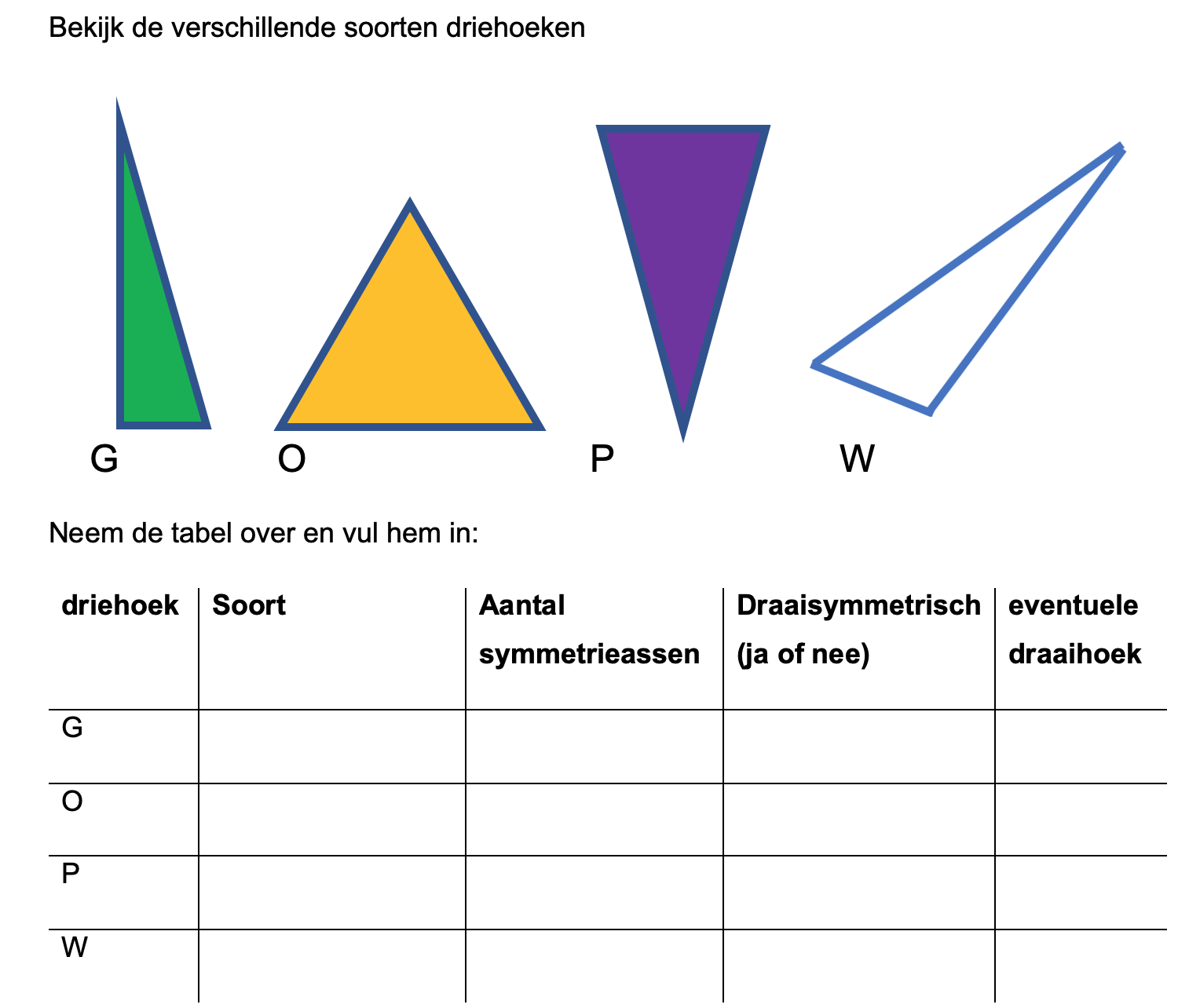
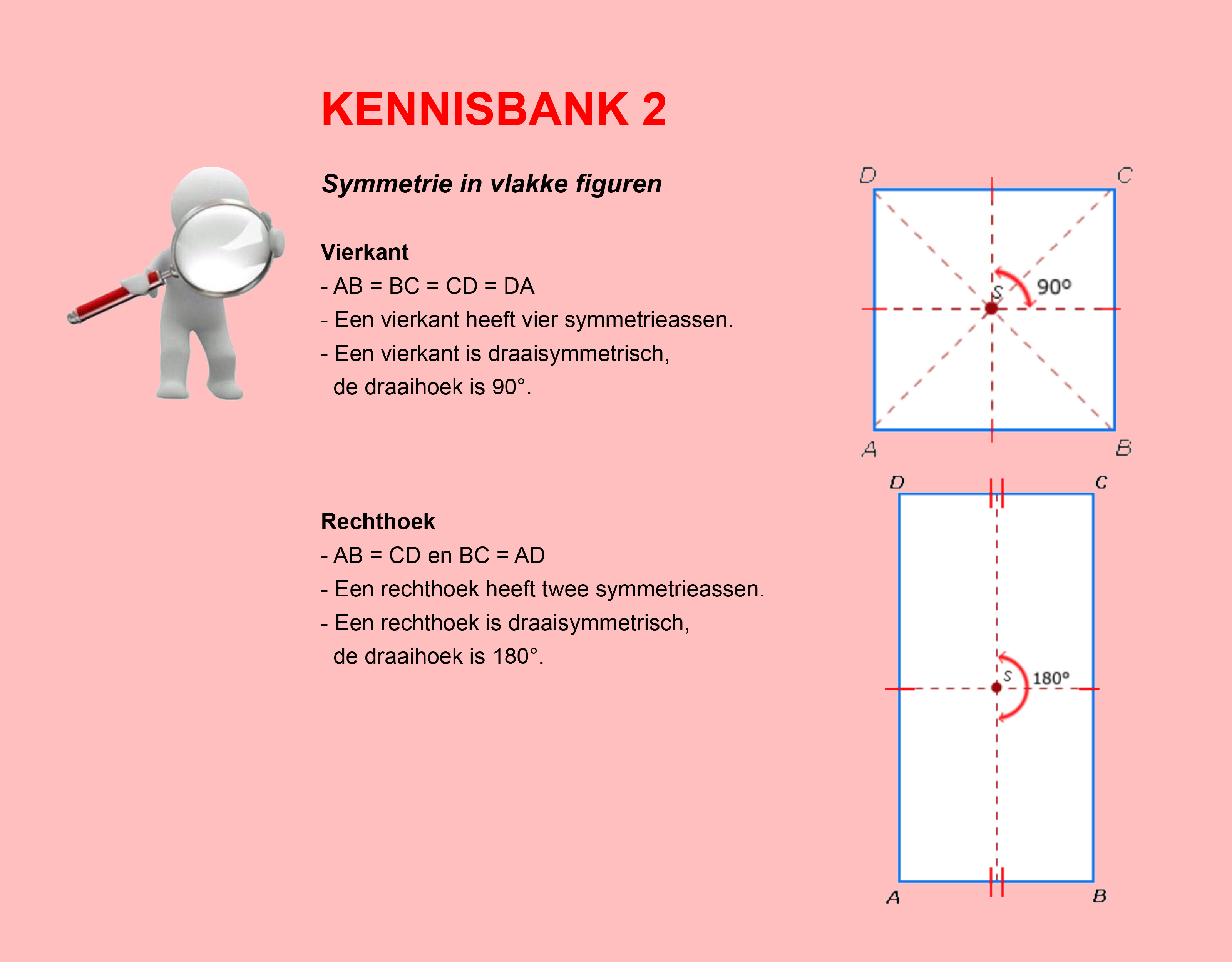
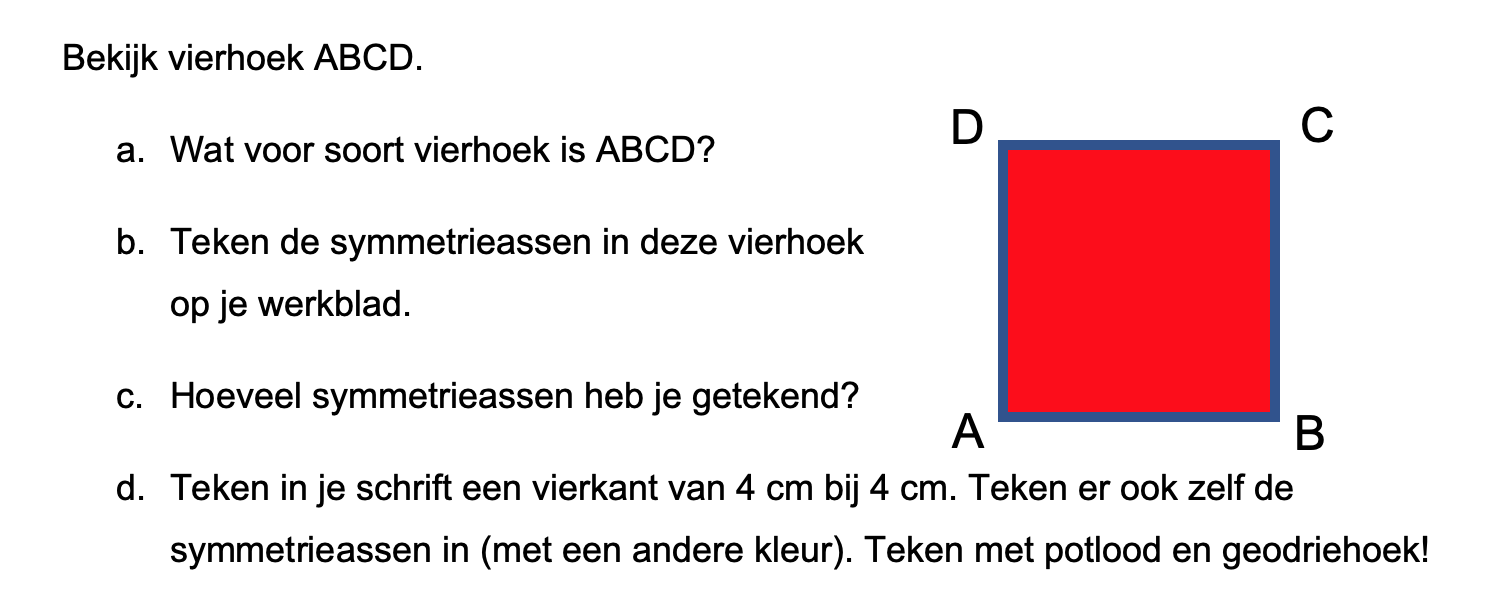
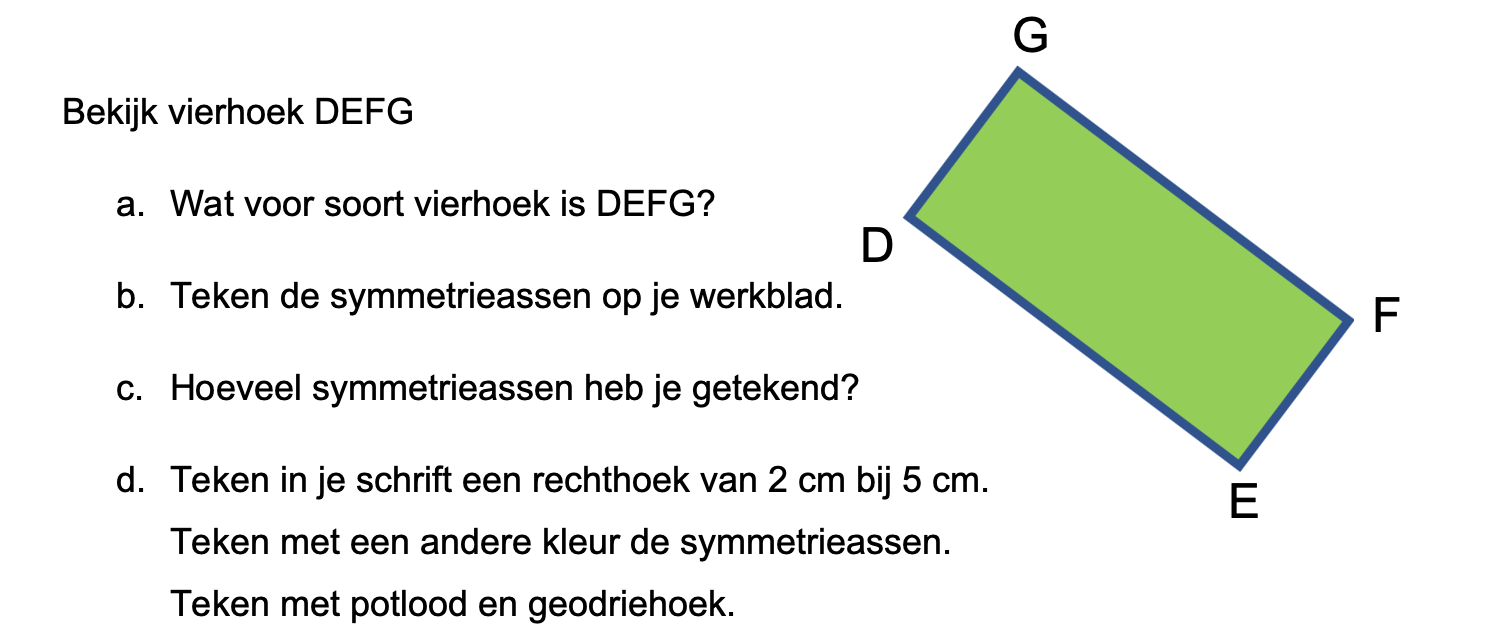
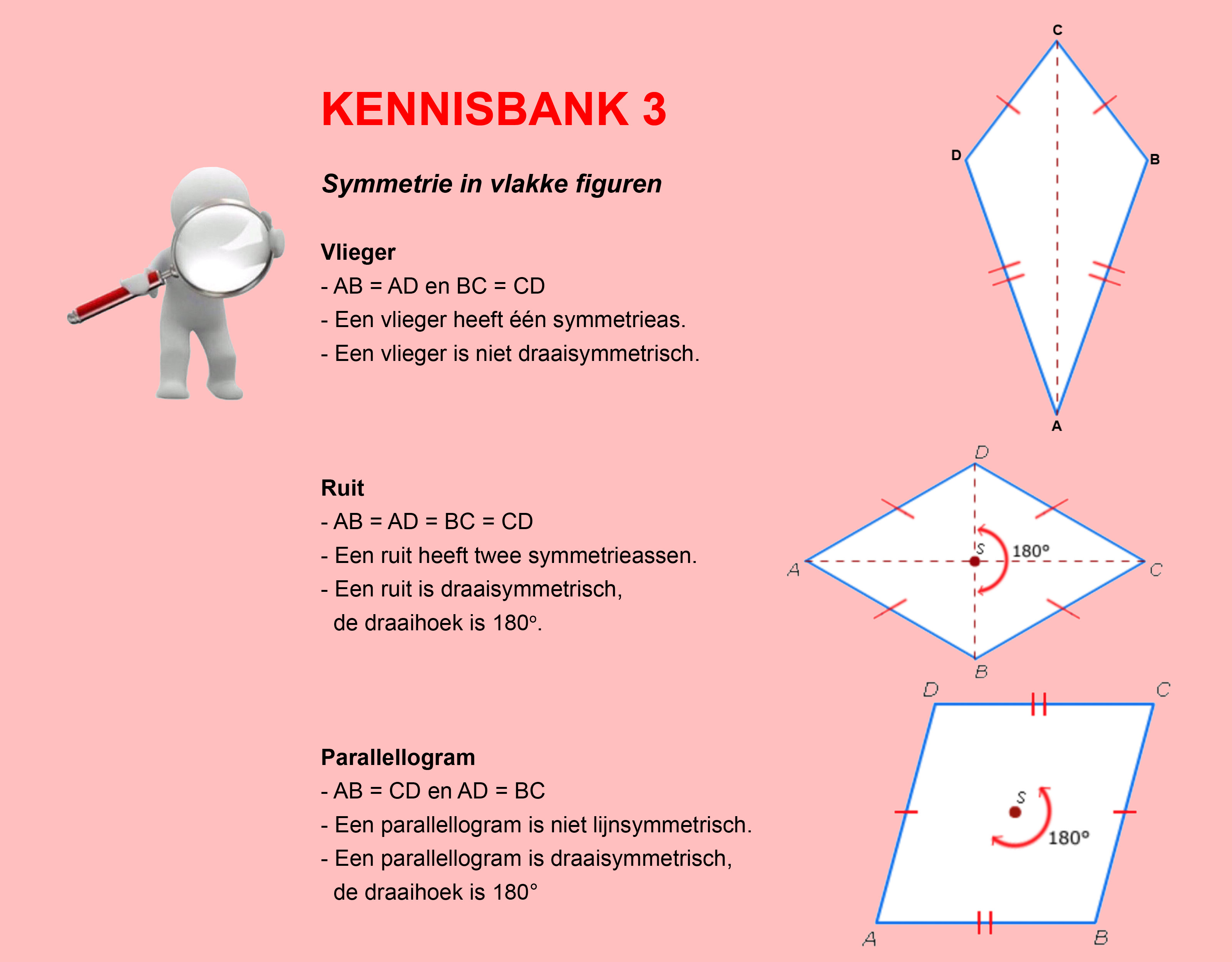


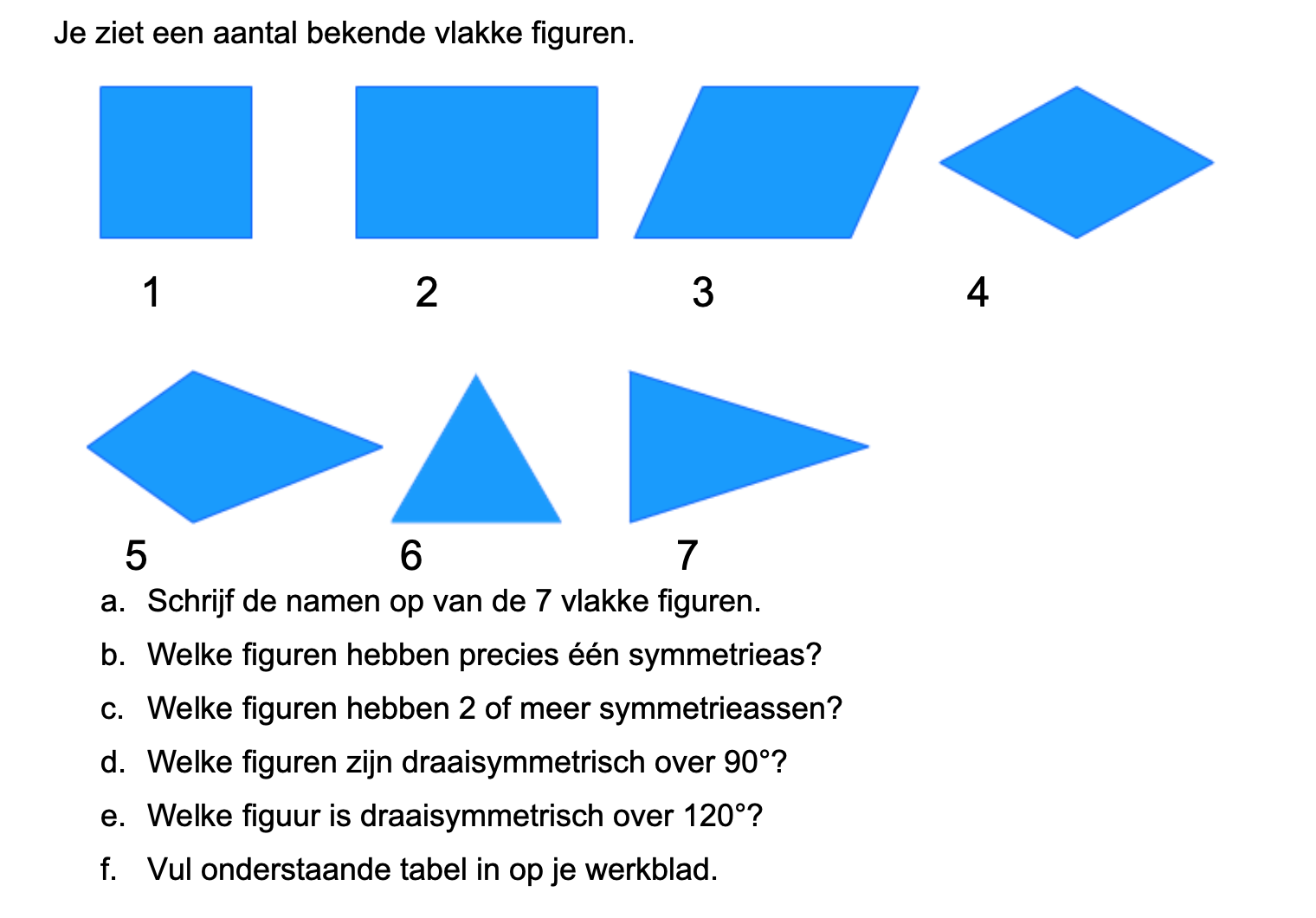
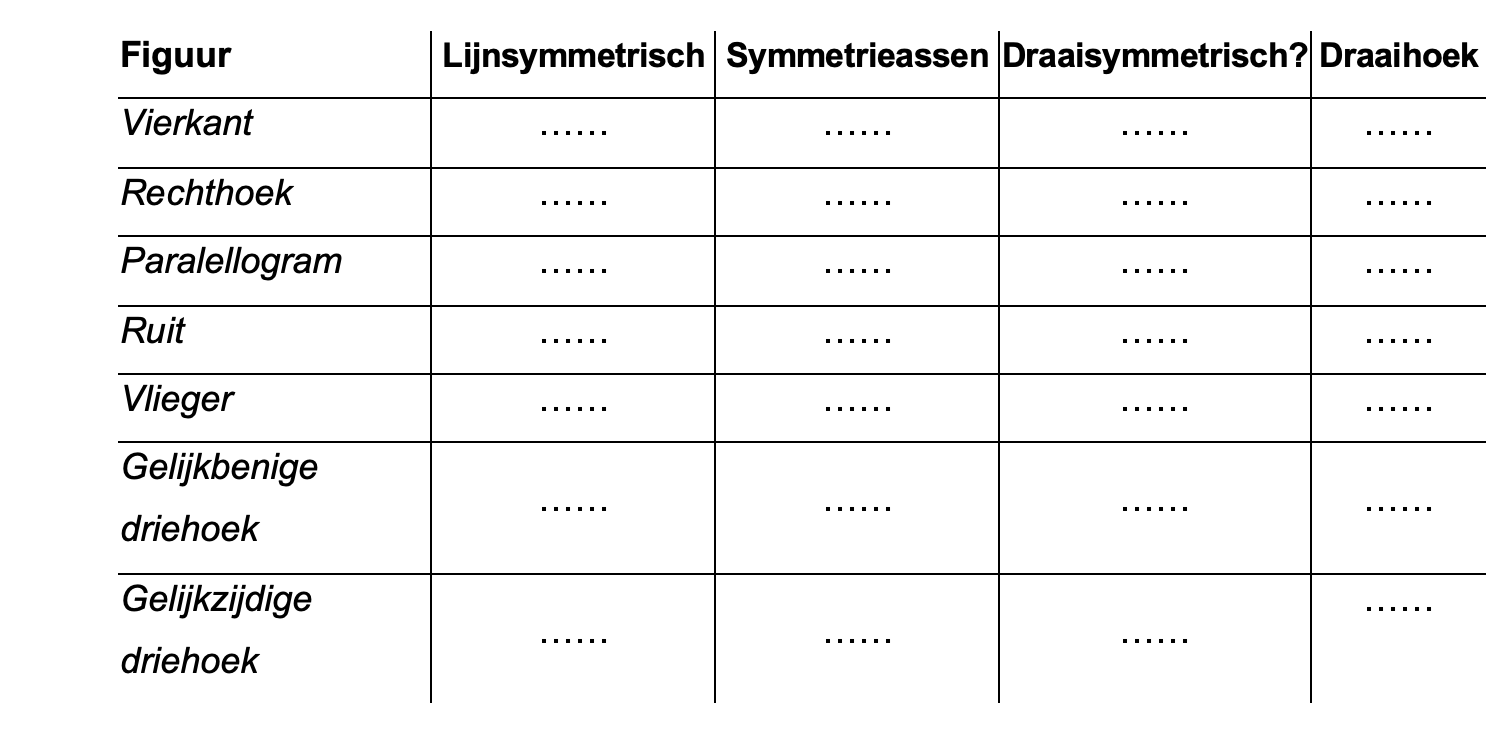

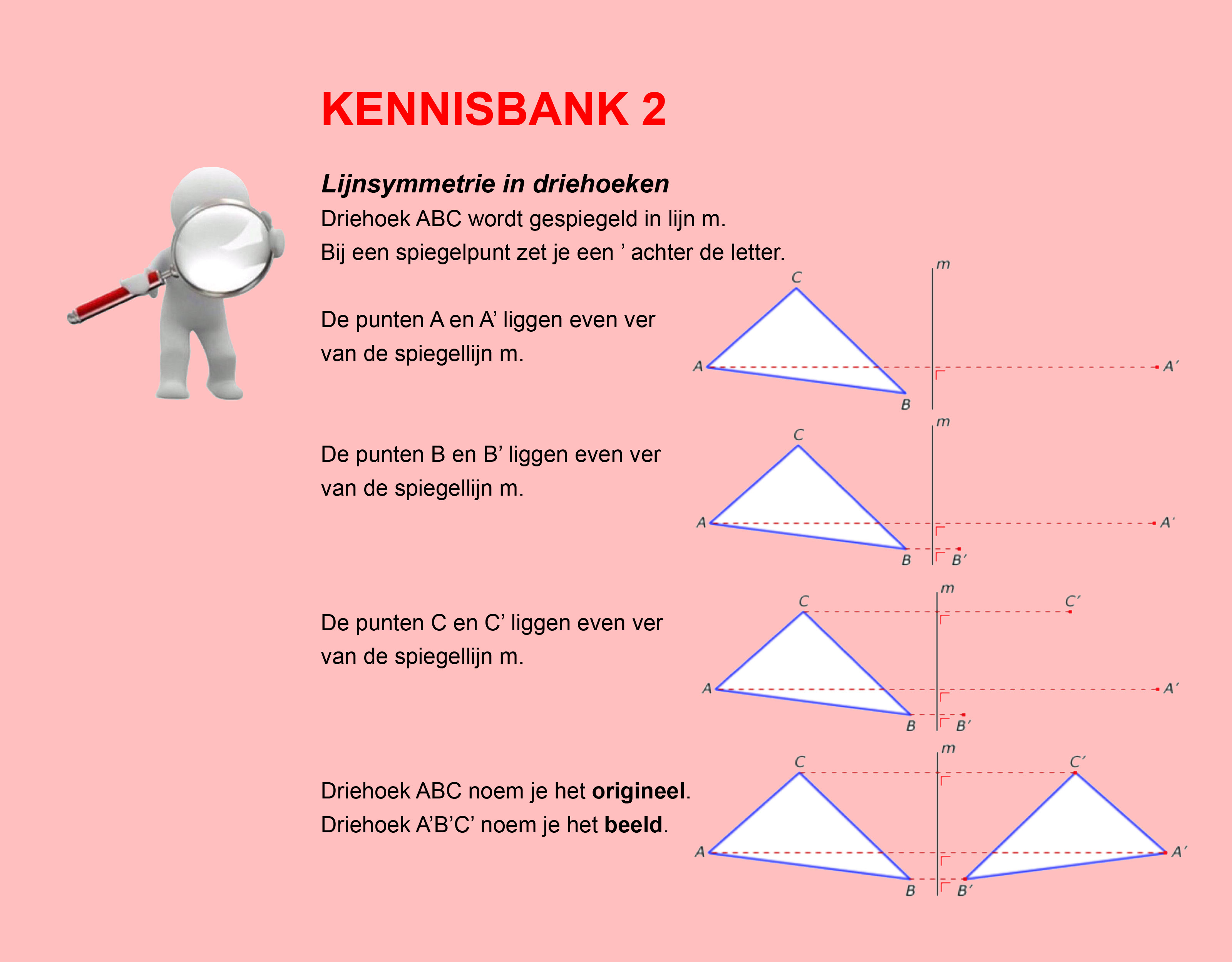







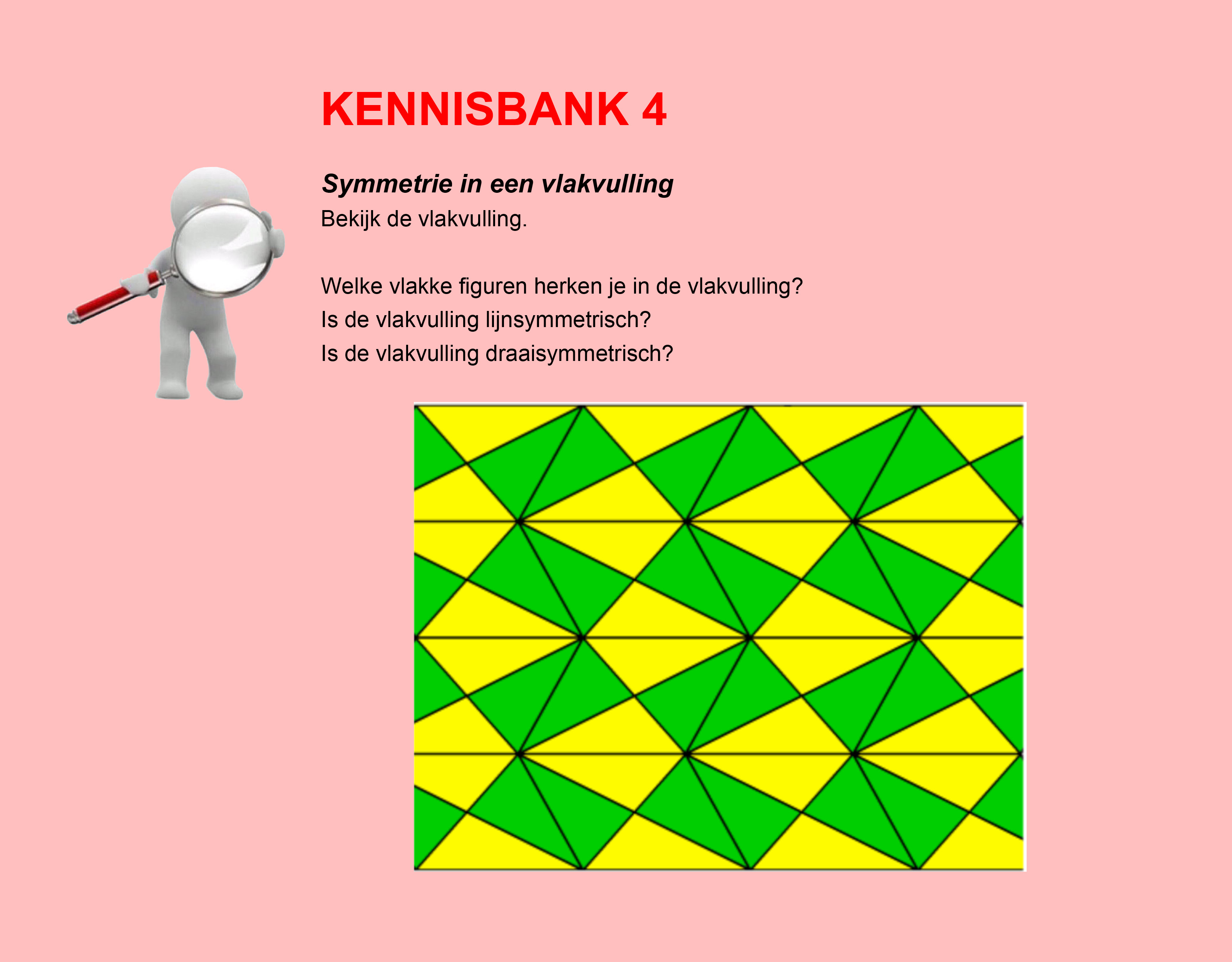


 Maak de volgende opgaven.
Maak de volgende opgaven.

 Hoe komt het, denk je, dat veel mensen die kasteeltuinen zo mooi vinden?
Hoe komt het, denk je, dat veel mensen die kasteeltuinen zo mooi vinden?

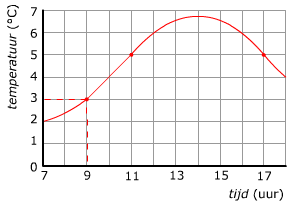
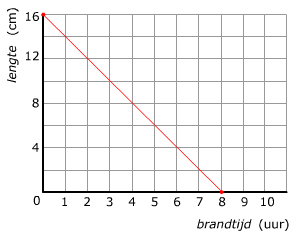
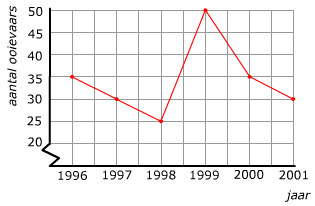
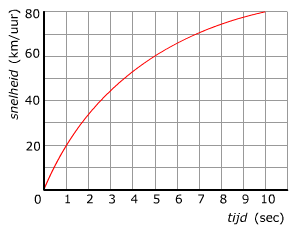





/s3/static.nrc.nl/bvhw/files/2016/09/ANP-1857035.jpg)








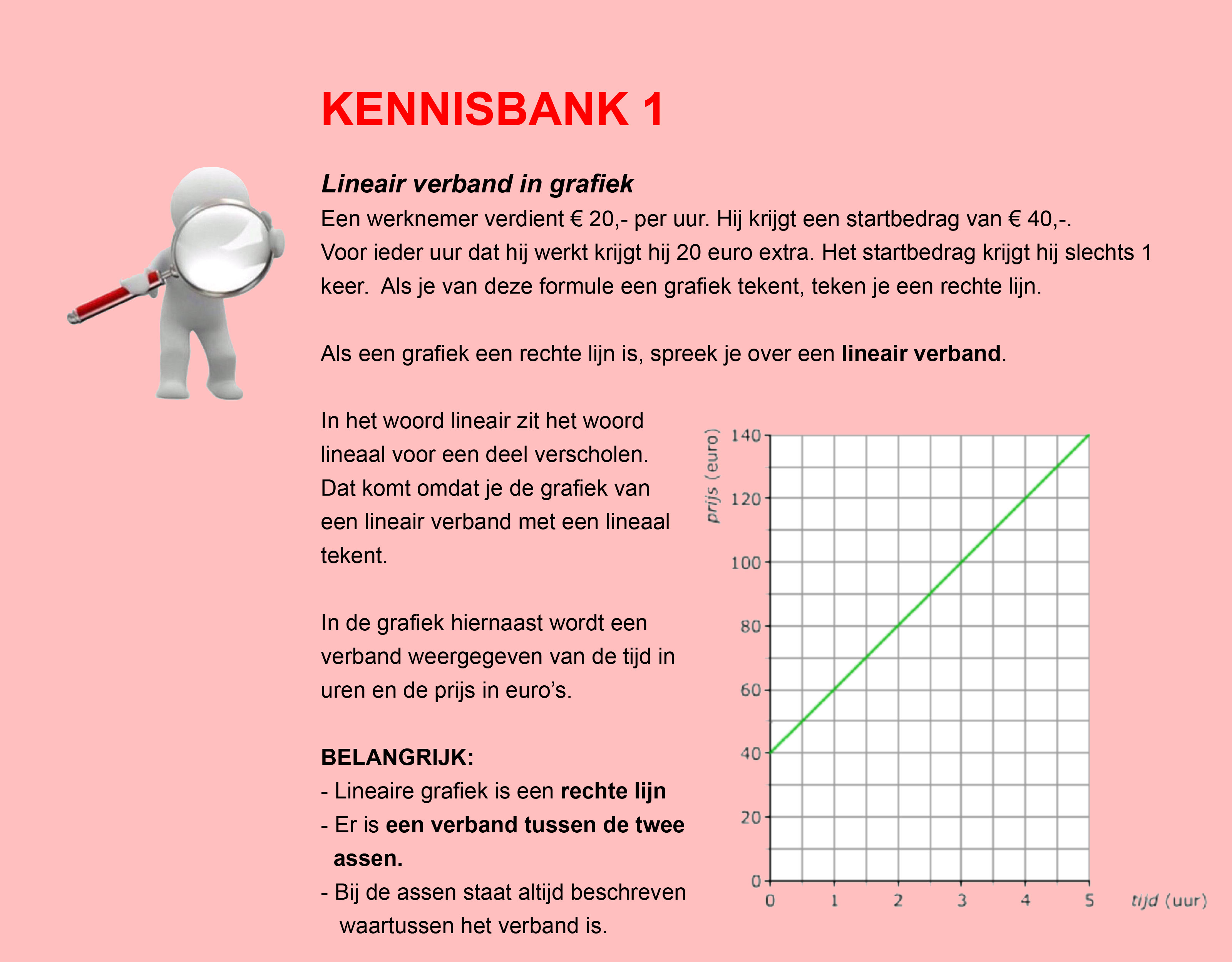




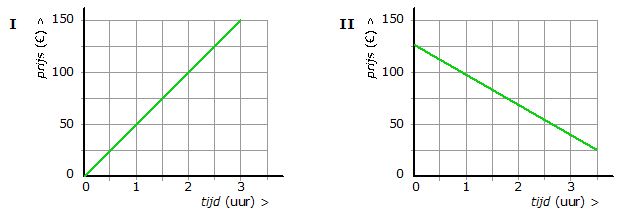

 Maak de volgende opgaven.
Maak de volgende opgaven.


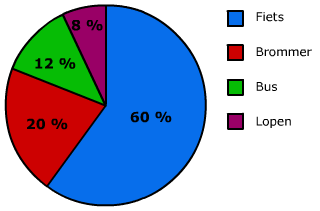







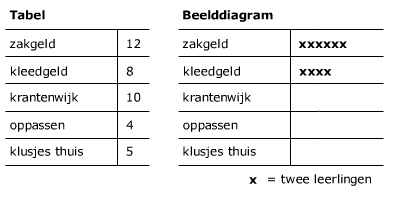
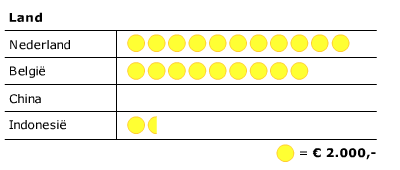
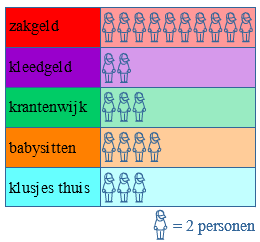

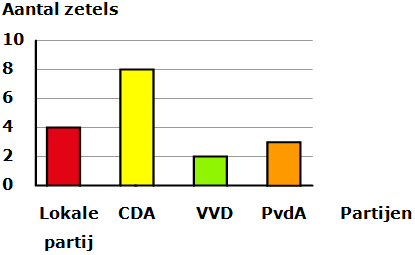
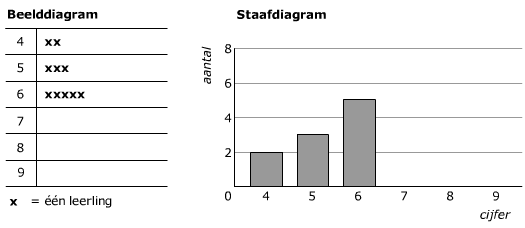



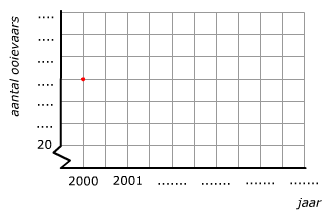


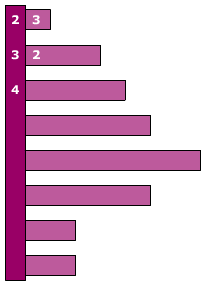
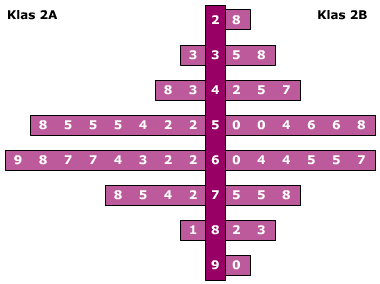

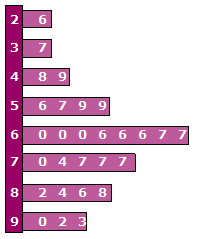
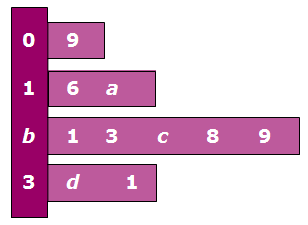
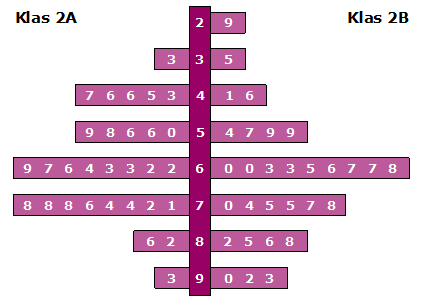
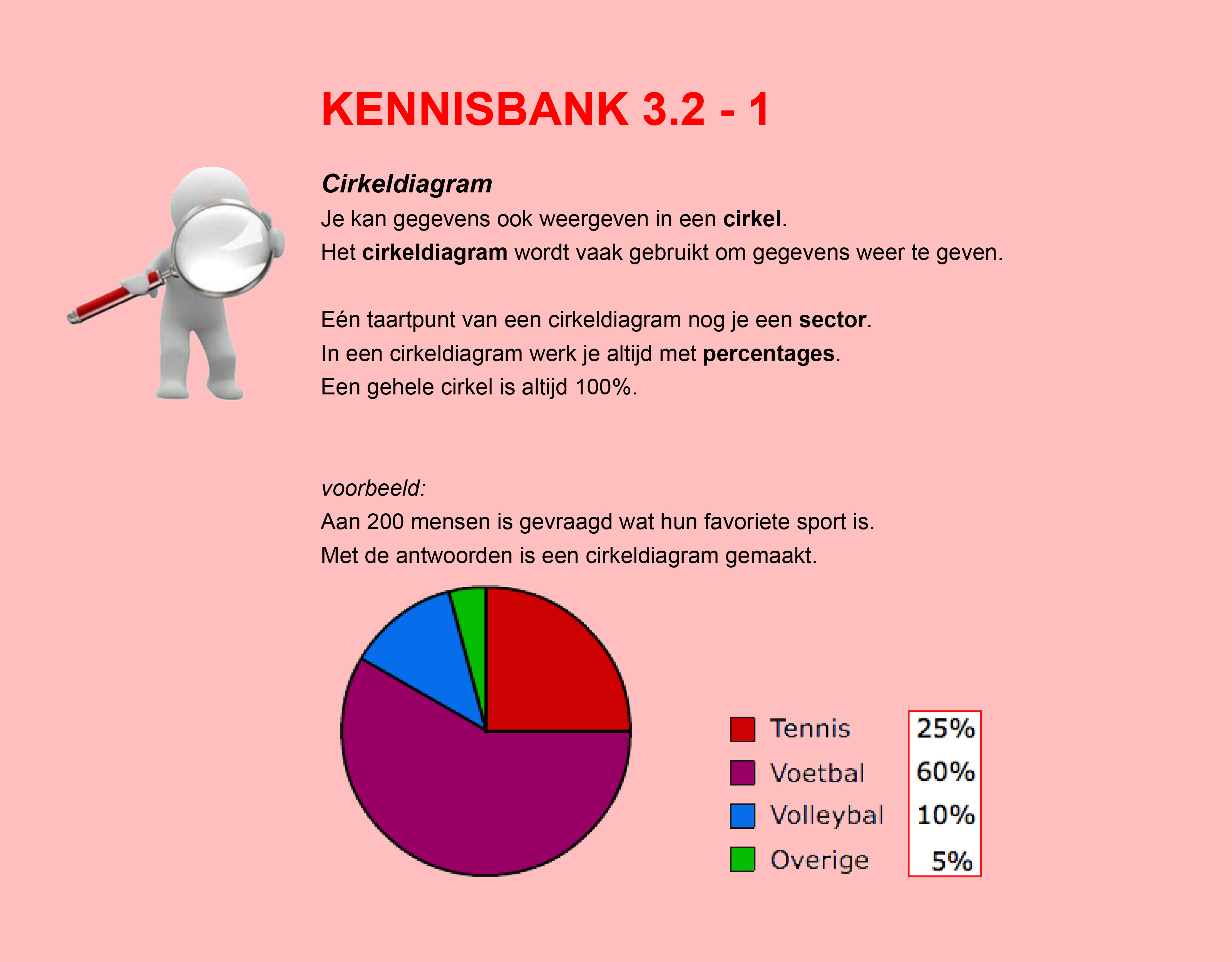





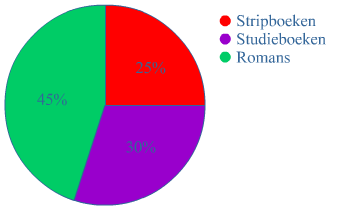
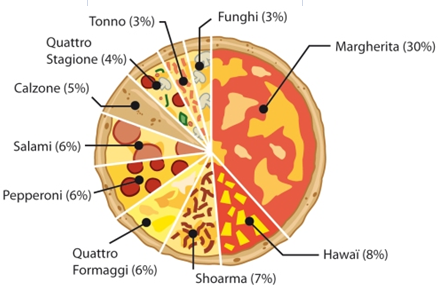
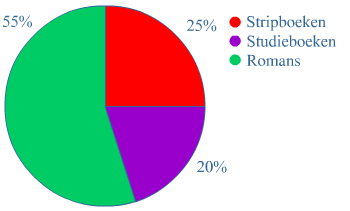

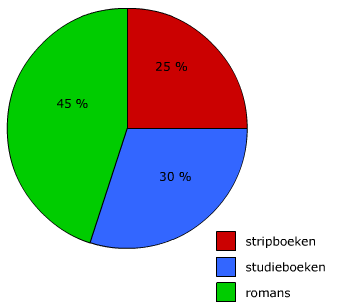
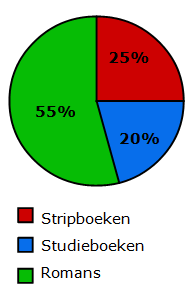

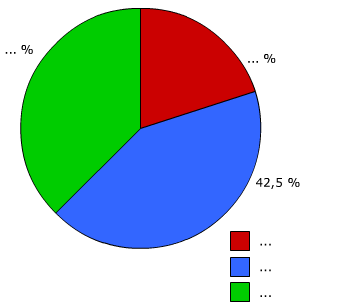
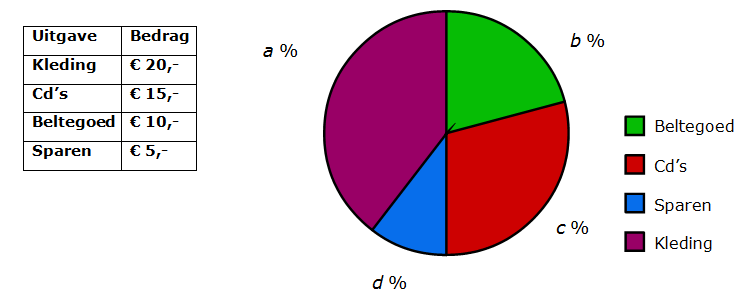


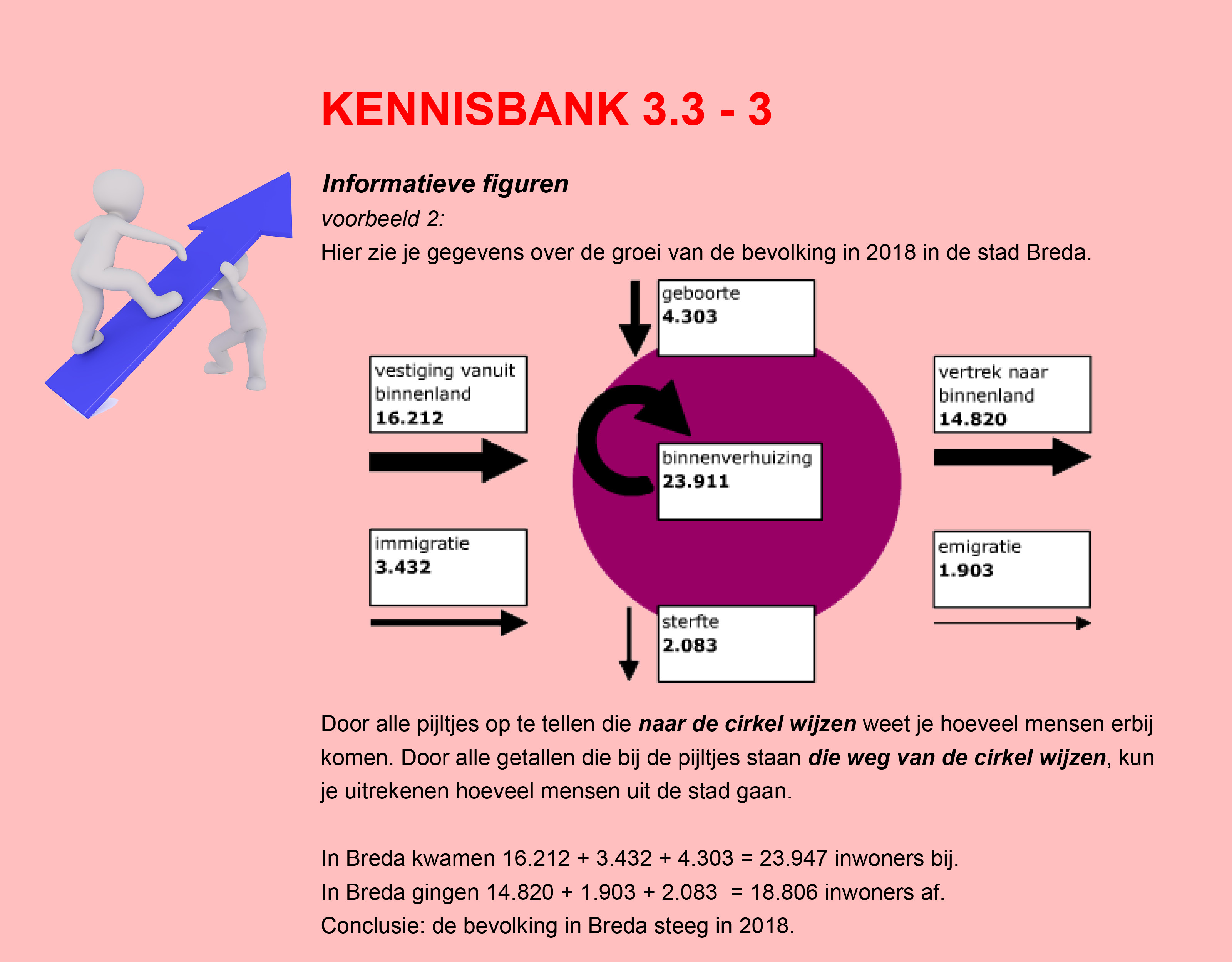


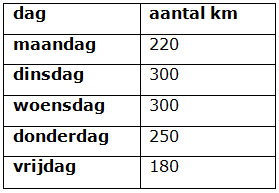


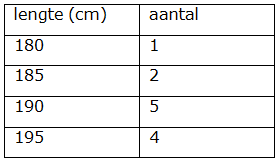
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Maak de volgende opgaven.
Maak de volgende opgaven.


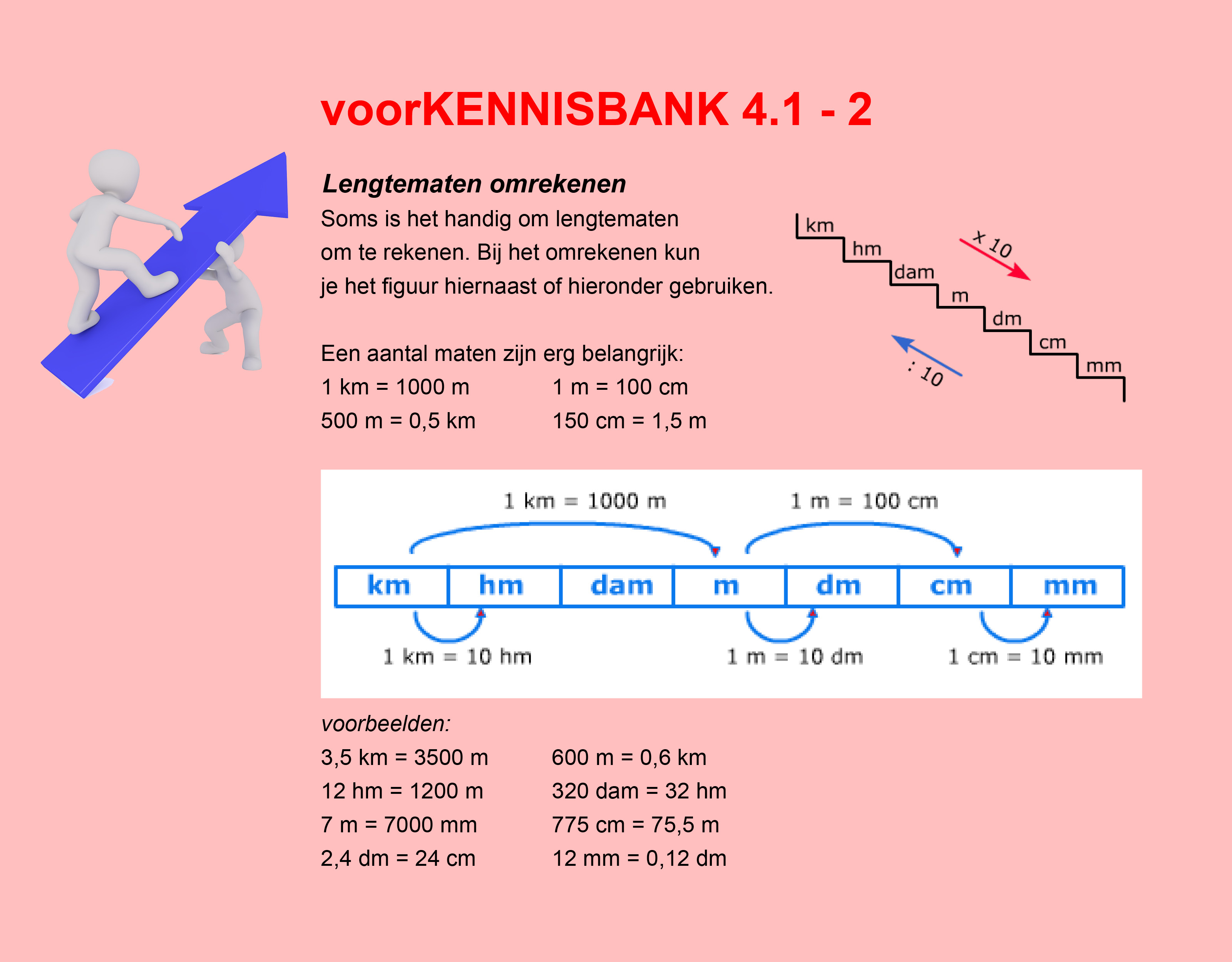


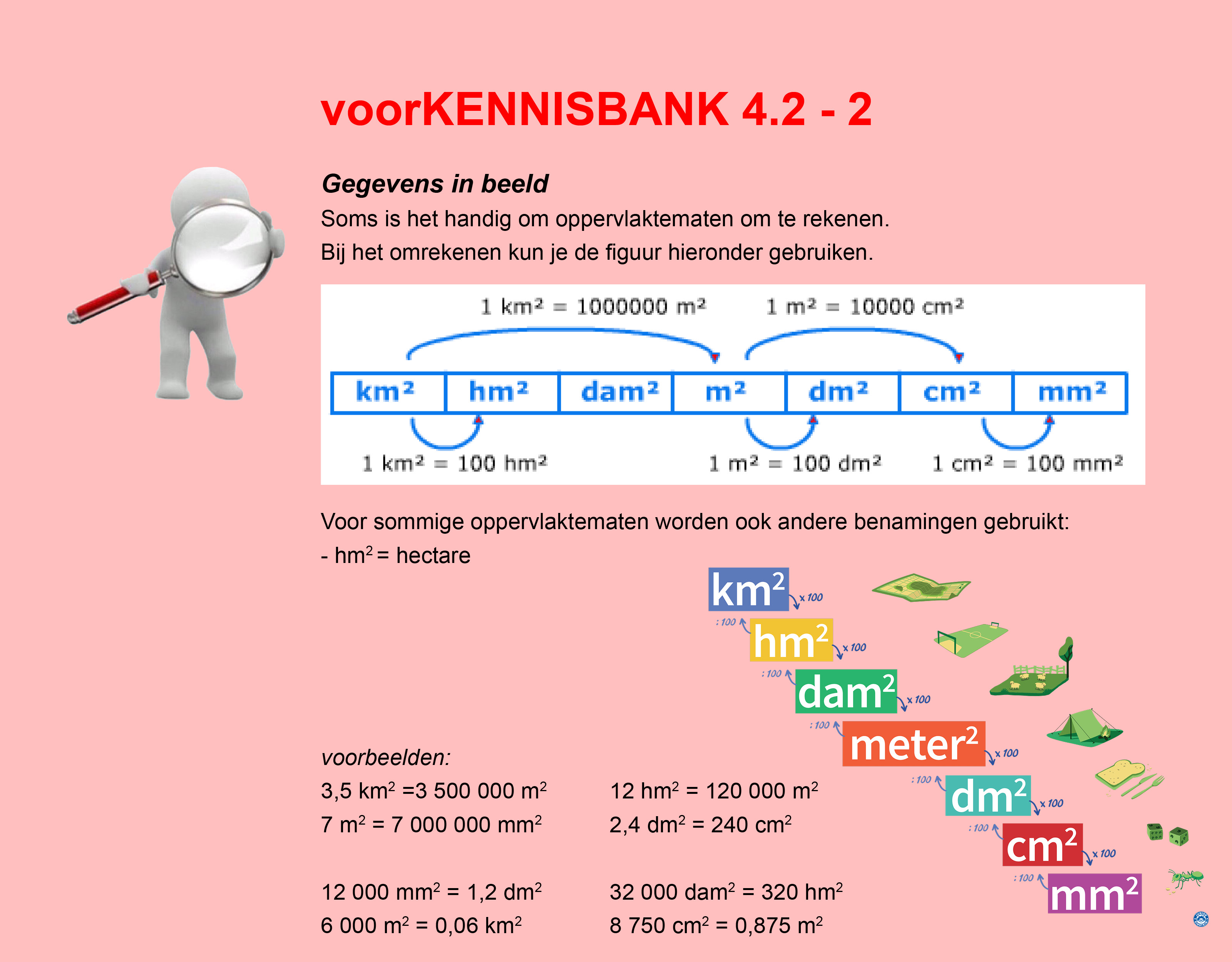



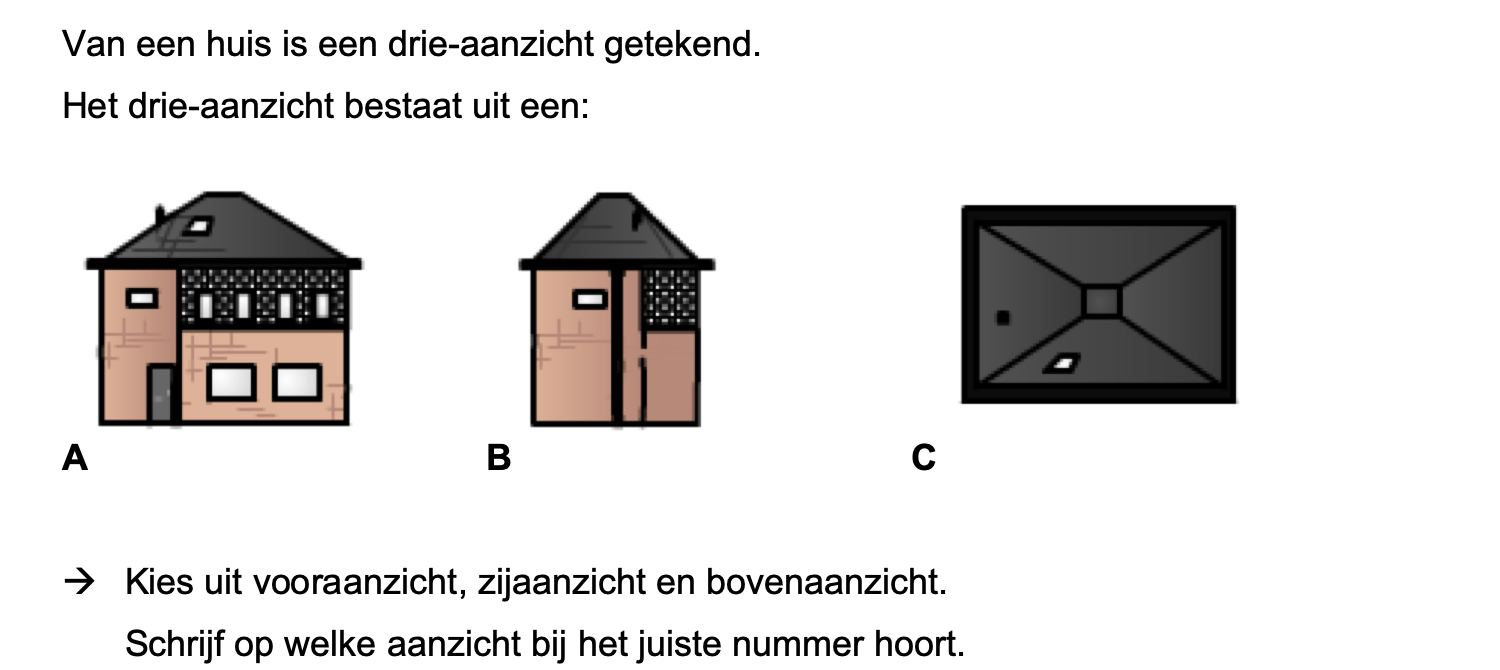

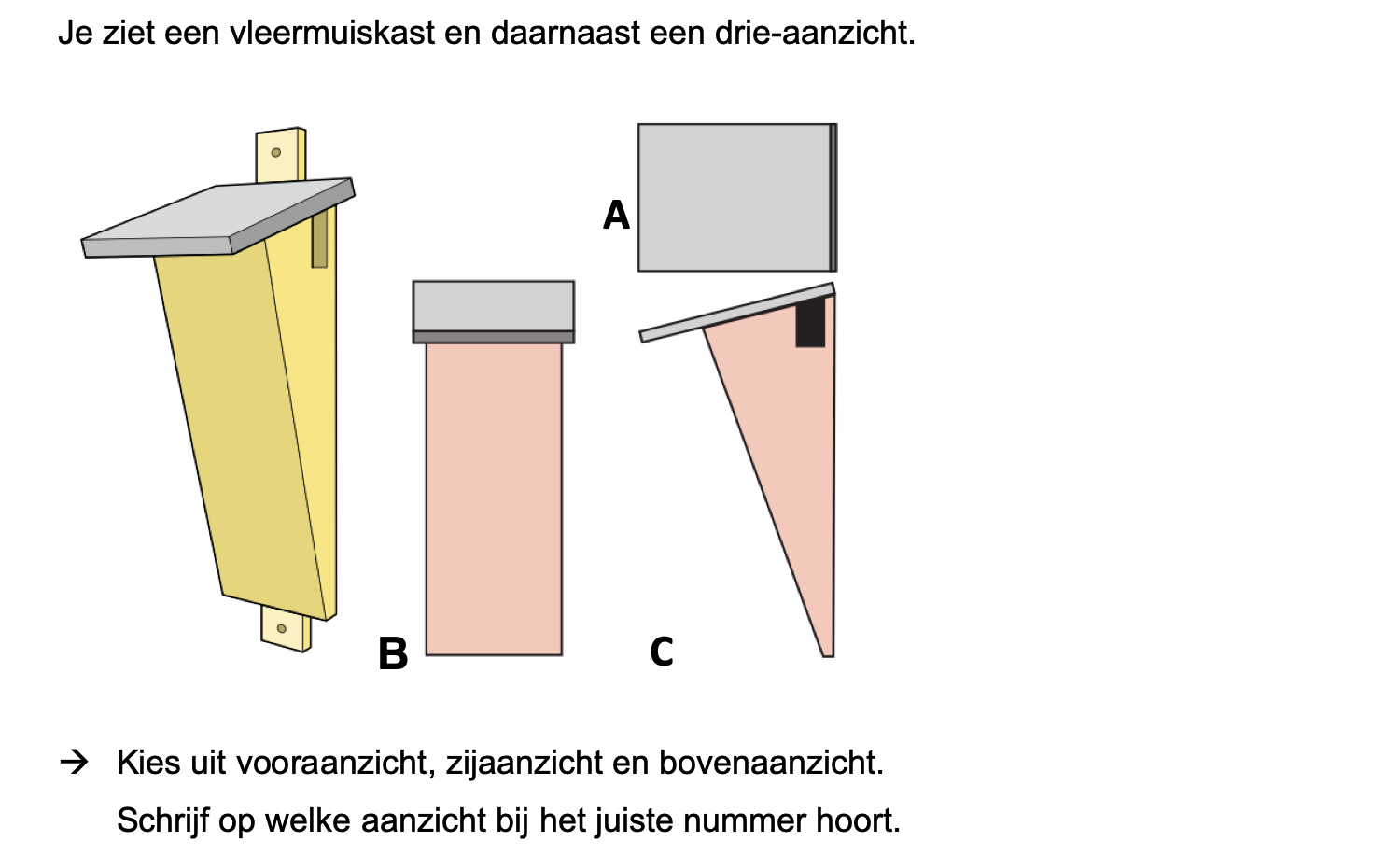
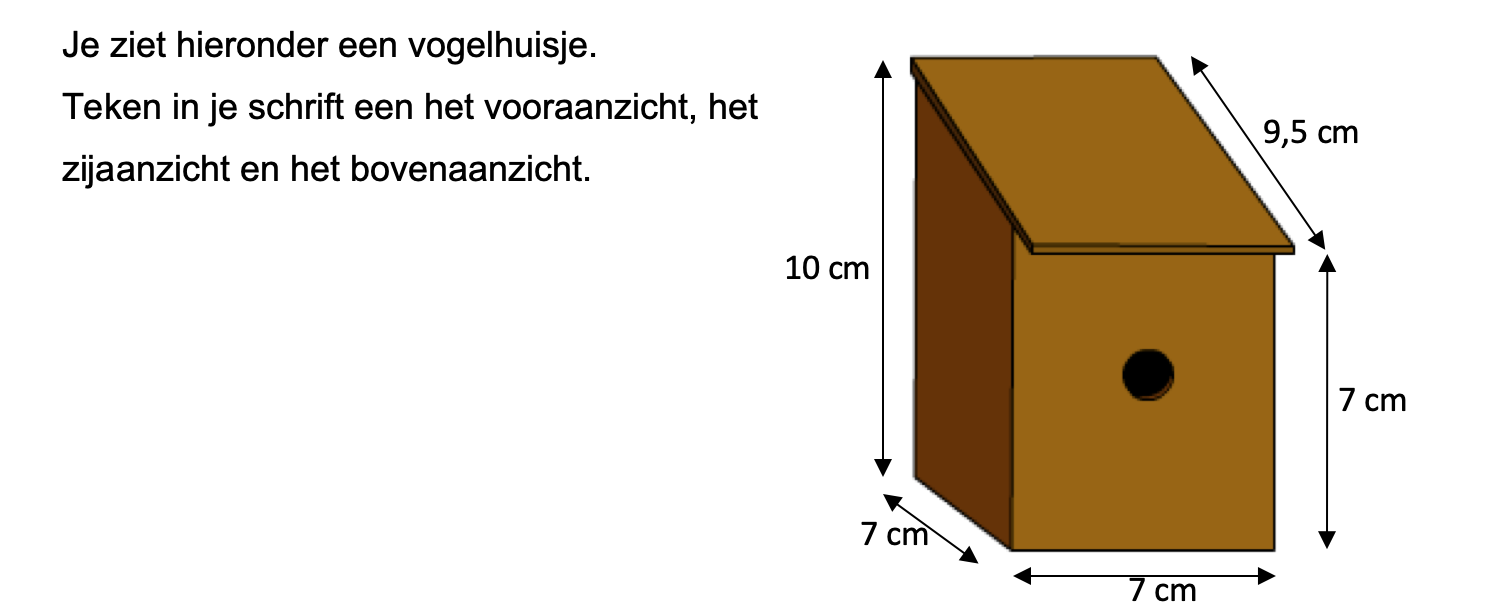


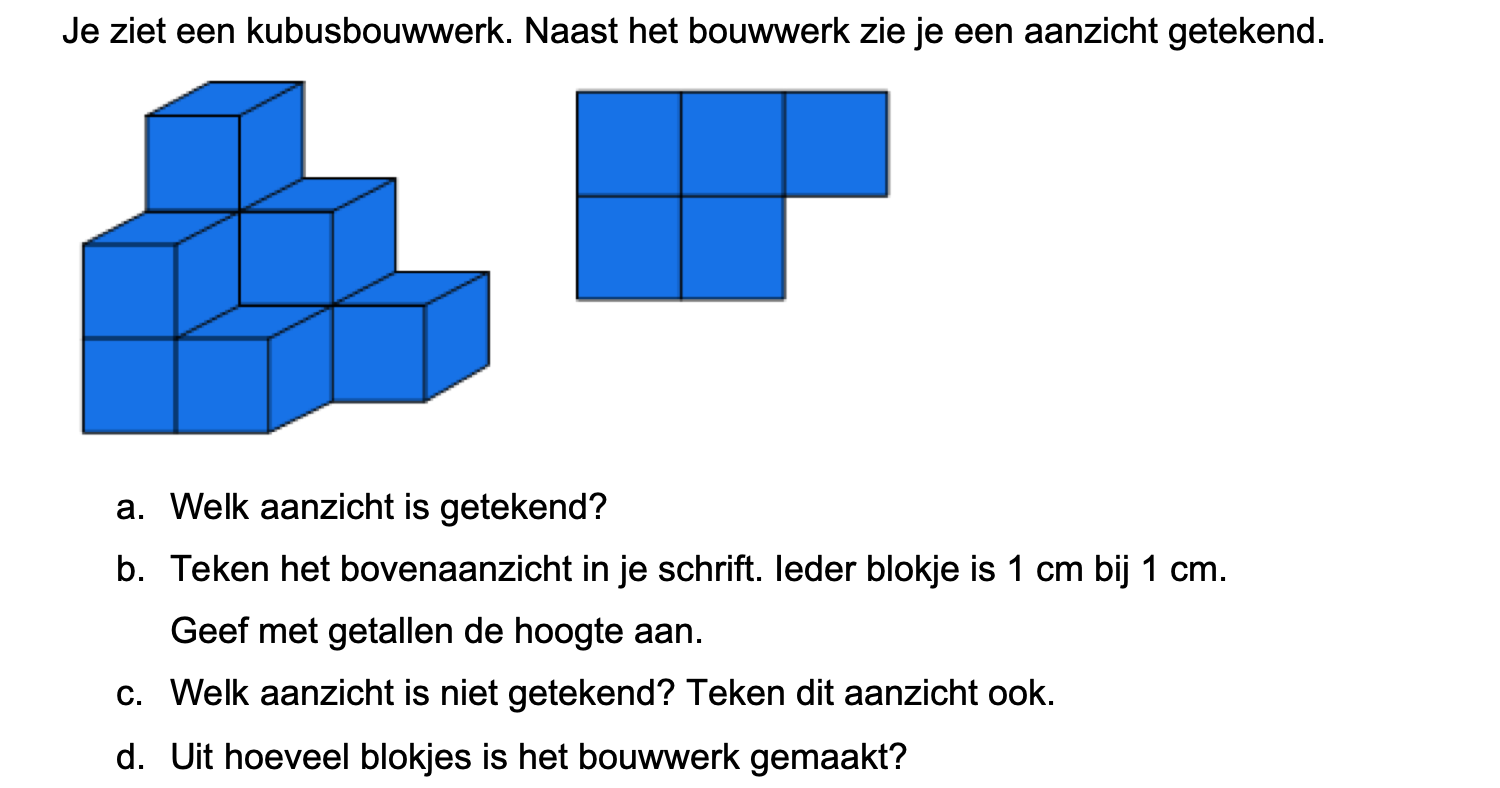
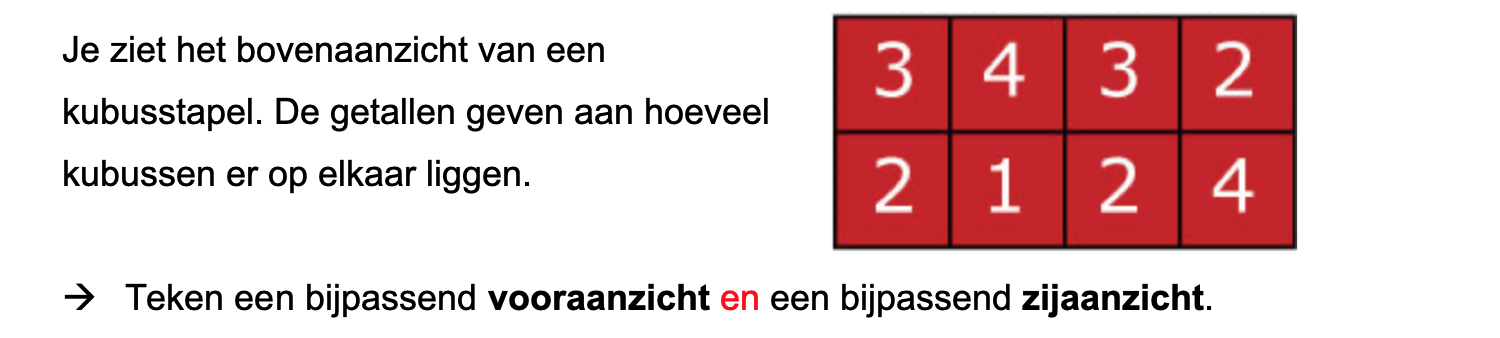
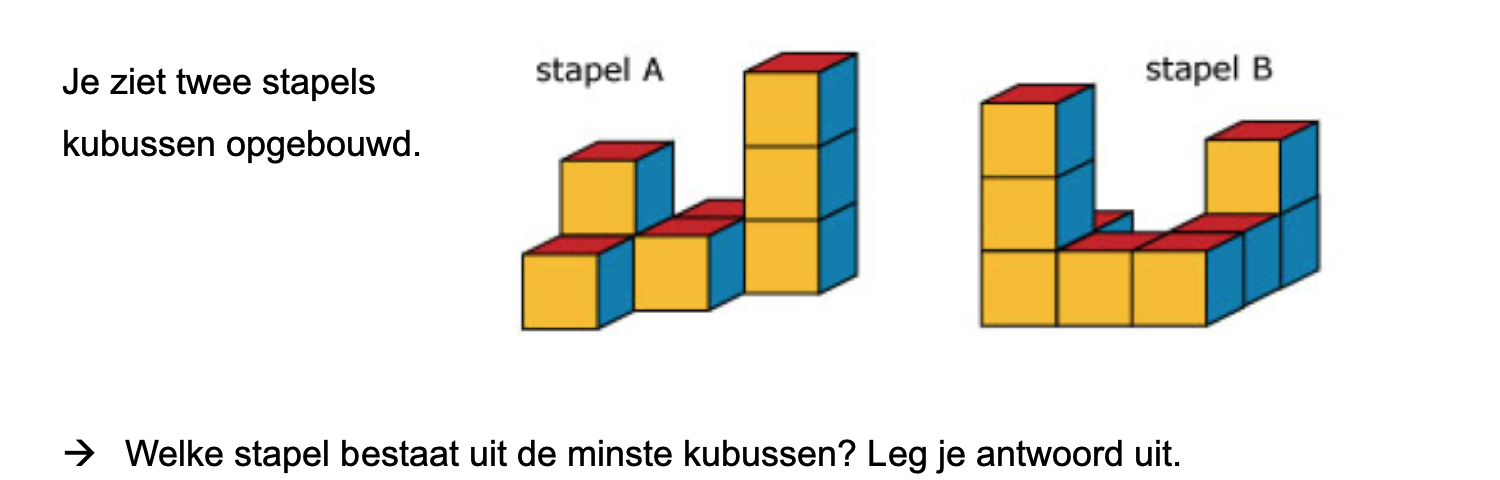
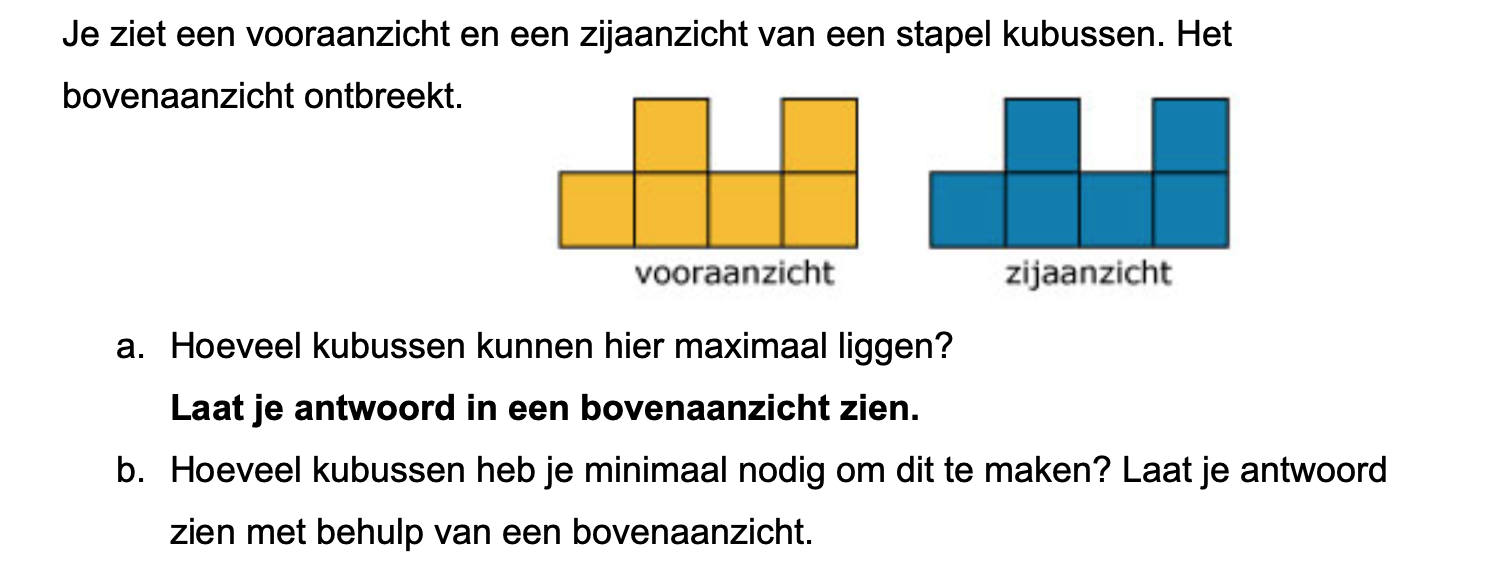
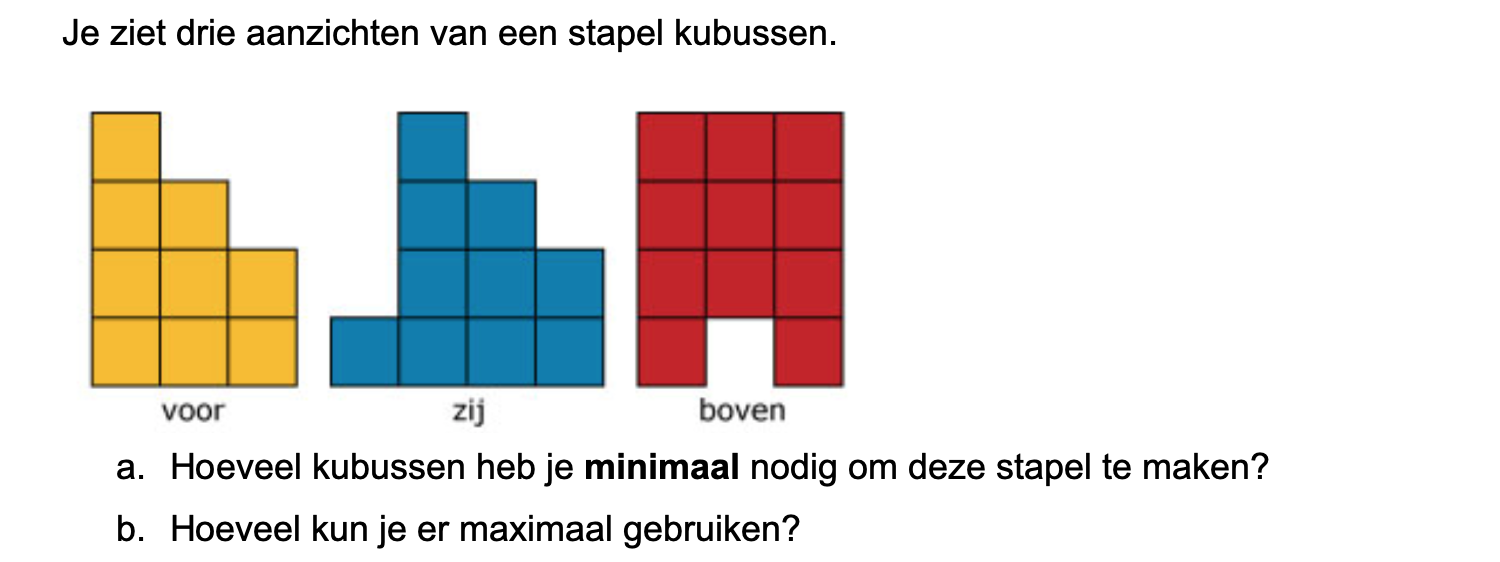
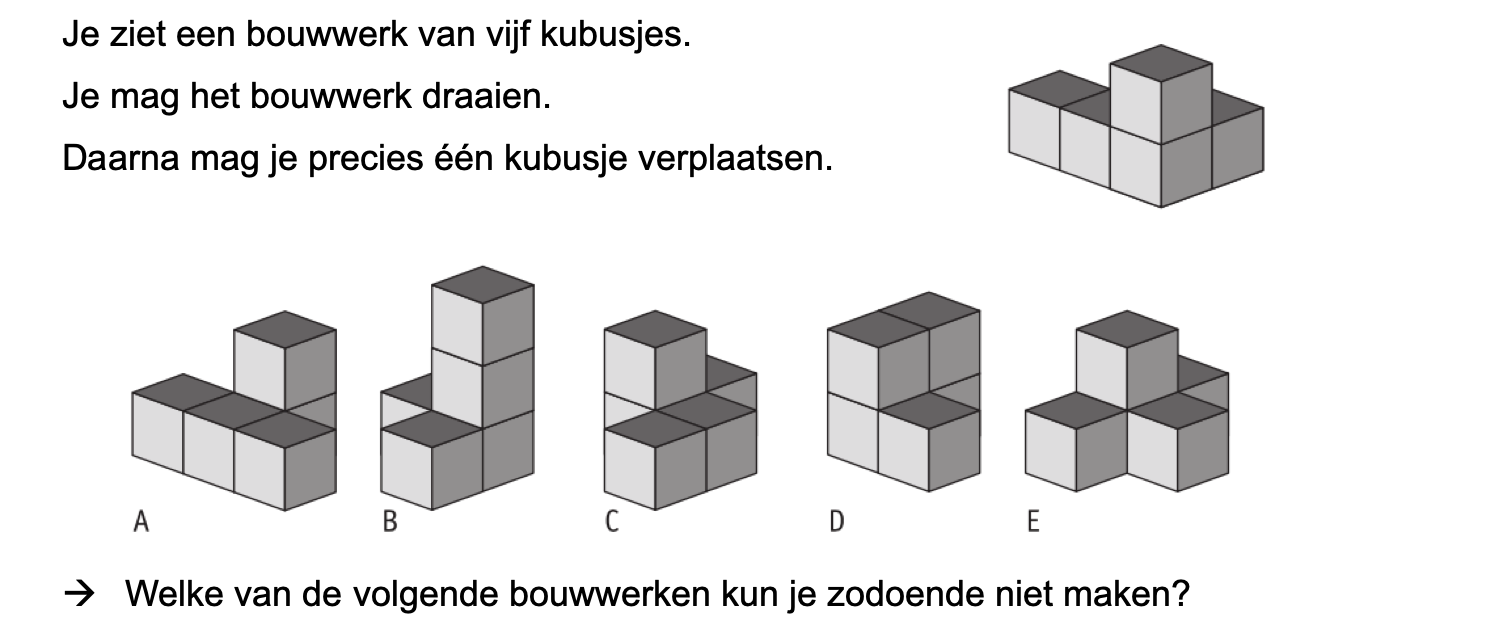



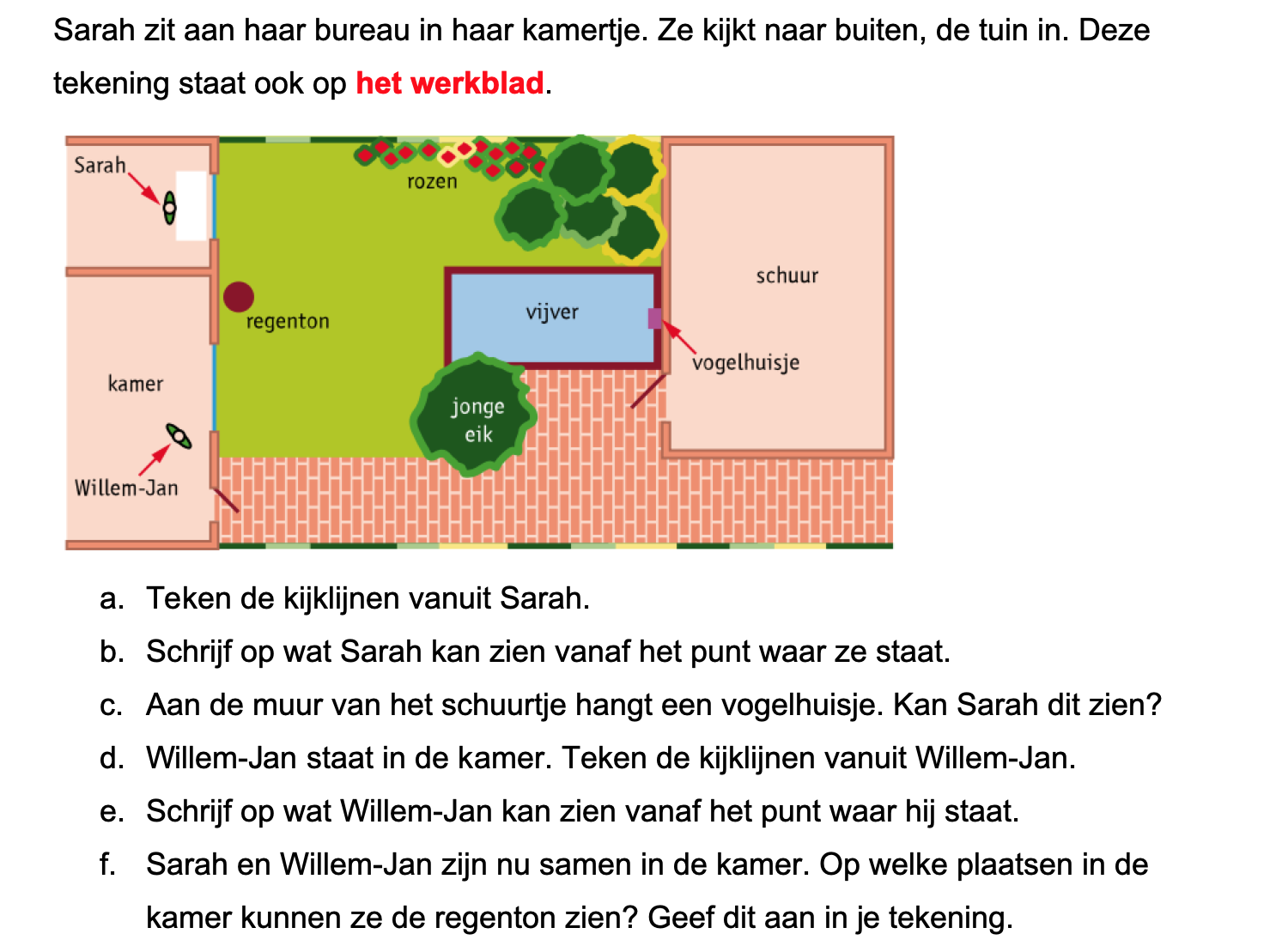
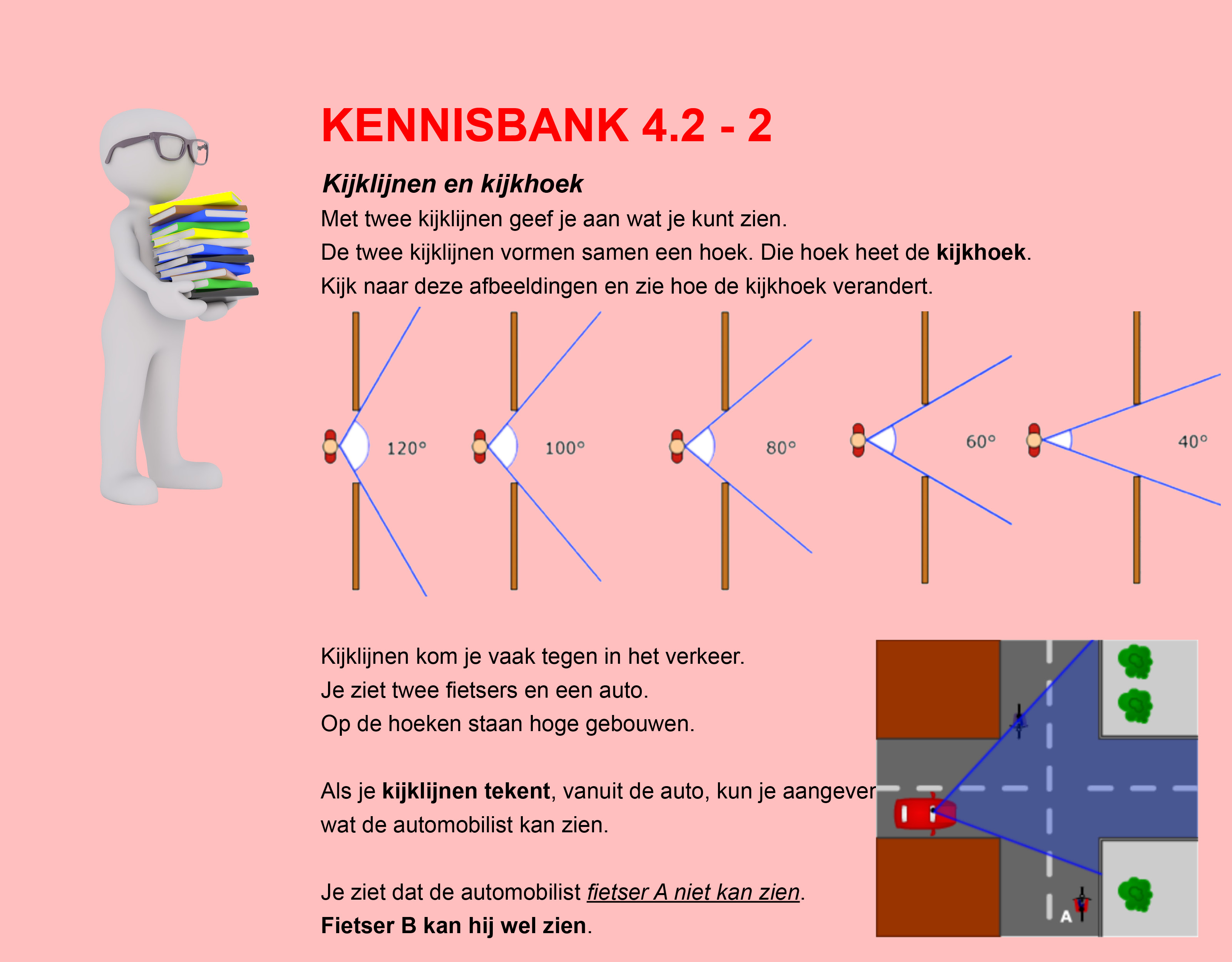
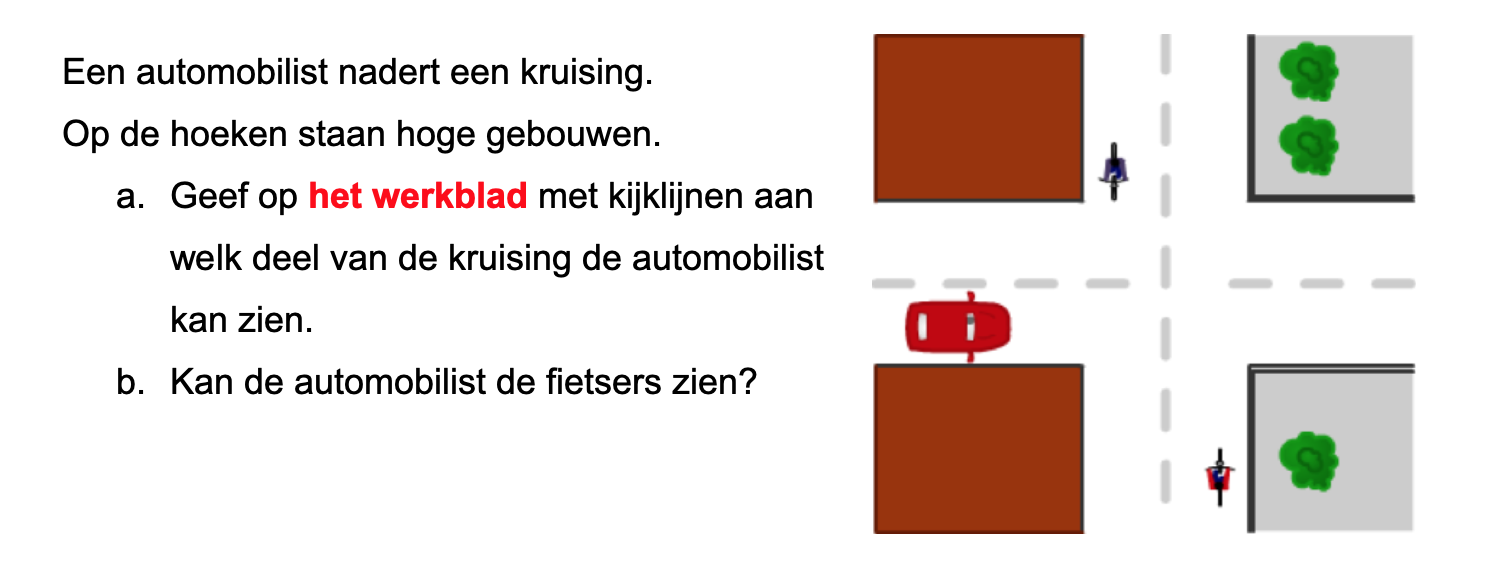
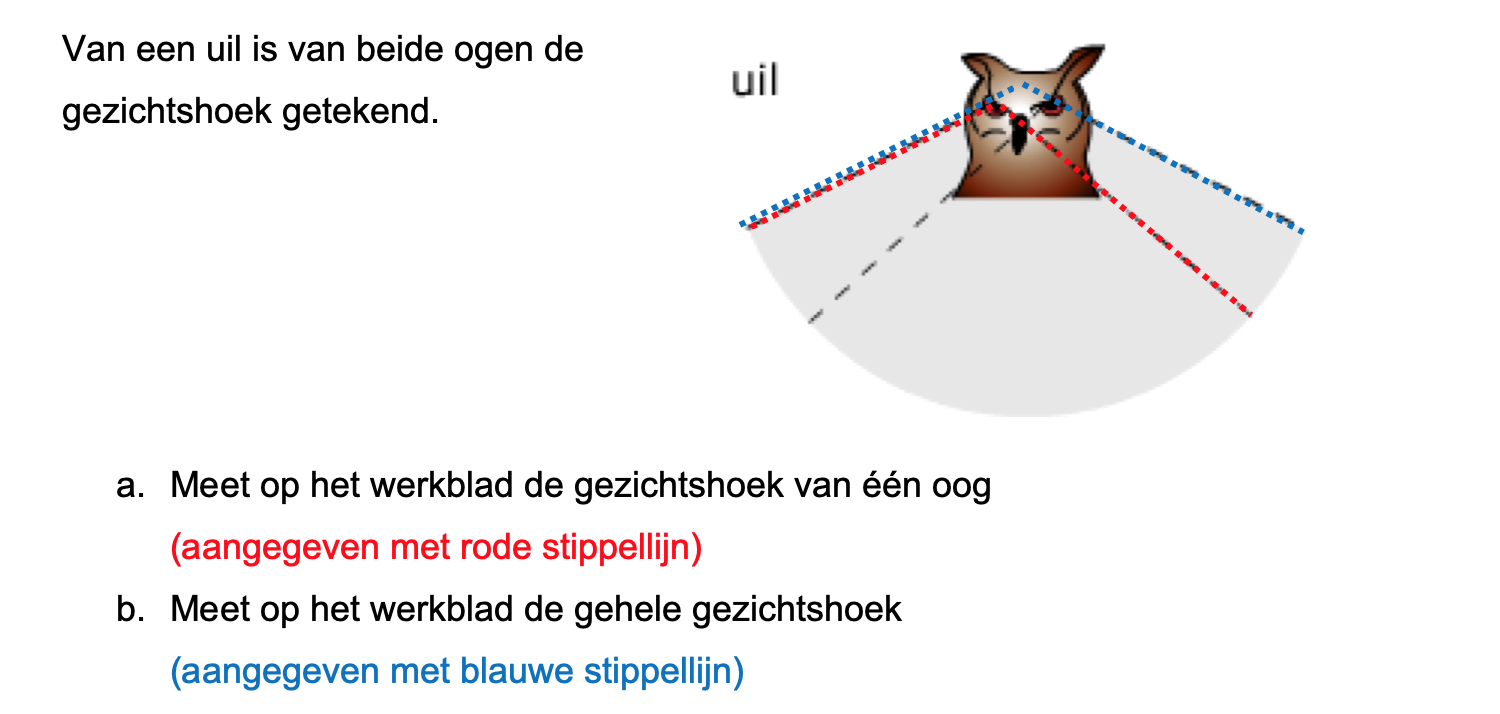
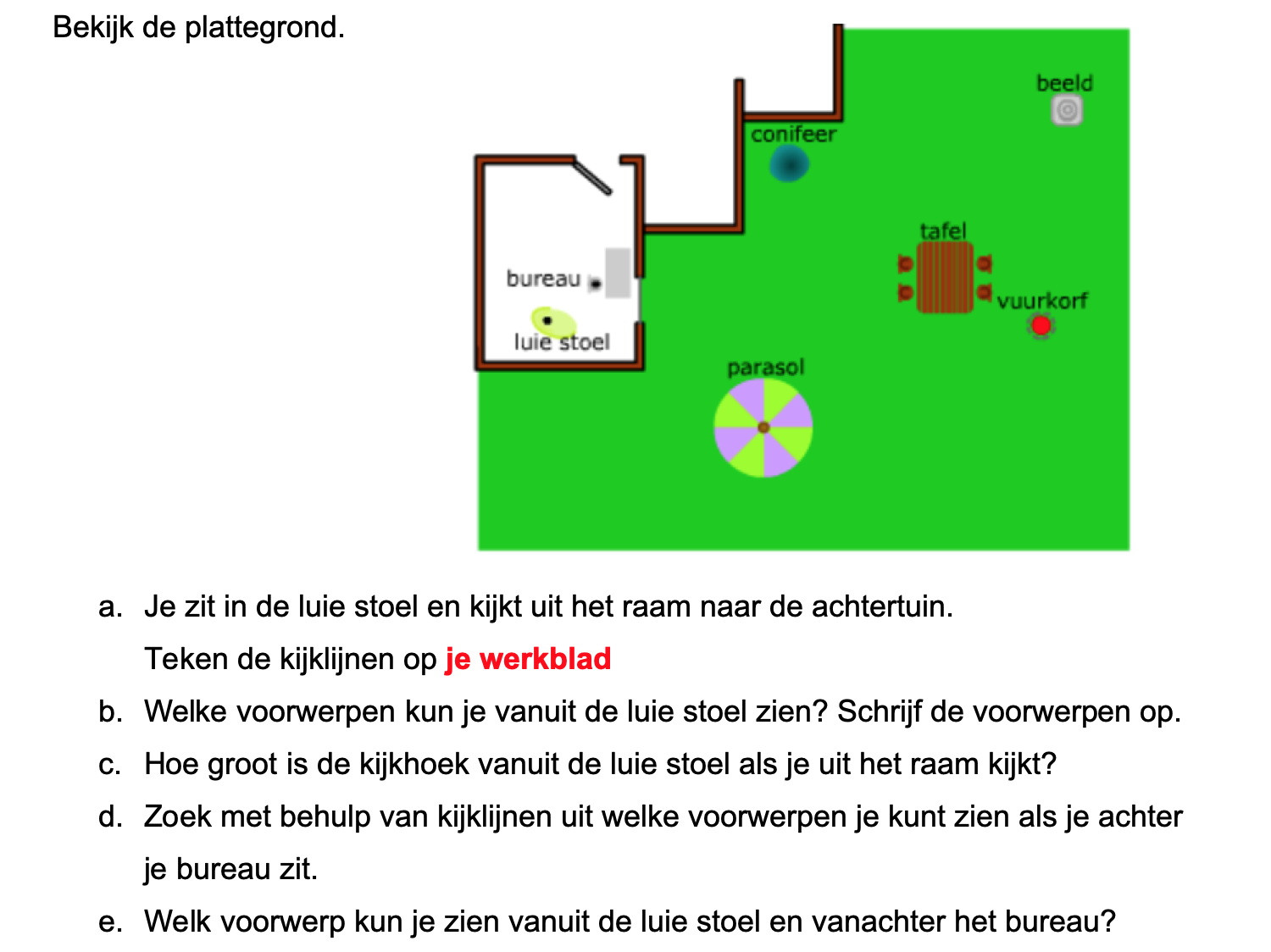
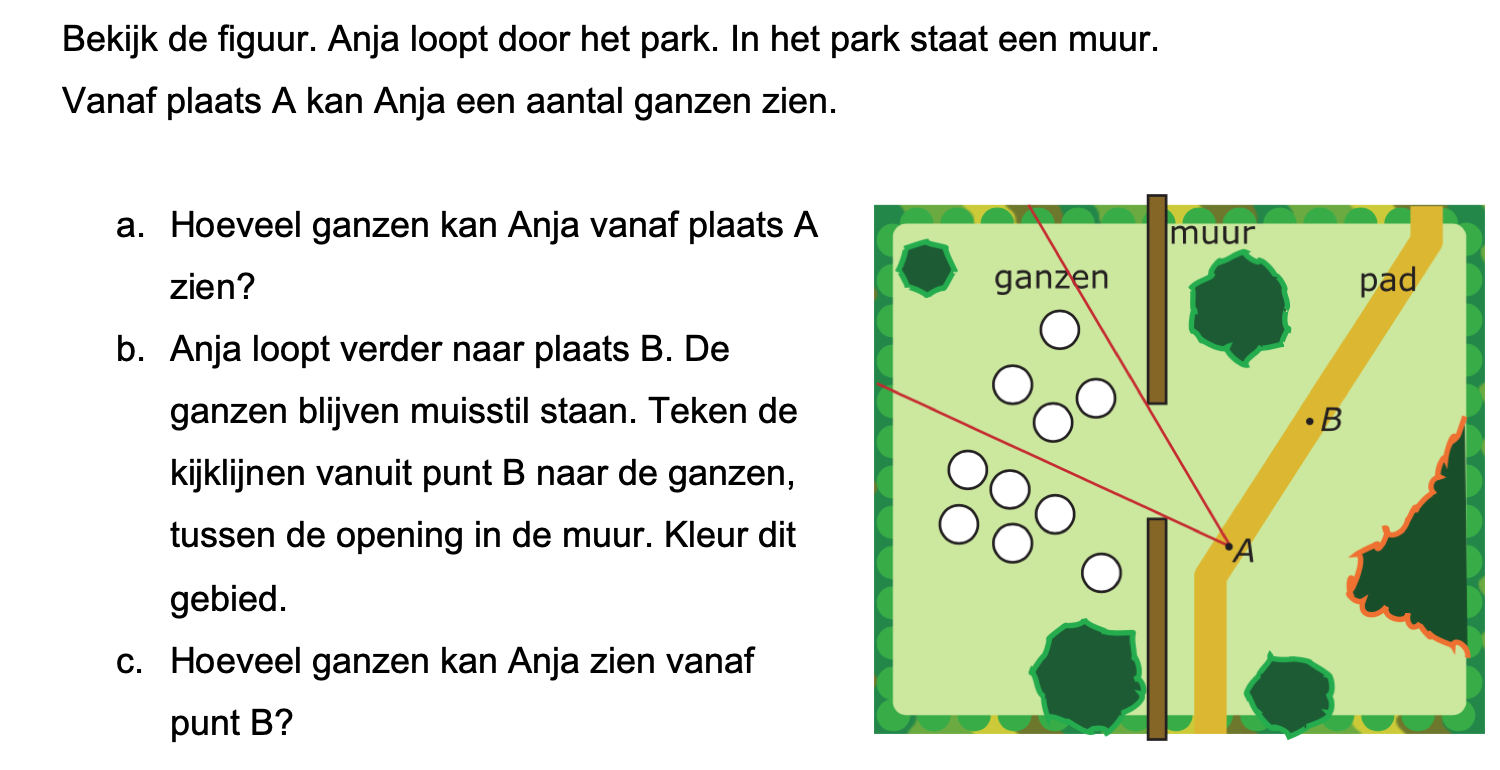
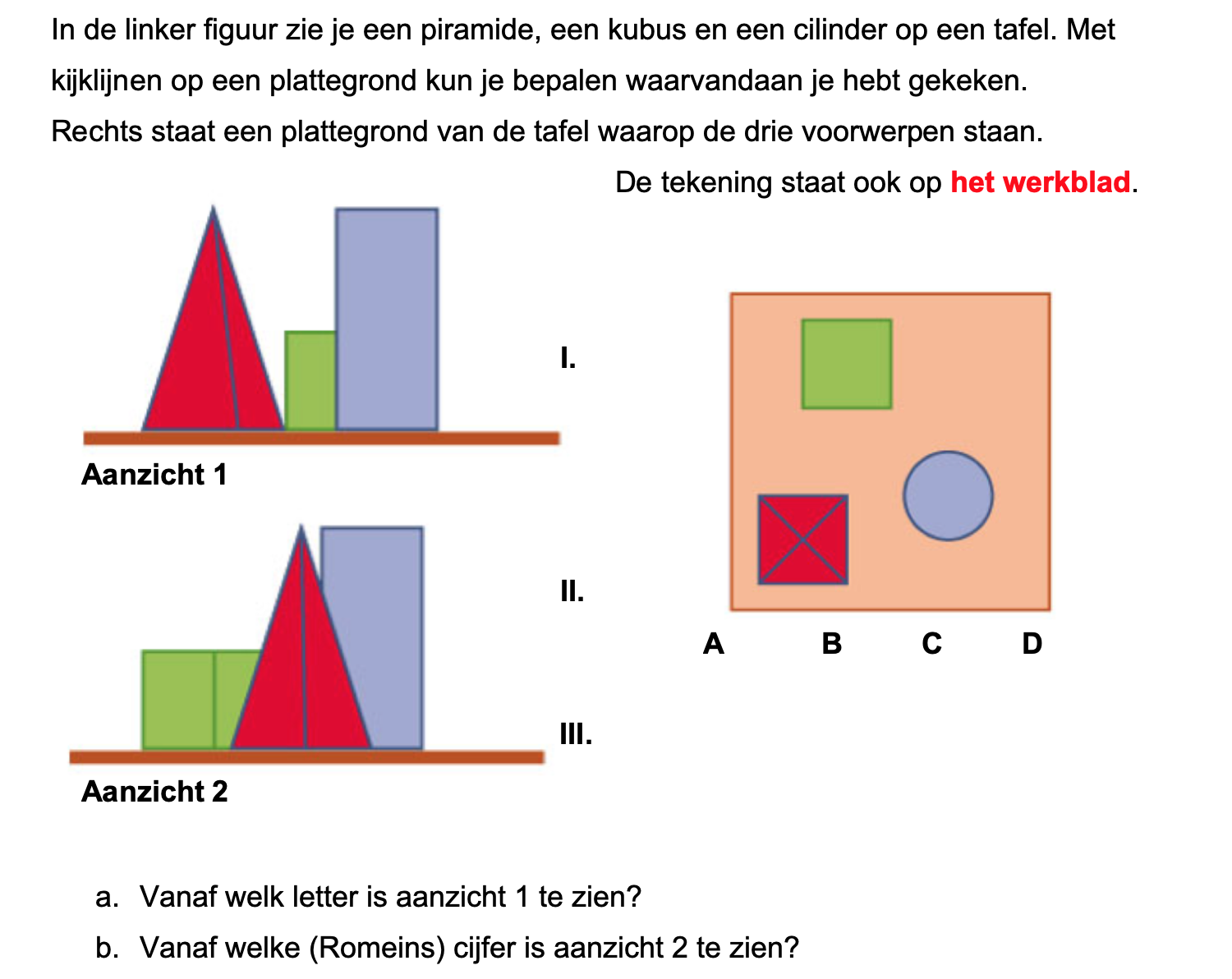

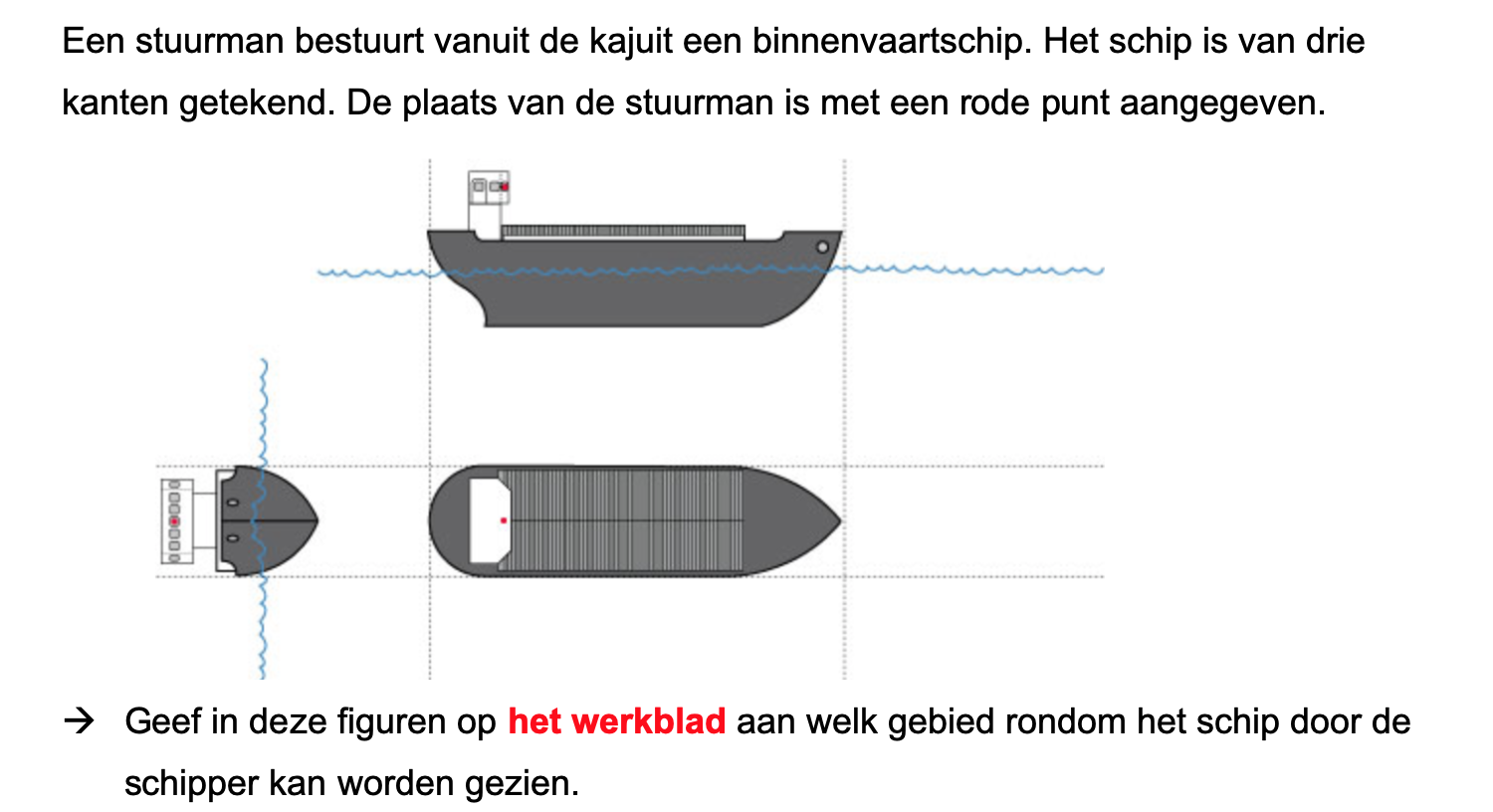
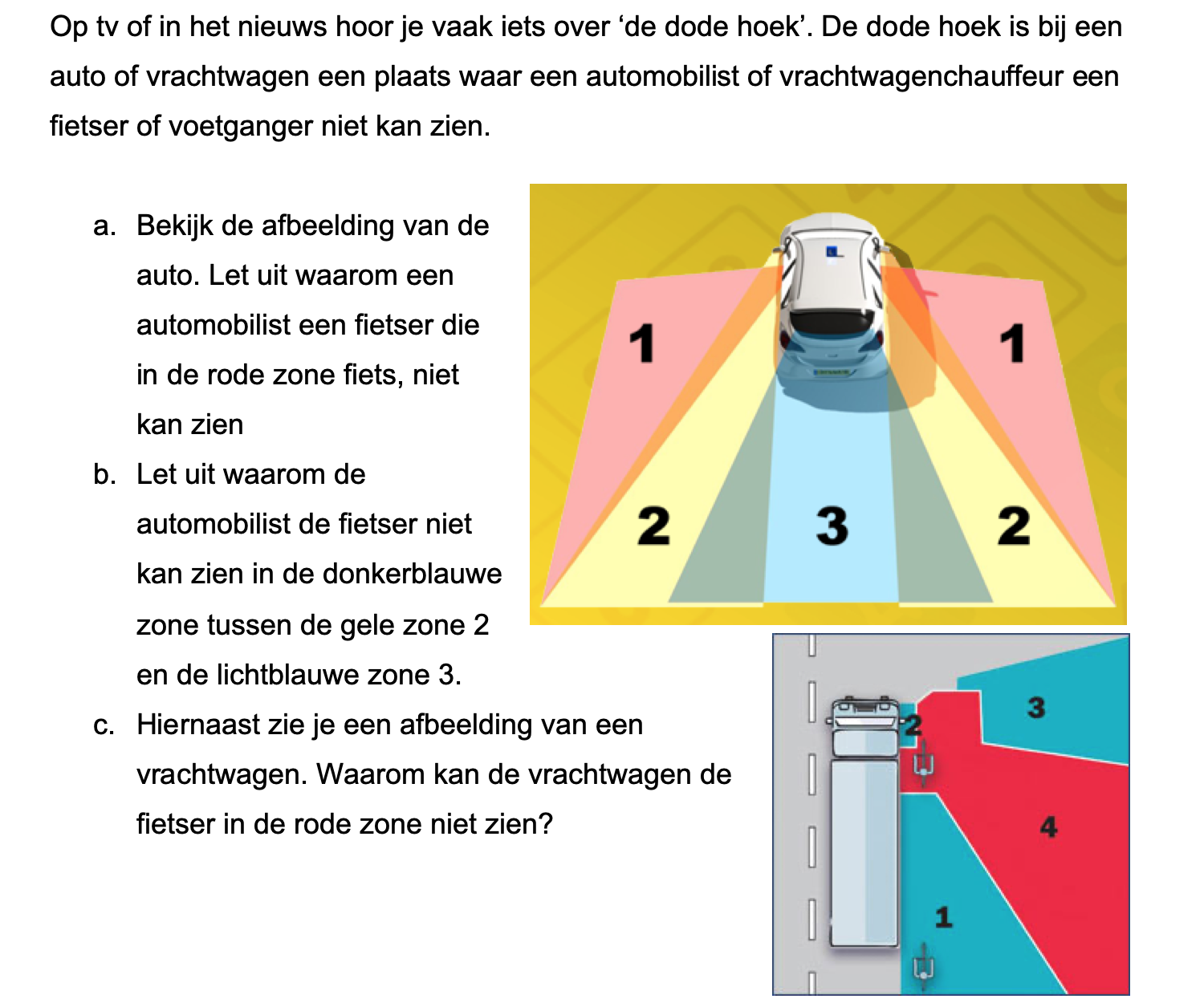
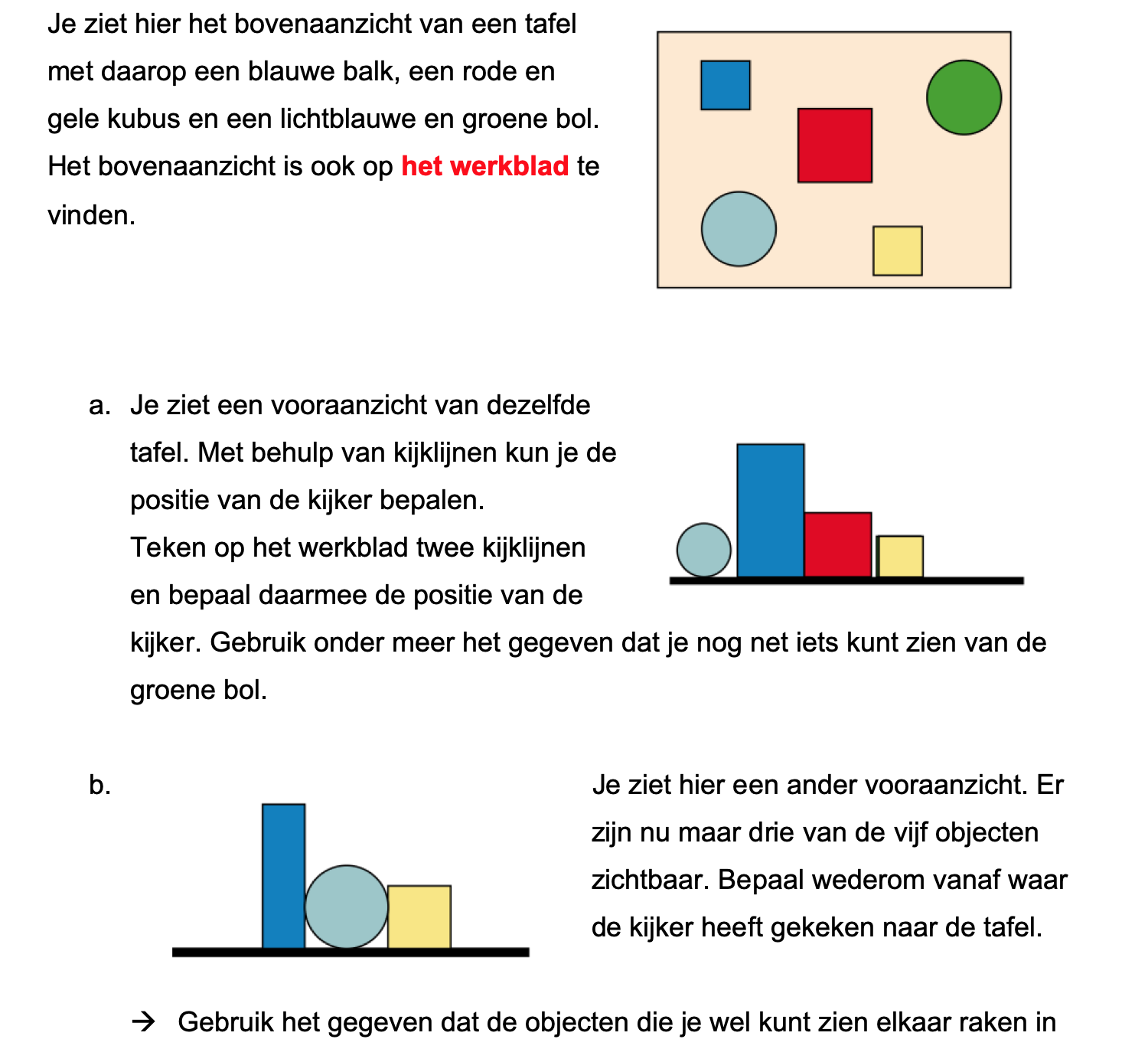
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
 Maak de volgende opgaven.
Maak de volgende opgaven.














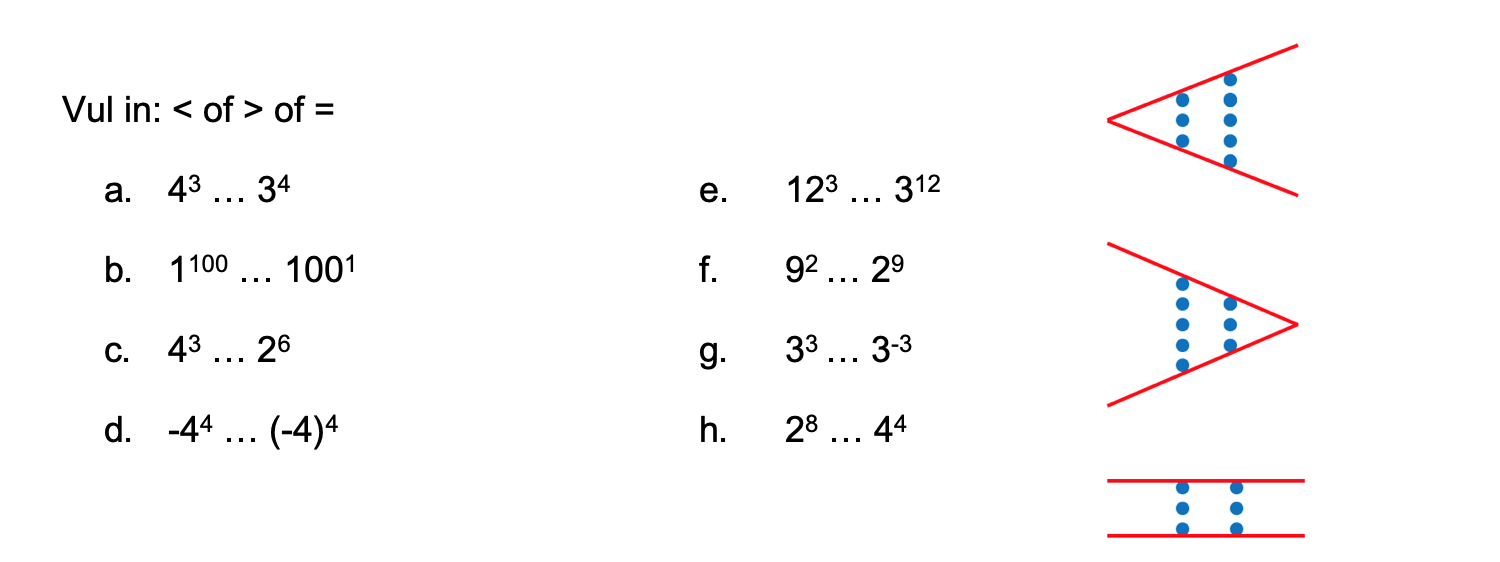
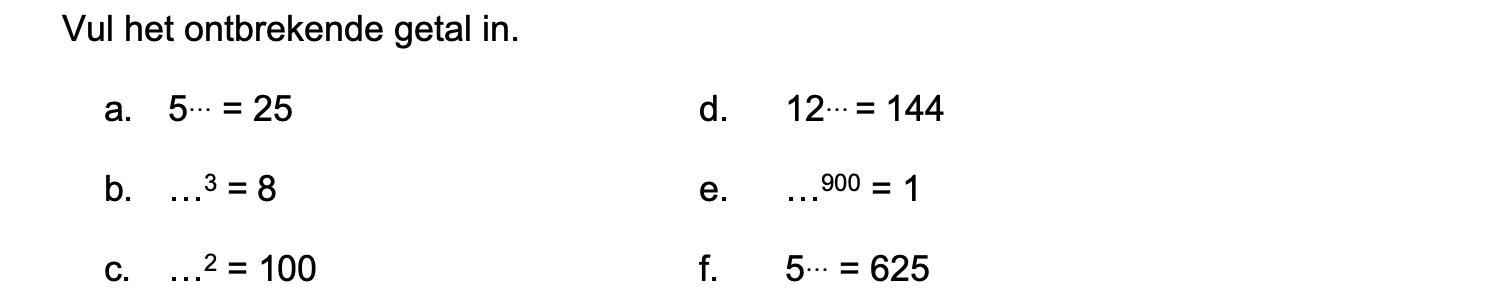


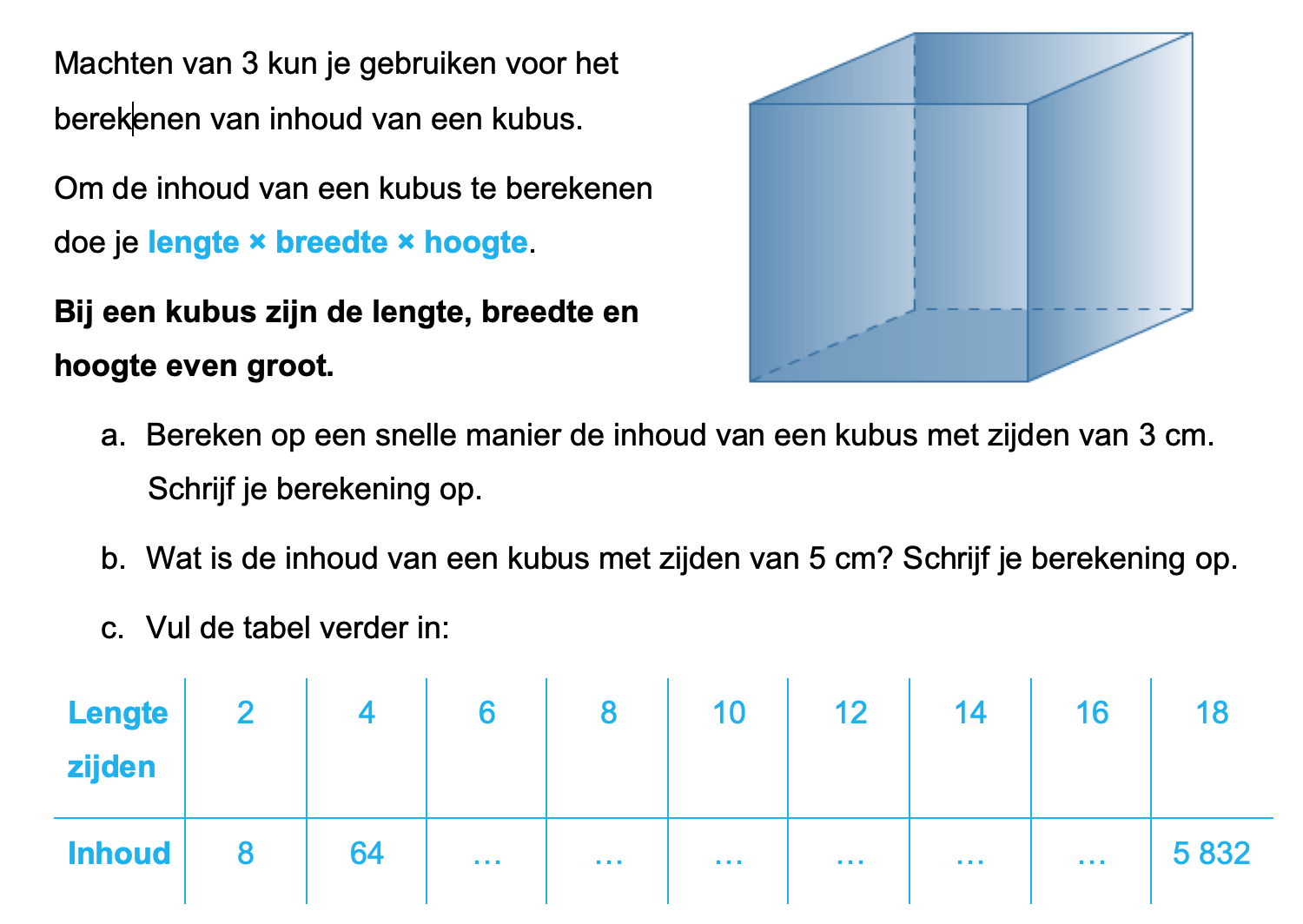

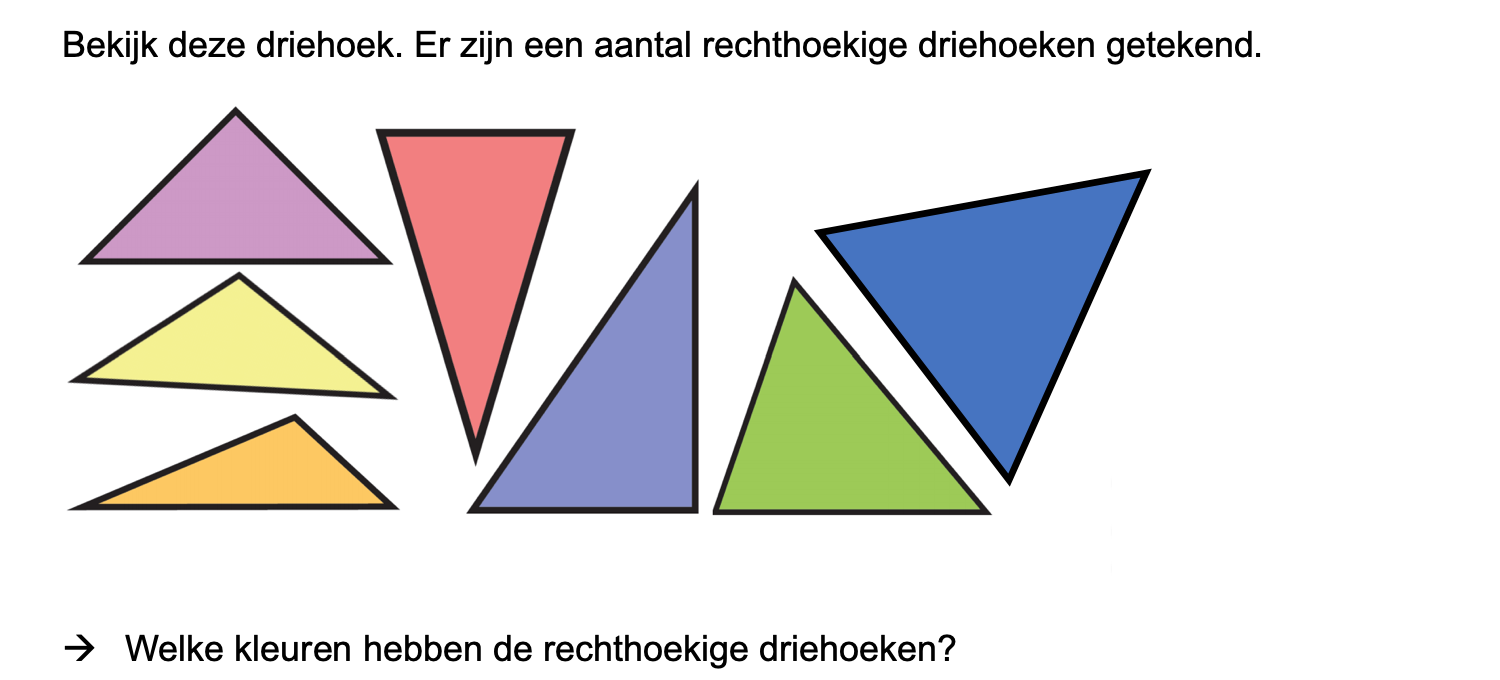
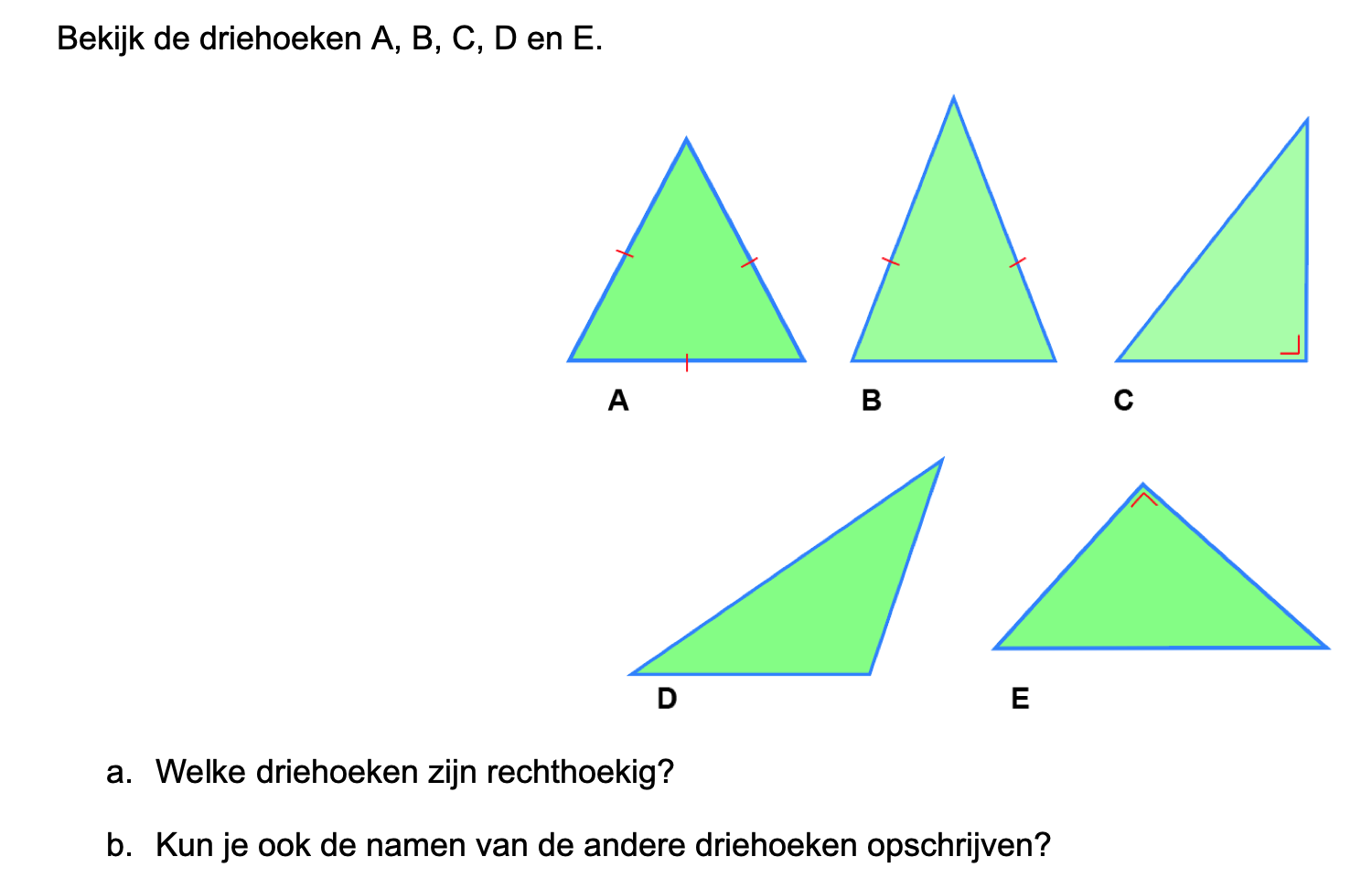

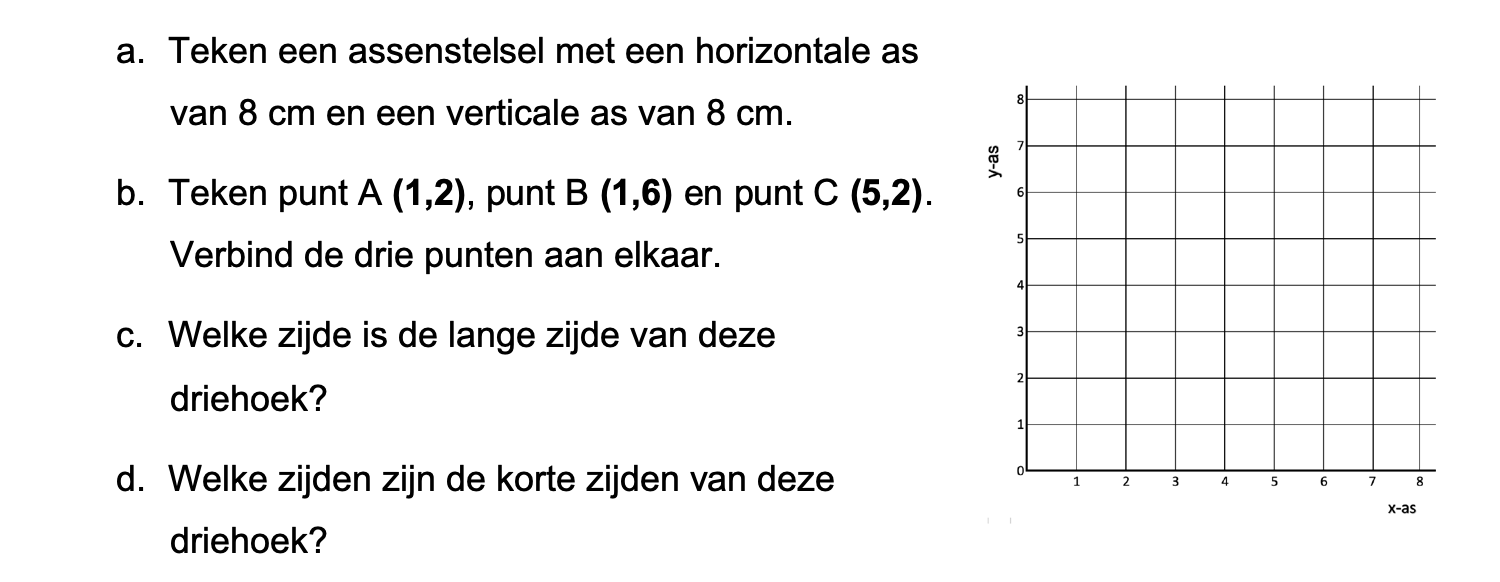


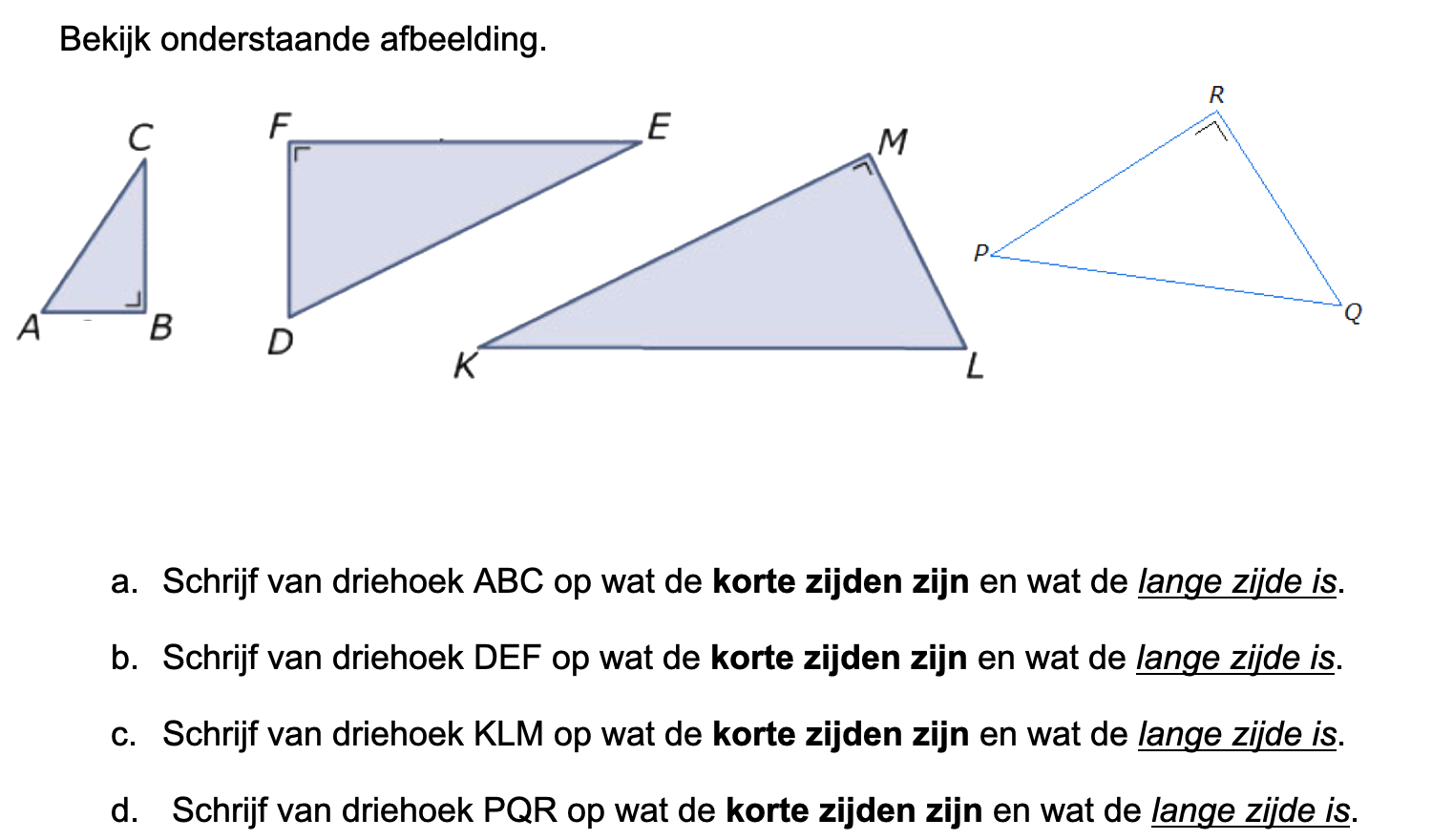
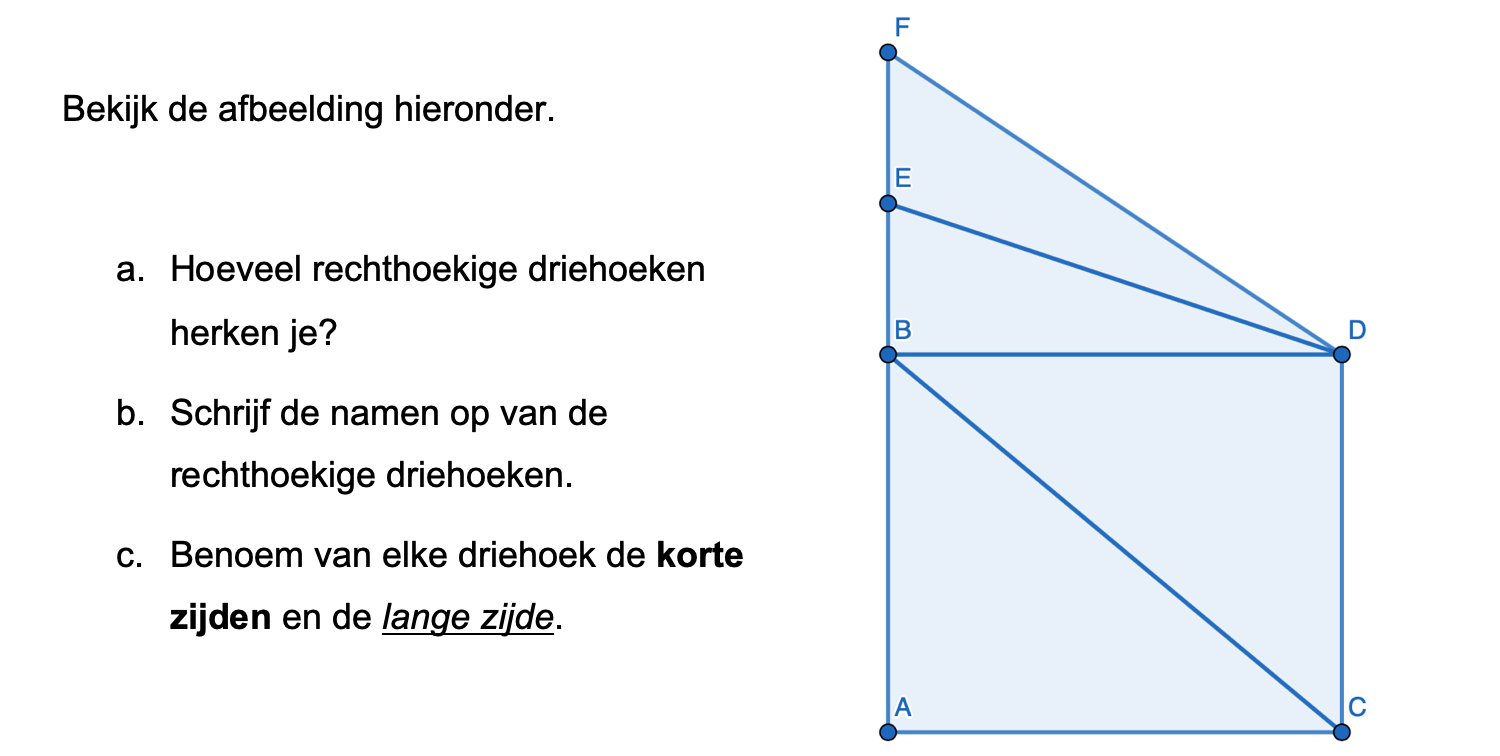


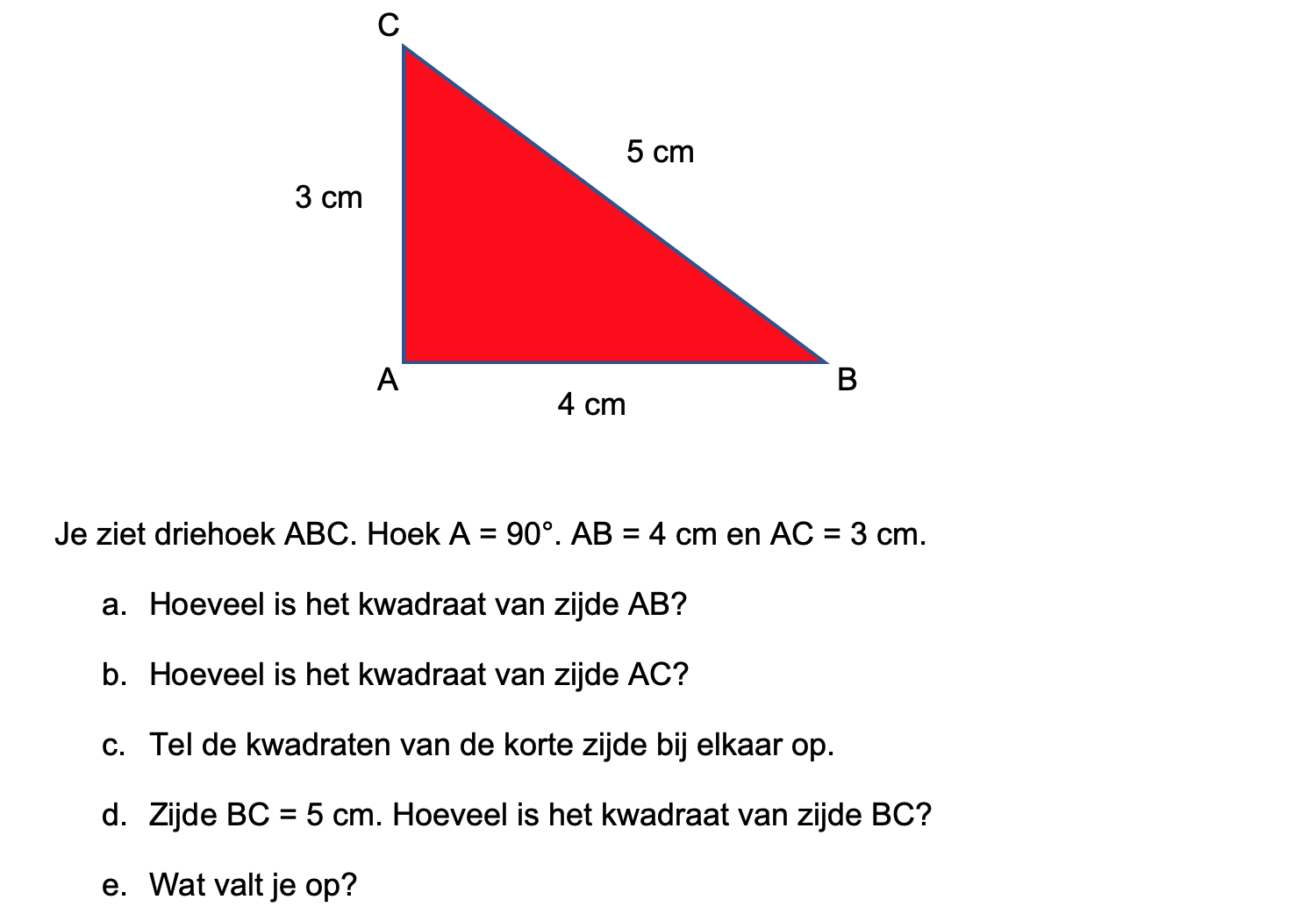
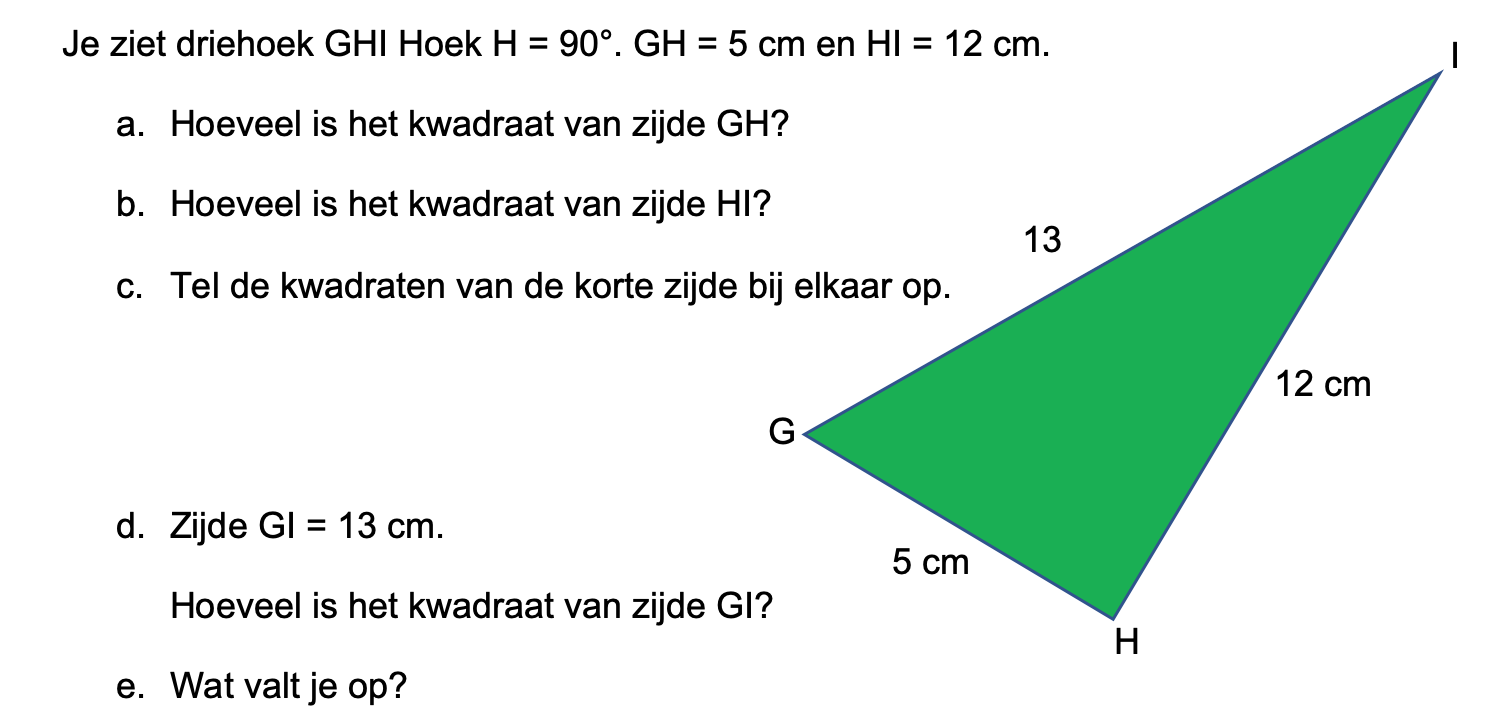
 \
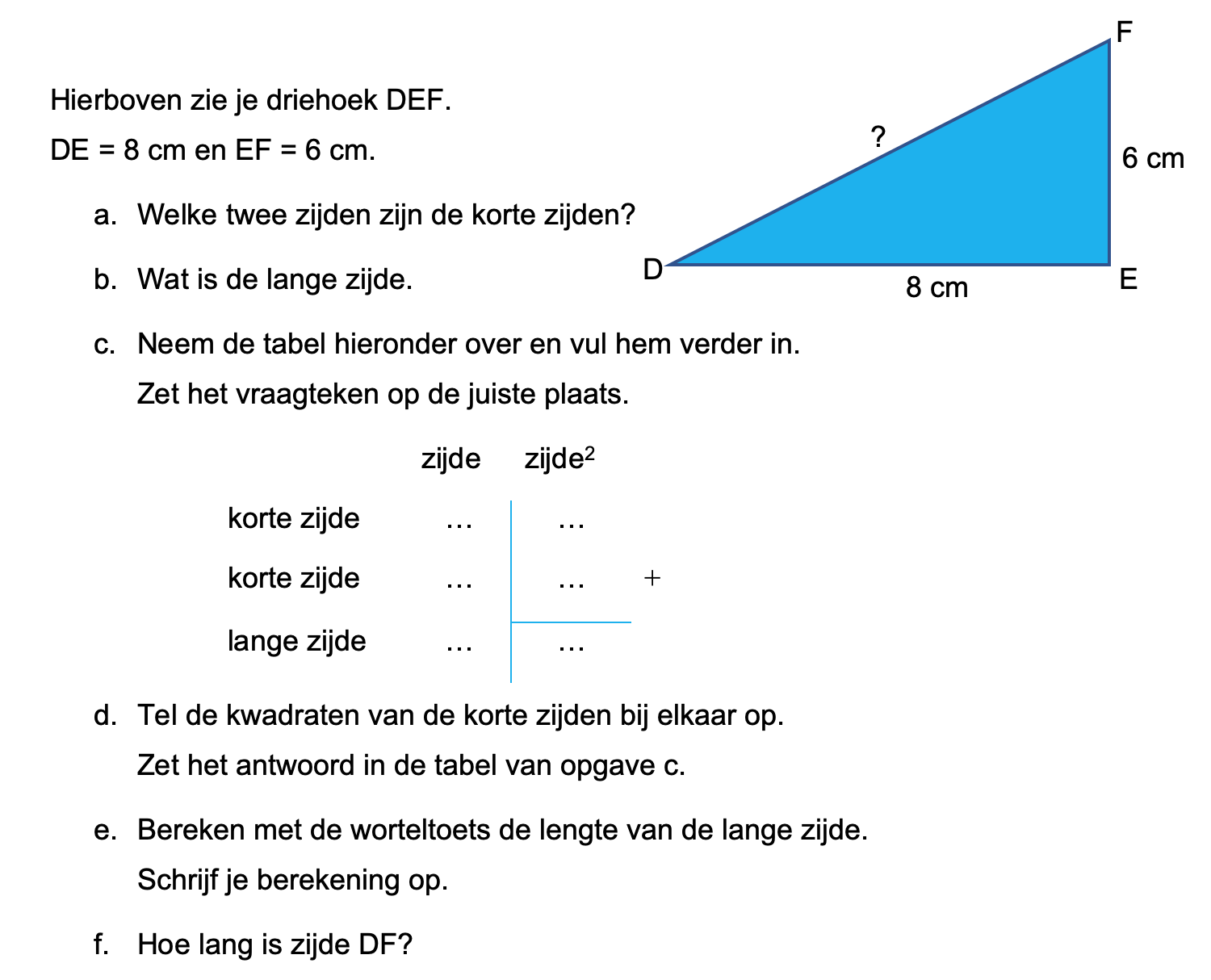
\
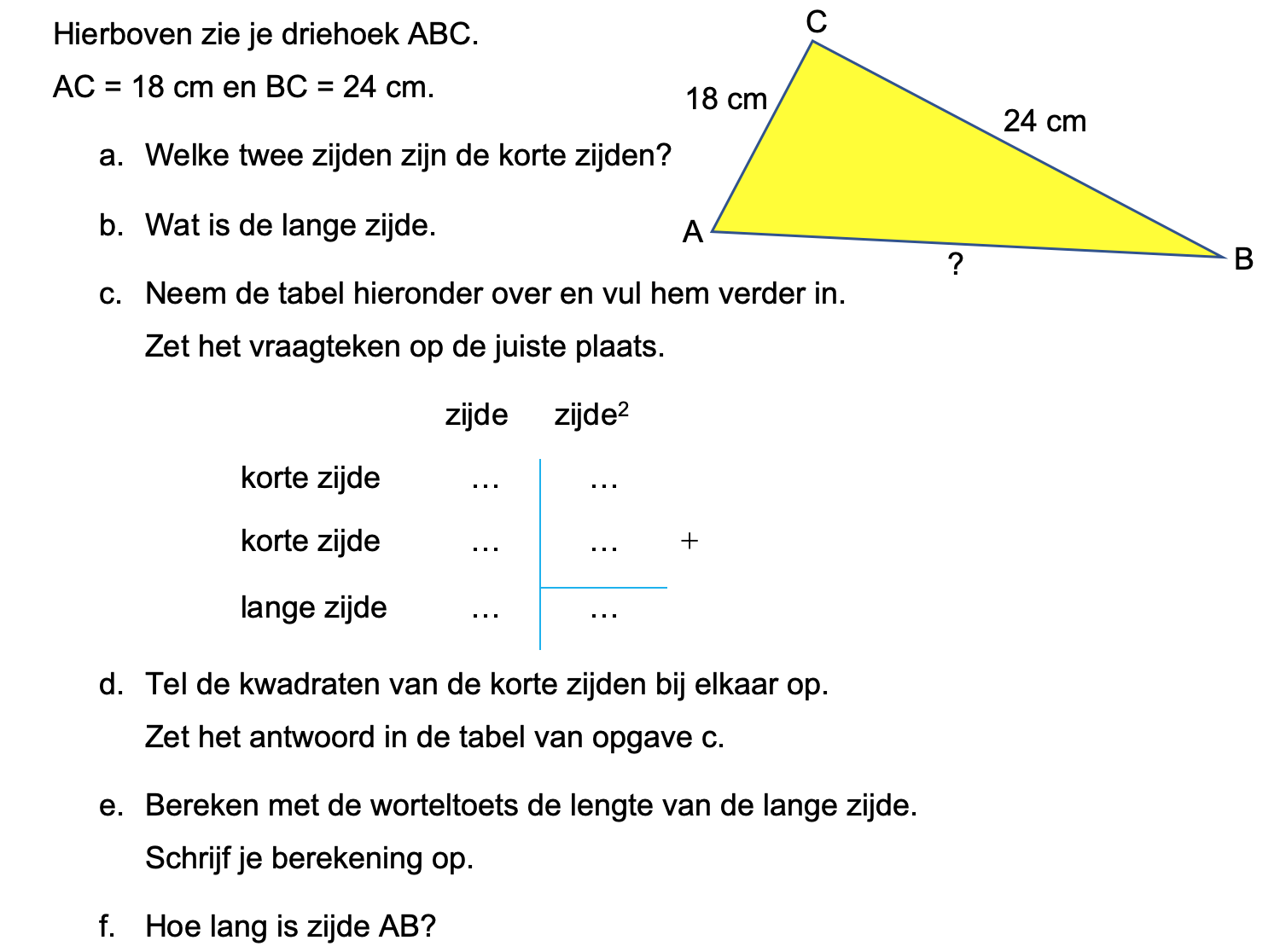

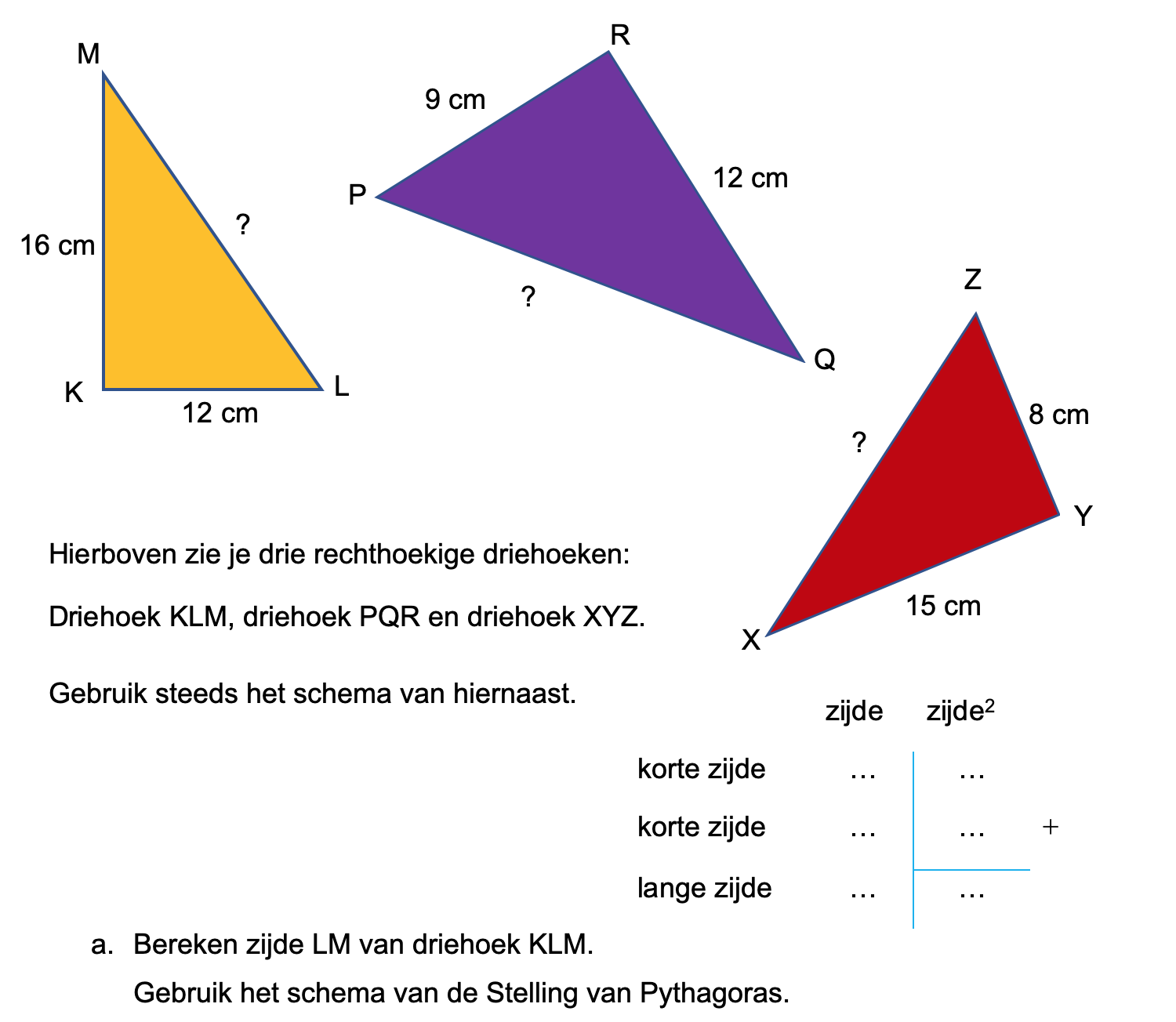

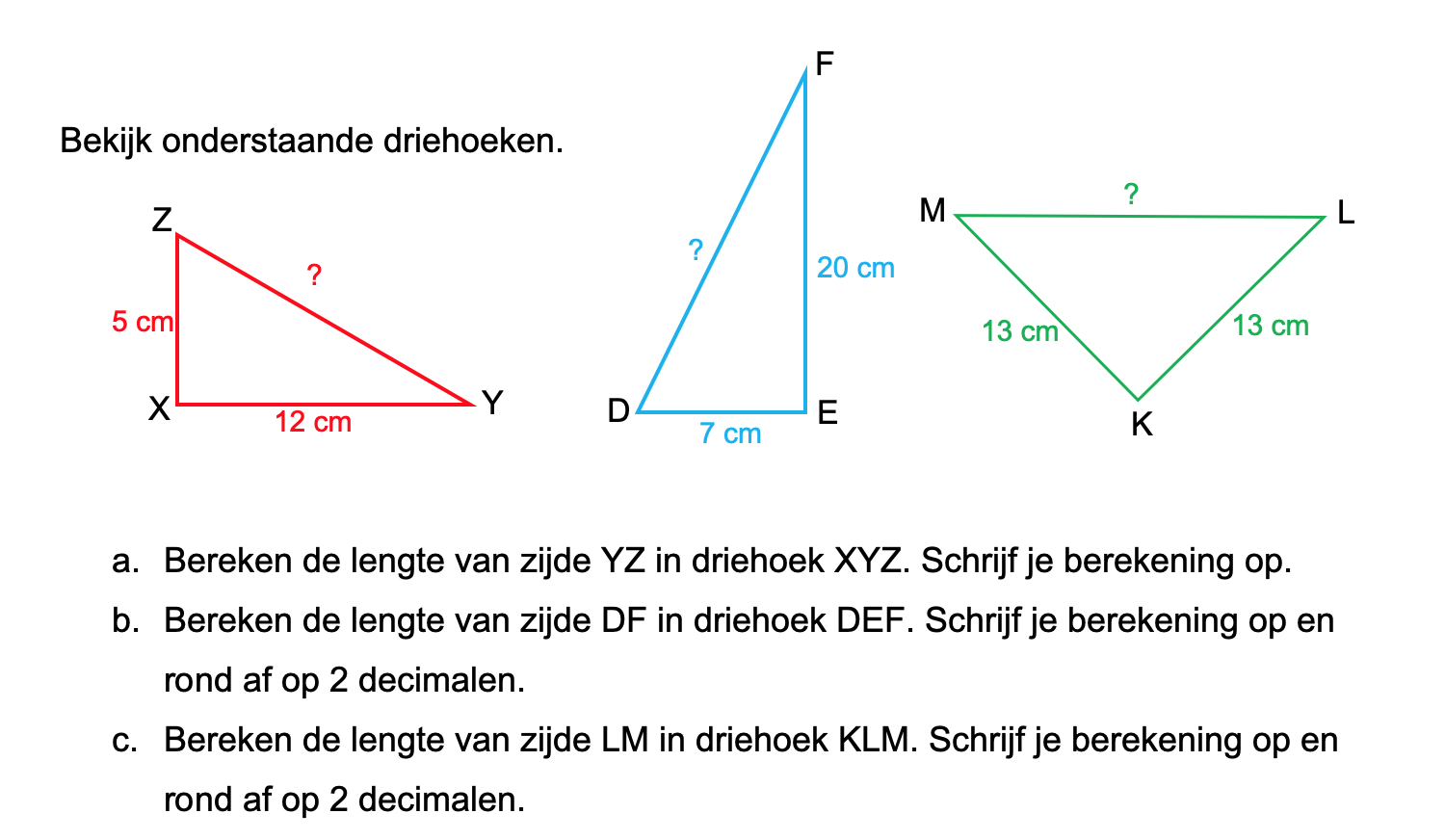
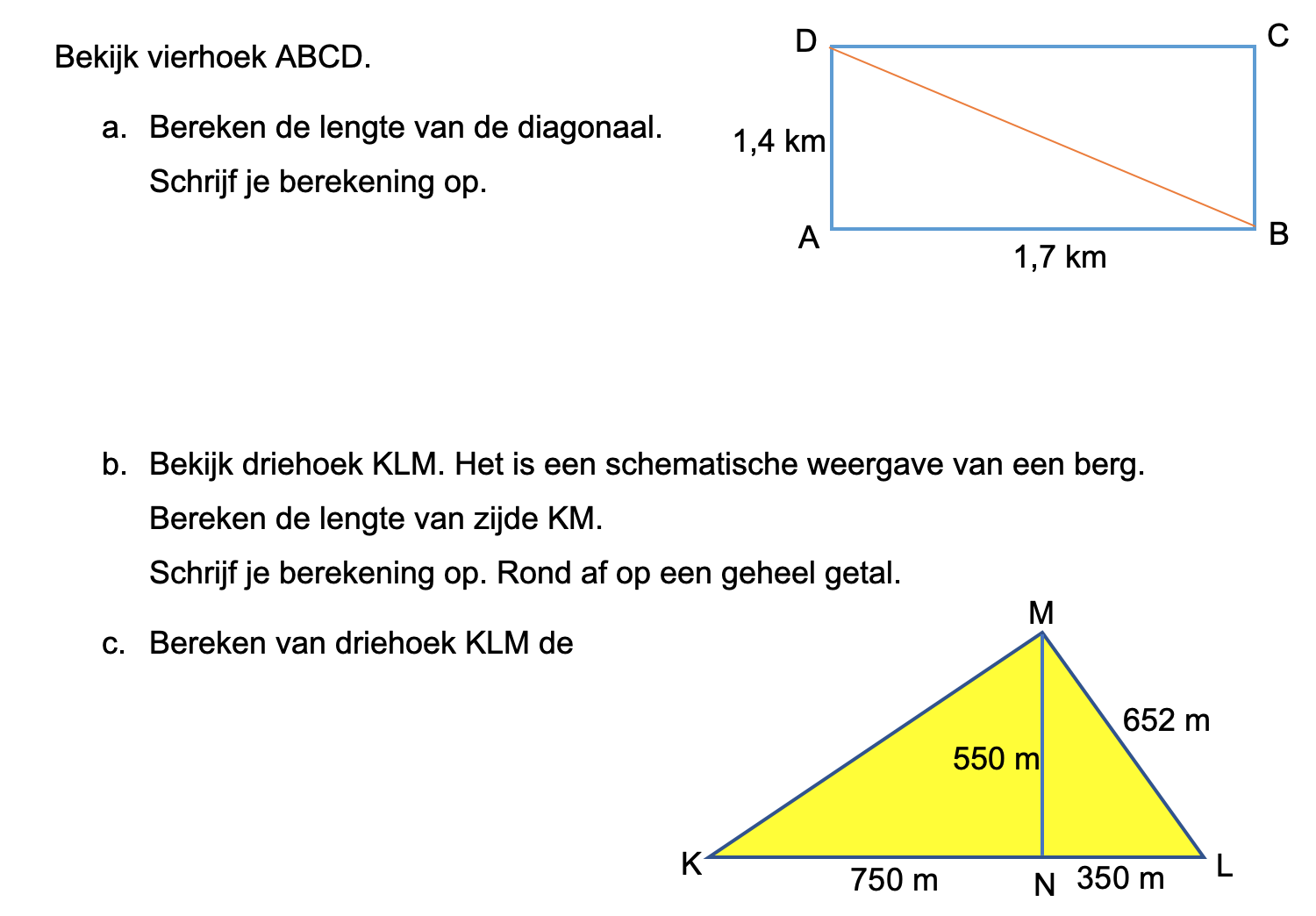





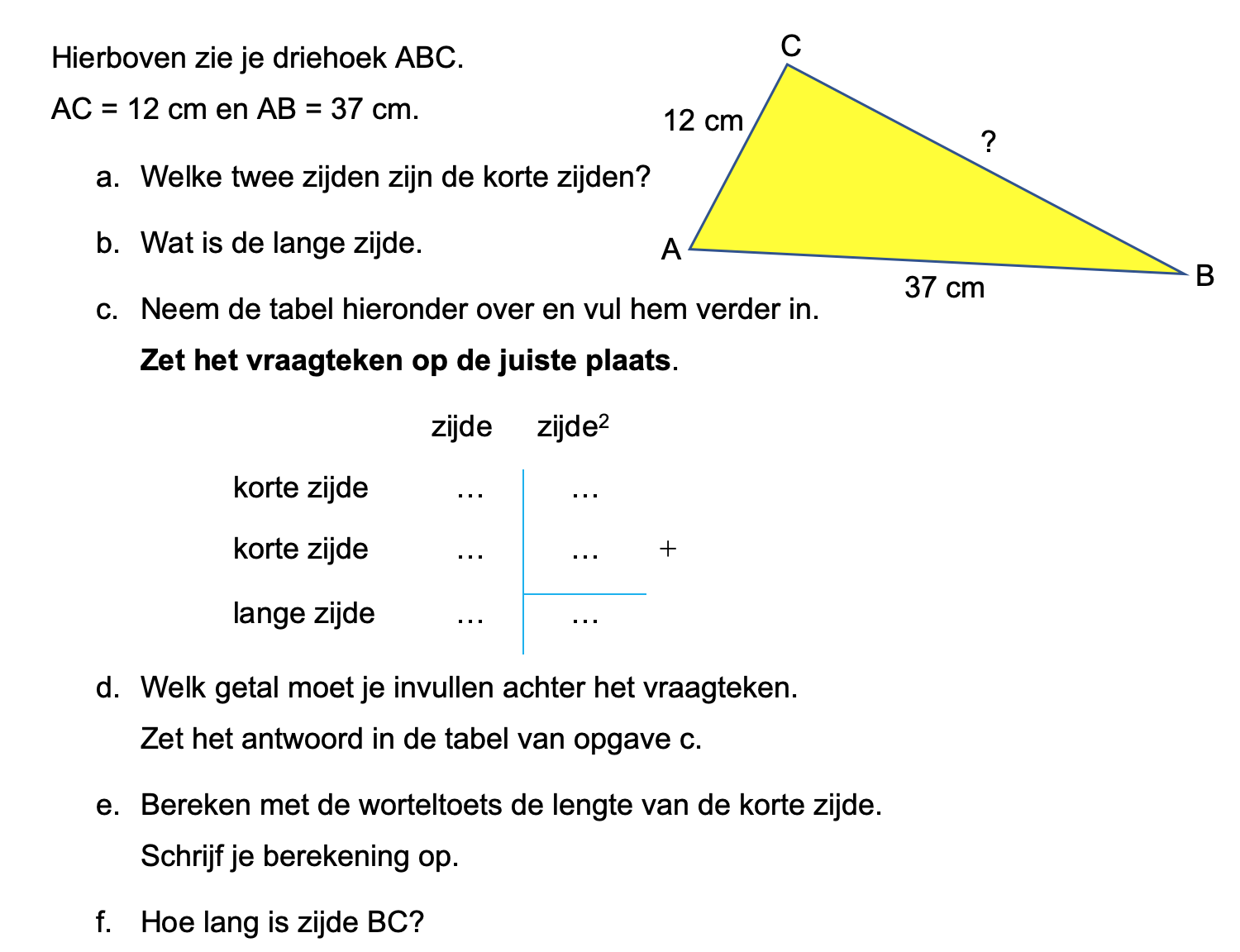
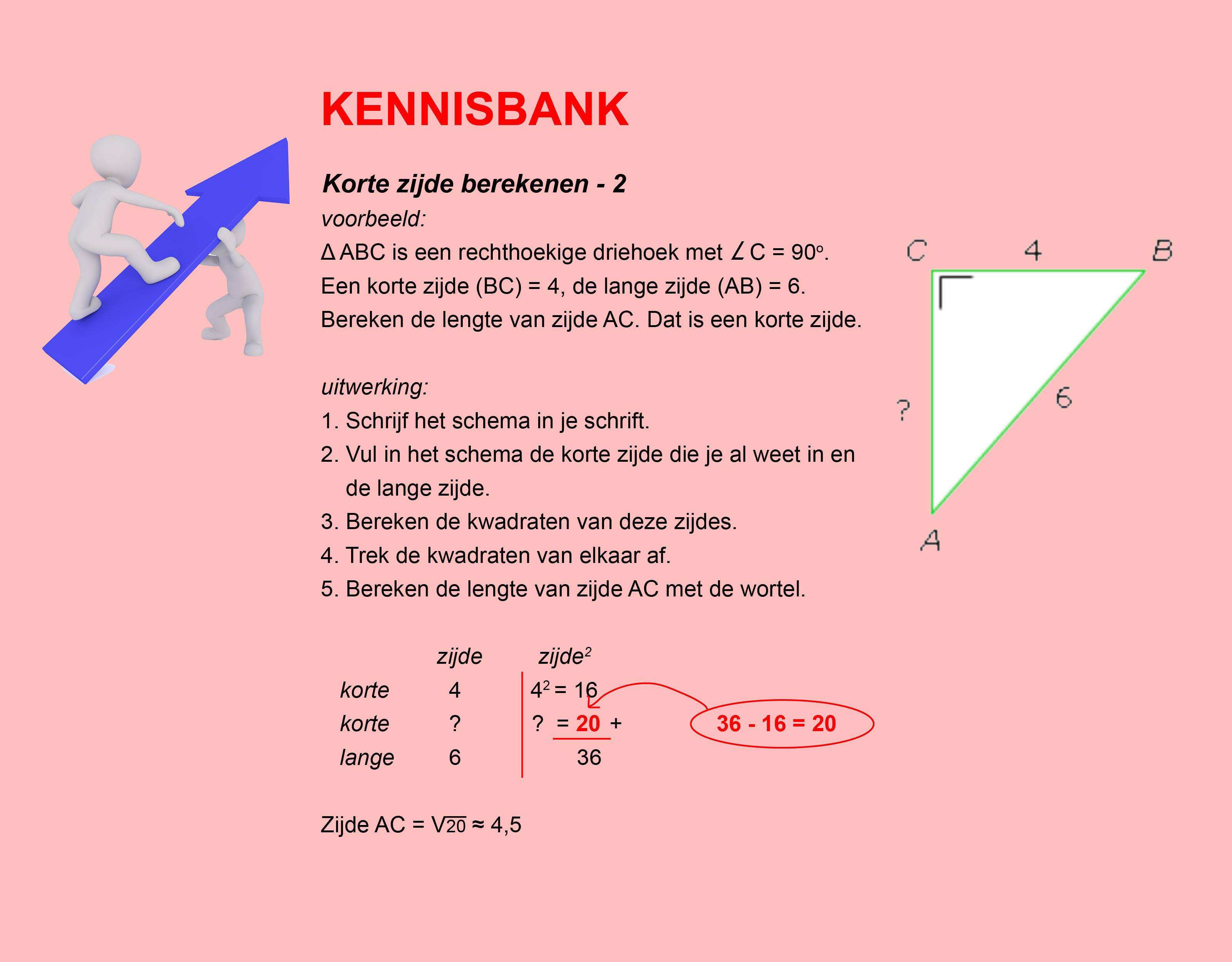
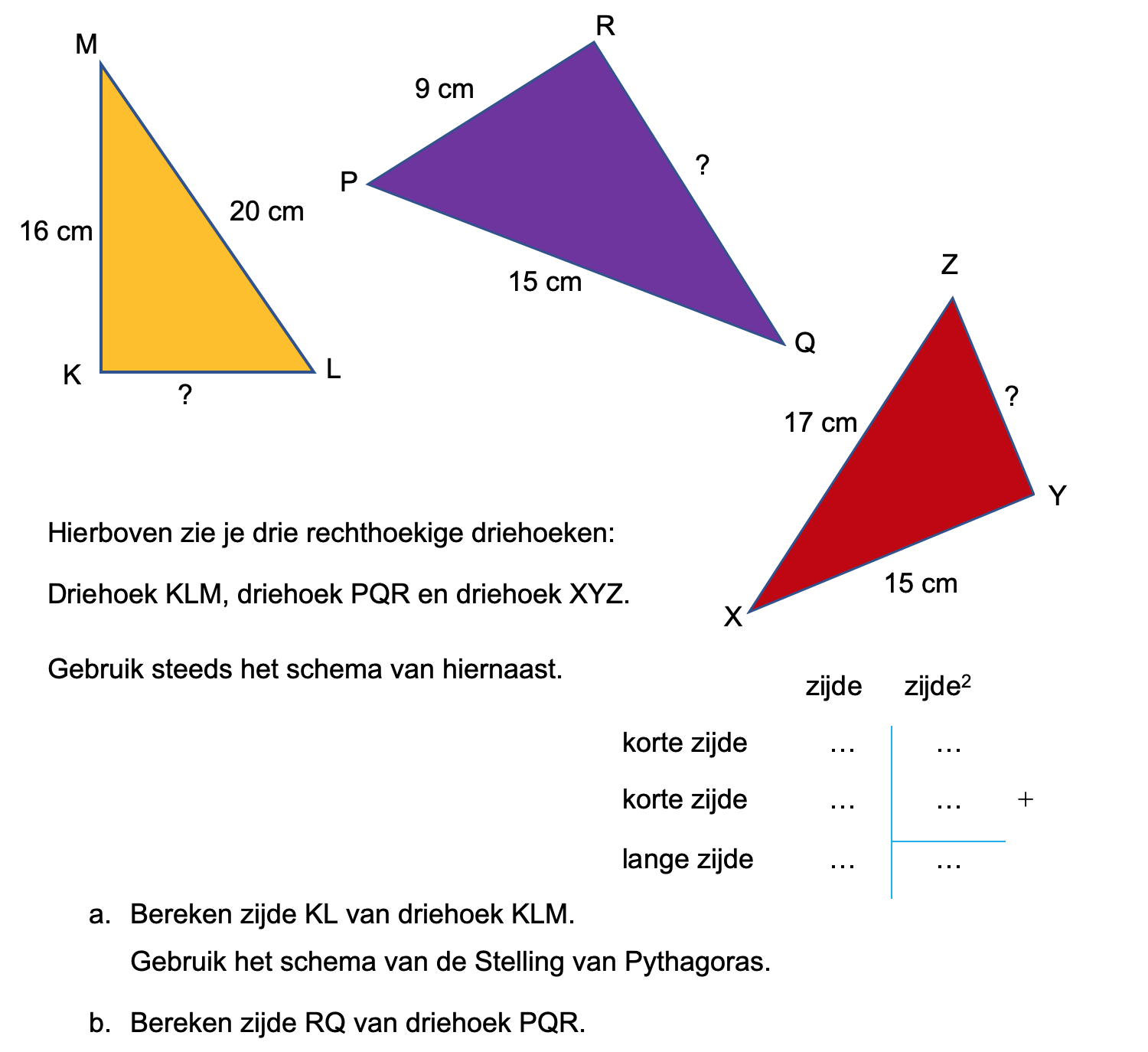

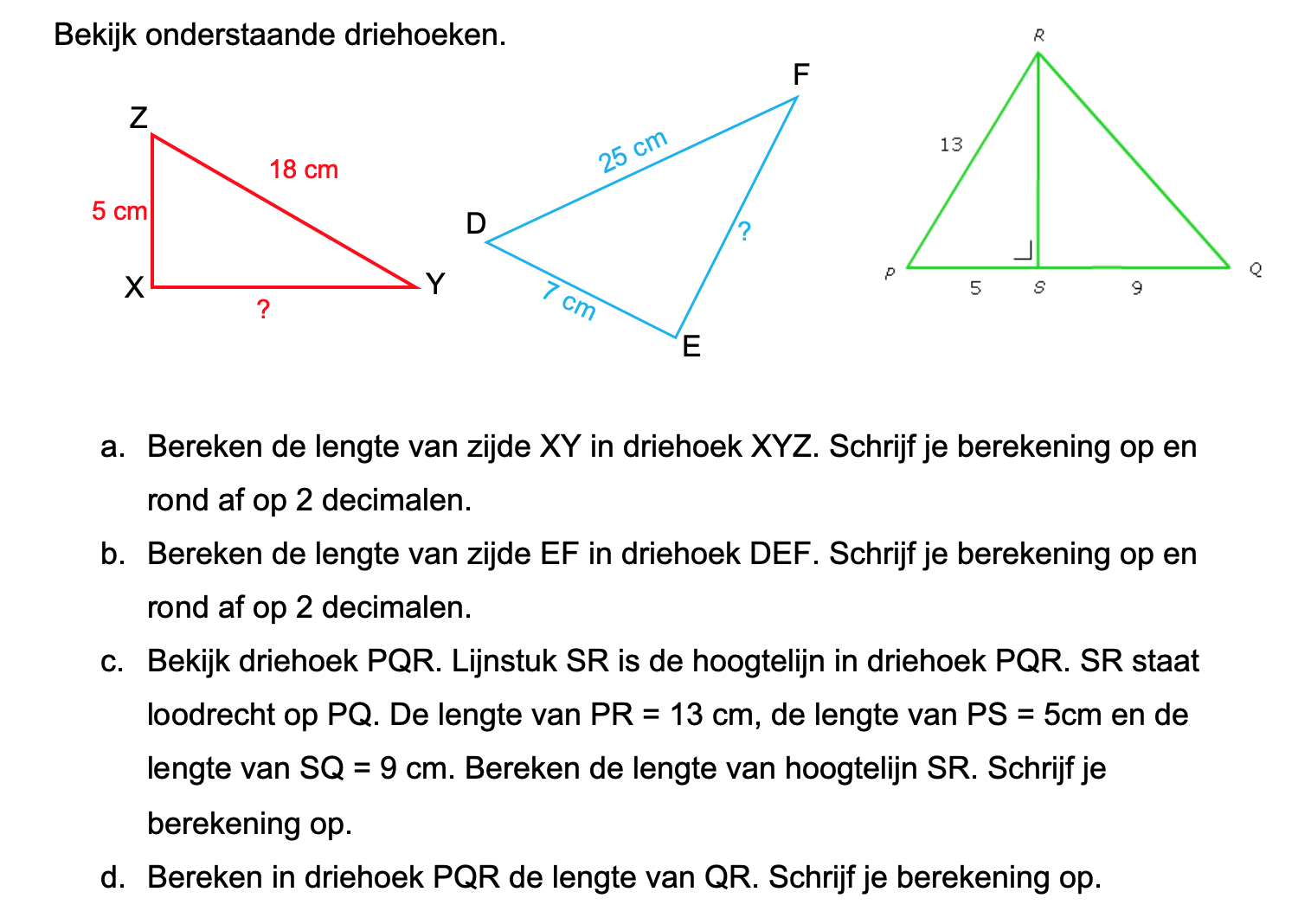
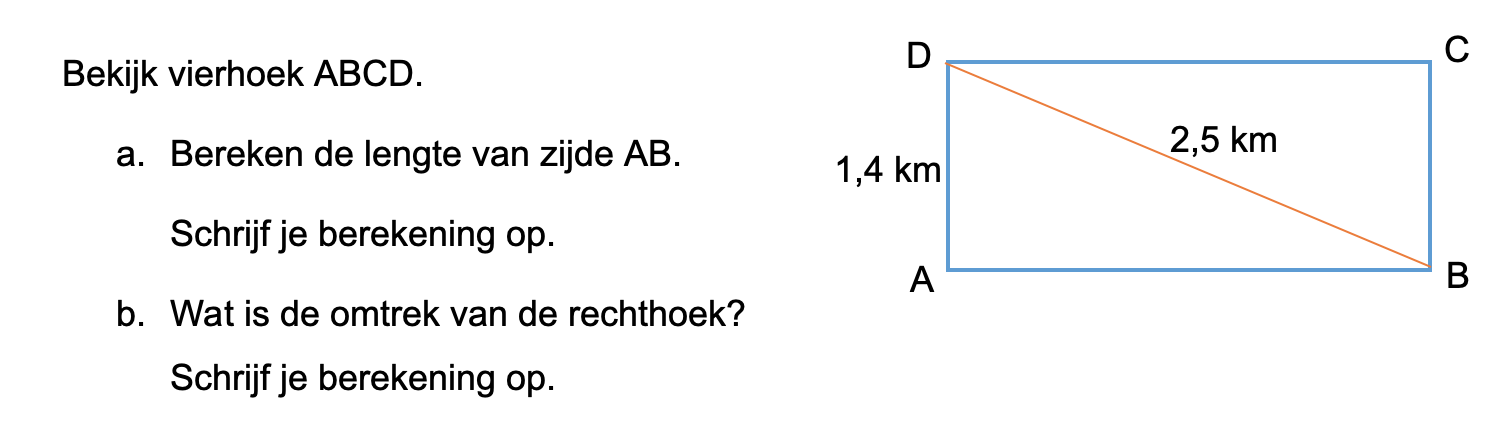
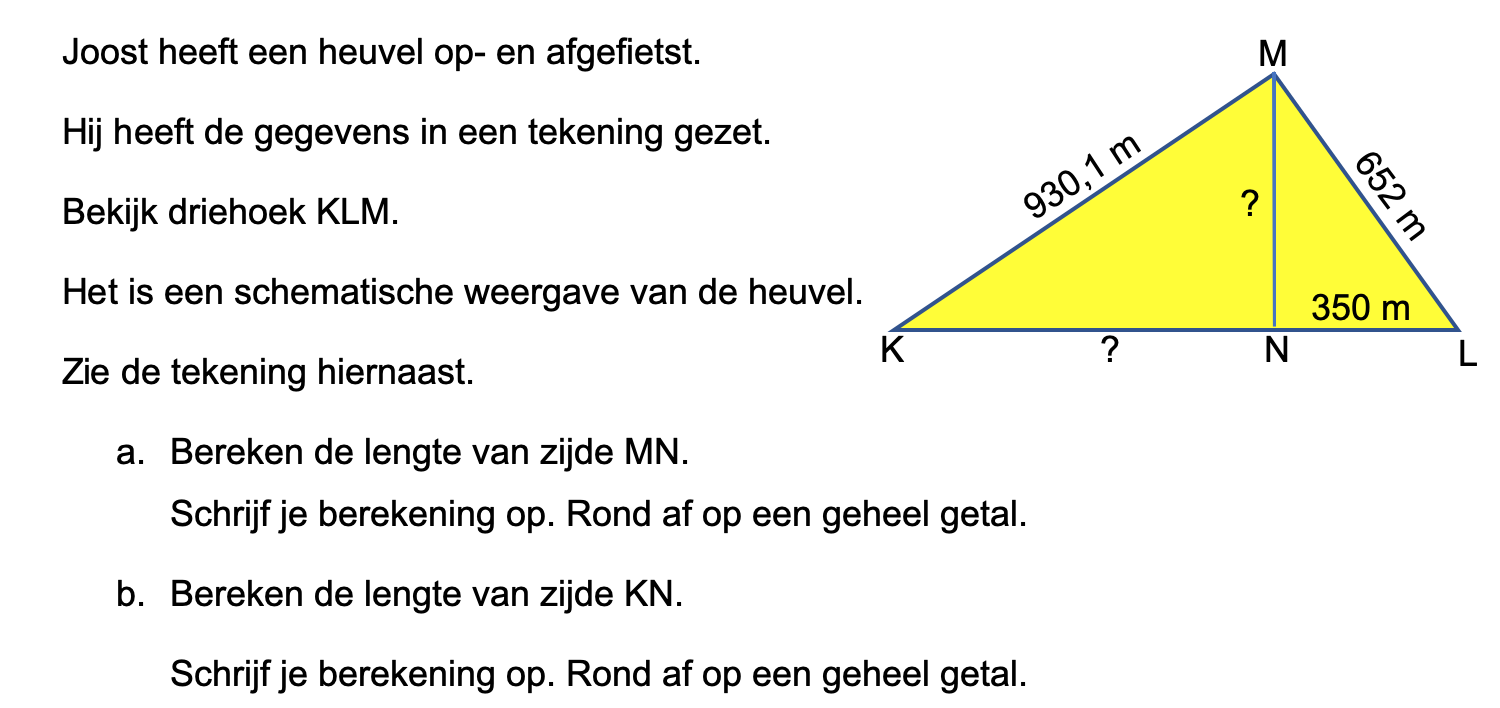


 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:







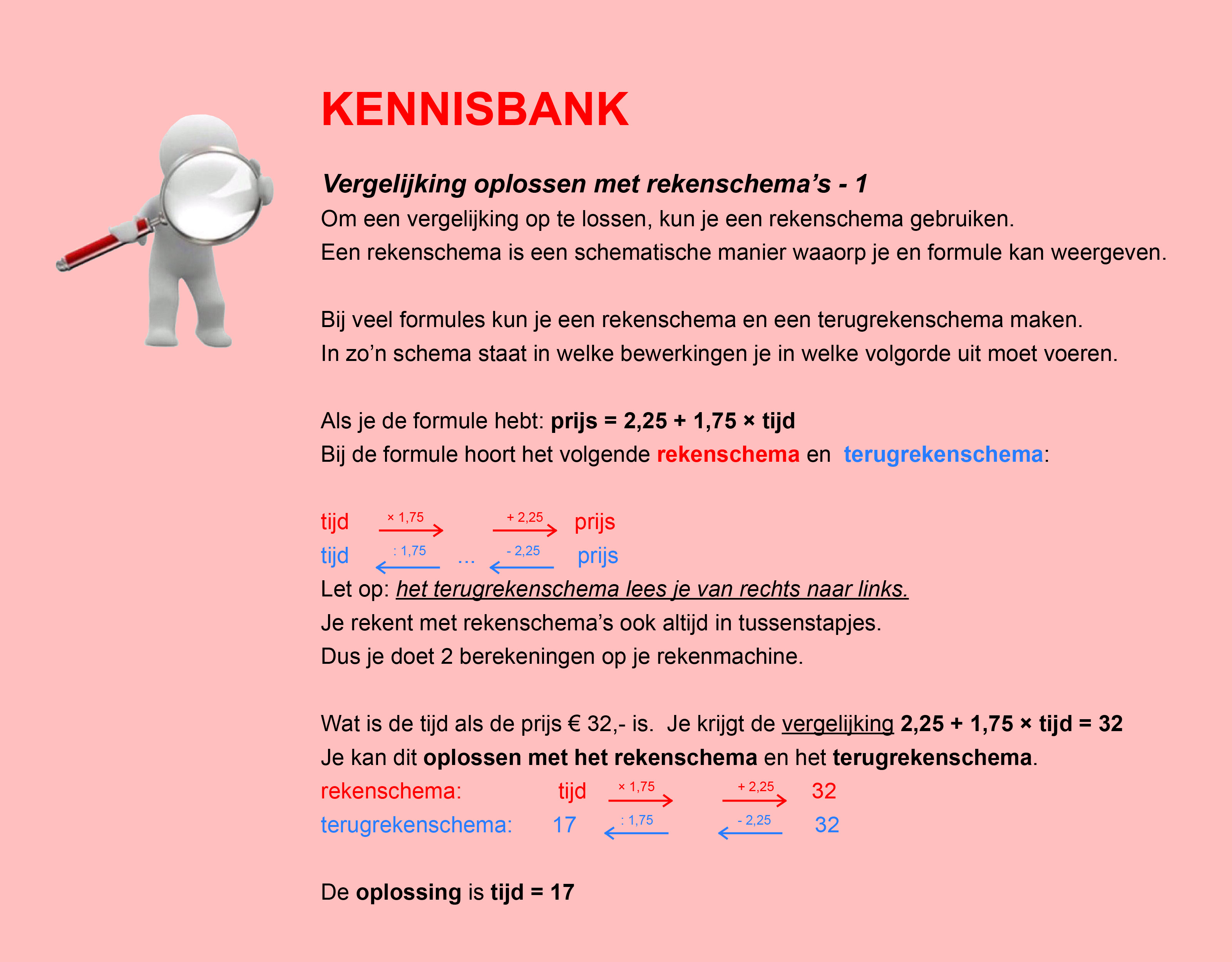









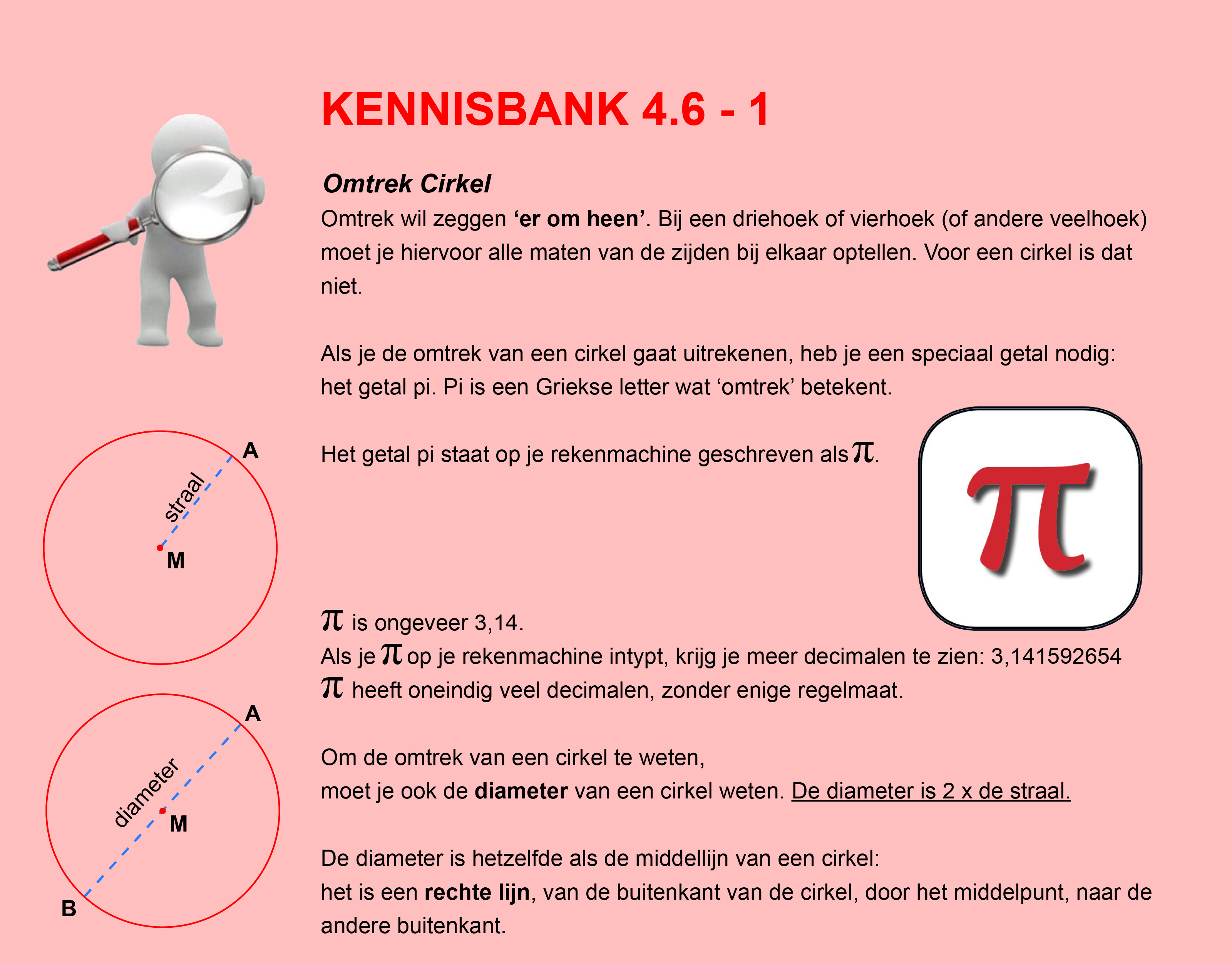


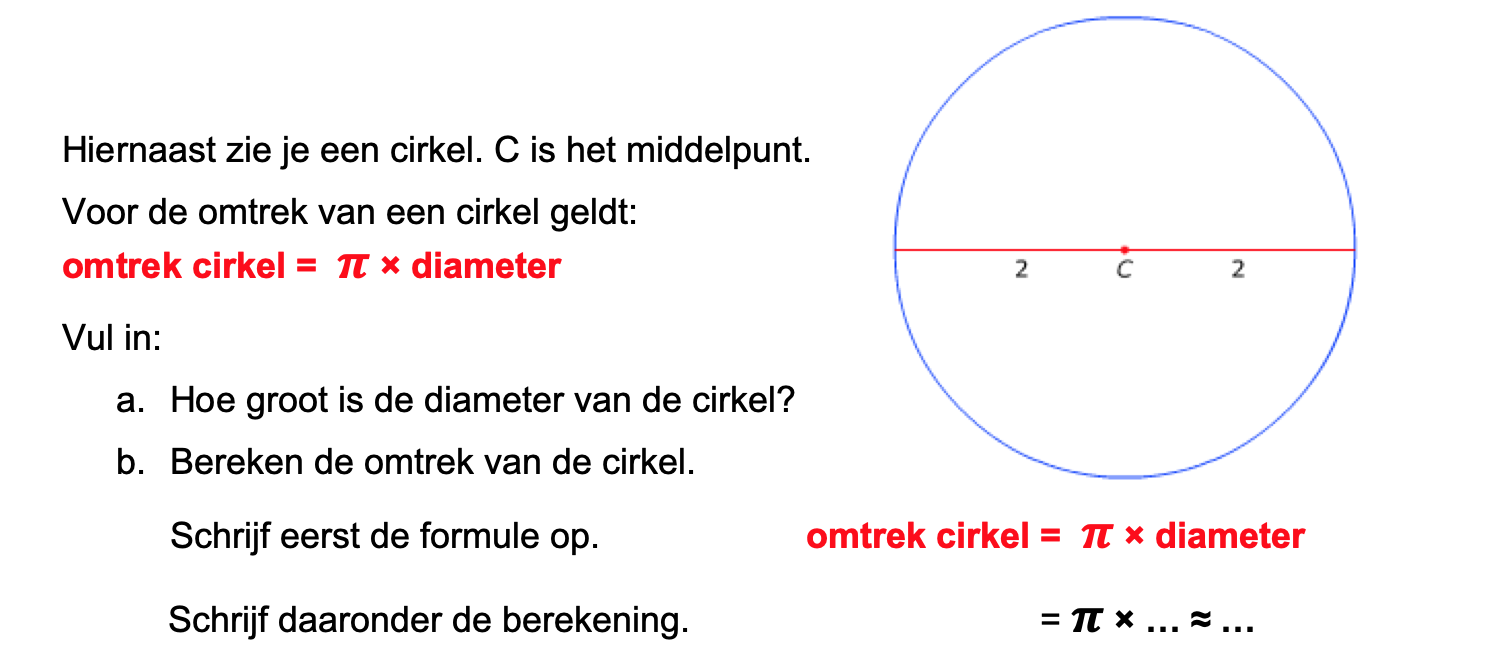

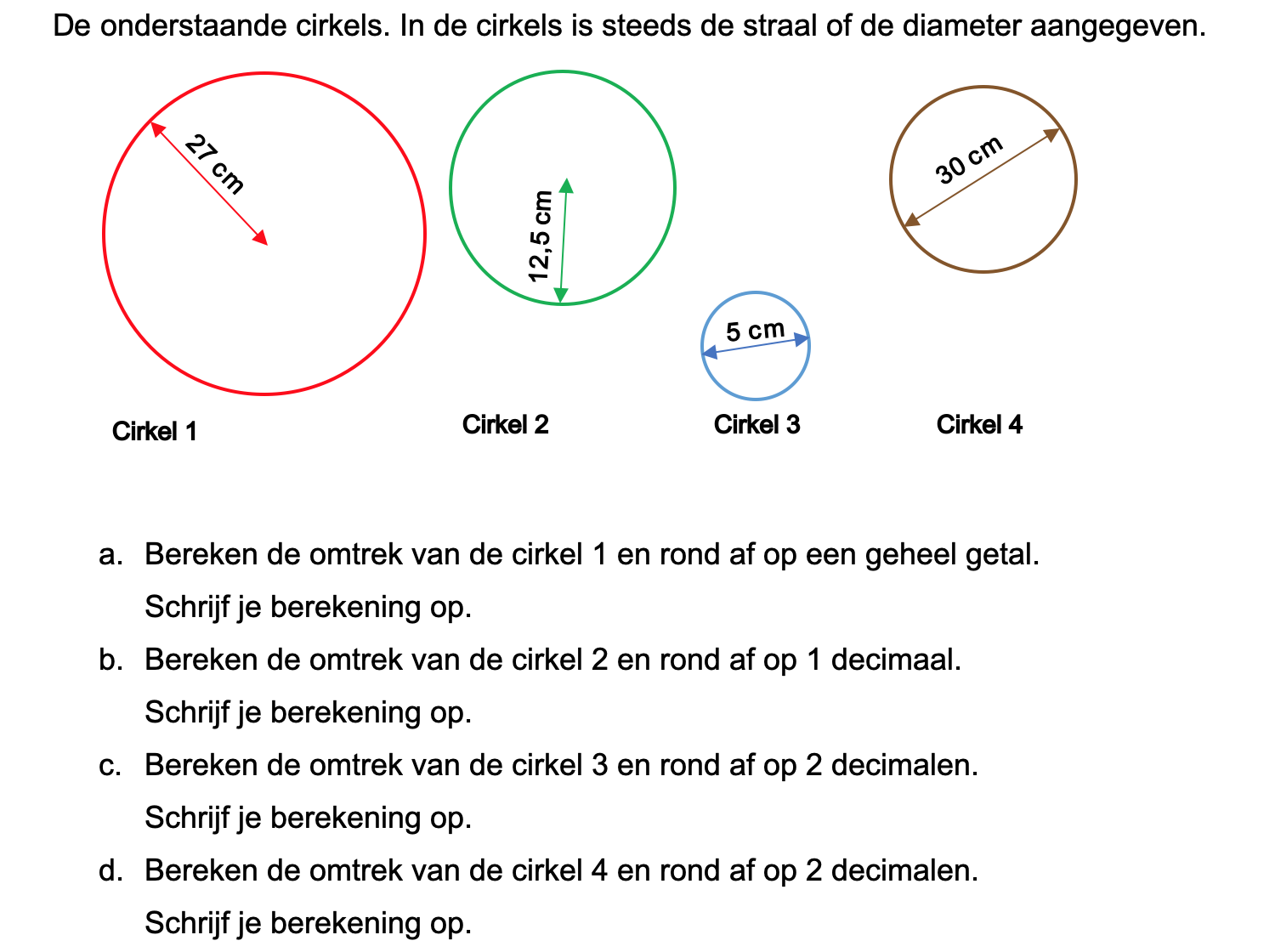
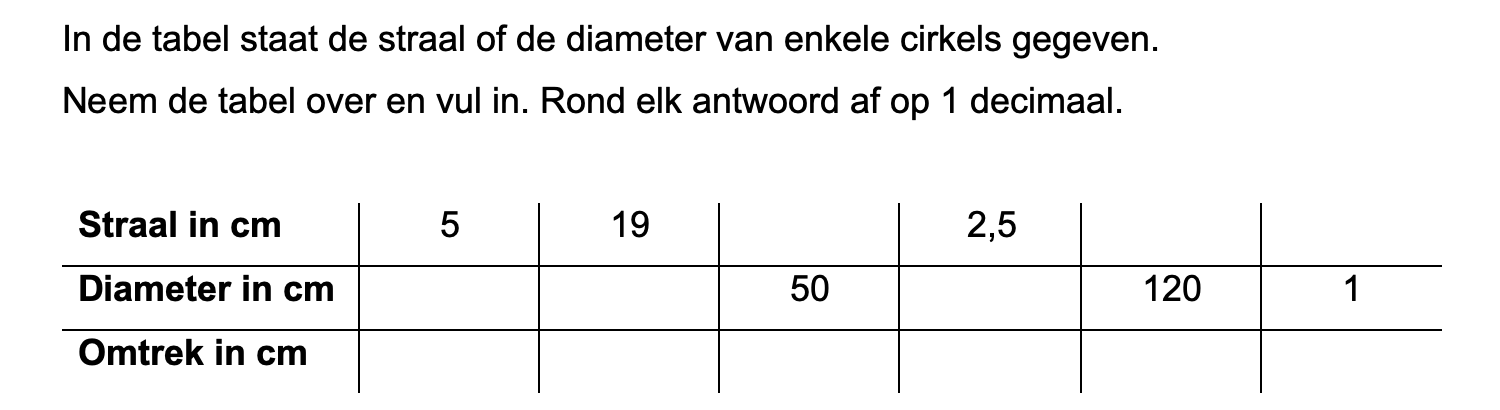



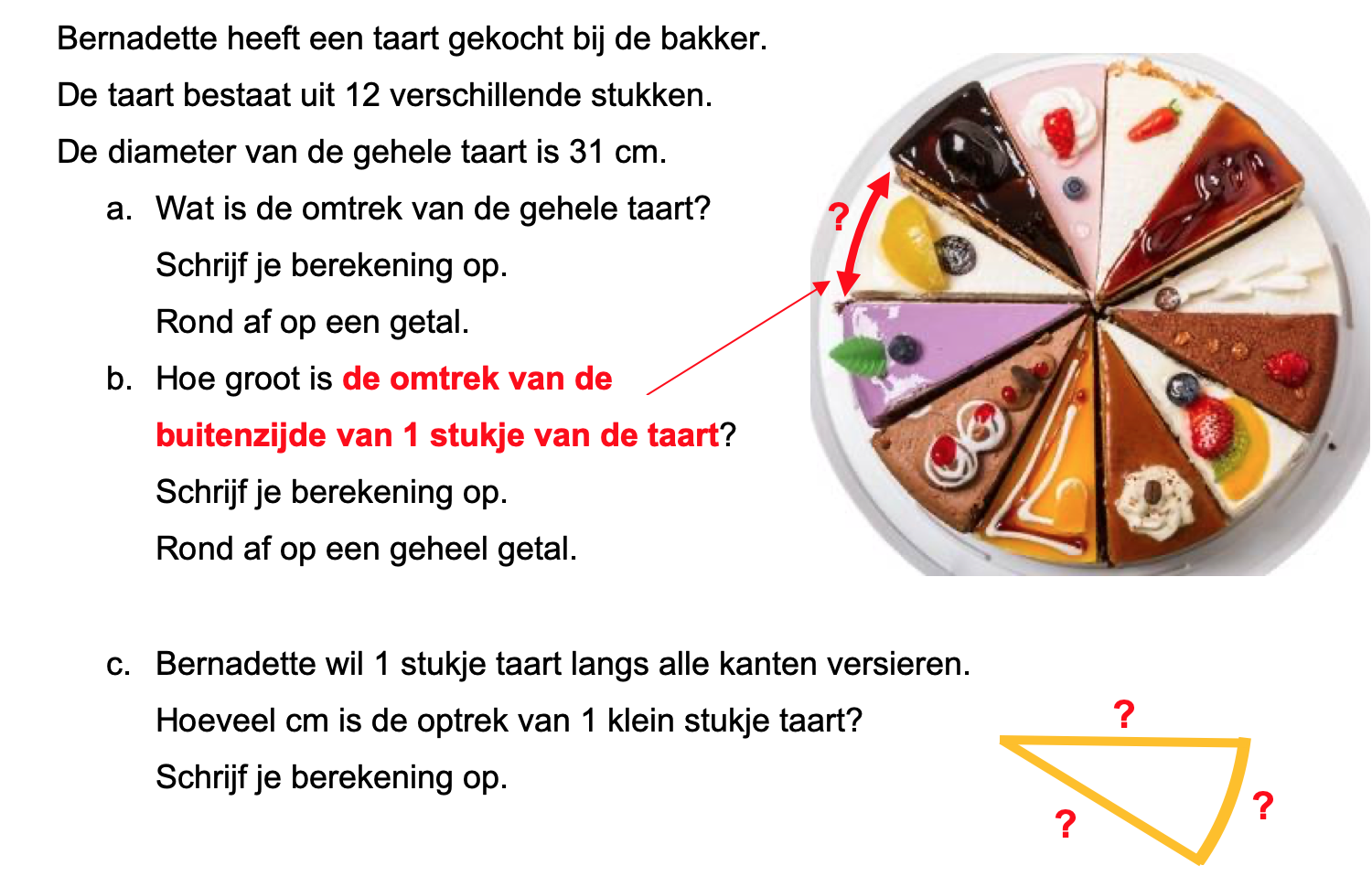




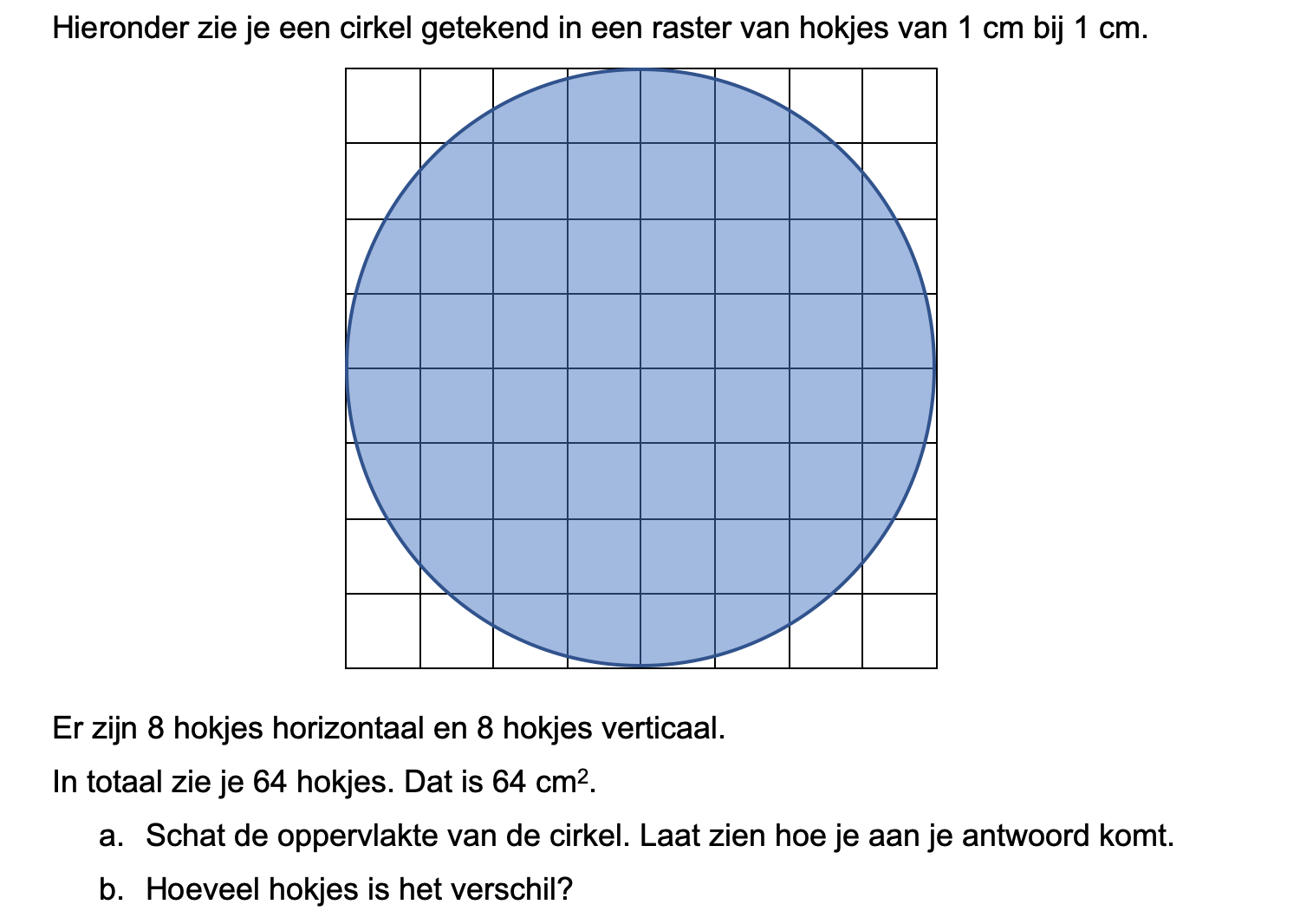
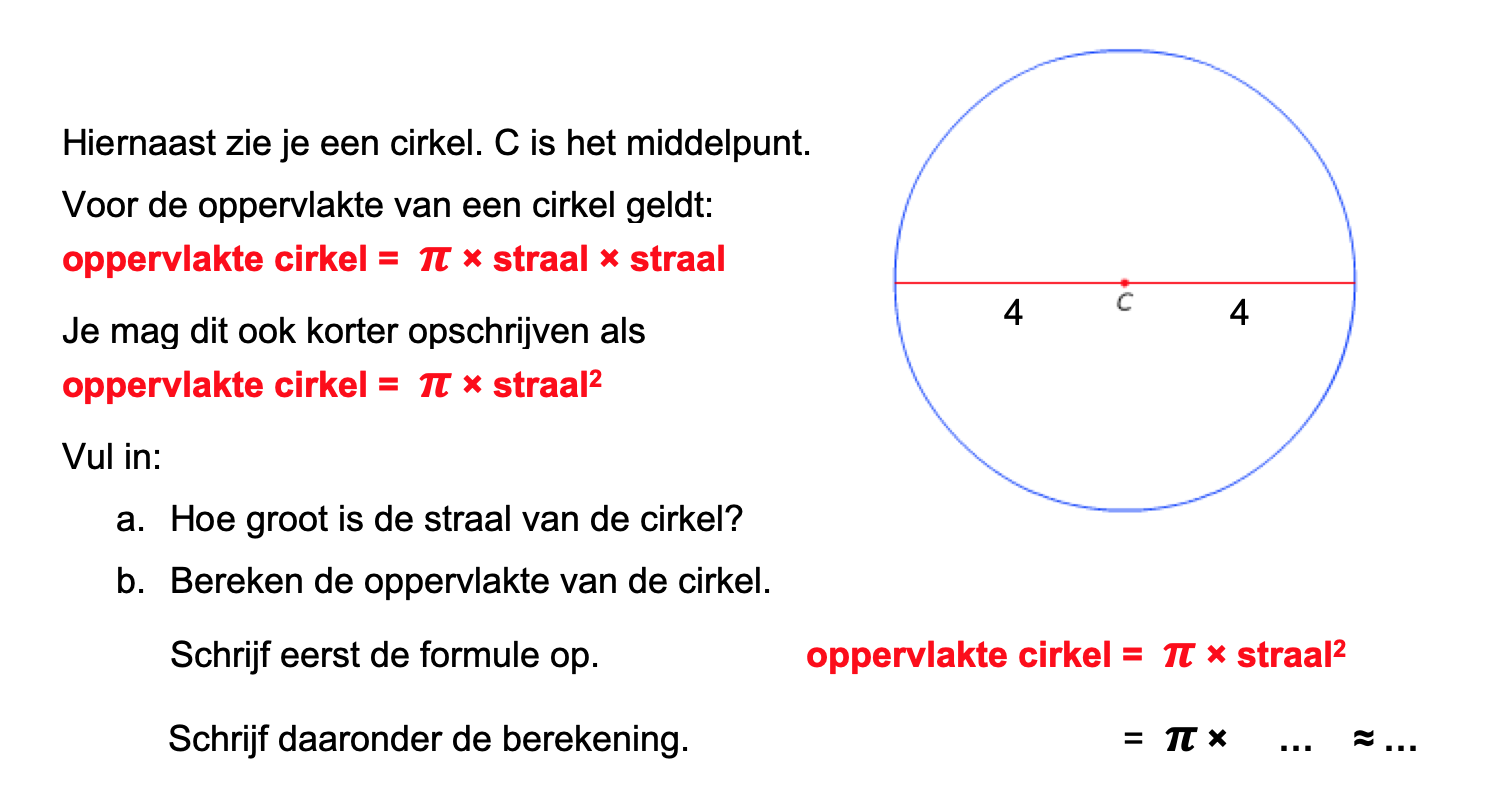

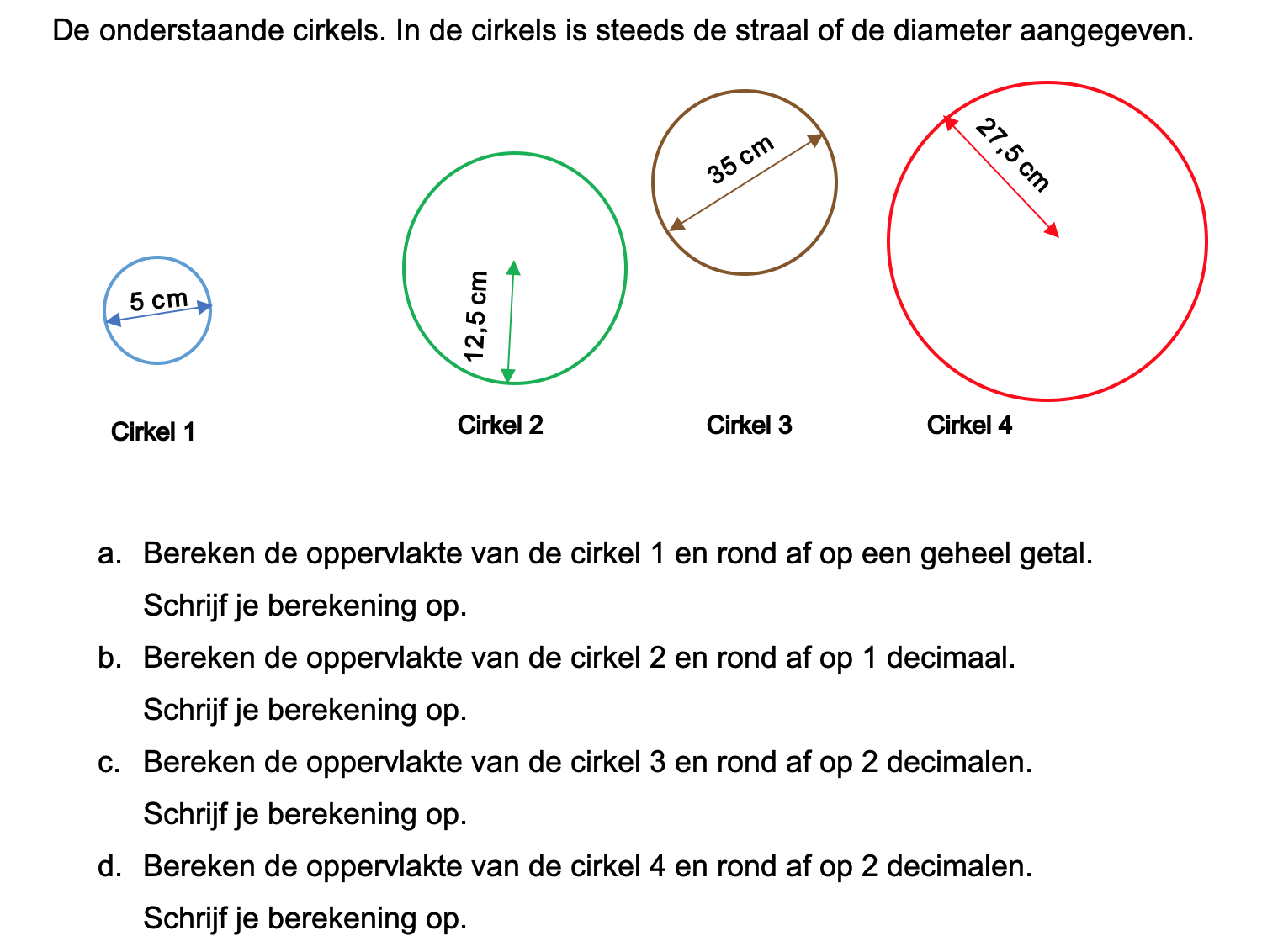




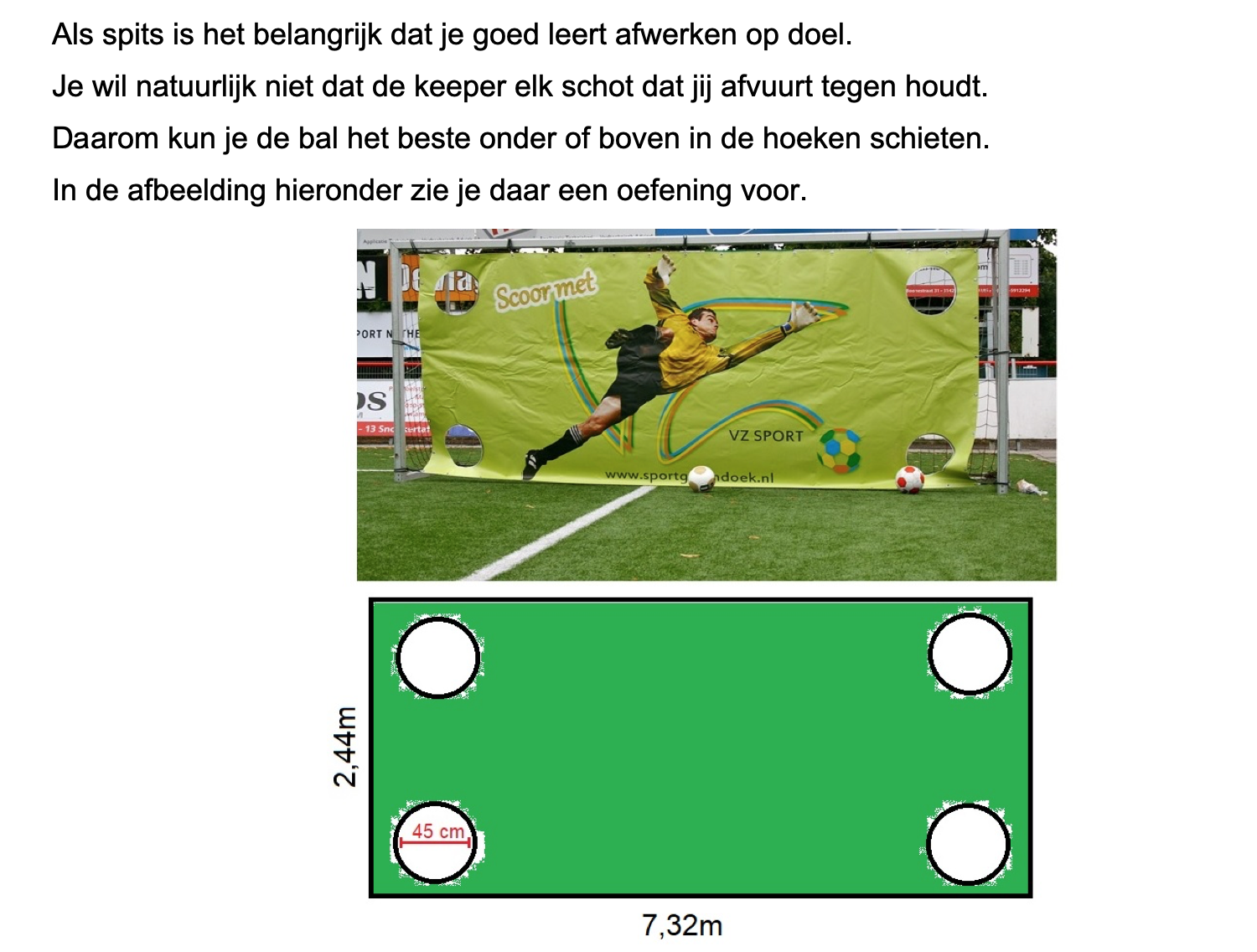



 Maak de volgende opgaven.
Maak de volgende opgaven.



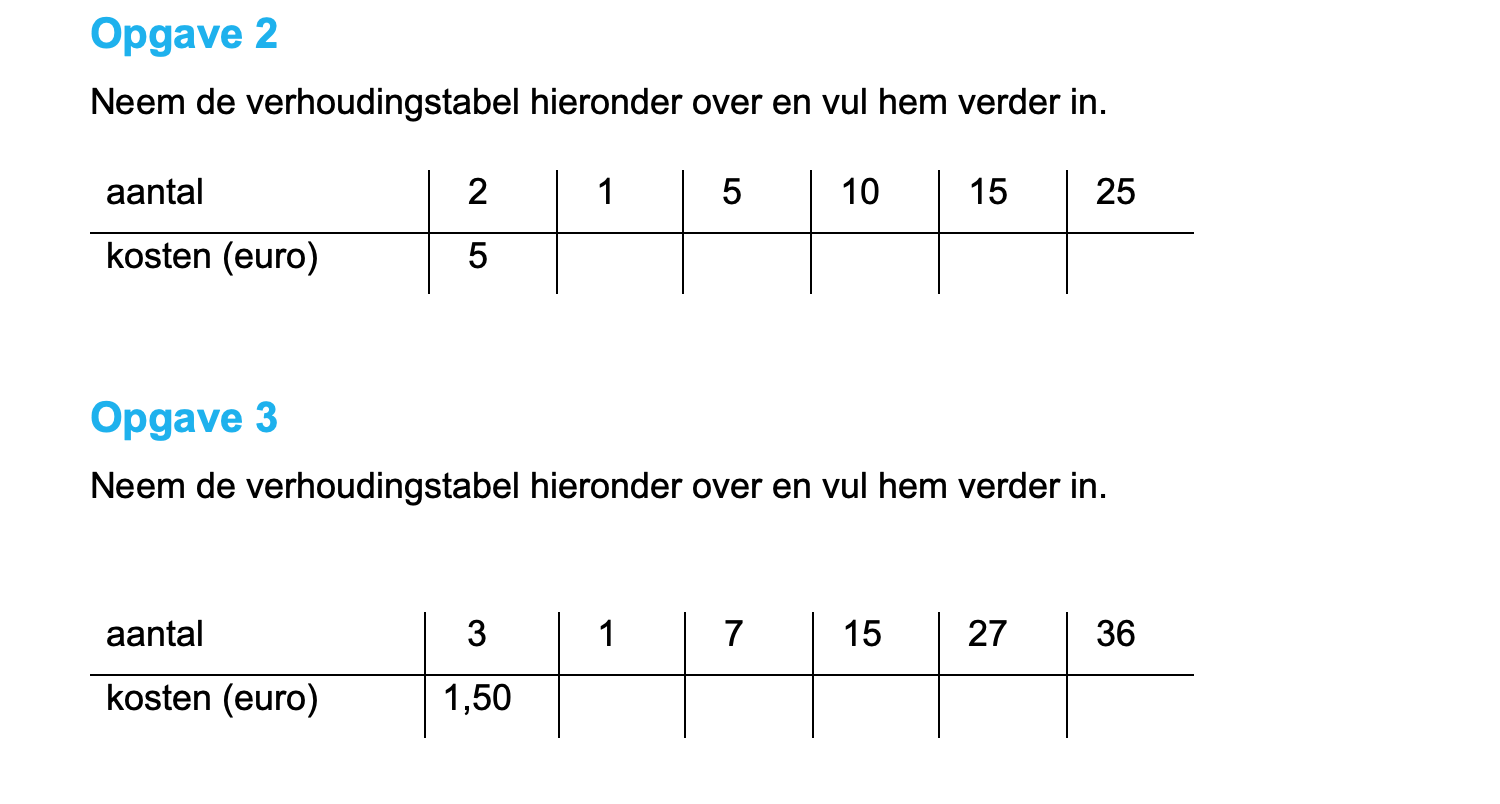
 \
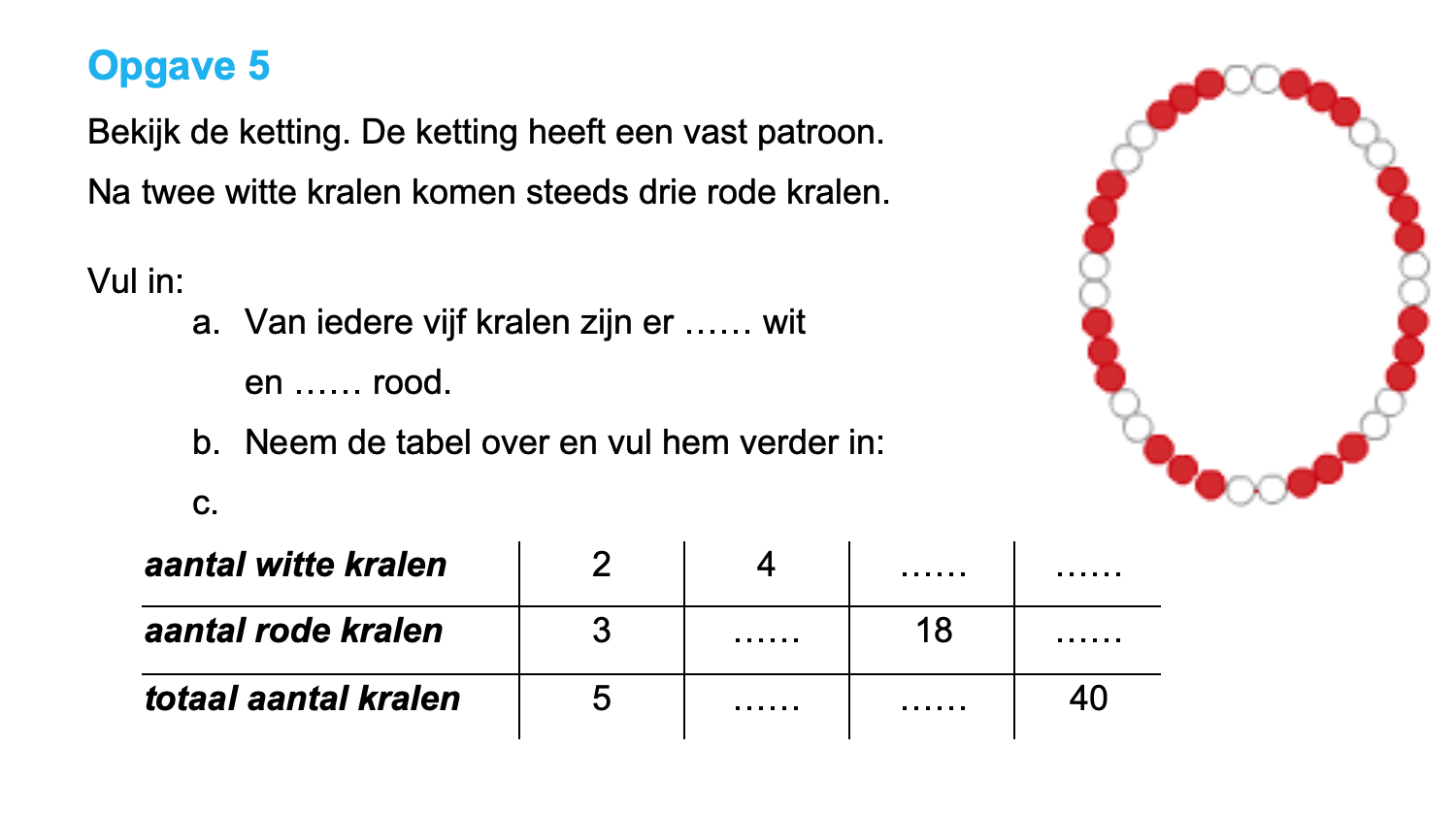
\







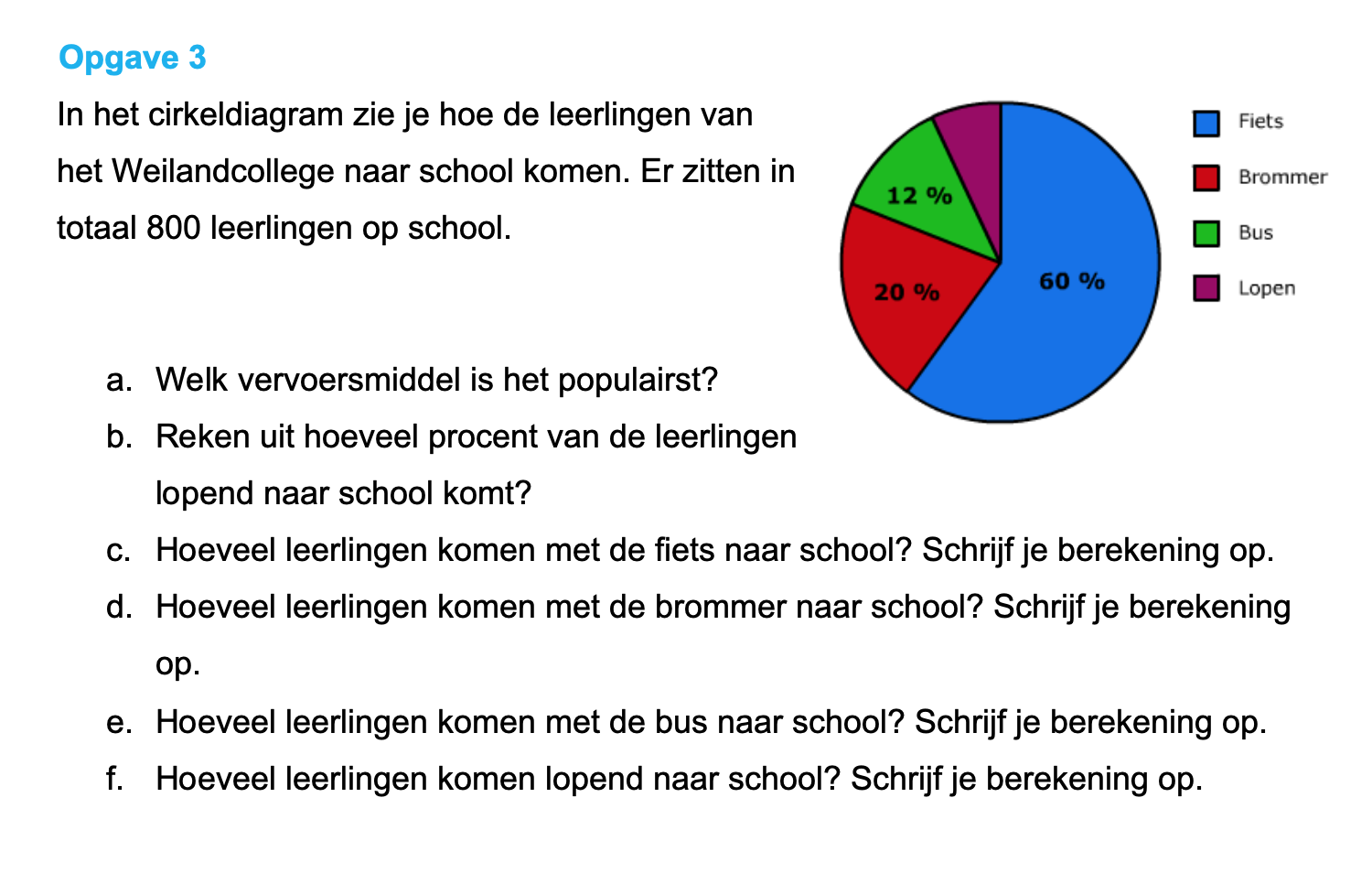


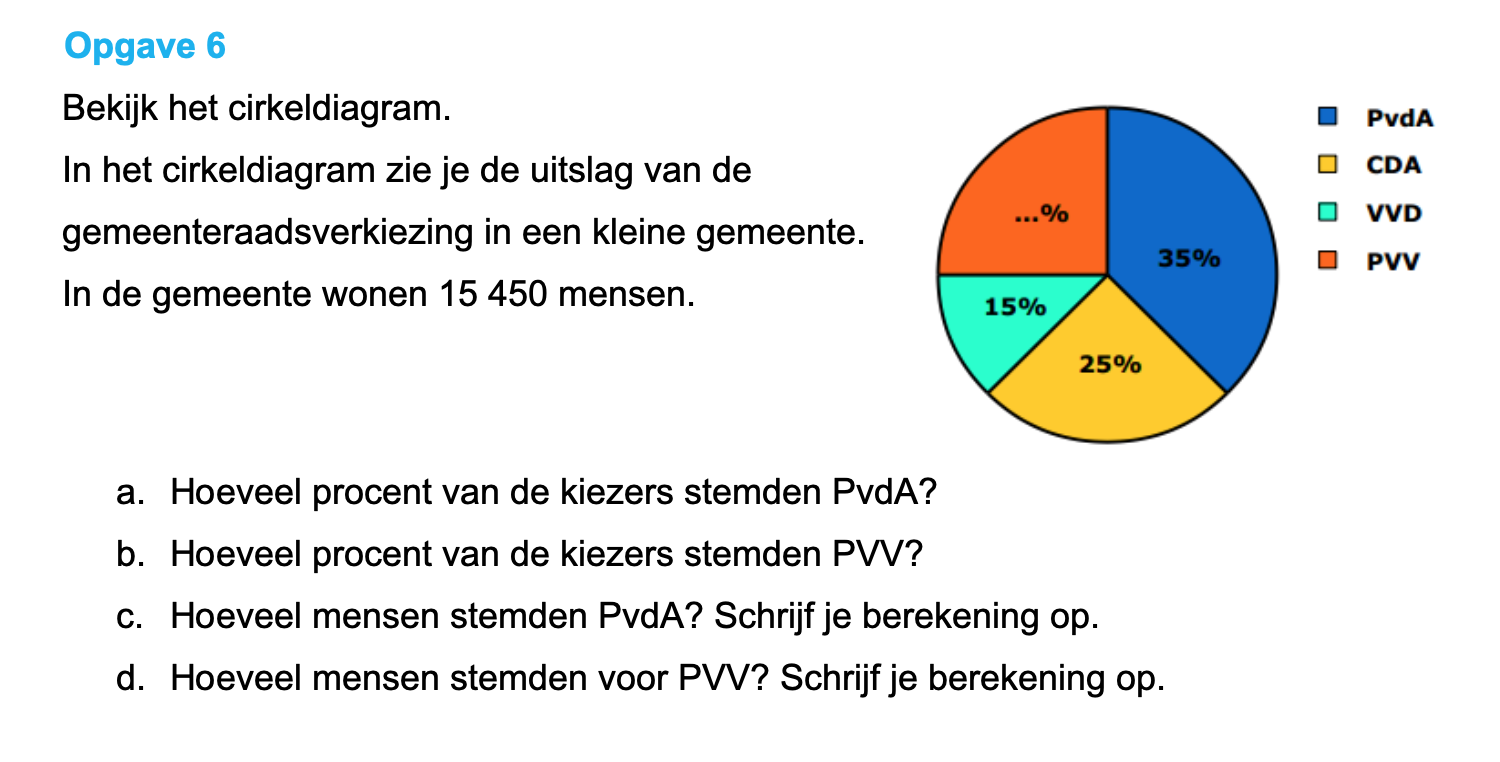



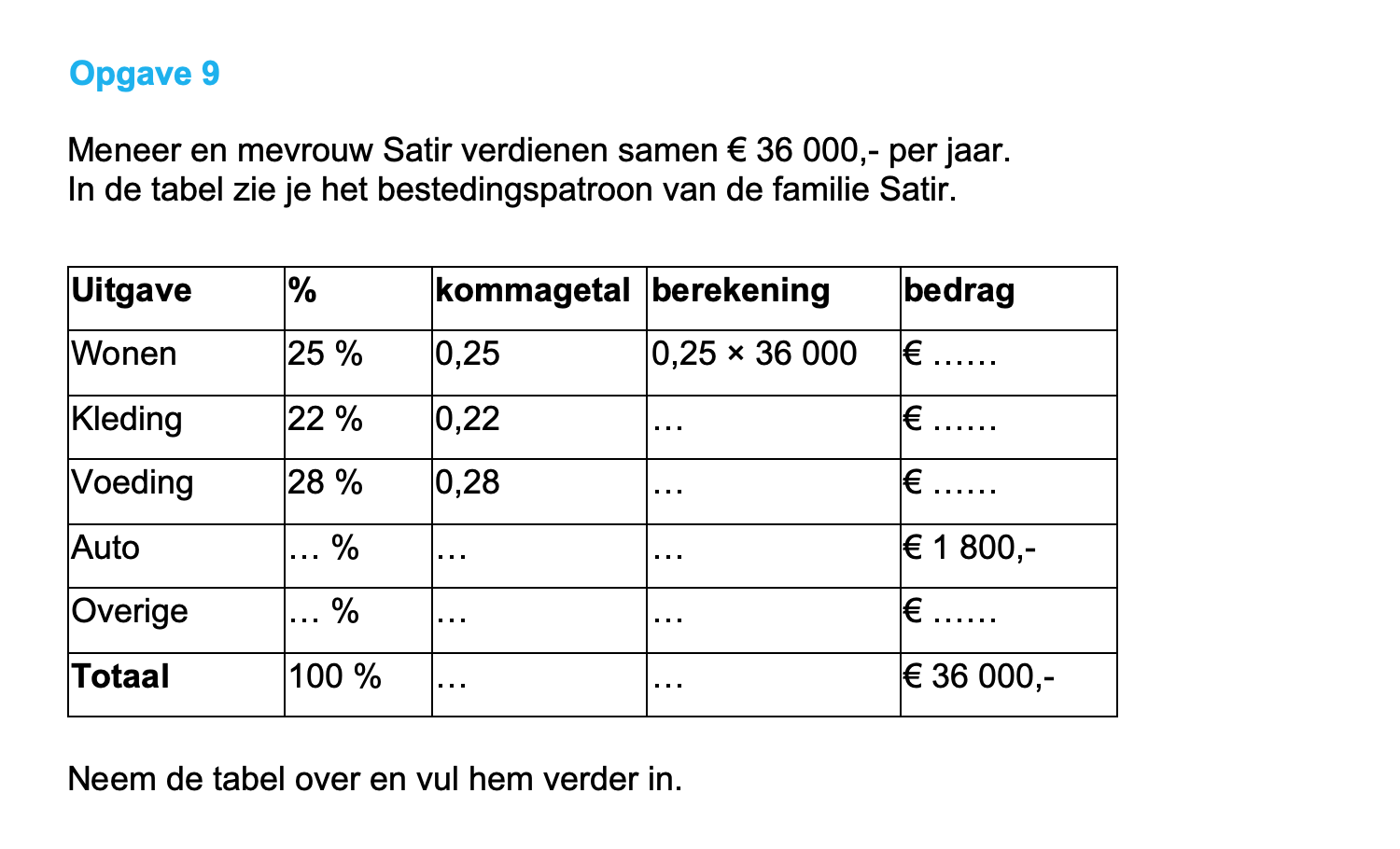

 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Maak de volgende opgaven.
Maak de volgende opgaven.
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Maak de volgende opgaven.
Maak de volgende opgaven.
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Veel oefenen is belangrijk.
Veel oefenen is belangrijk.
 Een bouwbedrijf wil een vakantiepark met vakantiehuisjes aanleggen.
Een bouwbedrijf wil een vakantiepark met vakantiehuisjes aanleggen. Klaar en tevreden?
Klaar en tevreden?


 Inleiding
Inleiding
 Inleiding
Inleiding Heb jij een mobiele telefoon? Vast wel. Tegenwoordig heeft bijna iedere leerling een mobiele telefoon. Bijvoorbeeld om even naar huis te bellen als je na moet blijven. Of om een sms-je te versturen naar een vriend of vriendin.
Heb jij een mobiele telefoon? Vast wel. Tegenwoordig heeft bijna iedere leerling een mobiele telefoon. Bijvoorbeeld om even naar huis te bellen als je na moet blijven. Of om een sms-je te versturen naar een vriend of vriendin.




 Inleiding
Inleiding

 De kubuswoningen in het centrum van Rotterdam zijn een opvallende en kleurrijke verschijning. De woningen zijn bedacht door de architect Piet Blom. In het volgende korte filmpje van YouTube krijg je
De kubuswoningen in het centrum van Rotterdam zijn een opvallende en kleurrijke verschijning. De woningen zijn bedacht door de architect Piet Blom. In het volgende korte filmpje van YouTube krijg je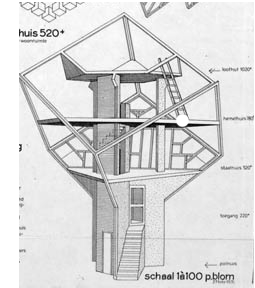 In de inleiding van dit thema heb je kennisgemaakt met de kubuswoningen in Rotterdam. Hiernaast zie je een bouwtekening van zo'n kubuswoning. In de tekening zie je dat de kubuswoning meerdere verdiepingen heeft.
In de inleiding van dit thema heb je kennisgemaakt met de kubuswoningen in Rotterdam. Hiernaast zie je een bouwtekening van zo'n kubuswoning. In de tekening zie je dat de kubuswoning meerdere verdiepingen heeft.