Het arrangement Sk-10 Rekenen in de chemie is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 02-01-2016 23:42:12
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 3.0 Nederland licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 3.0 Nederland licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
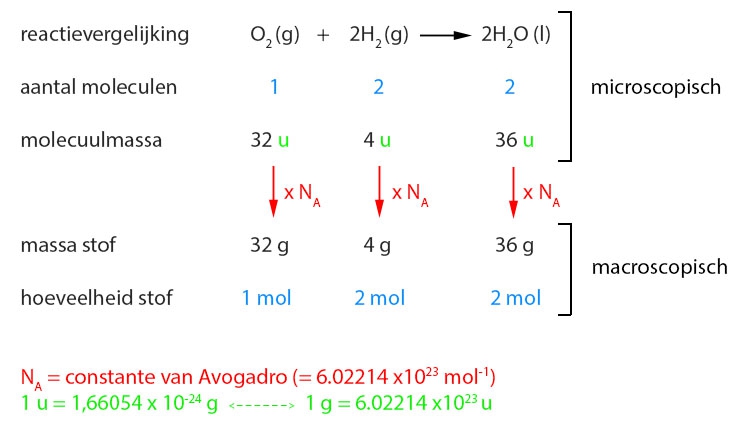
- Vakinhoudelijk deel van een thema 'Rekenen in de chemie', omgezet in een Wikiwijs arrangement vanuit een prototype van een kennisbank scheikunde van het voormalige Ruud de Moor Centrum van de OU; zie ook de colofon in het arrangement voor toelichting. Samenvatting Rekenen in de chemie gaat over kwantitatieve aspecten van de scheikunde. Behalve met de grootheden massa en volume werken we in dit thema met de grootheid hoeveelheid stof en de bijbehorende eenheid mol. We laten zien hoe we met behulp van de getalwaarde van de constante van Avogadro de 'microscopische' reactie tussen deeltjes kunnen vertalen naar een 'macroscopische' reactie tussen hoeveelheden stoffen (en omgekeerd). Maar eerst behandelen we de begrippen massabehoud en massaverhoudingen bij reacties wat uitgebreider dan we deden in een thema over chemische reacties en datzelfde doen we met de begrippen massasamenstelling (aansluitend op een thema over atomen en moleculen) en overmaat (dat we al eens tegenkwamen in een thema over zouten). Kennis van deze begrippen is van belang om te kunnen werken met het begrip mol. Om te kunnen rekenen aan reacties moeten we ook weten wat de begrippen concentratie en molariteit inhouden. Na behandeling van deze begrippen sluiten we dit hoofdstuk af met voorbeelden van berekeningen aan chemische reacties.
- Leerniveau
- HAVO 4; VWO 6; HAVO; VWO; HAVO 5; VWO 4; VWO 5;
- Leerinhoud en doelen
- Scheikunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 0 uur 50 minuten
Bronnen
| Bron | Type |
|---|---|
|
Reactievergelijkingen maken https://youtu.be/3hSObcW-mGY?rel=0 |
Video |
|
De mol, deel 1 https://youtu.be/YDgZJXciB2Y?rel=0 |
Video |
|
De mol, deel 2 https://youtu.be/j0otAjVDixQ?rel=0 |
Video |
|
Oefenen met de mol, deel 1 https://youtu.be/nOKF2sl4XaU?rel=0 |
Video |
|
Oefenen met de mol, deel 2 https://youtu.be/82n4e1IK9Ro?rel=0 |
Video |
|
Videosamenvatting van 'De mol, een SI-eenheid' https://youtu.be/zSjqELPevhA?rel=0 |
Video |
|
De molariteit, deel 1 https://youtu.be/rduJlCYlyoY?rel=0 |
Video |
|
De molariteit, deel 2 https://youtu.be/pH3bYsj7wgc?rel=0 |
Video |
|
Massapercentages berekenen https://youtu.be/APTIZjS0J1U?rel=0 |
Video |
|
Oefenen met de mol (1) https://youtu.be/nOKF2sl4XaU?rel=0 |
Video |
|
Oefenen met de mol (2) https://youtu.be/82n4e1IK9Ro?rel=0 |
Video |
|
Samenvatting https://youtu.be/zSjqELPevhA |
Video |
Gebruikte Wikiwijs Arrangementen
Lutgerink, Jan. (2013).
Sk-10 Rekenen in de chemie