Het arrangement Vmbo thematisch is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 09-12-2025 16:00:12
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Vmbo lessen volgens modeldidactiek
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Gebruikte Wikiwijs Arrangementen
Modeldidactiek. (2025).
03 Practicum schaduwen
Modeldidactiek. (2025).
04 Practicum spiegels met lichtkastjes
https://maken.wikiwijs.nl/214451/04_Practicum_spiegels_met_lichtkastjes
Modeldidactiek. (z.d.).
Bovenbouw havo/vwo thematisch
https://maken.wikiwijs.nl/212637/Bovenbouw_havo_vwo_thematisch
Modeldidactiek. (z.d.).
Demoles Optica: introductie licht
https://maken.wikiwijs.nl/207489/Demoles_Optica__introductie_licht
Modeldidactiek. (z.d.).
Oefening krachten tekenen met snelle feedback
https://maken.wikiwijs.nl/207479/Oefening_krachten_tekenen_met_snelle_feedback
Modeldidactiek. (z.d.).
Oefenles Optica: stralendiagrammen
https://maken.wikiwijs.nl/207522/Oefenles_Optica__stralendiagrammen
Modeldidactiek. (z.d.).
Practicum botsende treintjes
https://maken.wikiwijs.nl/207469/Practicum_botsende_treintjes
Modeldidactiek. (z.d.).
Practicum massa en gewicht
Modeldidactiek. (2025).
Practicum stofeigenschappen
https://maken.wikiwijs.nl/219373/Practicum_stofeigenschappen
Modeldidactiek. (2024).
Practicum Vaardigheden: Ohmse weerstand
https://maken.wikiwijs.nl/207526/Practicum_Vaardigheden__Ohmse_weerstand
Modeldidactiek. (z.d.).
Practicum Verdamping en Condensatie met Concept Cartoon
https://maken.wikiwijs.nl/207492/Practicum_Verdamping_en_Condensatie_met_Concept_Cartoon
Modeldidactiek. (z.d.).
Practicum videometen treintje
https://maken.wikiwijs.nl/207461/Practicum_videometen_treintje
Modeldidactiek. (z.d.).
Practicum Warmtetransport
Modeldidactiek. (2025).
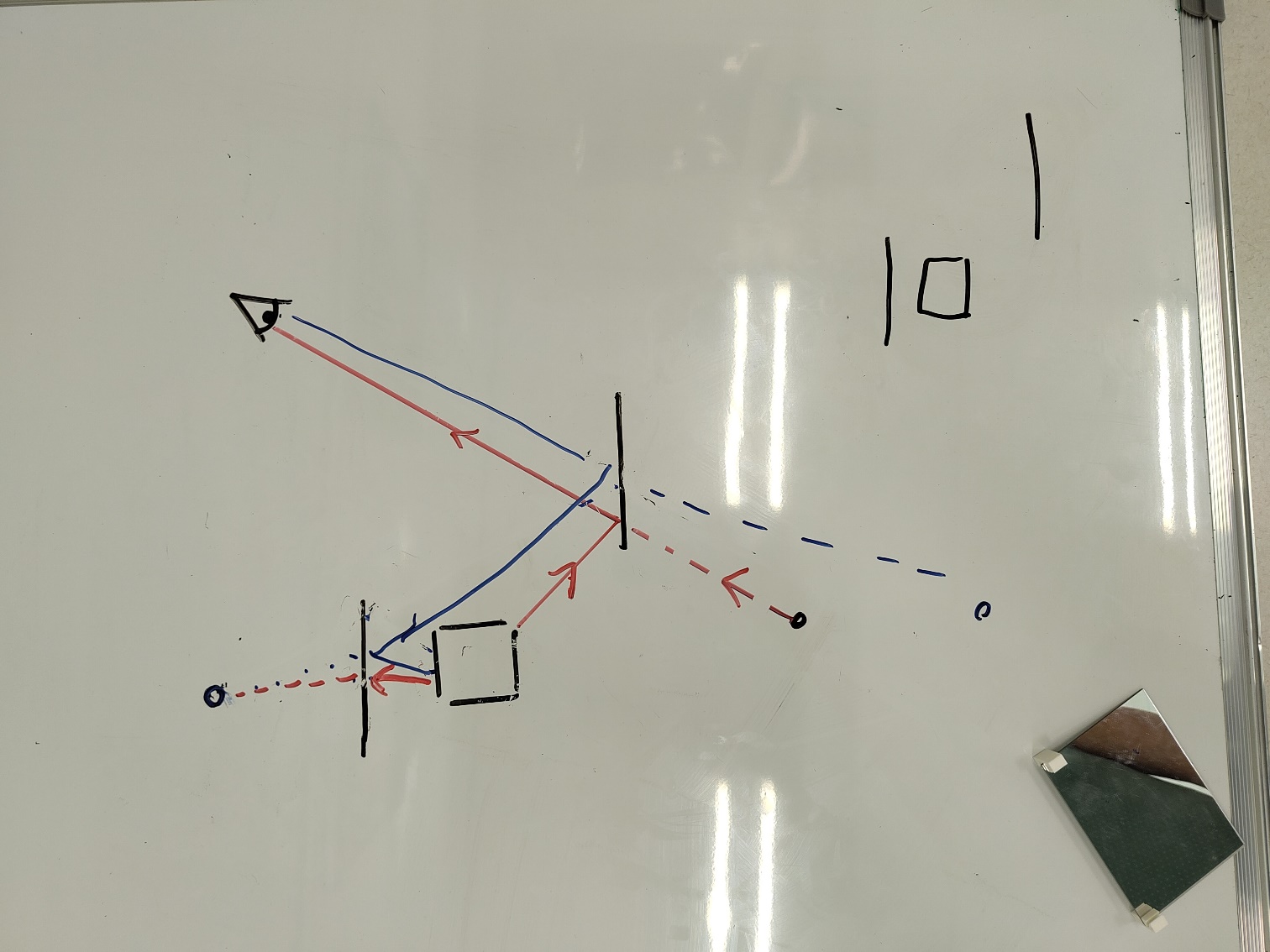
Practicum: Lichtstraal bij twee spiegels
https://maken.wikiwijs.nl/221361/Practicum__Lichtstraal_bij_twee_spiegels
Modeldidactiek. (2025).
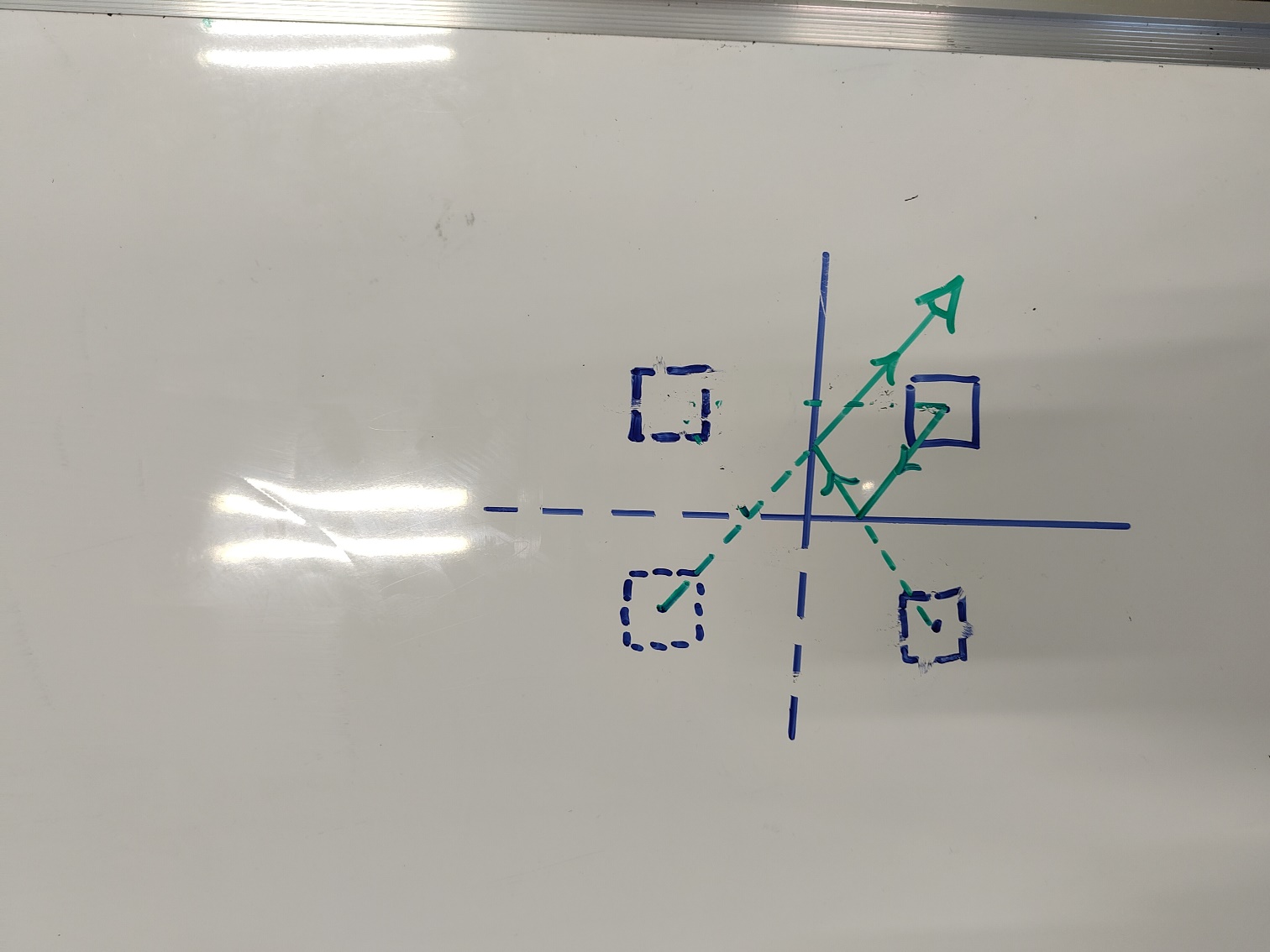
Practicum: spiegelen met blokken
https://maken.wikiwijs.nl/221360/Practicum__spiegelen_met_blokken


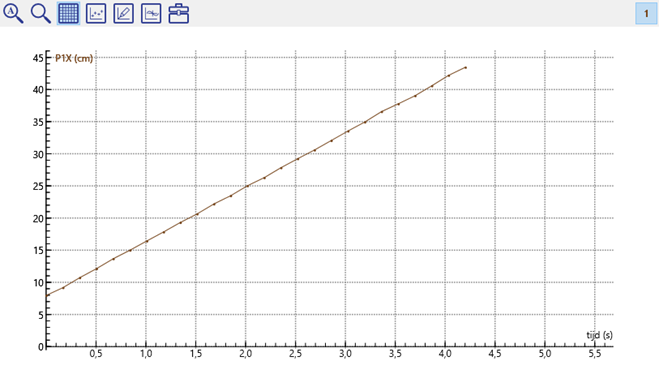
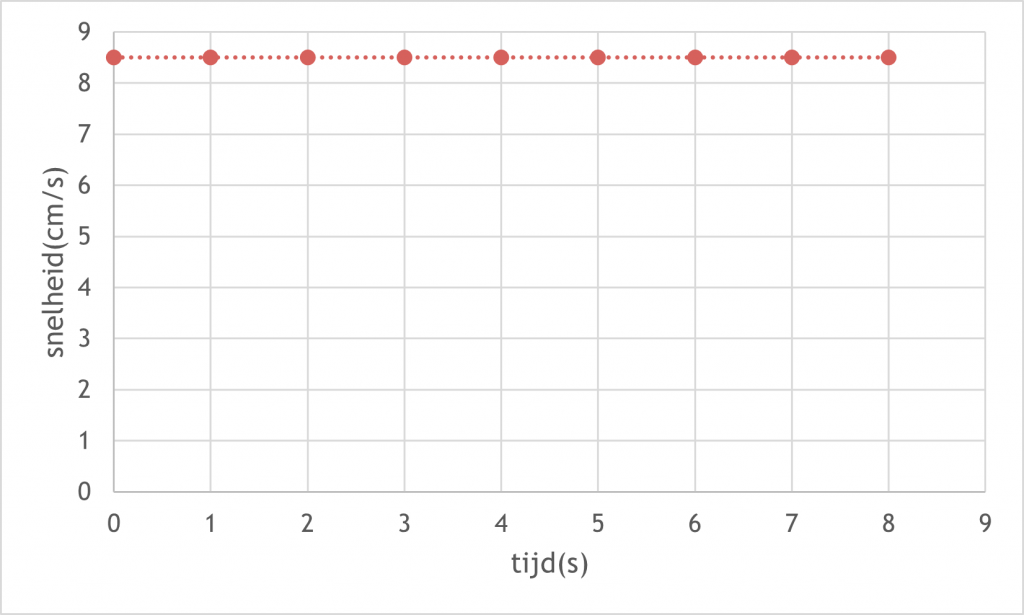
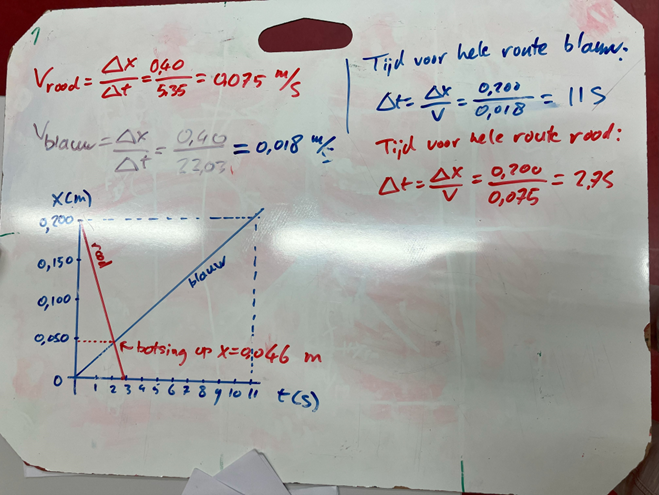
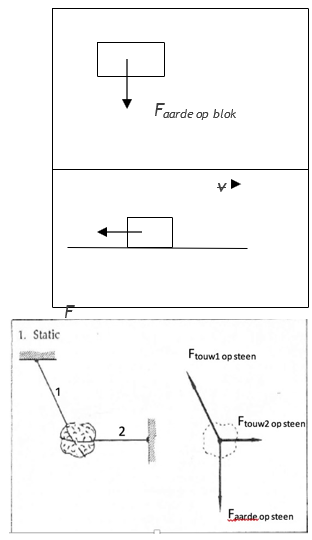
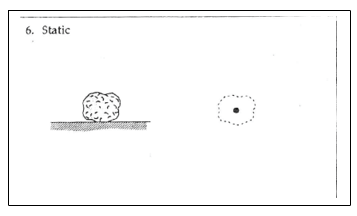
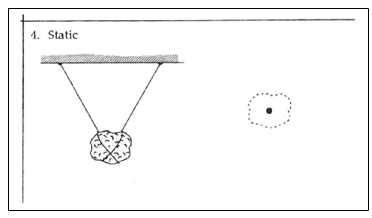
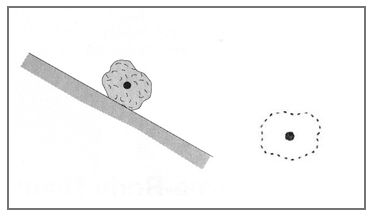
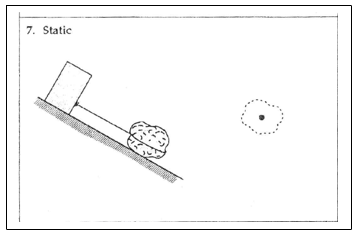
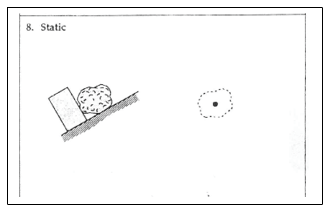
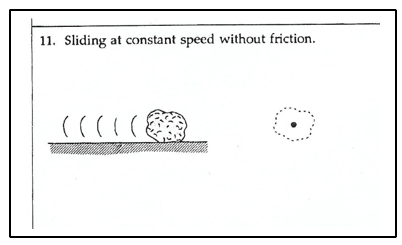
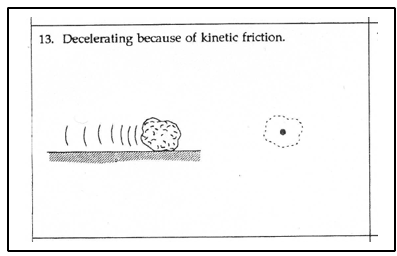


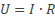
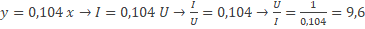

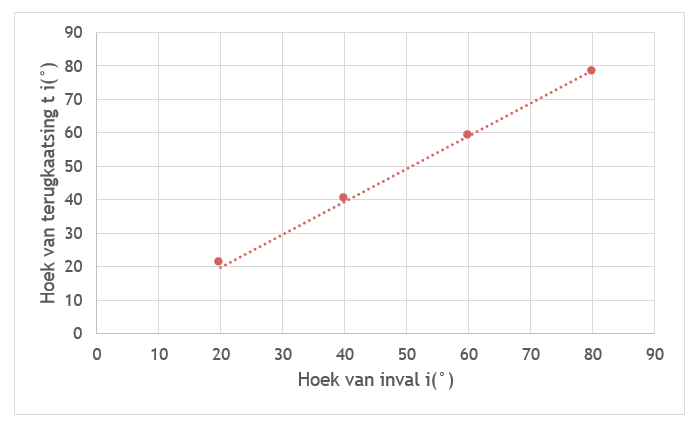


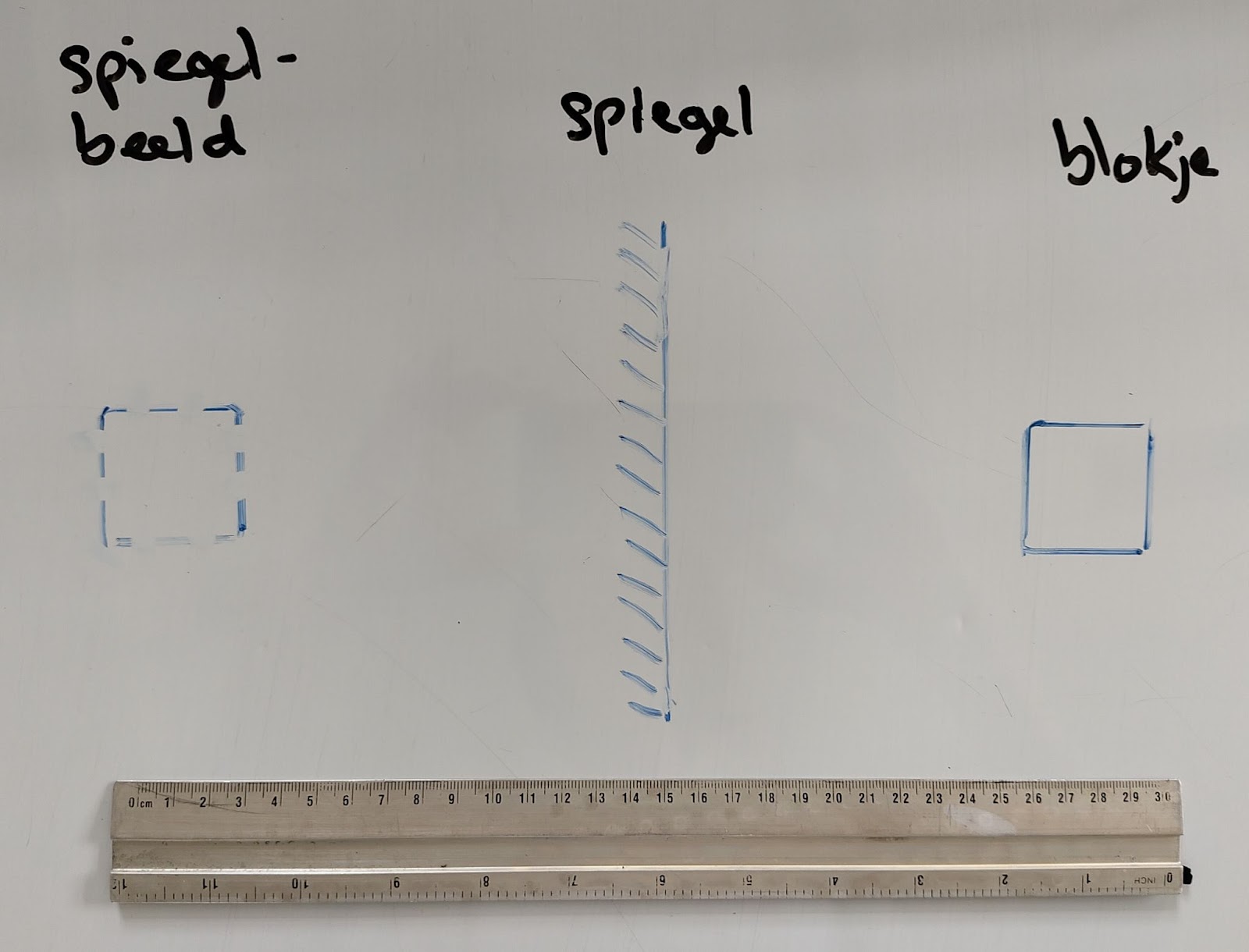


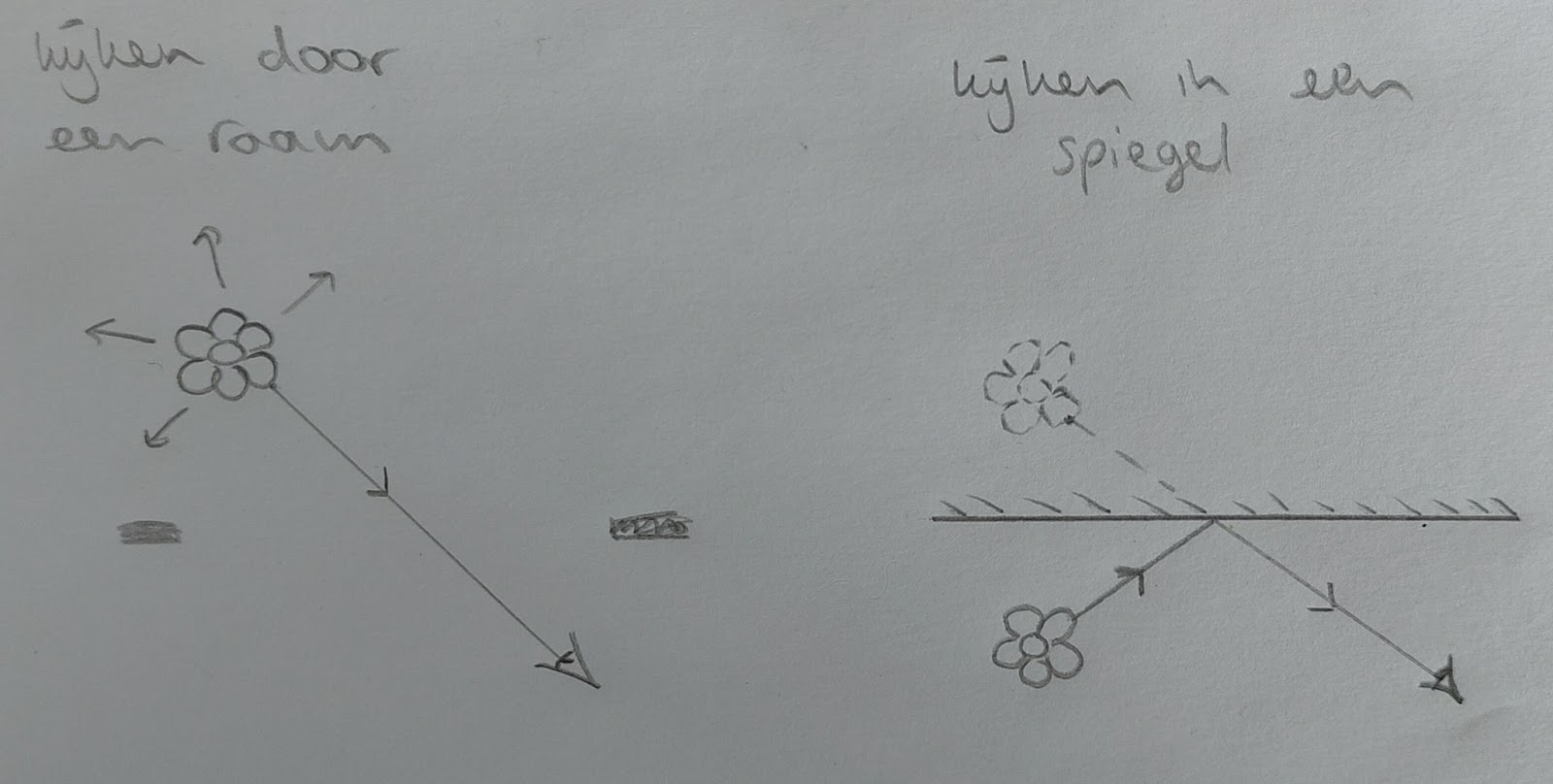
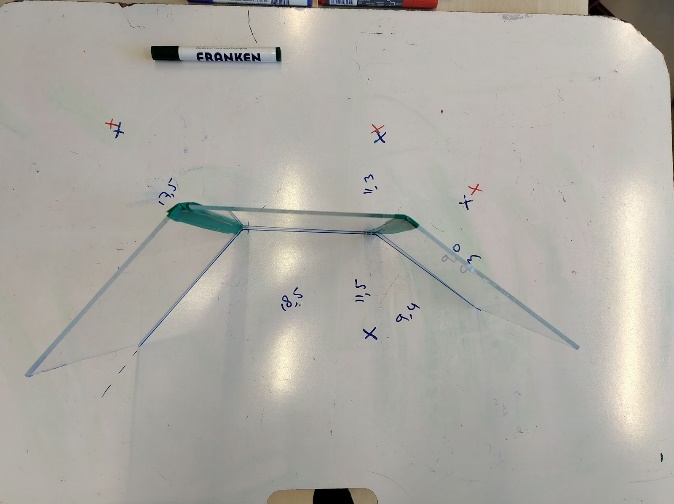
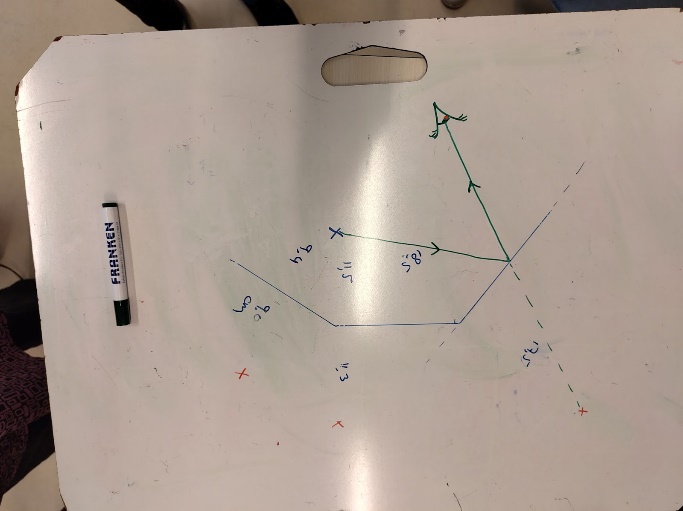
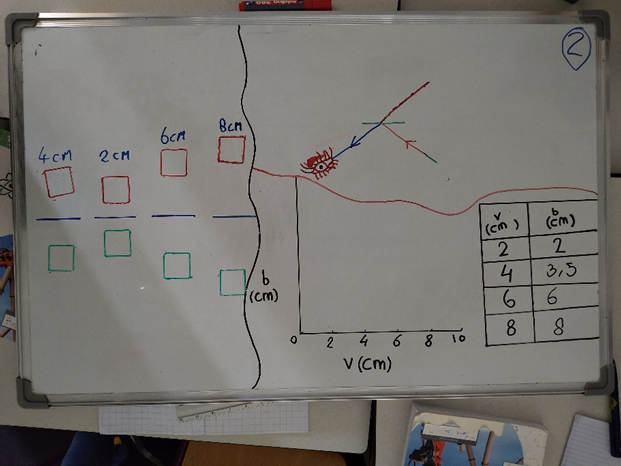











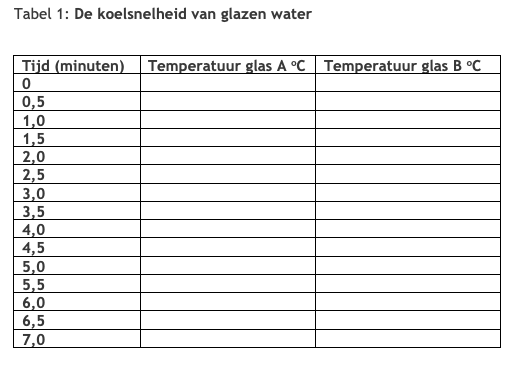
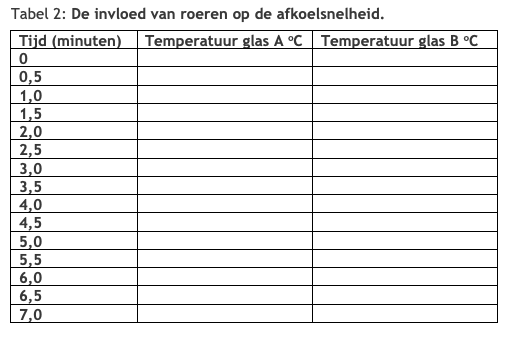

 Noteer dichtheid als verhouding:
Noteer dichtheid als verhouding: