Het arrangement Schrapselsom is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 14-11-2024 11:08:24
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
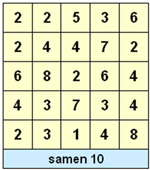
- Bij Schrapselsom gaat het officieel om optellen maar ook aanvullen tot .... komt aan bod. Het getalgebied tot 20 is favoriet. Splitskennis staat centraal. Met name de ?samen 10? schrapselsommen vormen in de groepen 3 en 4 een welkome variatie op de traditionele oefenstof rond het getal 10. Op speelse wijze kunnen die puzzels bijdragen aan kennis van relaties die onder de dekmantel van 10 verborgen zitten. Het gaat daarbij niet alleen om de bekende splitsingen zoals 6-4 en 2-8 maar ook om combinaties zoals 3-3-4 en 1-2-3-4. De schrapselsom van figuur 2 laat dat zien.
- Leerniveau
- Primair onderwijs; PO groep 4; PO groep 7; PO groep 6; PO groep 5;
- Leerinhoud en doelen
- Rekenen; Getallen en variabelen;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
- Trefwoorden
- fi, showcase_nl, spelhoek
Gebruikte Wikiwijs Arrangementen
Freudenthal Instituut. (z.d.).
Sjabloon [NIET WEGGOOIEN OF AANPASSEN!]
https://maken.wikiwijs.nl/207790/Sjabloon__NIET_WEGGOOIEN_OF_AANPASSEN__

 Universiteit Utrecht
Universiteit Utrecht