Colofon
Het arrangement Practicum 3 Trillingen: Energiehuishouding massa-veersysteem is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 17-12-2024 12:37:28
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Dit onderzoek bouwt verder op de meetgegevens van practicum 2. Leerlingen onderzoeken hier de energiehuishouding van het massa-veersysteem. Naast de metingen van practicum 2 heb je ook de massa en de veerconstante nodig van practicum 2. In dit practicum kun je de invloed van de zwaarte-energie meenemen of niet. Aan het eind van deze practicumbeschrijving wordt uitgelegd waarom je de invloed van de zwaarte-energie niet hoeft mee te nemen. Het is ook mogelijk om dit experiment uit te voeren op een luchtkussenbaan. Dan is er geen discussie over de zwaarte-energie.
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
- Trefwoorden
- iol, modeldidactiek, nvon, trillingen
Gebruikte Wikiwijs Arrangementen
Modeldidactiek. (z.d.).
Practicum 5 Trillingen: Bouw je eigen klok
https://maken.wikiwijs.nl/207487/Practicum_5_Trillingen__Bouw_je_eigen_klok










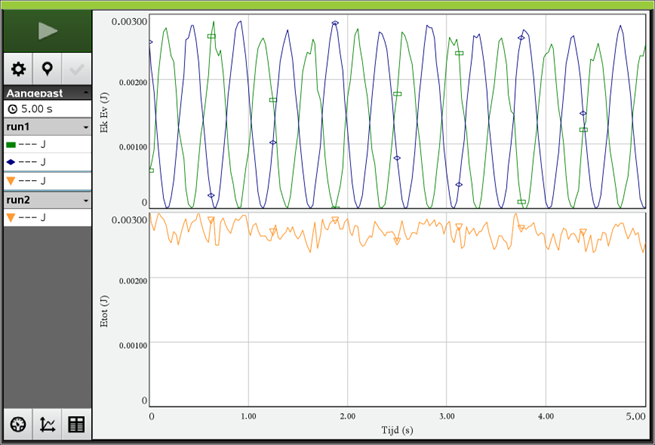

 In het figuur hiernaast zie je een massa aan een veer. Als er geen massa aanhangt dan komt de veer tot A. Met de massa er aan komt de veer in rust tot C. Hij rekt dan h uit. De veer oscilleert tussen B en D.
In het figuur hiernaast zie je een massa aan een veer. Als er geen massa aanhangt dan komt de veer tot A. Met de massa er aan komt de veer in rust tot C. Hij rekt dan h uit. De veer oscilleert tussen B en D.