Het arrangement Meetkunde is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 04-07-2023 01:34:34
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Het onderdeel van wiskunde dat zich bezighoudt met de eigenschappen van punten, lijnen en lichaam.
- Leerniveau
- MBO, Niveau 4: Middenkaderopleiding;
- Leerinhoud en doelen
- Rekenen/wiskunde; Meten en meetkunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld

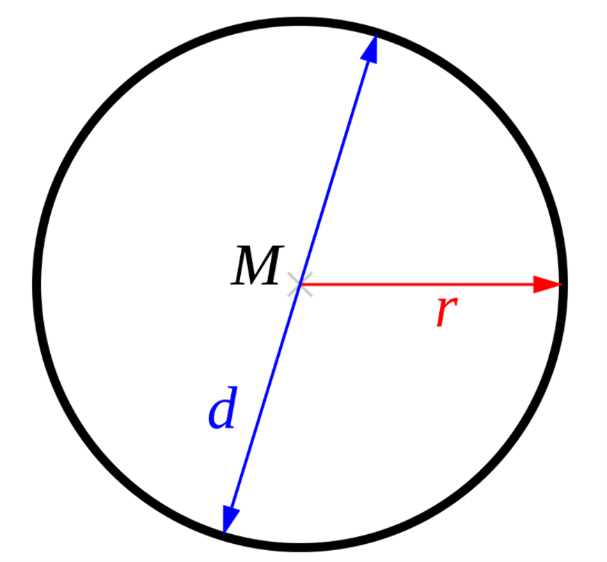
 Het is de afstand van cirkel tot cirkel door het middelpunt. De straal is de afstand van het middelpunt tot de cirkel, de straal kort je af met de letter
Het is de afstand van cirkel tot cirkel door het middelpunt. De straal is de afstand van het middelpunt tot de cirkel, de straal kort je af met de letter 
 Oppervlakte van een cirkel:
Oppervlakte van een cirkel: 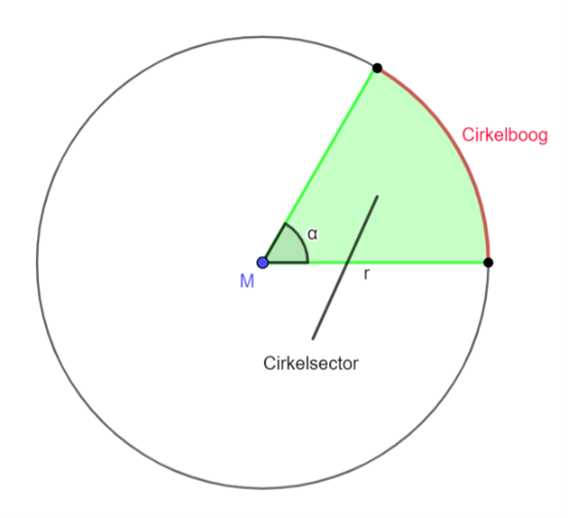

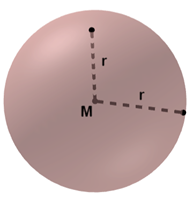 Is een cirkel een tweedimensionaal figuur, een bol is een driedimensionaal lichaam waarvan alle punten op het oppervlak van de bol op eenzelfde afstand tot het middelpunt van de bol liggen. Alle resterende punten van de bol liggen binnen dit oppervlak. Het oppervlak wordt ook sfeer genoemd. Veel voorwerpen uit de praktijk zijn een bol, denk aan een voetbal of tennisbal. Ook planeten zijn een bol, weliswaar zijn de polen van planeten wat afgeplat.
Is een cirkel een tweedimensionaal figuur, een bol is een driedimensionaal lichaam waarvan alle punten op het oppervlak van de bol op eenzelfde afstand tot het middelpunt van de bol liggen. Alle resterende punten van de bol liggen binnen dit oppervlak. Het oppervlak wordt ook sfeer genoemd. Veel voorwerpen uit de praktijk zijn een bol, denk aan een voetbal of tennisbal. Ook planeten zijn een bol, weliswaar zijn de polen van planeten wat afgeplat.
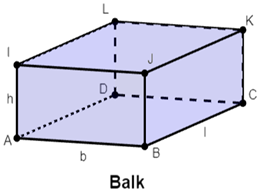
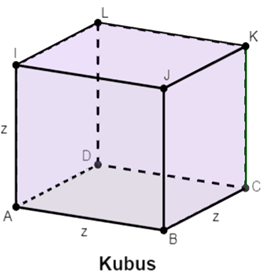
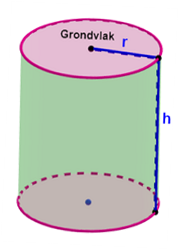
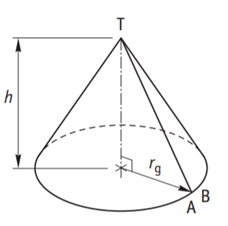
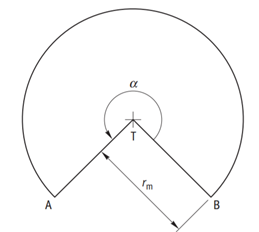
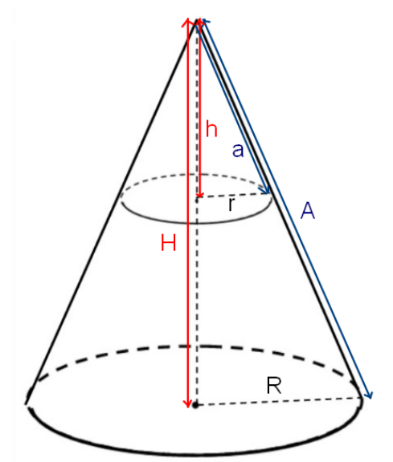
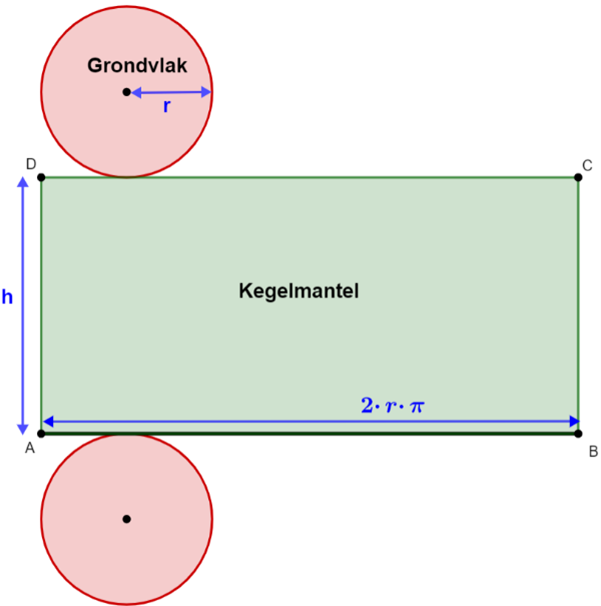 Om de oppervlakte van een cilinder te berekenen tel je de oppervlakte van de grondvlak, bovenvlak en de mantel van de cilinder bij elkaar op. De grond- en bovenvlak van een cilinder zijn cirkels. De oppervlakte van de cilindermantel bereken je door de breedte van de kegelmantel te vermenigvuldigen met de hoogte van de cilinder. Een kegelmantel heeft als breedte de omtrek van het grondvlak.
Om de oppervlakte van een cilinder te berekenen tel je de oppervlakte van de grondvlak, bovenvlak en de mantel van de cilinder bij elkaar op. De grond- en bovenvlak van een cilinder zijn cirkels. De oppervlakte van de cilindermantel bereken je door de breedte van de kegelmantel te vermenigvuldigen met de hoogte van de cilinder. Een kegelmantel heeft als breedte de omtrek van het grondvlak.