Het arrangement Kennisbanken Wiskunde vmbo-kgt12 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 04-10-2025 20:37:32
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- In dit arrangement vind je alle kennisbanken bij elkaar die gebruikt zijn voor de leerlijn Wiskunde vmbo-b12.
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Gebruikte Wikiwijs Arrangementen
VO-content - Kennisbanken. (2025).
Aftrekken met negatieve getallen
https://maken.wikiwijs.nl/107332/Aftrekken_met_negatieve_getallen
VO-content - Kennisbanken. (2023).
Aftreksommen met grote getallen
https://maken.wikiwijs.nl/197915/Aftreksommen_met_grote_getallen
VO-content - Kennisbanken. (2023).
Breuken optellen en aftrekken
https://maken.wikiwijs.nl/197916/Breuken_optellen_en_aftrekken
VO-content - Kennisbanken. (2023).
Breuken vergelijken
VO-content - Kennisbanken. (2023).
Breuken vermenigvuldigen
VO-content - Kennisbanken. (2023).
Decimale getallen
VO-content - Kennisbanken. (2023).
Grensvlakken en ribben
VO-content - Kennisbanken. (2023).
Hoeken berekenen
VO-content - Kennisbanken. (2025).
Inhoud kubus en balk
VO-content - Kennisbanken. (2025).
Kijklijnen en kijkhoeken
VO-content - Kennisbanken. (2025).
Lettervariabelen
VO-content - Kennisbanken. (2023).
Lijn, lijnstuk, punt
VO-content - Kennisbanken. (2025).
Negatief in het assenstelsel
https://maken.wikiwijs.nl/107334/Negatief_in_het_assenstelsel
VO-content - Kennisbanken. (2023).
Nog meer procenten
VO-content - Kennisbanken. (2025).
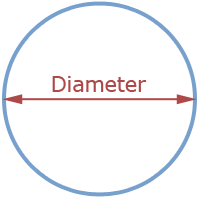
Oppervlakte cirkel
VO-content - Kennisbanken. (2025).
Oppervlakte parallellogram en driehoek
https://maken.wikiwijs.nl/204894/Oppervlakte_parallellogram_en_driehoek
VO-content - Kennisbanken. (2023).
Oppervlaktematen
VO-content - Kennisbanken. (2023).
Optellen en aftrekken
VO-content - Kennisbanken. (2023).
Optellen met grote getallen
https://maken.wikiwijs.nl/197919/Optellen_met_grote_getallen
VO-content - Kennisbanken. (2025).
Optellen met negatieve getallen
https://maken.wikiwijs.nl/107333/Optellen_met_negatieve_getallen
VO-content - Kennisbanken. (2023).
Passer en geodriehoek
VO-content - Kennisbanken. (2023).
Plaatsbepaling op de kaart
VO-content - Kennisbanken. (2023).
Procenten erbij of eraf
VO-content - Kennisbanken. (2025).
Rekenen met lettervariabelen
https://maken.wikiwijs.nl/107317/Rekenen_met_lettervariabelen
VO-content - Kennisbanken. (2023).
Rekenen met procenten
VO-content - Kennisbanken. (2025).
Rekenstappen in schema
VO-content - Kennisbanken. (2023).
Romeinse cijfers
VO-content - Kennisbanken. (2023).
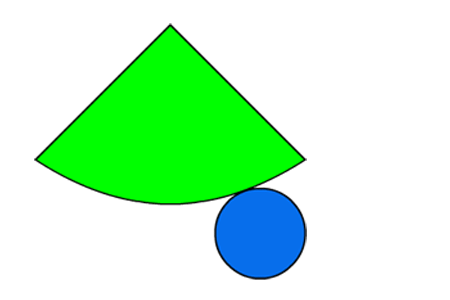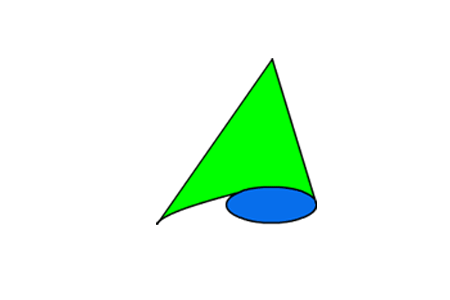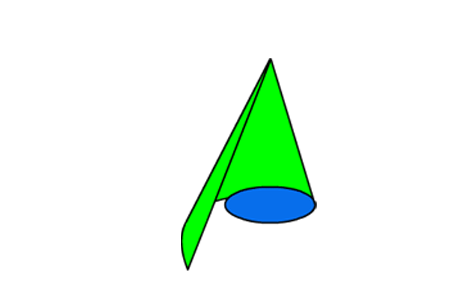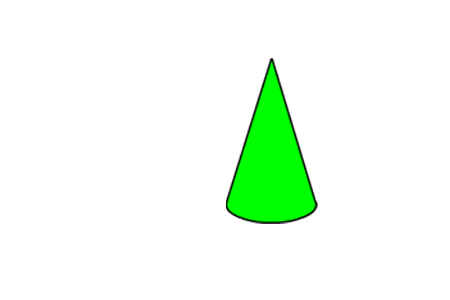
Ruimtelijke figuren
VO-content - Kennisbanken. (2023).
Som- en verschilgrafiek
VO-content - Kennisbanken. (2017).
Steel- en bladdiagram
VO-content - Kennisbanken. (2023).
Teller en noemer
VO-content - Kennisbanken. (2025).
Van formule naar grafiek
VO-content - Kennisbanken. (2023).
Verband en grafiek
VO-content - Kennisbanken. (2025).
Vergelijking en oplossing
VO-content - Kennisbanken. (2023).
Verhoudingen vergelijken
VO-content - Kennisbanken. (2023).
Verhoudingstabellen
VO-content - Kennisbanken. (2023).
Vermenigvuldigen
VO-content - Kennisbanken. (2023).
Vermenigvuldigen
VO-content - Kennisbanken. (2025).
Vermenigvuldigen met negatieve getallen
https://maken.wikiwijs.nl/107331/Vermenigvuldigen_met_negatieve_getallen
VO-content - Kennisbanken. (2025).
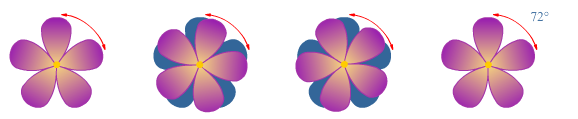
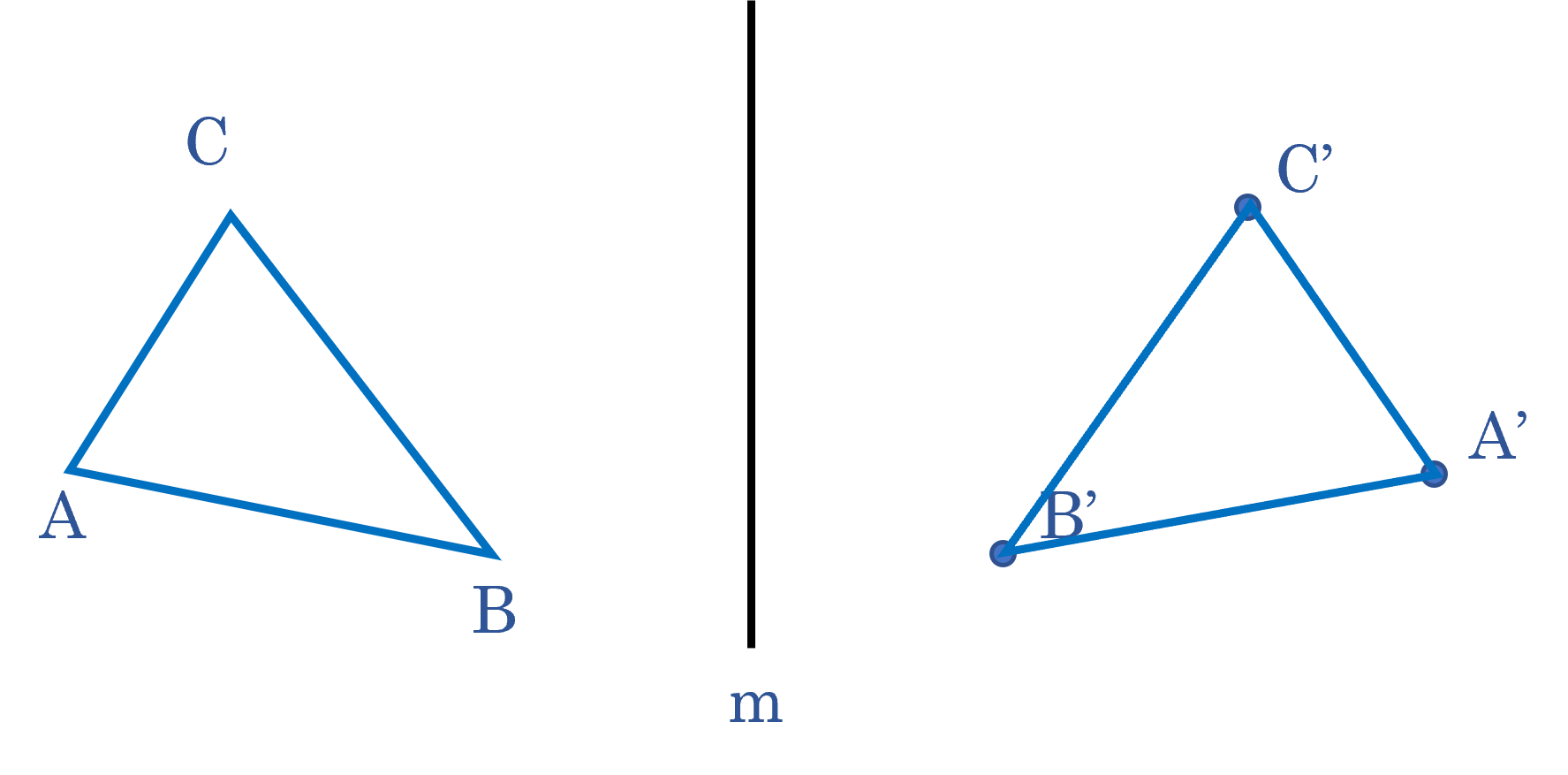
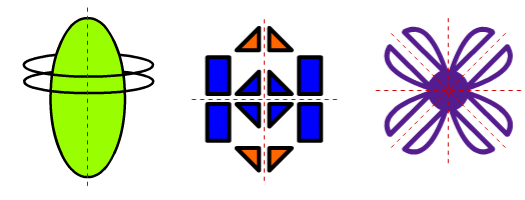
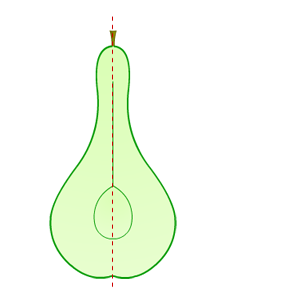
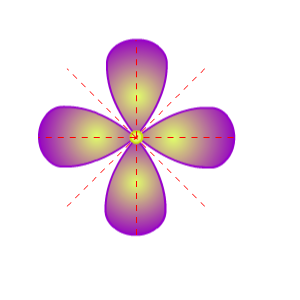
Vlakke figuren en symmetrie
https://maken.wikiwijs.nl/204973/Vlakke_figuren_en_symmetrie
VO-content - Kennisbanken. (2025).
Wat is negatief?

 Welkom bij de Kennisbank Wiskunde onderbouw vmbo.
Welkom bij de Kennisbank Wiskunde onderbouw vmbo.



 Emilie heeft drie proefwerken gehad voor wiskunde.
Emilie heeft drie proefwerken gehad voor wiskunde. Jochem heeft een fles cola.
Jochem heeft een fles cola.
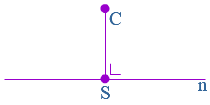
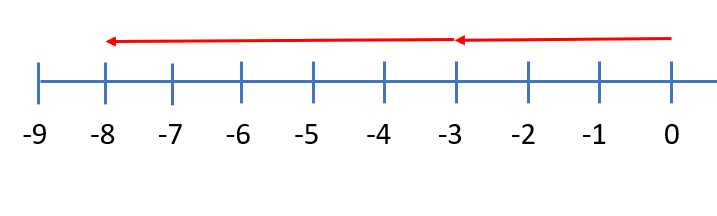
 Bekijk het verkeersbord.
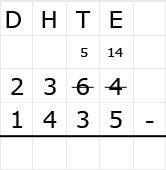
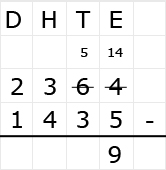
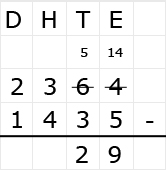
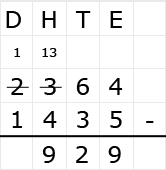
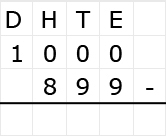
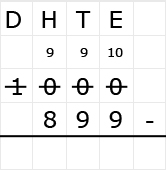
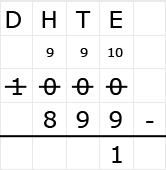
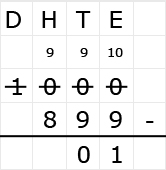
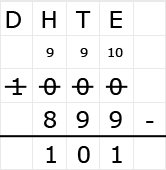
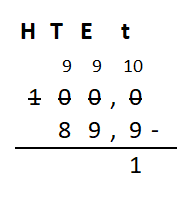
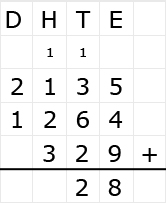
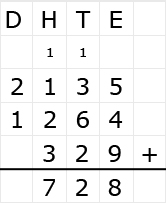
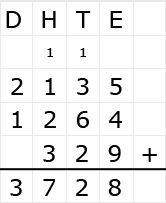
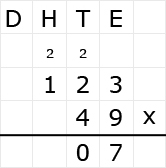
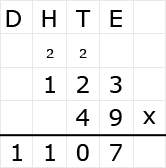
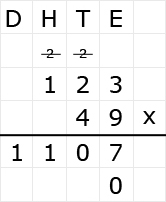
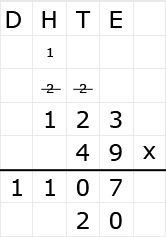
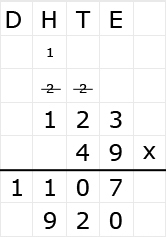
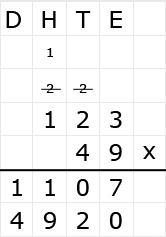
Bekijk het verkeersbord. Net als bij optelsommen, kun je aftreksommen met grote getallen het beste onder elkaar uitrekenen. Ook hiervoor hebben we weer een stappenplan.
Net als bij optelsommen, kun je aftreksommen met grote getallen het beste onder elkaar uitrekenen. Ook hiervoor hebben we weer een stappenplan. 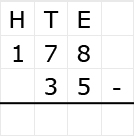

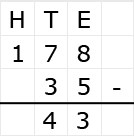
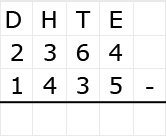
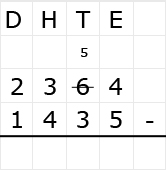
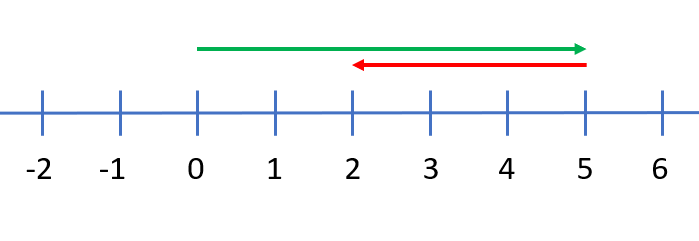
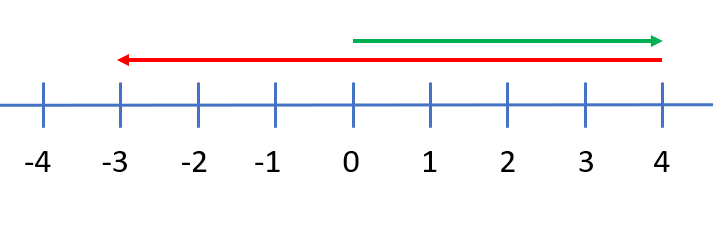
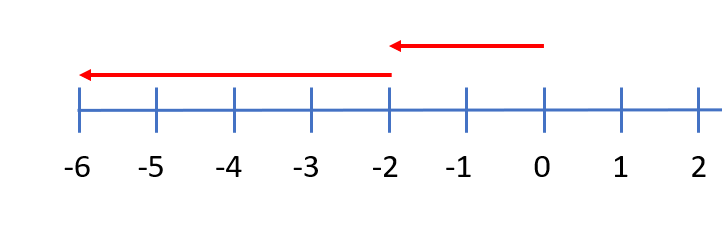
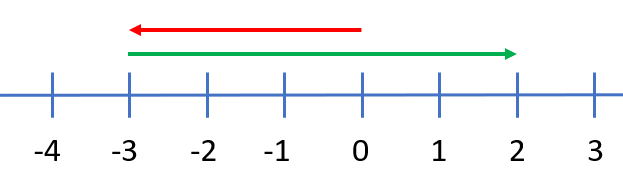
 Bij het aftrekken met negatieve getallen maak je gebruik van de regel:
Bij het aftrekken met negatieve getallen maak je gebruik van de regel: 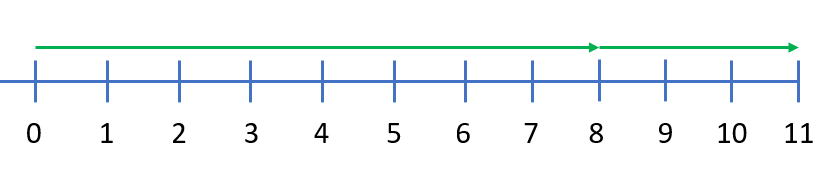
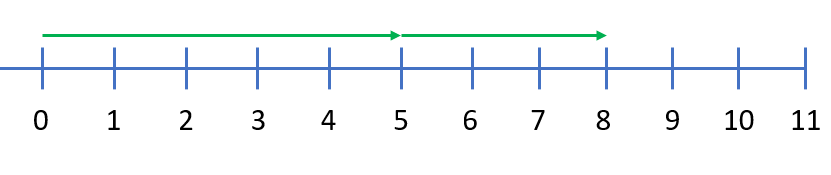

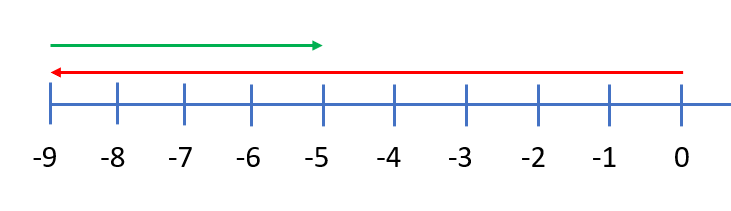




 Je ziet drie poppetjes. Een van de drie poppetjes is gekleurd.
Je ziet drie poppetjes. Een van de drie poppetjes is gekleurd.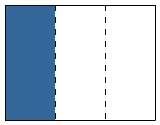 Breuken kun je zichtbaar maken in plaatjes.
Breuken kun je zichtbaar maken in plaatjes. Een breuk kun je als volgt in een decimaal getal omzetten. Je kunt dit controleren met je rekenmachine.
Een breuk kun je als volgt in een decimaal getal omzetten. Je kunt dit controleren met je rekenmachine. In een klas zitten evenveel jongens als meisjes.
In een klas zitten evenveel jongens als meisjes. Één vierde is hetzelfde als
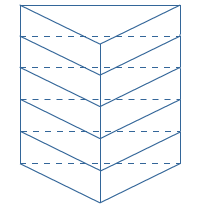
Één vierde is hetzelfde als  Bekijk de ketting hiernaast. De ketting heeft een vast patroon.
Bekijk de ketting hiernaast. De ketting heeft een vast patroon. In een klas zitten
In een klas zitten  In het stadion van FC Utrecht kunnen
In het stadion van FC Utrecht kunnen  De pizza is eerst in
De pizza is eerst in 



 Deze pizza is verdeeld in
Deze pizza is verdeeld in  Aan alle onderbouwleerlingen van een scholengemeenschap is gevraagd hoeveel zakgeld ze per maand krijgen.
Aan alle onderbouwleerlingen van een scholengemeenschap is gevraagd hoeveel zakgeld ze per maand krijgen. 

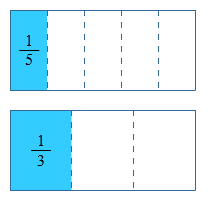 Soms helpt een plaatje bij het vergelijken van breuken.
Soms helpt een plaatje bij het vergelijken van breuken.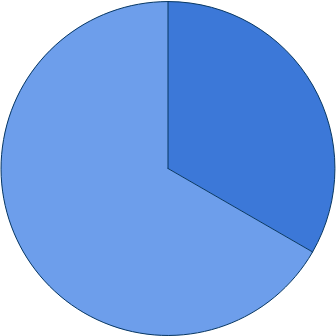
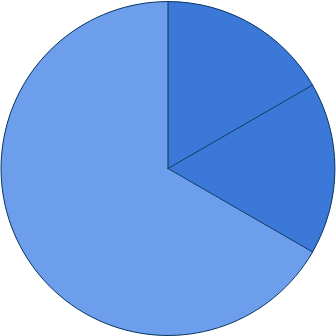
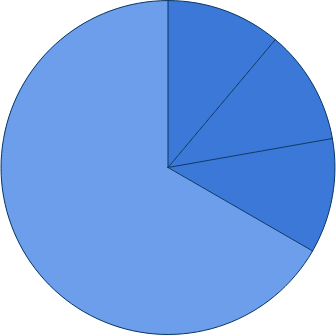





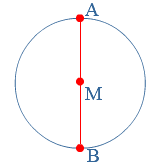
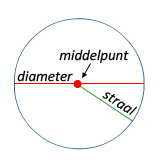
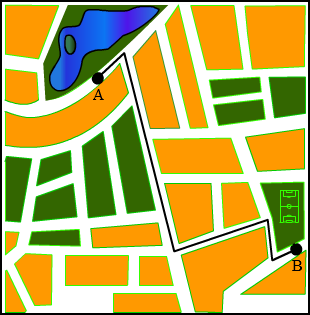
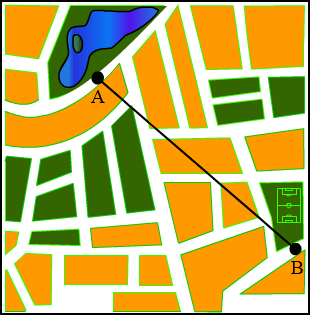
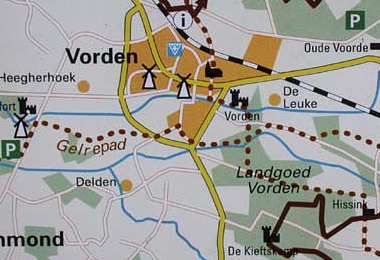
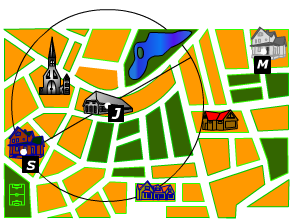 Je ziet de kaart van de stad waarin Joost woont.
Je ziet de kaart van de stad waarin Joost woont. Met een code schrijf je op een korte manier veel informatie op.
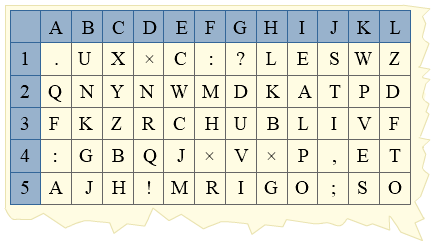
Met een code schrijf je op een korte manier veel informatie op.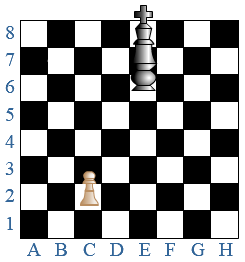 Je ziet een schaakbord.
Je ziet een schaakbord.

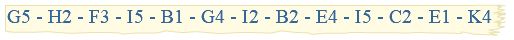
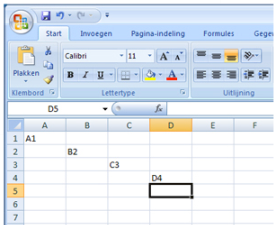 Het programma Excel is een rekenprogramma.
Het programma Excel is een rekenprogramma.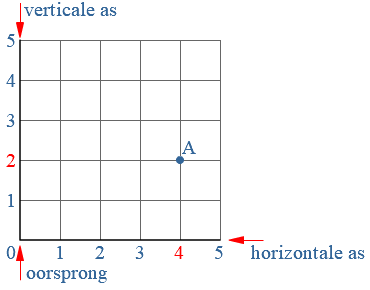 Een assenstelsel heeft een horizontale as en een verticale as.
Een assenstelsel heeft een horizontale as en een verticale as. Je werkt met decimale getallen.
Je werkt met decimale getallen.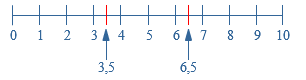
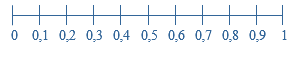
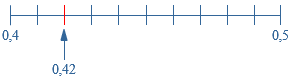

 Soms wil je getallen vermenigvuldigen.
Soms wil je getallen vermenigvuldigen.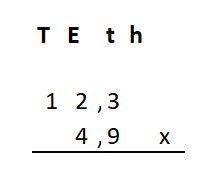
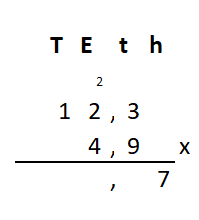
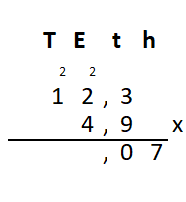
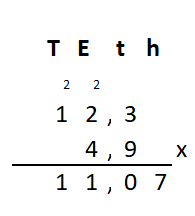
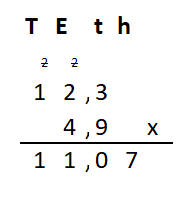
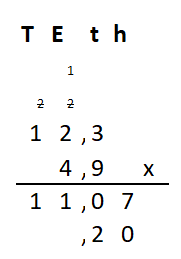
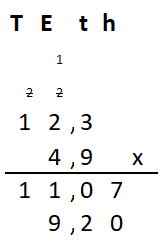
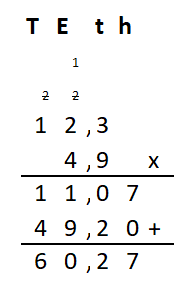

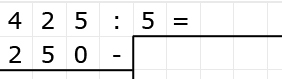
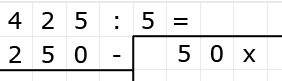
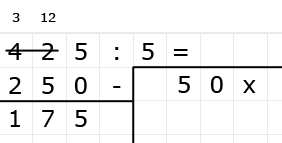
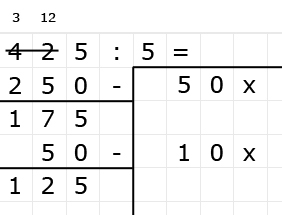
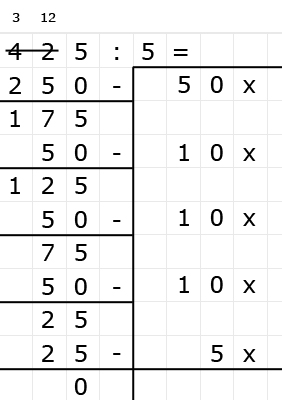
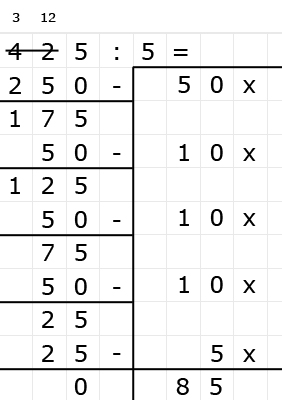
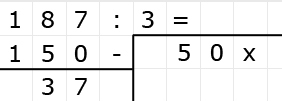
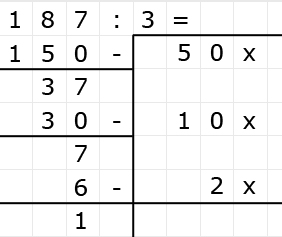
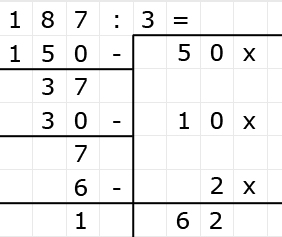
 Delen is precies het omgekeerde van vermenigvuldigen.
Delen is precies het omgekeerde van vermenigvuldigen.
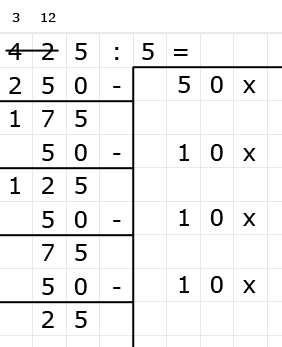


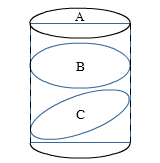
 Hier zie je een doorsnede van een boom.
Hier zie je een doorsnede van een boom.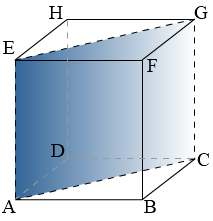

 Bij alles wat je doet, verbruik je energie.
Bij alles wat je doet, verbruik je energie.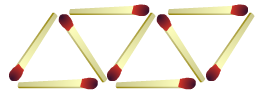 Met lucifers kun je driehoeken leggen.
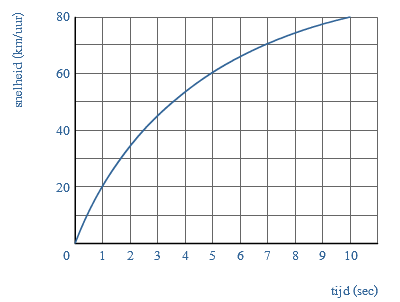
Met lucifers kun je driehoeken leggen. Je rijdt in een auto.
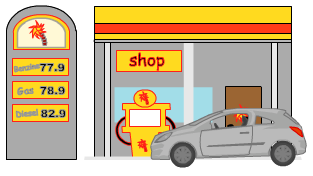
Je rijdt in een auto.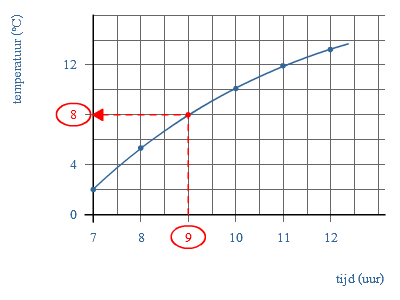
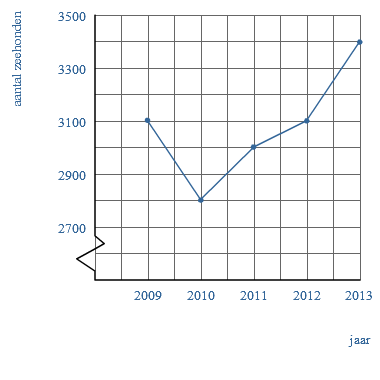 Een aantal jaar is het
Een aantal jaar is het 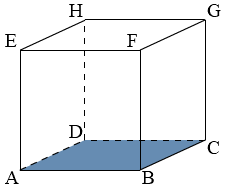
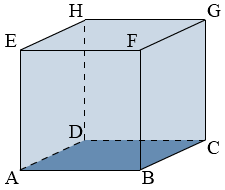
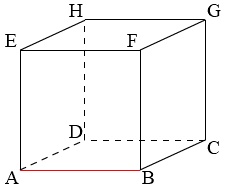
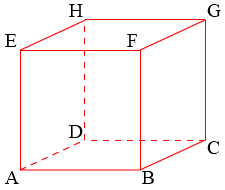
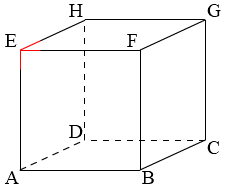

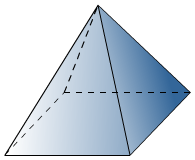
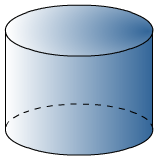

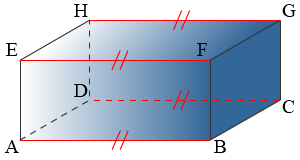
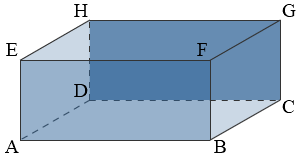
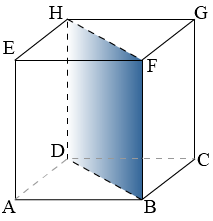
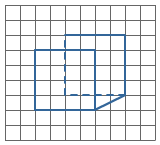
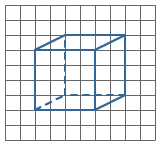
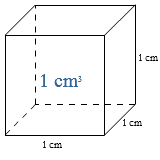
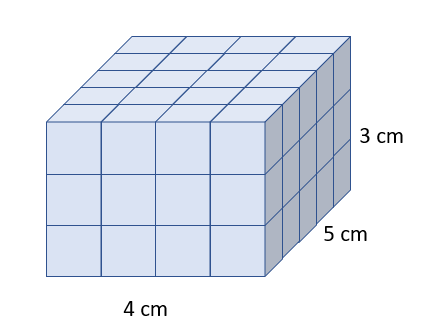
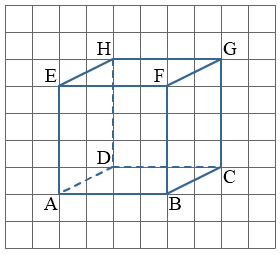 Van een kubus zijn alle ribben gelijk.
Van een kubus zijn alle ribben gelijk.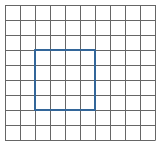
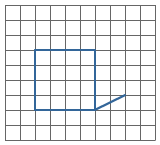
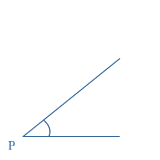
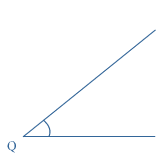
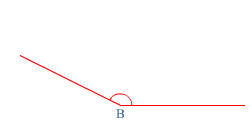
 Iedere hoek heeft een hoekpunt en twee benen.
Iedere hoek heeft een hoekpunt en twee benen.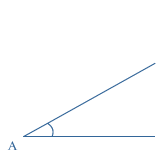
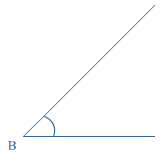


 Bekijk de klok.
Bekijk de klok.
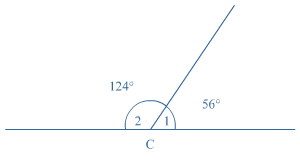
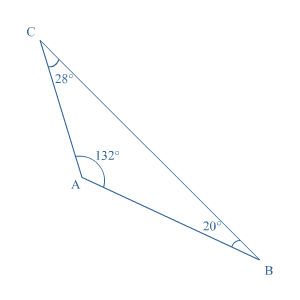 In iedere driehoek geldt dat de drie hoeken samen
In iedere driehoek geldt dat de drie hoeken samen 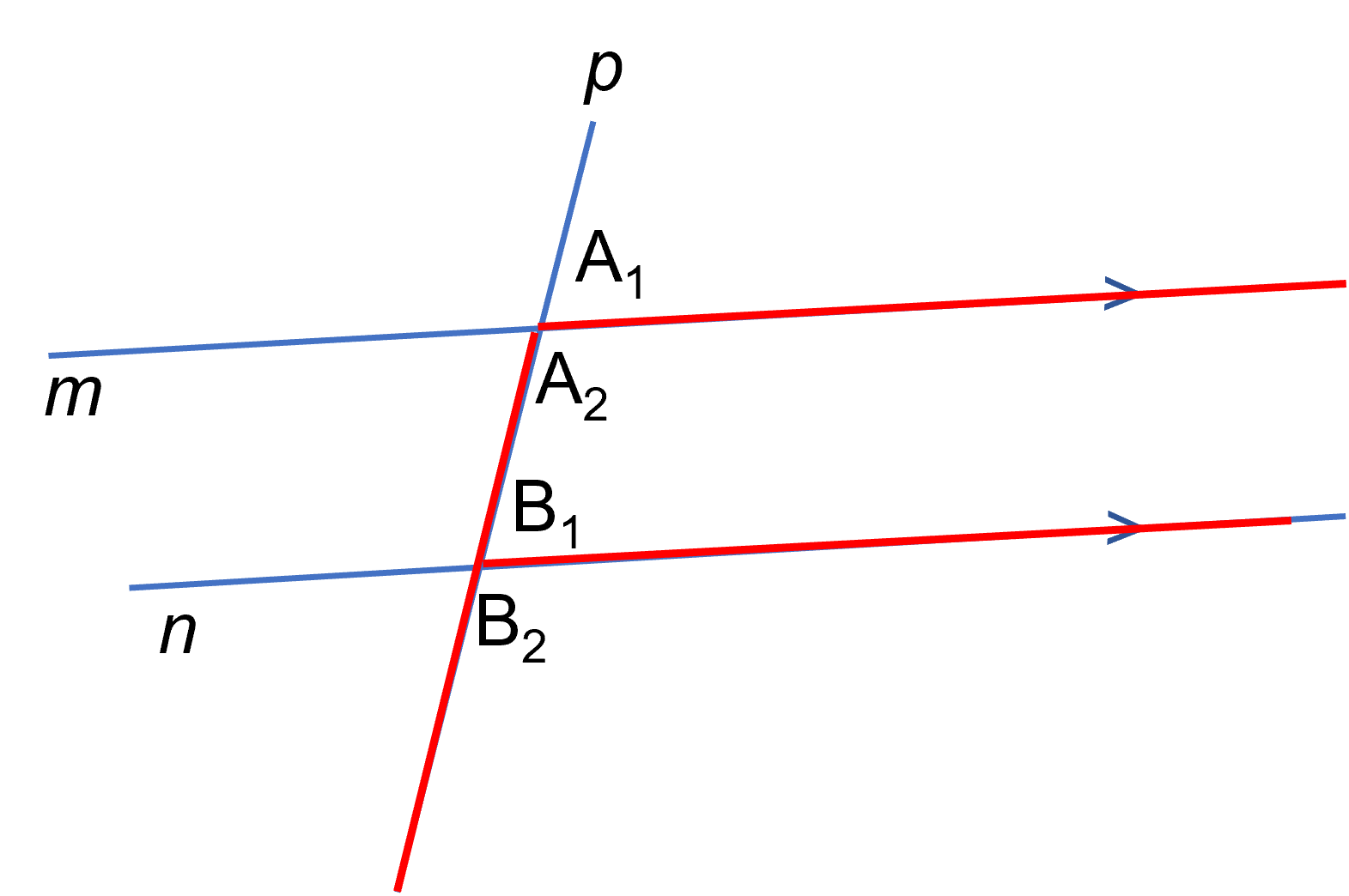
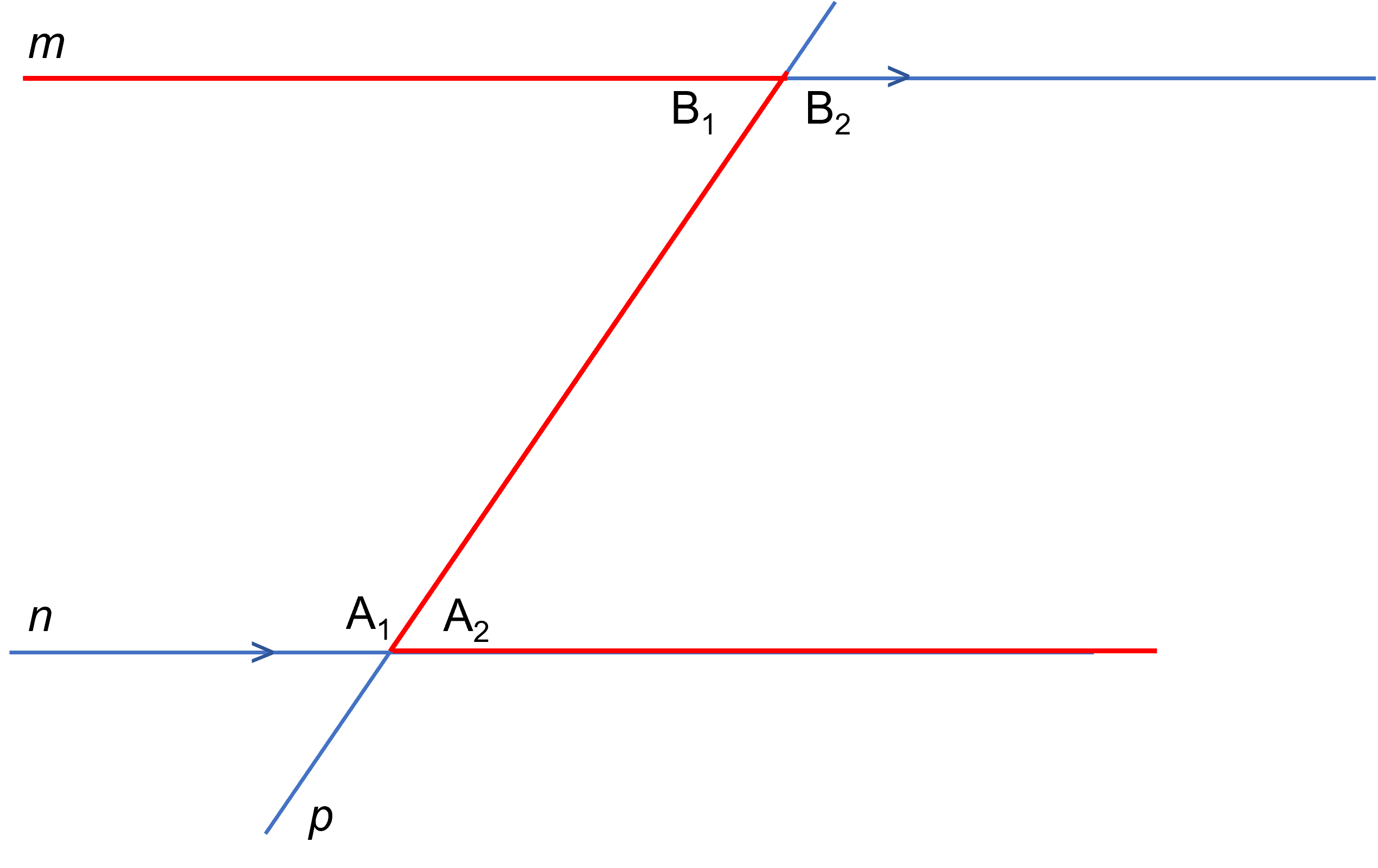
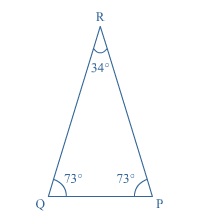 Je ziet driehoek
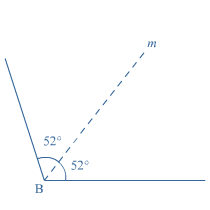
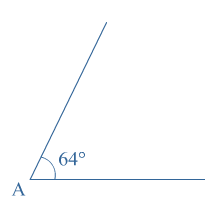
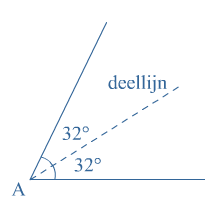
Je ziet driehoek  Een rechte hoek is verdeeld in
Een rechte hoek is verdeeld in 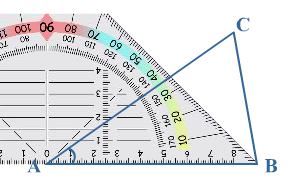
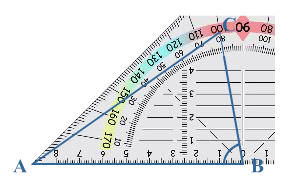
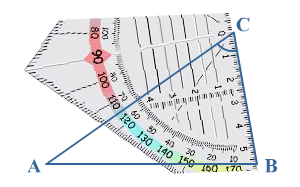
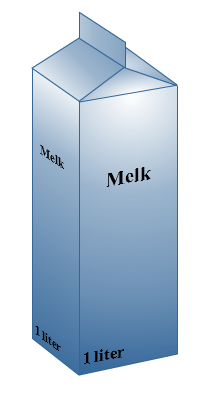 Hiernaast zie je een literpak melk.
Hiernaast zie je een literpak melk.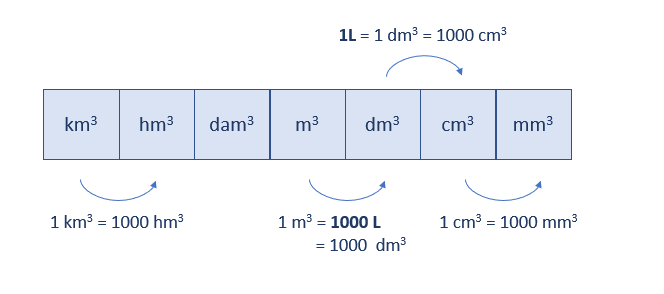
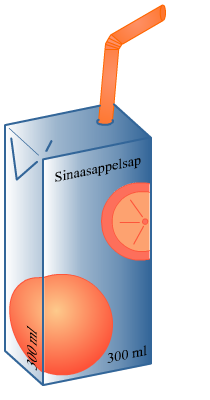 De bodem van het pakje
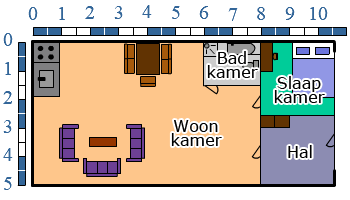
De bodem van het pakje 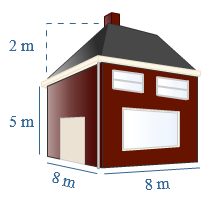 Hiernaast zie je een tekening van het huis.
Hiernaast zie je een tekening van het huis.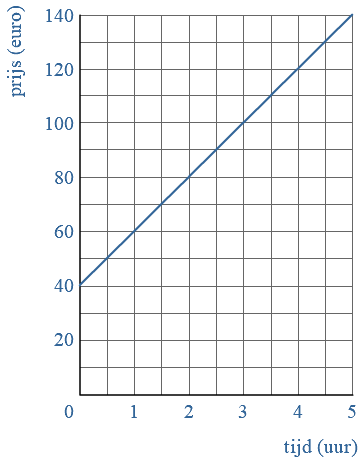 Lineair verband in een grafiek
Lineair verband in een grafiek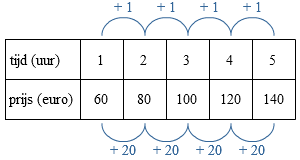
 Er zijn veel verschillende aanbieders van mobiele telefonie.
Er zijn veel verschillende aanbieders van mobiele telefonie.
 Een volledig spel kaarten bestaat uit: 52 kaarten.
Een volledig spel kaarten bestaat uit: 52 kaarten. Je hebt een toets.
Je hebt een toets.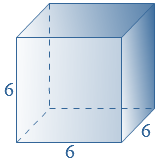 De ribben van de kubus zijn
De ribben van de kubus zijn 

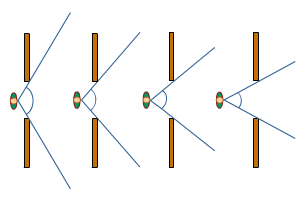
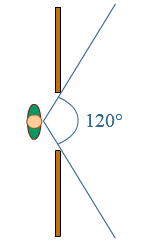
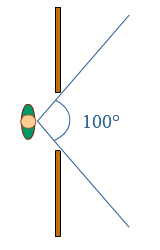
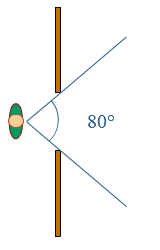
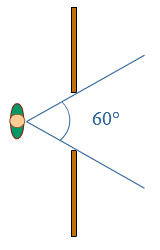
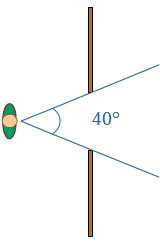
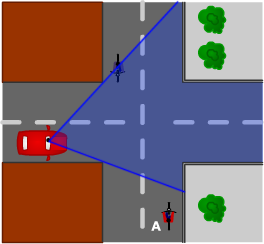 Je ziet twee fietsers en een auto.
Je ziet twee fietsers en een auto.


 Jelmer heeft een vierkant kamer.
Jelmer heeft een vierkant kamer.
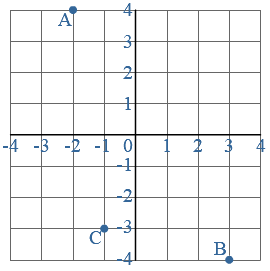
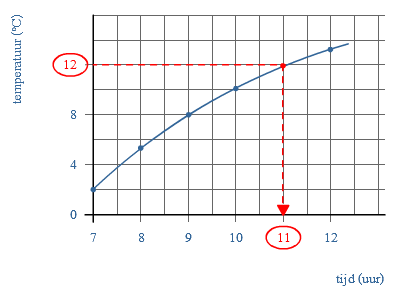
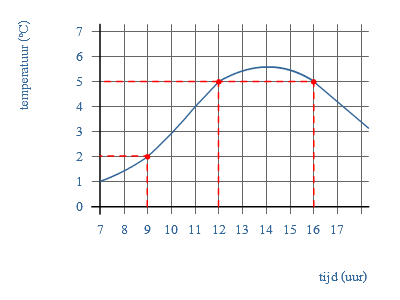
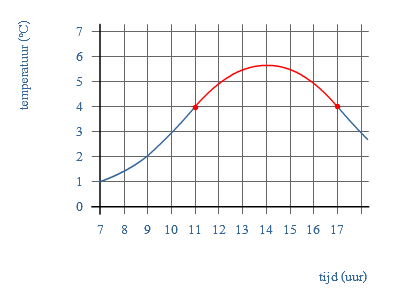
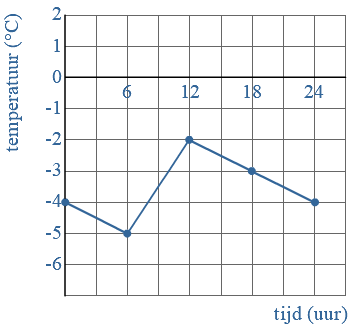 Hier zie je een temperatuur grafiek op een dag in januari.
Hier zie je een temperatuur grafiek op een dag in januari.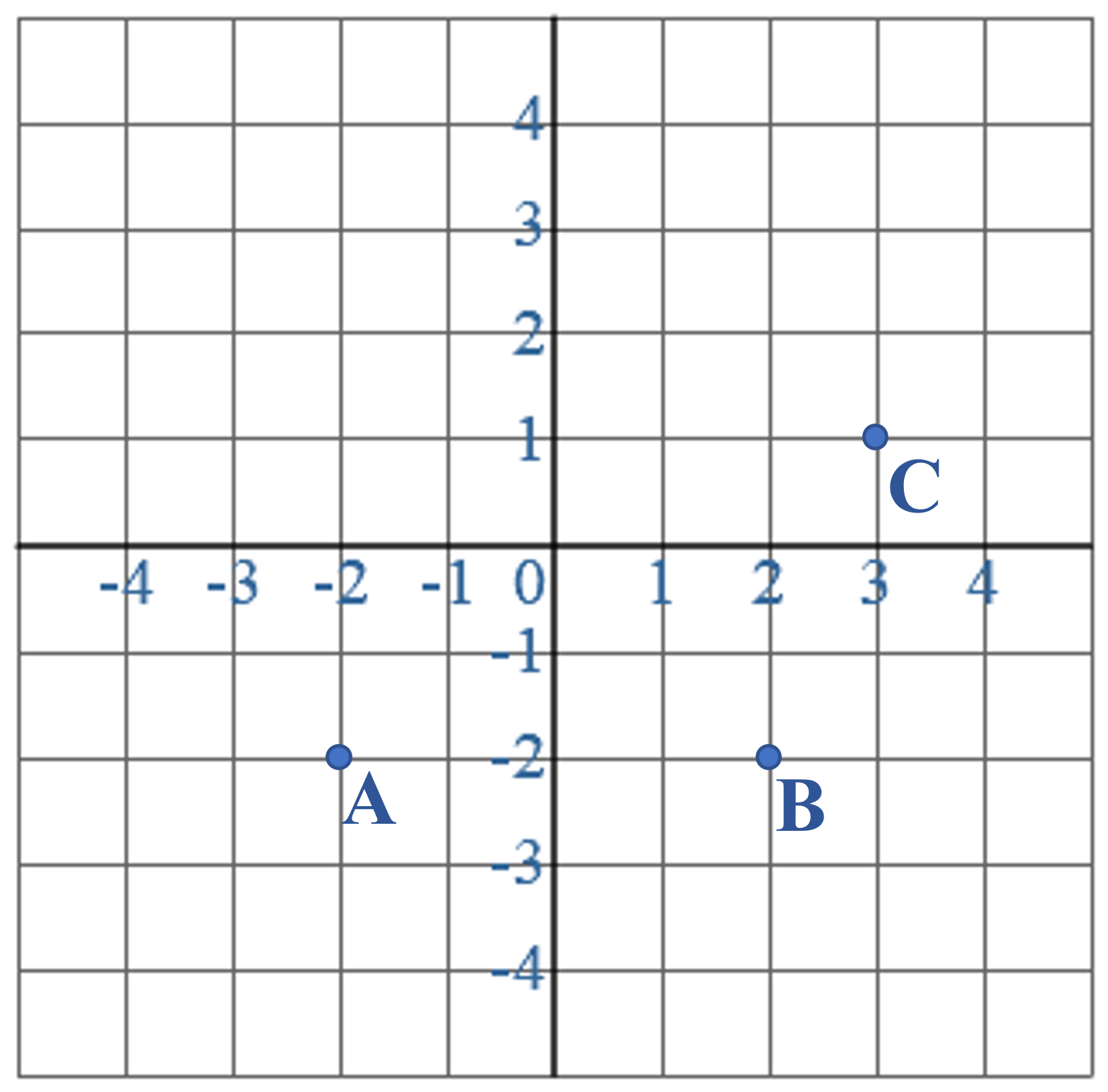
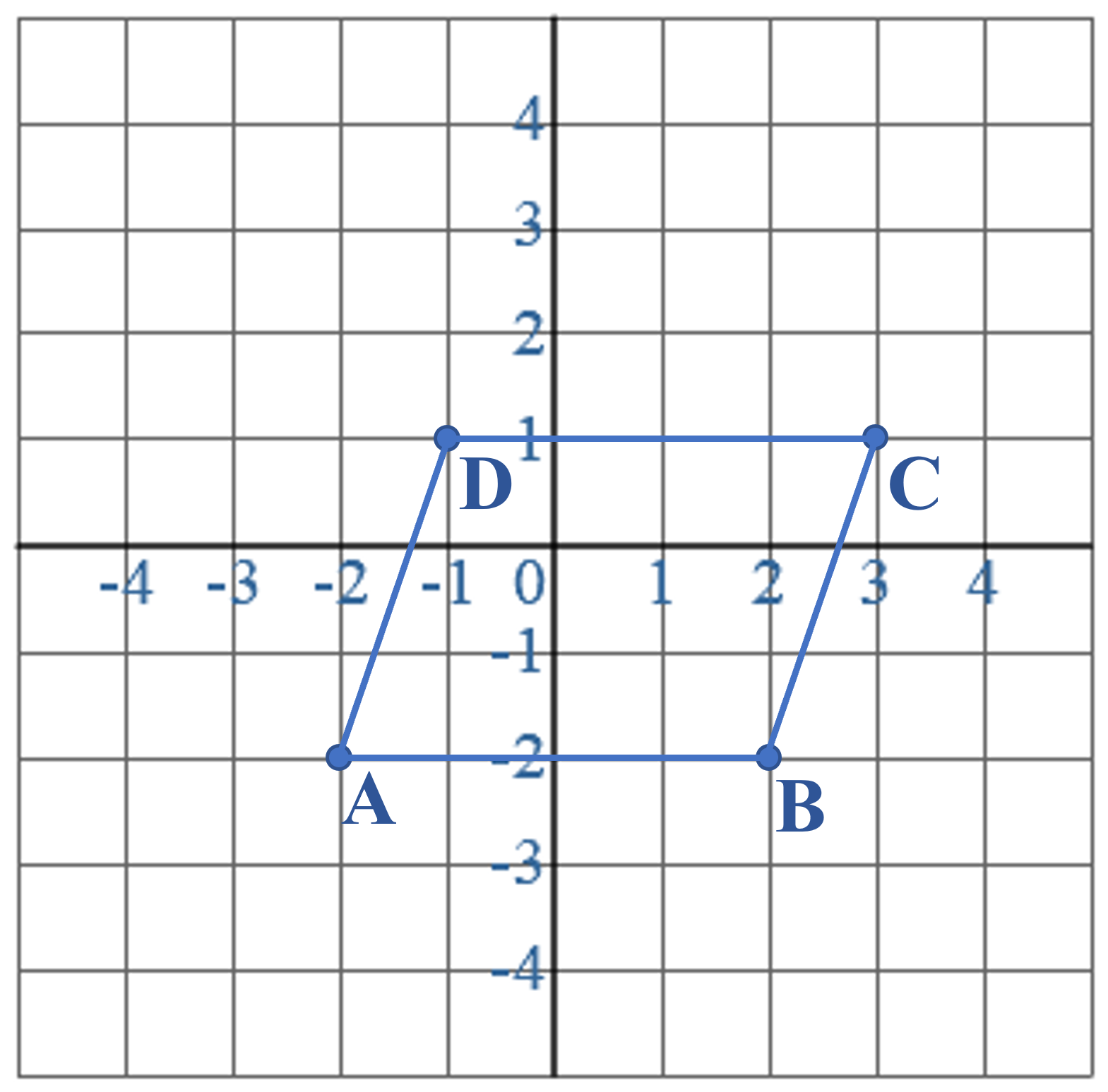
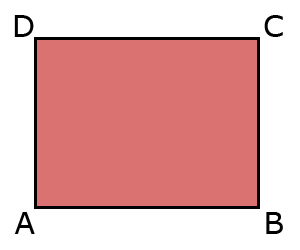 Je hebt in de vorige paragraaf de omtrek uitgerekend.
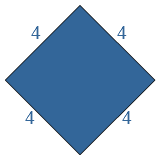
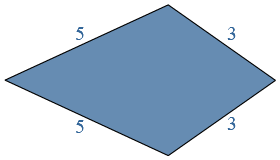
Je hebt in de vorige paragraaf de omtrek uitgerekend.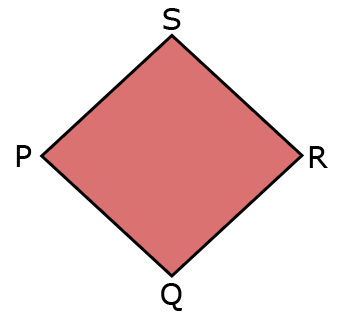 Van ruit
Van ruit 



 Bekijk de formule:
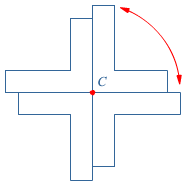
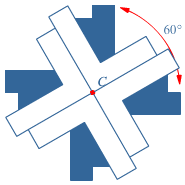
Bekijk de formule: 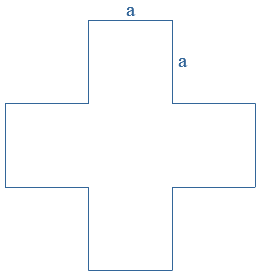 Hiernaast zie je een 'kruis' getekend.
Hiernaast zie je een 'kruis' getekend.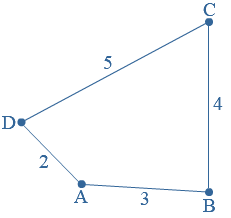 De
De 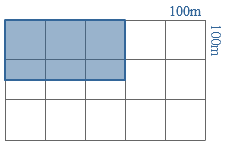

 Van een
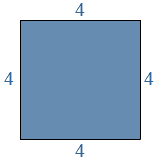
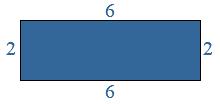
Van een 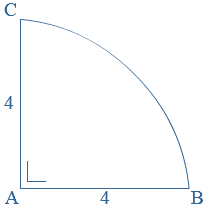 Ito wil de omtrek van de figuur hiernaast uitrekenen.
Ito wil de omtrek van de figuur hiernaast uitrekenen.

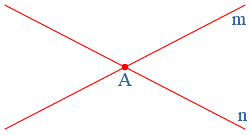
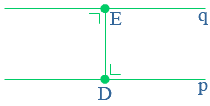
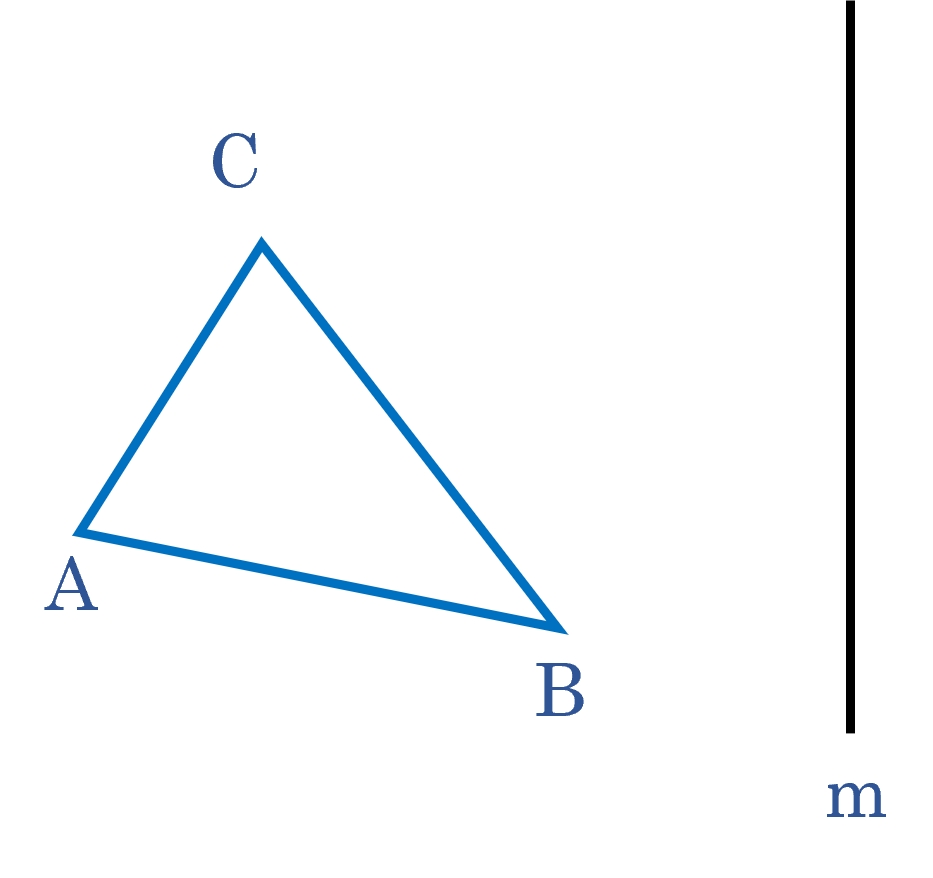
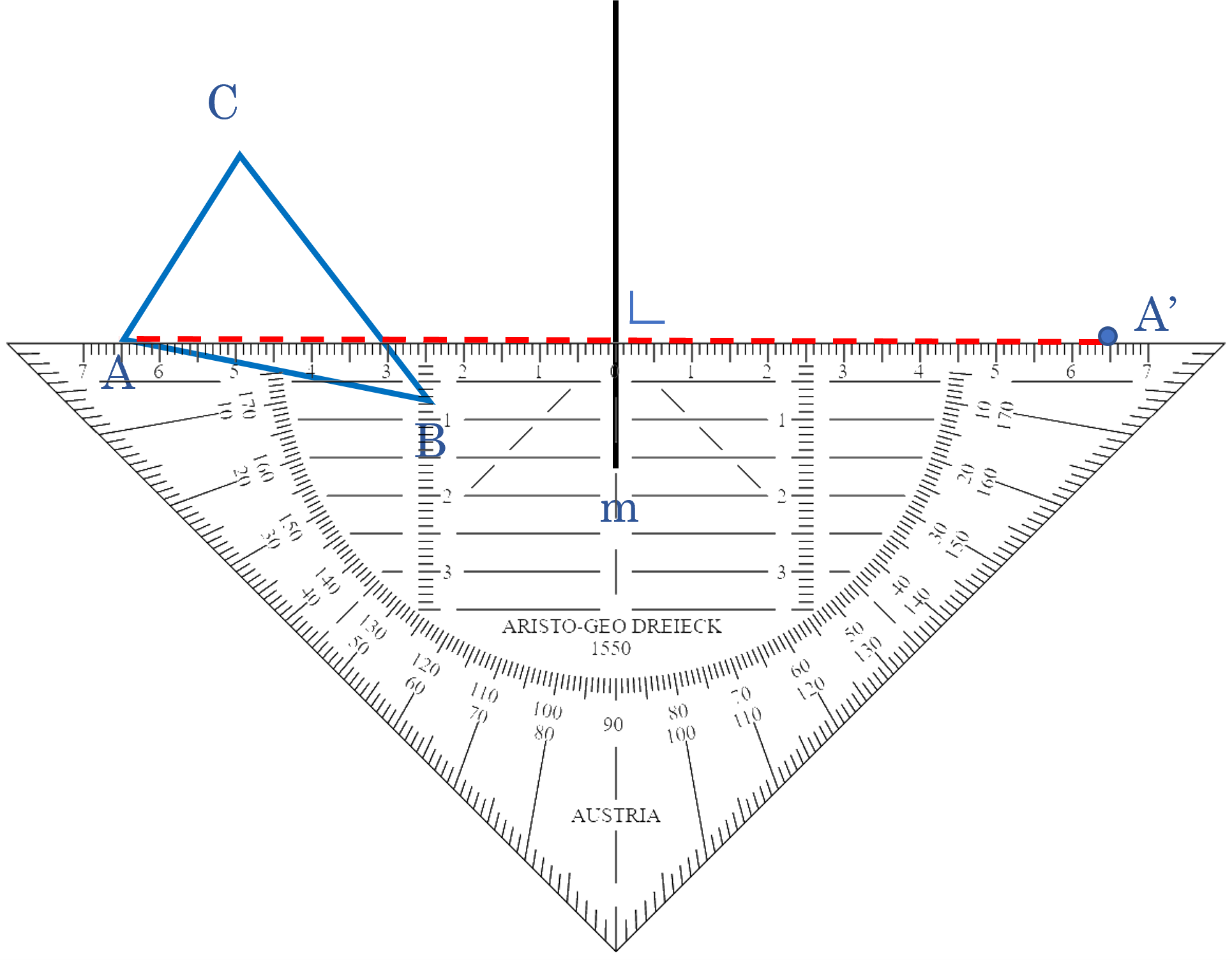
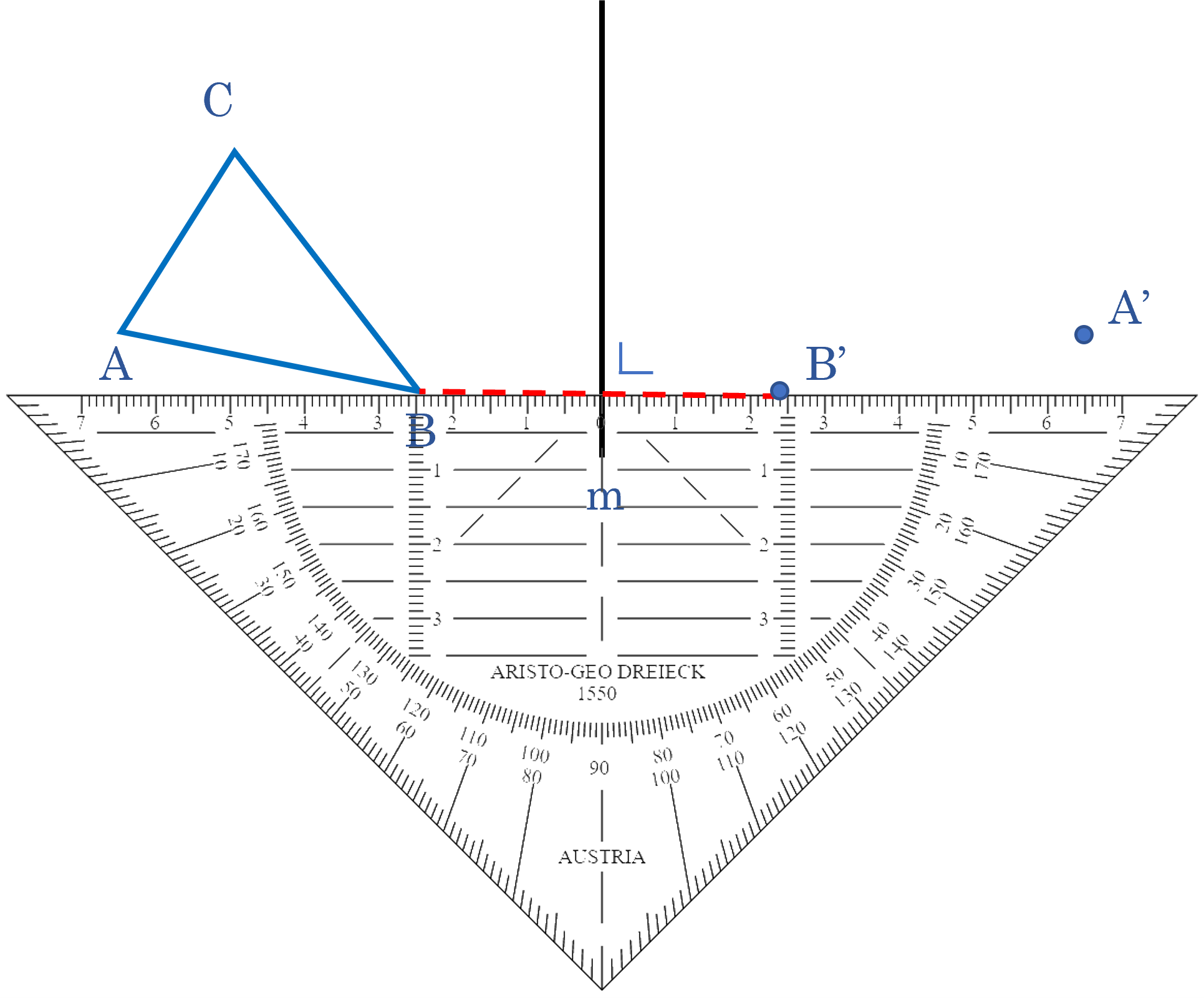
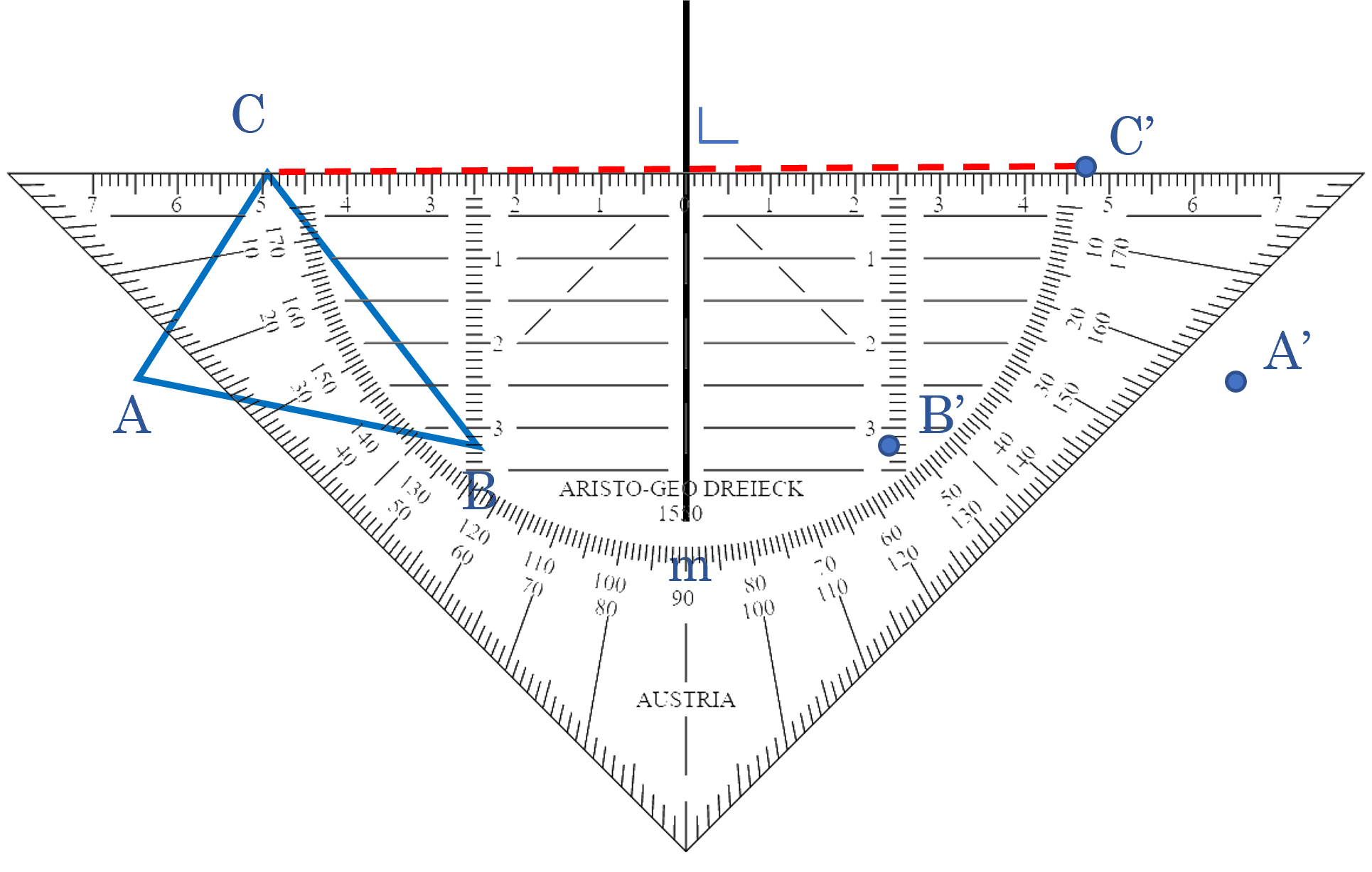
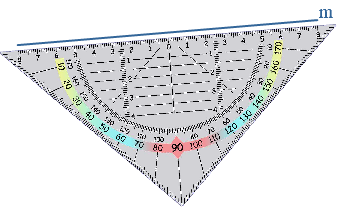
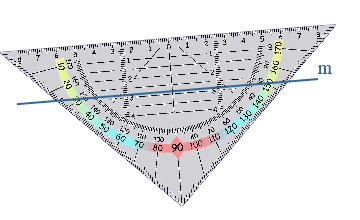
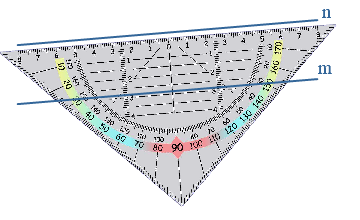
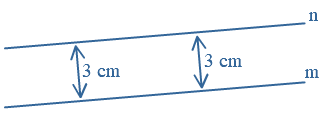
 betekent loodrecht, dit zul je vaak terug zien komen.
betekent loodrecht, dit zul je vaak terug zien komen.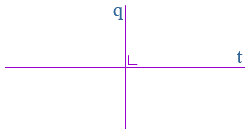
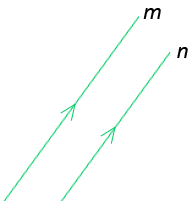




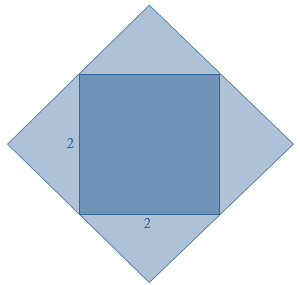
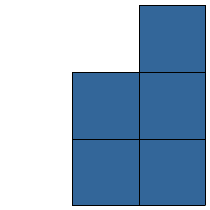
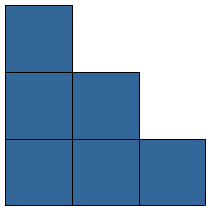
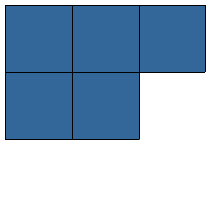
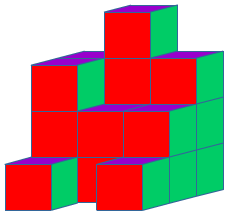
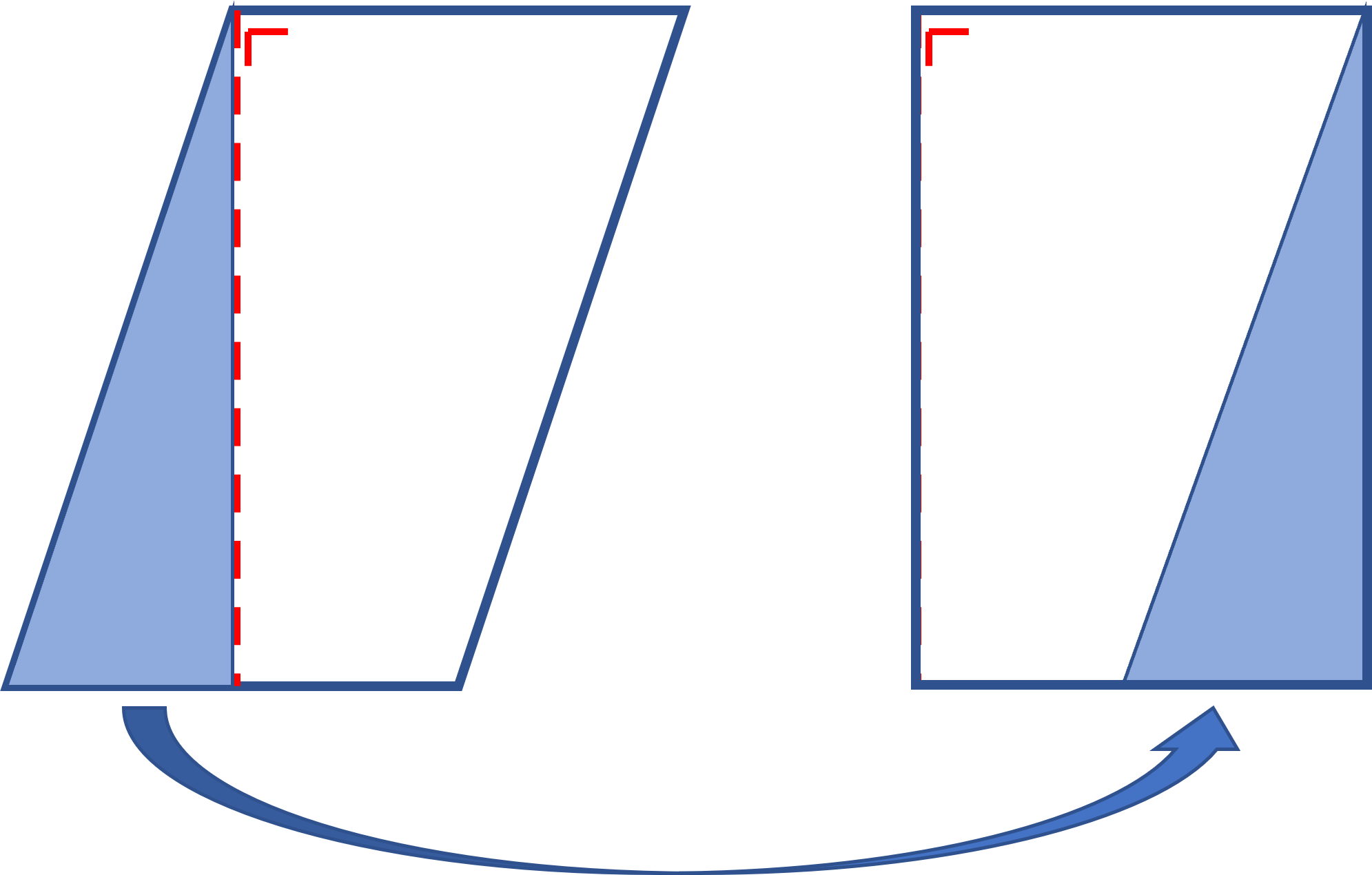
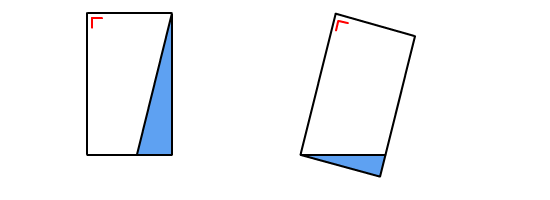
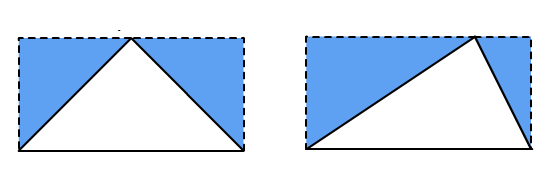
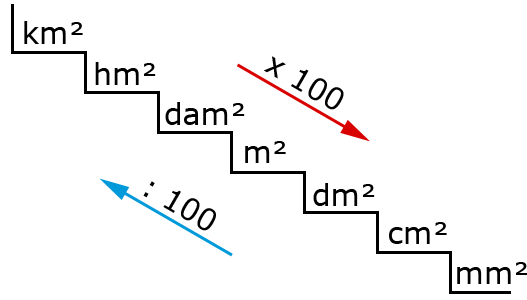
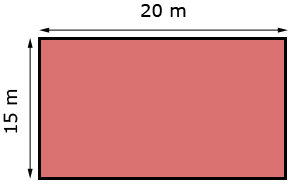 De oppervlakte reken je uit met lengte x breedte bij een rechthoekig figuur, zoals een vierkant of een rechthoek.
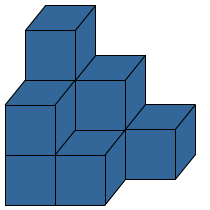
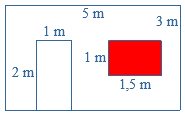
De oppervlakte reken je uit met lengte x breedte bij een rechthoekig figuur, zoals een vierkant of een rechthoek.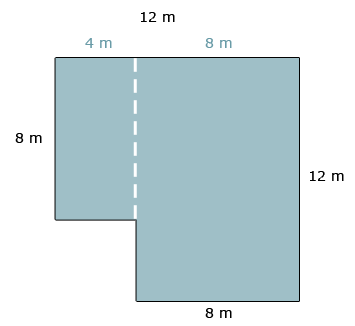 Wat is de totale oppervlakte van de figuur?
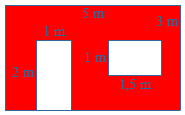
Wat is de totale oppervlakte van de figuur?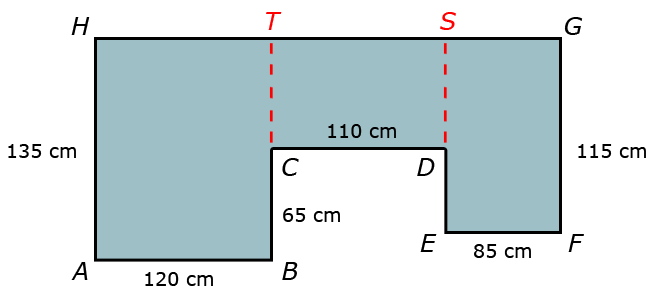 Je wilt de totale oppervlakte uitrekenen van figuur
Je wilt de totale oppervlakte uitrekenen van figuur 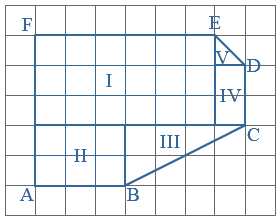 Bekijk de figuur. De figuur is
Bekijk de figuur. De figuur is 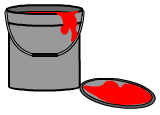 Joost wil een muur in zijn kamer verven.
Joost wil een muur in zijn kamer verven.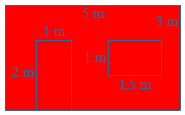
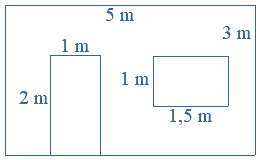 de oppervlakte van de deur is
de oppervlakte van de deur is 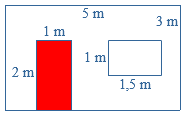
 Bekijk de figuur.
Bekijk de figuur.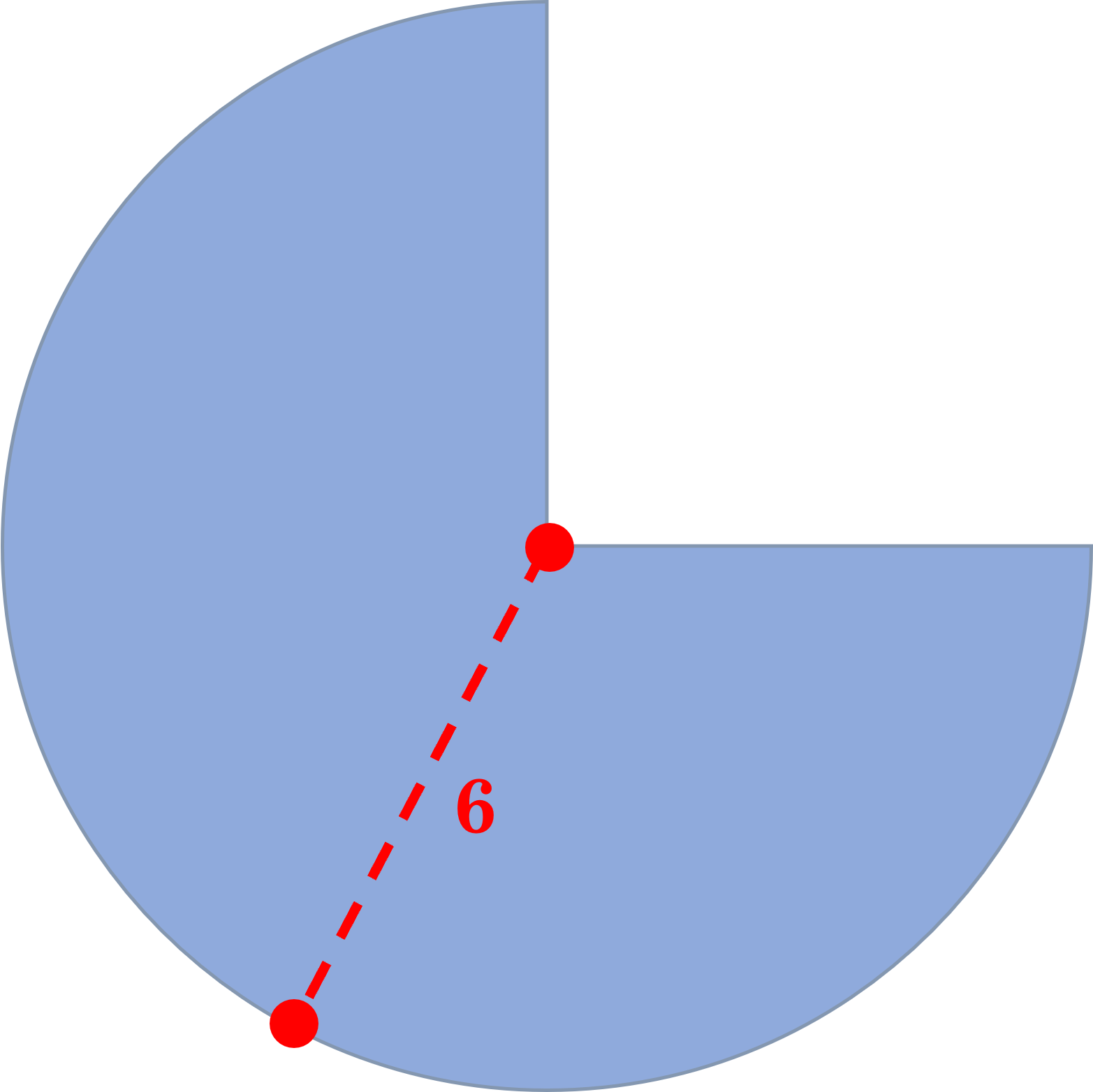
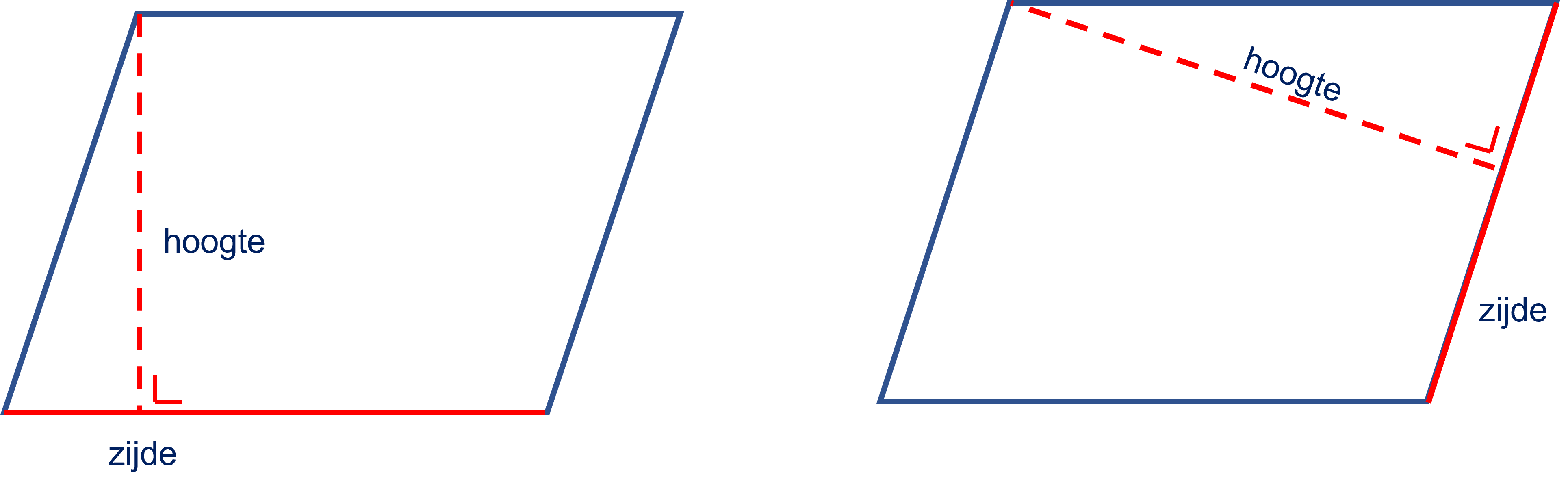

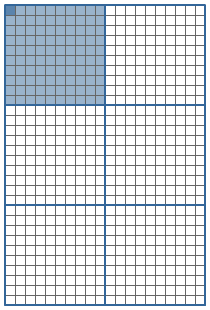 Hiernaast zie je een stukje millimeterpapier.
Hiernaast zie je een stukje millimeterpapier.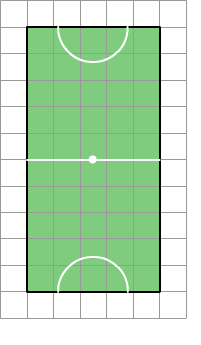 Hiernaast zie je een handbalveld getekend.
Hiernaast zie je een handbalveld getekend. Irma wil de vloer van haar kamer met vloertegels beleggen.
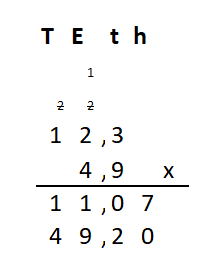
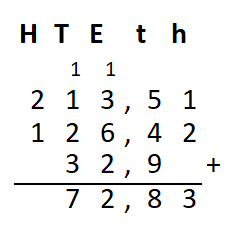
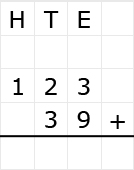
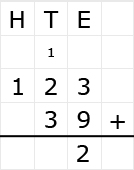
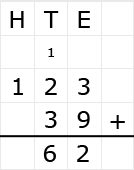
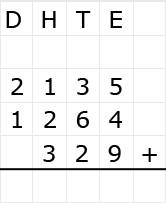
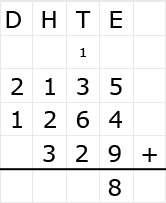
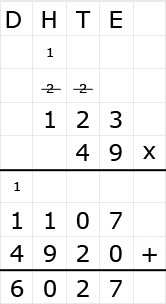
Irma wil de vloer van haar kamer met vloertegels beleggen. Optelsommen met decimale getallen kan je het beste onder elkaar uitrekenen met het stappenplan wat je eerder bij thema 1 Basisrekenen hebt gebruikt. Neem de voorbeeldsommen hieronder over in je schrift en voer de stappen hieronder ook zelf uit in je schrift. Dan onthoud je ze beter.
Optelsommen met decimale getallen kan je het beste onder elkaar uitrekenen met het stappenplan wat je eerder bij thema 1 Basisrekenen hebt gebruikt. Neem de voorbeeldsommen hieronder over in je schrift en voer de stappen hieronder ook zelf uit in je schrift. Dan onthoud je ze beter. 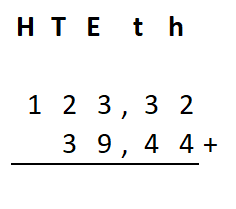
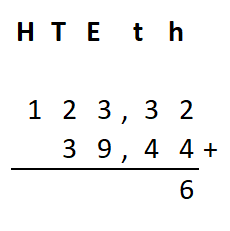
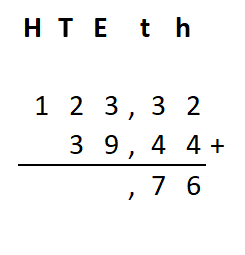
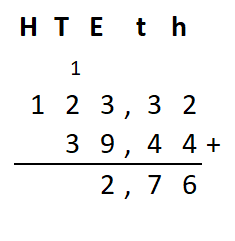
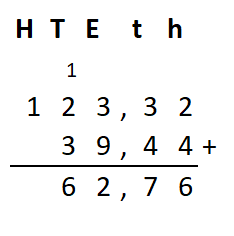
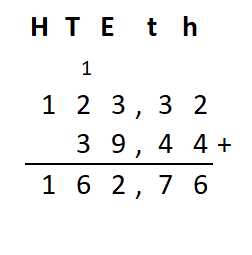
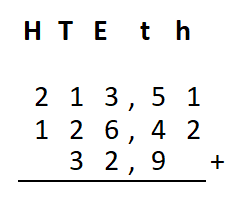
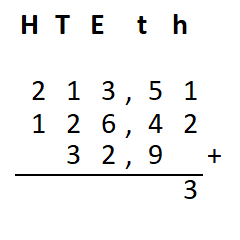
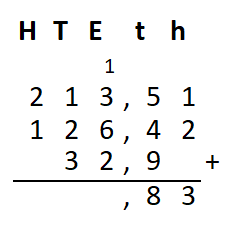
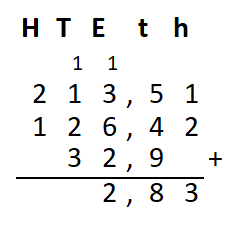
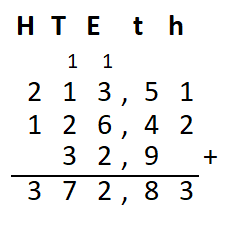
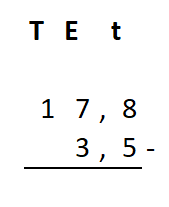
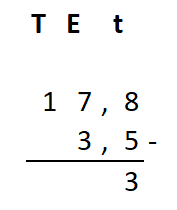
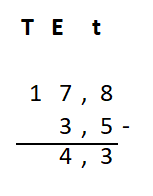
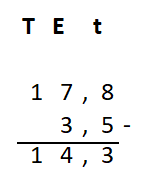
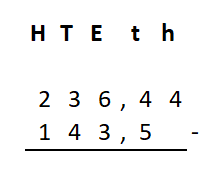
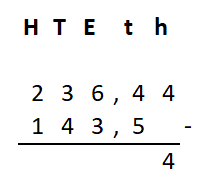
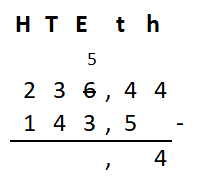
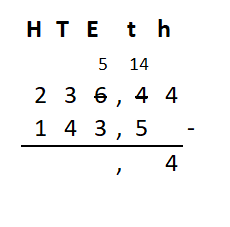
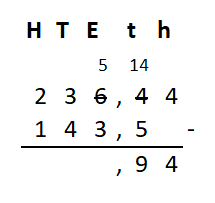
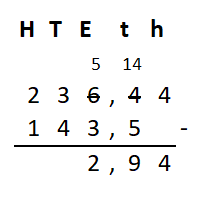
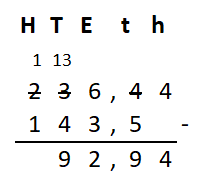
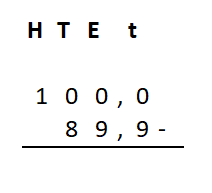
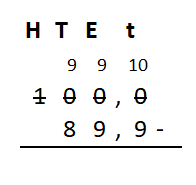
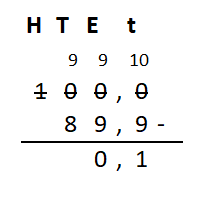
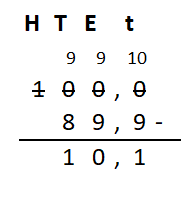



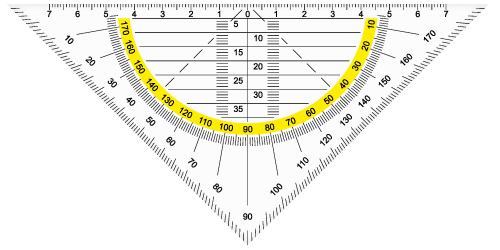
 Als je schrijft zie je vaak geen verschil tussen de
Als je schrijft zie je vaak geen verschil tussen de 





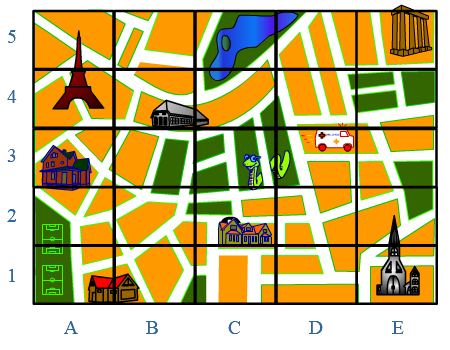
 Joost fietst naar de kerk.
Joost fietst naar de kerk.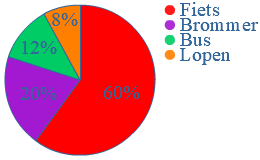 In het cirkeldiagram zie je hoe de leerlingen van het Hoge Zand college naar school komen.
In het cirkeldiagram zie je hoe de leerlingen van het Hoge Zand college naar school komen.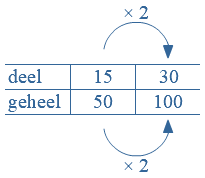




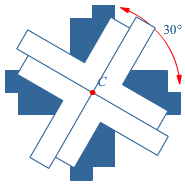
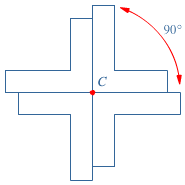
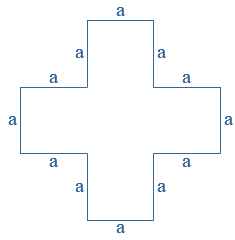 Hiernaast zie je een 'kruis' getekend.
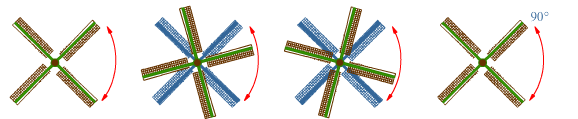
Hiernaast zie je een 'kruis' getekend.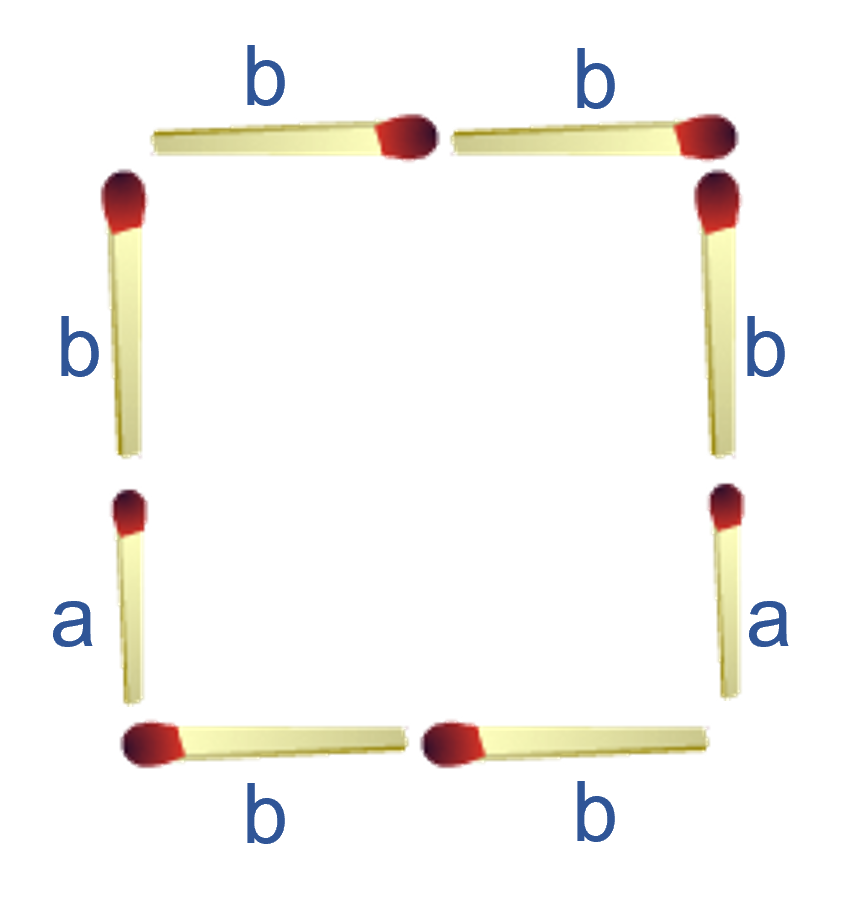 Voor de luciferfiguur zijn twee soorten lucifers gebruikt:
Voor de luciferfiguur zijn twee soorten lucifers gebruikt:

 George heeft
George heeft 

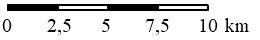

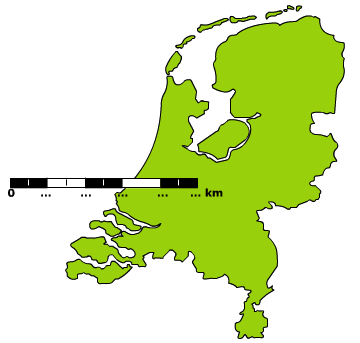
 Schatten in je eigen omgeving en in de wereld.
Schatten in je eigen omgeving en in de wereld.
 Je weet dan hoeveel tijd je ongeveer nodig hebt voor het lezen van het boek.
Je weet dan hoeveel tijd je ongeveer nodig hebt voor het lezen van het boek.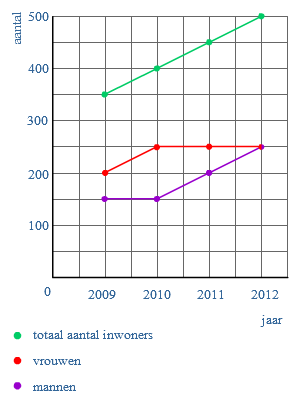 In een dorp is een aantal jaar het aantal mannen en vrouwen geteld.
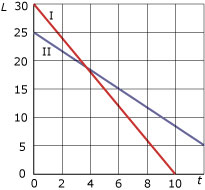
In een dorp is een aantal jaar het aantal mannen en vrouwen geteld.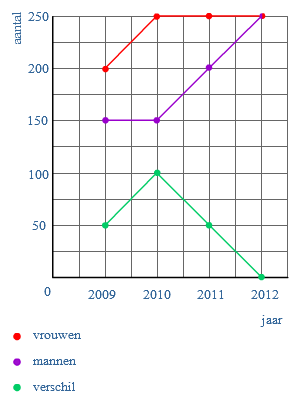 Naast de somgrafiek kennen we ook de verschilgrafiek.
Naast de somgrafiek kennen we ook de verschilgrafiek.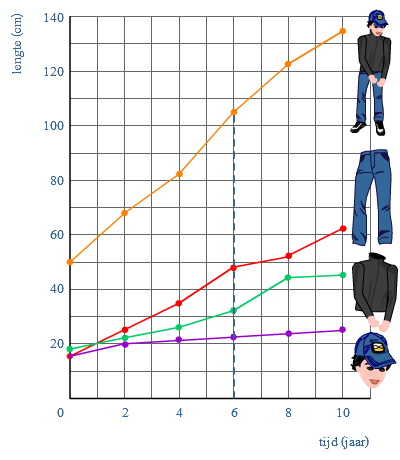 In de grafiek zie je de lengtegroei van Eric.
In de grafiek zie je de lengtegroei van Eric.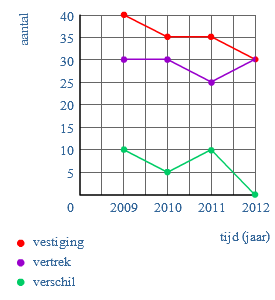 Een dorp heeft een aantal jaar bijgehouden hoeveel mensen naar het dorp verhuisd zijn (vestiging) en hoeveel mensen vanuit het dorp verhuisd zijn naar ergens anders (vertrek).
Een dorp heeft een aantal jaar bijgehouden hoeveel mensen naar het dorp verhuisd zijn (vestiging) en hoeveel mensen vanuit het dorp verhuisd zijn naar ergens anders (vertrek).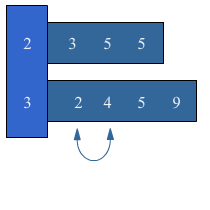 Gegevens kun je weergeven in een diagram.
Gegevens kun je weergeven in een diagram.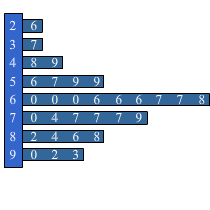 Hieronder zie je de cijfers voor een proefwerk wiskunde.
Hieronder zie je de cijfers voor een proefwerk wiskunde.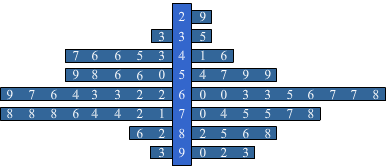
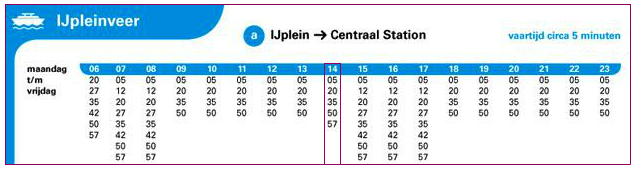
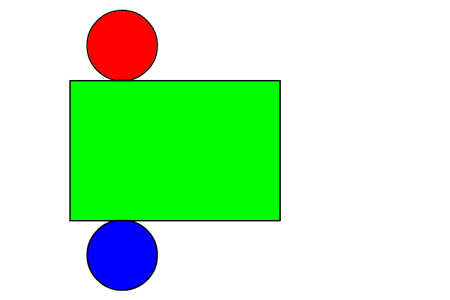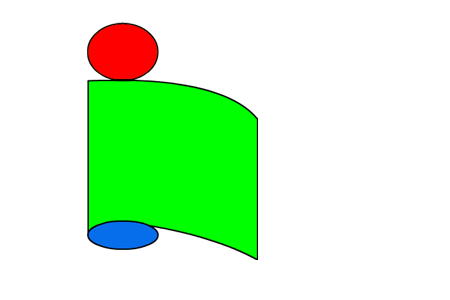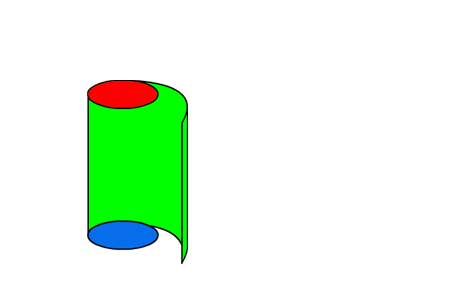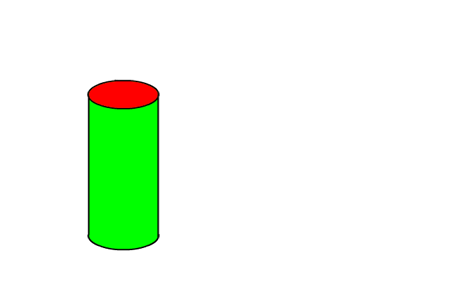
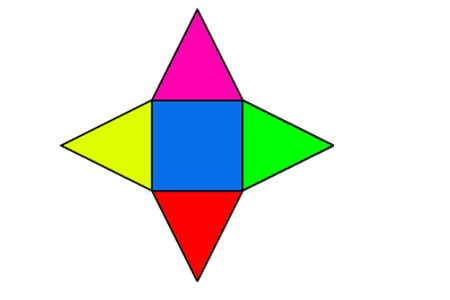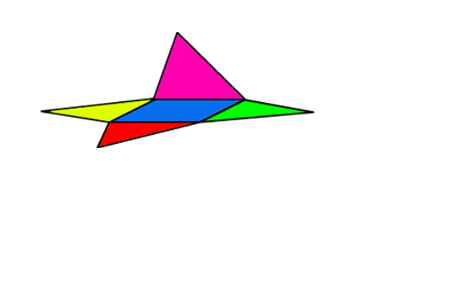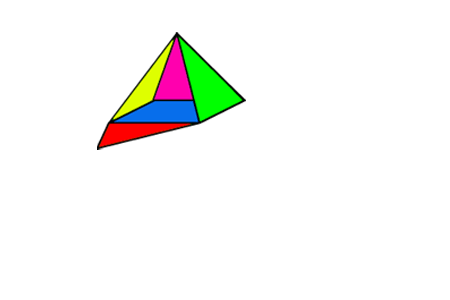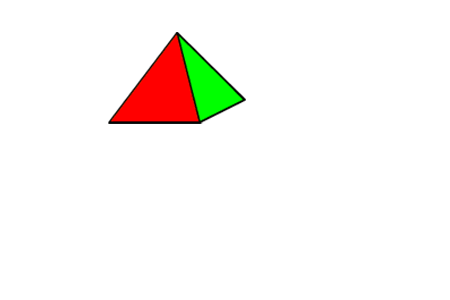
 Je ziet een uitslag van een kubus. In een uitslag staan alle grensvlakken van de kubus.
Je ziet een uitslag van een kubus. In een uitslag staan alle grensvlakken van de kubus.
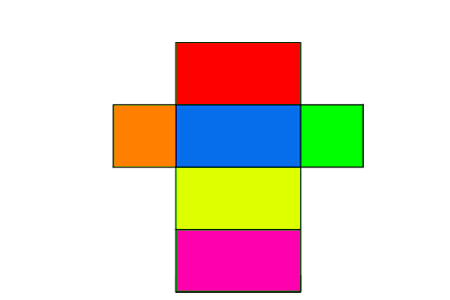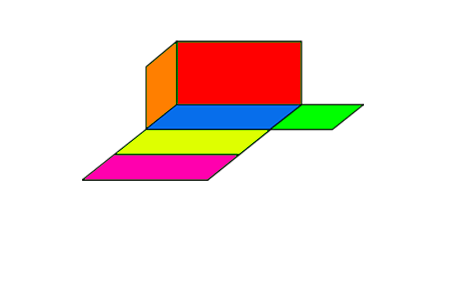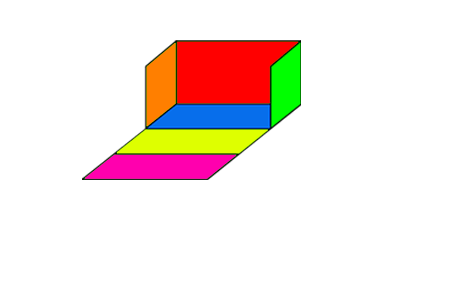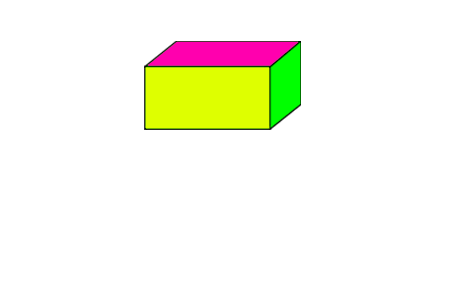
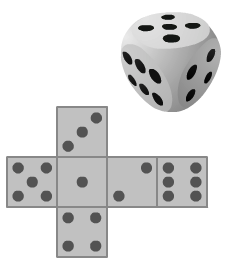 Je ziet hier een uitslag van een dobbelsteen.
Je ziet hier een uitslag van een dobbelsteen. Bron:
Bron: 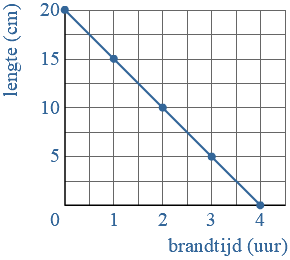 Bij een formule kun je een grafiek maken.
Bij een formule kun je een grafiek maken.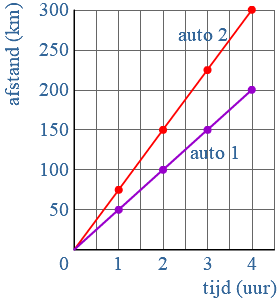 Auto
Auto 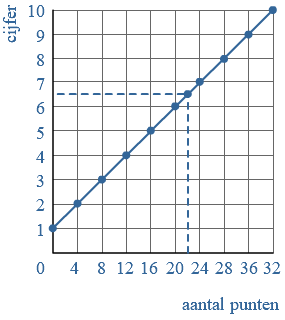 Voor een proefwerk kun je
Voor een proefwerk kun je 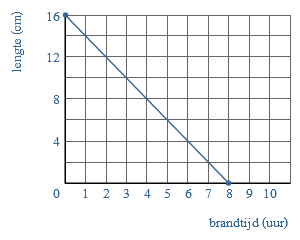 Een verband kun je weergeven in een grafiek.
Een verband kun je weergeven in een grafiek.

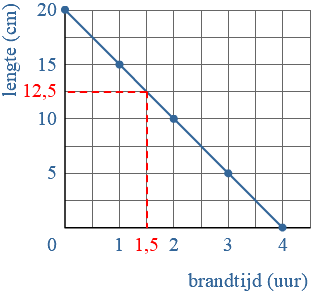
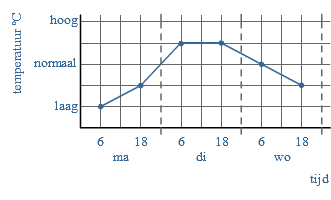 Janine ligt in het ziekenhuis.
Janine ligt in het ziekenhuis.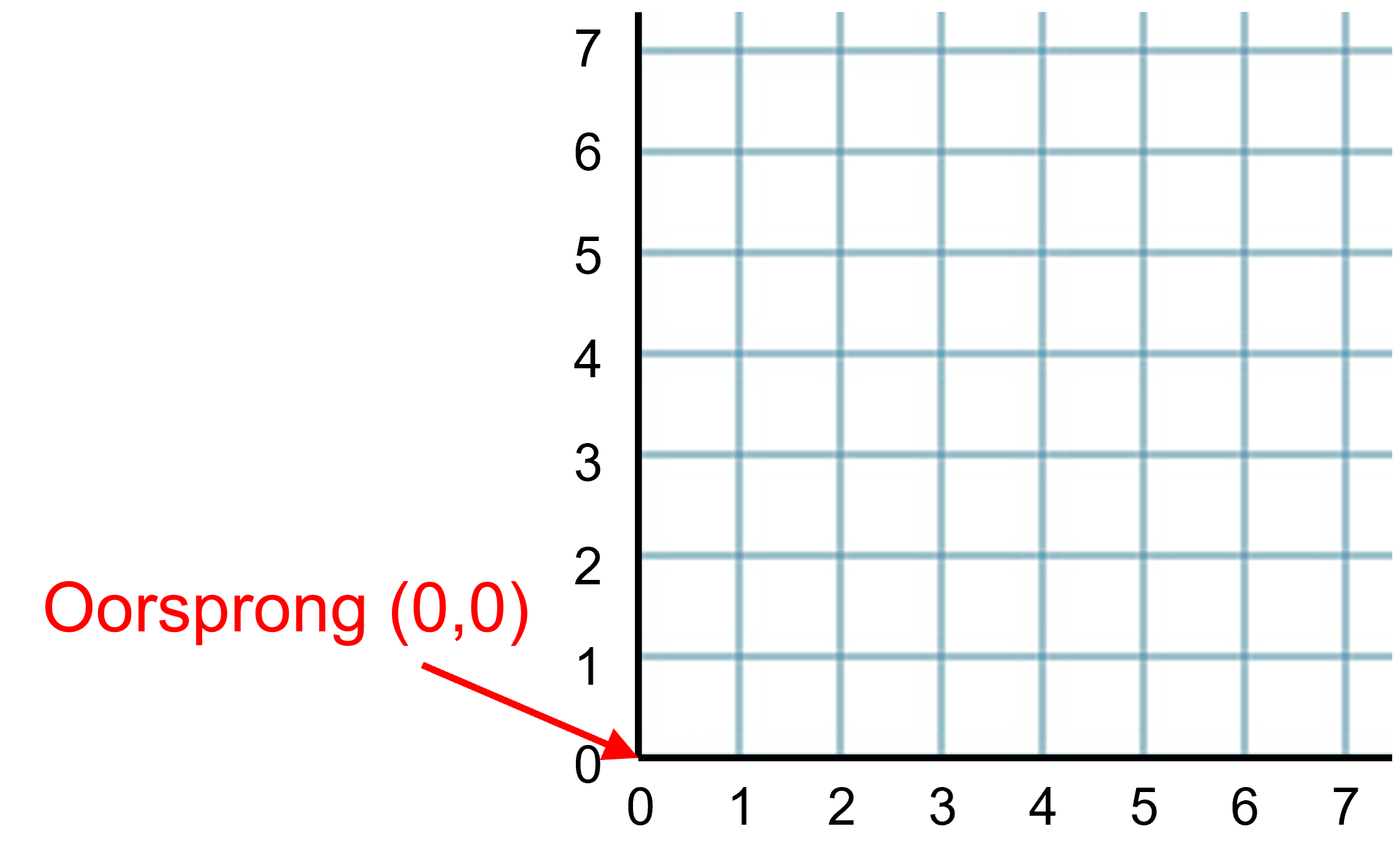
 Bekijk de formule:
Bekijk de formule: 











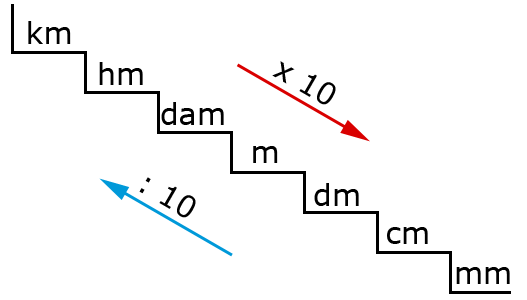
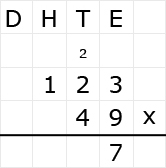
 Als je de tafels al goed kent, dan is vermenigvuldigen met 10 x iets, 100 x iets enzovoort niet moeilijk. Kijk maar eens naar het volgende voorbeeld:
Als je de tafels al goed kent, dan is vermenigvuldigen met 10 x iets, 100 x iets enzovoort niet moeilijk. Kijk maar eens naar het volgende voorbeeld: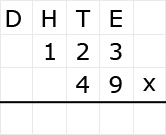
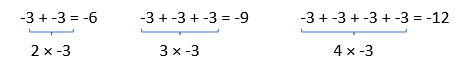

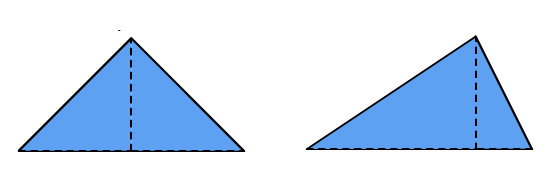
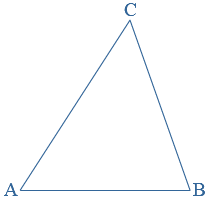 Een driehoek heeft drie hoekpunten en drie zijden.
Een driehoek heeft drie hoekpunten en drie zijden.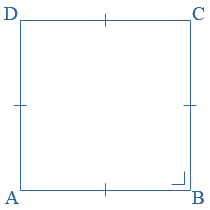

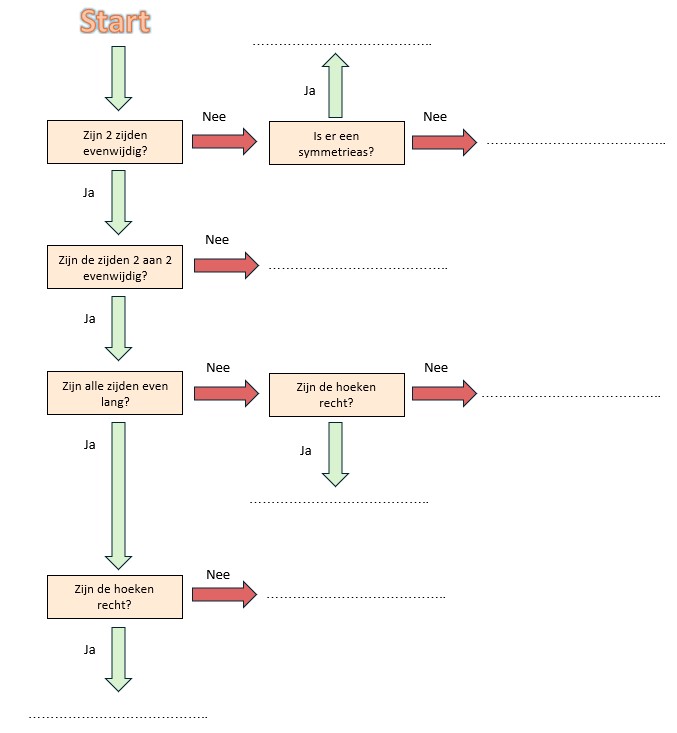

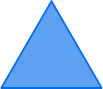





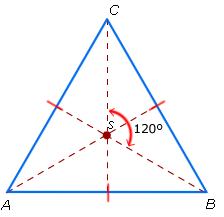 AB = AC = BC
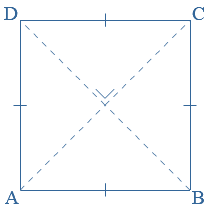
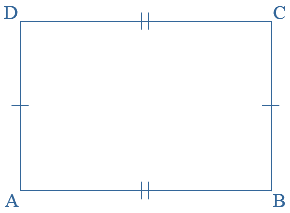
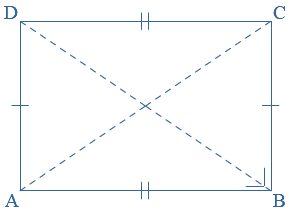
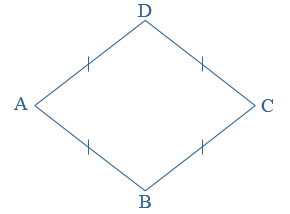
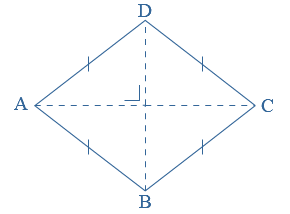
AB = AC = BC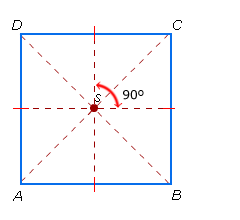 AB = BC = CD = DA
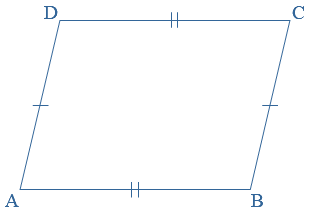
AB = BC = CD = DA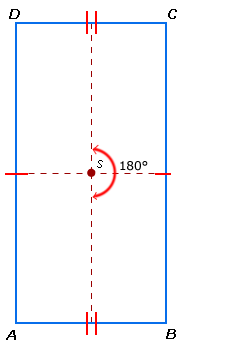 AB = CD en BC = AD
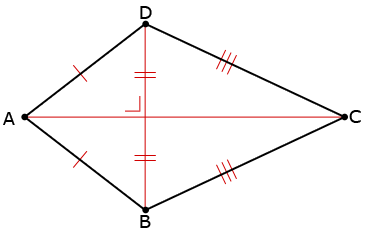
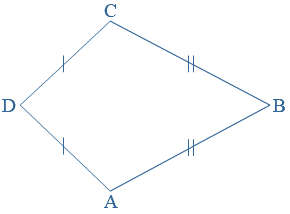
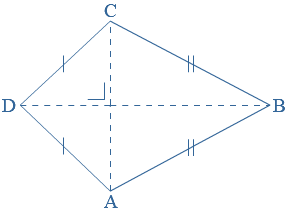
AB = CD en BC = AD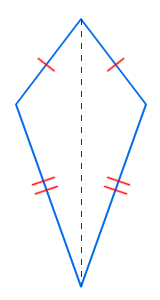 AB = AD en BC = CD
AB = AD en BC = CD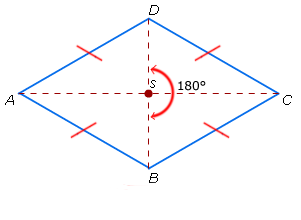
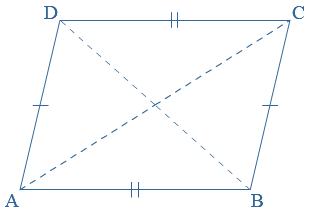
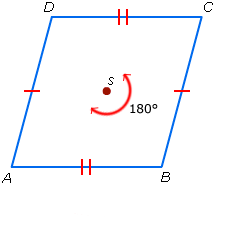 AB = CD en AD = BC
AB = CD en AD = BC AC = BC
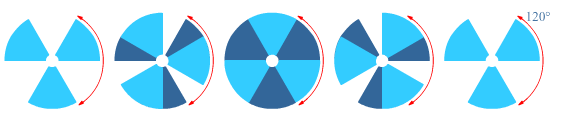
AC = BC Bekijk de vlakvulling.
Bekijk de vlakvulling. Evert krijgt iedere maand
Evert krijgt iedere maand 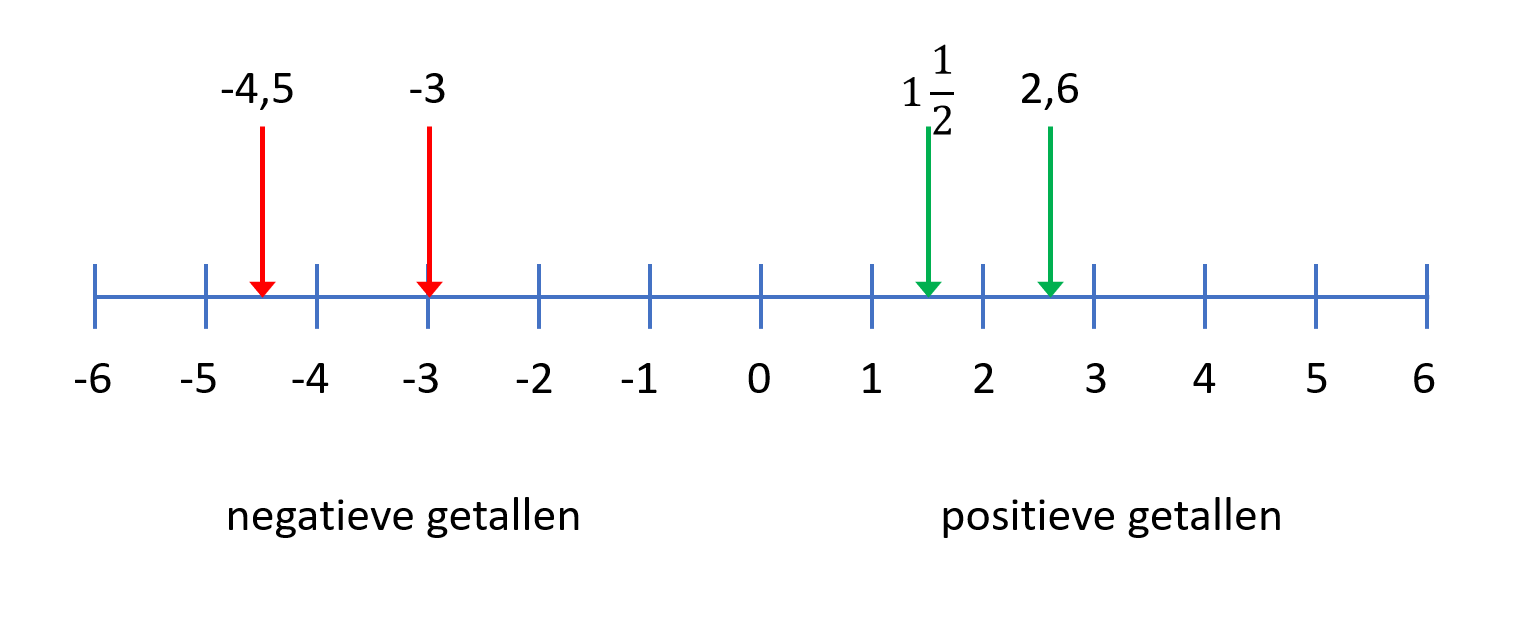
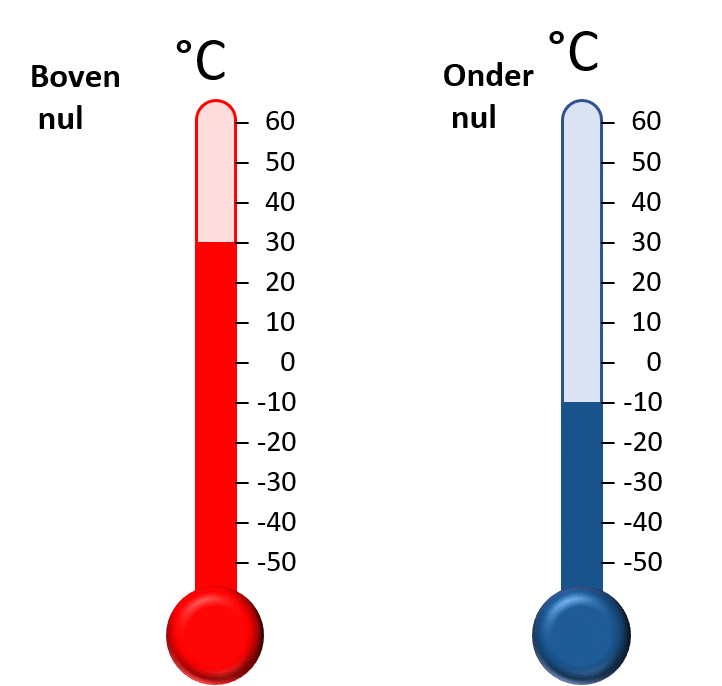
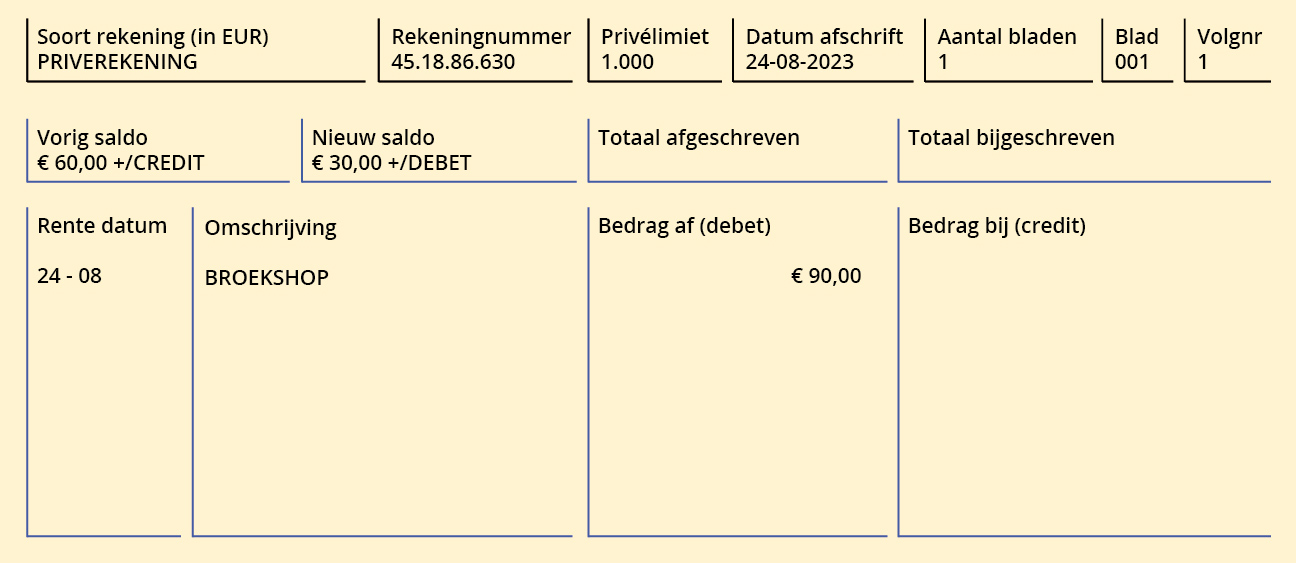


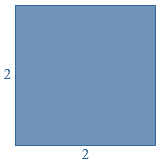
 Dit vierkant heeft een oppervlakte van
Dit vierkant heeft een oppervlakte van