Wikiwijs Hoofdstuk 5 (deel 1)

Wikiwijs Hoofdstuk 5 (deel 1)

Introductie hoofdstuk 5: 'Meten'

Hallo leerlingen uit de eerste klas!

 

Dit hoofdstuk gaat over het meten van allerlei situaties. Zo ga je leren over het meten van lengtes, oppervlakten en inhoud. We gaan niet alleen kijken naar de oppervlaktes van stoeptegels, maar naar die van voetbalvelden en bossen. Ook gaan we leren hoe we de oppervlakte van bijzondere figuren kunnen uitrekenen. Wil je weten wat je aan het einde van deze Wikiwijs kan en weet? Lees dan de onderstaande leerdoelen alvast door:

 

Aan het einde van deze Wikiwijs kan ik als leerling ...

... begrijpen en uitleggen wat een eenheid is.

... begrijpen en uitleggen wat een grootheid is.

... begrijpen en uitleggen wat lengte is.

... rekenen met verschillende eenheden van lengte.

... begrijpen en uitleggen wat oppervlakte is.

... rekenen met verschillende eenheden van oppervlakte.

... de oppervlakte van verschillende rechthoeken berekenen.

... de oppervlakte van verschillende driehoeken berekenen.

Voorkennis eenheden en grootheden

Beste leerlingen,

 

Vandaag starten wij met een nieuw hoofdstuk, namelijk hoofdstuk 5. Voordat wij hier echt mee kunnen gaan beginnen, gaan we naar het eerste nieuwe onderwerp kijken. Dit onderwerp is: Eenheden en grootheden. Kijk het filmpje hieronder, dan kunnen we daarna aan de slag met de opdrachten!

Wat zijn eenheden en grootheden?

Een grootheid is dus iets wat wij kunnen meten. Denk hierbij aan lengte, inhoud of zelfs gewicht. In wat we deze grootheden meten noemen we eenheden. De lengte van een persoon kan bijvoorbeeld in meters of centimeters worden gegeven. Wanneer je zegt dat een persoon 1,75 meter lang is, dan is de gebruikte eenheid meter.

Bij de grootheid gewicht gebruiken wij bijvoorbeeld de eenheid gram of kilogram. Afhankelijk van het voorwerp kies je de bijbehorende eenheid. We zeggen bijvoorbeeld niet dat een persoon 62000 gram weegt, maar in dit geval zeggen we 62 kilogram.

Maak nu de Educaplay hieronder:

Eenheden van lengte

Op de basisschool heb je al eerder gerekend met eenheden van lengte. Het enige verschil is dat je toen nog niet wist dat dit eenheden van lengte waren.

De meest voorkomende eenheden van lengte zijn de kilometer, meter en centimeter. Denk maar aan de blauwe verkeersborden op de snelweg, hier staan afstanden in kilometers genoteerd. Je eigen lengte vertel je vaak in meters. De breedte van je tafel of beeldscherm wordt vaak gegeven in centimeters.

Binnen de lessen wiskunde gebruiken wij afkortingen voor de eenheden van lengte. Zo noteren wij geen kilometer, maar 'km'. Ook kunnen de verschillende eenheden van lengte omgeschreven worden naar andere eenheden van lengte. Een lengte van 141 cm is bijvoorbeeld 14,1 dm en 1,41 m. Het schema hieronder kan handig zijn om hier mee te oefenen:

Tip!

 

Schrijf altijd de eenheid achter het getal. Wanneer je dit niet doet is het antwoord fout!

Eenheden van oppervlakte

Op de basisschool heb je waarschijnlijk ook al een keer les gekregen over oppervlakte. De oppervlakte is wat anders dan lengte, want oppervlakte is een gebied. We kunnen bijvoorbeeld zeggen dat een lokaal een oppervlakte van 36 m2 heeft. Je spreekt dit uit als '36 vierkante meter'.

Ook natuurgebieden kunnen weergegeven worden in eenheden van oppervlakte. Een bos kan bijvoorbeeld bestaan uit 100 ha. Een ha is een andere afkorting voor hm2. De afkorting ha spreek je uit als hectare en de afkorting hm2 spreek je uit als vierkante hectometer.

De eenheden van oppervlakte kunnen ook omgeschreven worden, kijk maar naar onderstaand schema:

Let bij dit schema op een aantal onderwerpen. Verschillende eenheden van oppervlakte hebben twee namen voor de eenheid. Zorg ervoor dat je deze dan beide kent. Opnieuw is het ook belangrijk om altijd de eenheid te noteren achter je antwoord.

Ten slotte is het belangrijk om te onthouden dat er bij eenheden van oppervlakte stappen van 100 zitten tussen de verschillende eenheden. Dit verschilt dus met de eenheden van lengte!

 

De oppervlakte van een rechthoek is eenvoudig te berekenen met een formule. De formule die we hiervoor gebruiken is:

Oppervlakte rechthoek = lengte • breedte

Of de versie met afkortingen:

Opp rh = l • b

Deze formule mag je alleen gebruiken als alle eenheden gelijk zijn. Je mag dus niet een lengte hebben die in dm staat en een breedte in m. Je moet er dan voor zorgen dat beide eenheden in dm of in m staan.

Bedenk ook dat deze formule geldt voor een vierkant. Een vierkant is immers een bijzondere rechthoek.

Kijk eens naar het volgende voorbeeld en probeer de oppervlakte uit te rekenen:

Als het goed is heb je de volgende berekening in je schrift gemaakt:

Oppervlakte rechthoek = lengte • breedte

Oppervlakte rechthoek = 15 • 20

Oppervlakte rechthoek = 300 m2.

Let er op dat je netjes onder elkaar alles uitwerkt en bij het antwoord niet vergeet de eenheid erachter te zetten.

Maak nu de vragen hieronder:

Oppervlakte driehoek

Oppervlakte driehoek door inlijsten

Nu hebben we een goede basis gelegd voor de volgende stap, het berekenen van de oppervlakte van een driehoek. Nu denk je misschien, hoe kan dit zo veel moeilijker zijn dan bij rechthoeken? Het grote verschil zit in de termen. Een driehoek heeft namelijk geen lengte en breedte, maar een zijde en (bijbehorende) hoogte. Hier komen we later op terug.

Een driehoek is technisch gezien de helft van een rechthoek, kijk maar naar de afbeelding hieronder:

De oppervlakte van een rechthoek konden we al uitrekenen met de formule: oppervlakte rechthoek = lengte • breedte. Nu we weten dat de driehoek eigenlijk de helft van de rechthoek is, kunnen we deze dus ook uitrekenen. Dit werkt op de volgende manier:

Oppervlakte rechthoek = lengte • breedte

Oppervlakte rechthoek = 4 • 2

Oppervlakte rechthoek = 8 cm2.

Oppervlakte driehoek ABC = 8 : 2

Oppervlakte driehoek ABC = 4 cm2.

Deze manier van de oppervlakte van een driehoek berekenen noemen we inlijsten.

Formule voor de oppervlakte van een driehoek

Niet alle driehoeken zijn mooi in te lijsten. Toch kunnen we van iedere driehoek de oppervlakte berekenen, zolang we de zijde en (bijbehorende) hoogte weten. Wat een zijde en (bijbehorende) hoogte is wordt laten zien bij de afbeelding hieronder:

Onthoud dus goed dat je bij een driehoek geen lengte en breedte hebt, maar zijde en hoogte. Bij een rechthoek horen lengte en breedte wel, maar daar spreken we weer niet van zijde en hoogte.

De formule voor het berekenen van de oppervlakte van een driehoek is:

Oppervlakte driehoek = 0,5 • zijde • hoogte

Of de versie met afkortingen:

Opp dh = 0,5 • z • h

Ga voor jezelf na of je bij de vorige driehoek met deze formule op dezelfde uitkomst uitkomt. Zo ja, dan is het goed gegaan en mag je doorgaan naar de volgende pagina. Lukte het nog niet? Probeer het nogmaals of vraag hulp.

Hieronder vind je een kennisclip over het berekenen van de oppervlakte van een driehoek:

Kennisclip berekenen oppervlakte van een driehoek

Oppervlakte stomphoekige driehoek

Bij een stomphoekige driehoek is de hoogte vinden niet altijd even makkelijk. Je hebt te maken met een stomphoekige driehoek wanneer één van de hoeken groter is dan 90o. In het voorbeeld hieronder zie je hoe deze situatie eruit kan zien:

Binnen dit voorbeeld is hoek R de hoek die groter is dan 90o. Ook is te zien dat we niet eenvoudig de hoogte bij QR kunnen vinden. Toch is dit wel mogelijk, namelijk met een hulplijn. In het volgende voorbeeld wordt laten zien hoe de hulplijn bij een stomphoekige driehoek getekend moet worden:

De hoogte bij KL is gestippeld en is 3 cm. Aan de hand hiervan kunnen we de formule van de oppervlakte van een driehoek gebruiken om deze te berekenen. Dit ziet er als volgt uit:

Oppervlakte driehoek KLM = 0,5 • zijde • hoogte

Oppervlakte driehoek KLM = 0,5 • 3 • 3

Oppervlakte driehoek KLM = 4,5 cm2.

Bereken nu voor jezelf de oppervlakte van driehoek PQR. Deze vraag komt ook terug binnen de oefeningen hieronder.

Voorbereiding op de toets

Om jullie extra te helpen bij het voorbereiden op de tussentijdse toets, staan hieronder twee verschillende tools. De Quizlet is bedoeld om jullie te helpen met de begrippen voor de toets. Wanneer je de begrippen goed kent, worden de vragen vaak makkelijker te begrijpen op de toets. De tweede tool is een oefentoets. Deze oefentoets geeft een goed beeld van wat voor soort vragen er gesteld kunnen worden op de toets.

Succes met het oefenen en leren!

Tussentijdse toets

Beste leerlingen, het is zover. Hieronder staat de tussentijdse toets over hoofdstuk 5 paragraaf 1 t/m 3. Bij het maken van deze toets heb je in principe geen hulpmiddelen nodig. Een rekenmachine is toegestaan, eveneens als kladpapier, een pen, potlood en geodriehoek. Denk bij iedere vraag rustig na. Heel veel succes!

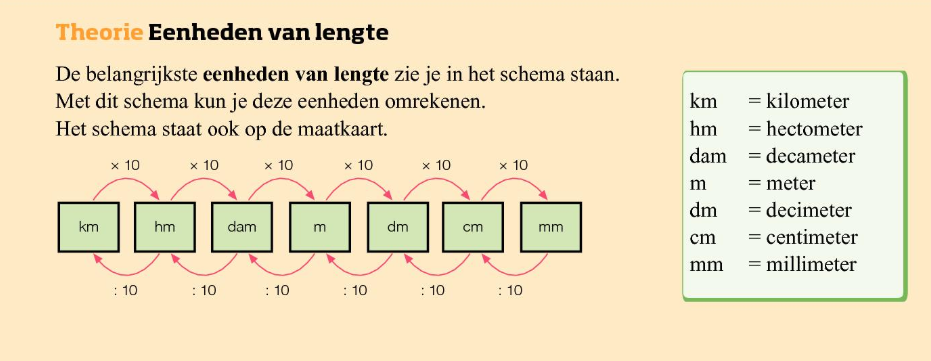
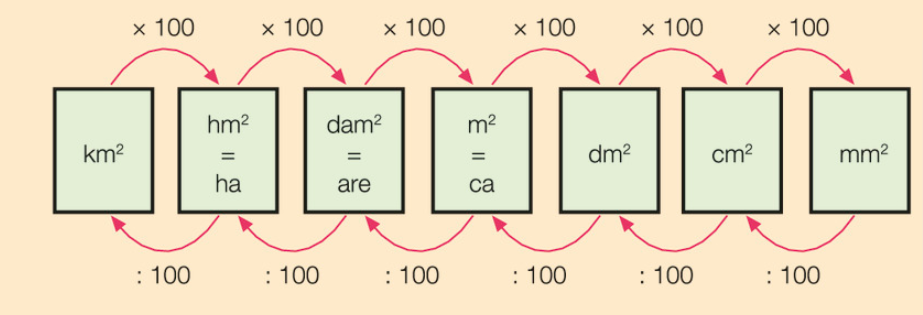
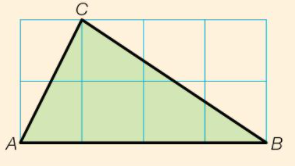
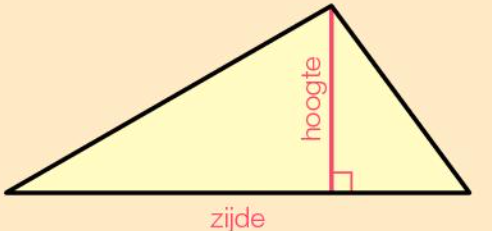
  • Het arrangement Wikiwijs Hoofdstuk 5 (deel 1) is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.

    Auteur
    Oscar Jager
    Laatst gewijzigd
    2022-01-27 21:26:05
    Licentie

    Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:

    • het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
    • het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
    • voor alle doeleinden, inclusief commerciële doeleinden.

    Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.

    Aanvullende informatie over dit lesmateriaal

    Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:

    Toelichting
    Het doel van deze wikiwijs is om de leerlingen van een eerste klas mavo/havo, met wiskunde te helpen eenheden en grootheden beter te begrijpen. Binnen deze wikiwijs wordt er gefocust op verschillende eenheden en grootheden en de toepassing hiervan. De leerdoelen concreet zijn: - De leerlingen kunnen aan het einde van deze wikiwijs een onderscheid maken tussen eenheden en grootheden. - De leerlingen kunnen rekenen met de eenheden mm, cm, dm, m, dam, hm en km aan het einde van deze wikiwijs. - De leerlingen kunnen tevens de lengte-eenheden omschrijven. - De leerlingen kunnen rekenen ook rekenen met de eenheden van oppervlakte. - De leerlingen kunnen tevens de oppervlakte-eenheden omschrijven. - De leerlingen kunnen de oppervlakte van een driehoek uitrekenen.
    Eindgebruiker
    leerling/student
    Moeilijkheidsgraad
    gemiddeld
    Studiebelasting
    4 uur 0 minuten

    Bronnen

    Bron Type
    Wat zijn eenheden en grootheden?
    https://www.youtube.com/watch?v=GGLFKgsA4nA     		Video
    Kennisclip berekenen oppervlakte van een driehoek
    https://youtu.be/6GbQ1-KmGL0     		Video

  • Downloaden

    Het volledige arrangement is in de onderstaande formaten te downloaden.

    Metadata

    LTI

    Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI koppeling aan te gaan.

    Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.

    Arrangement

    IMSCC package

    Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.

    Voor developers

    Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op onze Developers Wiki.

  • Gebruik
    Weergave
  • Wikiwijs is een dienst van