De oppervlakte van een driehoek

De oppervlakte van een driehoek

Hallo!

Welkom op de wikiwijs over de oppervlakte van een driehoek. In deze wikiwijs wordt er uitgelegd wat de oppervlakte van een driehoek is, hoe deze berekent wordt bij een scherpe driehoek en hoe je de oppervlakte berekent van een stomphoekige driehoek.

De wikiwijs is gemaakt voor mavo 1, maar kan ook ingezet worden voor andere niveaus.

Lesdoelen

Aan het eind van deze wikiwijs:

- Kan je de formule voor het berekenen van de oppervlakte van een driehoek uitleggen

- Kan je de oppervlakte van een driehoek berekenen

Introductie

Oppervlakte van een rechthoek

Voordat we leren hoe we de oppervlakte van een driehoek kunnen berekenen kijken we eerst naar een rechthoek.

Beantwoord eerst de volgende vraag voordat je verder gaat:

Oefenen

Nu je de formule gevonden hebt gaan we dit nu uitproberen aan de hand van een aantal opgaves.

Bereken de oppervlakte van de rechthoeken in het volgende rechthoeken:

 

Rechthoeken
Rechthoeken

Een halve rechthoek

Rechthoek met driehoek
Rechthoek met driehoek

In de afbeelding hierboven zien we een rechthoek met een lengte en een breedte. Daarnaast zien we in deze rechthoek ook nog een driehoek. De driehoek neemt precies de helft van de oppervlakte van de rechthoek in.

Je zou dus ook kunnen zeggen dat de oppervlakte van een driehoek de helft is van de oppervlakte van een rechthoek.

Als je de oppervlakte van een rechthoek weet, kan je de oppervlakte van een driehoek berekenen door deze te delen door 2.

De oppervlakte van ΔABD = 18 x 10 : 2 = 90

ΔABD spreek je uit als 'driehoek ABD'.

Oppervlakte driehoek

Formule

Driehoek ABC
Driehoek ABC

Om ΔABC is een rechthoek getekend. De rechthoek bestaat uit een lengte en een breedte. Deze breedte kunnen we in de driehoek zetten. Vervolgens krijgt deze in de driehoek een andere naam: de hoogte.

Driehoek ABC
Driehoek ABC

Om dus de oppervlakte van een driehoek te berekenen gebruiken we de volgende formule:

\(oppervlakte = 0,5\times zijde\times hoogte\)

Merk hierbij op dat de hoogte loodrecht op zijde AB staat. De hoogte van een driehoek moet altijd loodrecht op een zijde staan!

De hoogte kan dus anders zijn in verschillende driehoeken. Bijvoorbeeld:

 

Verschillende hoogtes
Verschillende hoogtes

Voorbeeld

Driehoek DEF
Driehoek DEF

Hoe bereken je de oppervlakte van ΔDEF?

Als eerst zoeken we de hoogte die loodrecht op een zijde staat. Dit is de hoogte DG en die staat loodrecht op zijde EF.

Daarna vullen de de formule in met de juiste waardes die we gevonden hebben:

\(oppervlakte = 0,5\times zijde\times hoogte\)

\(oppervlakte = 0,5\times EF\times DG\)

\(oppervlakte = 0,5\times 28\times24 = 336 mm²\)

Let hierbij op dat er eenheden staan bij de zijdes en hoogte dus dat de oppervlakte ook een eenheid krijgt!

Voor de toets is alleen de laatste regel belangrijk. De regels daarvoor zijn ter ondersteuning.

Oefenen

Maak opdracht 32 t/m 37 van hoofdstuk 5

Een stomphoekige driehoek

Bekijk de kennisclip over het berekenen van de oppervlakte van een stomphoekige driehoek.

Kennisclip

Alles door elkaar

Socrative
Klik op de link en maken de vragen die klaarstaan in Socrative. De roomname is: WIGWIS

Afsluitende toets
Maak deze toets als je alles doorgenomen en geoefend hebt. Je mag er zo lang over doen als je wilt.

Afsluiten

Je bent aan het eind van de wikiwijs gekomen. Je kan nu de oppervlakte van een driehoek berekenen en de formule daarbij uitleggen. Dit kan je zowel voor scherpe als stomphoekige driehoeken.

Als laatste zou ik willen vragen of je de volgende evaluatie wilt invullen.

Evaluatie wikiwijs

Succes met leren voor je toets! :-)

  • Het arrangement De oppervlakte van een driehoek is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.

    Auteur
    Robin
    Laatst gewijzigd
    04-03-2022 12:33:35
    Licentie

    Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:

    • het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
    • het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
    • voor alle doeleinden, inclusief commerciële doeleinden.

    Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.

    Bronnen:

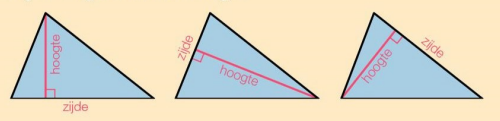
    Verschillende hoogtes: Noordhoff Uitgevers bv. (z.d.). Getal & Ruimte 1 vmbo-t/havo. Geraadpleegd op 1/11-2021 via: https://getalenruimte.digitaal.noordhoff.nl/home/ibookviewer?iBookId=4c750860-28b5-494b-8d3e-e61806eee5e2

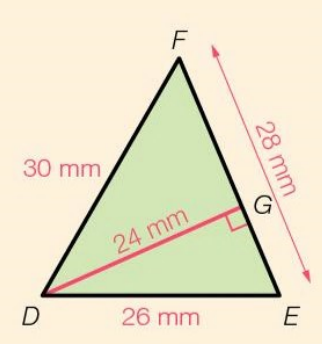
    Driehoek DEF: Noordhoff Uitgevers bv. (z.d.). Getal & Ruimte 1 vmbo-t/havo. Geraadpleegd op 1/11-2021 via: https://getalenruimte.digitaal.noordhoff.nl/home/ibookviewer?iBookId=4c750860-28b5-494b-8d3e-e61806eee5e2

    Aanvullende informatie over dit lesmateriaal

    Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:

    Toelichting
    In deze les voor mavo 1 komt de uitleg voor het berekenen van de oppervlakte van een driehoek naar voren.
    Eindgebruiker
    leerling/student
    Moeilijkheidsgraad
    gemiddeld
    Trefwoorden
    driehoek, mavo, oppervlakte, rechthoek, wiskunde

    Bronnen

    Bron Type
    Kennisclip
    https://edpuzzle.com/embed/assignments/6221f8f66d53b442a7d395b8/watch     		Video
    Socrative
    https://b.socrative.com/login/student/     		Link
    Afsluitende toets
    https://forms.gle/5V5LTiesZ5m2BWgr9     		Link
    Evaluatie wikiwijs
    https://forms.gle/S5ktBEdTULBektPT9     		Link

  • Downloaden

    Het volledige arrangement is in de onderstaande formaten te downloaden.

    Metadata

    LTI

    Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI koppeling aan te gaan.

    Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.

    Arrangement

    IMSCC package

    Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.

    Voor developers

    Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op onze Developers Wiki.

  • Wikiwijs is een dienst van