Het arrangement T4 Meetkunde: Vlakke Figuren 21/22 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteurs
- Laatst gewijzigd
- 20-09-2023 15:06:40
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- -
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten

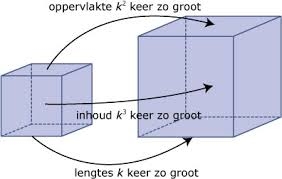
 regelmatig zult tegenkomen. Je kijkt naar de eigenschappen van deze figuren, je rekent met hoeken en je kijkt wat er gebeurt als je de figuren vergroot of verkleint.
regelmatig zult tegenkomen. Je kijkt naar de eigenschappen van deze figuren, je rekent met hoeken en je kijkt wat er gebeurt als je de figuren vergroot of verkleint.
 Leerdoelen
Leerdoelen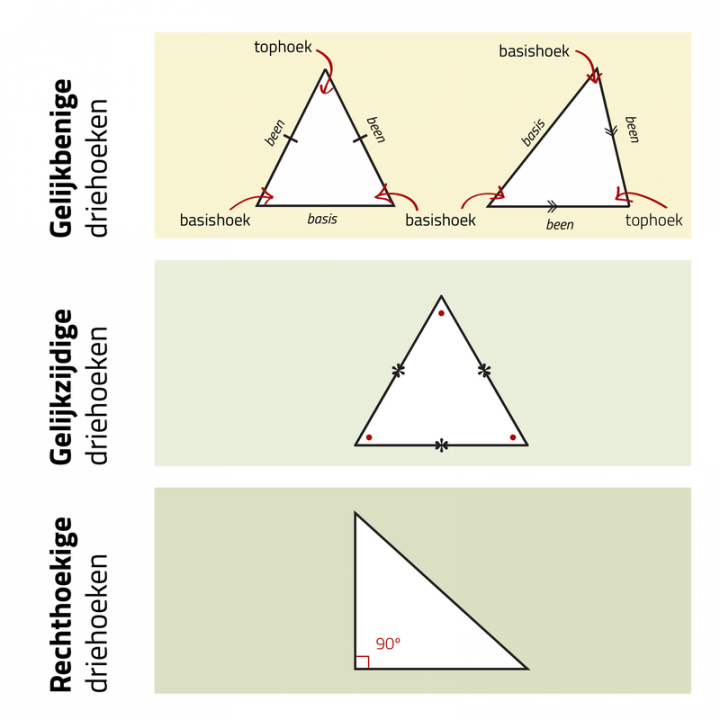

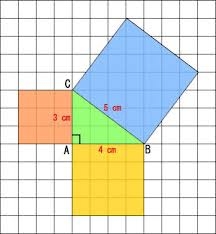
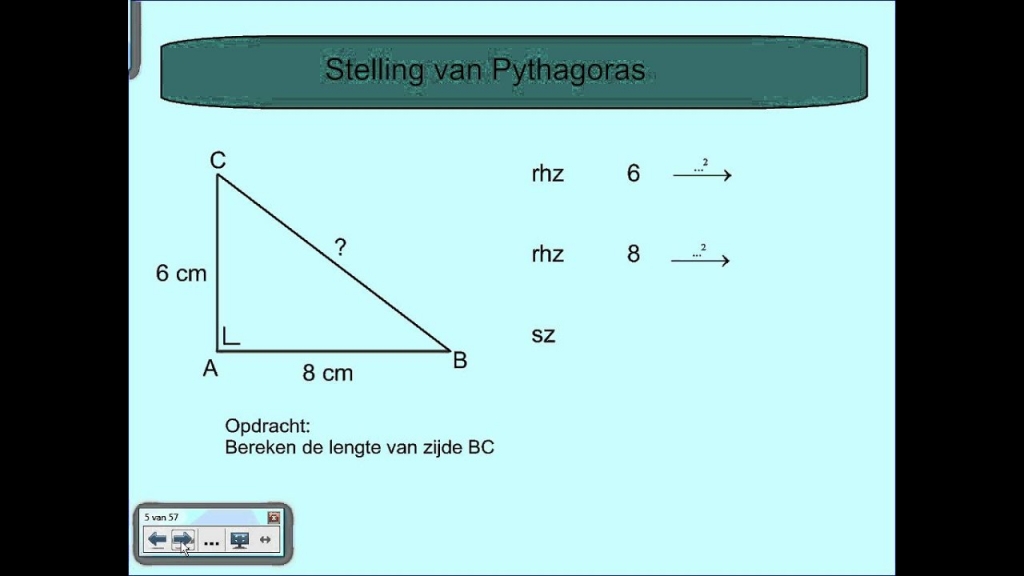
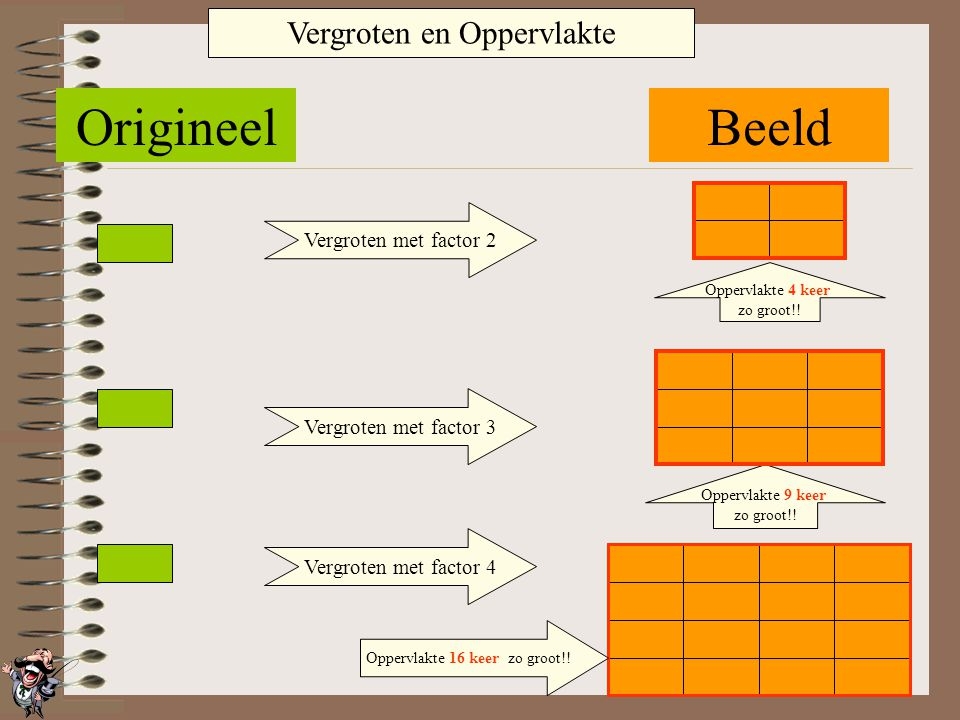

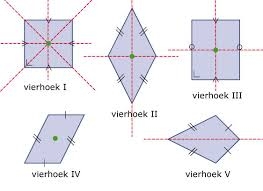
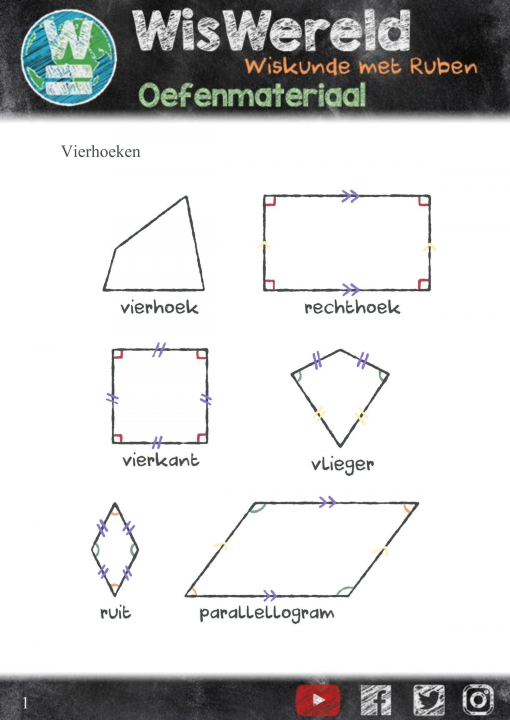
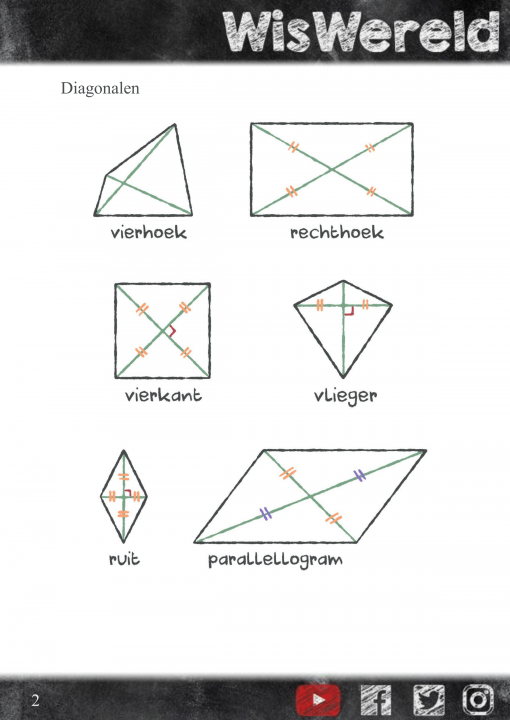
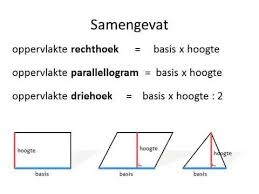
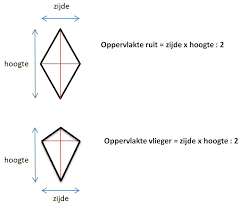
 De tweede paragraaf van dit thema is de paragraaf 'Vierhoeken'.
De tweede paragraaf van dit thema is de paragraaf 'Vierhoeken'.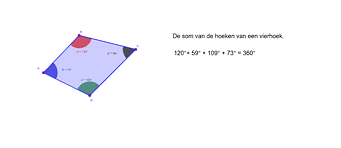

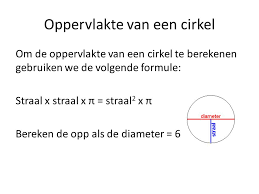
 In de derde paragraaf staat de cirkel centraal.
In de derde paragraaf staat de cirkel centraal.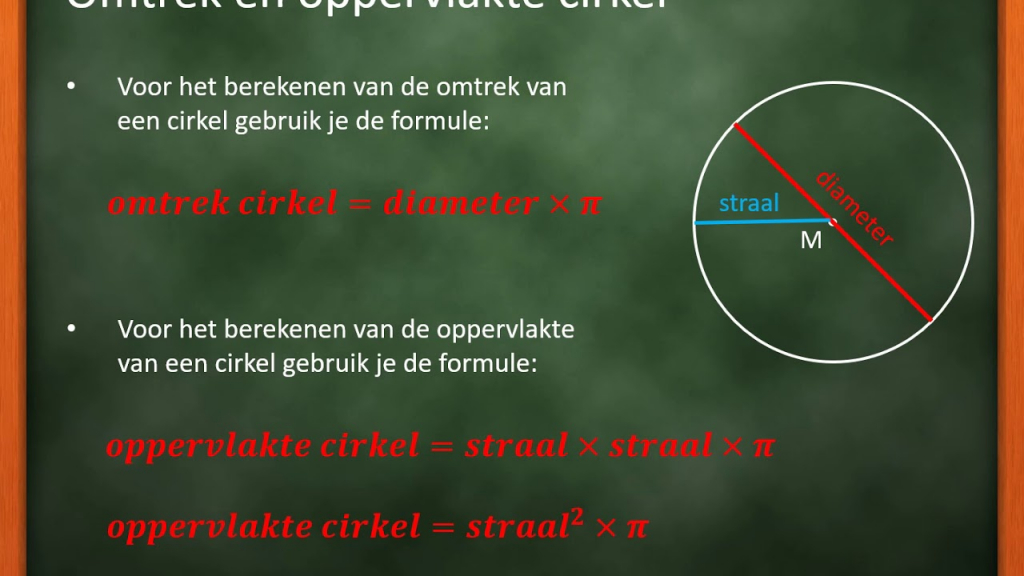


 Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren.