Het arrangement 2 M Ravelijn is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 04-10-2020 17:51:08
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
Bronnen
| Bron | Type |
|---|---|
|
Hoe teken je een grafiek bij een tabel (1) https://www.youtube.com/watch?v=faAJ9bY8SWQ |
Video |
|
Hoe teken je een grafiek bij een tabel (2) https://www.youtube.com/watch?v=lqRhertbEt4 |
Video |
Gebruikte Wikiwijs Arrangementen
Giessen, D.. (z.d.).
2H06 §2 Werken met verbanden
https://maken.wikiwijs.nl/149981/2H06__2_Werken_met_verbanden
Giessen, D.. (z.d.).
2H06 §3 Kwadratische verbanden
https://maken.wikiwijs.nl/149982/2H06__3_Kwadratische_verbanden
Giessen, D.. (z.d.).
2H06 §4 Kwadratische verbanden toepassen
https://maken.wikiwijs.nl/149983/2H06__4_Kwadratische_verbanden_toepassen
Giessen, D.. (z.d.).
2H06 §5 Vergelijkingen oplossen
https://maken.wikiwijs.nl/149984/2H06__5_Vergelijkingen_oplossen
Giessen, D.. (z.d.).
2H06 §6 Gemengde opgaven
Giessen, D.. (z.d.).
2KGT H02 Vergelijkingen
Giessen, D.. (z.d.).
2KGT H04 Kwadratische verbanden
https://maken.wikiwijs.nl/150016/2KGT_H04_Kwadratische_verbanden


 ‘t Ravelijn is een middelbare school in Steenbergen voor mavo en voorbereidend MBO
‘t Ravelijn is een middelbare school in Steenbergen voor mavo en voorbereidend MBO
 Welkom in leerjaar 2.
Welkom in leerjaar 2.






 Elke ochtend kijk je vast even in de spiegel. Je bent dan met symmetrie bezig zonder dat je het door hebt. Of knipt jou vader of moeder de heg in de tuin ook altijd zo netjes? Ook dan ben je met symmetrie bezig.
Elke ochtend kijk je vast even in de spiegel. Je bent dan met symmetrie bezig zonder dat je het door hebt. Of knipt jou vader of moeder de heg in de tuin ook altijd zo netjes? Ook dan ben je met symmetrie bezig. Ik kan in een figuur lijnsymmetrie herkennen.
Ik kan in een figuur lijnsymmetrie herkennen.


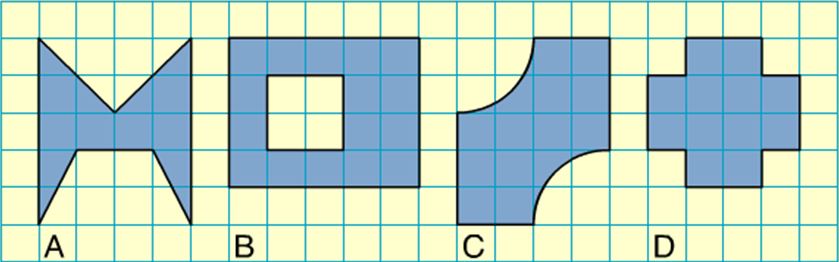 Maak een schema in je schrift:
Maak een schema in je schrift: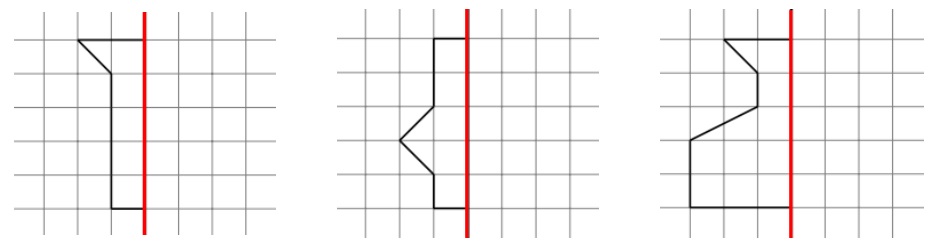
 Op je werkblad zie je de afbeelding zoals die hiernaast staat.
Op je werkblad zie je de afbeelding zoals die hiernaast staat.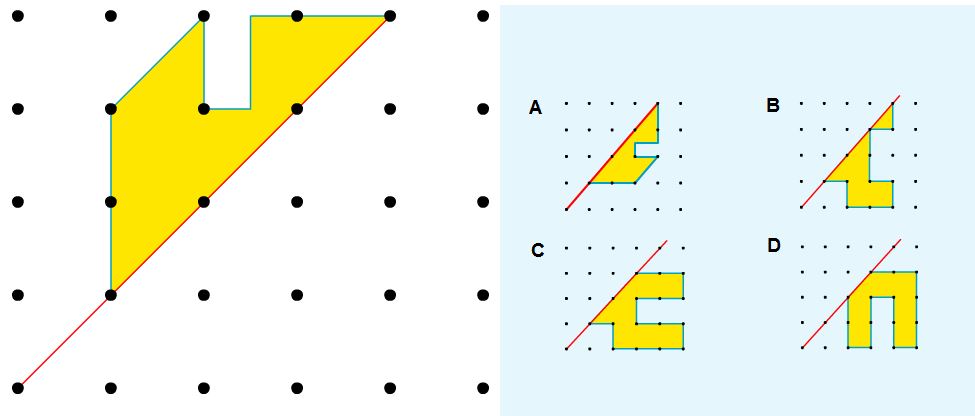
 De vierhoek hiernaast past bij draaiing vier keer op zichzelf.
De vierhoek hiernaast past bij draaiing vier keer op zichzelf. Kijk maar.
Kijk maar.
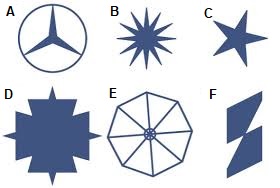 Hiernaast zie je een aantal draaisymmetrische figuren.
Hiernaast zie je een aantal draaisymmetrische figuren.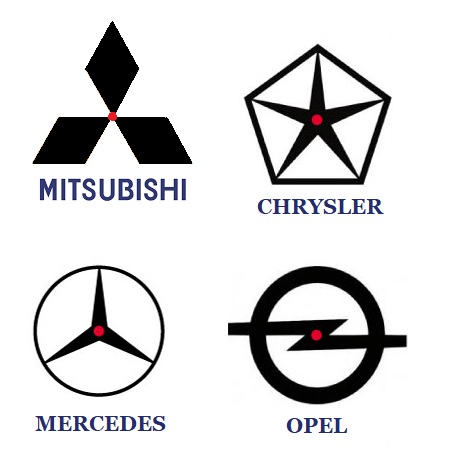 Hiernaast zien we vier logo's van vier verschillende auto merken. De logo's zijn draaisymmetrisch. Bereken van ieder logo de kleinste draaihoek. Schrijf de berekeningen netjes in je schrift.
Hiernaast zien we vier logo's van vier verschillende auto merken. De logo's zijn draaisymmetrisch. Bereken van ieder logo de kleinste draaihoek. Schrijf de berekeningen netjes in je schrift.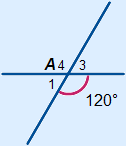
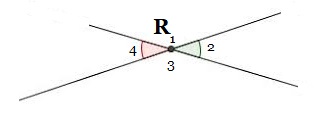 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.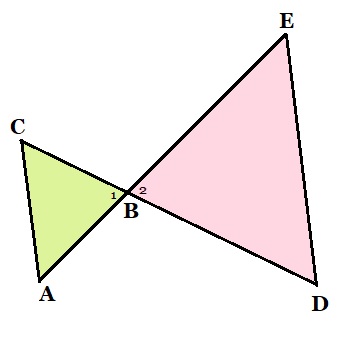 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.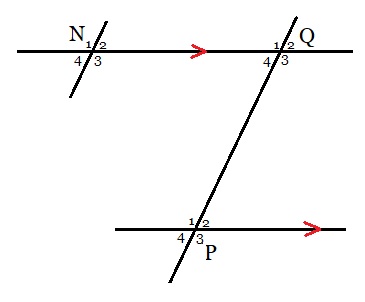 Bekijk de afbeelding hiernaast. Je ziet hier de hoeken N, P en Q. Alle hoeken zijn onderverdeelt in vier stukken.
Bekijk de afbeelding hiernaast. Je ziet hier de hoeken N, P en Q. Alle hoeken zijn onderverdeelt in vier stukken.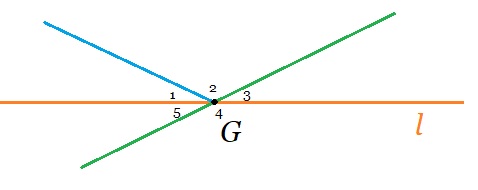 Hiernaast zie je hoek G. Hoek G is verdeeld in 5 stukken.
Hiernaast zie je hoek G. Hoek G is verdeeld in 5 stukken.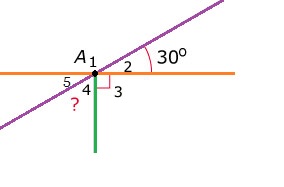 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.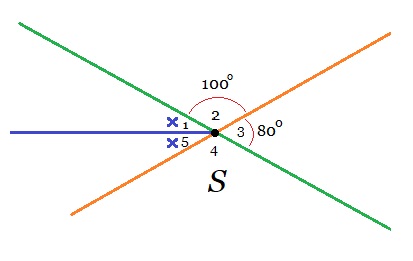 Bekijk de afbeelding hiernaast.
Bekijk de afbeelding hiernaast.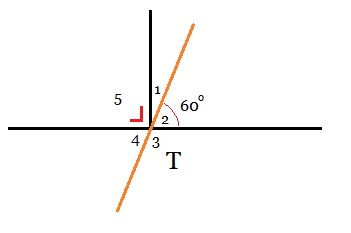 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.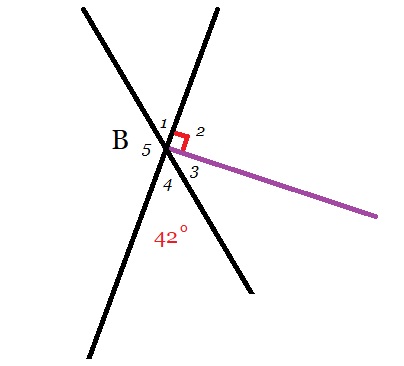 Bekijk de afbeelding hiernaast.
Bekijk de afbeelding hiernaast. Bekijk de acht afbeeldingen hiernaast.
Bekijk de acht afbeeldingen hiernaast.
 Een driehoek met een rechte hoek.
Een driehoek met een rechte hoek. Een driehoek met twee gelijke zijden. Deze driehoek heeft één symmetrieas.
Een driehoek met twee gelijke zijden. Deze driehoek heeft één symmetrieas.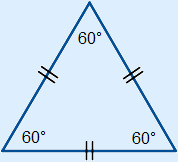 Een driehoek met drie gelijke zijden. Alle zijden van deze driehoek zijn even lang.
Een driehoek met drie gelijke zijden. Alle zijden van deze driehoek zijn even lang.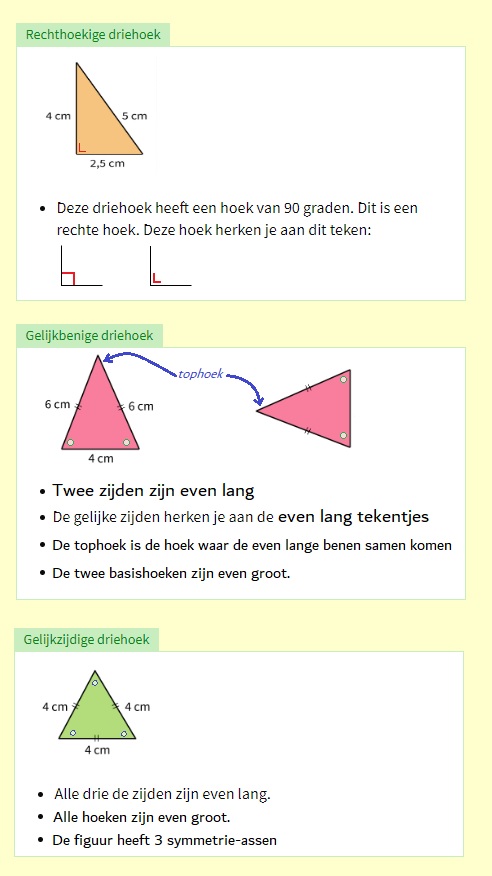
 Bekijk de driehoek op het plaatje. Deze staat ook op je werkblad. Gebruik je geodriehoek om de zijden eventueel op te meten.
Bekijk de driehoek op het plaatje. Deze staat ook op je werkblad. Gebruik je geodriehoek om de zijden eventueel op te meten. Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast. Bekijk de afbeelding hiernaast.
Bekijk de afbeelding hiernaast. Bekijk de verkeersborden hiernaast. Deze staan ook op je werkblad.
Bekijk de verkeersborden hiernaast. Deze staan ook op je werkblad. De lijnen m en n snijden elkaar in punt A.
De lijnen m en n snijden elkaar in punt A.
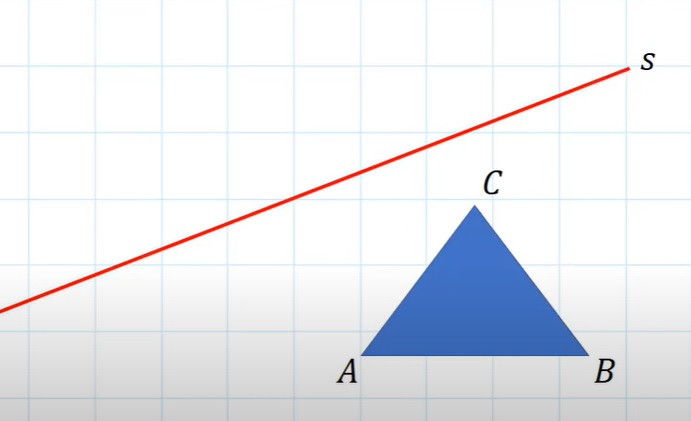
 De lijnen r en s snijden elkaar niet.
De lijnen r en s snijden elkaar niet.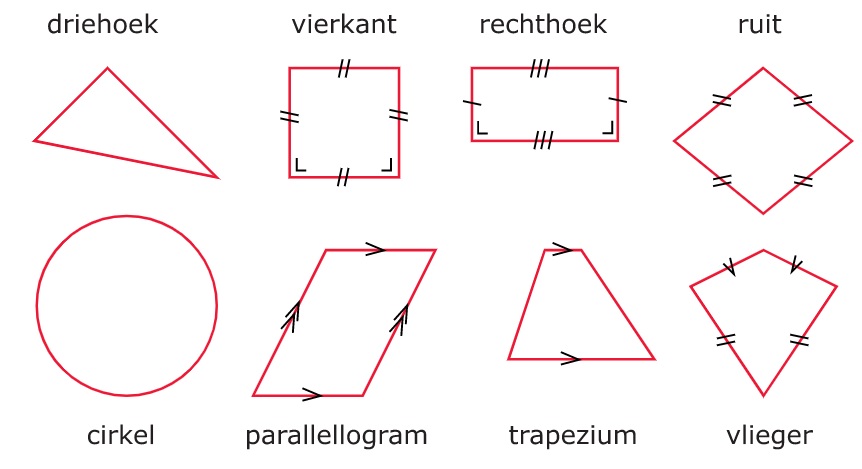
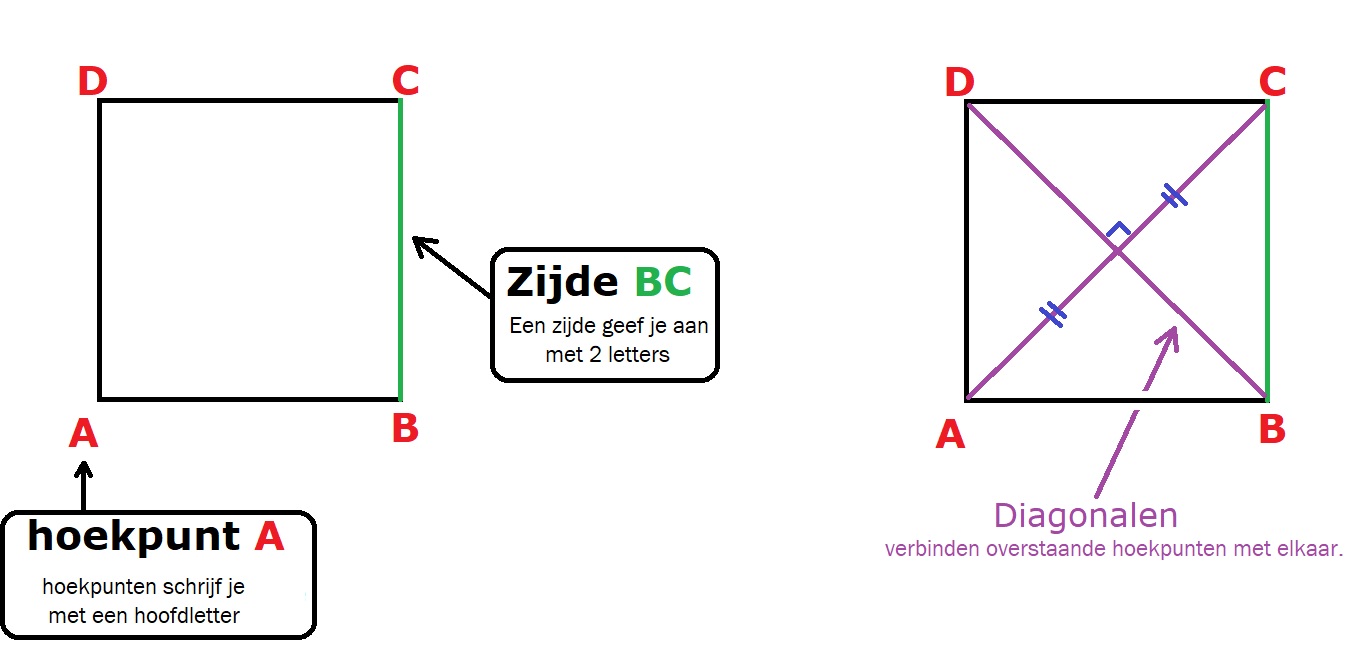
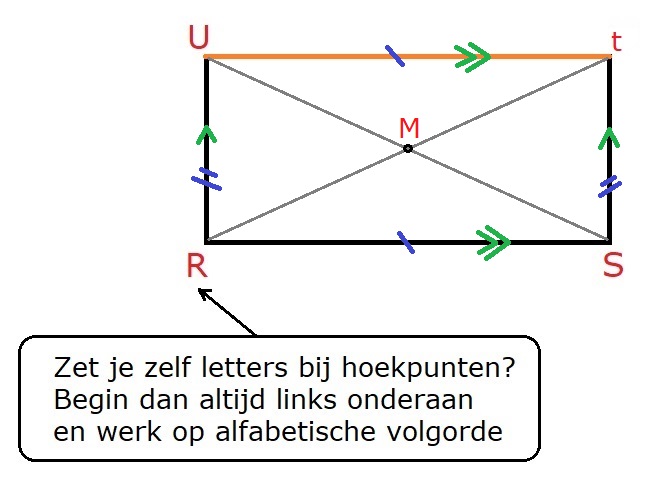 Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op.
Bekijk de rechthoek hiernaast, beantwoord dan de vragen. Schrijf de antwoorden op je ruitjespapier op. ,
,  en
en  wordt genoteerd als
wordt genoteerd als  .
.
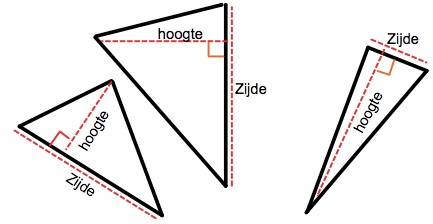
 Opp cirkel =
Opp cirkel = 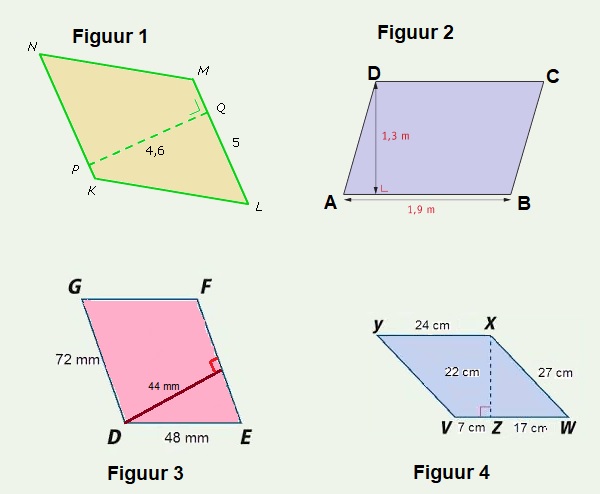 Bekijk de vier parallellogrammen hiernaast.
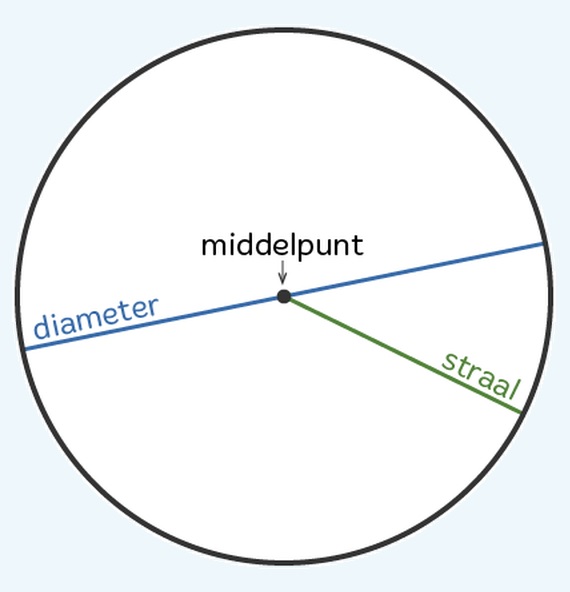
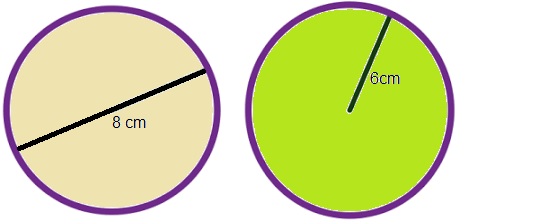
Bekijk de vier parallellogrammen hiernaast. Bekijk de cirkels hiernaast.
Bekijk de cirkels hiernaast.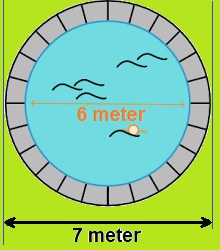 Over het zwembad hiernaast moet een zeil komen dat het zwembad beschermt tegen regen en het water schoon houdt. Ook de rand met tegels komt onder het zeil te liggen.
Over het zwembad hiernaast moet een zeil komen dat het zwembad beschermt tegen regen en het water schoon houdt. Ook de rand met tegels komt onder het zeil te liggen.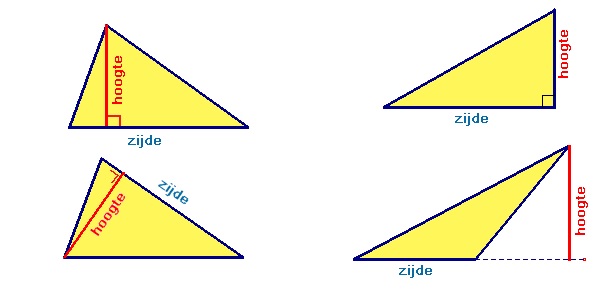
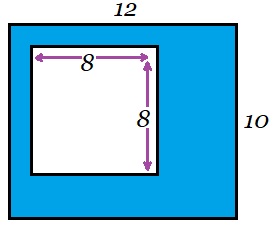 Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.
Hiernaast zie je een blauwe rechthoek waar een stukje uit gesneden is. We willen alleen de oppervlakte van het blauwe stuk weten.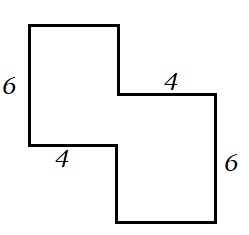 Bekijk de figuur hiernaast.
Bekijk de figuur hiernaast.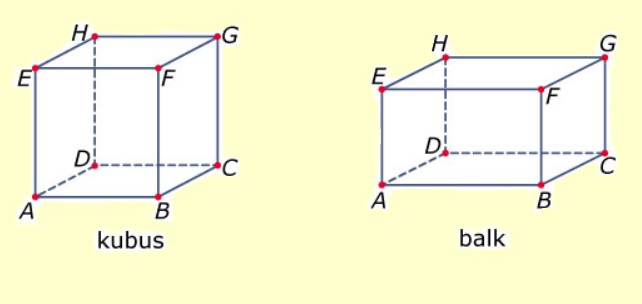

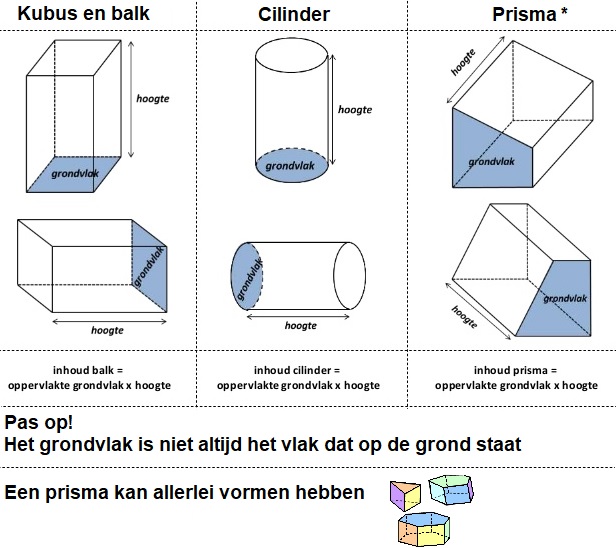
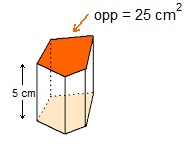 Bekijk het prisma hiernaast.
Bekijk het prisma hiernaast.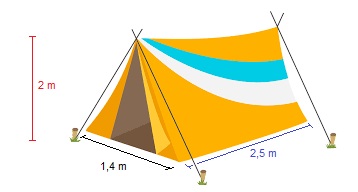 De voorkant van deze 'tent' is een gelijkbenige driehoek.
De voorkant van deze 'tent' is een gelijkbenige driehoek.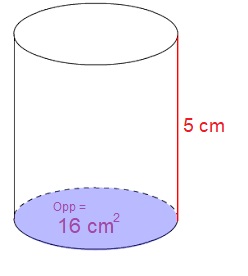 Bekijk het plaatje hiernaast.
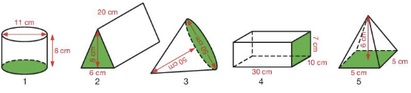
Bekijk het plaatje hiernaast.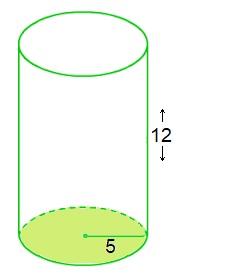 Het grondvlak van een cilinder heeft een straal van van 5 cm.
Het grondvlak van een cilinder heeft een straal van van 5 cm.
 De jacuzzi is 1,2 meter hoog en heeft een diameter van 1,6 m.
De jacuzzi is 1,2 meter hoog en heeft een diameter van 1,6 m.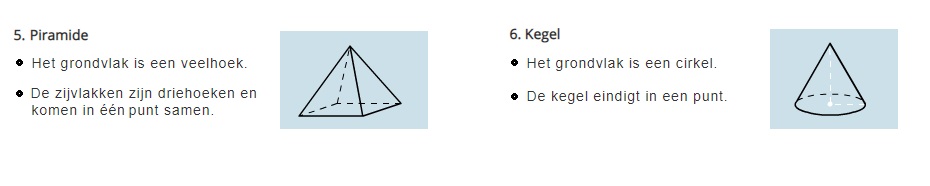
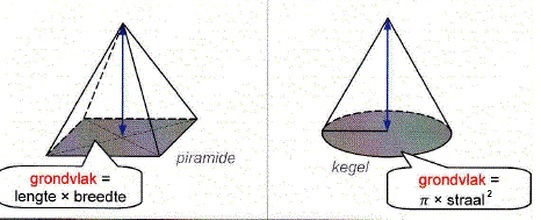
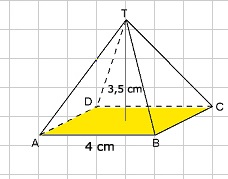 Het grondvlak van de piramide hieronder is een vierkant met zijde van 4 cm. De hoogte van de piramide is 3,5 cm.
Het grondvlak van de piramide hieronder is een vierkant met zijde van 4 cm. De hoogte van de piramide is 3,5 cm.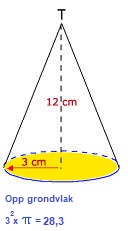 Het grondvlak van de kegel hieronder is een cirkel met een straal van 3 cm.
Het grondvlak van de kegel hieronder is een cirkel met een straal van 3 cm.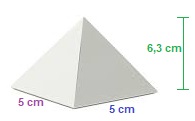 De piramide hieronder heeft een grondvlak met een oppervlakte van 25 cm². De hoogte is 6,3 cm.
De piramide hieronder heeft een grondvlak met een oppervlakte van 25 cm². De hoogte is 6,3 cm.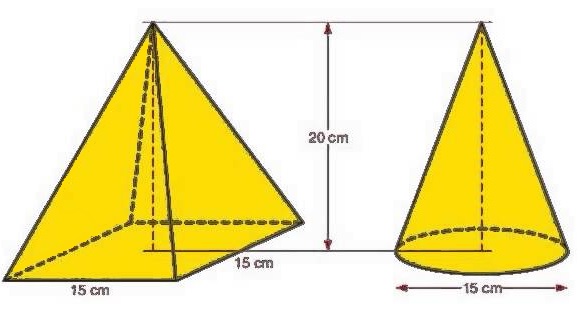 Hiernaast zie je een piramide en een kegel. Laat door middel van
Hiernaast zie je een piramide en een kegel. Laat door middel van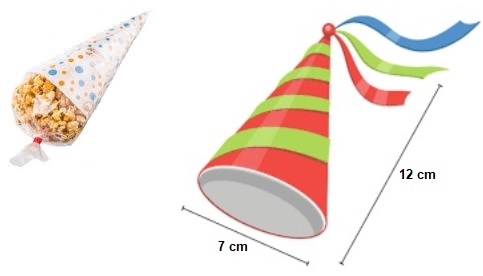 Sanne is jarig en wil in haar klas een kleine tractatie uitdelen. Ze besluit feesthoedjes te vullen met popcorn.
Sanne is jarig en wil in haar klas een kleine tractatie uitdelen. Ze besluit feesthoedjes te vullen met popcorn.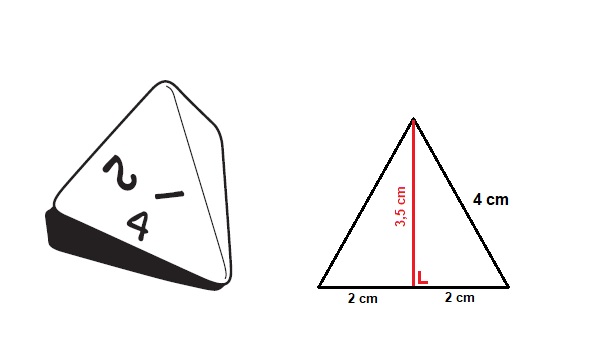 Niet iedere piramide heeft een rechthoek of een vierkant als grondvlak. Kijk maar eens naar de dobbelsteen hiernaast. Je ziet daar een piramide met een gelijkzijdige driehoek als grondvlak.
Niet iedere piramide heeft een rechthoek of een vierkant als grondvlak. Kijk maar eens naar de dobbelsteen hiernaast. Je ziet daar een piramide met een gelijkzijdige driehoek als grondvlak.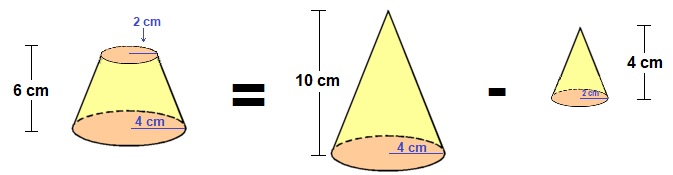
 Het theezakje hieronder bestaat uit allemaal gelijkzijdige driehoeken met zijden van 3 cm. De hoogte van het zakje is ook 3cm.
Het theezakje hieronder bestaat uit allemaal gelijkzijdige driehoeken met zijden van 3 cm. De hoogte van het zakje is ook 3cm. De wereld om ons heen bestaat niet enkel uit losse ruimtefiguren (lichamen). Heel veel objecten zijn opgebouwd uit twee of meer ruimtefiguren samen. Kijk maar naar het huis hiernaast. Dit huis bestaat uit twee balken en een prisma als dak.
De wereld om ons heen bestaat niet enkel uit losse ruimtefiguren (lichamen). Heel veel objecten zijn opgebouwd uit twee of meer ruimtefiguren samen. Kijk maar naar het huis hiernaast. Dit huis bestaat uit twee balken en een prisma als dak.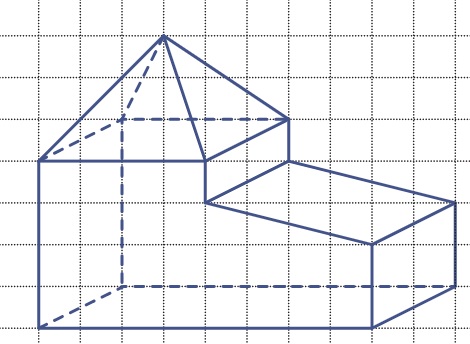 Bekijk de afbeelding hiernaast.
Bekijk de afbeelding hiernaast.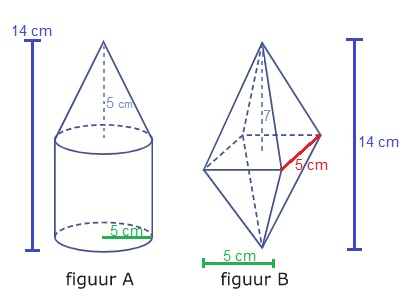
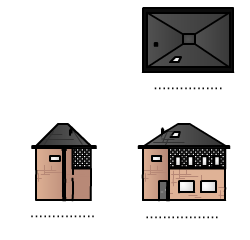
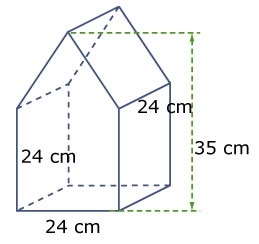 Hiernaast zien we de contouren van een huisje.
Hiernaast zien we de contouren van een huisje.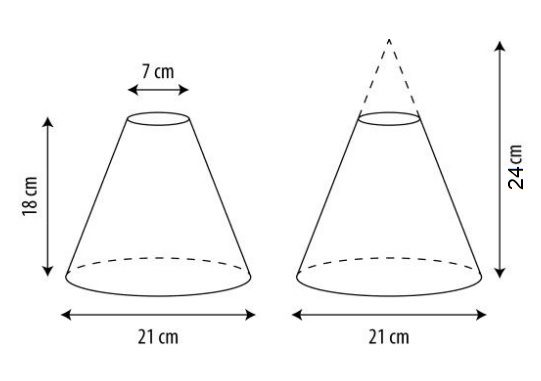 Hiernaast zien we een afgeknotte kegel. Voor het gemak is ernaast gezet welk stukje er afgesneden is.
Hiernaast zien we een afgeknotte kegel. Voor het gemak is ernaast gezet welk stukje er afgesneden is. Bereken de inhoud van het huis hiernaast.
Bereken de inhoud van het huis hiernaast.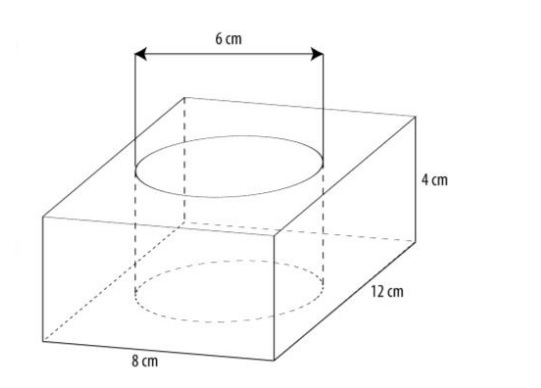 Hiernaast zien we een kaarsenhouder. Deze balkvormige houder heeft in het midden een cilindervormig gat waar de kaars precies in past.
Hiernaast zien we een kaarsenhouder. Deze balkvormige houder heeft in het midden een cilindervormig gat waar de kaars precies in past. Hiernaast zie je hou handdoekrollen worden vervoert. Op het plaatje kun je zien dat er zes rollen in één doos passen, twee naast elkaar en drie achter elkaar.
Hiernaast zie je hou handdoekrollen worden vervoert. Op het plaatje kun je zien dat er zes rollen in één doos passen, twee naast elkaar en drie achter elkaar. Van een kubus zijn alle ribben gelijk.
Van een kubus zijn alle ribben gelijk. lijnstukken die "naar achteren lopen" teken je een beetje schuin;
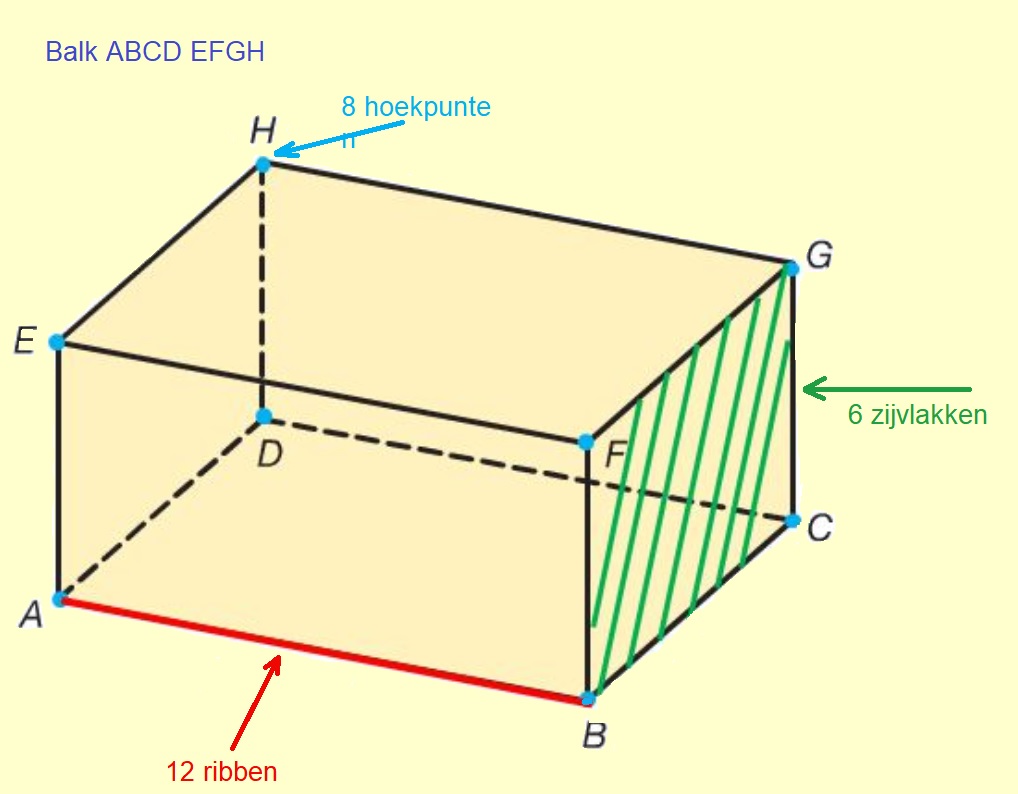
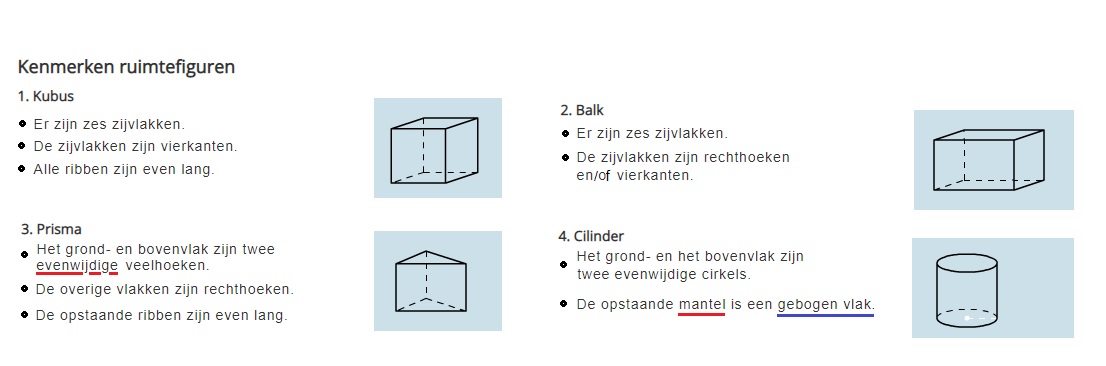
lijnstukken die "naar achteren lopen" teken je een beetje schuin;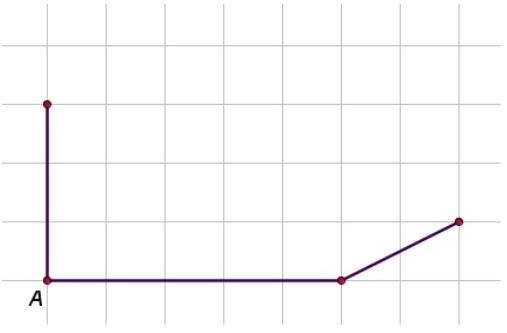 Op je werkblad is het begin van een balk ABCD EFGH getekend.
Op je werkblad is het begin van een balk ABCD EFGH getekend.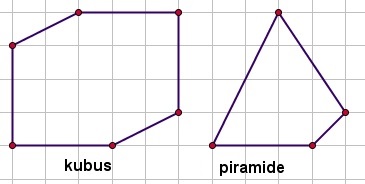 Teken op je werkblad de figuren 'af'.
Teken op je werkblad de figuren 'af'.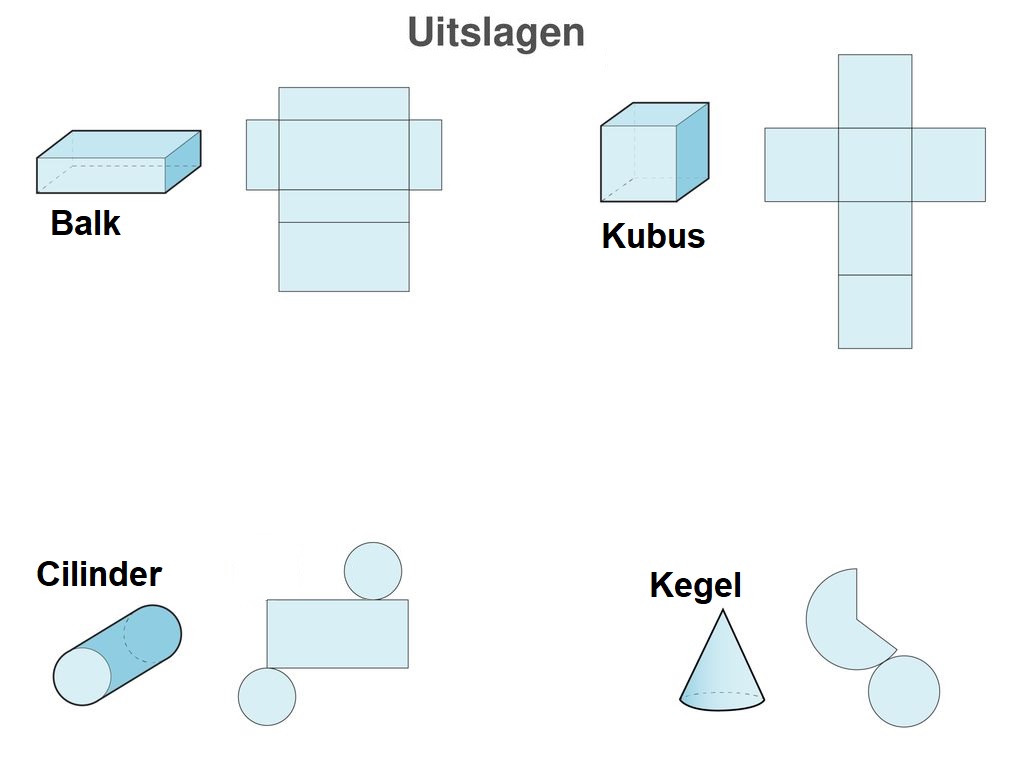
 Wat wel eens lastig kan zijn is dat je van ruimtefiguren vaak verschillende uitslagen kan maken. let daarbij wel op de uitslag moet met terugvouwen altijd weer het oorspronkelijke ruimtelijke figuur opleveren.
Wat wel eens lastig kan zijn is dat je van ruimtefiguren vaak verschillende uitslagen kan maken. let daarbij wel op de uitslag moet met terugvouwen altijd weer het oorspronkelijke ruimtelijke figuur opleveren.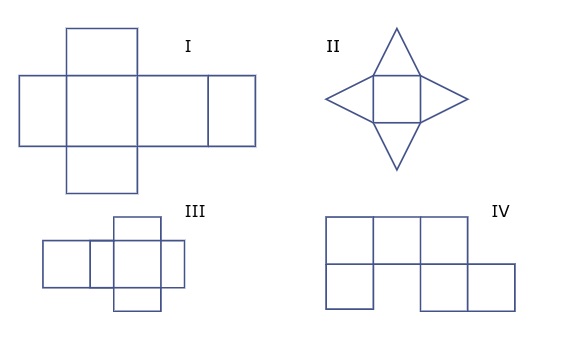 Bekijk de vier uitslagen van ruimtefiguren hiernaast.
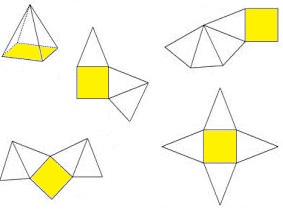
Bekijk de vier uitslagen van ruimtefiguren hiernaast.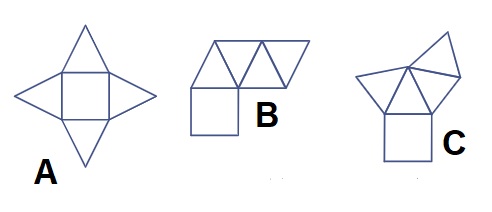 Bekijk de afbeelding met daarop verschillende uitslagen van een piramide.
Bekijk de afbeelding met daarop verschillende uitslagen van een piramide.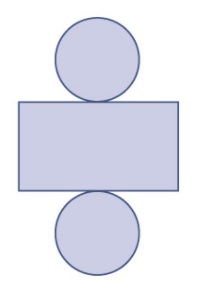 Maaike heeft geprobeerd de uitslag van een cilinder te tekenen.
Maaike heeft geprobeerd de uitslag van een cilinder te tekenen.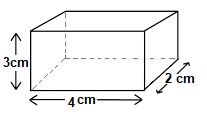 Hiernaast zie je een balk. Teken een mogelijke uitslag van de balk op ware grootte. Zet in je uitslag ook de woordjes onderkant, bovenkant, voorkant, achterkant, rechts en links.
Hiernaast zie je een balk. Teken een mogelijke uitslag van de balk op ware grootte. Zet in je uitslag ook de woordjes onderkant, bovenkant, voorkant, achterkant, rechts en links.




 WERKBLAD 7.2
WERKBLAD 7.2

 Op een pak gezeefde tomaten staat: Inhoud 500 ml.
Op een pak gezeefde tomaten staat: Inhoud 500 ml.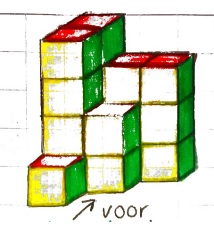 Sanne schetst het bouwwerk dat je hiernaast ziet.
Sanne schetst het bouwwerk dat je hiernaast ziet.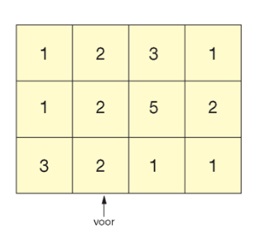 In de figuur hiernaast zie je het bovenaanzicht van een blokkenbouwwerk. De getallen geven de hoeveelheid blokjes aan die gestapeld zijn.
In de figuur hiernaast zie je het bovenaanzicht van een blokkenbouwwerk. De getallen geven de hoeveelheid blokjes aan die gestapeld zijn.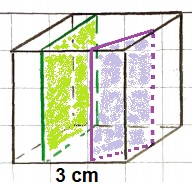 Hiernaast zie je eens schets van een kubus met daarin 2 gekleurde vlakken.
Hiernaast zie je eens schets van een kubus met daarin 2 gekleurde vlakken.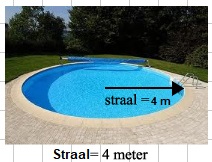 Bereken de oppervlakte van het zwembad hiernaast.
Bereken de oppervlakte van het zwembad hiernaast.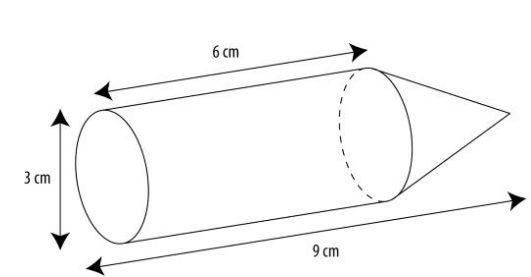 De figuur hiernaast is samengesteld uit twee ruimtefiguren.
De figuur hiernaast is samengesteld uit twee ruimtefiguren.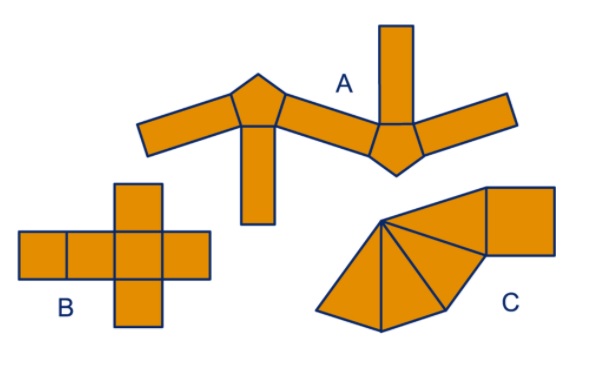 Hiernaast zie je drie uitslagen.
Hiernaast zie je drie uitslagen.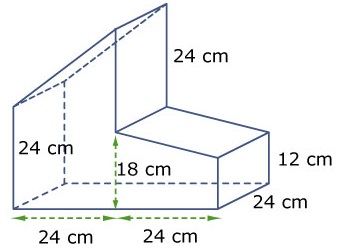 Hiernaast zien we een draadmodel van een huisje. De architect wil graag weten wat de inhoud van dit modelhuis is.
Hiernaast zien we een draadmodel van een huisje. De architect wil graag weten wat de inhoud van dit modelhuis is. Een diagnostische toets is een onderzoek naar eventuele gaten in jouw kennis of vaardigheden. Het doel van de diagnostische toets is het vaststellen wat je al kan, en waar je de komende tijd nog wat extra aandacht aan moet besteden.
Een diagnostische toets is een onderzoek naar eventuele gaten in jouw kennis of vaardigheden. Het doel van de diagnostische toets is het vaststellen wat je al kan, en waar je de komende tijd nog wat extra aandacht aan moet besteden.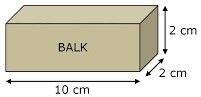
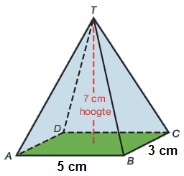 Bereken de inhoud van de piramide.
Bereken de inhoud van de piramide.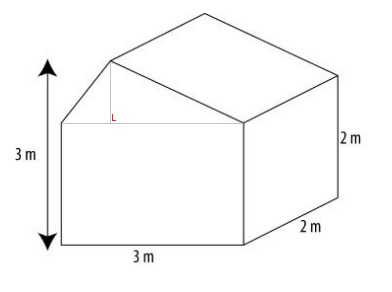 Hiernaast zien we een samengestelde ruimtefiguur.
Hiernaast zien we een samengestelde ruimtefiguur.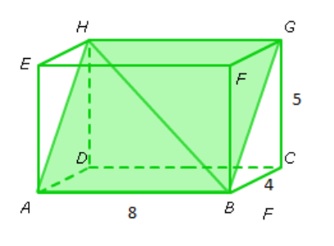
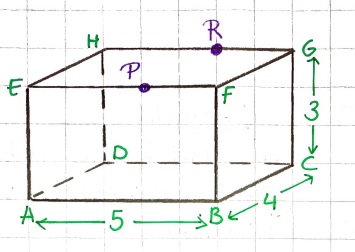 Hiernaast zie je een tekening van een balk. HR = EP en RG = 2 cm.
Hiernaast zie je een tekening van een balk. HR = EP en RG = 2 cm.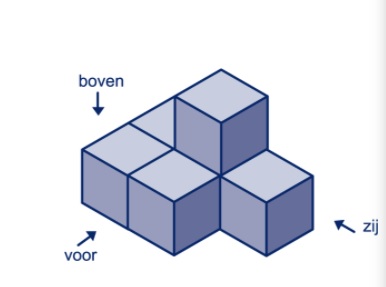 Bekijk het bouwwerkje hiernaast.
Bekijk het bouwwerkje hiernaast.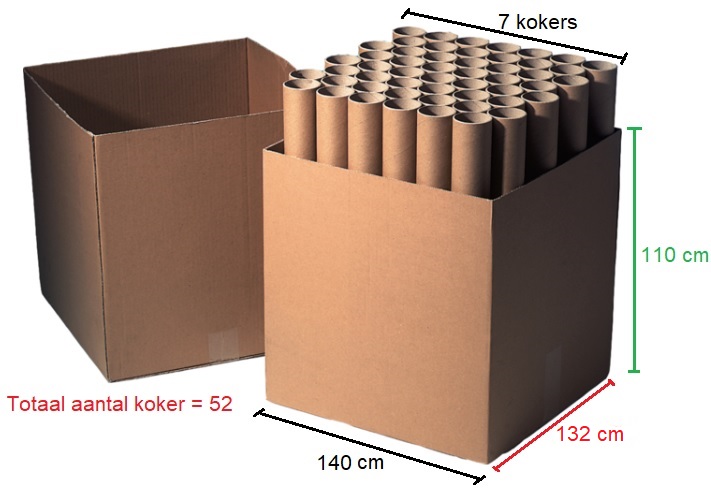 Wanneer je een grote hoeveelheid posters besteld worden deze in apparte kokers naar je toegezonden. Een koker heeft een diameter van 20 cm en is net zo hoog als de doos.
Wanneer je een grote hoeveelheid posters besteld worden deze in apparte kokers naar je toegezonden. Een koker heeft een diameter van 20 cm en is net zo hoog als de doos.
 Het hoofdstuk vergelijkingen hoort bij het onderwerp algebra. Algebra houdt zich bij wiskunde bezig met verbanden ook wel formules genoemd. In bijna alle beroepen kom je wel formules tegen. Mensen die werken met logistiek (vervoer over de weg, door de lucht of over het water maar ook telefoonverbindingen, wifi netwerken en elektriciteitskabels aanleggen), accountants (boekhouders), de lucht en ruimtevaart, civiele techniek (ontwerpen en bouwen van wegen, bruggen, dammen, dijken) werken dagelijks met verbanden. Eigenlijk werkt bijna iedereen wel eens een keer in de week met een verband. Al is het maar om je loon of de winst van je eigen bedrijf te kunnen berekenen
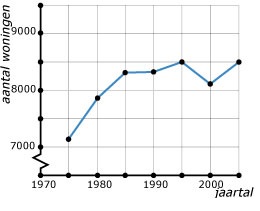
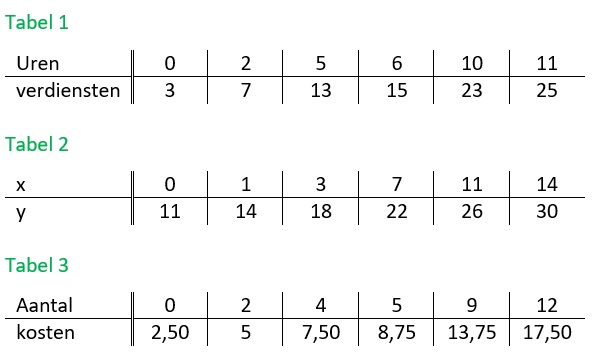
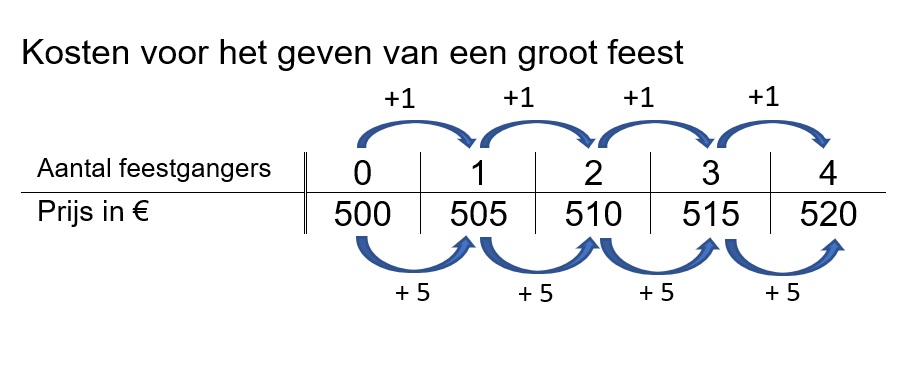
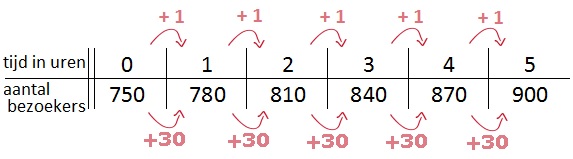
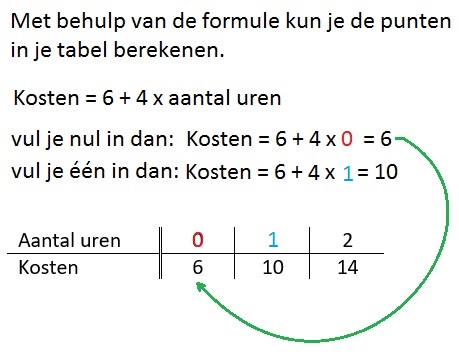
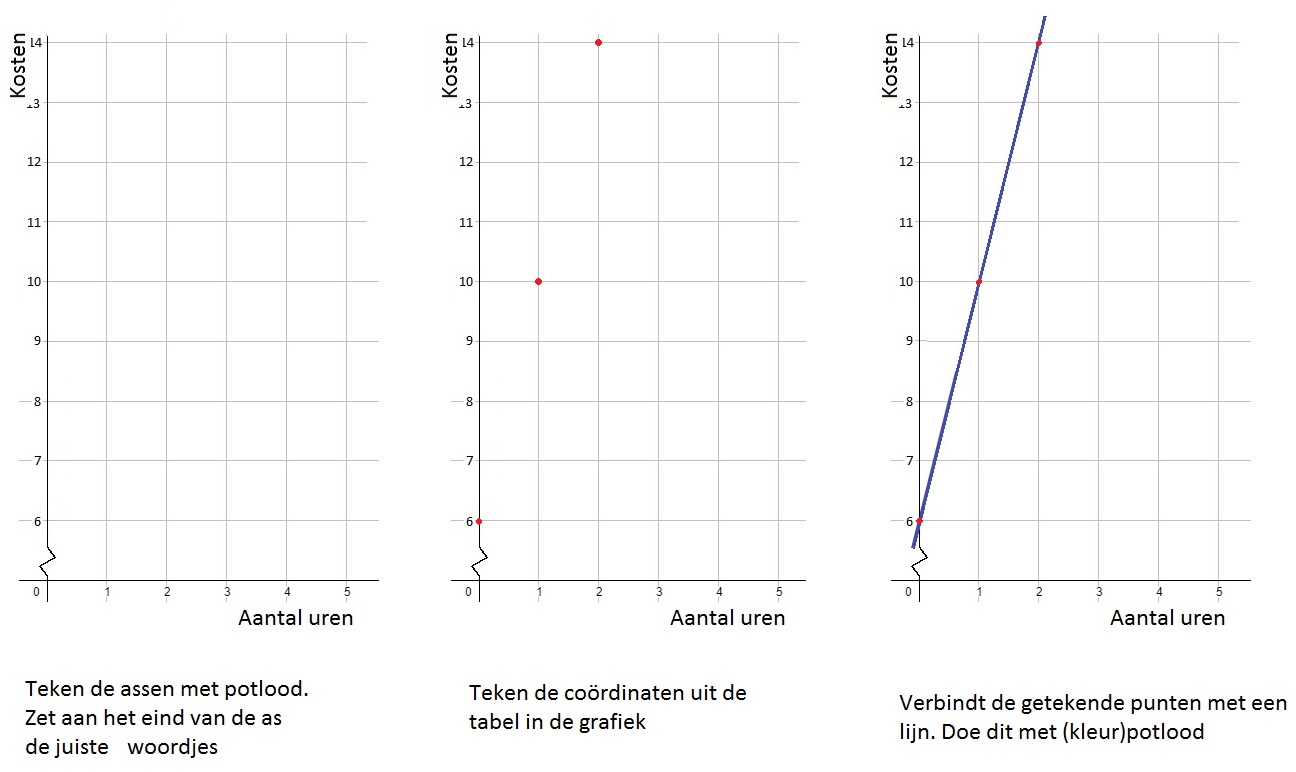
Het hoofdstuk vergelijkingen hoort bij het onderwerp algebra. Algebra houdt zich bij wiskunde bezig met verbanden ook wel formules genoemd. In bijna alle beroepen kom je wel formules tegen. Mensen die werken met logistiek (vervoer over de weg, door de lucht of over het water maar ook telefoonverbindingen, wifi netwerken en elektriciteitskabels aanleggen), accountants (boekhouders), de lucht en ruimtevaart, civiele techniek (ontwerpen en bouwen van wegen, bruggen, dammen, dijken) werken dagelijks met verbanden. Eigenlijk werkt bijna iedereen wel eens een keer in de week met een verband. Al is het maar om je loon of de winst van je eigen bedrijf te kunnen berekenen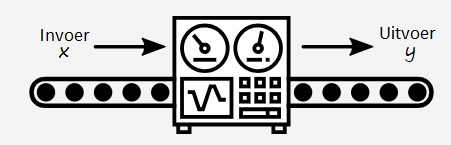 Een tabel bestaat uit twee onderdelen: invoer en uitvoer.
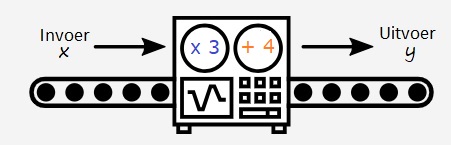
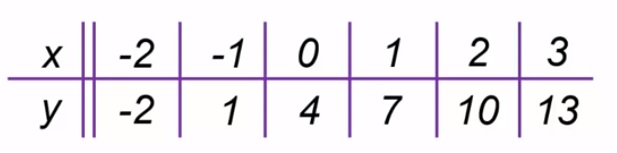
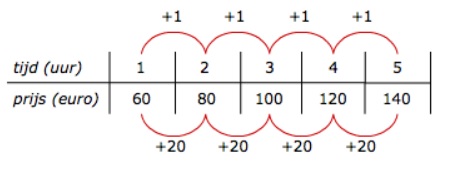
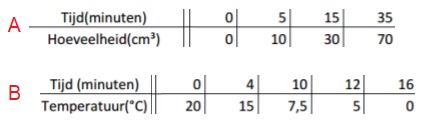
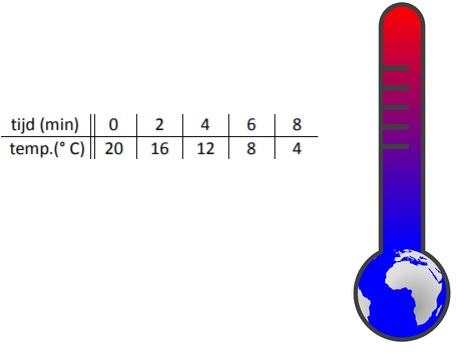
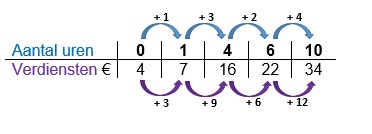
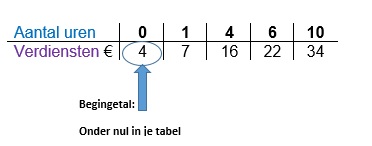
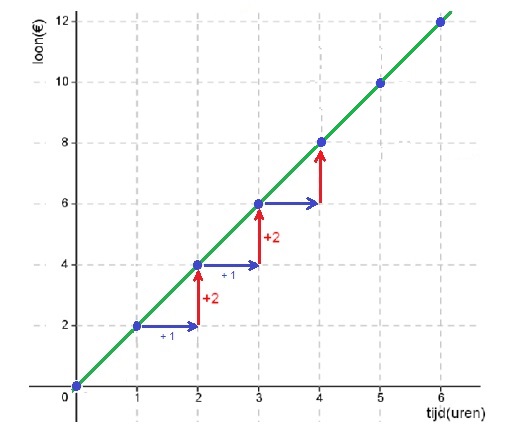
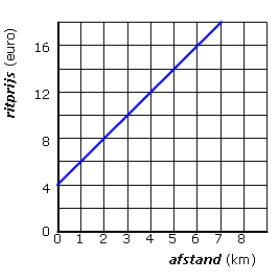
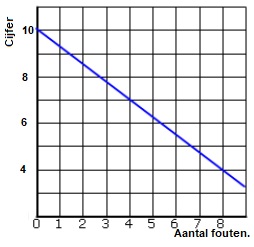
Een tabel bestaat uit twee onderdelen: invoer en uitvoer. 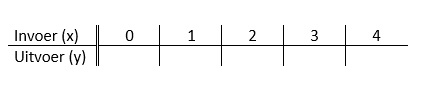
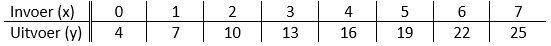
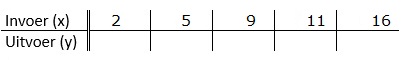
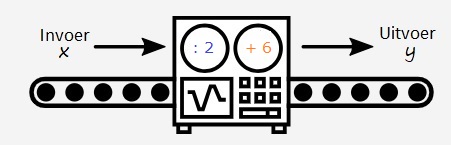

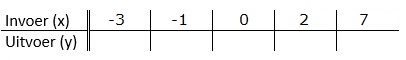
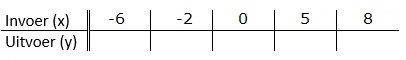

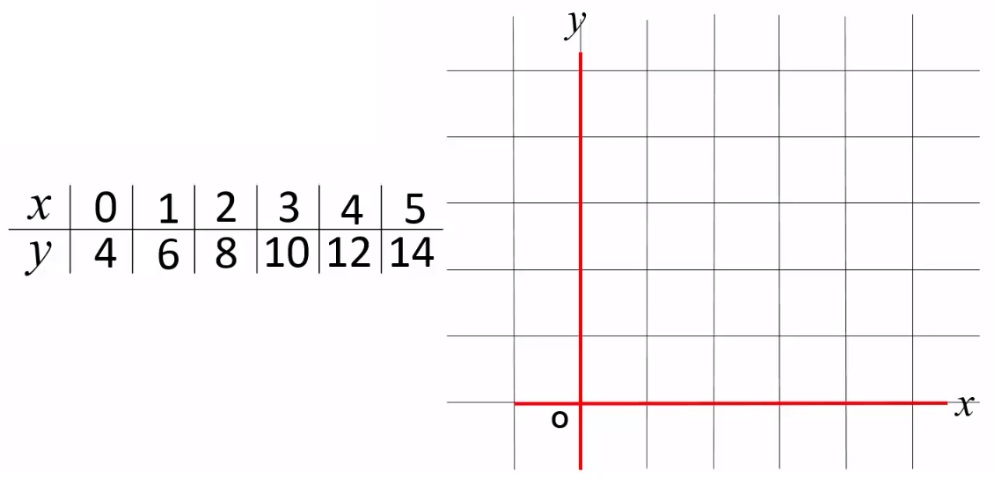




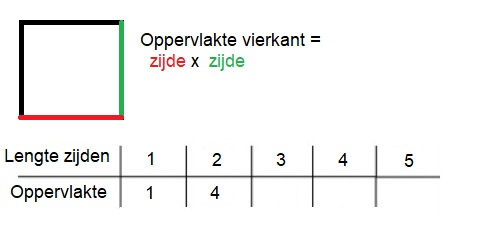
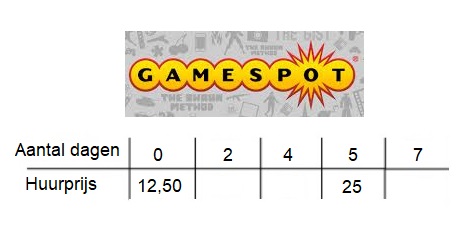
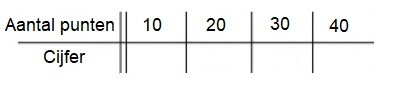
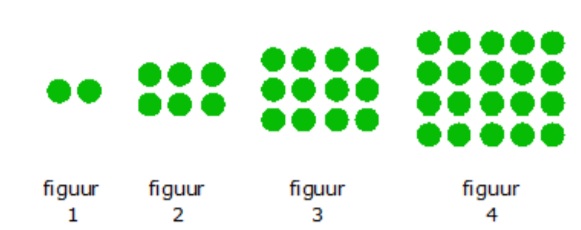


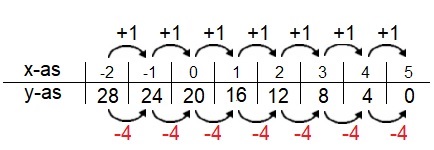
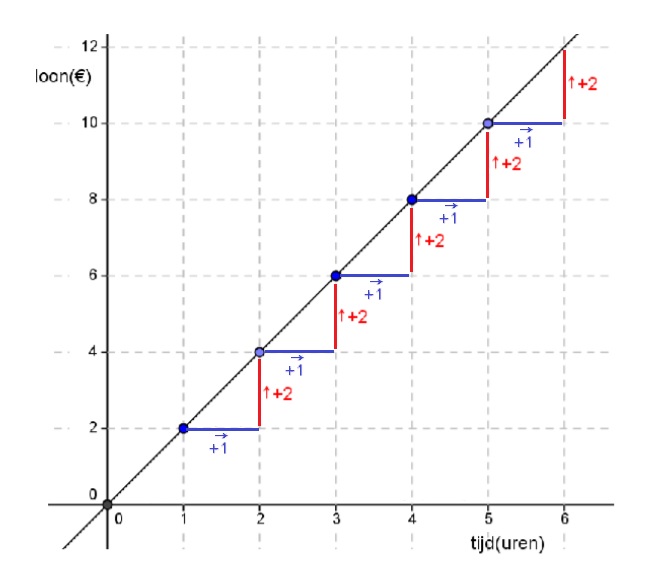
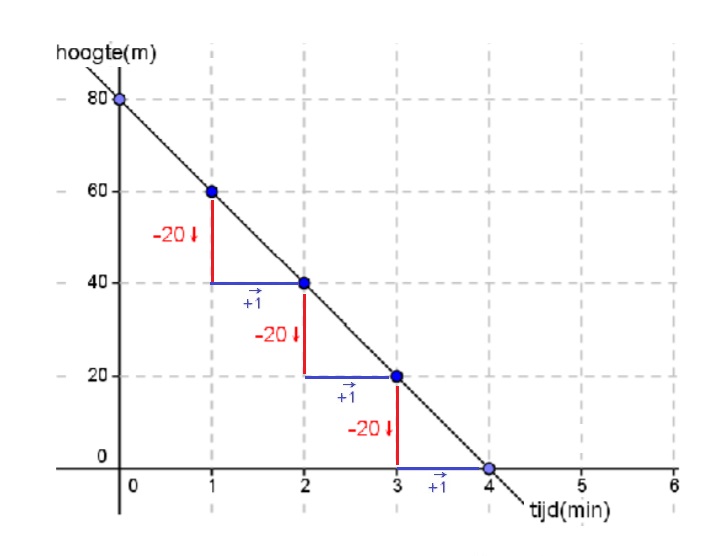
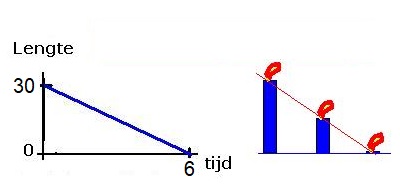
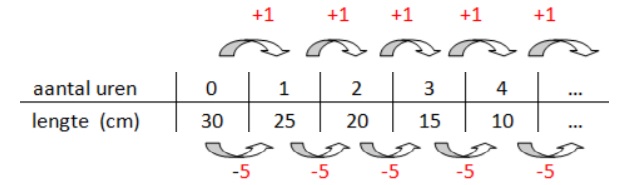
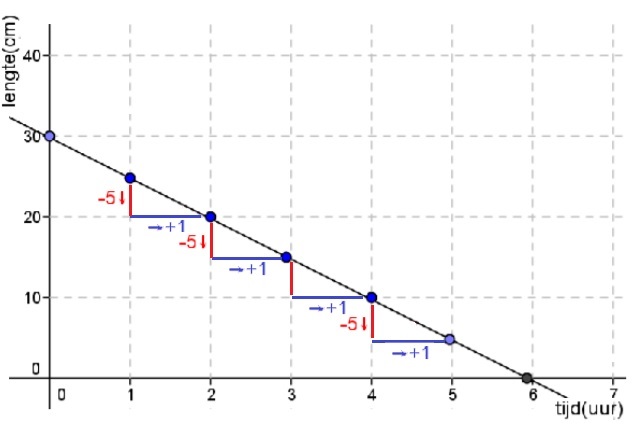
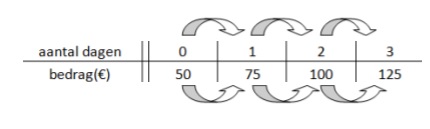
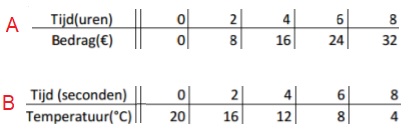





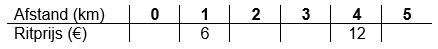
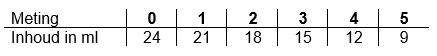


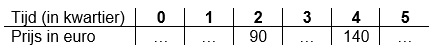


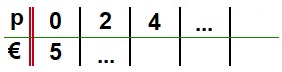
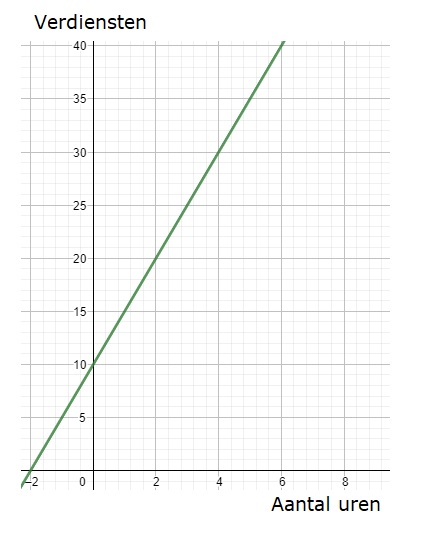
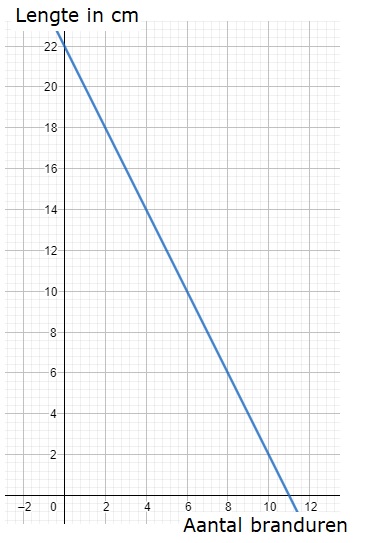
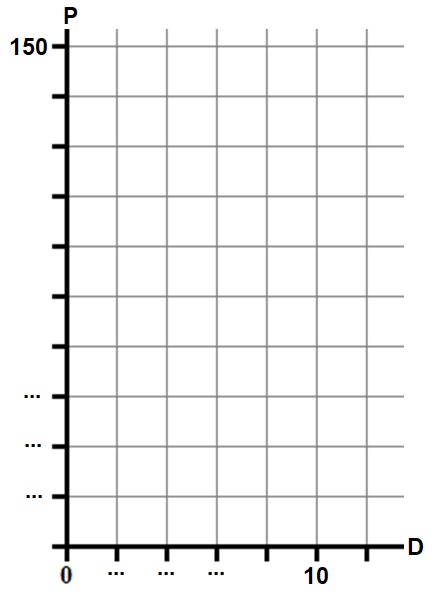

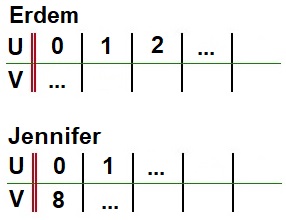


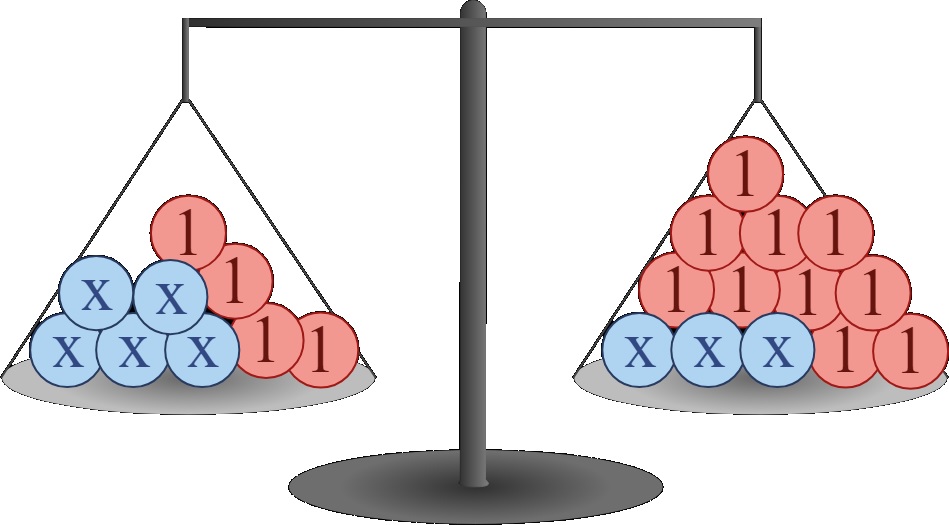
 Hier rechts zie je de balans uit het filmpje.
Hier rechts zie je de balans uit het filmpje.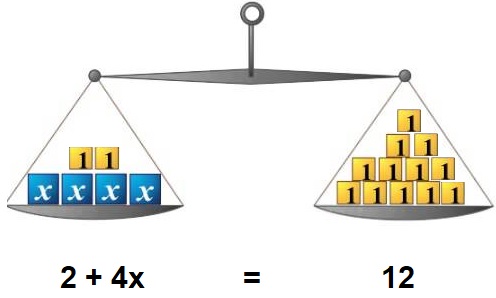
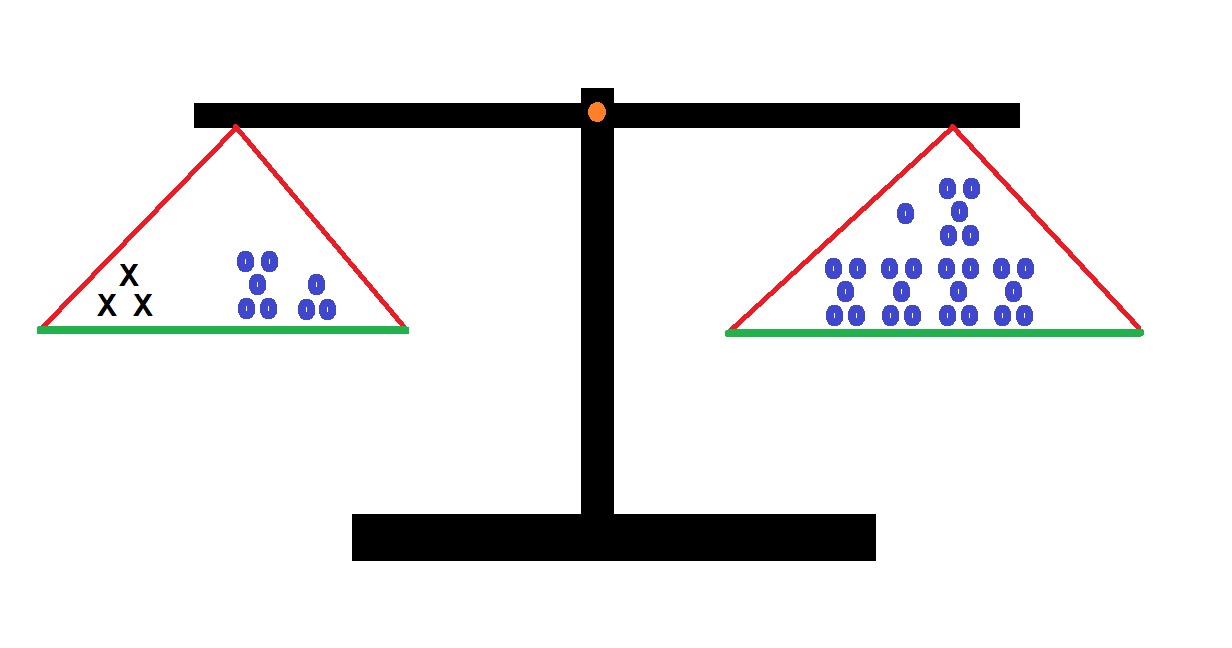 Hiernaast zie je een balans getekend.
Hiernaast zie je een balans getekend.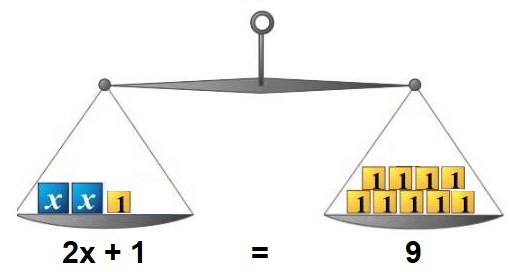



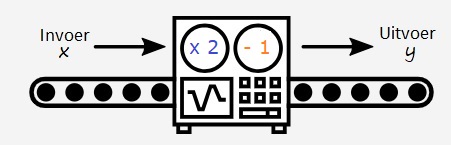
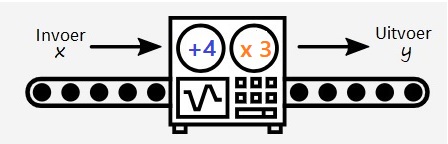 Bekijk het machientjes schema hiernaast. Schrijf daarna netjes je berekening op.
Bekijk het machientjes schema hiernaast. Schrijf daarna netjes je berekening op.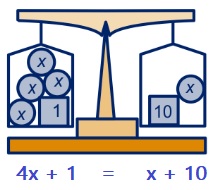 Hiernaast zie je een ouderwetse balans met daaronder de bijbehorende vergelijking:
Hiernaast zie je een ouderwetse balans met daaronder de bijbehorende vergelijking:



 of
of  )
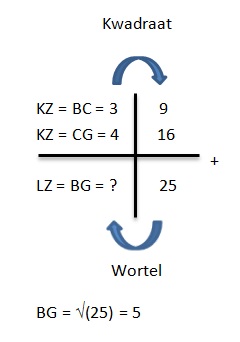
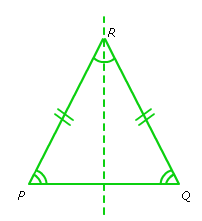
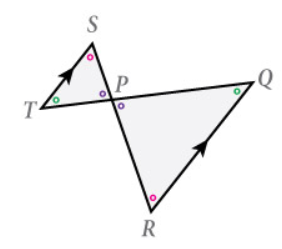
)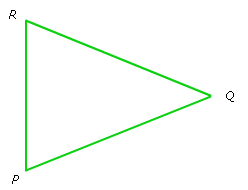 Bekijk de figuur. ΔPQR is een gelijkbenige driehoek.
Bekijk de figuur. ΔPQR is een gelijkbenige driehoek.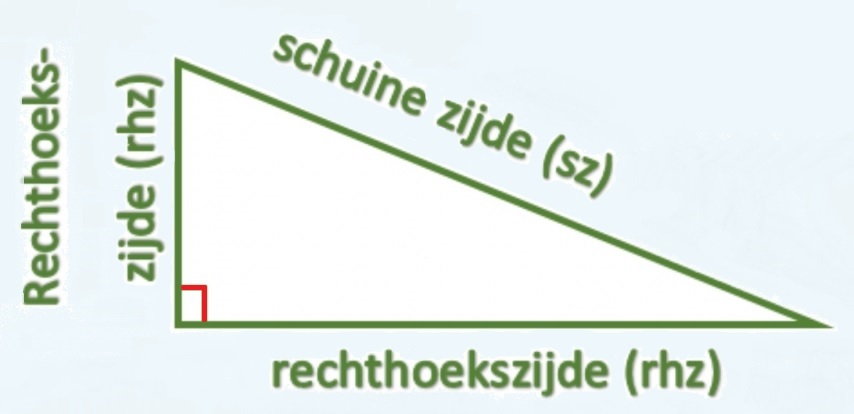
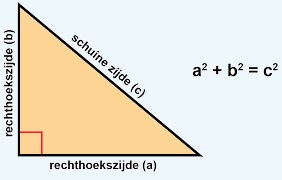 Waarom je de zijden moet kunnen benoemen? Dit heeft te maken met het hoofdonderwerp van dit hoofdstuk: de stelling van Pythagoras en het onderwerp goniometrie dat we in klas 3 behandelen.
Waarom je de zijden moet kunnen benoemen? Dit heeft te maken met het hoofdonderwerp van dit hoofdstuk: de stelling van Pythagoras en het onderwerp goniometrie dat we in klas 3 behandelen.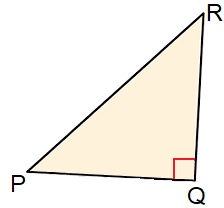 Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.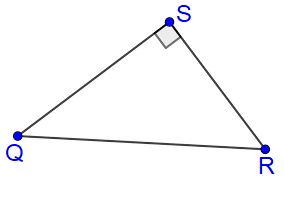 Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.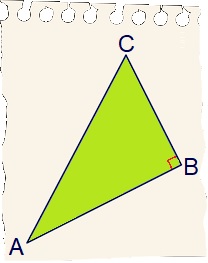 Bekijk de driehoek hiernaast. Beantwoord daarna de vragen in je schrift.
Bekijk de driehoek hiernaast. Beantwoord daarna de vragen in je schrift.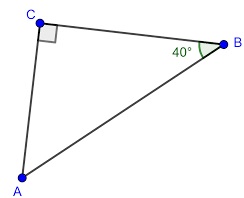 Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.
Bekijk de driehoek hiernaast, beantwoord daarna de vragen in je schrift.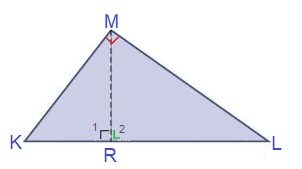 Bekijk de driehoek hiernaast, de driehoek is een samengestelde driehoek.
Bekijk de driehoek hiernaast, de driehoek is een samengestelde driehoek. Dit hoofdstuk is het tweede hoofdstuk over verbanden dit jaar. We kijken dit keer naar kwadratische verbanden want behalven kwadraten uitrekenen kun je ook formules maken met daarin een kwadraat. Waneer je werk met een kwadratische formule (verband) dan krijg je iets anders dan regelmaat in je tabel en de grafiek ziet er al helemaal anders uit.
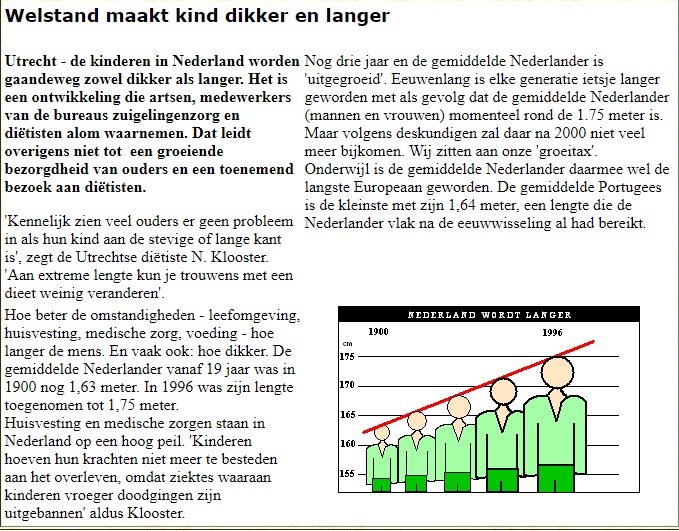
Dit hoofdstuk is het tweede hoofdstuk over verbanden dit jaar. We kijken dit keer naar kwadratische verbanden want behalven kwadraten uitrekenen kun je ook formules maken met daarin een kwadraat. Waneer je werk met een kwadratische formule (verband) dan krijg je iets anders dan regelmaat in je tabel en de grafiek ziet er al helemaal anders uit. Werken met verbanden hoort bij het onderwerp algebra. Binnen algebra houden we ons bezig met getallen en formules (verbanden). Een architect of bouwkundige krijgt veel te maken met kwadratische verbanden. Maar ook wanneer je met radiogolven werkt, bijvoorbeeld bij communicatie tussen twee telefoons of een wifinetwerk krijg je te maken met kwadratische verbanden. Zo zie je maar, wiskunde is een heel veelzijdig vak en komt in heel veel beroepen in de wereld om je heen voor.
Werken met verbanden hoort bij het onderwerp algebra. Binnen algebra houden we ons bezig met getallen en formules (verbanden). Een architect of bouwkundige krijgt veel te maken met kwadratische verbanden. Maar ook wanneer je met radiogolven werkt, bijvoorbeeld bij communicatie tussen twee telefoons of een wifinetwerk krijg je te maken met kwadratische verbanden. Zo zie je maar, wiskunde is een heel veelzijdig vak en komt in heel veel beroepen in de wereld om je heen voor.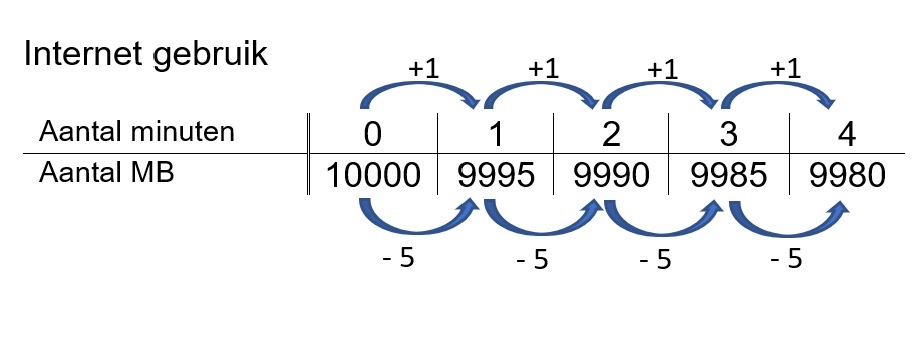
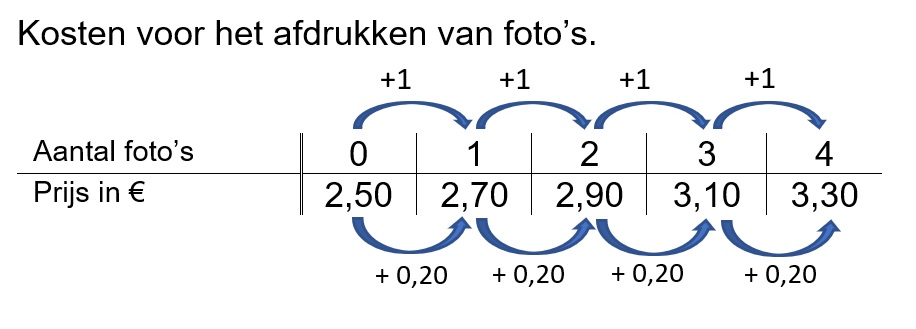
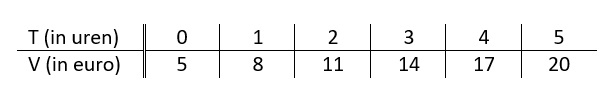
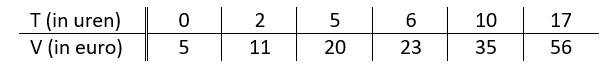


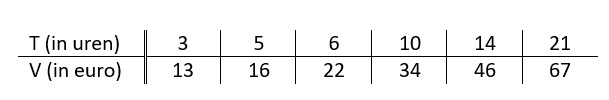
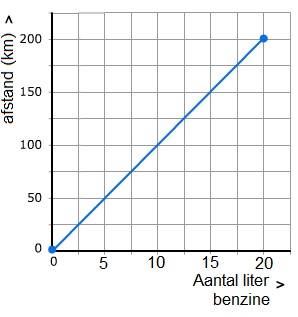
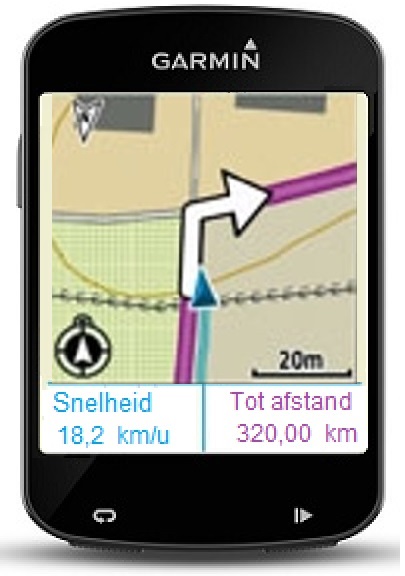 Rosalie fietst elke dag van huis naar school en weer terug. Dat is elke dag 16 km in totaal.
Rosalie fietst elke dag van huis naar school en weer terug. Dat is elke dag 16 km in totaal.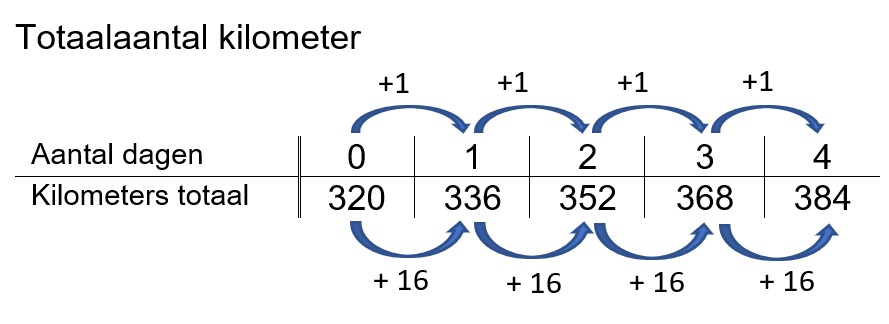
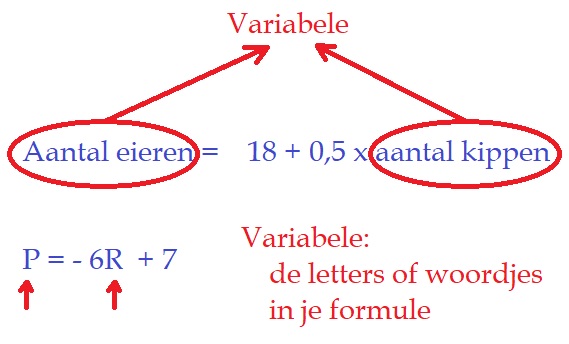


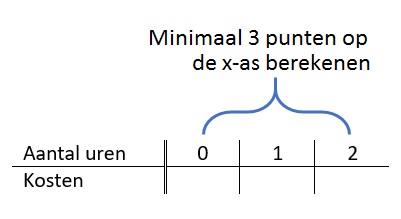
 Bij het branden van een cilindervormige kaars kun je ook een formule maken.
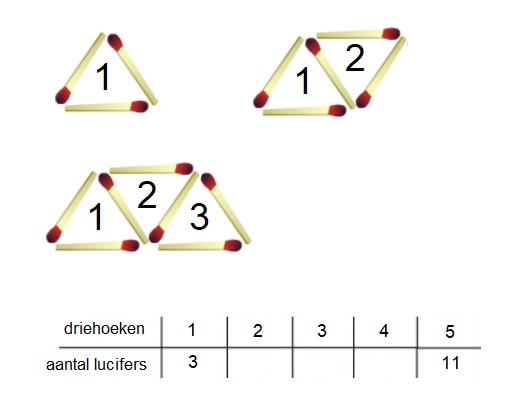
Bij het branden van een cilindervormige kaars kun je ook een formule maken.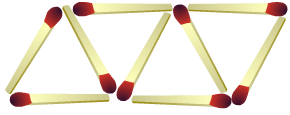 Met lucifers kun je allerlei patronen leggen, bekijk de figuren hiernaast maar eens.
Met lucifers kun je allerlei patronen leggen, bekijk de figuren hiernaast maar eens.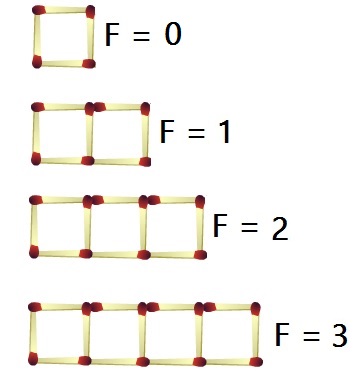 Behalve dat je driehoeken met lucifers kunt leggen kun je natuurlijk ook andere patronen maken bijvoorbeeld vierkanten.
Behalve dat je driehoeken met lucifers kunt leggen kun je natuurlijk ook andere patronen maken bijvoorbeeld vierkanten.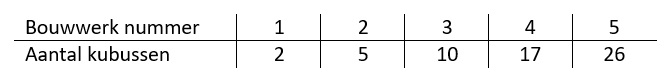

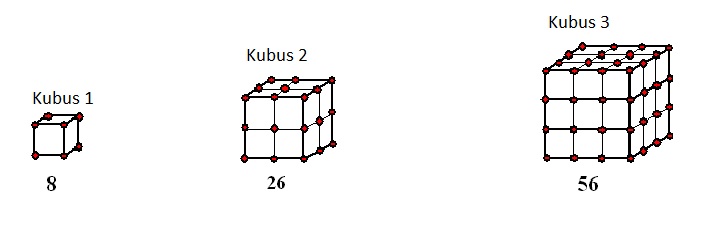
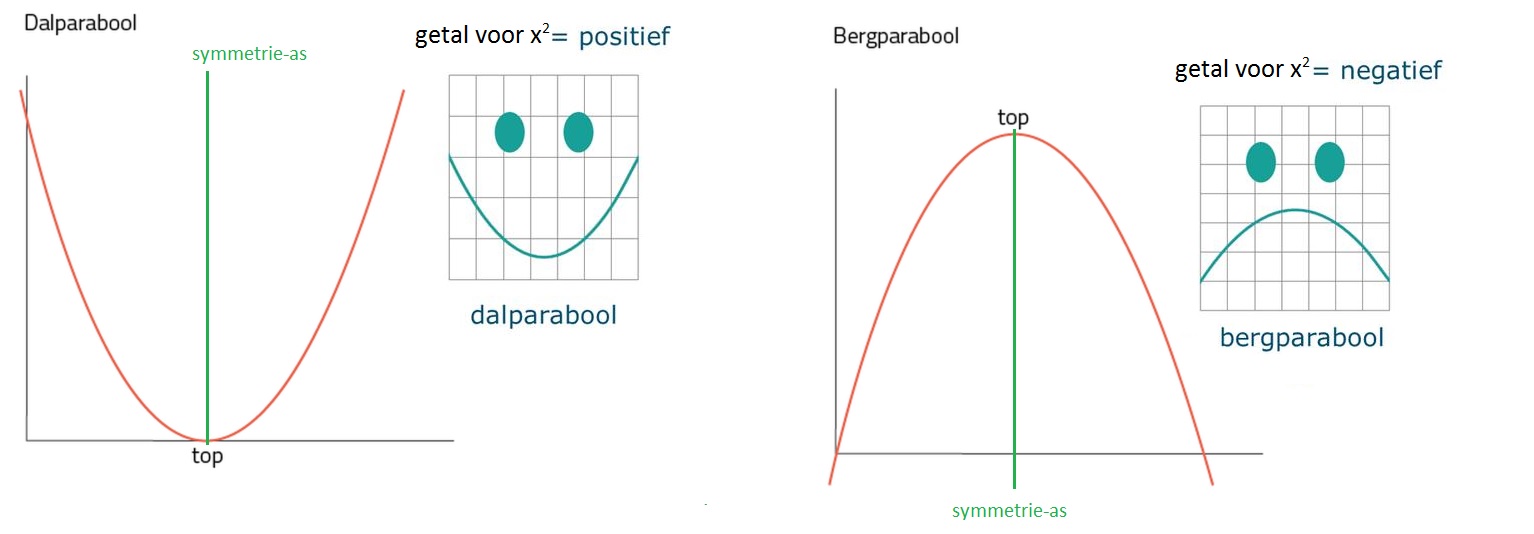
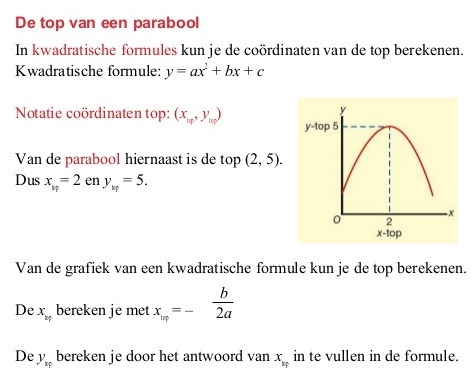
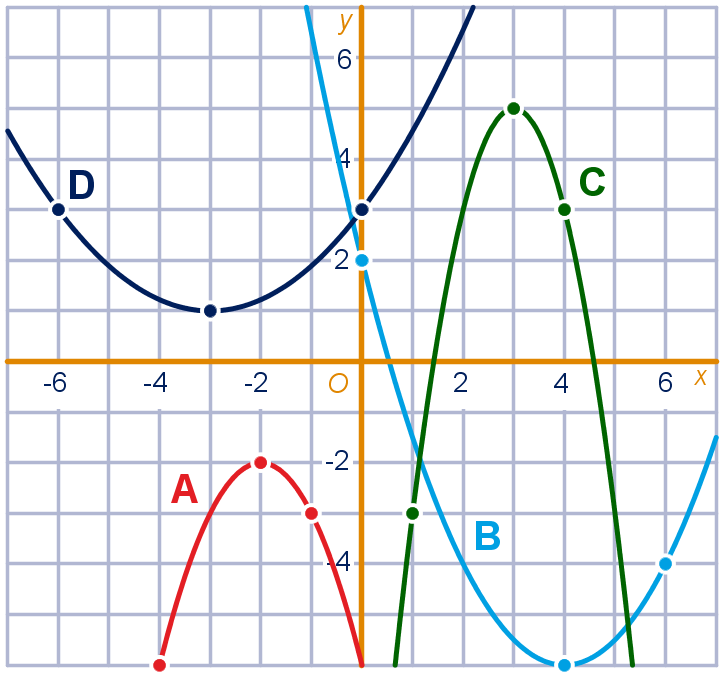 De grafiek wordt een parabool vanwege het kwadraat.
De grafiek wordt een parabool vanwege het kwadraat.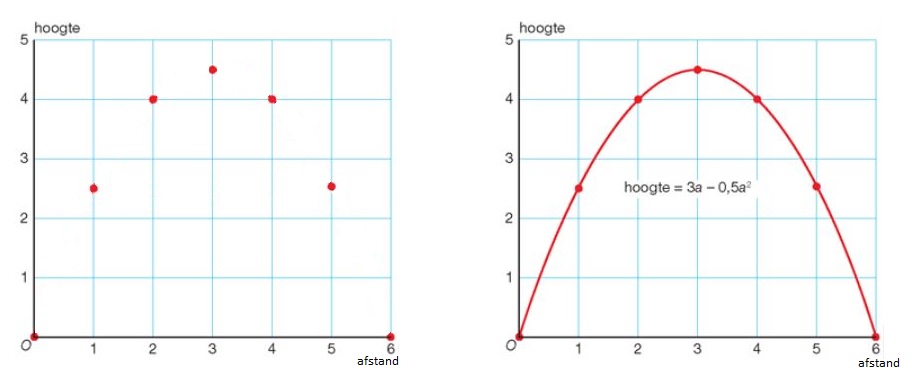
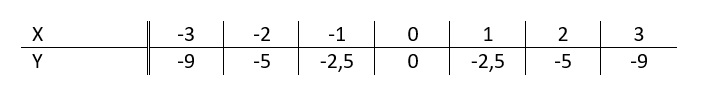
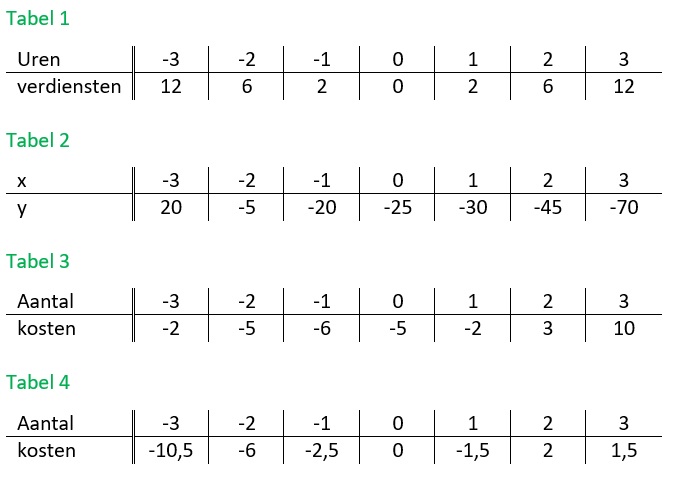
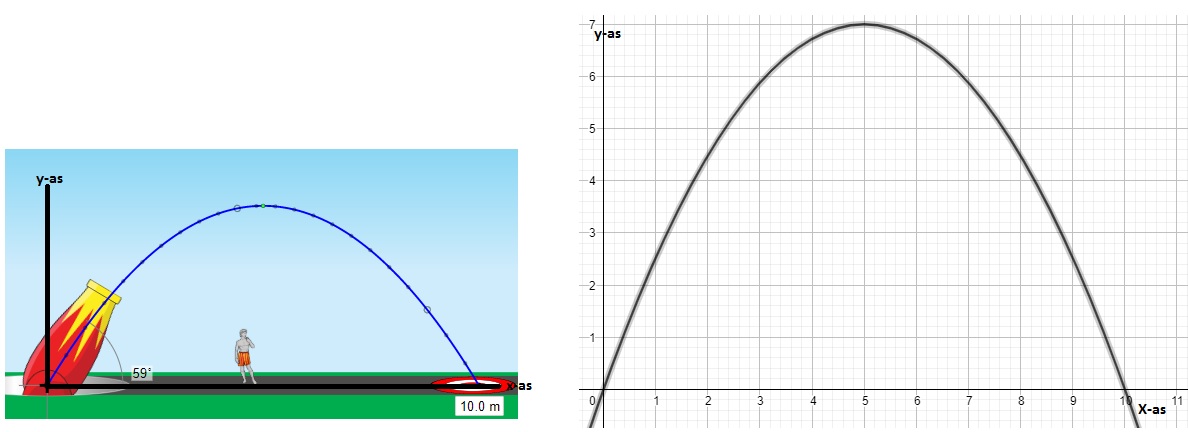
 Kenneth is keeper van een voetbalelftal. Kenneth oefent veel op het nemen van een doeltrap zodat hij de bal met een vere trap naar de spits van het elftal kan schieten. Bij de baan die de bal aflegt wanneer je deze wegtrapt hoort een kwadratische formule.
Kenneth is keeper van een voetbalelftal. Kenneth oefent veel op het nemen van een doeltrap zodat hij de bal met een vere trap naar de spits van het elftal kan schieten. Bij de baan die de bal aflegt wanneer je deze wegtrapt hoort een kwadratische formule.
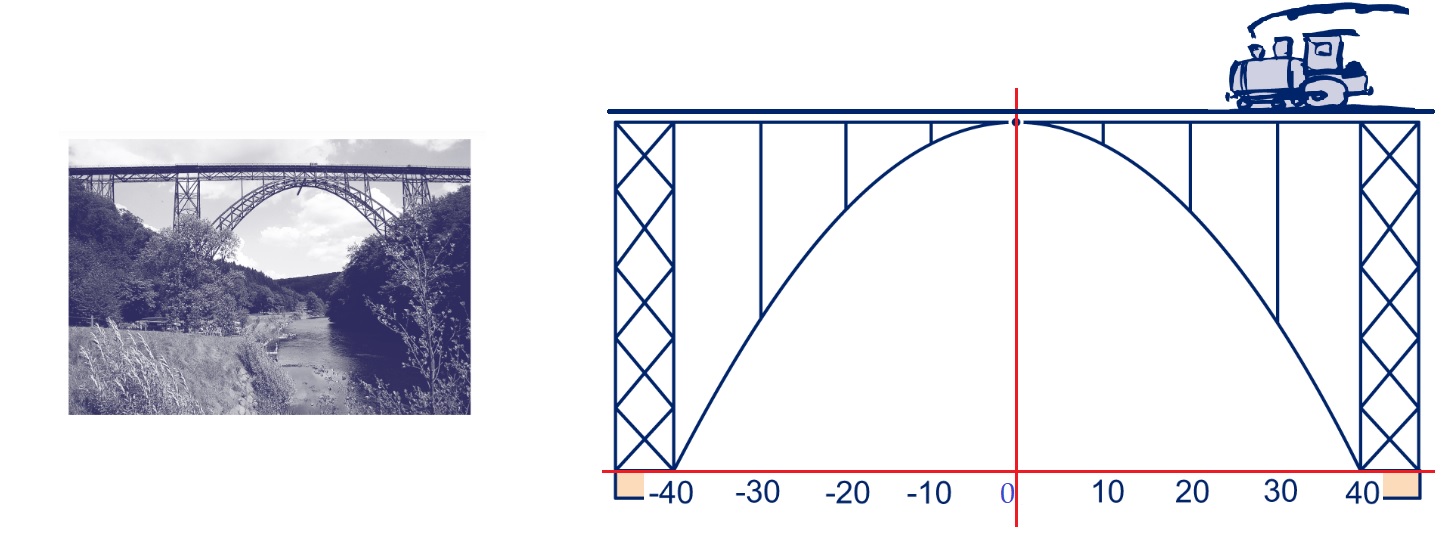
 Aan het eind van de wereldhavendagen wordt er in rotterdam een grote vuurwerkshow gehouden. Bij het afschieten van een vuurpijl hoort ook een kwadratische formule. De baan van de vuurpijl heeft namelijk de vorm van een parabool.
Aan het eind van de wereldhavendagen wordt er in rotterdam een grote vuurwerkshow gehouden. Bij het afschieten van een vuurpijl hoort ook een kwadratische formule. De baan van de vuurpijl heeft namelijk de vorm van een parabool.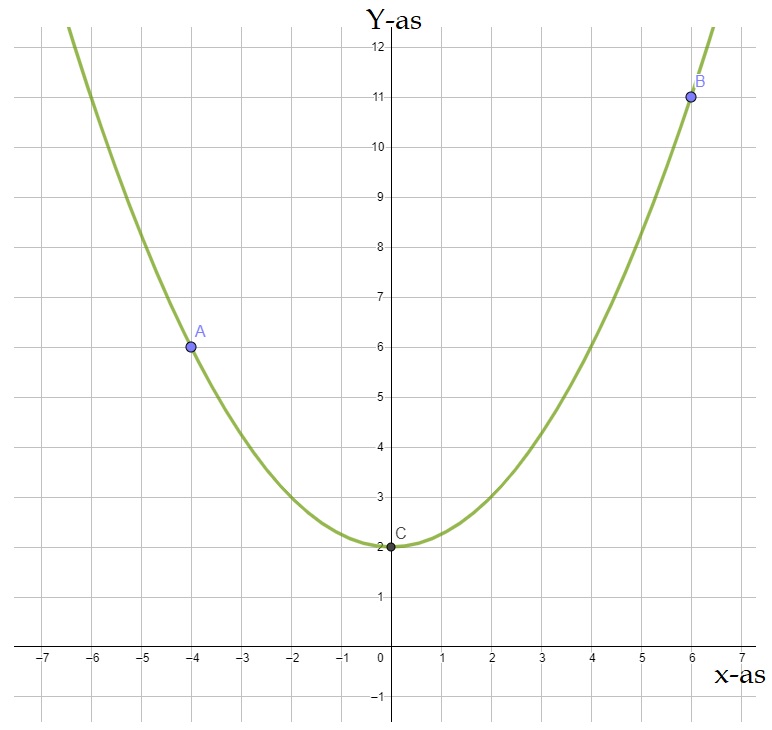

 Hiernaast zie je een balans getekend.
Hiernaast zie je een balans getekend.

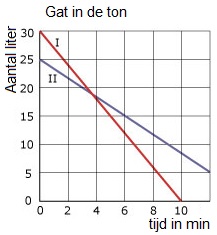
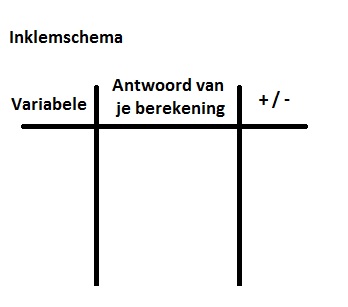 Is de formule waarmee je werkt niet-lineair, dan kun je een vergelijking oplossen met de inklem-methode. De inklem-methode is als het ware gokken. Je vult net zo lang getallen in tot je het goede antwoord hebt gevonden. Bij inklemmen houdt je in een schema bij wat je allemaal geprobeerd hebt.
Is de formule waarmee je werkt niet-lineair, dan kun je een vergelijking oplossen met de inklem-methode. De inklem-methode is als het ware gokken. Je vult net zo lang getallen in tot je het goede antwoord hebt gevonden. Bij inklemmen houdt je in een schema bij wat je allemaal geprobeerd hebt.
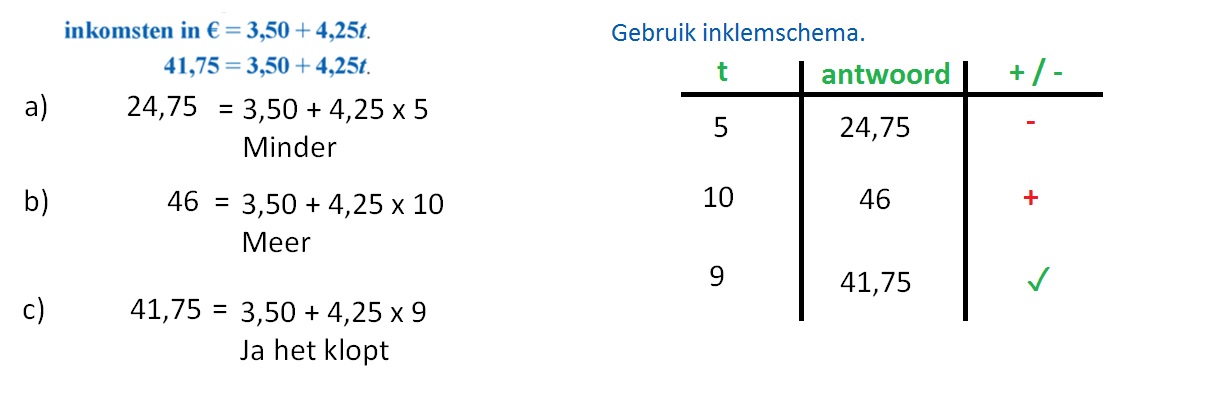
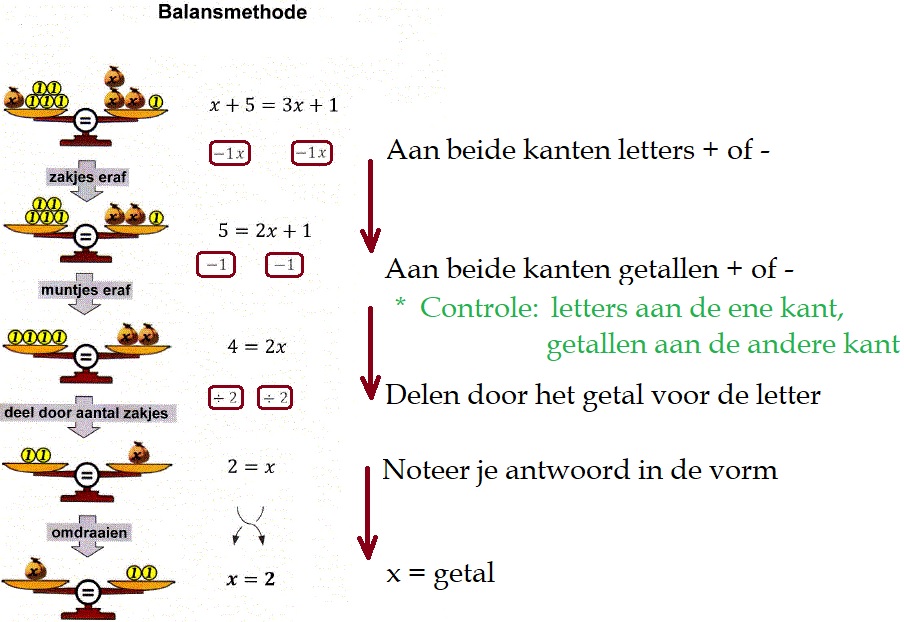
 In opgave 1 t/m 5 heb je jouw kennis over de balansmethode weer even herhaalt. Je werkte in al die opgaven met lineaire formule. Is de formule niet-lineair, dan kun je de balansmethode niet gebruiken, je gebruikt dan de inklemmethode.
In opgave 1 t/m 5 heb je jouw kennis over de balansmethode weer even herhaalt. Je werkte in al die opgaven met lineaire formule. Is de formule niet-lineair, dan kun je de balansmethode niet gebruiken, je gebruikt dan de inklemmethode.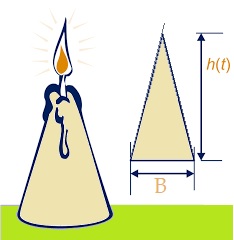 Hiernaast zie je een kaars. Een formule die ongeveer het verband tussen de hoogte van deze kaars en de brandtijd aangeeft, is:
Hiernaast zie je een kaars. Een formule die ongeveer het verband tussen de hoogte van deze kaars en de brandtijd aangeeft, is: Hiernaast zie je een foto van de Red-Bull Cliffdive competitie. Hierbij hoort een verband tussen de hoogte van het plateau en de tijdsduur van de sprong in seconden. Voor dit verband geldt de volgende formule
Hiernaast zie je een foto van de Red-Bull Cliffdive competitie. Hierbij hoort een verband tussen de hoogte van het plateau en de tijdsduur van de sprong in seconden. Voor dit verband geldt de volgende formule Sarah is bloemiste, zij heeft een eigen bloemenzaak.
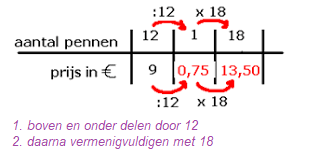
Sarah is bloemiste, zij heeft een eigen bloemenzaak.
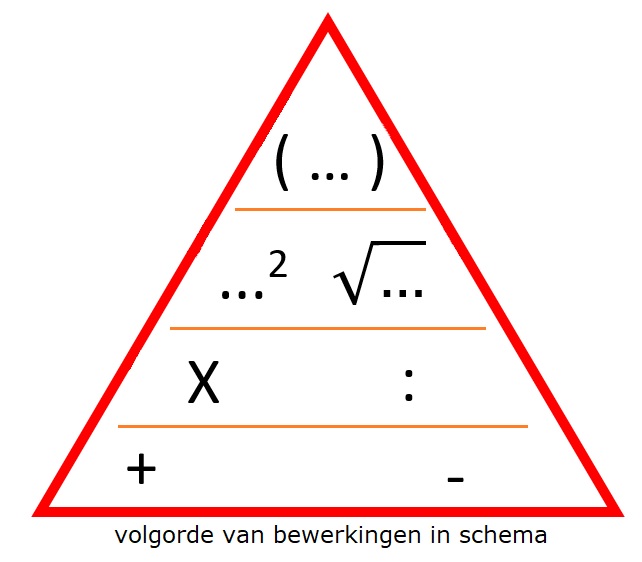
 Volgorde van bewerkingen (voorrangregels)
Volgorde van bewerkingen (voorrangregels)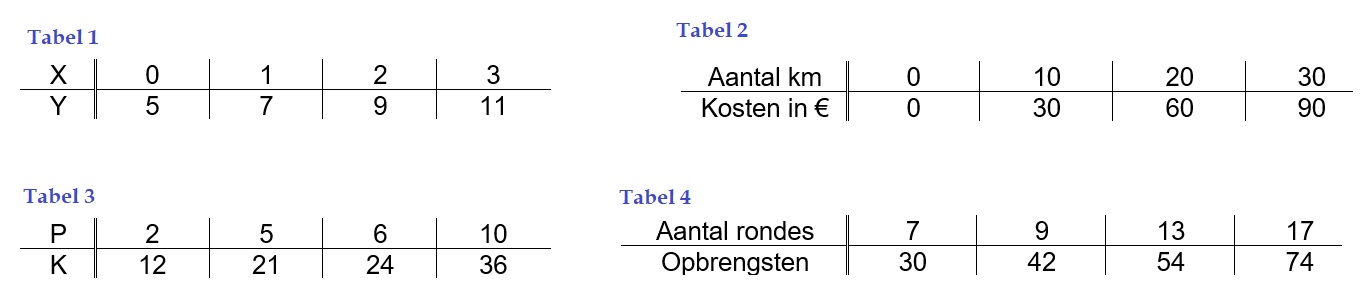
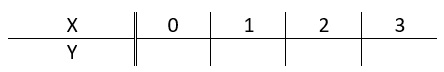
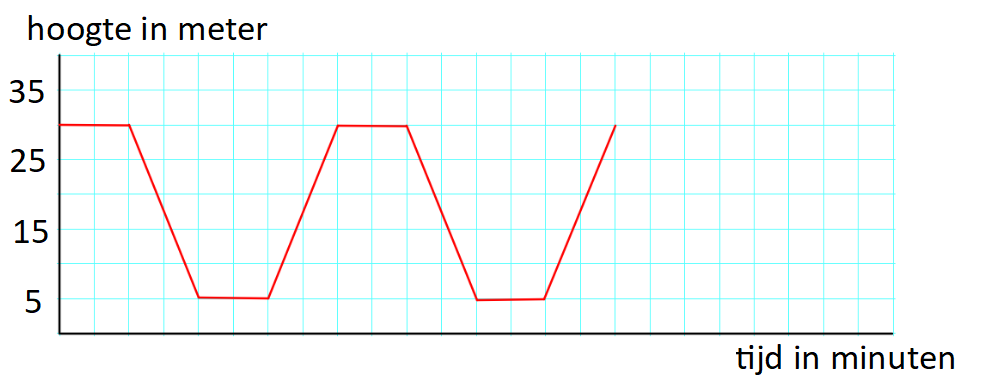
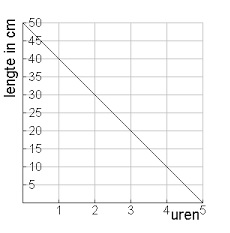
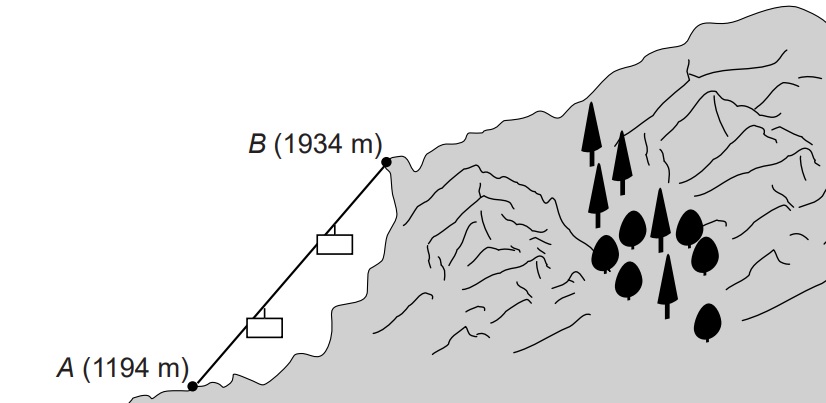 Jasmina en Mitchell gaan een wandeltocht maken in de bergen. Voor de steilste stukken in de tocht maken ze gebruik van cabineliften.
Jasmina en Mitchell gaan een wandeltocht maken in de bergen. Voor de steilste stukken in de tocht maken ze gebruik van cabineliften. Hiernaast zie je een tekening van een stuk sierbestrating. De stenen die hiervoor gebruikt worden heten klinkers. De klinkers worden in drietallen naast elkaar gelegd. Zo ontstaat telkens een vierkant.
Hiernaast zie je een tekening van een stuk sierbestrating. De stenen die hiervoor gebruikt worden heten klinkers. De klinkers worden in drietallen naast elkaar gelegd. Zo ontstaat telkens een vierkant.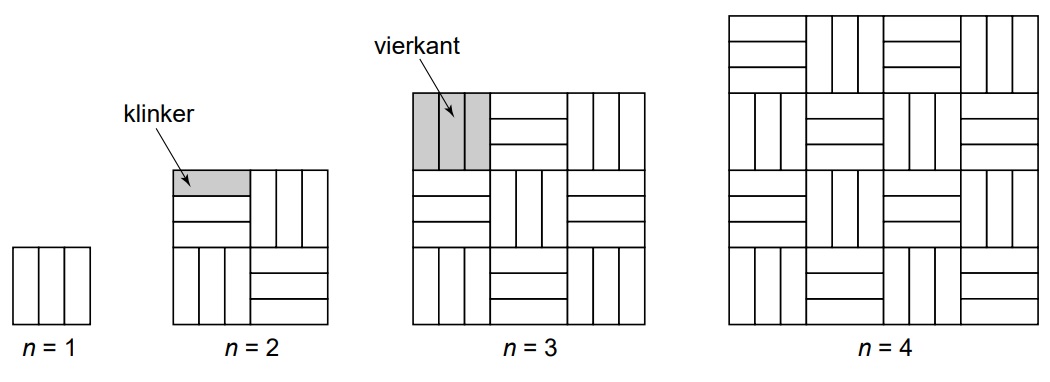
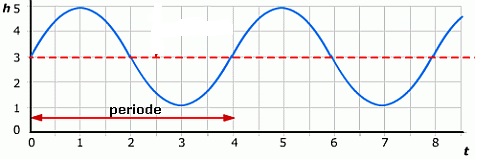
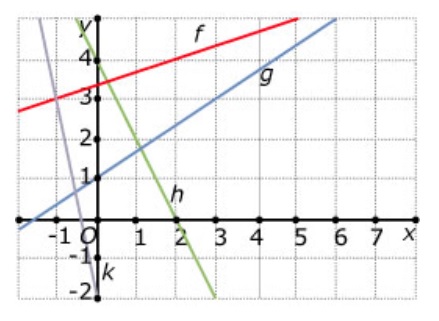
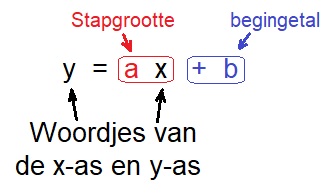
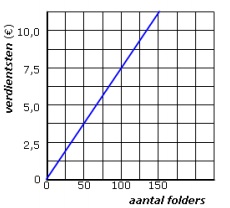
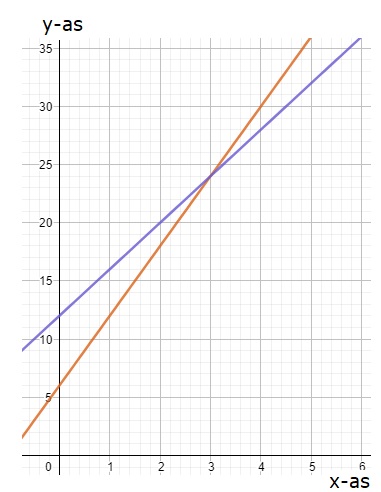
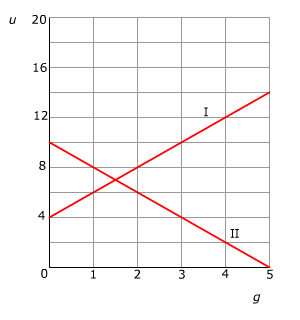
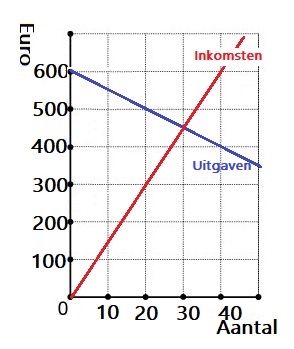
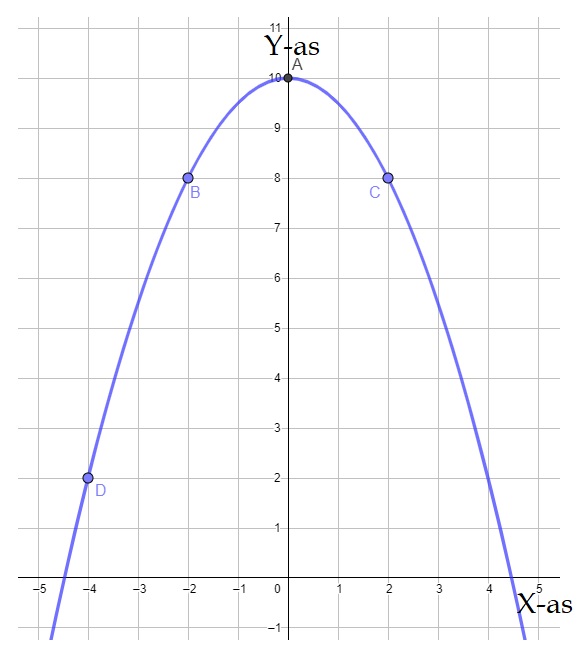
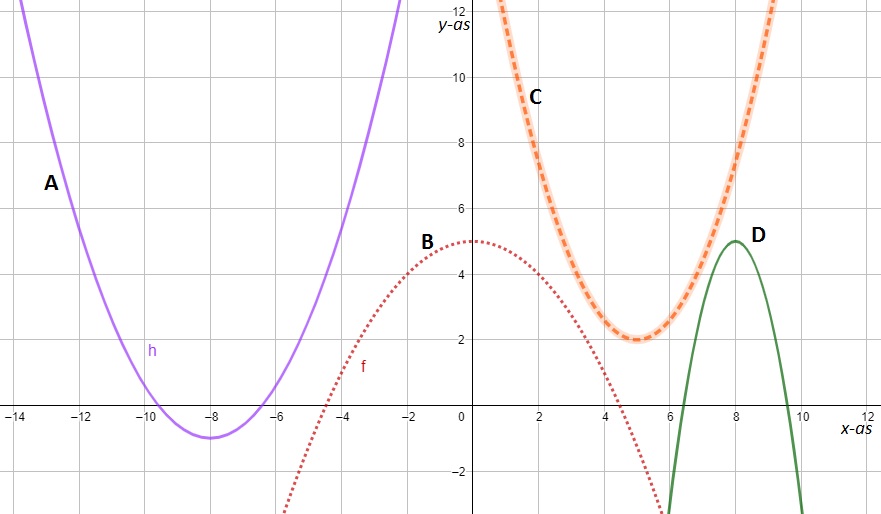
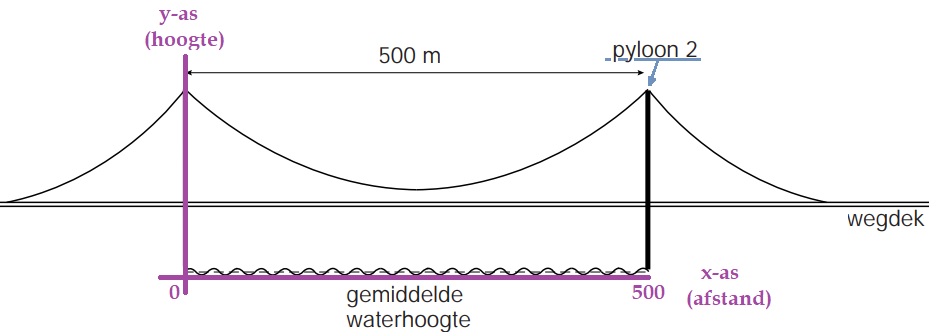
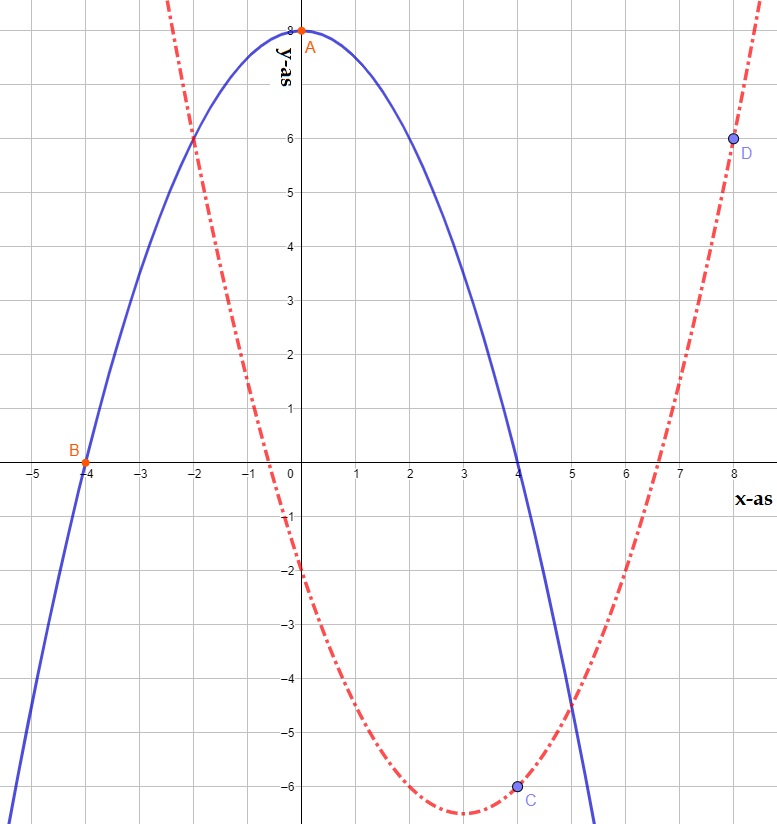 Bij de blauwe grafiek hoort de formule:
Bij de blauwe grafiek hoort de formule:
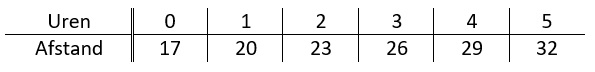
 Los op met inklemmen: (als je niet meer weet hoe dit moet, kijk dan naar het filmpje in de uitleg)
Los op met inklemmen: (als je niet meer weet hoe dit moet, kijk dan naar het filmpje in de uitleg)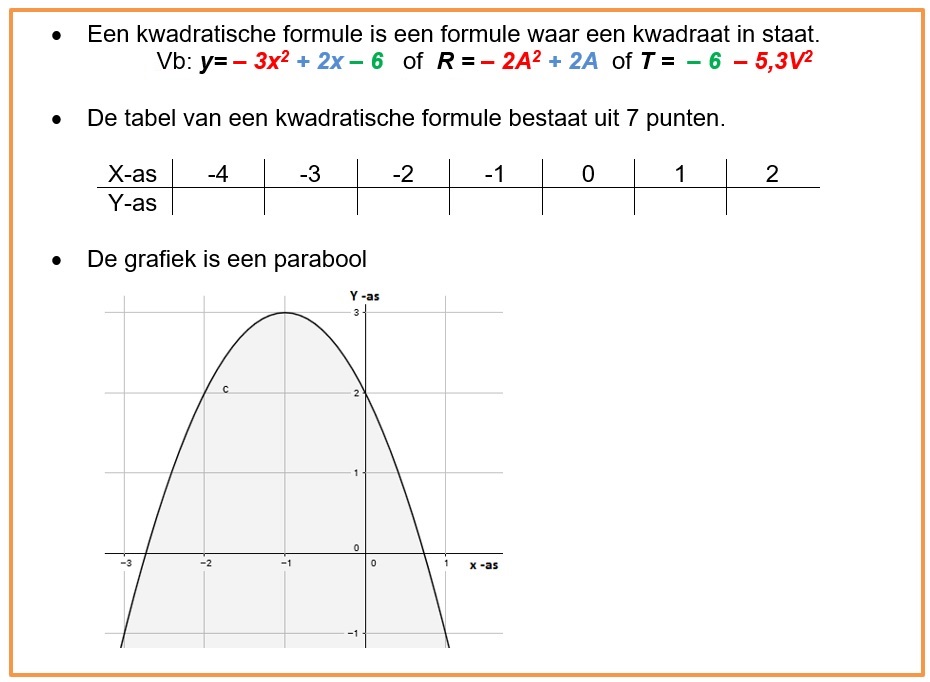
 In het zesde hoofdstuk van dit jaar gaan we aan de slag met procenten en verhoudingen.
In het zesde hoofdstuk van dit jaar gaan we aan de slag met procenten en verhoudingen.









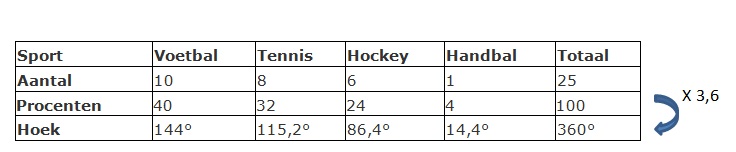
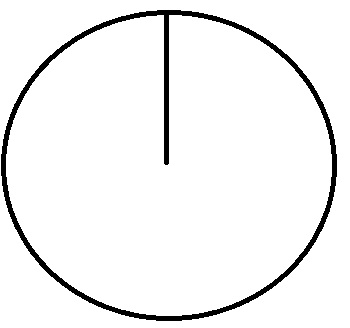
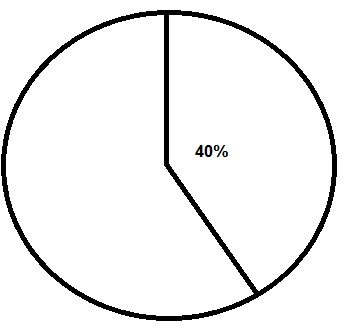
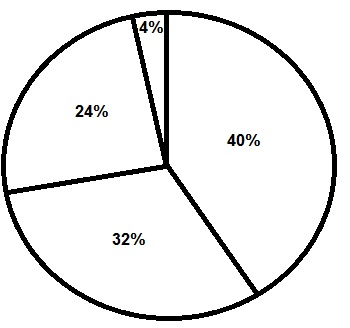
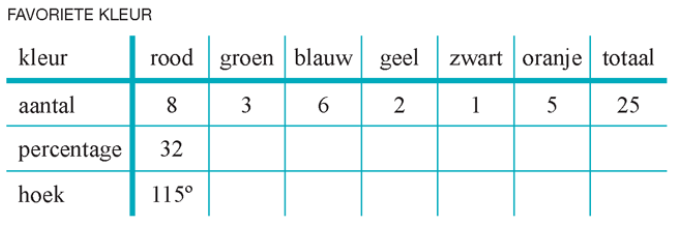
 Voorbeeld
Voorbeeld
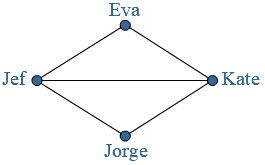
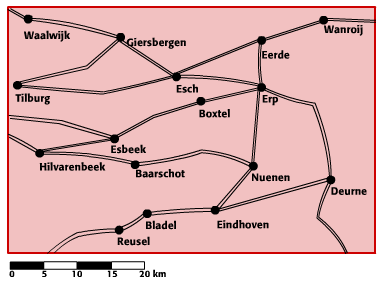
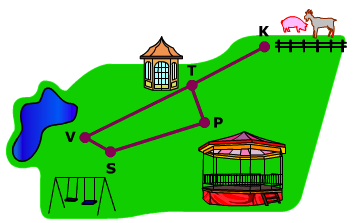 In een park zijn vijf ontmoetingsplaatsen:
In een park zijn vijf ontmoetingsplaatsen:














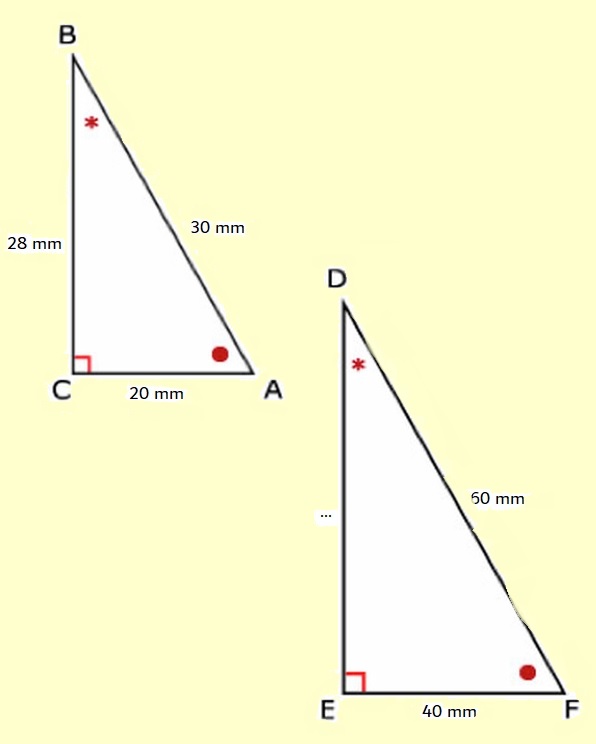
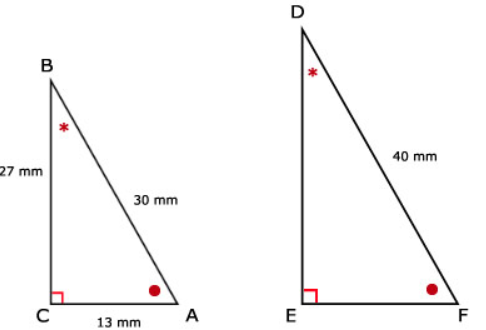
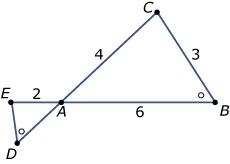
 Bekijk de twee driehoeken hiernaast.
Bekijk de twee driehoeken hiernaast.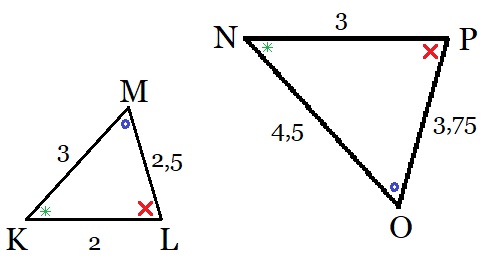 Bekijk de twee driehoeken hiernaast.
Bekijk de twee driehoeken hiernaast.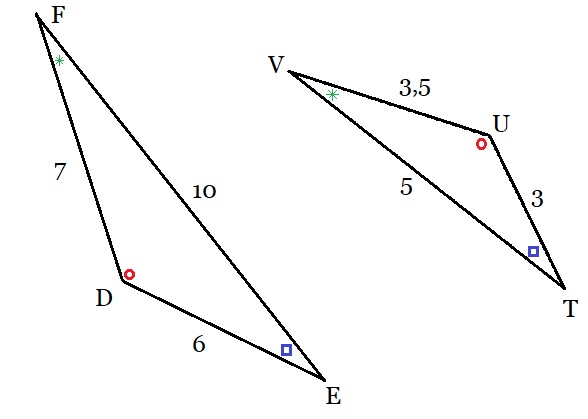 Bekijk de twee driehoeken hiernaast.
Bekijk de twee driehoeken hiernaast.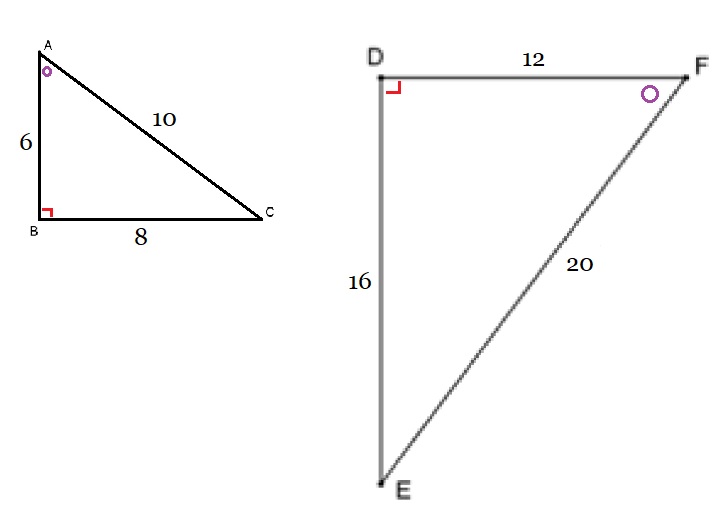
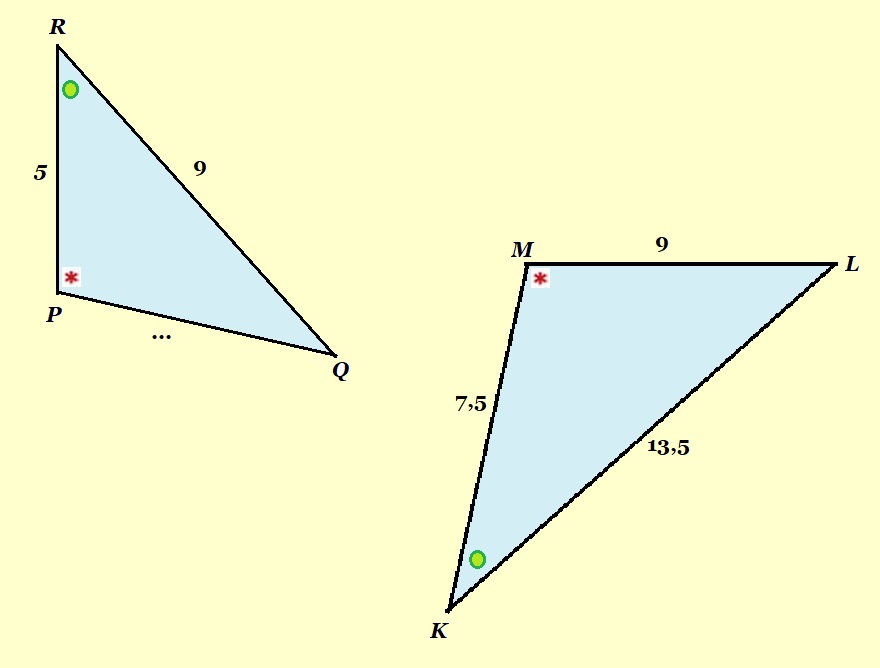
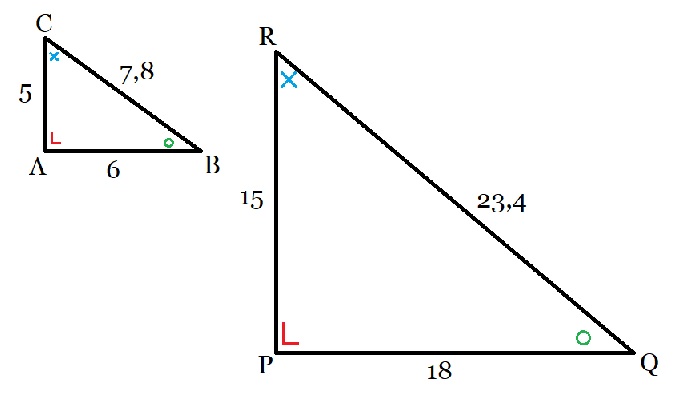
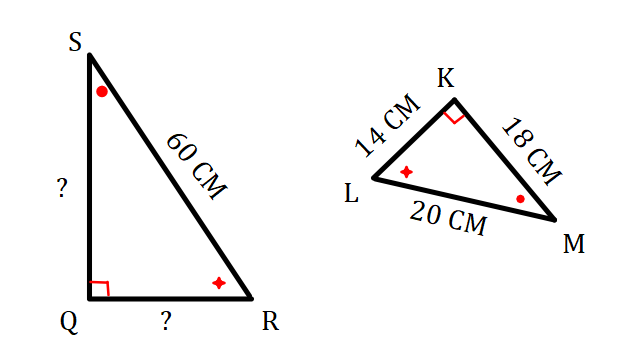
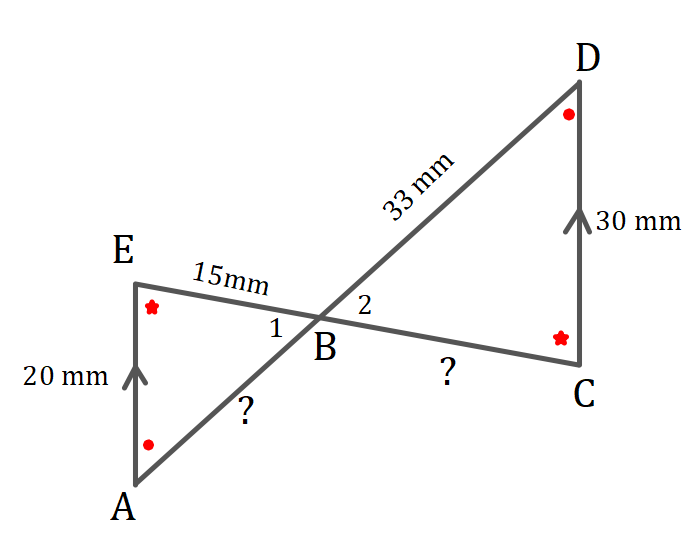
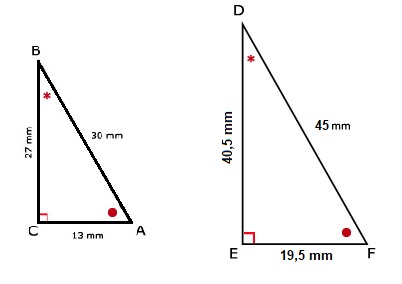 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.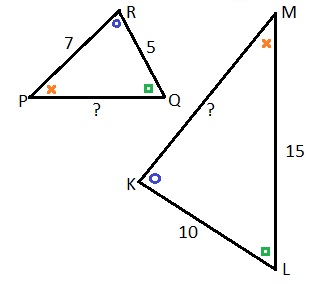 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.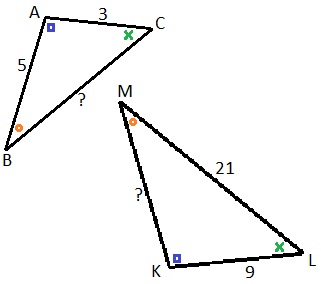 Bekijk de driehoeken hiernaast.
Bekijk de driehoeken hiernaast.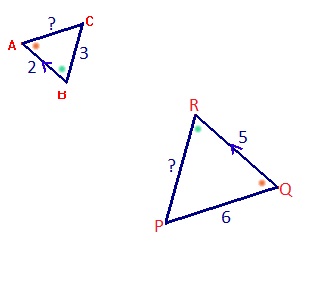 Bekijk de driehoeken hiernaast.
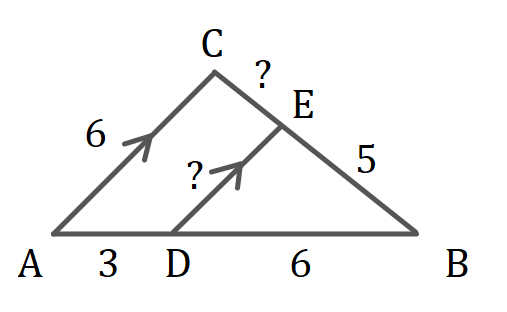
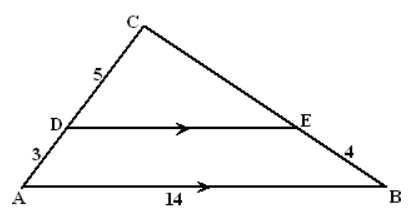
Bekijk de driehoeken hiernaast.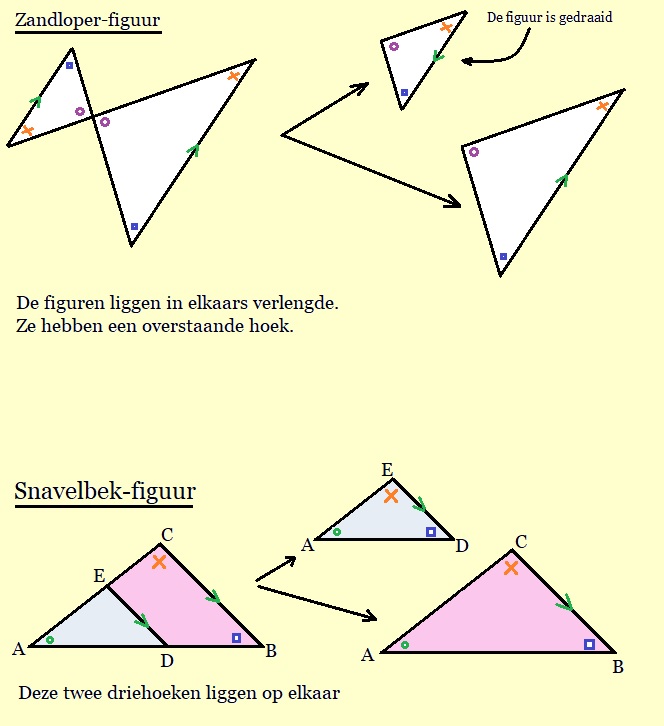
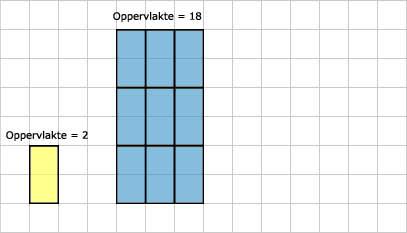
 oppervlakte = 5 cm2
oppervlakte = 5 cm2
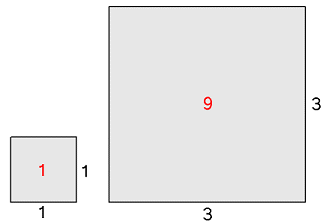
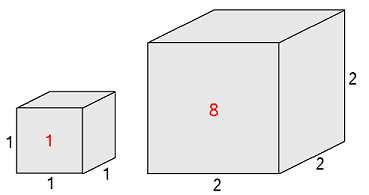




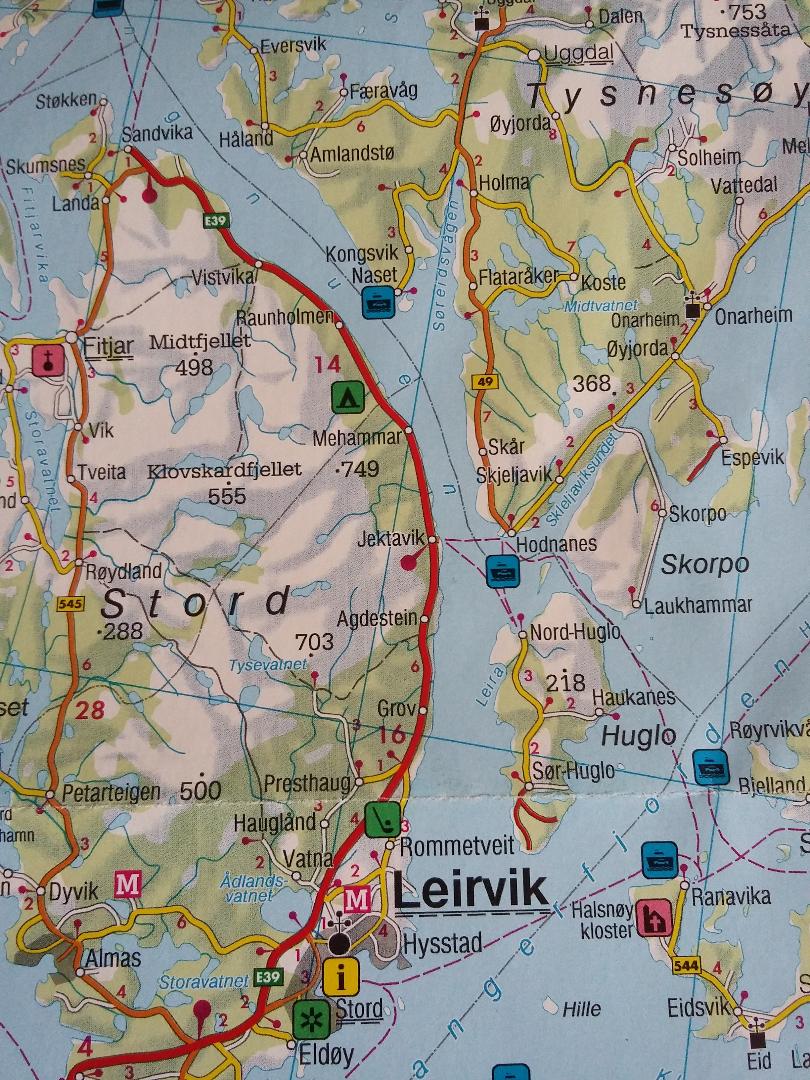
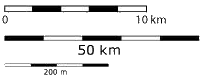
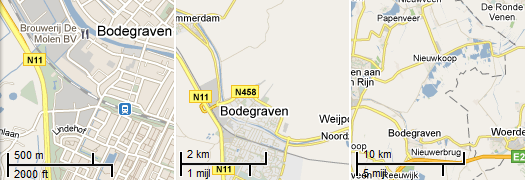
 Schaalmodel Land Rover 1 : 24
Schaalmodel Land Rover 1 : 24 Schaalmodel Volkswagen bus 1962 1 : 43
Schaalmodel Volkswagen bus 1962 1 : 43 Schaalmodel boot 1 : 110
Schaalmodel boot 1 : 110
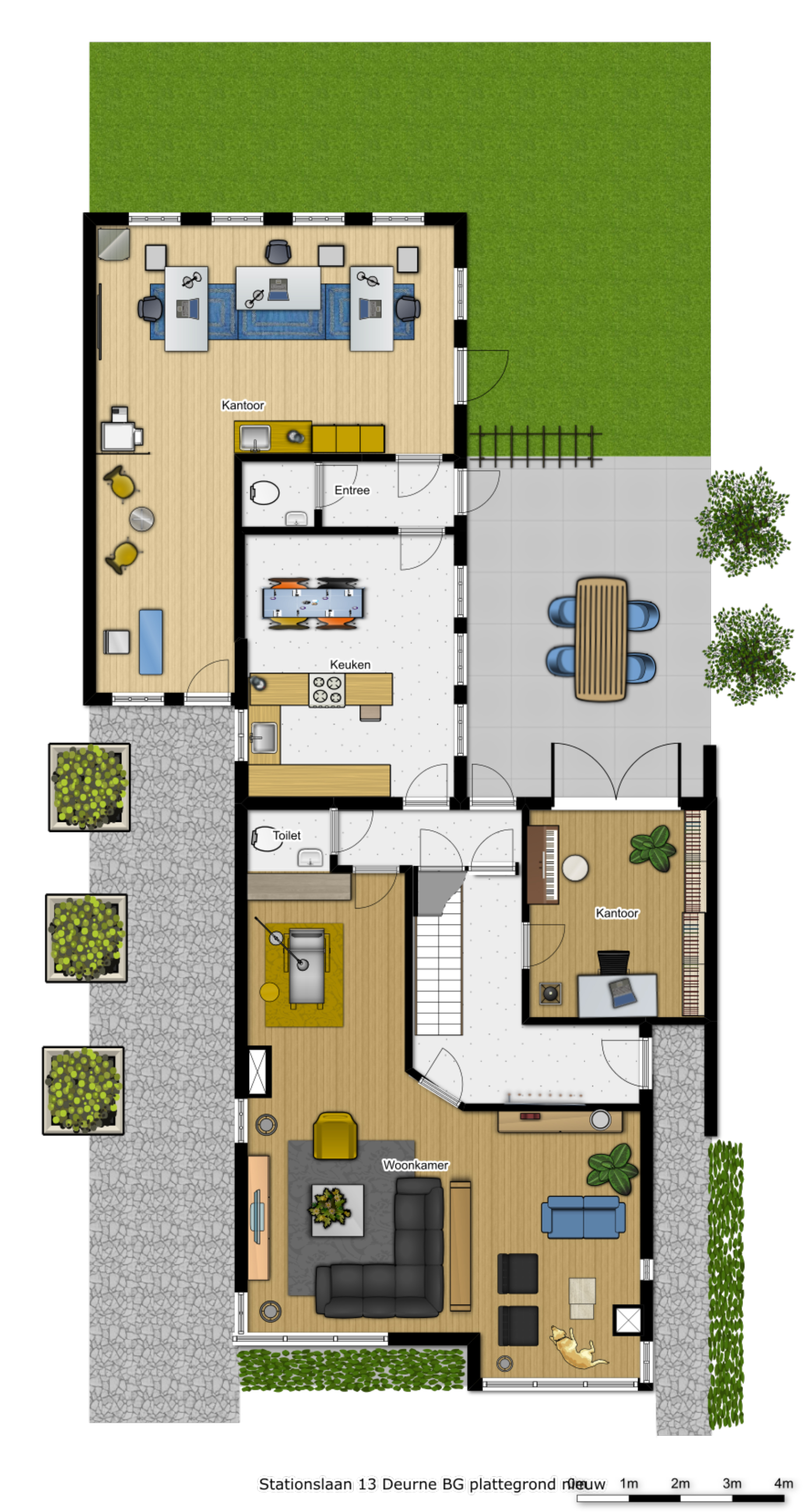

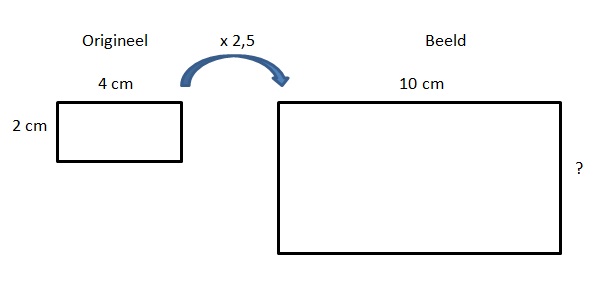
 Hiernaast zie je links het origineel van een foto. De afbeeldingen staan ook op je werkblad.
Hiernaast zie je links het origineel van een foto. De afbeeldingen staan ook op je werkblad. Hiernaast zie je links het origineel van een foto. De afbeeldingen staan ook op je werkblad.
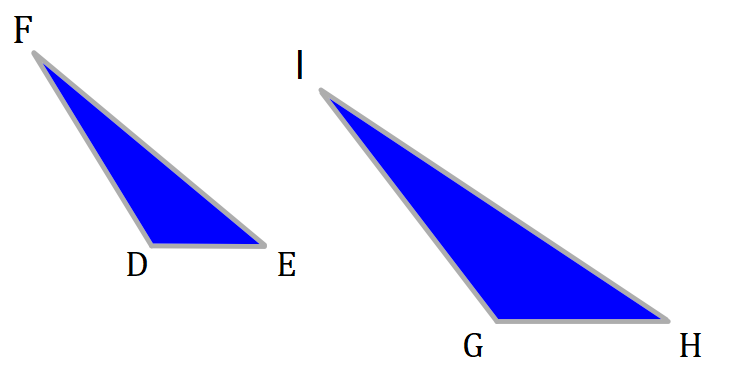
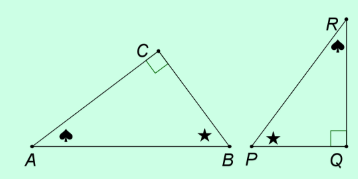
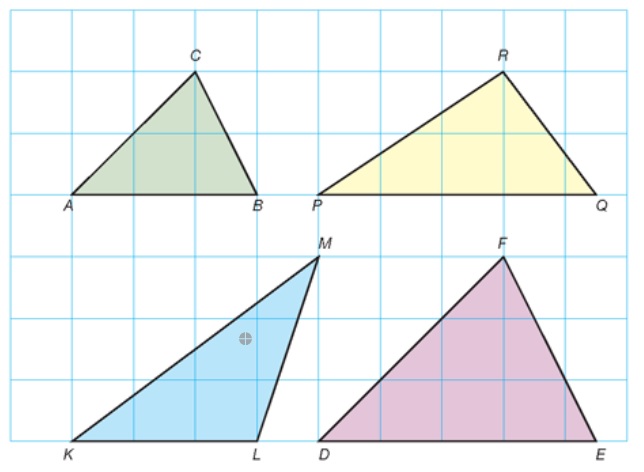
Hiernaast zie je links het origineel van een foto. De afbeeldingen staan ook op je werkblad.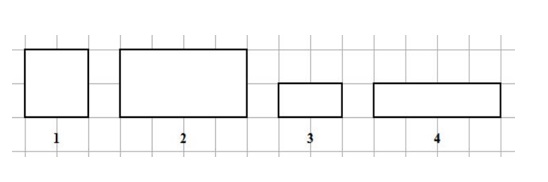 Welke twee figuren hieronder zijn gelijkvormig? Leg ook uit waarom de anderen niet gelijkvormig zijn.
Welke twee figuren hieronder zijn gelijkvormig? Leg ook uit waarom de anderen niet gelijkvormig zijn.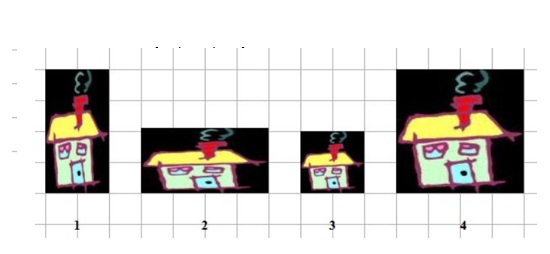 Welke twee figuren zijn gelijkvormig? Bereken van deze figuren de vergrotingsfactor.
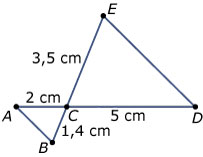
Welke twee figuren zijn gelijkvormig? Bereken van deze figuren de vergrotingsfactor.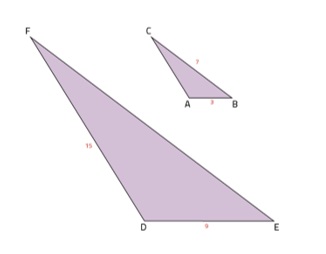 Bekijk de driehoeken hieronder. De afbeelding staat ook op je werkblad.
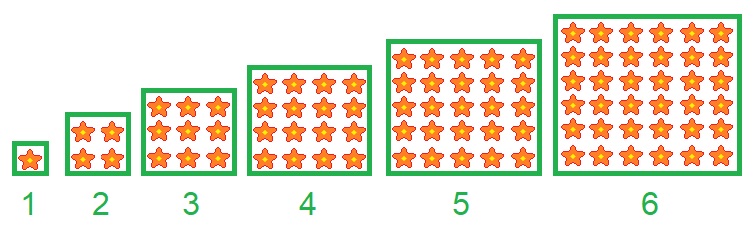
Bekijk de driehoeken hieronder. De afbeelding staat ook op je werkblad.  De oppervlakte van de kleine smiley is 4 cm².
De oppervlakte van de kleine smiley is 4 cm². De oppervlakte van de kleine foto is 12 cm². De rechter foto is een vergroting van deze foto. De vergrotingsfactor is 7. Bereken de oppervlakte van de grote foto in m²
De oppervlakte van de kleine foto is 12 cm². De rechter foto is een vergroting van deze foto. De vergrotingsfactor is 7. Bereken de oppervlakte van de grote foto in m² De kopjes zijn vergrotingen van elkaar. De vergrotingsfactor is 0,8.
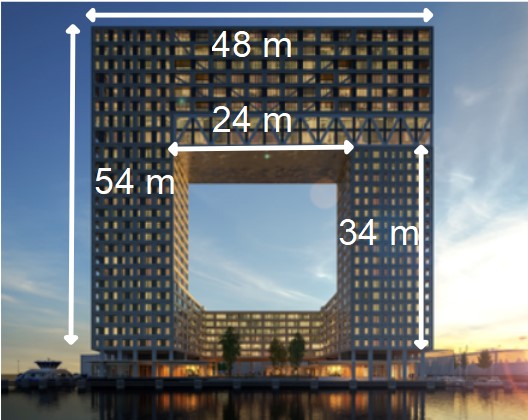
De kopjes zijn vergrotingen van elkaar. De vergrotingsfactor is 0,8. 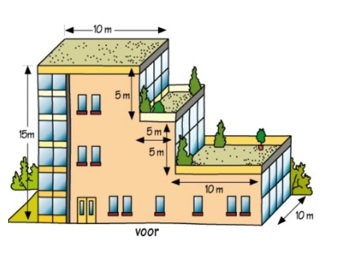 Teken in je schrift het vooraanzicht van het flatgebouw.
Teken in je schrift het vooraanzicht van het flatgebouw.