Het arrangement K3 Thema rechthoekige driehoeken, Pythagoras en tangens is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 01-06-2020 13:34:37
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Het thema 'Vlakke figuren' is ontwikkeld door auteurs en medewerkers van StudioVO.
Fair Use
In de Stercollecties van StudioVO wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- eigenschappen driehoeken, soorten driehoeken, oppervlakte en omtrek driehoeken, pythagoras, tangens.
- Leerniveau
- VMBO kaderberoepsgerichte leerweg, 4; VMBO kaderberoepsgerichte leerweg, 3;
- Leerinhoud en doelen
- Rekenen/wiskunde; Meten en meetkunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 25 uur 20 minuten
- Trefwoorden
- arrangeerbaar, leerlijn, leerlijnen, rearrangeerbare

 Inleiding
Inleiding Leerdoelen
Leerdoelen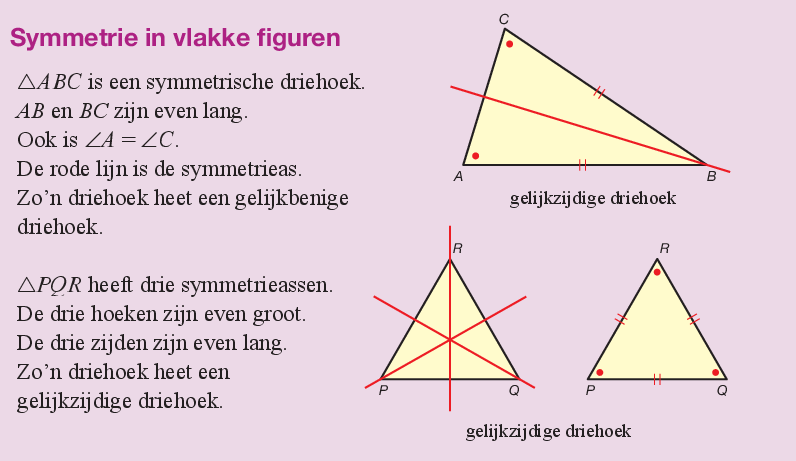


 Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren.
Op deze en de volgende pagina's vind je een aantal examenvragen uit examens van vorige jaren.