Het arrangement Module: Enigma - Grondslagen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 19-07-2025 08:54:41
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Deze module is onderdeel van de arrangeerbare leerlijn van de Stercollecties voor het kerndeel van Informatica voor hv456. In de module Grondslagen behandelen we de basisprincipes van informatie en rekenen. In de informatica is rekenen het manipuleren van vormen, volgens bepaalde regels. Deze voorschriften noem je ook wel algoritmes. In deze module leer je daarmee werken. Daarnaast ga je meer leren over informatieprocessen en verschillende structuren die daarbij passen. In ieder onderdeel vind je, verdeeld over verschillende pagina's, informatie in de vorm van teksten, afbeeldingen en video's. Daarnaast ga je zelf aan de slag met toepassingsopdrachten en toetsen. Van de toetsen wordt je voortgang bijgehouden en deze voortgang zal zowel door jou als je docent te bekijken zijn. Veel succes!
- Leerniveau
- HAVO 4; VWO 6; HAVO 5; VWO 4; VWO 5;
- Leerinhoud en doelen
- Informatica;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- algoritme, arrangeerbaar, boomstructuren, enigma- grondslagen, hv456, informatica, informatie, informatieproces, kerndeel, stercollectie

 In de module Grondslagen behandelen we de basisprincipes van informatie en rekenen.
In de module Grondslagen behandelen we de basisprincipes van informatie en rekenen.

 Je bent begonnen in de module Grondslagen.
Je bent begonnen in de module Grondslagen.
 Geef drie voorbeelden van
Geef drie voorbeelden van  Zoek op het web naar algoritmisch gegenereerde afbeeldingen van “natuur”, zoals planten of landschappen.
Zoek op het web naar algoritmisch gegenereerde afbeeldingen van “natuur”, zoals planten of landschappen. 1. Bedenk in welke van de volgende situaties een programma als Google Translate beter werkt:
1. Bedenk in welke van de volgende situaties een programma als Google Translate beter werkt: TED-presentatie:
TED-presentatie:  Een belangrijk maar ook lastig begrip in de informatica is informatie.
Een belangrijk maar ook lastig begrip in de informatica is informatie.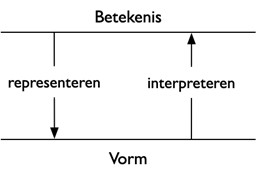
 Informatie gaat verloren als de vorm verloren gaat, of als de manier om die vorm betekenis te geven verloren raakt.
Informatie gaat verloren als de vorm verloren gaat, of als de manier om die vorm betekenis te geven verloren raakt. Niet alle aspecten van een vorm dragen op eenzelfde manier bij aan de betekenis.
Niet alle aspecten van een vorm dragen op eenzelfde manier bij aan de betekenis. Sommige woorden in het Nederlands klinken hetzelfde maar hebben verschillende betekenissen:
Sommige woorden in het Nederlands klinken hetzelfde maar hebben verschillende betekenissen: Welke fysieke dragers heb je nodig voor de onderstaande vormen?
Welke fysieke dragers heb je nodig voor de onderstaande vormen?
 De notatie
De notatie 
 Zoals eerder gezegd, hebben we een grote vrijheid in het kiezen van vormen voor het uitdrukken van een bepaalde betekenis. Vaak laten we ons daarbij leiden door de traditie (conventie).
Zoals eerder gezegd, hebben we een grote vrijheid in het kiezen van vormen voor het uitdrukken van een bepaalde betekenis. Vaak laten we ons daarbij leiden door de traditie (conventie). Een analoge vorm is gelijkvormig aan het origineel.
Een analoge vorm is gelijkvormig aan het origineel.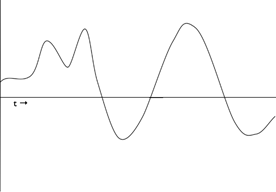
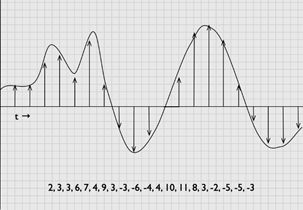
 In de tekst wordt besproken hoe bepaalde notaties handiger zijn voor specifieke toepassingen, zoals het decimale systeem voor rekenen en het binaire systeem voor computers. Het hexadecimaal systeem is vergelijkbaar in zijn handigheid, omdat het een compacte en efficiënte manier biedt om kleuren weer te geven in webdesign.
In de tekst wordt besproken hoe bepaalde notaties handiger zijn voor specifieke toepassingen, zoals het decimale systeem voor rekenen en het binaire systeem voor computers. Het hexadecimaal systeem is vergelijkbaar in zijn handigheid, omdat het een compacte en efficiënte manier biedt om kleuren weer te geven in webdesign. Een ander voorbeeld van omzetting van analoog naar digitaal vind je in een digitale camera: deze zet het oorspronkelijke beeld om in een groot aantal discrete pixels.
Een ander voorbeeld van omzetting van analoog naar digitaal vind je in een digitale camera: deze zet het oorspronkelijke beeld om in een groot aantal discrete pixels. Geef een aantal voorbeelden van symbolische vormen die al bestonden voor de komst van de computer.
Geef een aantal voorbeelden van symbolische vormen die al bestonden voor de komst van de computer. Welke van de onderstaande vormen zijn analoog, welke symbolisch?
Welke van de onderstaande vormen zijn analoog, welke symbolisch? Computers werken met vormen op een erg letterlijke manier.
Computers werken met vormen op een erg letterlijke manier.


 Bij de PTT gebruikte men vroeger de leus: wij hebben geen boodschap aan de boodschap.
Bij de PTT gebruikte men vroeger de leus: wij hebben geen boodschap aan de boodschap.
 Een belangrijke structuur die je overal in de informatica tegenkomt, is de boom.
Een belangrijke structuur die je overal in de informatica tegenkomt, is de boom.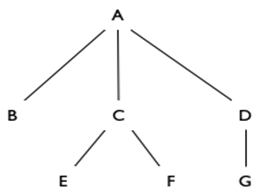
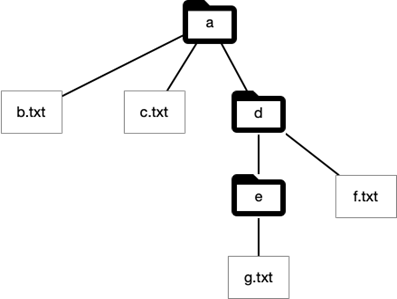
 Een recursieve structuur is een structuur waarbij één of meer delen dezelfde structuur hebben als het geheel. In de informatica zie je bij bomen deze recursieve structuur terug.
Een recursieve structuur is een structuur waarbij één of meer delen dezelfde structuur hebben als het geheel. In de informatica zie je bij bomen deze recursieve structuur terug.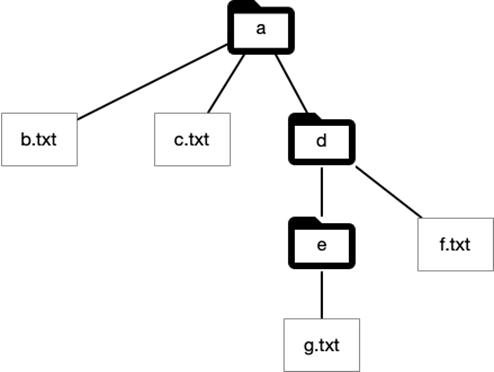
 Het beginpunt van de boom, bijvoorbeeld de map op het hoogste niveau, noemen we de wortel of root. In Linux spreek je over de root directory, aangegeven als /.
Het beginpunt van de boom, bijvoorbeeld de map op het hoogste niveau, noemen we de wortel of root. In Linux spreek je over de root directory, aangegeven als /.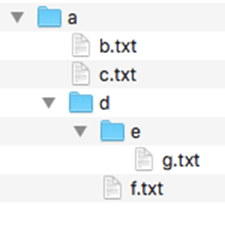
 1. Zoek voorbeelden van een horizontale weergave van een boom.
1. Zoek voorbeelden van een horizontale weergave van een boom.
 Maak in het Operating System op je computer de bestanden aan volgens de structuur van de voorbeeld-figuur.
Maak in het Operating System op je computer de bestanden aan volgens de structuur van de voorbeeld-figuur. Zoek uit wat een outline editor is (voor tekstdocumenten).
Zoek uit wat een outline editor is (voor tekstdocumenten). Bestudeer hoe in een project voor een website de bestanden georganiseerd zijn (bijvoorbeeld via GitHub). Geef een beschrijving van de gebruikte aanpak.
Bestudeer hoe in een project voor een website de bestanden georganiseerd zijn (bijvoorbeeld via GitHub). Geef een beschrijving van de gebruikte aanpak.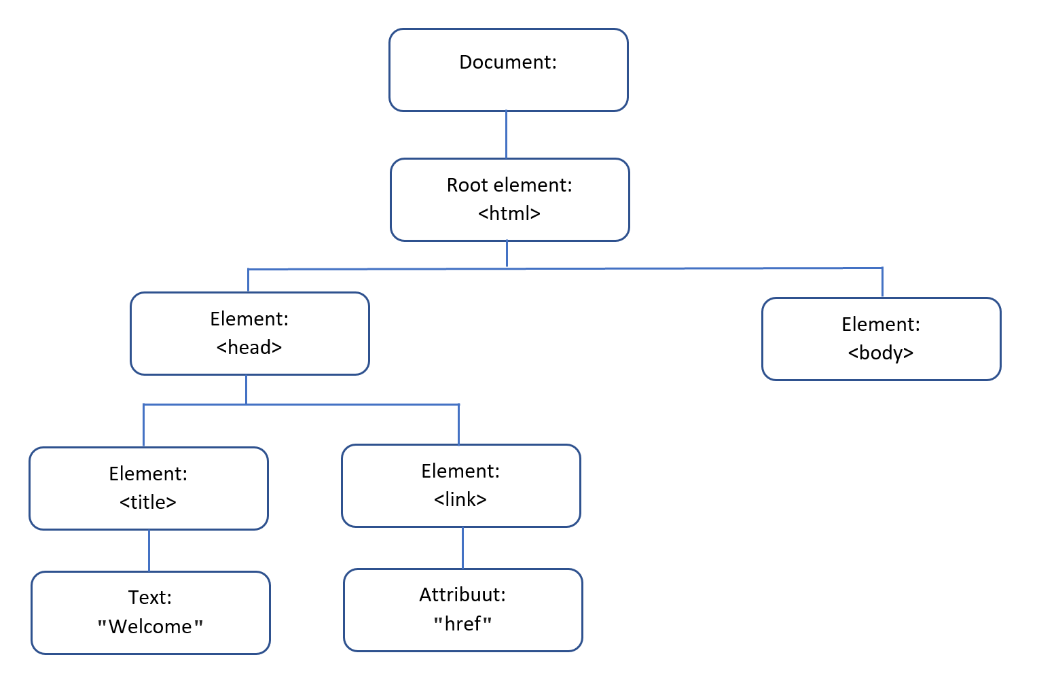
 Een HTML DOM model wordt opgebouwd als een boom die bestaat uit objecten.
Een HTML DOM model wordt opgebouwd als een boom die bestaat uit objecten. 1. Met behulp van de webontwikkelaar-hulpmiddelen van de browser kun je de DOM als “horizontale boomstructuur” te zien krijgen.
1. Met behulp van de webontwikkelaar-hulpmiddelen van de browser kun je de DOM als “horizontale boomstructuur” te zien krijgen. Voor de structuur van een webpagina wordt HTML gebruikt.
Voor de structuur van een webpagina wordt HTML gebruikt.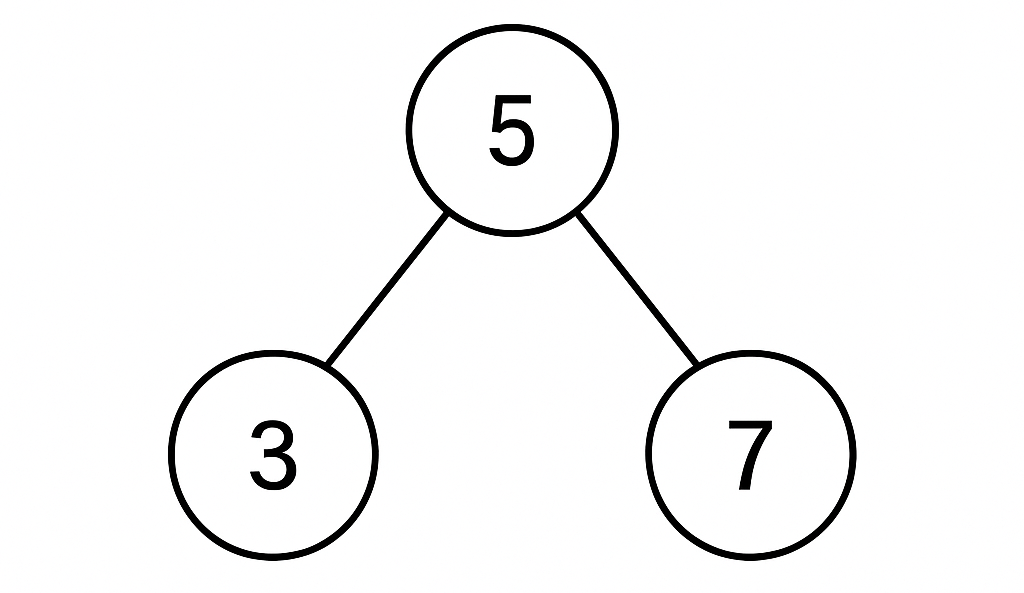
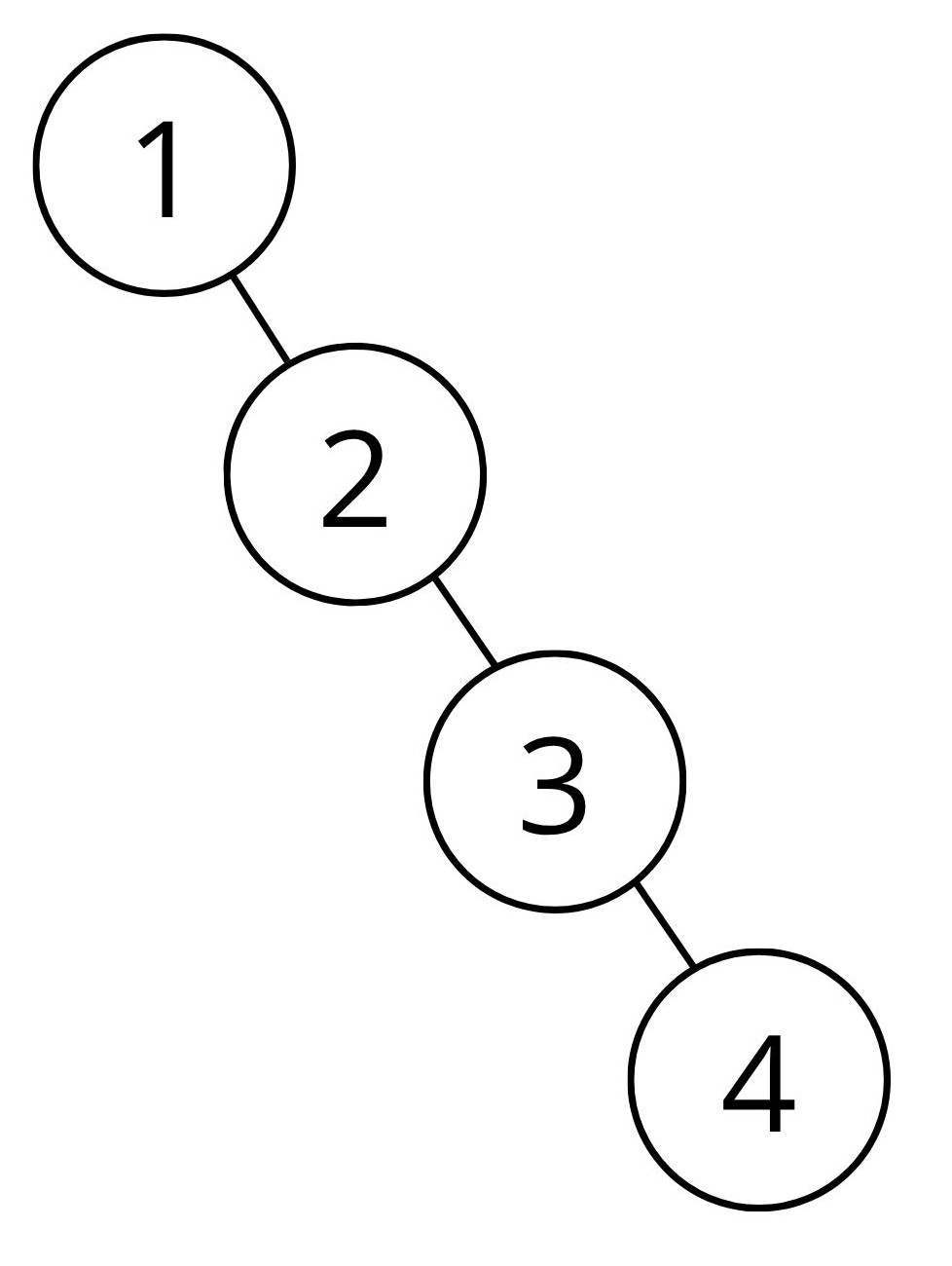
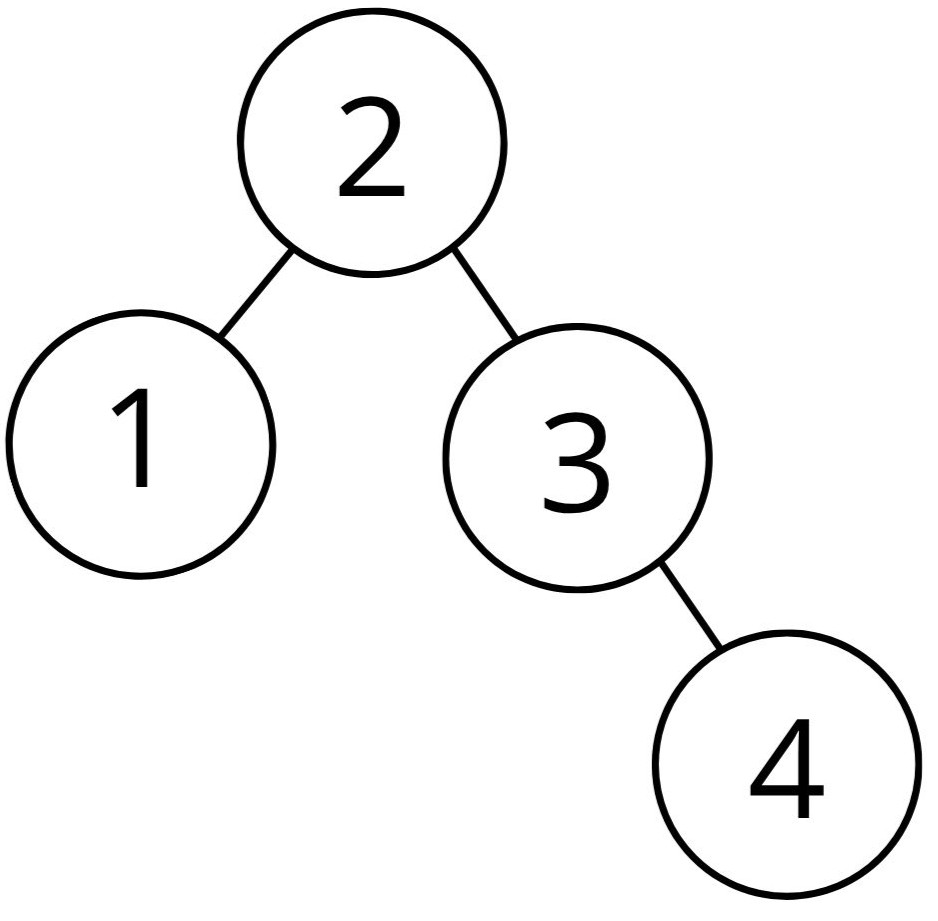
 Gegeven is de volgende zoekboom.
Gegeven is de volgende zoekboom.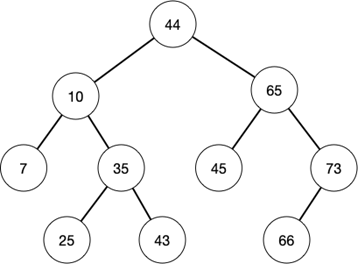
 Hieronder zie je een ontleedboom.
Hieronder zie je een ontleedboom.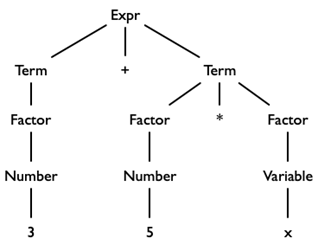

 Bij rekenen denk je meestal aan het werken met getallen.
Bij rekenen denk je meestal aan het werken met getallen. Enkele begrippen rond algoritmen (en programmeren) komen we ook in het dagelijks leven tegen.
Enkele begrippen rond algoritmen (en programmeren) komen we ook in het dagelijks leven tegen.
 1. Kijk op het web naar de video "
1. Kijk op het web naar de video " Als het algoritme effectief is (of correct) krijg je, als je de stappen precies uitvoert, altijd het beoogde resultaat, voor elke acceptabele waarde van de invoer.
Als het algoritme effectief is (of correct) krijg je, als je de stappen precies uitvoert, altijd het beoogde resultaat, voor elke acceptabele waarde van de invoer. Een algoritme is niet afhankelijk van de technologie: je kunt eenzelfde algoritme met verschillende technologieën uitvoeren. Je kunt verschillende programmeertalen gebruiken, en verschillende processoren. Maar je kunt ook een compleet andere technologie gebruiken.
Een algoritme is niet afhankelijk van de technologie: je kunt eenzelfde algoritme met verschillende technologieën uitvoeren. Je kunt verschillende programmeertalen gebruiken, en verschillende processoren. Maar je kunt ook een compleet andere technologie gebruiken. In de volgende onderdelen gaan we verder in op algoritmen en automaten.
In de volgende onderdelen gaan we verder in op algoritmen en automaten. 1. Plaats de volgende termen in het juiste vak:
1. Plaats de volgende termen in het juiste vak: Call centra maken vaak gebruik van call scripts.
Call centra maken vaak gebruik van call scripts. Breien als algoritme
Breien als algoritme Optellen
Optellen Zoekalgoritme
Zoekalgoritme Charles Babbage (1792-1871) is vooral bekend geworden door zijn ontwerpen voor mechanische rekenmachines. In de 17e eeuw hadden Blaise Pascal en Gottfried Wilhelm Leibniz ook al mechanische rekenmachines ontworpen.
Charles Babbage (1792-1871) is vooral bekend geworden door zijn ontwerpen voor mechanische rekenmachines. In de 17e eeuw hadden Blaise Pascal en Gottfried Wilhelm Leibniz ook al mechanische rekenmachines ontworpen. Het speelveld van Conway’s Game of Life is een oneindig rechthoekig rooster van vierkante cellen.
Het speelveld van Conway’s Game of Life is een oneindig rechthoekig rooster van vierkante cellen.
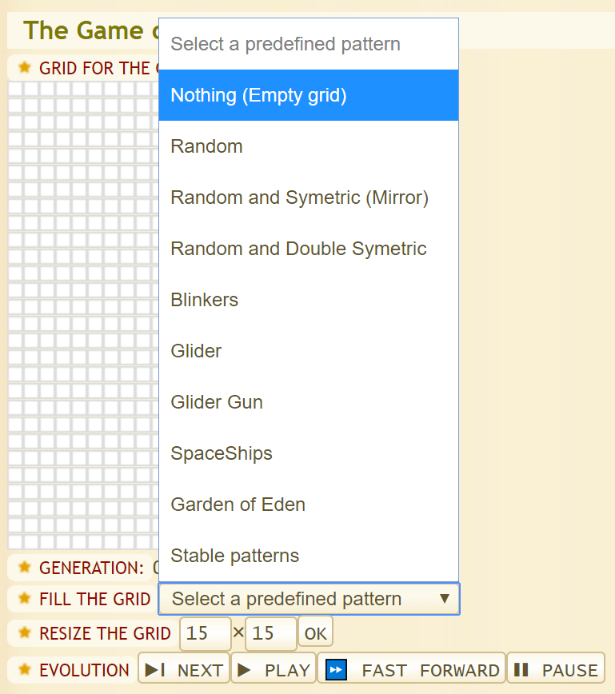

 Bekijk de onderstaande video:
Bekijk de onderstaande video: Zoek op het web (YouTube) naar video’s van de Game of Life.
Zoek op het web (YouTube) naar video’s van de Game of Life. Er zijn allerlei varianten op de regels mogelijk, maar niet alle varianten geven aanleiding tot interessant gedrag. Met de online-simulator
Er zijn allerlei varianten op de regels mogelijk, maar niet alle varianten geven aanleiding tot interessant gedrag. Met de online-simulator  De regels van een cellulaire automaat beschrijven hoe je uit de huidige toestand (vorm) de volgende toestand bepaalt. De uitvoering van deze regels resulteert in een proces als opeenvolging van deze toestanden.
De regels van een cellulaire automaat beschrijven hoe je uit de huidige toestand (vorm) de volgende toestand bepaalt. De uitvoering van deze regels resulteert in een proces als opeenvolging van deze toestanden.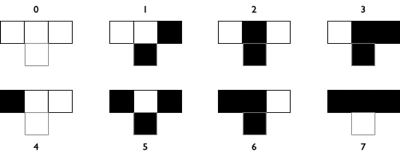
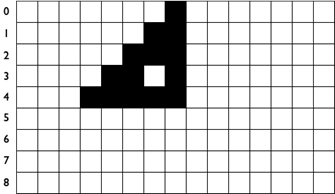
 De cellulaire automaat hierboven heet “regel 110”. Bedenk waar deze naam vandaan komt.
De cellulaire automaat hierboven heet “regel 110”. Bedenk waar deze naam vandaan komt. 
 Je kunt in de spreadsheet ook experimenteren met andere regels.
Je kunt in de spreadsheet ook experimenteren met andere regels. We behandelen hier een ander soort automaten: eindige automaten.
We behandelen hier een ander soort automaten: eindige automaten.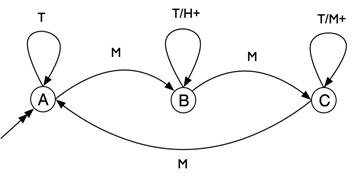
 1. Teken een eindige automaat die de verkeerslichten bij een kruispunt beschrijft.
1. Teken een eindige automaat die de verkeerslichten bij een kruispunt beschrijft.
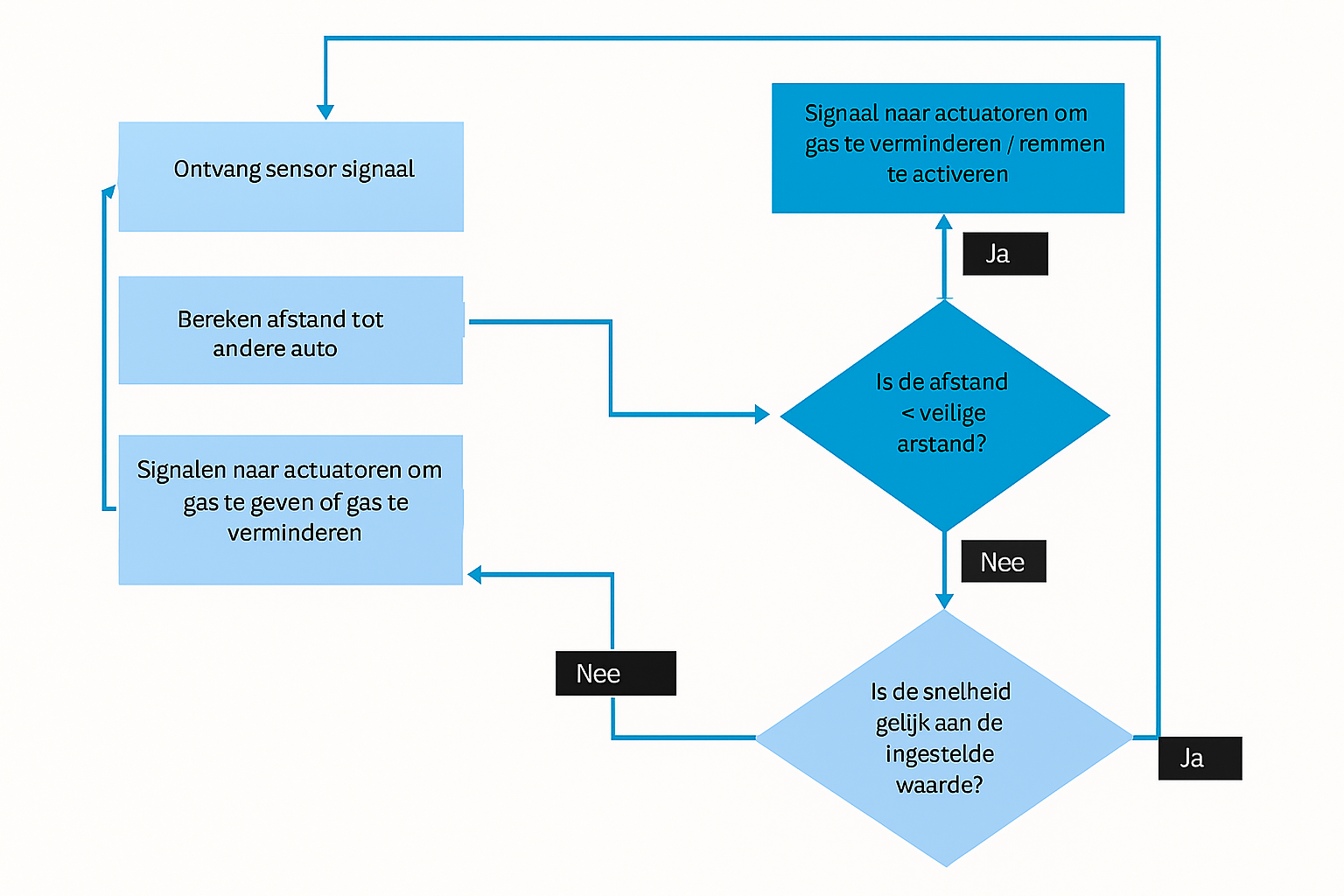
 In de definitie van een eindige automaat hierboven staat dat een overgang “gewoonlijk” een invoersymbool heeft en een uitvoersymbool.
In de definitie van een eindige automaat hierboven staat dat een overgang “gewoonlijk” een invoersymbool heeft en een uitvoersymbool.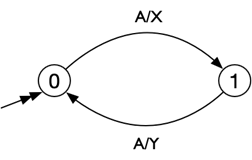
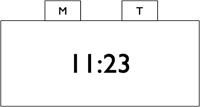
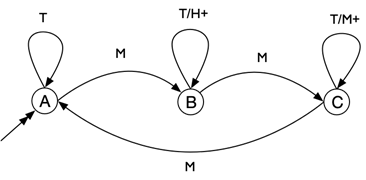
 De onderstaande figuur beschrijft een snoepautomaat.
De onderstaande figuur beschrijft een snoepautomaat.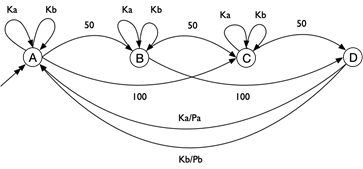
 Beschouw de volgende automaat:
Beschouw de volgende automaat: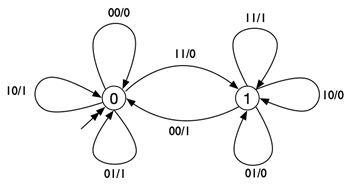
 Zoeken komt in veel toepassingen voor, bijvoorbeeld het zoeken van het nulpunt van een functie, of als onderdeel van “opslaan en terugzoeken”.
Zoeken komt in veel toepassingen voor, bijvoorbeeld het zoeken van het nulpunt van een functie, of als onderdeel van “opslaan en terugzoeken”.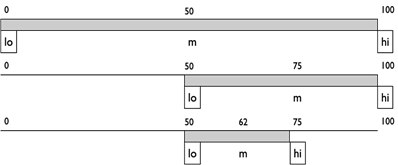
 Welke reeks waarden voor lo en hi krijg je bij het raden
Welke reeks waarden voor lo en hi krijg je bij het raden Je hebt 10 munten waarvan je weet dat er 1 vals is, met een afwijkend gewicht.
Je hebt 10 munten waarvan je weet dat er 1 vals is, met een afwijkend gewicht. Je hebt een (lange) lijst met namen en bijbehorende telefoonnummers.
Je hebt een (lange) lijst met namen en bijbehorende telefoonnummers. In het spreadsheet-voorbeeld hebben we ook een demonstratie van het sorteren van een reeks getallen.
In het spreadsheet-voorbeeld hebben we ook een demonstratie van het sorteren van een reeks getallen. Zoals we gezien hebben, heeft het gegeven algoritme voor het sorteren van een reeks van N getallen N stappen nodig.
Zoals we gezien hebben, heeft het gegeven algoritme voor het sorteren van een reeks van N getallen N stappen nodig. In dit gedeelte behandelen we enkele patronen voor het rekenen met rijen van waarden zoals je die in bijvoorbeeld spreadsheets vaak tegenkomt.
In dit gedeelte behandelen we enkele patronen voor het rekenen met rijen van waarden zoals je die in bijvoorbeeld spreadsheets vaak tegenkomt. (map)
(map)  (map/reduce)
(map/reduce)  (map/reduce)
(map/reduce) (map/reduce)
(map/reduce) We hebben hiervoor rekenen beschreven als “spelen met vormen”.
We hebben hiervoor rekenen beschreven als “spelen met vormen”. Met behulp van een grammatica van een taal kun je twee dingen:
Met behulp van een grammatica van een taal kun je twee dingen: Een eerste manier om bepaalde volgordes van woorden af te dwingen is met behulp van een eindige automaat.
Een eerste manier om bepaalde volgordes van woorden af te dwingen is met behulp van een eindige automaat.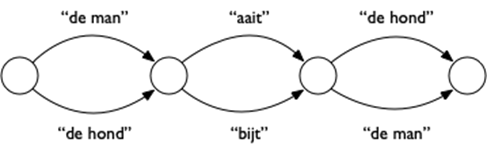

 Een volgende stap is het gebruik van grammatica’s met herschrijfregels. Zo’n grammatica bestaat uit de volgende onderdelen:
Een volgende stap is het gebruik van grammatica’s met herschrijfregels. Zo’n grammatica bestaat uit de volgende onderdelen: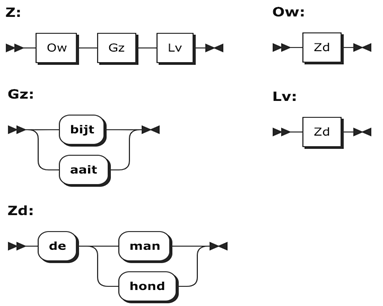
 Geef de afleiding van de zin “de hond bijt de man”.
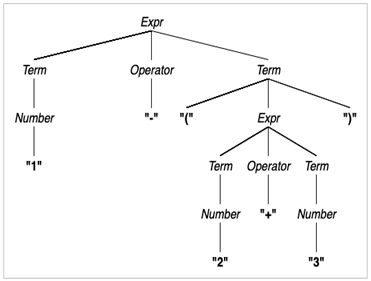
Geef de afleiding van de zin “de hond bijt de man”. Het volgende voorbeeld is een grammatica voor eenvoudige expressies.
Het volgende voorbeeld is een grammatica voor eenvoudige expressies.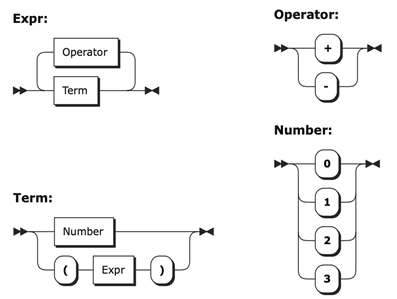
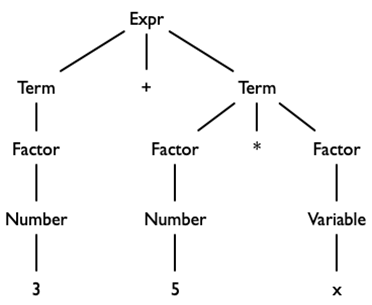
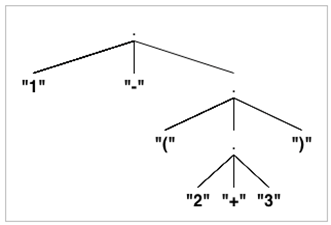
 Gegeven is de onderstaande grammatica voor expressies.
Gegeven is de onderstaande grammatica voor expressies. Gegeven is de volgende grammatica voor (iets minder eenvoudige) zinnen.
Gegeven is de volgende grammatica voor (iets minder eenvoudige) zinnen. In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp grondslagen.
In de volgende toets wordt getoetst wat je inmiddels zou moeten weten over het onderwerp grondslagen.
 Bekijk hier je voortgang
Bekijk hier je voortgang