Het arrangement Combinaties is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 22-12-2021 18:26:33
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Dit thema valt onder de arrangeerbare leerlijn van de Stercollecties voor wiskunde A voor havo leerjaar 4. De volgende onderdelen worden behandeld: je gaat in deze paragraaf leren hoe je een bepaald type telproblemen kunt vertalen naar een rooster. En dit tellen in het rooster kun je dan weer direct op je grafische rekenmachine uitrekenen met de zogenaamde combinatiegetallen
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
- Trefwoorden
- arrangeerbaar, combinatiegetallen, grafische rekenmachine, havo 4, rooster, stercollectie, telproblemen, wiskunde a
Gebruikte Wikiwijs Arrangementen
Wiskunde Wageningse Methode OUD. (z.d.).
Systematisch uitschrijven

 Je gaat in deze paragraaf leren hoe je een bepaald type telproblemen kunt vertalen naar een rooster.
Je gaat in deze paragraaf leren hoe je een bepaald type telproblemen kunt vertalen naar een rooster.
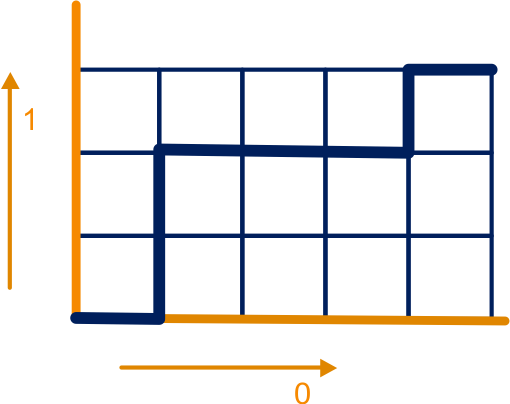 Bij ieder drietal hoort zo’n rijtje met vijf keer een ‘0’ en drie keer een ‘1’. Ieder rijtje (bestaande uit vijf nullen en drie enen) kan dan worden voorgesteld door een route in een rooster. Zo’n route bestaat uit acht stappen: je moet vijf keer naar rechts en drie keer naar boven. De route die bij het drietal B-C-G hoort, zie je hiernaast. Het aantal mogelijke drietallen is daarom gelijk aan het aantal kortste routes van
Bij ieder drietal hoort zo’n rijtje met vijf keer een ‘0’ en drie keer een ‘1’. Ieder rijtje (bestaande uit vijf nullen en drie enen) kan dan worden voorgesteld door een route in een rooster. Zo’n route bestaat uit acht stappen: je moet vijf keer naar rechts en drie keer naar boven. De route die bij het drietal B-C-G hoort, zie je hiernaast. Het aantal mogelijke drietallen is daarom gelijk aan het aantal kortste routes van 
