Je gaat in deze paragraaf leren hoe je sommige telproblemen op kunt lossen met de zogenaamde 'combinatiegetallen'. Deze ben je tegengekomen bij het tellen in roosters in de vorige paragraaf. Ze komen ook voor in de driehoek van Pascal.
Dit type telproblemen zul je straks nog erg veel tegenkomen: je zult in deze paragraaf leren in welke situaties dat is. Daarbij is met name van belang dat bij dit type telproblemen de volgorde niet van belang is.
Opgaven
Wegenstructuur
De wegenstructuur in Amerikaanse steden is in het algemeen erg overzichtelijk. In de benaming van de wegen is die overzichtelijkheid terug te vinden: 1st street, 2nd street ... en 1st avenue, 2nd avenue,... .
Het karakteristieke schaakbordpatroon van veel
merikaanse steden.
Noord-zuid lopen de avenue’s, oost-west de streets.
Randy Walker wandelt van het kruispunt 2nd street, 1st avenue naar het kruispunt 3rd street, 4th avenue zonder omwegen.
Plattegrond
In de plattegrond hiernaast wordt bij elk kruispunt vermeld hoeveel routes er zonder omwegen naar dat kruispunt leiden, gerekend vanaf het stadhuis. Bij drie kruispunten is het aantal routes al ingevuld.
Routes van A naar B
Bij het tellen van het aantal routes raak je makkelijk in de knoop. Daarom is het handig om bij elk ‘tussenpunt’ het aantal routes naar dat punt te schrijven.
Punt B ligt vier hokjes rechts van A en drie hokjes boven A. Nils heeft geteld dat er \(20\) kortste routes zijn van A naar het punt links van B; hij heeft ook geteld dat er \(15\) kortste routes zijn van A naar het punt onder B. Die aantallen staan bij de betreffende kruispunten.
Kortste routes in situaties
Je hebt nu een principe ontdekt waarmee je aantallen kortste routes in een rooster kunt uitrekenen.
Noteer het getal \(1\) bij elk punt in het rooster dat op maar één manier te bereiken is.
Gebruik vervolgens de optelmethode om het aantal routes naar de overige roosterpunten te bepalen.
Tuin in Square City
In Square City is een fraaie tuin aangelegd die niet door voetgangers mag worden betreden.
Historie driehoek van Pascal
Blaise Pascal
(1623 - 1662)
Veel telproblemen kunnen worden opgelost met behulp van het onderstaande getallenpatroon: de driehoek van Pascal. Elk getal (\(≠1\)) is de som van zijn twee bovenburen.
Het getallenpatroon is genoemd naar de Franse filosoof en wiskundige Blaise Pascal. Het werd onder zijn naam in 1665 (postuum) gepubliceerd.
Pascal was overigens niet de eerste wiskundige die de tabel ontdekte en gebruikte. In een Chinees wiskundeboek, van de schrijvers Ssu Yuan Yu en Chuh Shih Chieh, uit het jaar 1303, is de tabel al te vinden. En dat de tabel nog veel ouder is, blijkt uit het feit dat hij in het Chinese boek ‘de antieke tabel’ wordt genoemd.
Bekijk de driehoek van Pascal. De driehoek begint met regel 0; de onderste regel is regel 9.
Driehoek van Pascal
Nog een keer de driehoek van Pascal maar nu in de vorm van een plattegrond.
Op regel 0 staat \(1\). De getallen op regel 1 zijn opgeteld \(2\). De getallen op regel 2 zijn opgeteld \(4\).
Kanaal door Square City
Dwars door Square City loopt een kanaal, zoals je al eerder gezien hebt. Langs het kanaal is een mooie boulevard aangelegd met gezellige restaurants en barretjes.
Een inwoonster van Square city wil vanuit punt A zo snel mogelijk naar de boulevard.
Kortste routes in driehoek van Pascal
In opgave "Routes van A naar B" heb je berekend hoeveel kortste routes er zijn in een rooster van \((0,0)\) naar \((4,3)\). Zie figuur linksonder. Als het goed is, kwam je aan \(35\). Elke kortste route bestaat uit \(7\) stappen (een stap is \(1\) naar boven of \(1\) naar rechts). Van die \(7\) stappen moet je er \(3\) naar boven doen (en \(4\) naar rechts). Het aantal kortste routes vind je in de driehoek van Pascal in de \(7\)e rij. Zie figuur rechtsonder.
Combinatiegetal
Als je met behulp van de driehoek van Pascal het aantal kortste routes van \((0,0)\) naar \((14,6)\) wilt bepalen, moet je de driehoek aanvullen tot en met de 20e rij. Dat is een heel karwei. Dit getal kun je gelukkig ook eenvoudig op je (grafische) rekenmachine berekenen met de optie \(\text {nCr}\).
De rekenmachine geeft \(20\space \text {nCr} \space 6=38.760\).
De \(20\) staat voor het totaal aantal stappen van \((0,0)\) naar \((14,6)\) en de \(6\) staat voor het aantal stappen dat je naar boven gaat.
Het aantal kortste routes van \((0,0)\) naar \((14,6)\) noteren we met het combinatiegetal \(\left( {\begin{array}{*{20}{c}}
{20} \\
6
\end{array}} \right)\); spreek uit: twintig boven zes.
Het arrangement De driehoek van Pascal is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
Dit thema valt onder de arrangeerbare leerlijn van de Stercollecties voor wiskunde A voor havo leerjaar 4. Je gaat in deze paragraaf leren hoe je sommige telproblemen op kunt lossen met de zogenaamde 'combinatiegetallen'. Deze ben je tegengekomen bij het tellen in roosters in de vorige paragraaf. Ze komen ook voor in de driehoek van Pascal.
Leerniveau
HAVO 4;
Leerinhoud en doelen
Wiskunde A;
Eindgebruiker
leerling/student
Moeilijkheidsgraad
gemiddeld
Studiebelasting
4 uur en 0 minuten
Trefwoorden
arrangeerbaar, combinatiegetallen, driehoek van pascal, havo 4, roosters, stercollectie, telproblemen, wiskunde a
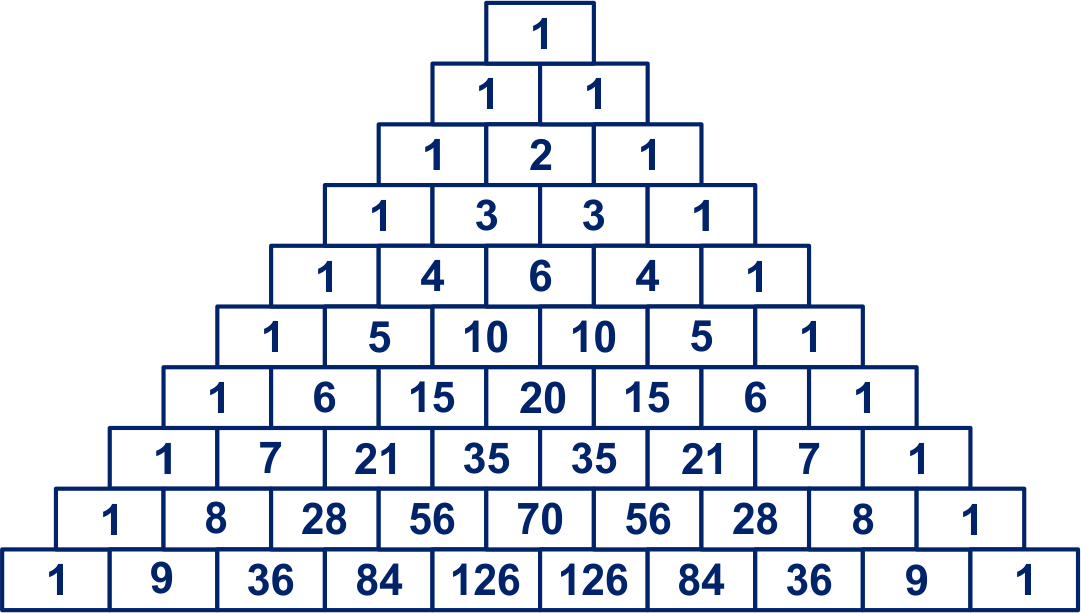
Dit thema valt onder de arrangeerbare leerlijn van de Stercollecties voor wiskunde A voor havo leerjaar 4. Je gaat in deze paragraaf leren hoe je sommige telproblemen op kunt lossen met de zogenaamde 'combinatiegetallen'. Deze ben je tegengekomen bij het tellen in roosters in de vorige paragraaf. Ze komen ook voor in de driehoek van Pascal.
Je gaat in deze paragraaf leren hoe je sommige telproblemen op kunt lossen met de zogenaamde 'combinatiegetallen'. Deze ben je tegengekomen bij het tellen in roosters in de vorige paragraaf. Ze komen ook voor in de driehoek van Pascal.
De wegenstructuur in Amerikaanse steden is in het algemeen erg overzichtelijk. In de benaming van de wegen is die overzichtelijkheid terug te vinden: 1st street, 2nd street ... en 1st avenue, 2nd avenue,... .
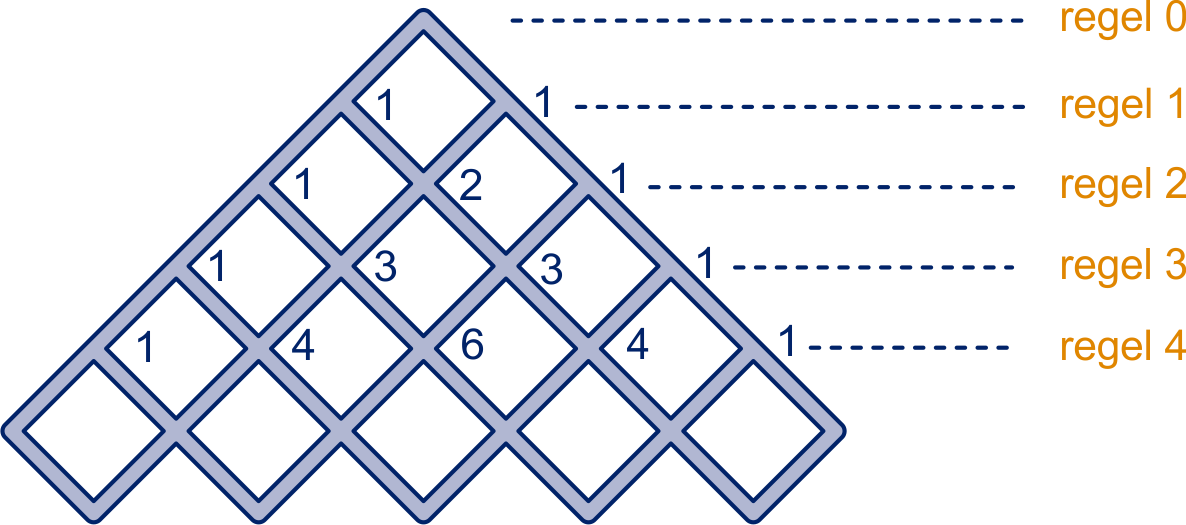
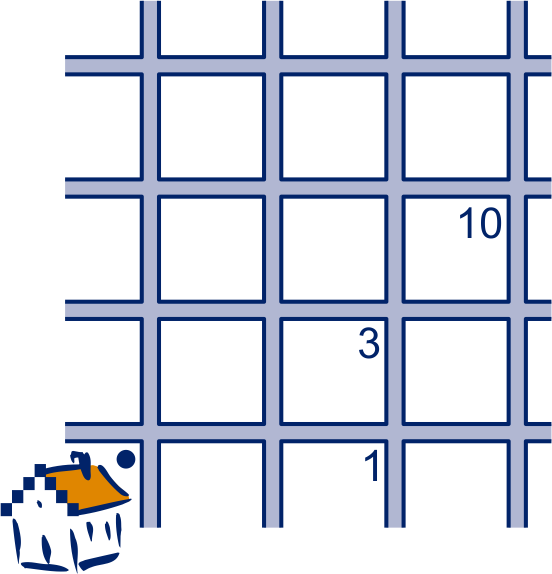In de plattegrond hiernaast wordt bij elk kruispunt vermeld hoeveel routes er zonder omwegen naar dat kruispunt leiden, gerekend vanaf het stadhuis. Bij drie kruispunten is het aantal routes al ingevuld.
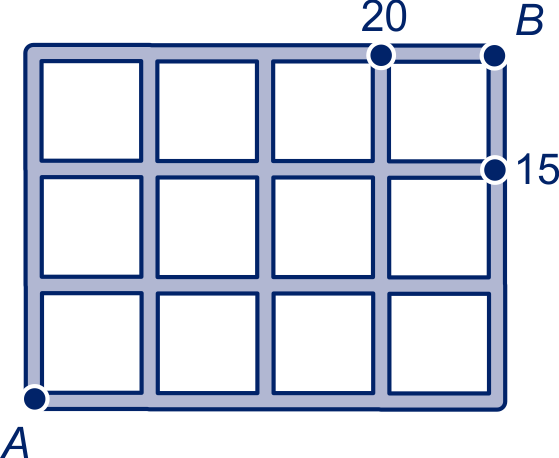Punt B ligt vier hokjes rechts van A en drie hokjes boven A. Nils heeft geteld dat er 
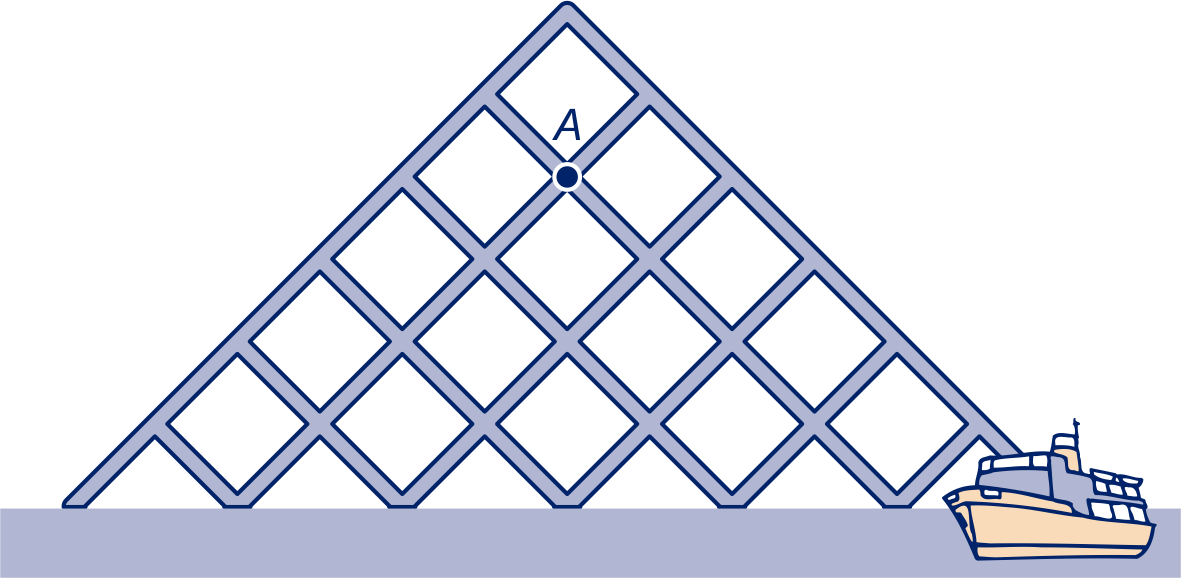
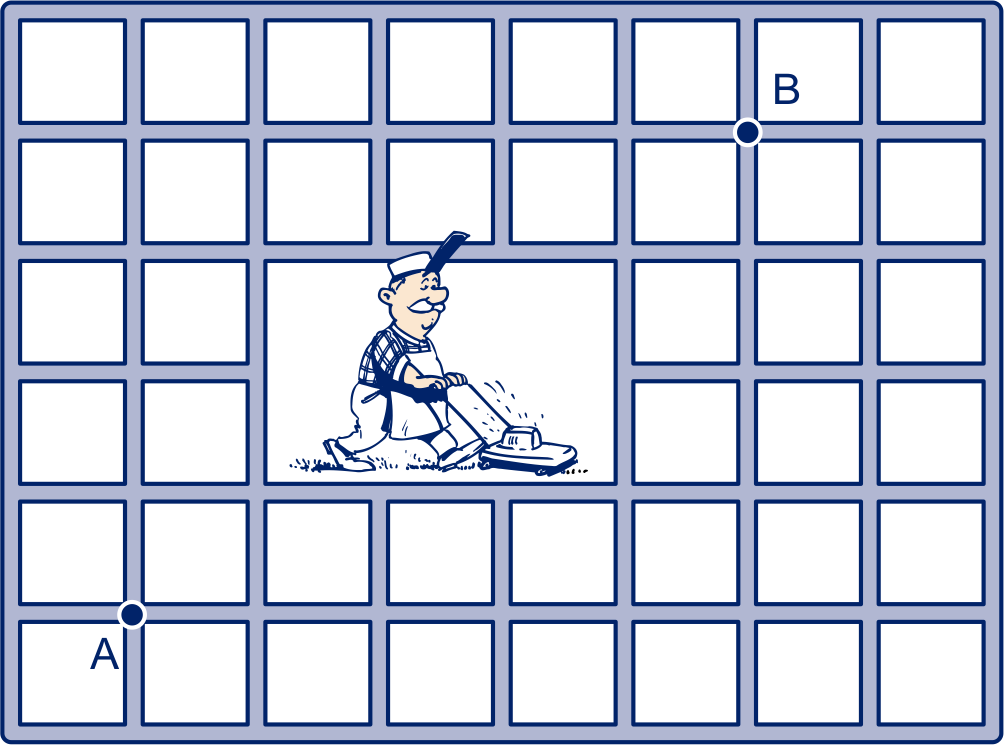In Square City is een fraaie tuin aangelegd die niet door voetgangers mag worden betreden.
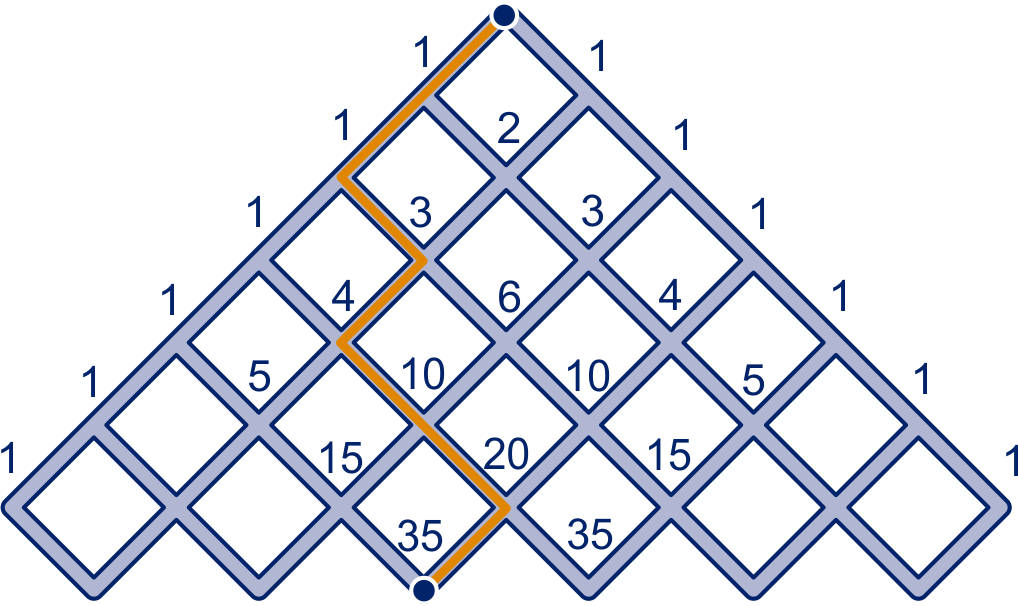
Als je met behulp van de driehoek van Pascal het aantal kortste routes van 
