Het arrangement Cirkels is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 29-07-2022 14:50:01
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
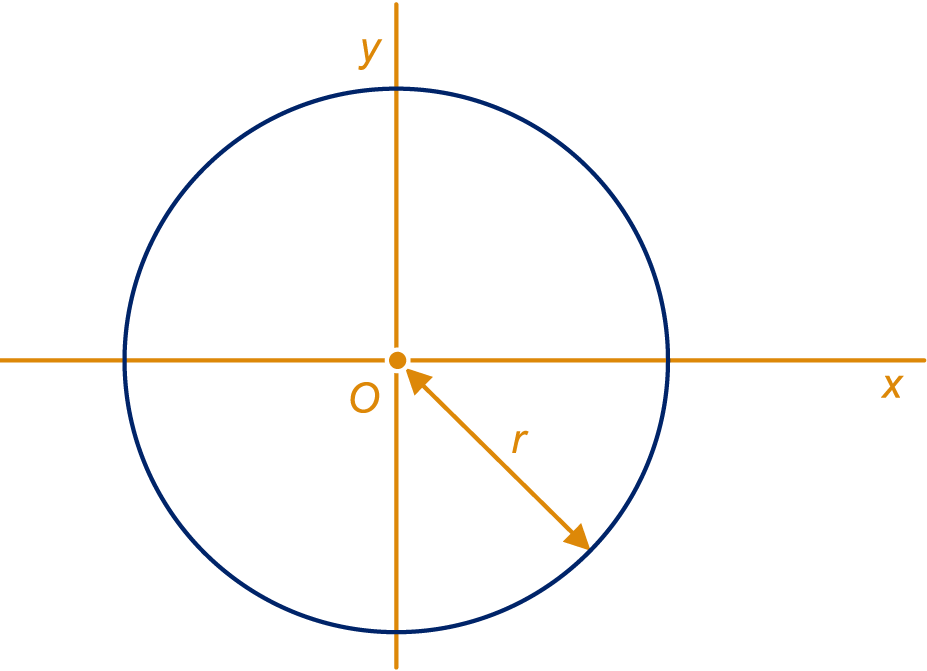
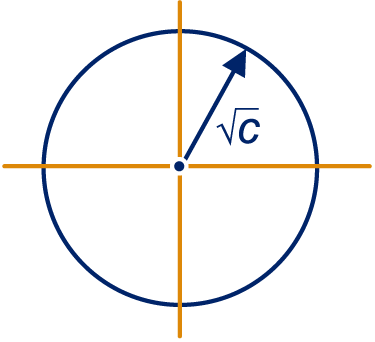
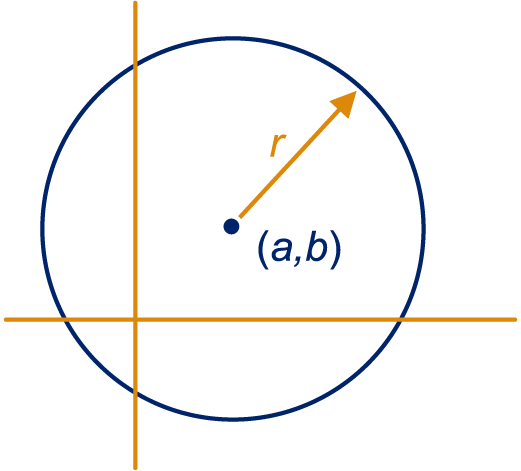
- Deze les valt onder de arrangeerbare leerlijn van de Stercollectie voor wiskunde B voor havo leerjaar 4. Dit is thema ’Lijnen en cirkels'. Het onderwerp van deze les is: cirkels. Punten op een lijn hebben bijvoorbeeld de eigenschap dat de x -coördinaat en de y -coördinaat opgeteld bij elkaar 4 zijn. Zo heb je nog veel meer mogelijkheden, die je allemaal al hebt gezien. Wanneer we echter gaan kijken naar alle punten die op dezelfde afstand van een punt M af liggen, krijgen we geen lijn. We krijgen een cirkel. Omdat de eigenschap van de punten die hieraan voldoen verschilt van de punten die op een lijn liggen, hebben cirkels ook een andere formule. Deze vergelijking ga je in verschillende gevallen opstellen en je gaat het middelpunt van een cirkel en zijn straal berekenen door de vergelijking in middelpuntsvorm te zetten.
- Leerniveau
- HAVO 4;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 4 uur 0 minuten
- Trefwoorden
- arrangeerbaar, cirkel, havo 4, middelpuntsvorm, stercollectie, vergelijking, wiskunde b
Gebruikte Wikiwijs Arrangementen
Wiskunde Wageningse Methode OUD. (z.d.).
Rechte lijnen

 Punten op een lijn hebben bijvoorbeeld de eigenschap dat de
Punten op een lijn hebben bijvoorbeeld de eigenschap dat de