Wanneer je twee lijnen in hetzelfde assenstelsel tekent, is de kans groot dat die lijnen elkaar ergens snijden.
Dit snijpunt kun je berekenen. Hiervoor kun je substitutie gebruiken, of vergelijkingen omschrijven.
Om dit gemakkelijk te doen zul je een paar trucjes leren.
Ook zal je leren wat een lijnenbundel is en hoe je ermee werkt.
Opgaven
Snijpunt van rechte lijnen
Substitutie
Twee lijnen
Soms heb je twee lijnen met vergelijkingen in de vorm \(\small ax+by=c\).
Om dan het snijpunt van de twee lijnen uit te rekenen heb je de volgende mogelijkheden:
Beide vergelijkingen omzetten in de vorm \(\small y=\ldots\) en dan aan elkaar gelijkstellen.
Eén van beide vergelijkingen omzetten in de vorm \(\small y=\ldots\) (of \(\small x=\ldots\)) en deze dan in de andere substitueren.
Lijnenbundel
Gegeven is voor elke waarde van \(a\) lijn \(\small k_a\) met vergelijking \(\small y=a(x−1)+3\).
Voor elke waarde van \(\small a\) krijg je een andere lijn.
Als je bijvoorbeeld \(\small a=2\) neemt, krijg je de lijn \(\small k_2\) met vergelijking \(\small y=2(x−1)+3\), ofwel \(\small y=2x+1\).
En \(\small a=\text{-}3\) geeft lijn \(\small k_{\text{-}3}\): \(\small y=\text{-}3(x−1)+3=\text{-}3x+6\).
In de figuur hieronder staan voor negen verschillende waarden van \(\small a\) de grafiek van \(\small k_a\) getekend.
Je ziet dat je een zogenaamde lijnenbundel of lijnenwaaier krijgt:
lijn \(\small k_a\) gaat voor elke waarde van \(\small a\) door het punt \(\small (1,3)\), met telkens een andere richtingscoëfficiënt.
Voorbeeld:
Voor welke waarde van \(\small a\) gaat lijn \(\small k_a\) door de oorsprong?
Oplossing
Vul punt \(\small (0,0)\) in de vergelijking van \(\small k_a\) in.
Je krijg \(\small 0=a\cdot (0-1)+3\), ofwel \(\small \text{‐}a+3=0\). Dus \(\small a=3\).
Lijn m
Lijn n
Punten op lijnen
Lijn PQ
Voor elke a hetzelfde
In de vorige opgave kreeg je vier keer hetzelfde antwoord (als je die opgave goed gemaakt hebt).
In de volgende opgave gaan we dat begrijpen.
Het arrangement Rekenen met rechte lijnen is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
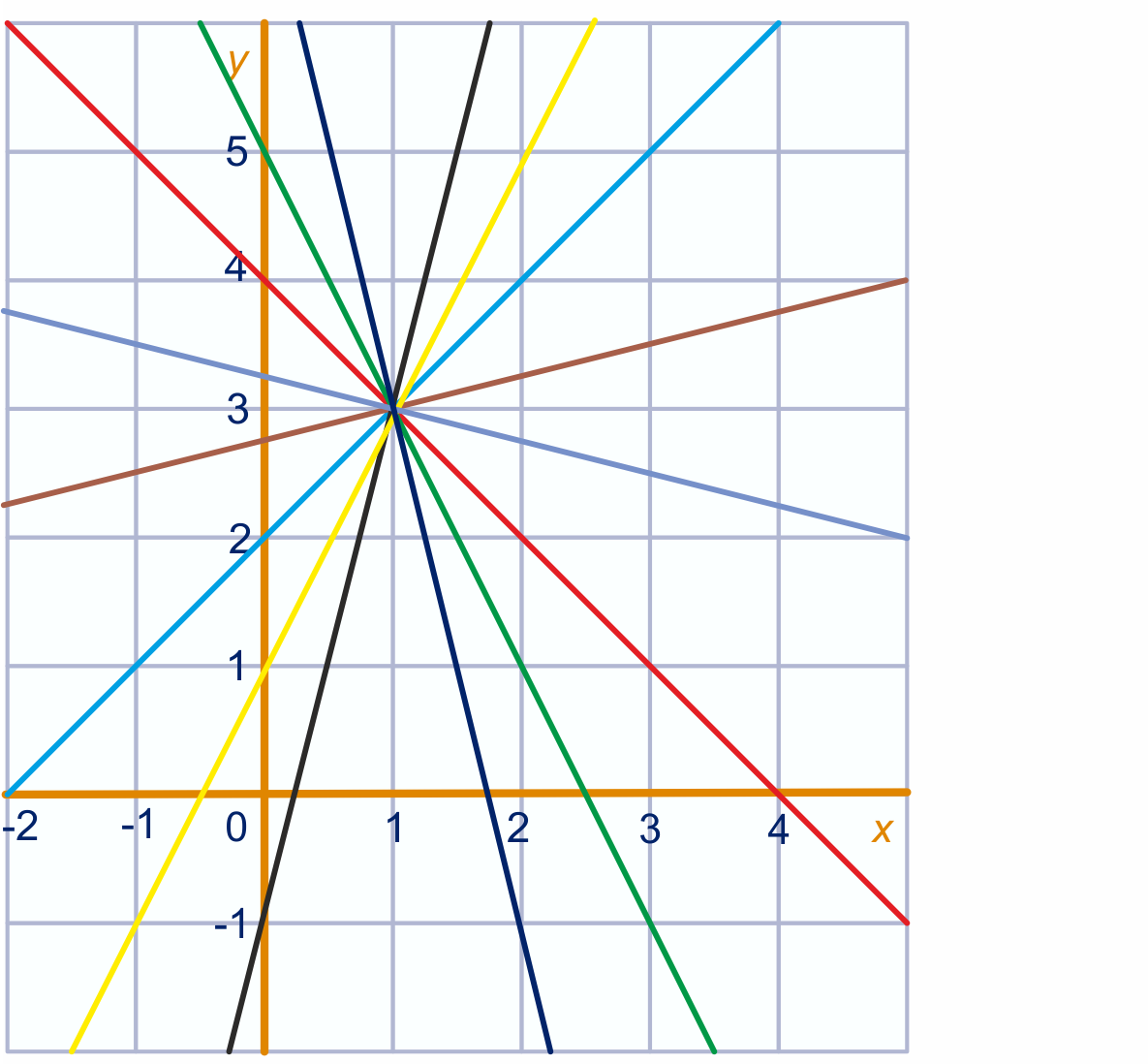
Deze les valt onder de arrangeerbare leerlijn van de Stercollectie voor wiskunde B voor havo leerjaar 4. Dit is thema ’Hellingen'. Het onderwerp van deze les is: rekenen met rechte lijnen.
Wanneer je twee lijnen in hetzelfde assenstelsel tekent, is de kans groot dat die lijnen elkaar ergens snijden.
Dit snijpunt kun je berekenen. Hiervoor kun je substitutie gebruiken, of vergelijkingen omschrijven.
Om dit gemakkelijk te doen zul je een paar trucjes leren.
Ook zal je leren wat een lijnenbundel is en hoe je ermee werkt.
Leerniveau
HAVO 4;
Eindgebruiker
leerling/student
Moeilijkheidsgraad
gemiddeld
Studiebelasting
4 uur en 0 minuten
Trefwoorden
arrangeerbaar, assenstelsel, havo 4, lijnenbundel, snijpunt, stercollectie, substitutie, wiskunde b
Deze les valt onder de arrangeerbare leerlijn van de Stercollectie voor wiskunde B voor havo leerjaar 4. Dit is thema ’Hellingen'. Het onderwerp van deze les is: rekenen met rechte lijnen.
Wanneer je twee lijnen in hetzelfde assenstelsel tekent, is de kans groot dat die lijnen elkaar ergens snijden.
Dit snijpunt kun je berekenen. Hiervoor kun je substitutie gebruiken, of vergelijkingen omschrijven.
Om dit gemakkelijk te doen zul je een paar trucjes leren.
Ook zal je leren wat een lijnenbundel is en hoe je ermee werkt.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
