Het arrangement Wiskunde vmbo basis leerjaar 2 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteurs
- Laatst gewijzigd
- 07-10-2019 08:51:52
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
StudioVO
Deze module is ontwikkeld door medewerkers van StudioVO.
Fair Use
In de Stercollecties van StudioVO wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Rearrangeerbare stercollectie wiskunde voor leerjaar 1 en 2 VMBO B van Stichting VO-content. De stercollectie is ontwikkeld op basis van de kerndoelen basisvorming en de door de SLO ontwikkelde inhoud- en leerdoelspecificaties voor het vak wiskunde. Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO.
- Leerniveau
- VMBO basisberoepsgerichte leerweg, 1; VMBO basisberoepsgerichte leerweg, 2;
- Leerinhoud en doelen
- Rekenen/wiskunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 100 uur 0 minuten
- Trefwoorden
- arrangeerbare, arrangeerbare leerlijn, hoofdarrangement, leerlijn, rearrangeerbaar, rearrangeerbare, vo-content
Gebruikte Wikiwijs Arrangementen
VO-content - Leerlijnen. (2025).
Wiskunde vmbo-b12



 Weet jij hoeveel jullie thuis per maand aan energie betalen?
Weet jij hoeveel jullie thuis per maand aan energie betalen? Hoeveel geld geeft een gezin uit aan eten, drinken en wonen?
Hoeveel geld geeft een gezin uit aan eten, drinken en wonen? Een bouwbedrijf wil een vakantiepark met vakantiehuisjes aanleggen. Het park komt bij het plaatsje Opperdam. De naam van het park wordt “Heideheuvel”. De vakantiehuisjes gaan ze verkopen.
Een bouwbedrijf wil een vakantiepark met vakantiehuisjes aanleggen. Het park komt bij het plaatsje Opperdam. De naam van het park wordt “Heideheuvel”. De vakantiehuisjes gaan ze verkopen. Het spel ganzenbord ken je vast wel.
Het spel ganzenbord ken je vast wel. Bij veel kastelen is er de mogelijkheid om een bezoek te brengen aan de kasteeltuin. Na een wandeling door de tuin rusten ze dan graag uit op het mooie terras om de vijver.
Bij veel kastelen is er de mogelijkheid om een bezoek te brengen aan de kasteeltuin. Na een wandeling door de tuin rusten ze dan graag uit op het mooie terras om de vijver. In het dagelijkse praktijk heb je regelmatig te maken met de omtrek en oppervlakte van figuren. Op internet kun je filmpjes vinden waarin uitgelegd wordt hoe je iets uit kunt rekenen. Zou jij zo'n filmpje zelf kunnen maken? Dat ga je aan het eind van dit thema samen met een klasgenoot doen.
In het dagelijkse praktijk heb je regelmatig te maken met de omtrek en oppervlakte van figuren. Op internet kun je filmpjes vinden waarin uitgelegd wordt hoe je iets uit kunt rekenen. Zou jij zo'n filmpje zelf kunnen maken? Dat ga je aan het eind van dit thema samen met een klasgenoot doen. Heb jij een mobiele telefoon? Vast wel. Tegenwoordig heeft bijna iedere leerling een mobiele telefoon. Bijvoorbeeld om even naar huis te bellen als je na moet blijven. Of om een sms-je te versturen naar een vriend of vriendin.
Heb jij een mobiele telefoon? Vast wel. Tegenwoordig heeft bijna iedere leerling een mobiele telefoon. Bijvoorbeeld om even naar huis te bellen als je na moet blijven. Of om een sms-je te versturen naar een vriend of vriendin.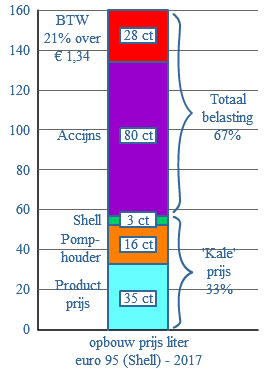 Heb je je ouders wel eens horen klagen over de benzineprijs? Vast wel!
Heb je je ouders wel eens horen klagen over de benzineprijs? Vast wel! Je ziet al een hele tijd op school.
Je ziet al een hele tijd op school. In het centrum van Rotterdam staan kubuswoningen.
In het centrum van Rotterdam staan kubuswoningen.