De lengte van de dunne darm van de mens is ruim 5 meter en heeft een oppervlakte van 150 à 200 m2 (de grootte van een tennisveld). Dat hij toch in je buik past, komt doordat hij erg gekronkeld is. Ook is het oppervlak geen gladde buis, maar bestaat hij uit talloze plooien.
De totale lengte van het menselijk bloedvatenstelsel is bijna 1500 km. Bij deze lengte zijn ook de kleinste haarvaten meegerekend.
Als je alle zenuwbanen van het menselijk lichaam achter elkaar legt, blijkt de totale lengte van het perifere zenuwstelsel ongeveer 150.000 kilometer te zijn. Dat is bijna vier keer de aarde rond.
Wat kan ik straks?
Aan het einde van dit thema kan je:
de oppervlakte van een paralellogram uitrekenen
de oppervlakte van een driehoek uitrekenen
de oppervlakte van allerlei figuren uitrekenen door ze te verdelen in bekende figuren
de oppervlakte van rechthoeken met dezelfde omtrek uitrekenen
de oppervlakte en omtrek van een cirkel uitrekenen
Wat kan ik al?
In dit hoodstuk leren we hoe we de oppervlakte van diverse figuren kunnen bepalen. Je weet al hoe je de oppervlakte en de omtrek van een rechthoek kan berekenen.
Het thema Cijfers in orde bestaat uit de volgende onderdelen:
Onderdeel
Tijd in lesuren
Start
Inleiding
0,5 uur
Wat kan ik straks?
Wat kan ik al?
Wat ga ik doen?
Paragrafen
De oppervlakte van een parallellogram
1,5 uur
De oppervlakte van een driehoek
1 uur
Allerlei oppervlaktes
1,5 uur
Rechthoeken met dezelfde omtrek
1 uur
Oppervlakte en omtrek van een cirkel
1,5 uur
Afsluiting
Samenvatting
Thema-opdracht
2 uur
Diagnostische toets
0,5 uur
Extra opgaven
0,5 uur
Terugblik
Totaal
10 uur
Gewone opgaven en Super opgaven
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
Die Super variant is wel wat moeilijker. Let op: Je hoeft dan niet ook de 'normale' variant te maken.
Je herkent de opgaven waar een Super variant van is aan dit teken
Als je op dit teken klikt, dan ga je naar de Super variant.
In de Super variant staat dit teken
Als je daarop klikt, ga je weer terug naar de gewone opgave.
De Super opgaven staan ook steeds bij elkaar onder aan iedere paragraaf.
Paragrafen
In dit thema gaan we aan de slag met oppervlakte.
In de volgende paragrafen leer je om de oppervlakte van verschillende figuren uit te rekenen en complexere figuren te verdelen in eenvoduige figuren waarvan je de oppervlakte makkelijker kunt uitrekenen. Je leert dat rechthoeken met dezelfde omtrek niet altijd dezelfde oppervlakte hebben en om de oppervlakte en omtrek van een cirkel uit te rekenen.
De oppervlakte van een parallellogram bereken je zo.
Kies een van de zijden als basis. Neem de bijbehorende hoogte van het parallellogram.
De oppervlakte is \(basis × hoogte\).
Oppervlakte van een driehoek
De oppervlakte van een driehoek bereken je zo.
Kies een van de zijden als basis. Neem de bijbehorende hoogte van de driehoek
De oppervlakte is \(\frac{1}{2}\) × basis × hoogte.
Omtrek en oppervlakte van een cirkel
De omtrek van een cirkel met straal \(r\) is \(2πr\).
De oppervlakte van een cirkel met straal \(r\) is \(πr^2\).
Oppervlakte van een vlieger
De oppervlakte van een vlieger is het halve product van de diagonalen.
Oppervlakte van een veelhoek
De oppervlakte van een veelhoek kun je vaak berekenen door hem in driehoeken te verdelen.
Voorbeeld De oppervlakte van het trapezium is: \(\frac{1}{2}⋅4⋅9+\frac{1}{2}⋅4⋅5=28\).
Thema-opdracht
Wiskunde als kunst. We zien het overal om ons heen. Mondriaan is een van de bekendste voorbeelden hiervan. Maar kijk naar de logo’s van bedrijven om je heen en je ontdekt de meest bijzondere vormen.
Deze eindopdracht kijken we naar verschillende manieren om een vierkant gedeeltelijk in te kleuren.
Het arrangement Thema: Oppervlakte - 2V is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Dit thema is ontwikkeld door auteurs en medewerkers van de Wageningse Methode.
Fair Use
In de Stercollecties van VO-content wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Wat kan ik al?
Diagnostische toets "Oppervlakte"
Extra oefening Basis
Extra oefening Plus
Terugblik
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
De lengte van de dunne darm van de mens is ruim 5 meter en heeft een oppervlakte van 150 à 200 m2 (de grootte van een tennisveld). Dat hij toch in je buik past, komt doordat hij erg gekronkeld is. Ook is het oppervlak geen gladde buis, maar bestaat hij uit talloze plooien.
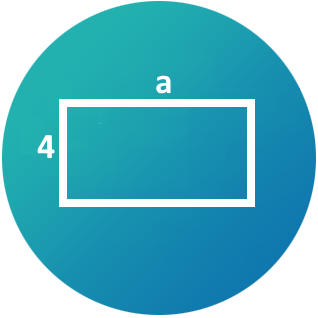In dit hoodstuk leren we hoe we de oppervlakte van diverse figuren kunnen bepalen. Je weet al hoe je de oppervlakte en de omtrek van een rechthoek kan berekenen.
Het thema Cijfers in orde bestaat uit de volgende onderdelen:
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
In dit thema gaan we aan de slag met oppervlakte.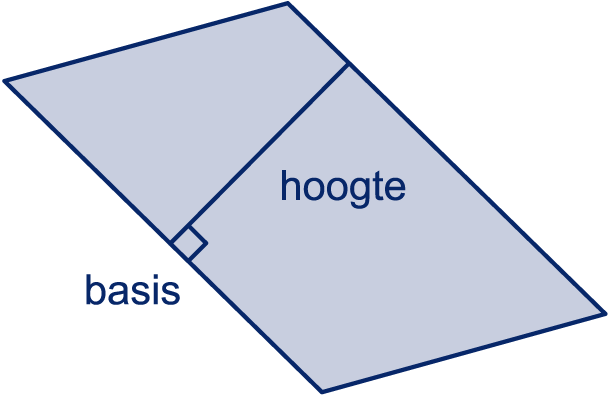
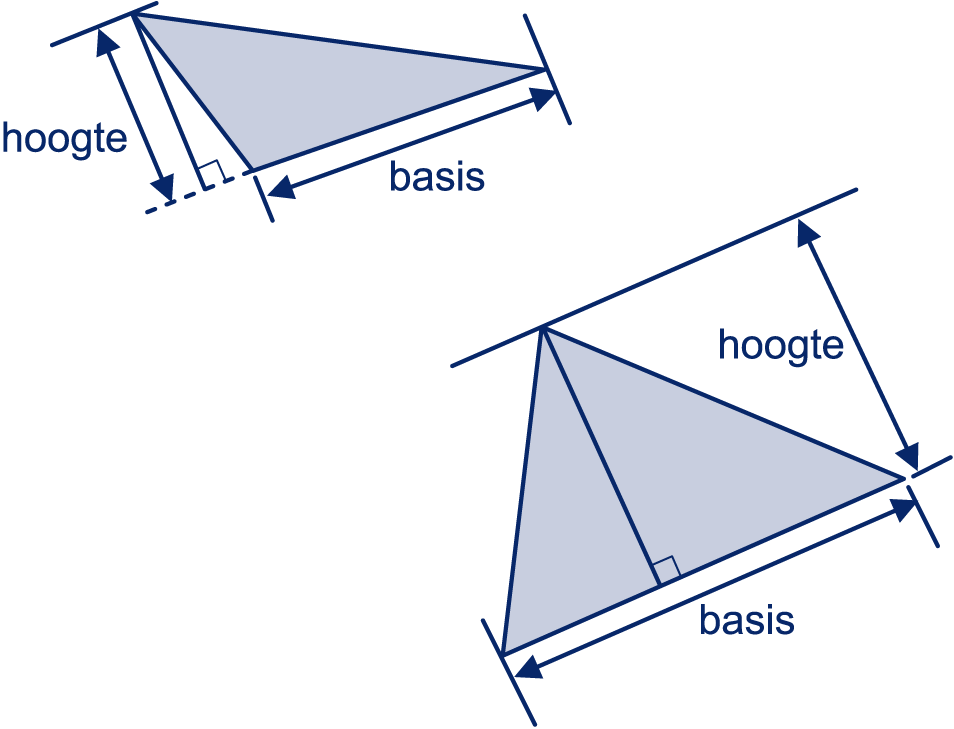driehoek bereken je zo.
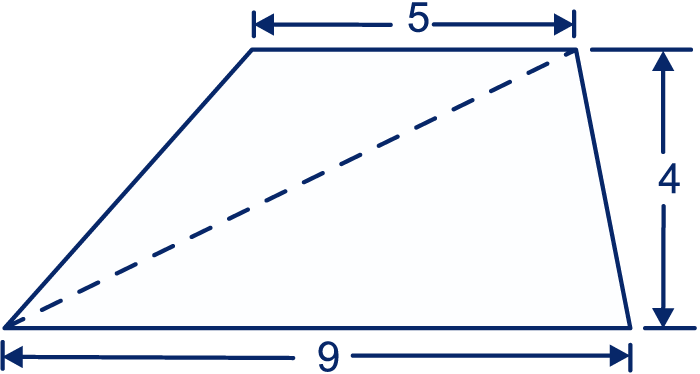De oppervlakte van het trapezium is:
Je gaat nu een aantal gevarieerde opgaven maken waarin je kunt laten zien of je de geleerde stof uit de voorgaande paragrafen beheerst.
Je ziet hier twee Extra oefeningen. Je hoeft er maar één te doen.
