Het arrangement Thema 13 Symmetrie - vwo2 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 07-08-2025 11:18:52
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Dit thema is ontwikkeld door auteurs en medewerkers van de Wageningse Methode.
Fair Use
In de Stercollecties van VO-content wordt gebruik gemaakt van beeld- en filmmateriaal dat beschikbaar is op internet. Bij het gebruik zijn we uitgegaan van fair use. Meer informatie: Fair use
Mocht u vragen/opmerkingen hebben, neem dan contact op via de helpdesk VO-content.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Rearrangeerbare lessenserie wiskunde stercollectie VO-content wiskunde vwo
- Leerniveau
- VWO 2;
- Leerinhoud en doelen
- Lengte, omtrek, oppervlakte en inhoud; Rekenen/wiskunde; Vormen en figuren; Redeneren in de (vlakke) meetkunde; Meten en meetkunde; Tekenen en construeren;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 13 uur 0 minuten
- Trefwoorden
- leerlijn, rearrangeerbare, vo-content


 Vouw een vierkant vel papier diagonaal doormidden. Vouw nu de ontstane driehoek weer doormidden.
Vouw een vierkant vel papier diagonaal doormidden. Vouw nu de ontstane driehoek weer doormidden. Het zijn allemaal open vragen. Die moet je dadelijk zelf eerlijk nakijken.
Het zijn allemaal open vragen. Die moet je dadelijk zelf eerlijk nakijken.

 Het thema Symmetrie bestaat uit de volgende onderdelen:
Het thema Symmetrie bestaat uit de volgende onderdelen: Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.
Voor een aantal opgaven in dit hoofdstuk is een Super variant beschikbaar.

 In dit thema gaan we aan de slag met de verschillende vormen van symmetrie.
In dit thema gaan we aan de slag met de verschillende vormen van symmetrie.


 Een figuur is spiegelsymmetrisch als hij een symmetrieas (=spiegelas) heeft: de delen aan weerszijden van de spiegelas passen precies op elkaar.
Een figuur is spiegelsymmetrisch als hij een symmetrieas (=spiegelas) heeft: de delen aan weerszijden van de spiegelas passen precies op elkaar. Een figuur is puntsymmetrisch als hij is opgebouwd door een deel te spiegelen in een punt, het zogenaamde symmetriepunt.
Een figuur is puntsymmetrisch als hij is opgebouwd door een deel te spiegelen in een punt, het zogenaamde symmetriepunt.
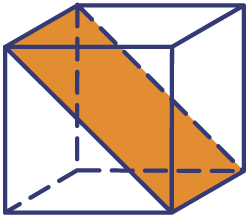
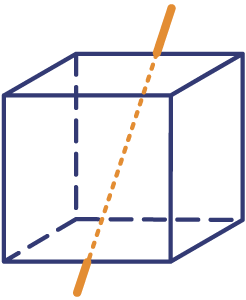
 In deze opdracht gaan jullie aan de slag met het combineren van symmetrievormen. Jullie gaan je verdiepen in patronen die je kan maken met één tegel.
In deze opdracht gaan jullie aan de slag met het combineren van symmetrievormen. Jullie gaan je verdiepen in patronen die je kan maken met één tegel.



