De wereld om je heen zit vol met wiskunde, je moet het alleen wel herkennen.
Wist jij dat wanneer je over een brug fietst deze is ontworpen met behulp van wiskunde.
De vorm van de brug, hoeveel kilo de brug kan dragen, hoeveel verkeer er per uur over de brug heen kan rijden, wat het kost om de brug te bouwen en te onderhouden zijn allemaal zaken die met wiskunde te maken hebben.
In hoofdstuk 6 van dit jaar hebben we het weer over verbanden. Dit jaar heb je al leren werken met lineaire verbanden. Het onderwerp verbanden komt ieder jaar meerdere keren terug. We herhalen telkens je kennis over verbanden en breiden dit elk hoofdstuk een klein beetje uit.
In hoofdstuk 6 herhalen we kort onze kennis over lineaire verbanden en leren we werken met kwadratisch verbanden. We leren een berekening maken bij een kwadratisch verband, een tabel tekenen en invullen en natuurlijk de grafiek bij de tabel tekenen. Ook leer je hoe je een vergelijking oplost bij een kwadratisch verband.
Leerdoelen
Leerdoelen bij hoofdstuk 6. Werken met kwadratische verbanden
Leerdoel
Beginnend
Op weg
Gevorderd
Expert
Voorrangregels
Ik kan een eenvoudige samengestelde rekenopgave oplossen in de vorm van
6 + 2 x 3 =
Ik kan een samengestelde rekenopgave met meer dan 2 stappen oplossen
3 x ( 2 + 6 ) : 12 =
Ik kan een samengestelde rekenopgave oplossen met kwadraten en wortels
32 + \(\sqrt{25} \) : (2 + 3)
Ik kan een samengestelde rekenopgave oplossen met machten, wortels en negatieve getallen.
-3 x 4 + (-2)4 : -\(\sqrt{16}\)
Formule bij een regelmatige tabel
Ik ken de vaste opbouw van een lineaire formule uit mijn hoofd opschrijven
Ik kan in een tabel het begingetal aflezen en ik kan de regelmaat in een tabel aangeven met boogjes
Ik kan de formule van een regelmatige tabel opschrijven. Ik gebruik hierbij de woorden begingetal en stapgrootte
Ik kan de regelmaat van een tabel controleren en wanneer de tabel regelmatig is hierbij de formule opschrijven.
Lineair verband
Ik begrijp wat een formule is met x en y.
Ik kan bij een lineaire formule een tabel maken. Ik gebruik een tabel met minimaal 3 punten
Ik kan bij een lineaire formule een tabel en een lijngrafiek tekenen in een assenstelsel.
Ik kan een lineaire vergelijking oplossen door deze met grafieken te tekenen en af te lezen
Kwadratisch verband
Ik herken een kwadratische formule aan het feit dat hier een kwadraat in zit.
Ik kan bij een kwadratische formule een tabel maken. Ik gebruik een tabel met 7 punten.
Ik kan bij een kwadratische formule en een tabel een parabool tekenen in een assenstelsel.
Ik kan een lijngrafiek en een parabool in één assenstelsel tekenen.
Kwadratisch verband toepassen
Ik kan bij een gegeven kwadratisch verband een berekening maken
Ik kan in een parabool één of meerdere punten aflezen
Lineaire vergelijking oplossen
Ik herken een lineaire formule aan de vaste opbouw
Ik kan een eenvoudige balans oplossen in de vorm
37 = 3x + 7
Ik kan een vergelijking oplossen in de vorm
2x + 10 = 4x + 2
Ik kan een vergelijking met negatieve getallen oplossen in de vorm
-5x + 10 = 3x -14
Niet-lineaire vergelijking oplossen
Ik herken niet lineaire vergelijkingen aan hun vorm.
Ik kan een inklemschema tekenen en begrijp dat bij inklemmen er minimaal 3 pogingen gevraagd worden
Ik kan een eenvoudige niet-linaire vergelijking oplossen ket inklemmen (één antwoord vinden)
Ik kan een complexe niet-linaire vergelijking oplossen met inklemmen (twee mogelijke antwoorden vinden)
Werkbladen
Ben jij de werkbladen kwijt geraakt?
Geen paniek, hieronder kun je ze nog eens uitprinten.
De voorkennis bij hoofdstuk 6 sluit aan bij het hoofdstuk over lineaire formules.
In de voorkennis herhalen we het werken met de rekenvolgorde.
In hoofdstuk 2 heb je kennis gemaakt met een lineair verband. We hebben geleerd dat een lineair verband een vaste opbouw heeft, dat je bij een lineair verband een tabel en een grafiek kunt maken.
Andersom hebben we ook geleerd hoe je bij een regelmatigetabel een formule kunt maken.
Hoe maak je ook al weer berekeningen wanneer de formule gegeven is en hoe teken je een tabel en een grafiek bij een gegeven formule. Dit zijn de onderwerpen van paragraaf 2.
Binnen het VMBO leer je werken met verschillende soorten verbanden. Er zijn namelijk niet alleen situaties die passen bij een lineair verband, er zijn allerlei soorten situaties. Er zijn dus ook allerlei soorten verbanden die we de komende tijd en jaren met elkaar gaan behandelen.
Hieronder zie je welke verbanden we de komende tijd gaan leren herkennen.
Lineaire verband.
Kwadratisch verband.
Exponentiël verband.
Machtsverband.
Wortelverband.
Omgekeerd evenredig verband.
Periodiek verband.
In deze paragraaf leer je hoe je werkt met kwadratische verbanden.
In de gemengde opgaven oefen je de verschillende onderdelen van het hoofdstuk nog eens door elkaar heen. Dit is een goede voorbereiding op de komende toets.
Merk je dat je bepaalde opgaven nog niet helemaal beheerst, lees dan eerste de uitleg in de paragraaf waar de opgave bij hoort, kijk het instructiefilmpje en probeer de opgave nog een keer.
Lukt het nog niet om de opgave zelfstandig op te lossen vraag dan hulp. Stel vragen in de lessen of vraag aan een leerling uit de klas of hij/zij je kan helpen met het zetten van de juiste stappen.
Je kunt deze d-toets gebruiken om na te gaan of je alle onderdelen van het hoofdstuk voldoende beheerst.
Zijn er paragrafen die je moeilijk vond, of wijst deze d-toets uit dat je delen nog niet beheerst, oefen de betreffende paragrafen dan nog eens.
Lees de uitleg van de paragraaf waar je veel foutjes in maakt, maak per stukje uitleg telkens 2 a 3 opgaven. Net als met sporten zul je moeten trainen, oefenen, zweten, fouten maken en het nog eens op nieuw moeten proberen. Wie weet waar hij/zij moeite mee heeft en dit veel oefent komt goed voorbereid naar de toets.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Aan het eind van het hoofdstuk, vlak voor de repetitie kun je nog eens testen of je alle onderdelen van het hoofdstuk begrepen hebt. Je maakt daarvoor de herhalingsopgaven.
Doe dit serieus, zo krijg je een goed beeld van de paragrafen die goed gaan en paragrafen waar je echt nog een keer extra mee moet gaan oefenen.
Ben je vergeten hoe bepaalde opgaven uitgewerkt moeten worden, blader dan terug in je schrift, neem de bijbehorende paragraaf voor je en bekijk de uitleg nog eens.
Als laatste redmiddel zijn er nog korte instructiefilmpje toegevoegd aan de herhaling.
Succes met de voorbereidingen op de komende toets.
In dit hoofdstuk heb je het volgende geleerd over kwadratische formules.
Je hebt ontdekt dat de tabel bij een kwadratische formule een evenwijdig figuur oplevert, de parabool. Dit kon een bergparabool zijn zoals hierboven is afgebeeld of een dalparabool.
Maak nu opgave 1, 2 en 3.
Vaste opbouw van een kwadratische formule.
we gaan de theorie over kwadratische formules een stuk uitbreiden. Je kunt namelijk aan de opbouw van de formule een aantal zaken afleiden.
Een kwadratische formule is altijd opgebouwd volgens het volgende principe.
y = ax2+ bx+ c.
Op de plek van de letters a, b en c kun je elk denkbaar getal invullen dus ook een breuk of een negatief getal.
Kijk maar:
y = ax2+ bx+ c
y = ax2+ bx+ c
y = 3x2- 2x+ 8.
y = -2x2+ 0,5x+ 2
In dit voorbeeld is:
In dit voorbeeld is:
voor a het getal 3 ingevuld 3x2
voor a het getal 3 ingevuld -2x2
voor b is het getal - 2 ingevuld - 2x
voor b is het getal - 2 ingevuld + 0,5x
voor c is het getal 8 ingevuld + 8
voor c is het getal 8 ingevuld + 2
Pas wel op, als je het getal 0 (nul) invult, dan valt het stukje weg! Het heeft dan namelijk geen waarde meer. kijk maar:
y = ax2+ bx+ c.
y = ax2+ bx+ c.
y = -2,5x2+ 2
y = 0,5x2+ 7x
In dit voorbeeld is:
In dit voorbeeld is:
voor a het getal 3 ingevuld -2,5x2
voor a het getal 3 ingevuld 0,5x2
voor b is het getal 0 ingevuld (is er niet)
voor b is het getal - 2 ingevuld + 07x
voor c is het getal 8 ingevuld + 2
voor c is het getal 8 ingevuld (is er niet)
Maak nu opdracht 4 en opdracht 5 Lees daarna de rest van de uitleg door.
Hoe bereken je de top van een parabool.
Bekijk onderstaande video
In deze video maak je kennis met de formule
Xtop = \(-b \over 2a\) voor Ytop voer je jouw gevonden xtop in de formule in.
Vindt je het nog wat onduidelijk? Hieronder staat nog een video waarin je ziet hoe je de coördinaten van de top van een parabool kunt berekenen
Maak nu opgave 6 t/m 10
Opgaven
..1.
Tabel bij een kwadratische formule
Maak bij onderstaande formules tabellen en vul deze in.
Y= -0,5X2 + 1
G = A2 – 4
..2.
Evenwijdige figuur
Leg uit hoe het komt dat je bij x = – 2 en bij x = 2 dezelfde antwoorden krijgt. Illustreer dit met een voorbeeld. (Maak een tabel en teken de grafiek of laat dit met berekeningen zien)
..3.
Grafieken tekenen
Teken in één assenstelsel de grafieken van y = 1x2 – 4x + 0 en y = –2x2 + 5 x + 3
* tip(maak eerst 2 tabellen gebruik hier in de getallen –2 tot en met 4)
Lees nu het tweede stukje uitleg, ga daarna verder met de opgaven hieronder.
..4.
formules vormen
y = ax2+ bx+ c
Schrijf steeds de bijbehorende kwadratische formule op. Vul in het bovenstaande functievoorschrift (formule) steeds op de juiste plaats de getallen in.
a = 2b = -3 en c = 2
a = –4b = 6 en c = –8
a = 3b = 0 en c = 4
a = –0,5b = 1,5 en c = 0
..5.
Formules vormen.
Waarom mag je voor het stukje ax2 nooit het getal nul invullen?
Lees nu eerst het laatste stukje van de uitleg. Ga daarna verder met de vragen hieronder.
..6.
Top van een parabool
Gegeven is de formule x2 + 4
Neem de tabel hieronder over en vul deze verder in
x
-3
-2
-2
0
1
2
3
y
8
13
Teken de grafiek die bij de tabel hoort.
Teken in de grafiek de symmetrie as
Reken de coördinaten top van de parabool na met de formule Xtop= \({-b \over 2a}\) en Ytop.
..7.
Top van een parabool
Gegeven is de formule -x2 + 4x
Neem de tabel hieronder over en vul deze verder in
x
0
1
2
3
4
5
y
0
4
Teken de grafiek die bij de tabel hoort.
Teken in de grafiek de symmetrie as
Reken de coördinaten top van de parabool na met de formule Xtop= \({-b \over 2a}\) en Ytop
..8.
Top van de parabool berekenen
Bereken de coördinaten van de top van de volgende parabolen
y = -2x2 + 28x + 8 .
y = 5x2 + 60x - 125 .
y = x2 - 12x + 4 .
y = 0,5x2 - 4x + 1
..9.
De brug over de Rijn bij Emmerich is met een lengte van 1228 meter de langste hangbrug van Duitsland. De afstand tussen de twee pylonen is 500 meter.
De kabel tussen de twee pylonen vormt bij benadering een dalparabool. De hoogte van de kabel van de brug boven het water kun je berekenen met de formule
hoogte kabel = 0,0005a2 – 0,2a + 70 Hierin is a de afstand gemeten vanaf de eerste pylon
Het wegdek is 62 meter boven boven het water.
Bereken de kleinste afstand tussen de kabel en het wegdek in hele meters volgens de formules. Schrijf je berekening op.
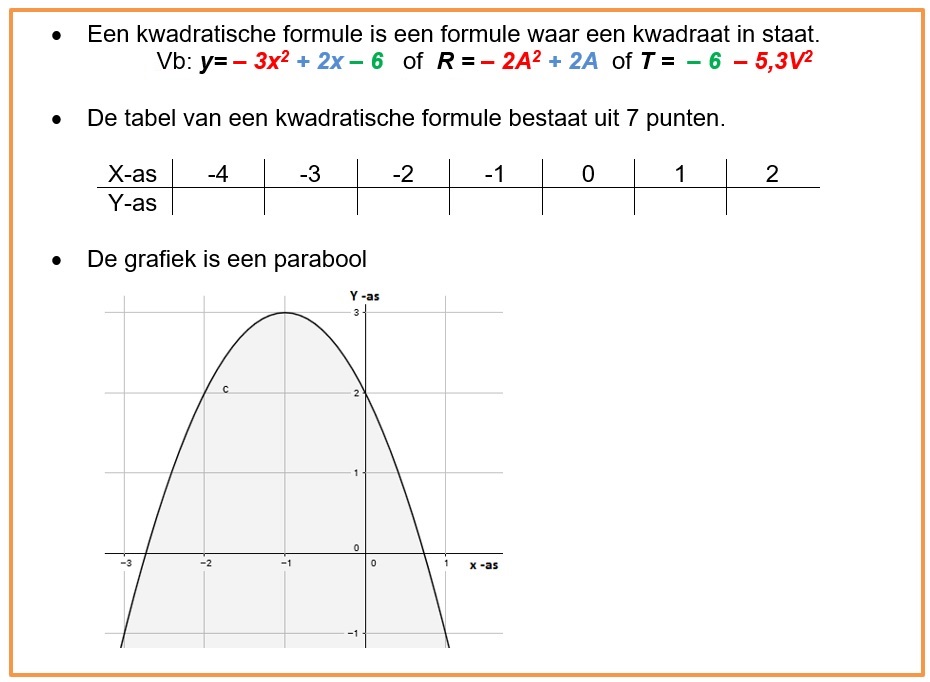
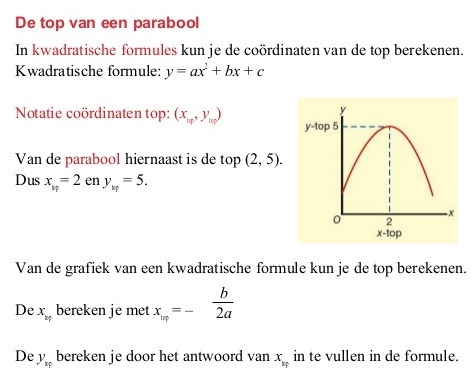
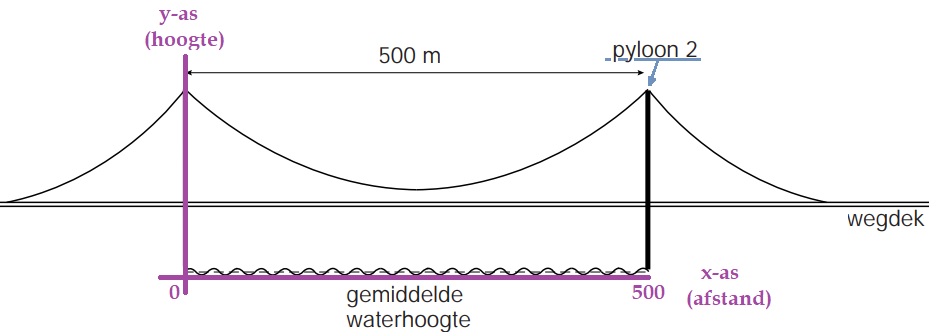
Het arrangement 2KGT H04 Kwadratische verbanden is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
D. Giessen
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-07-03 12:04:54
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Diagnostische toets
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
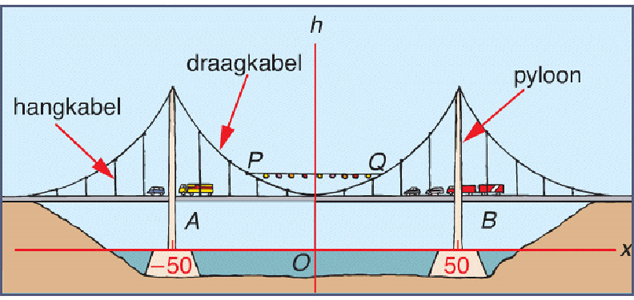Wist jij dat wanneer je over een brug fietst deze is ontworpen met behulp van wiskunde.
De voorkennis bij hoofdstuk 6 sluit aan bij het hoofdstuk over lineaire formules.
Hoe maak je ook al weer berekeningen wanneer de formule gegeven is en hoe teken je een tabel en een grafiek bij een gegeven formule. Dit zijn de onderwerpen van paragraaf 2.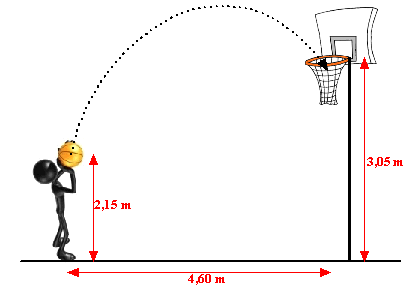
Binnen het VMBO leer je werken met verschillende soorten verbanden. Er zijn namelijk niet alleen situaties die passen bij een lineair verband, er zijn allerlei soorten situaties. Er zijn dus ook allerlei soorten verbanden die we de komende tijd en jaren met elkaar gaan behandelen.
In de vierde paragraaf van dit hoofdstuk werken we verder met kwadratische verbanden.
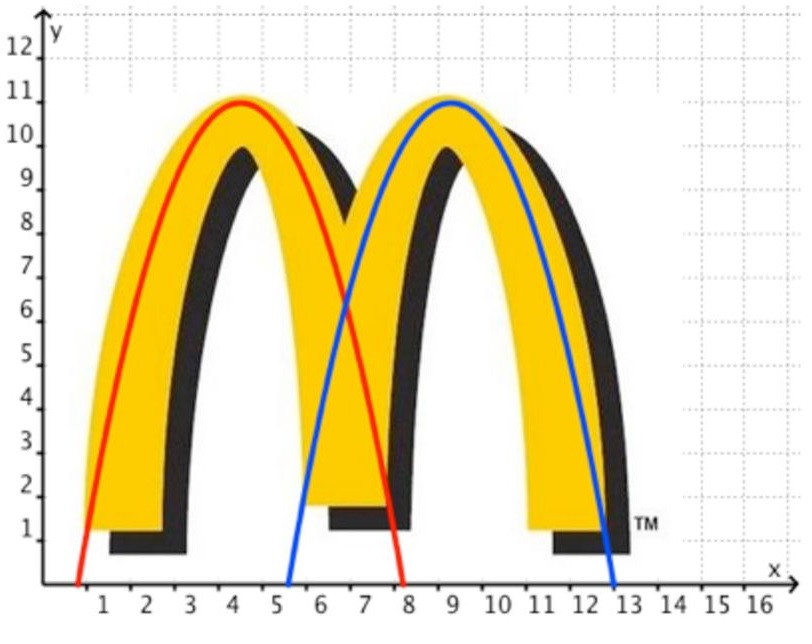In paragraaf 5 herhalen we onze kennis over de balansmethode en leren we hoe je een niet lineaire vergelijking kunt oplossen.
In de gemengde opgaven oefen je de verschillende onderdelen van het hoofdstuk nog eens door elkaar heen. Dit is een goede voorbereiding op de komende toets.
