Het arrangement 1KGT H05 Procenten en verhoudingen is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 02-07-2020 10:41:48
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Gebruikte Wikiwijs Arrangementen
Giessen, D.. (z.d.).
§2 Schaal en schaallijntjes
https://maken.wikiwijs.nl/152101/_2_Schaal_en_schaallijntjes

 Als je je fiets in een lagere versnelling zet, hoef je minder zwaar te trappen.
Als je je fiets in een lagere versnelling zet, hoef je minder zwaar te trappen. Aan het eind van dit hoofdstuk weet ik:
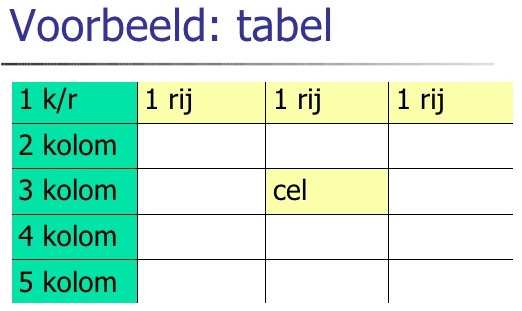
Aan het eind van dit hoofdstuk weet ik: De eerste paragraaf gaat over verhoudingstabellen.
De eerste paragraaf gaat over verhoudingstabellen.




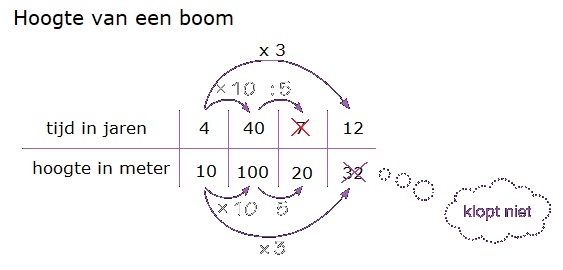
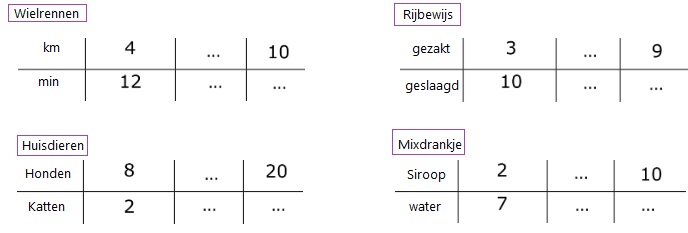
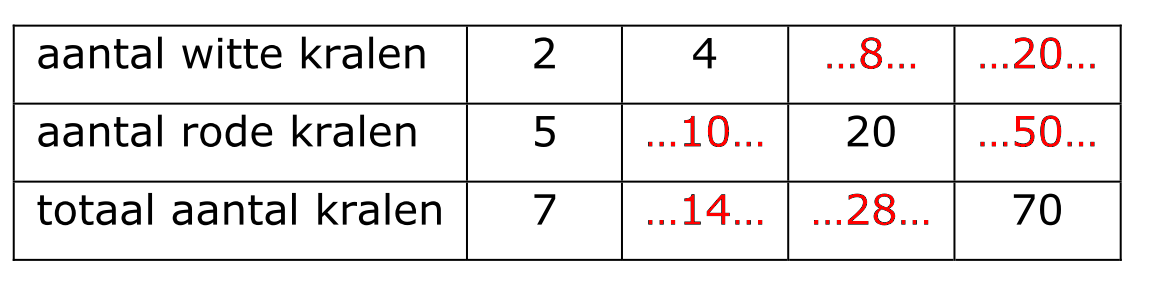
 In een doos met legostenen zitten in totaal 80 stenen.
In een doos met legostenen zitten in totaal 80 stenen.


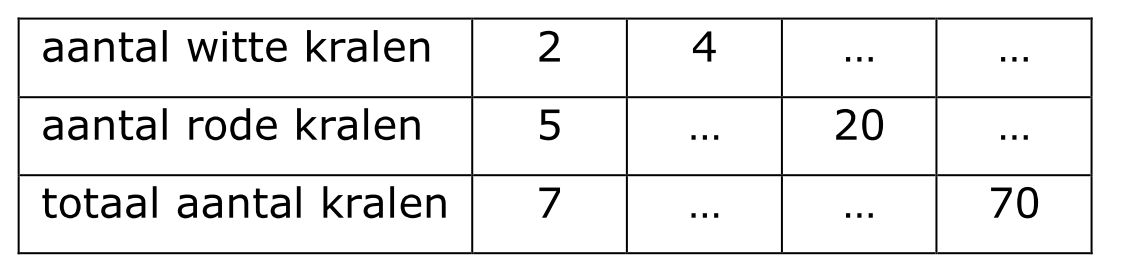
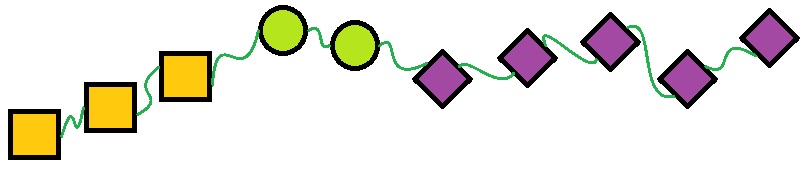 Suzhanna vindt het leuk om in haar vrije tijd kettingen te rijgen. Hiernaast zie je één van haar ontwerpen. De verhouding bij deze ketting is 3:2:5 (3 oranje, 2 groen, 5 paarse kralen.)
Suzhanna vindt het leuk om in haar vrije tijd kettingen te rijgen. Hiernaast zie je één van haar ontwerpen. De verhouding bij deze ketting is 3:2:5 (3 oranje, 2 groen, 5 paarse kralen.)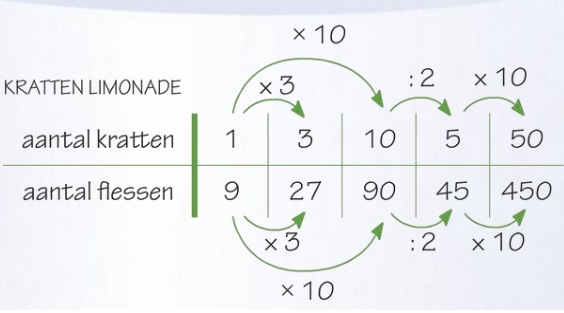
 Nathan heeft een volle tank benzine. Dat is 40 liter. Hiermee kan hij 800 km rijden.
Nathan heeft een volle tank benzine. Dat is 40 liter. Hiermee kan hij 800 km rijden.


 De naam van de paragraaf zegt het al.
De naam van de paragraaf zegt het al.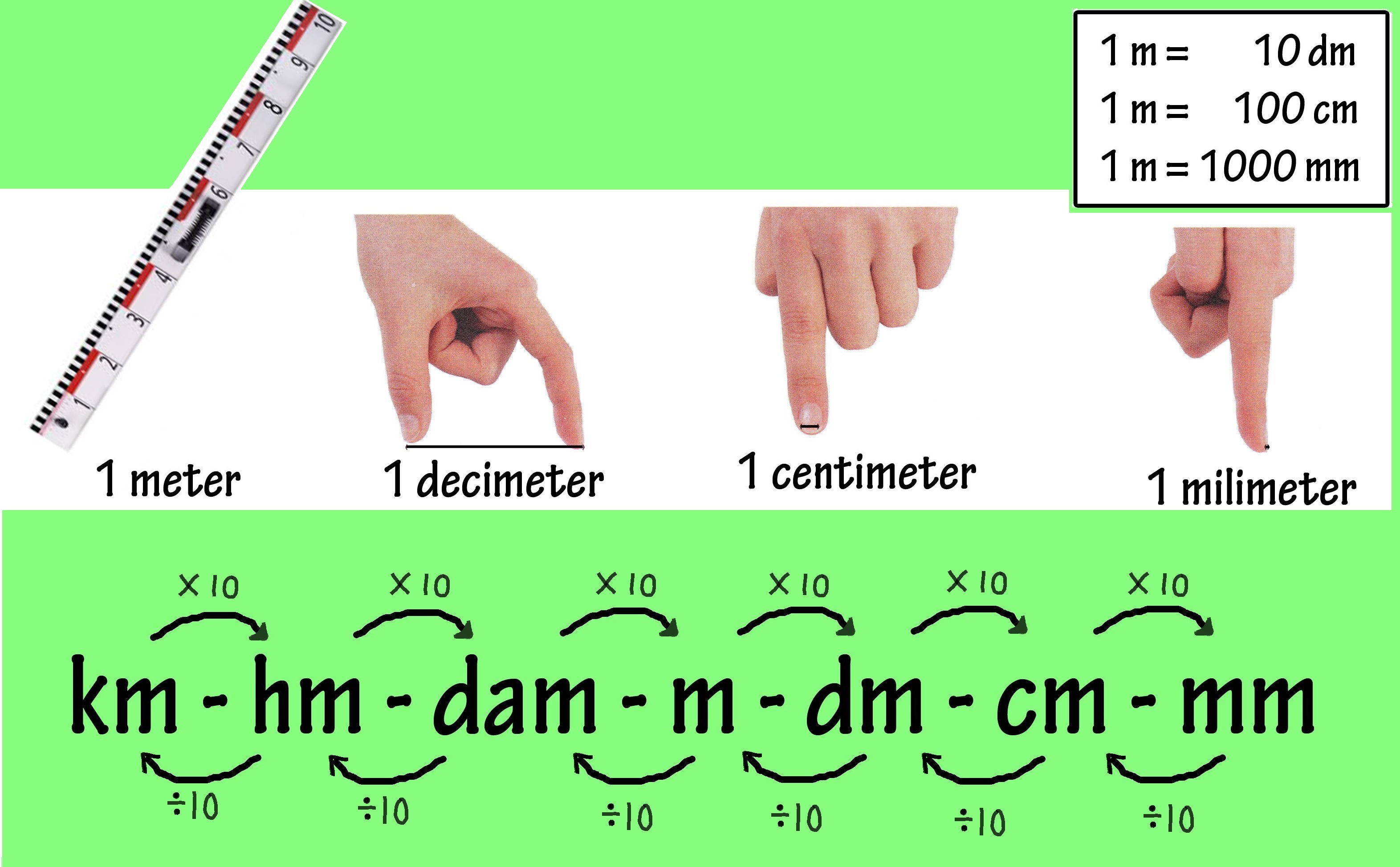
 Op het plaatje hiernaast zie je het Unity.
Op het plaatje hiernaast zie je het Unity.%20-%20kopie-750x750.jpg) Wie later in de mode en ontwerpwereld aan de slag wil krijgt ook te maken met werken op schaal.
Wie later in de mode en ontwerpwereld aan de slag wil krijgt ook te maken met werken op schaal.

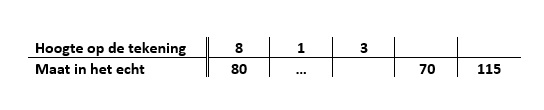
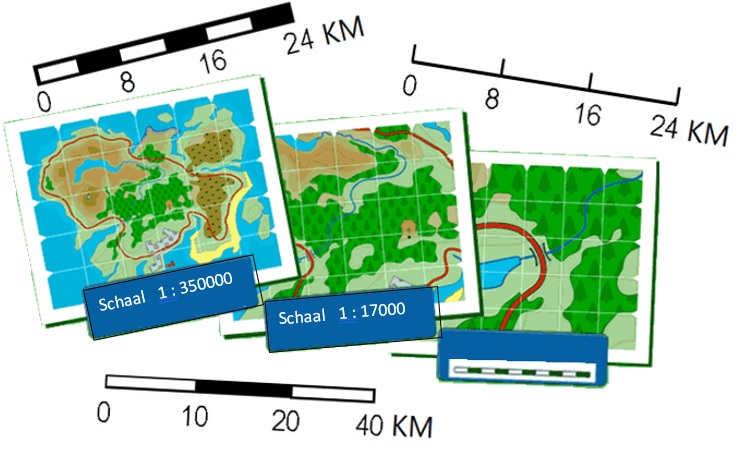
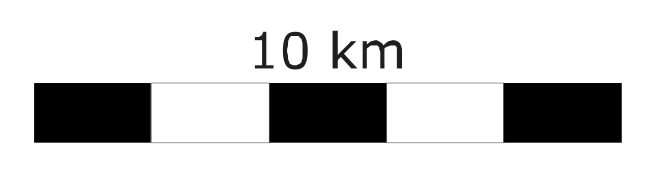 Hiernaast staat een schaallijntje. Het schaallijntje bestaat uit 5 blokjes, de schaallijn is dus 5 cm lang. In werkelijkheid komt dat overeen met een afstand van 10 km.
Hiernaast staat een schaallijntje. Het schaallijntje bestaat uit 5 blokjes, de schaallijn is dus 5 cm lang. In werkelijkheid komt dat overeen met een afstand van 10 km. 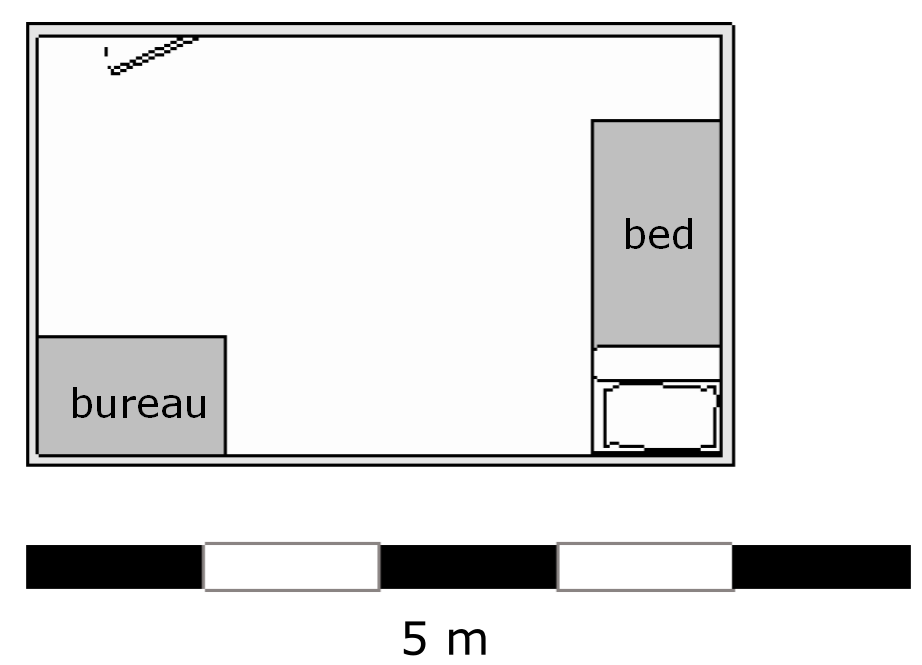
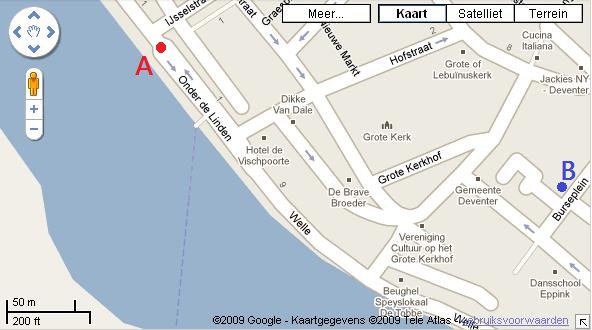
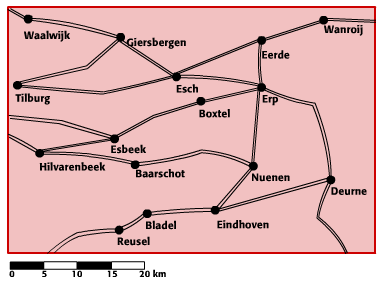 Bekijk het kaartje hiernaast, de kaart staat ook op je werkblad.
Bekijk het kaartje hiernaast, de kaart staat ook op je werkblad.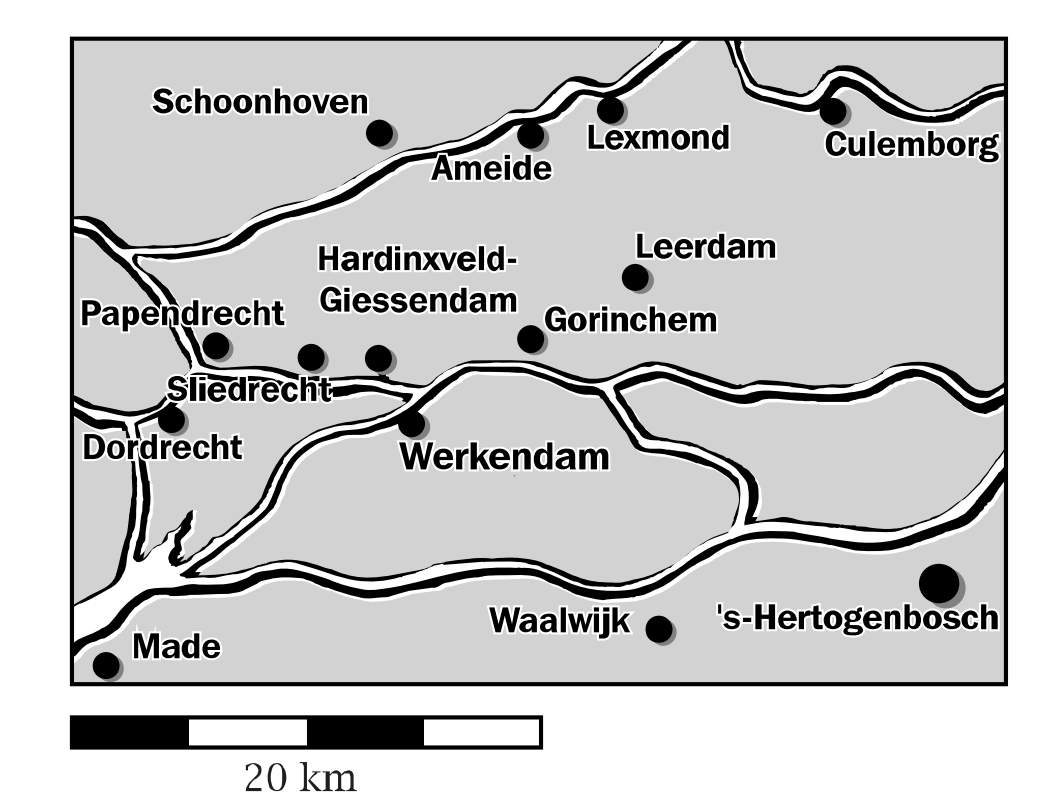
 In de derde paragraaf gaat het over het berekenen van een gemiddelde snelheid.
In de derde paragraaf gaat het over het berekenen van een gemiddelde snelheid.
 Orlando wil graag fit blijven, daarom gaat Orlando vaak een stukje hardlopen in het park.
Orlando wil graag fit blijven, daarom gaat Orlando vaak een stukje hardlopen in het park. Rick is 12 minuten geleden met de fiets van huis gegaan.
Rick is 12 minuten geleden met de fiets van huis gegaan. Op 16 augustus 2009 liep Usain Bolt het wereldrecord op de 100m sprint.
Op 16 augustus 2009 liep Usain Bolt het wereldrecord op de 100m sprint.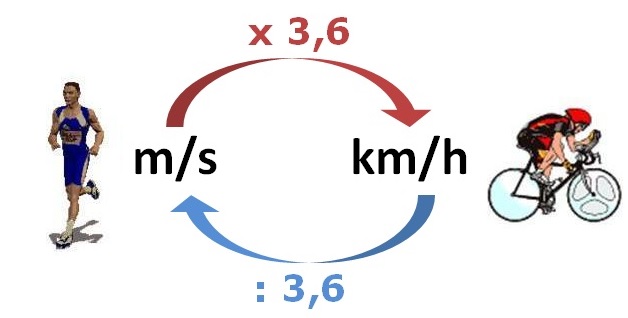
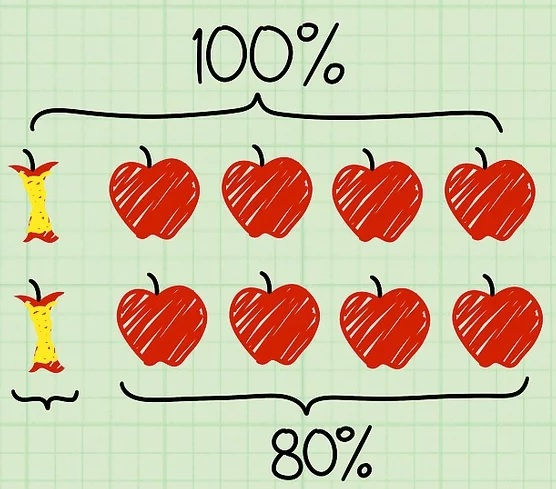 Ieder jaar komt het onderwerp 'werken met percentages '(opgaven met procenten)terug. Je herhaalt je kennis die je de afgelopen jaren hebt opgedaan en krijgt natuurlijk ook weer een klein stukje nieuwe kennis aangeboden.
Ieder jaar komt het onderwerp 'werken met percentages '(opgaven met procenten)terug. Je herhaalt je kennis die je de afgelopen jaren hebt opgedaan en krijgt natuurlijk ook weer een klein stukje nieuwe kennis aangeboden. Net als bij een breuk is een procent gewoon een deel van een geheel. Bij een taart die in 3 stukken is verdeeld, heten de stukken één derde,
Net als bij een breuk is een procent gewoon een deel van een geheel. Bij een taart die in 3 stukken is verdeeld, heten de stukken één derde, 
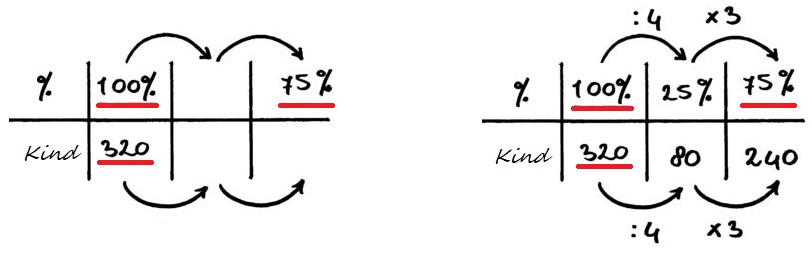

 Onder studenten is een enquete gehouden.
Onder studenten is een enquete gehouden. Een pizzabakker heeft bij gehouden welke extra ingrediënten mensen op hun pizza bestellen. In het diagram hiernaast zie je welke ingrediënten er zoal extra besteld worden.
Een pizzabakker heeft bij gehouden welke extra ingrediënten mensen op hun pizza bestellen. In het diagram hiernaast zie je welke ingrediënten er zoal extra besteld worden. Dit is de tweede paragraaf over procenten. Je kunt op dit moment dus al één type opgave oplossen met behulp van een tabel. Nu kijken we naar een ander type opgave, namelijk wanneer je moet berekenen welk deel (het percentage) er bekend is.
Dit is de tweede paragraaf over procenten. Je kunt op dit moment dus al één type opgave oplossen met behulp van een tabel. Nu kijken we naar een ander type opgave, namelijk wanneer je moet berekenen welk deel (het percentage) er bekend is.
 In de herfst en wintermaanden regent het vaker dan in de zomermaanden.
In de herfst en wintermaanden regent het vaker dan in de zomermaanden.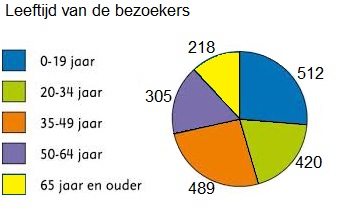
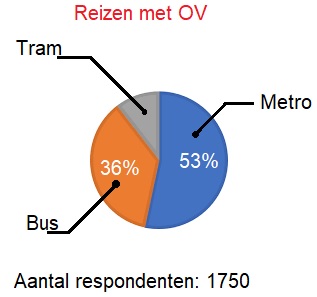
 Hiernaast zie je de top 3 vervoersmiddelen om mee op vakantie te gaan. Er ontbreken er natuurlijk ook nog een aantal, denk bijvoorbeeld aan de boot, fiets of bus.
Hiernaast zie je de top 3 vervoersmiddelen om mee op vakantie te gaan. Er ontbreken er natuurlijk ook nog een aantal, denk bijvoorbeeld aan de boot, fiets of bus. Neem voordat je begint aan de gemengde opgaven even de tijd om na te denken over de paragrafen die je gemaakt hebt. Welke paragraaf vond je lastig? In welke paragraaf heb je de meeste antwoorden niet helemaal goed berekend? Lees de uitleg van die twee paragrafen nog eens door voordat je begint
Neem voordat je begint aan de gemengde opgaven even de tijd om na te denken over de paragrafen die je gemaakt hebt. Welke paragraaf vond je lastig? In welke paragraaf heb je de meeste antwoorden niet helemaal goed berekend? Lees de uitleg van die twee paragrafen nog eens door voordat je begint Het is kortingsvierdaagse bij je favoriete gameshop.
Het is kortingsvierdaagse bij je favoriete gameshop.
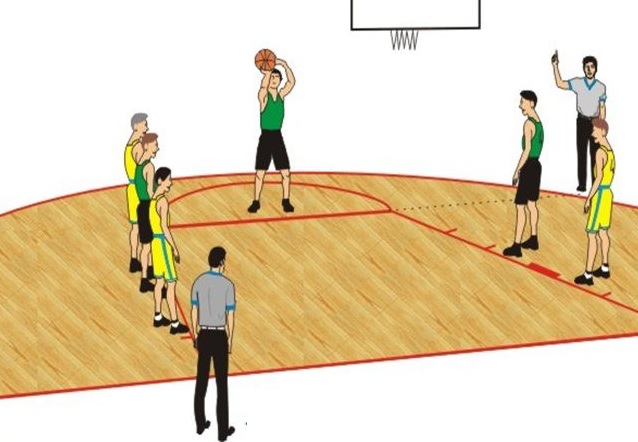 Tijdens het schieten van vrije worpen gooit Mohammed er 7 van de 12 in.
Tijdens het schieten van vrije worpen gooit Mohammed er 7 van de 12 in.