Symmetrie
Inleiding
 1H08 Inleiding ...............................................................................................
1H08 Inleiding ...............................................................................................
Bij veel kastelen is er de mogelijkheid om een bezoek te brengen aan de kasteeltuin. Na een wandeling door de tuin rusten ze dan graag uit op het mooie terras om de vijver.
Hiernaast zie je aantal kasteeltuinen. Hoe komt het, denk je, dat veel mensen die kasteeltuinen zo mooi vinden? Het heeft vast te maken met de planten en de bloemen die je in de tuinen kunt vinden, maar er is meer. Veel mensen vinden de tuinen mooi vanwege de vaste patronen die zich regelmatig herhalen.
Zou jij zo'n tuin kunnen ontwerpen?
Als je een kasteeltuin wilt ontwerpen, moet je iets weten over symmetrie en over vlakke figuren. En dat ga jij nu juist leren in dit thema.
Leerdoelen
 1H08 Leerdoelen ...........................................................................................
1H08 Leerdoelen ...........................................................................................
Aan het eind van dit thema:
- weet je wat lijnsymmetrie is;
- kun je in een lijnsymmetrische figuur de symmetrieas aanwijzen;
- kun je een figuur spiegeln in een lijn
- weet je wat draaisymmetrie is;
- kun je van een draaisymmetrische figuur het draaicentrum en de kleinste draaihoek bepalen;
- weet je van de bekendste vlakke figuren of ze symmetrisch zijn;
- weet je wat een motief en een patroon is
- kun je symmetrie gebruiken om een patroon te maken;
- weet je wat schuifsymmetrie is
Verdieping:
- kun je in figuren F-hoeken en Z-hoeken herkennen en gebruiken
Eindproduct
 1H08 Eindproduct ............................................................................................
1H08 Eindproduct ............................................................................................
Ter afsluiting van het thema zijn er verschillende opdrachten.
In ieder geval ga aan de slag met je eigen portretfoto en maak je daarmee een opdracht over lijnsymmetrie.
De andere opdracht gaat over het ontwerpen van een symmetrisch terras.
Mogelijk heeft je docent ook nog een opdracht buiten voor je.
Werkbladen
1H08 Werkbladen Symmetrie .................................................................................... ..............
..............
Bij veel opgaven heb je werkbladen nodig.
Die krijg je van de docent, maar je kunt ze ook zelf downloaden en afdrukken.
Paragrafen
Lijnsymmetrie
1H08.1 Paragraaflink ........................................................................................................
De eerste paragraaf van dit hoodstuk gaat over Lijnsymmetrie.
Lijnsymmetrie noemen we ook wel spiegelsymmetrie of vouwsymmetrie
Klik hier om de paragraaf te openen:
Lijnsymmetrie
Draaisymmetrie
 1H08.2 Paragraaflink ......................................................................................................
1H08.2 Paragraaflink ......................................................................................................
De tweede paragraaf van dit hoofdstuk gaat over Draaisymmetrie.
Klik hier om de paragraaf te openen:
Draaisymmetrie
Vlakke figuren en symmetrie
1H08.3 Paragraaf link ..............................................................................................................
De derde paragraaf van dit hoofdstuk gaat over vlakke figuren en symmetrie.
Klik hier om de paragraaf te openen:
Vlakke figuren en symmetrie
Patroon en motief
1H08.4 Paragraaf link ...........................................................................................................
De vierde paragraaf van dit hoofdstuk gaat over patroon en motief.
Klik hier om de paragraaf te openen:
Patroon en motief
D-toets
D-toets
1H08.D D-toets ................................................................................................
Je sluit het thema 'Symmetrie' af met de eindtoets.
Succes!
Extra opgaven
Opgaven
1H08.E Opgaven .............................................................................................................
| 1 |
 |
Verkeersborden |
Hieronder zie je tien verkeersborden.
 |
 |
 |
 |
 |
| I |
II |
III |
IV |
V |
| |
|
|
|
|
 |
 |
 |
 |
 |
| VI |
VII |
VIII |
IX |
X |
- Welke verkeersborden zijn lijnsymmetrisch?
- Welke verkeersborden zijn draaisymmetrisch?
- Welke verkeersborden zijn lijnsymmetrisch en draaisymmetrisch?
- teken de symmetrieas(-sen) van de de lijnsymmetrische verkeersborden.
- Bereken de kleinste draaihoek van de draaisymmetrische verkeersborden
| 2 |
 |
Logo's |
Bekijk de logo’s hieronder.





I II III IV V





VI VII VII IX X
- Welke logo's zijn lijnsymmetrisch?
- Welke logo's zijn draaisymmetrisch?
- Welke logo's zijn lijnsymmetrisch en draaisymmetrisch?
- Teken de symmetrieas(-sen) van de de lijnsymmetrische logo's.
- Bereken de kleinste draaihoek van de draaisymmetrische logo's
| 3 |
|
Driehoek in een assenstelsel |
- Teken in een assenstelsel de punten K( 5,4), M(3, -4) en L(2,1).
Teken  KLM.
KLM.
- Spiegel
 KLM in de y-as. Zet bij de hoekpunten de letters K', L' en M'.
KLM in de y-as. Zet bij de hoekpunten de letters K', L' en M'.
| 4 |
 |
Drie maal spiegelen |
- Teken in een assenstelsel de punten D(2,-1), E(3, -4) en F(5, -2).
Teken  DEF.
DEF.
- Spiegel
 DEF in de y-as. Noem de beeldfiguur D'E'F'.
DEF in de y-as. Noem de beeldfiguur D'E'F'.
- Spiegel
 DEF in de x-as. Noem de beeldfiguur D''E''F''.
DEF in de x-as. Noem de beeldfiguur D''E''F''.
- Met welke spiegeling kun je nu een derde beeldfiguur krijgen links-boven in je assenstelsel?
Maak ook hiermee de beeldfiguur.
| 5 |
|
Rechthoek in een assenstelsel |
- Teken in een assenstelsel de punten A(-2, -3), B(2, -1) C(3, 5) en D(-1, 3).
Teken vierhoek ABCD.
- Wat voor vierhoek is ABCD?
 Spiegel vierhoek ABCD in de y-as. Noem de beeldfiguur A'B'C'D'.
Spiegel vierhoek ABCD in de y-as. Noem de beeldfiguur A'B'C'D'.
| 6 |
 |
Spiegelen in een lijn |
Je ziet hiernaast rechthoek ABCD getekend.
De rechthoek wordt gespiegeld in lijn m.
Teken het beeld van rechthoek ABCD. Gebruik je geodriehoek.
Noem de beeldfiguur A’B’C’D’.

| 7 |
|
Spiegelen in een assenstelsel |
- Teken in een assenstelsel de punten A(3,0) en B(0,5).
Teken lijnstuk AB.
- Spiegel lijnstuk AB in de y-as. Het beeldpunt van A noem je A'.
- Teken nu ook lijnstuk AA'.
Je hebt nu in het assenstelsel de  A'AB getekend.
A'AB getekend.
- Welke twee zijden van deze driehoek zijn even lang?
- Wat voor driehoek is
 A'AB ?
A'AB ?
- Spiegel nu
 A'AB in de x-as.
A'AB in de x-as.
- Wat voor vierhoek is A'B'AB ?
Uitwerkingen
1H08.E Uitwerkingen ..................................................................................................................
- De borden I, II, IV, VIII, IX en X zijn lijnsymmetrisch.
Bord V lijkt dat ook, maar als je heel goed kijkt zul je zien dat de 3 net niet lijnsymmetrisch is. Heb je wel een symmetrieas getekend, dan mag je die hier nu goed rekenen, maar je ziet dat het eigenlijk best heel nauw komt!
- De borden III, VI, VII, VIII, IX en X zijn draaisymmetrisch
- De borden VIII, IX en X zijn lijnsymmetrisch en draaisymmetrisch.
- Bord X heeft oneindig veel symmetrieassen, die kun je dus niet tekenen

- Bord X heeft geen kleinste draaihoek; die kun je om elke hoek draaien.
Kleinste draaihoeken:
III: 360o : 3 = 120o
VI: 360o : 2 = 180o
VII: 360o : 3 = 120o
VIII: 360o : 4 = 90o
IX: 360o : 3 = 120o
- De logo's II, II, IV, VI, VII, VIII en X zijn lijnsymmetrisch.
- De logo's I, II, IV, V, VIII, IX en X zijn draaisymmetrisch.
- De logo's II, IV, VIII en X zijn lijnsymmetrisch en draaisymmetrisch.

- Kleinste draaihoeken
I: 360o : 3 = 120o
II: 360o : 3 = 120o
IV: 360o : 2 = 180o
V: 360o : 3 = 120o
VIII: 360o : 18 = 20o
IX: 360o : 2 = 180o
X: 360o : 5 = 72o

- b. c.

- Je kunt D'E'F' spiegelen in de x-as of D''E''F'' spiegelen in de y-as.
[ je kunt ook DEF draaien om de oorsprong over 180o ]
- c.

- ABCD is een parallellogram

- b. c. e.

- A'AB is een gelijkbenige driehoek
- A'B'AB is een ruit
Herhalingsopgaven
Opgaven
1H08.H Intro ................................................................................................................
Bij deze opgaven horen werkbladen. Die krijg je van je docent, maar je kunt ze ook hier downloaden:
1H08.H Opgaven ...........................................................................................................
Sleep in de volgende applet de figuren uit het bovenste veld naar het juiste getal in het onderste veld.
Klik op onderstaande knop om de applet te starten:

| |
|
WERKBLAD: Extra oefeningen 1 |
Spiegel de figuren steeds in de spiegelas s:

Spiegel driehoek ABC in lijn l. Noem de beeldfiguur A’B’C’.

Spiegel rechthoek ABCD in lijn m. Noem de beeldfiguur A’B’C’D’.

Geef in ondertstaande figuren het draaicentrum aan met een duidelijke stip en bereken de kleinste draaihoek van elke figuur.
Als er symmetrieassen zijn, teken die dan ook allemaal.


| |
|
WERKBLAD: Extra oefeningen 2 |
Bepaal van onderstaande verkeersborden of ze draaisymmetrisch zijn.
Zo ja, geef dan het draaicentrum aan en bereken de kleinste draaihoek.
Als er symmetrieassen zijn, teken die dan.




| 2 |
|
Driehoek in een assenstelsel |
- Teken in een assenstelsel de punten A(-3, -2), B(3, -2) en C(0, 4).
- Teken ∆ABC.
- Wat voor soort driehoek is ∆ABC?
- Geef met tekentjes aan welke onderdelen van de driehoek gelijk zijn.
- Spiegel de driehoek in de x-as. Noem de beeldfiguur A’B’C’.
| 3 |
|
Vierhoek in een assenstelsel |
- Teken in een assenstelsel de punten A(-6, 0), B(-3, -4), C(2, -4) en D(5,0).
- Teken vierhoek ABCD
- Wat voor soort vierhoek is ABCD?
- Teken in vierhoek ABCD met rood de symmetrieas.
- Spiegel vierhoek ABCD in de x-as
| |
|
WERKBLAD: Extra oefeningen 3 |
Je ziet hier een aantal patronen.
Kleur in elk patroon één motief.



Je ziet hier een plaatje van een kralenketting.
Teken het motief van deze ketting.
Wat is het motief in de ketting die hiernaast is afgebeeld?
Je ziet hier een deel van een kralenketting.
Kleur de overgebleven witte kralen in met de juiste kleuren.
Uitwerkingen
1H08.H Uitwerkingen Werkblad 1 ..........................................................................................................






1H08.H Uitwerkingen Werkblad 2 ..........................................................................................

∆ABC is een gelijkbenige drfiehoek.

Vierhoek ABCD is een trapezium

1H08.H Uitwerkingen Werkblad 3 ...........................................................................................






Alle uitleg bij elkaar
Lijnsymmetrie
|
Bekijk de figuur hiernaast.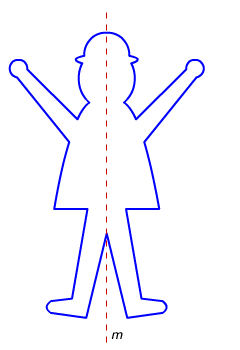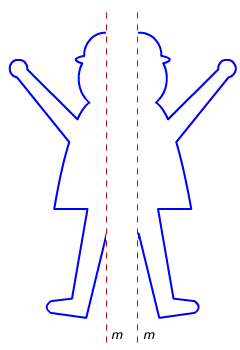
Lijn m deelt de figuur in twee stukken.
Die twee stukken zijn elkaars spiegelbeeld.
De stippellijn is de symmetrieas van de figuur.
De figuur is lijnsymmetrisch.
Lijnsymmetrie noemen we ook wel:
vouwsymmetrie of spiegelsymmetrie.
De symmetrieas noemen we ook wel:
vouwlijn, spiegellijn of spiegelas.
|
|
Driehoek ABC wordt gespiegeld in lijn m.
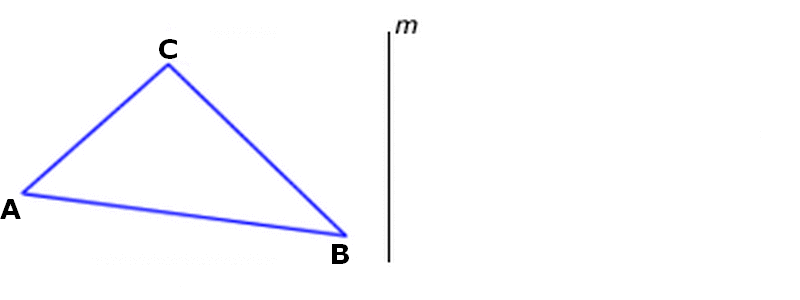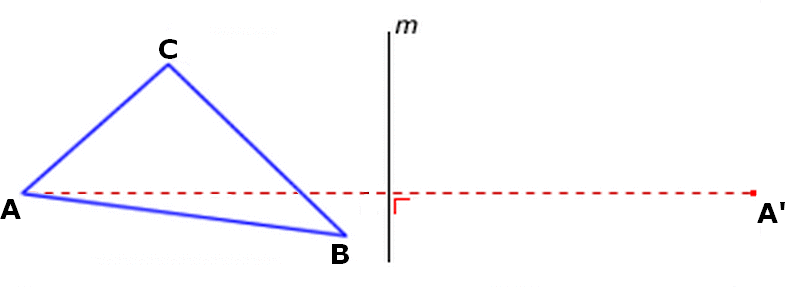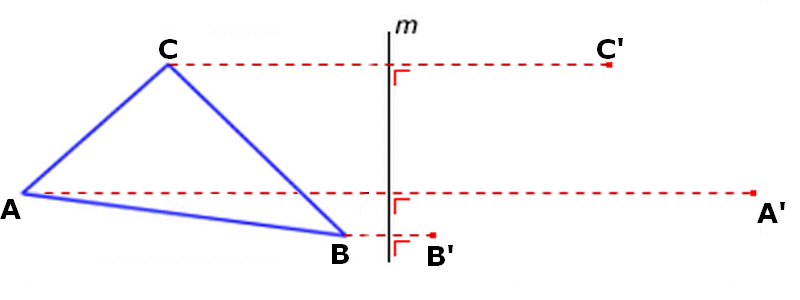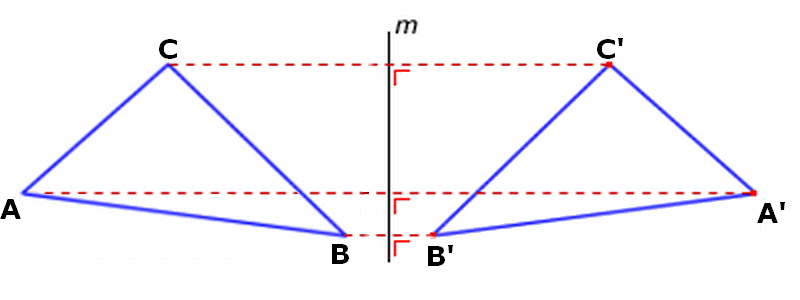
De punten A en A' liggen even ver van de spiegellijn m.
De punten B en B' liggen even ver van de spiegellijn m.
De punten C en C' liggen even ver van de spiegellijn m.
Driehoek ABC noem je het origineel.
Driehoek A'B'C' noem je het beeld.
|
Bekijk de logo's hieronder.
Al deze logo's zijn lijnsymmetrisch.
Sommige hebben zelfs meerdere symmetrieassen.
   |
|
In de natuur kom je regelmatig lijnsymmetrische figuren tegen. Zie onderstaande voorbeelden.
  
|
Draaisymmetrie
|
Bekijk de figuur.

Als je de figuur 90° draait om het centrum C dan lijkt het of er niets veranderd is.
De figuur is een voorbeeld van een draaisymmetrisch figuur.
De draaihoek is 90°.
|
Bekijk de logo's hieronder.


Al deze logo's zijn draaisymmetrisch.
Bij beide logo's is de draaihoek aangegeven.
Het eerste logo kun je in 3 stappen passend ronddraaien. De draaihoek is dan 360o : 3 = 120o
Het tweede logo kun je in 2 stappen passend ronddraaien. De draaihoek is 360o : 2 = 180o
Als je naar buiten kijkt kom je regelmatig draaisymmetrische figuren tegen.
Kijk maar naar de voorbeelden hieronder.


Vlakke figuren en symmetrie
|
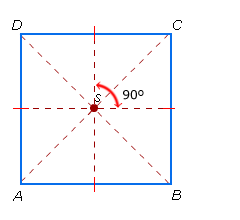 Vierkant Vierkant
- AB = BC = CD = DA
- Een vierkant heeft vier symmetrieassen.
- Een vierkant is draaisymmetrisch.
De draaihoek is 90°.
|
|
Rechthoek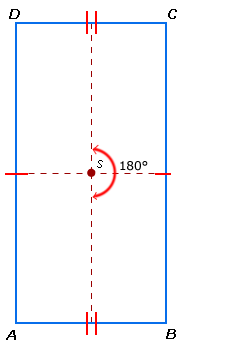
- AB = CD en BC = AD
- Een rechthoek heeft twee symmetrieassen.
- Een rechthoek is draaisymmetrisch.
De draaihoek is 180°.
|
|
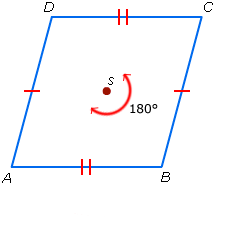 Parallellogram Parallellogram
- AB = CD en AD = BC
- Een parallellogram is niet lijnsymmetrisch.
- Een parallellogram is draaisymmetrisch.
De draaihoek is 180°.
|
|
Vlieger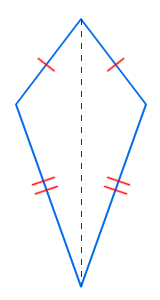
- AB = AD en BC = CD
- Een vlieger heeft één symmetrieas.
- Een vlieger is niet draaisymmetrisch.
|
|
Ruit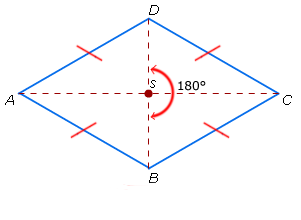
- AB = AD en BC = CD
- Een ruit heeft twee symmetrieassen.
- Een ruit is draaisymmetrisch.
De draaihoek is 180o.
|
|
Gelijkzijdige driehoek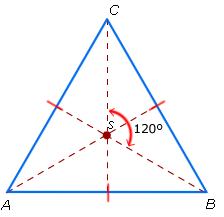
- AB = AC = BC
- Een gelijkzijdige driehoek heeft drie symmetrieassen.
- Een gelijkzijdige driehoek is draaisymmetrisch
De draaihoek is 120°.
|
|
Gelijkbenige driehoek
- AC = BC
- Een gelijkbenige driehoek heeft één symmetrieas.
- Een gelijkbenige driehoek is niet draaisymmetrisch
|
Patroon en motief
|
Als een figuur bestaat uit een herhaling van steeds dezelfde stukjes, dan is er sprake van schuifsymmetrie*.

De figuur heeft dan een patroon dat is opgebouwd uit een aantal herhalingen van een motief.
Het motief is een zo klein mogelijk stukje waarmee je het hele patroon kunt maken.
* als je meer wilt weten over schuifsymmetrie, bekijk dan het onderdeel Verdieping aan het einde van dit hoofdstuk.
|
|
In de figuur hieronder zie je een voorbeeld van een patroon en een bijbehorend motief:
patroon motief
 
|
|
Vaak kun je het motief ook op een andere manier kiezen, bijvoorbeeld:
 of of  of of 
Met elk van deze motieven kun je, door steeds te schuiven, het gehele patroon maken.
|
|
Een eenvoudiger voorbeeld is onderstaand tegelplateau:

Het motief is dan één zeskantige tegel.
|
|
Ingewikkelder kan ook:
patroon mogelijk motief:
  
|
Herken je de schuifsymmetrie in de volgende figuren?
 
Deze tegelpatronen vind je in Rome, in de kerk "Santa Maria in Cosmedin", bij de "Bocca Della Verità"
Kijk hier voor een foto via Google Streetview
|
Verdieping
Schuifsymmetrie
1H08.5 Paragraaflink ...........................................................................................................
De verdiepingsparagraaf van dit hoofdstuk gaat over Schuifsymmetrie en evenwijdige lijnen
Klik hier om de paragraaf te openen:
Schuifsymmetrie II
Thema-opdracht I
Vooraf
1H08.TI Themaopdracht .........................................................................................................
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je niet meer dan 1 lesuur nodig.
Voor deze opdracht krijg je van je docent een strip met foto's van jezelf.
Het werkblad bij deze opdracht krijg je van je docent, maar kun je ook hier downloaden:
Stap 1
Bij deze opdracht ga je aan de slag met een drietal foto's.
Twee foto's zijn normaal afgedrukt, de derde in spiegelbeeld.
Zie het voorbeeld hieronder:

De eerste foto knip je uit en plak je op je uitwerkingenblad.
Stap 2
De tweede en derde foto moet je doorknippen, maar wel zo, dat je zo goed
mogelijk het gezicht middendoor knipt: midden over kin, mond, neus,
voorhoofd, ...
Hieronder zie je hoe dat met de tweede en de derde foto gedaan is:

Omdat het gezicht schuin op de foto staat, is hier de foto schuin doorgeknipt, zodat het gezicht precies middendoor gedeeld is!
Stap 3
Nu komt het echte puzzelwerk:
Neem de linkerhelft van foto 2 en de rechterhelft van foto 3 en leg die zo tegen
elkaar dat weer één gezicht ontstaat.

Stap 4
Daarna moet je hetzelfde kunstje uithalen met de rechterhelft van foto 2 en de
linkerhelft van foto 3:

Stap 5
Als het gelukt is van de tweede en de derde foto de juiste helften bij elkaar te vinden, dan mag je die op je uitwerkingenblad plakken.
Twijfel je nog?
Vraag dan hulp aan je docent!
Als de foto's zijn opgeplakt, beantwoord dan ook de vragen op je werkblad.

Alles klaar?
Inleveren maar!
Thema-opdracht II
Vooraf

Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je 2 lesuren nodig. Je maakt samen met een klasgenoot een ontwerp voor een symmetrisch terras. Jullie berekenen ook de oppervlakte van het terras.
Benodigheden
Stap 1
Stap 1
Bekijk het volgende filmpje uit de serie 'Wat en waar is wiskunde?'.
In het filmpje zie je hoe ze een symmetrische versie van het beroemde schilderij de 'Mona Lisa' maken.
Je kunt ook zelf een symmetrisch portret maken. Dat kan bijvoorbeeld in het computerprogramma Paint.
Bekijk onderstaand filmpje:
Natuurlijk mag je met een foto van je eigen gezicht in Paint een mooi kunstwerkje maken.
Stap 2

Stap 2
Jullie gaan beginnen met het maken van het eindproduct: een symmetrisch terras rond een vijver in de kasteeltuin. Download het lege ontwerp voor een terras. Op het lege ontwerp staat een plattegrond van een vijver. De ruimte er omheen kun je gebruiken voor het terras.
Voor het ontwerp mogen jullie verschillende soorten tegels gebruiken (vierkant, rechthoek, driehoek, parallellogram, ruit, vlieger). Jullie mogen ook verschillende kleuren gebruiken (grijs, zwart, rood, beige).
Natuurlijk zorgen jullie er voor dat het terras symmetrisch blijft!
Stap 3

Stap 3
Jullie moeten ook de oppervlakte van het terras uitrekenen. Bepaal van alle verschillende tegels die jullie hebben gebruikt de oppervlakte. Bepaal ook de oppervlakte van het hele terras. Schrijf de berekening van de oppervlakte van het terras op jullie ontwerp (eventueel op de achterkant).
Klaar en tevreden?
Laat het ontwerp van het terras en de berekening van de oppervlakte beoordelen door jullie docent.

 1H08 Inleiding ...............................................................................................
1H08 Inleiding ............................................................................................... 1H08 Werkbladen
1H08 Werkbladen



















 Vierkant
Vierkant
 Parallellogram
Parallellogram





