Welkom! Ik ben student-docent en volg de opleiding voor leraar wiskunde. Ik heb voor jullie een digitale les gemaakt van het boek Moderne Wiskunde, Hfst 8-2, 10e editie. Ik heb deze digitale les zo goed mogelijk opgezet, in hoop dat jullie zo ver mogelijk kunnen komen. Een digitale les echter, is geen vervanging voor een normale les.
Vooral met het onderdeel meetkunde (waar dit onderwerp onder valt), kan een digitale les wat lastiger zijn. Door de beperkingen in Wikiwijs, kan ik bijvoorbeeld geen tabellen invoegen. Bij het uitrekenen van de stelling van Pythagoras is dit erg vervelend. Ik verwacht dat jullie zelf op kladpapier die tabel kunnen maken. Deze tabel is een belangrijk hulpmiddel hiervoor. Bewaar je uitwerkingen goed. De opgaven die je maakt komen uit dezelfde paragraaf (en hoofdstuk) en kun je dus terugvinden, om ze thuis nog een keer te maken voor de eindtoets van het hele hoofdstuk.
Dit hoofdstuk gaat over het berekenen van de oppervlakte van een parallellogram. Dit is een bijzonder mooi figuur in de wiskunde, met bijzondere eigenschappen. Deze bijzondere eigenschappen gaan jullie leren in deze les.
Ik heb deze les met een gemiddelde moeilijkheidsgraad van het theorieboek opgezet. Zo je het dan nog te makkelijk vindt, kan je zelf de 'extra-oefeningen', zoals 'basis', 'gemengd' of 'complex' maken uit het Moderne Wiskunde boek. Zo je het te moeilijk vindt, kijk dan vooral de filmpjes nog een keer extra.
Deze les wordt afgesloten met een eindtoets. Je mag pas de eindtoets gaan maken wanneer je de oefentoets 1 en 2 goed kan maken. Deze eindtoets is alleen van deze paragraaf en niet van heel het hoofdstuk.
Aan de linkerkant van het scherm staan 'knoppen'. Je kan hiermee snel terugspringen in de digitale les. Normaal gesproken klik je om door te gaan op de pijl rechts onderaan de pagina en ga je door naar de volgende bladzijde
Ik verwacht dat het jullie lukt! Zo jullie vragen hebben, twijfel niet, raadpleeg jullie (onmisbare) docent!
Ik wens jullie heel veel succes!
M. vd Nieuwendijk
Lesdoel hfst 8-2 Wat is de oppervlakte van een parallellogram?
Wat moet je kennen?
•Wat is een parallellogram?
•Wat is de formule voor het oppervlak van het parallellogram.
Wat moet je kunnen?
•De formule goed kunnen toepassen en de oppervlakte van het parallellogram kunnen berekenen.
Aandachtsrichter
Bron: Wikimedia Commons; Gelabeld voor niet-commercieel hergebruik, inclusief aanpassing.
Het gele figuur is gescheiden in twee figuren d.m.v. een rode lijn. Hoe heten deze gele figuren afzonderlijk?
De twee gele figuren aan elkaar vormen één figuur. Hoe heet dit figuur?
(Geef hieronder antwoord, klik op het rondje en druk op 'controleer')
Oprakelen voorkennis 1
Wat is de oppervlakte van een driehoek?
(Type in het venster hieronder de ontbrekende woorden op de stippellijntjes en zet er 'x' tussen en druk op 'controleer')
Oprakelen voorkennis 2
Wat is een parallellogram?
Bron: mathplanet.com; Gelabeld voor niet-commercieel hergebruik, inclusief aanpassing.
•Een parallellogram is een vierhoek waarbij de tegenover elkaar liggende zijden evenwijdig én even lang zijn.
•Tegenover elkaar liggende hoeken zijn even groot.
Let op! Omdat de overstaande hoeken even groot zijn geldt altijd: de evenwijdige zijden zijn even lang in een parallellogram!
Wanneer het figuur een parallellogram wordt genoemd, moet je aanemen dat de bovenstaande eigenschappen gelden voor het figuur.
Wat is de ‘basis’ en de ‘hoogte’ in een parallellogram?
De hoogte staat ALTIJD loodrecht op de basis!
Let op het rechthoeksteken! Deze is altijd precies 90 0 , dus loodrecht.
Bron: Moderne Wiskunde, Hfst 8-2, deel 2havo/vwo, 10 editie
De 'hoogte' kan ook verstopt staan
Let op! De 'hoogte' staat altijd loodrecht op de 'basis' (of op de 'zijde' daarvan).
De 'hoogte' kan ook wel eens aangegeven staan 'buiten' het parallellogram. Het rechthoeksteken staat daar dan ook bij (zo herken je het). Je mag die 'hoogte' dan verschuiven richting het parallellogram of 'in' het parallellogram!
Copyright 2018, M.W. v.d. Nieuwendijk
Definitie oppervlakte parallellogram
Voor de oppervlakte van een parallellogram geldt:
Oppervlakte = basis x hoogte
Of korter gezegd: A = b x h
Bron: Moderne Wiskunde, Hfst 8-2, deel 2havo/vwo, 10 editie
Het arrangement Parallellogram- oppervlakte berekenen is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Auteur
Marcel Nieuwendijk
Je moet eerst inloggen om feedback aan de auteur te kunnen geven.
Laatst gewijzigd
2020-03-20 15:52:42
Licentie
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
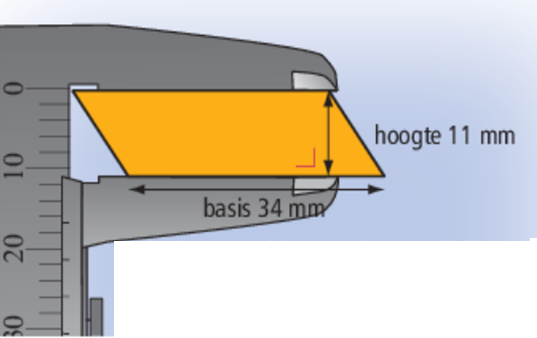
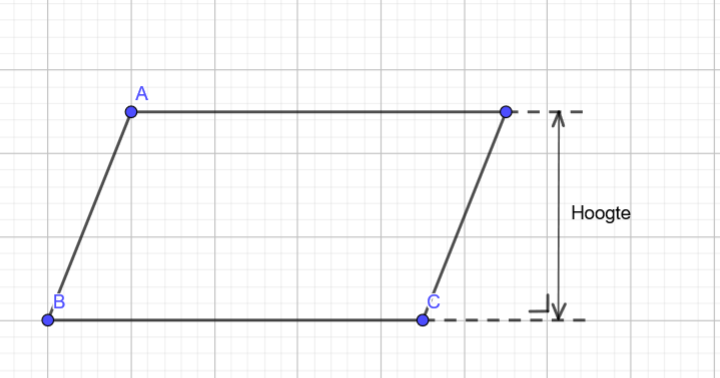
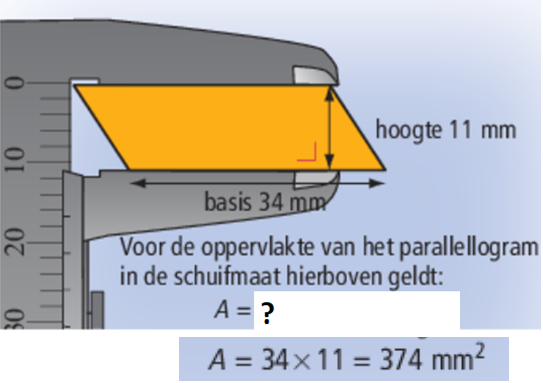
Hoe bereken je de oppervlakte van een parallellogram?
Leerniveau
VSO;
HAVO 2;
Leerinhoud en doelen
Lengte, omtrek, oppervlakte en inhoud;
Vaktaal meetkundige figuren en symbolen;
Rekenen/wiskunde;
Rekenen in de meetkunde;
Vormen en figuren;
Meten en meetkunde;
Tekenen en construeren;
Voorbeeld 1-videoclip- Copyright 2018, M.W. v.d. Nieuwendijk
