Het arrangement 2 Kader-Mavo is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 03-08-2023 15:23:14
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Deze methode is samengesteld door Dhr. J. Vriends. Voor vragen of opmerkingen kunt u contact opnemen met Dhr. Vriends (docent/ontwikkelaar wiskunde).
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- Rearrangeerbare stercollectie wiskunde voor leerjaar 2 VMBO KGT van Stichting VO-content, aangepast door docenten van 't R@velijn. De stercollectie is ontwikkeld op basis van de kerndoelen basisvorming en de door de SLO ontwikkelde inhoud- en leerdoelspecificaties voor het vak wiskunde. Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO.
- Leerniveau
- VMBO gemengde leerweg, 2; VMBO kaderberoepsgerichte leerweg, 1; VMBO kaderberoepsgerichte leerweg, 2; VMBO theoretische leerweg, 1; VMBO gemengde leerweg, 1; VMBO theoretische leerweg, 2;
- Leerinhoud en doelen
- Rekenen/wiskunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Studiebelasting
- 100 uur 0 minuten
- Trefwoorden
- arrangeerbare, arrangeerbare leerlijn, hoofdarrangement, leerlijn, rearrangeerbaar, rearrangeerbare, vo-content
Bronnen
Gebruikte Wikiwijs Arrangementen
VO-content - Leerlijnen. (2025).
Wiskunde vmbo-kgt12
Wiskunde Ravelijn. (z.d.).
H13.1 Kijklijnen en kijkhoeken
https://maken.wikiwijs.nl/109322/H13_1_Kijklijnen_en_kijkhoeken
Wiskunde Ravelijn. (z.d.).
K2 H14 Vergelijkingen
Wiskunde Ravelijn. (z.d.).
K2 H17 Machten en wortels
Wiskunde Ravelijn. (z.d.).
K2 H18 omtrek en oppervlakte
https://maken.wikiwijs.nl/109487/K2_H18_omtrek_en_oppervlakte
Wiskunde Ravelijn. (z.d.).
K2 H19 Liniaire verbanden
Wiskunde Ravelijn. (z.d.).
K2 H20 Verhoudingen en procenten
https://maken.wikiwijs.nl/109489/K2_H20_Verhoudingen_en_procenten
Wiskunde Ravelijn. (z.d.).
K2 H21 Statistiek en kans
Wiskunde Ravelijn. (z.d.).
K2 H22 doorsnede en inhoud
Wiskunde Ravelijn. (z.d.).
K2 H23 niet-liniair verband
https://maken.wikiwijs.nl/109492/K2_H23_niet_liniair_verband
Wiskunde Ravelijn. (z.d.).
K2 H24 Stelling van Pythagoras
https://maken.wikiwijs.nl/109493/K2_H24_Stelling_van_Pythagoras
Wiskunde Ravelijn. (z.d.).
Parallellogram en driehoek vmbo-kgt12
https://maken.wikiwijs.nl/119466/Parallellogram_en_driehoek_vmbo_kgt12


 't Ravelijn is een middelbare school in Steenbergen voor mavo en voorbereidend MBO
't Ravelijn is een middelbare school in Steenbergen voor mavo en voorbereidend MBO






 Inleiding
Inleiding
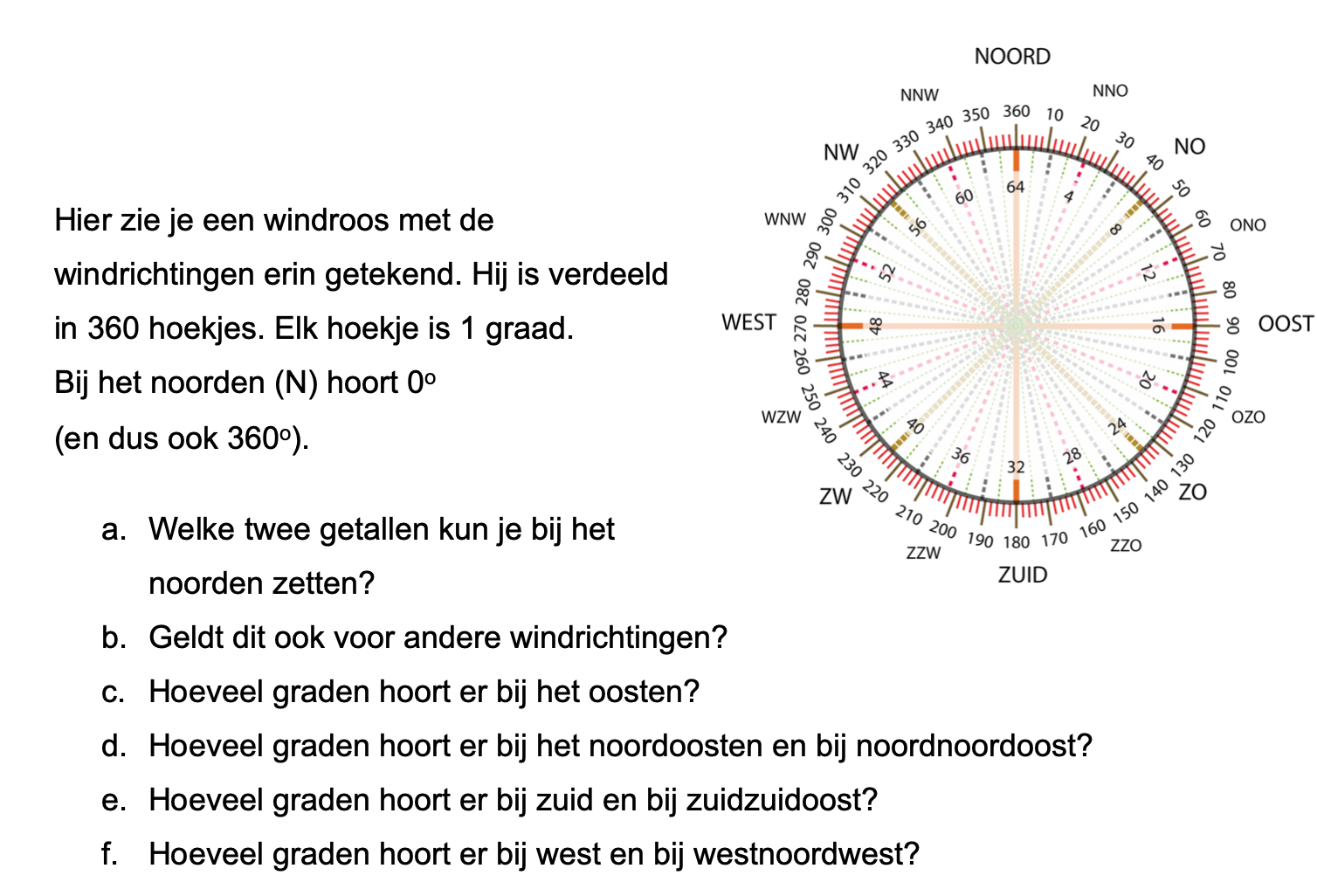











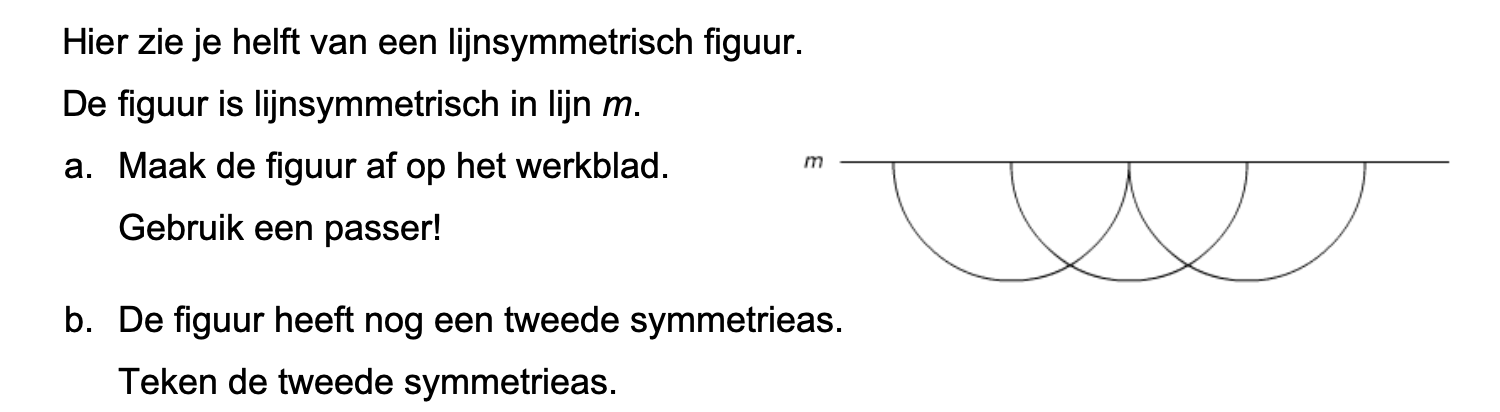
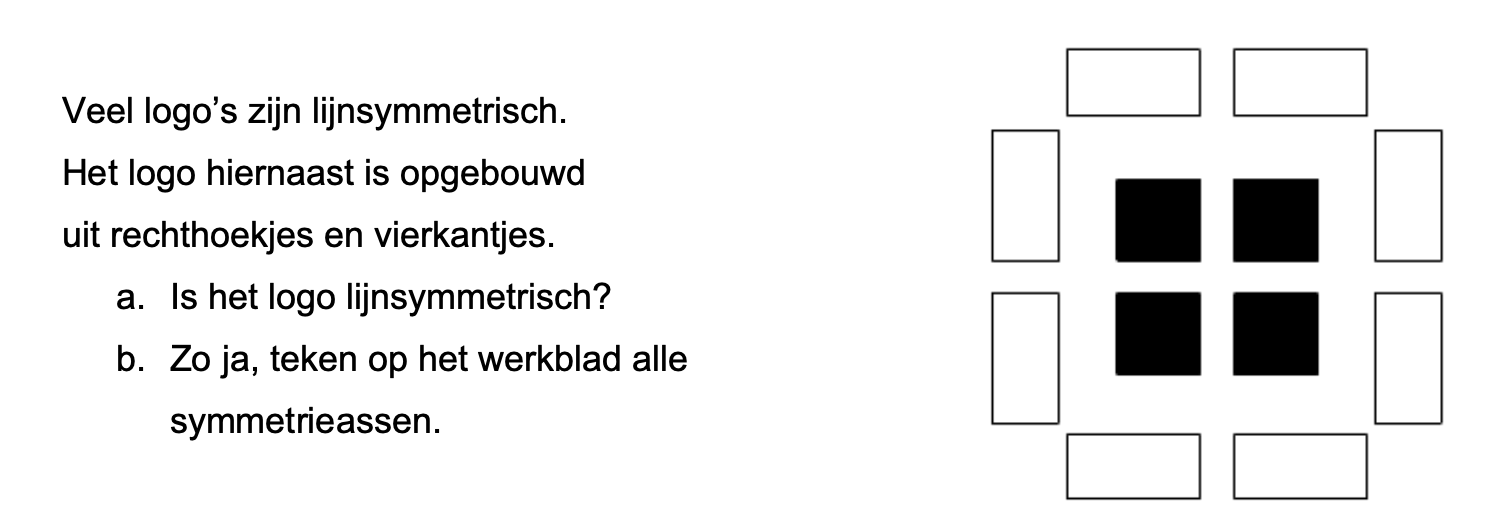



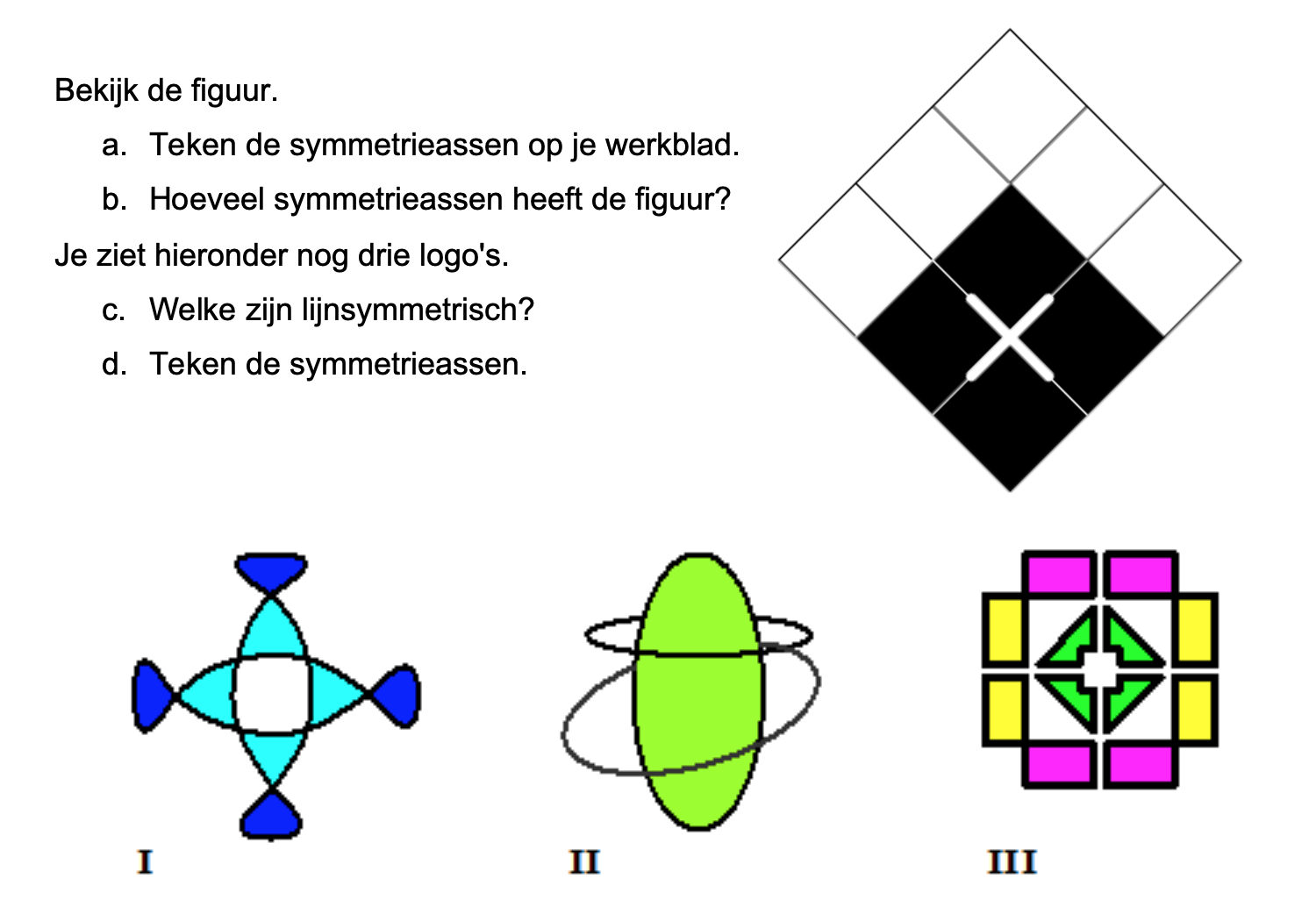




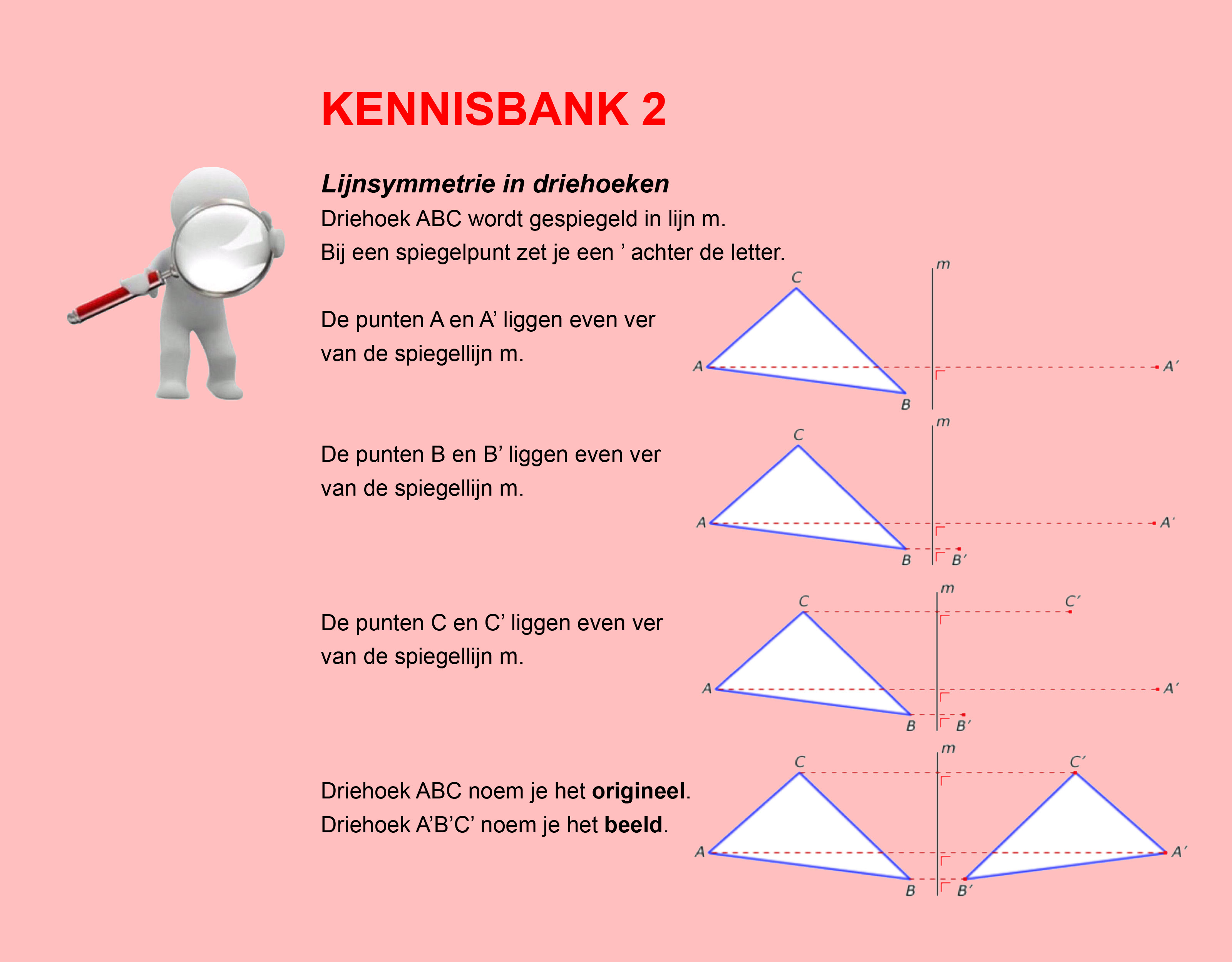
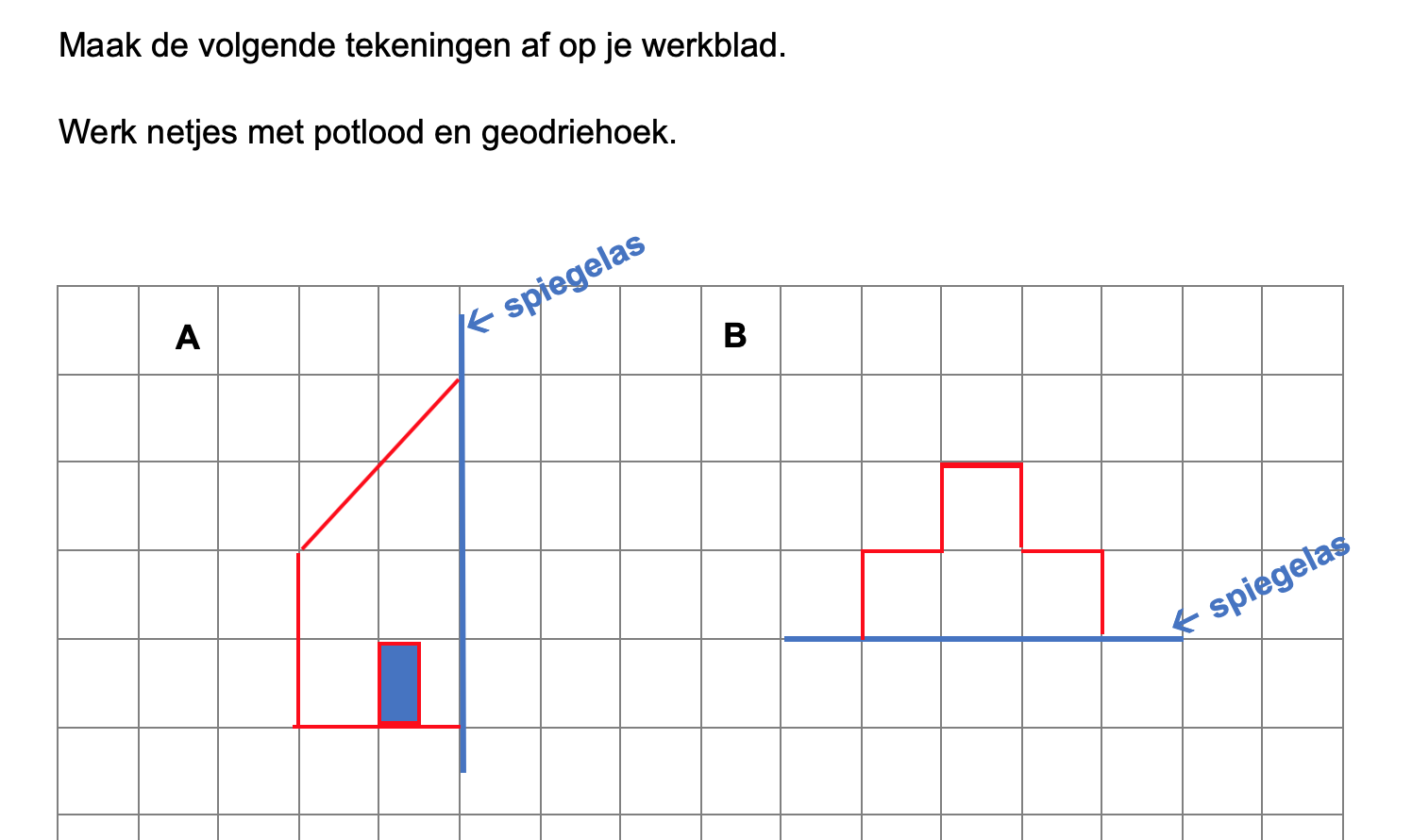
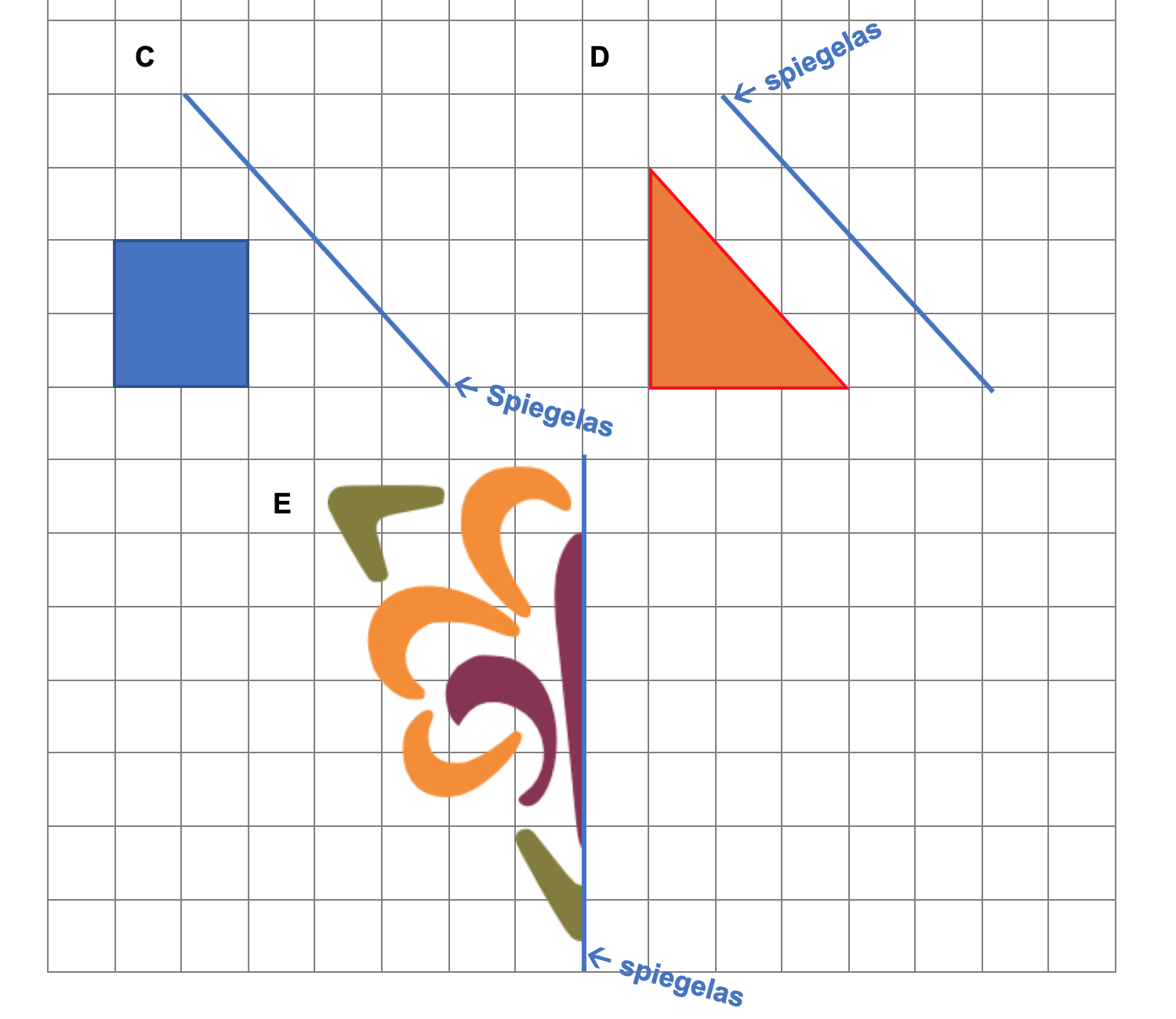
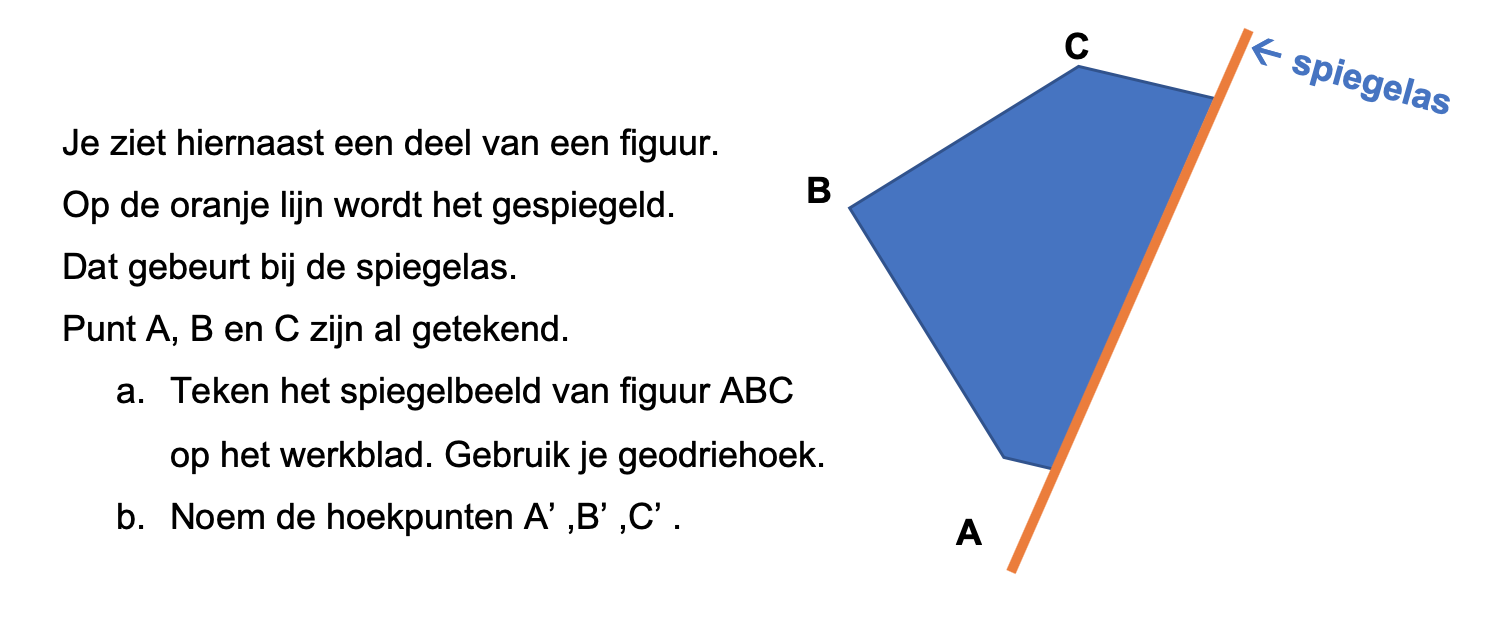
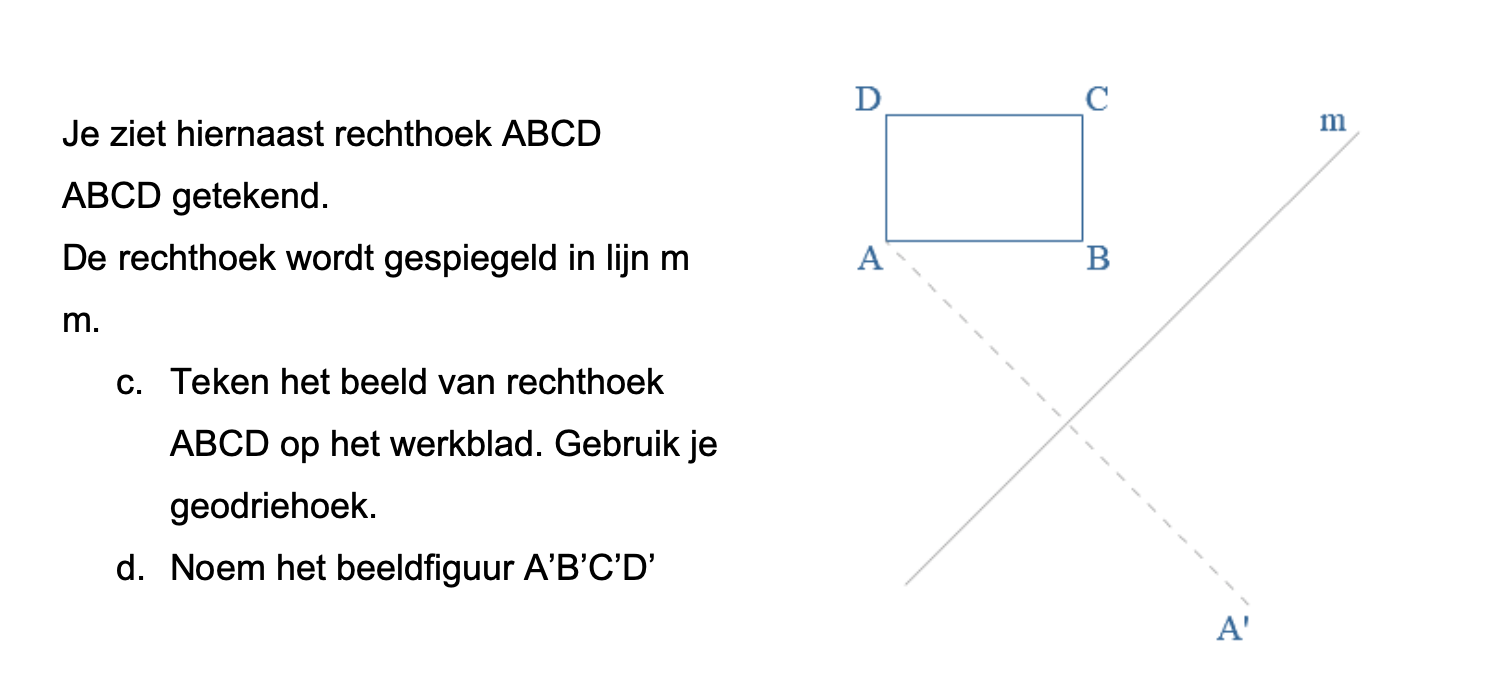
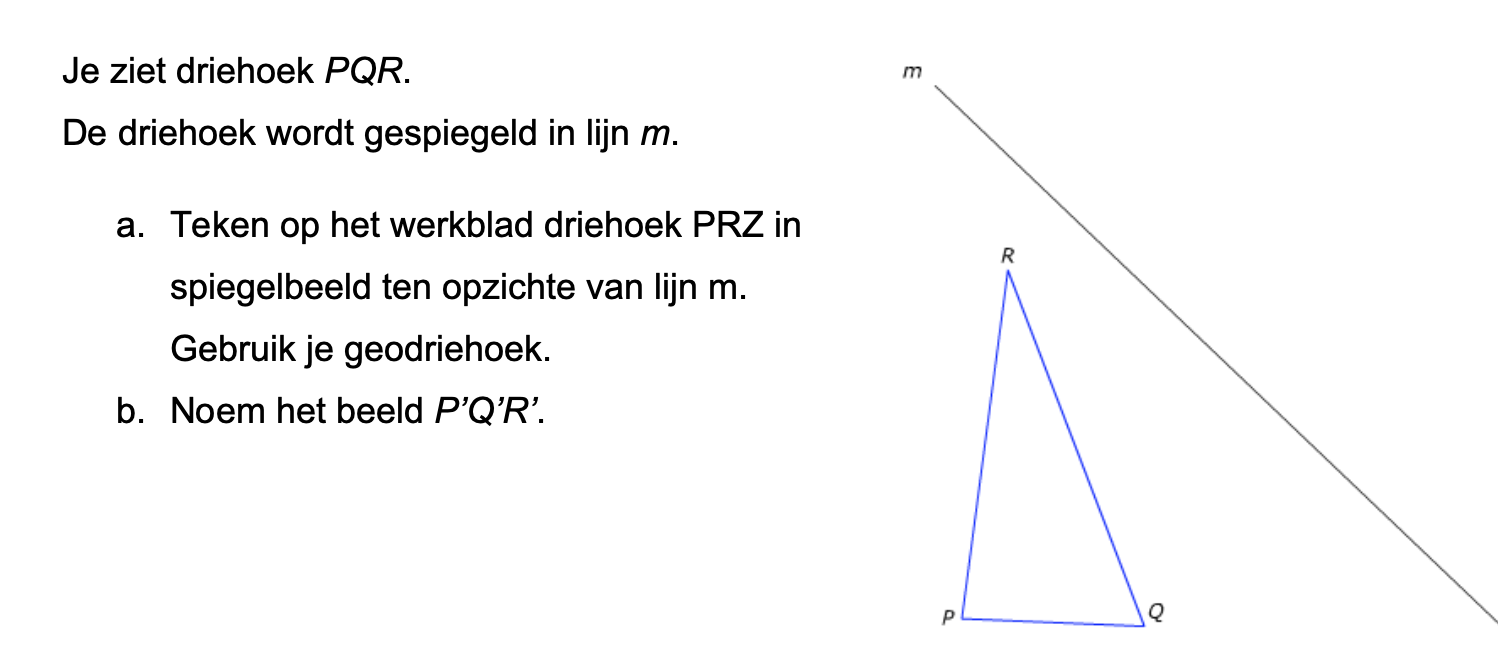

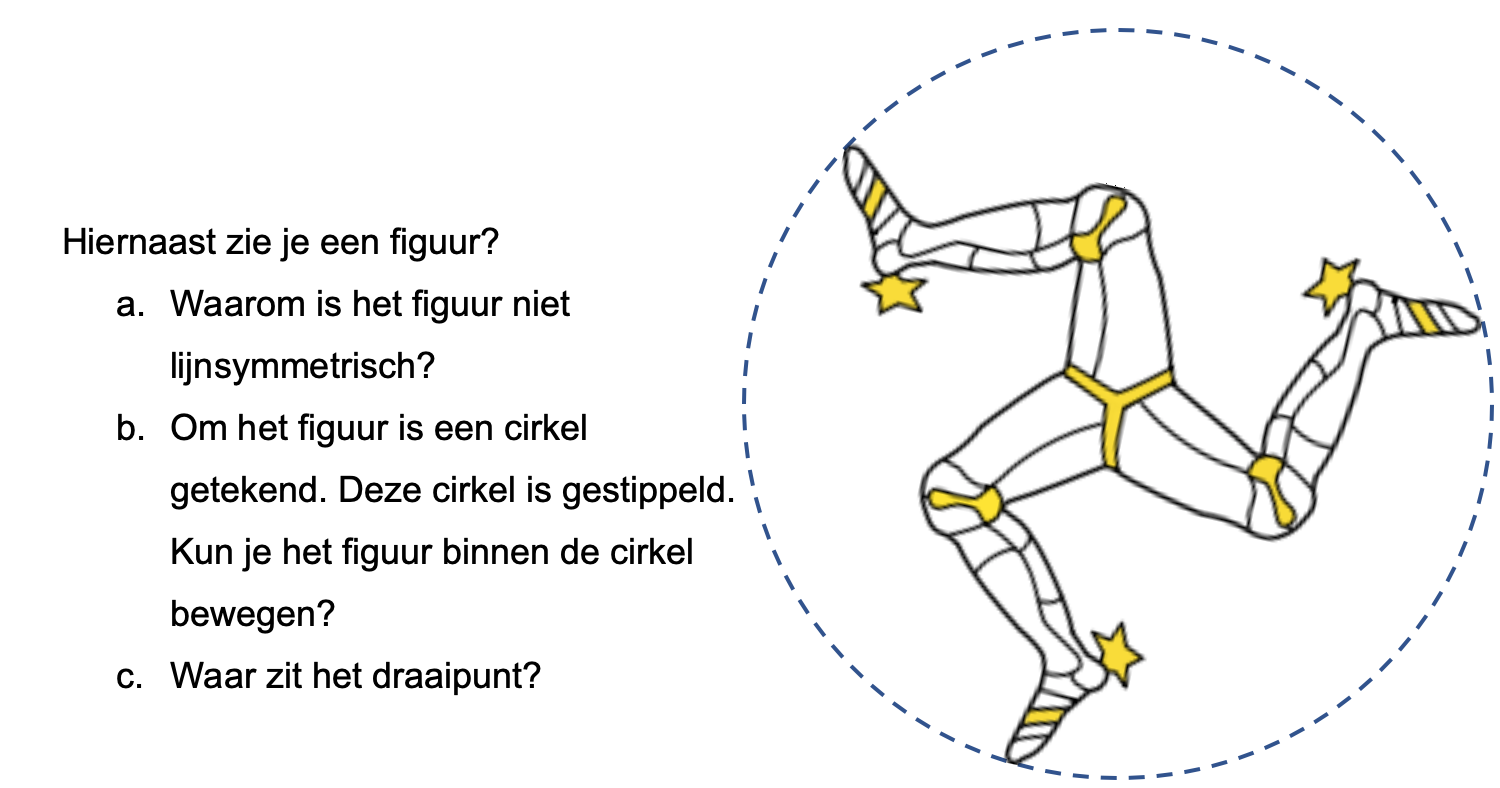

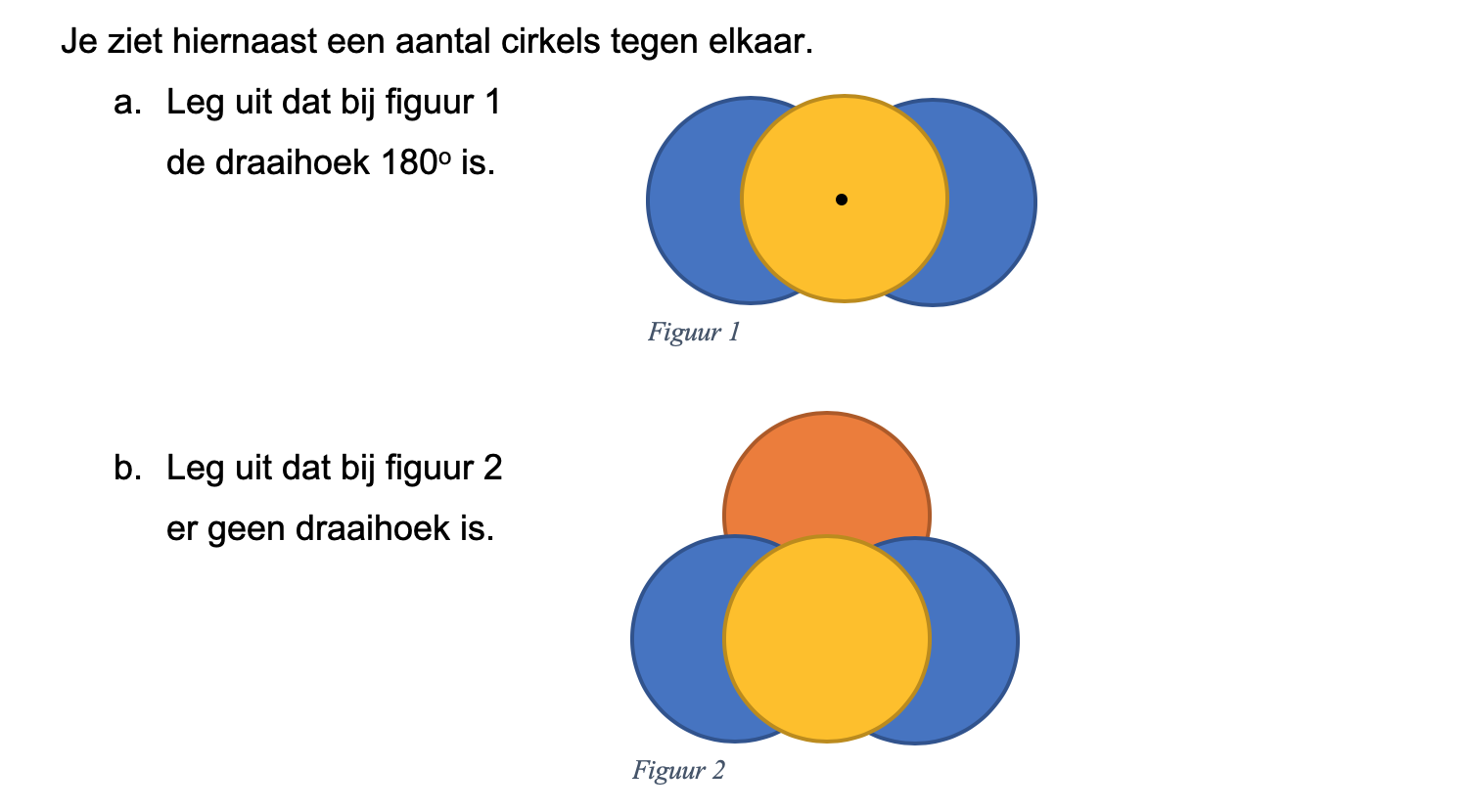




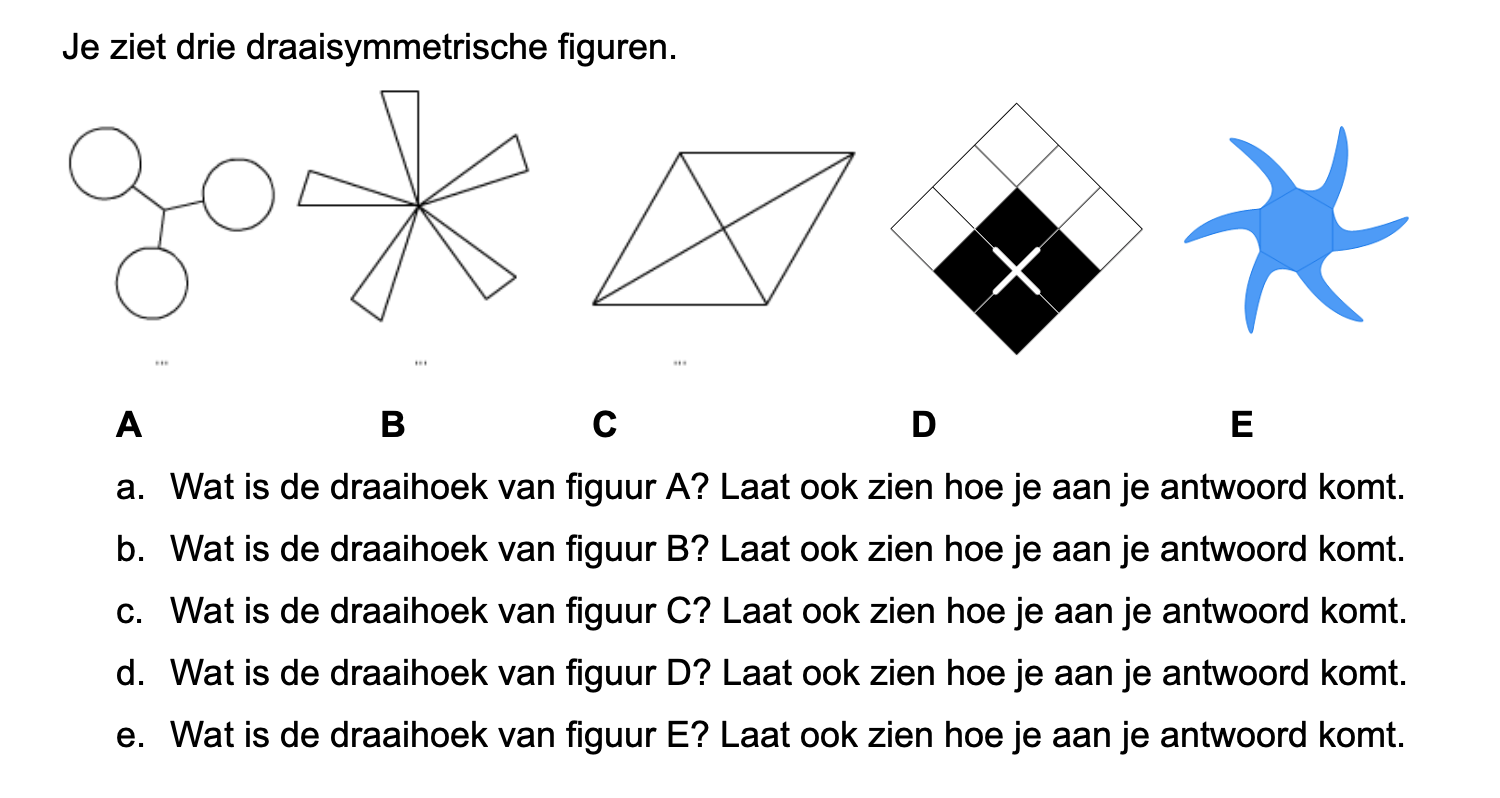





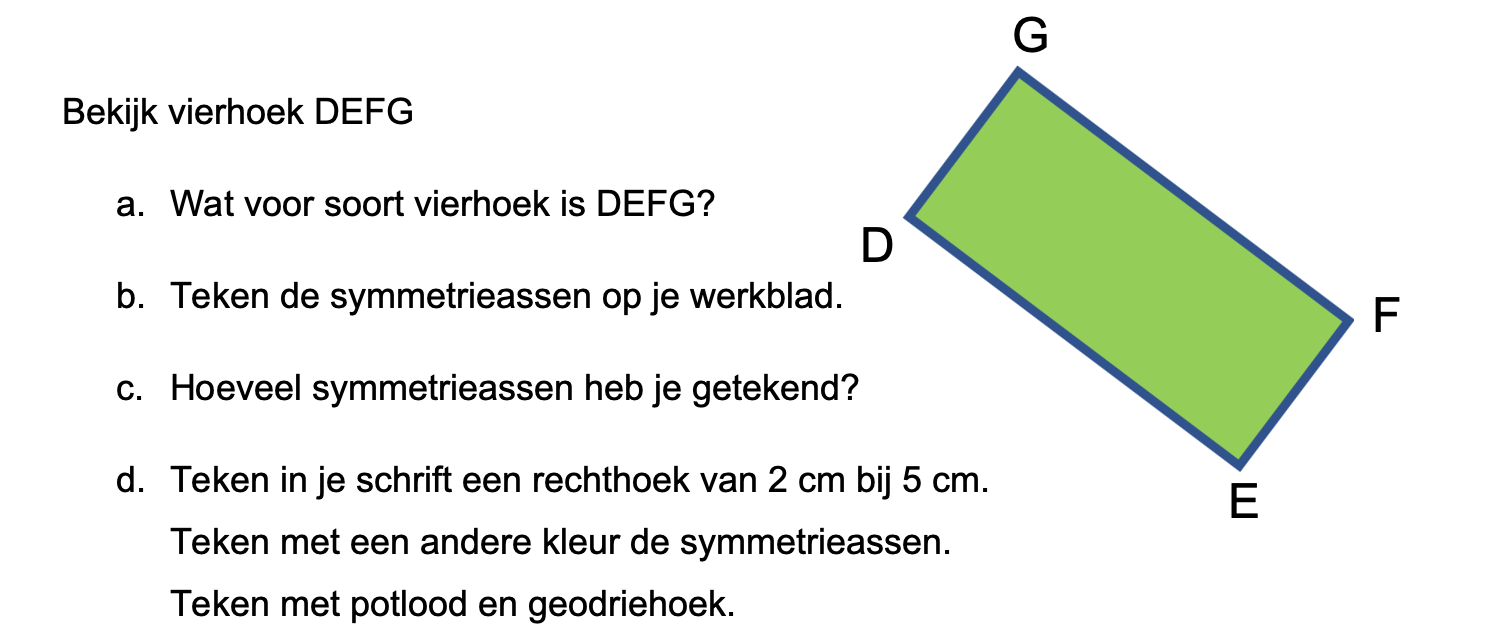


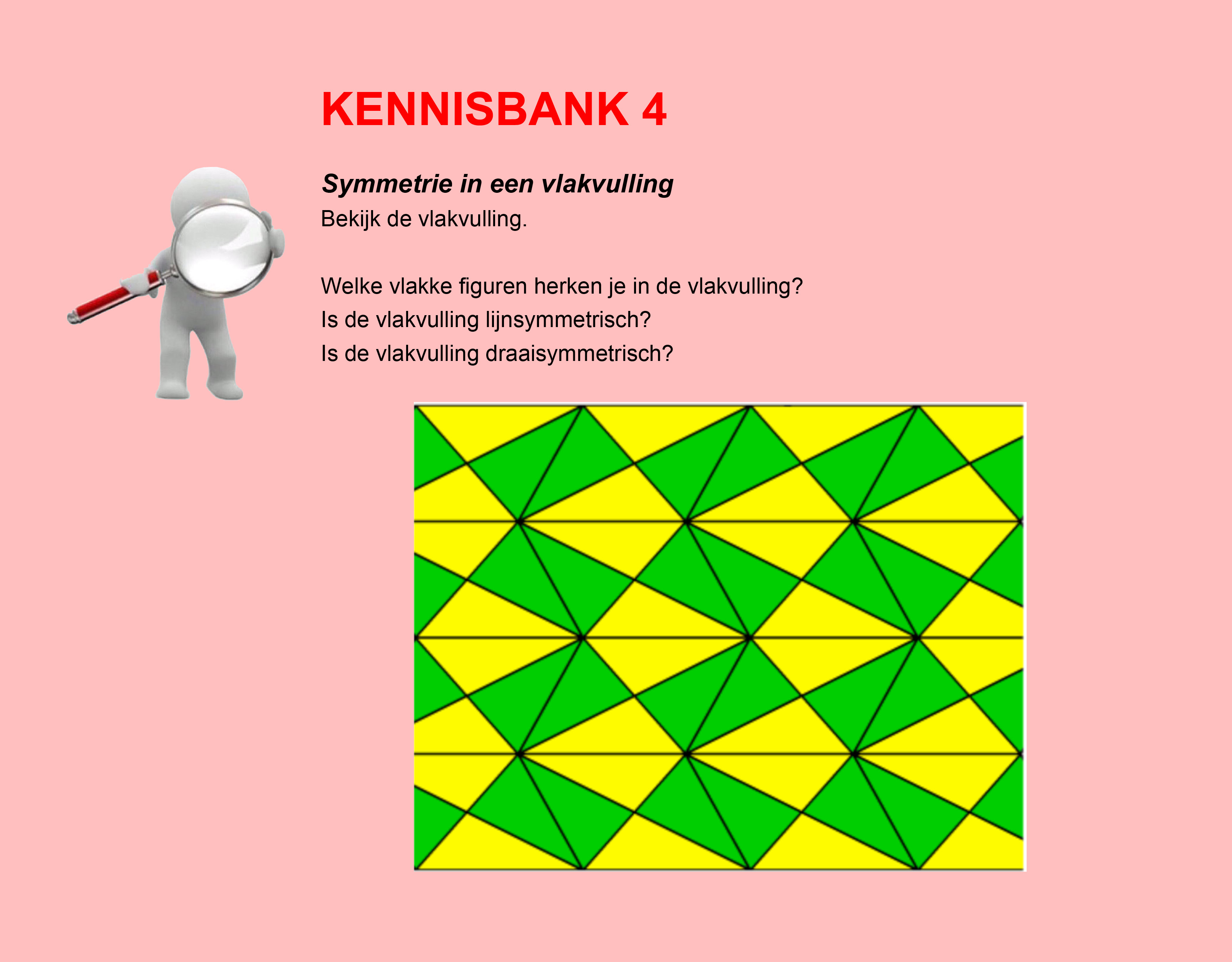
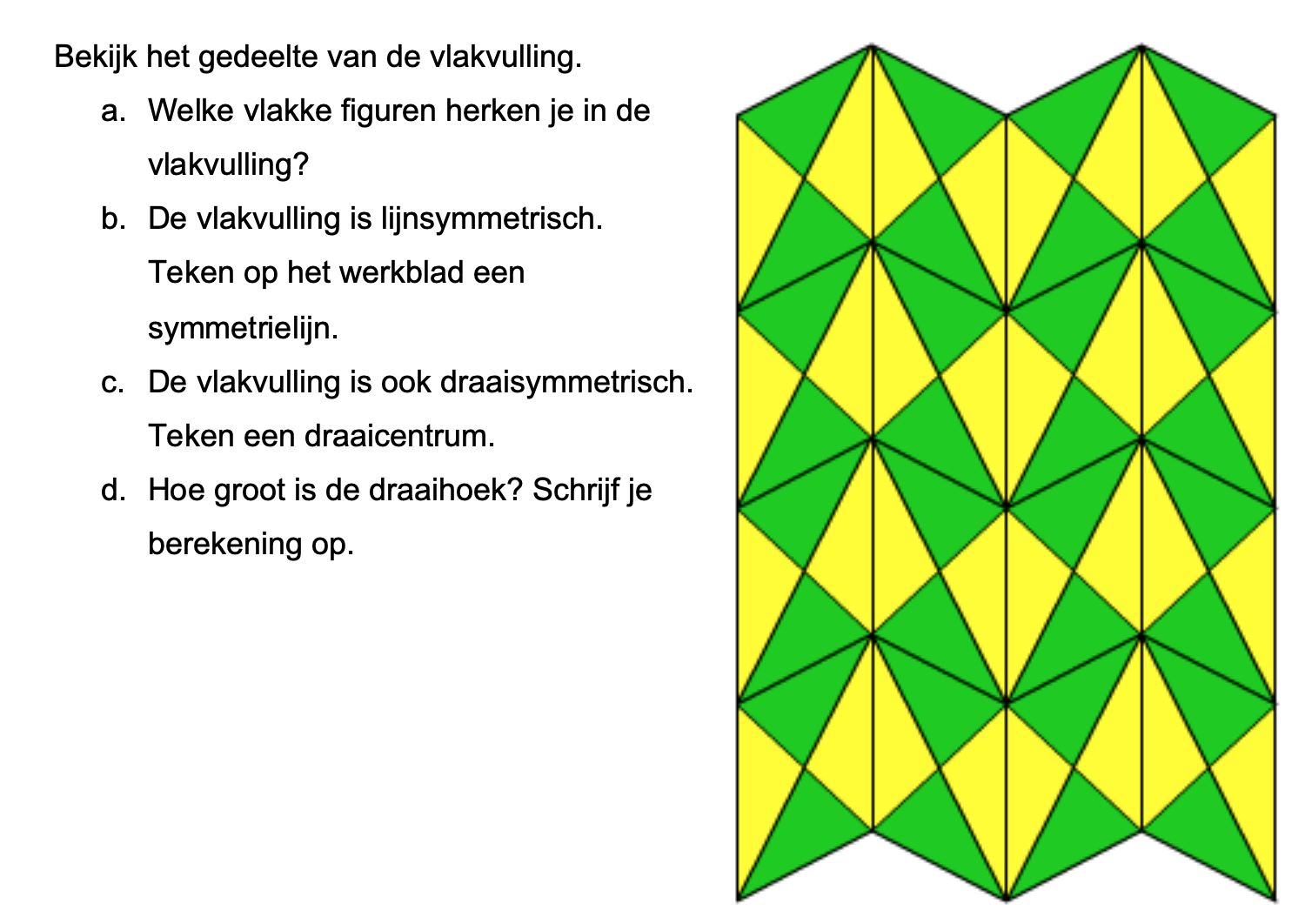

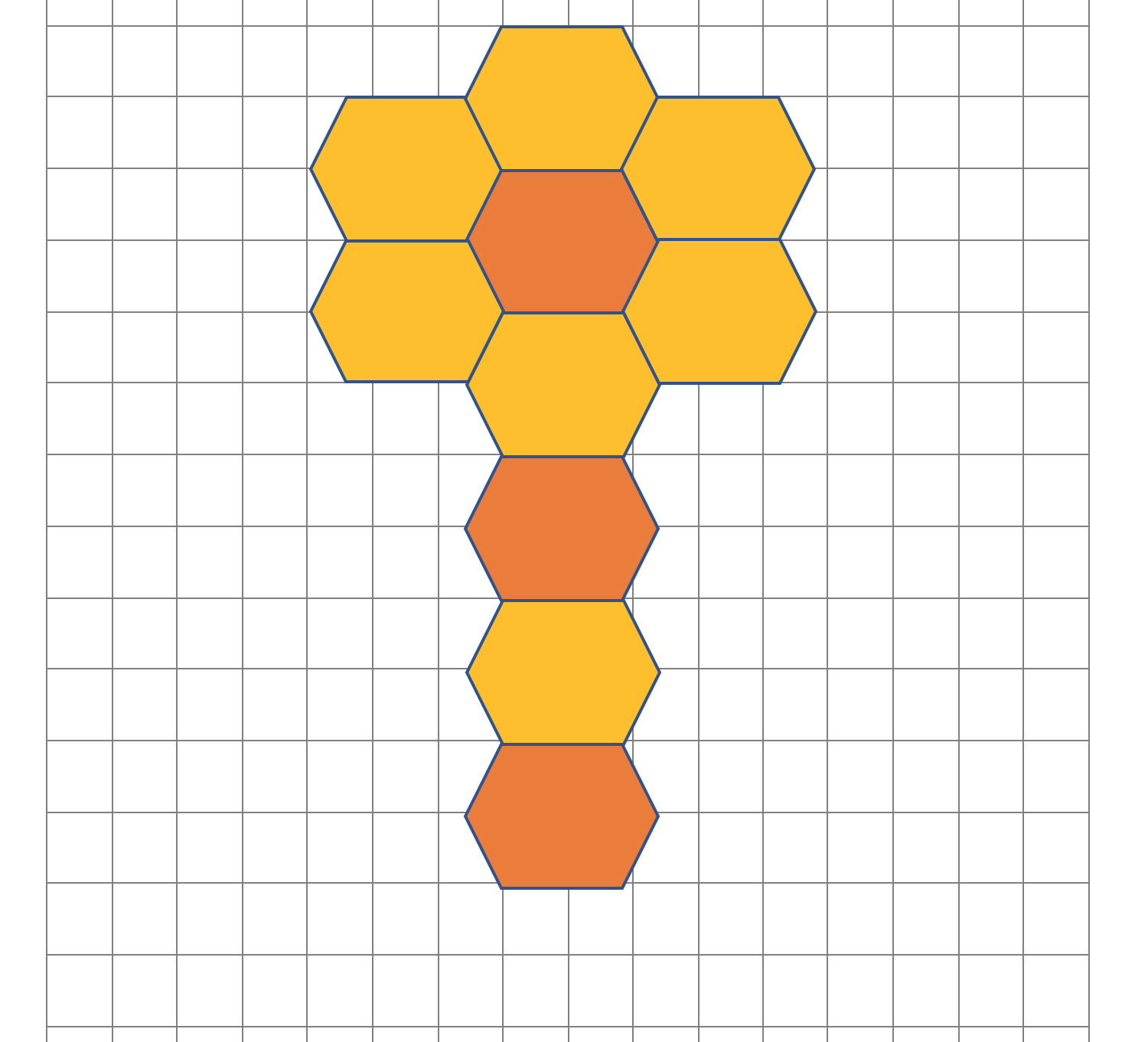












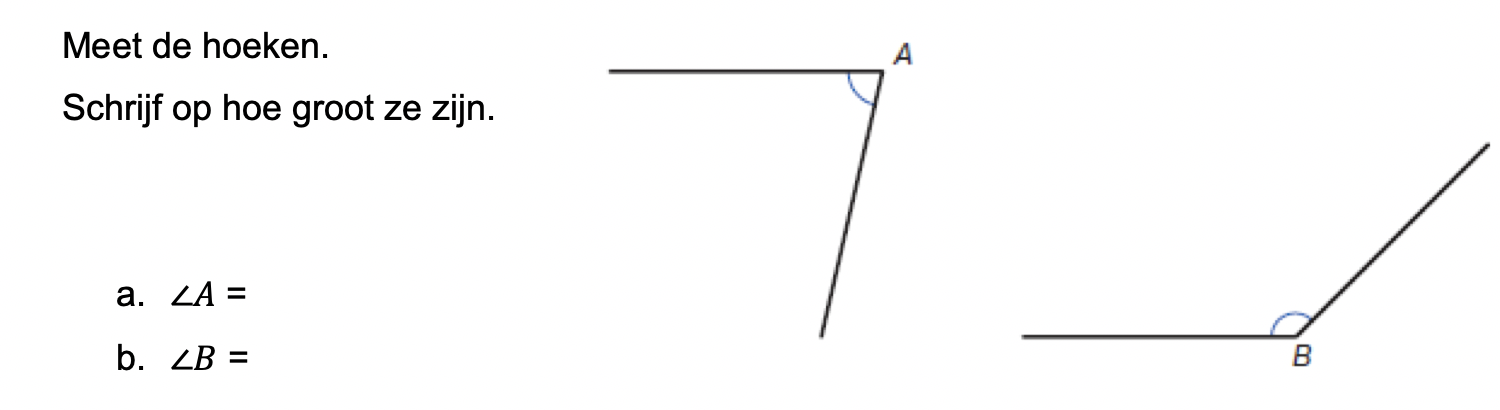


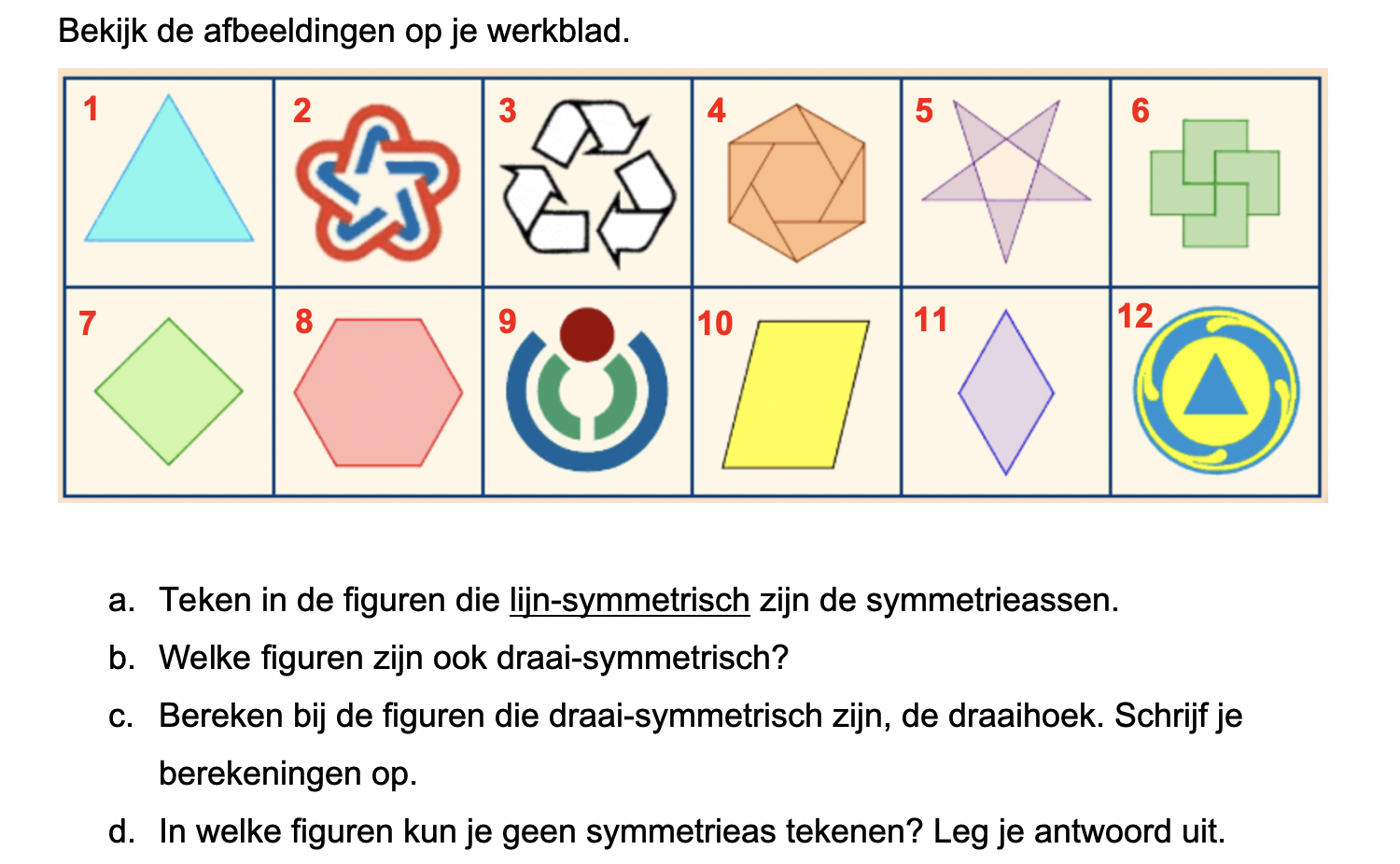
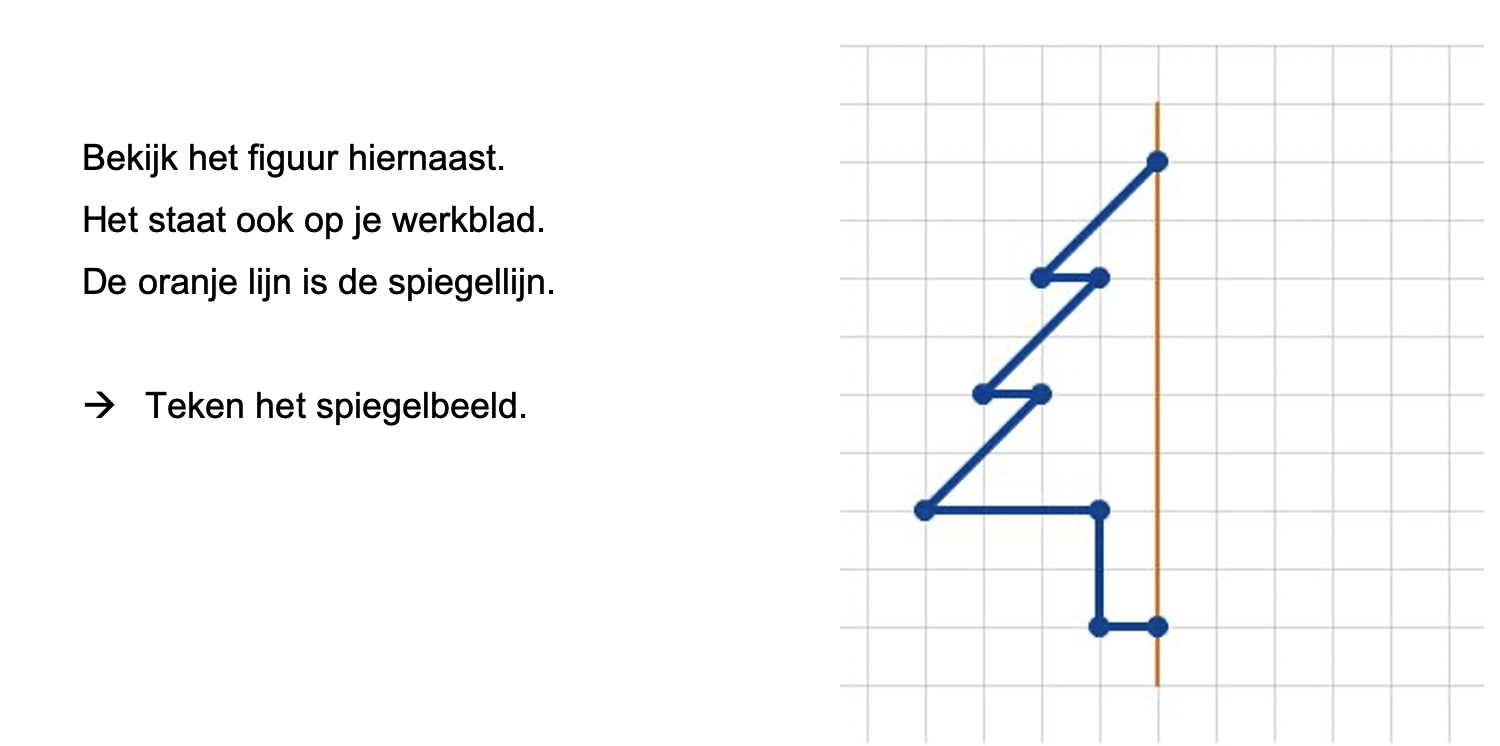
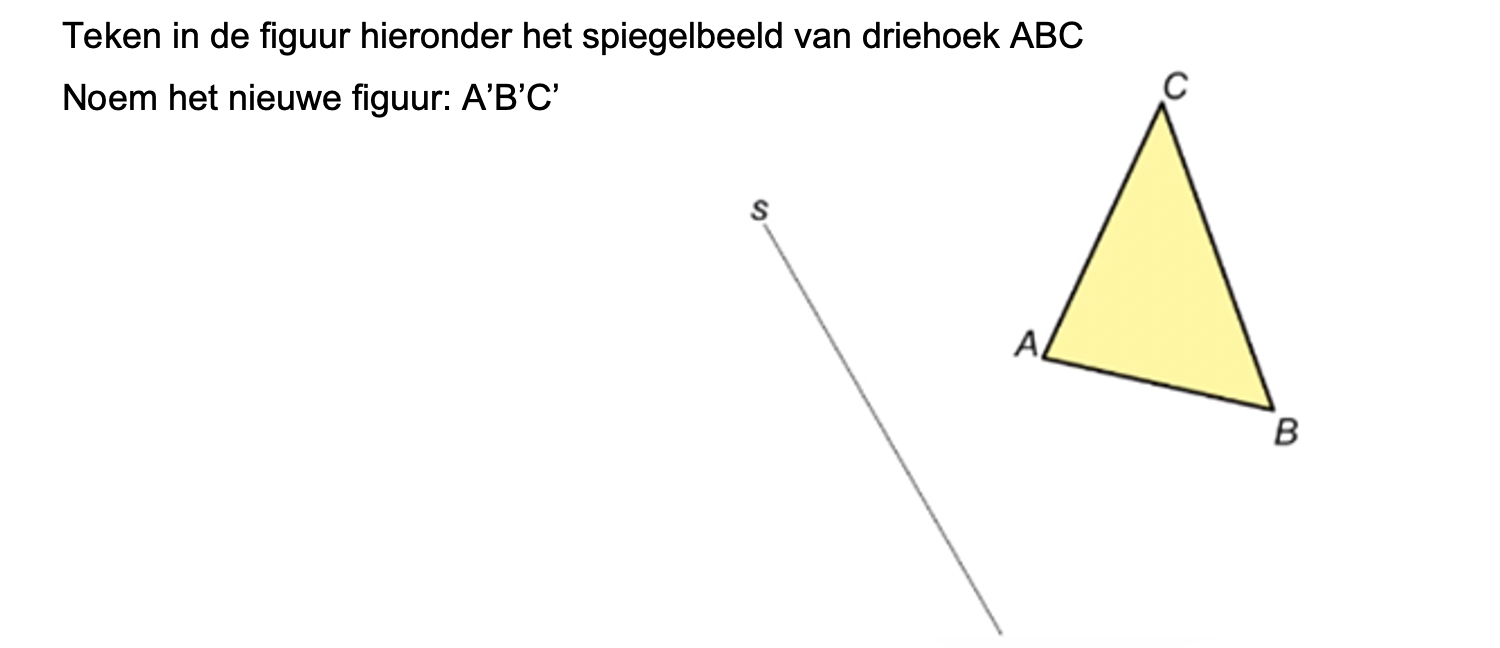
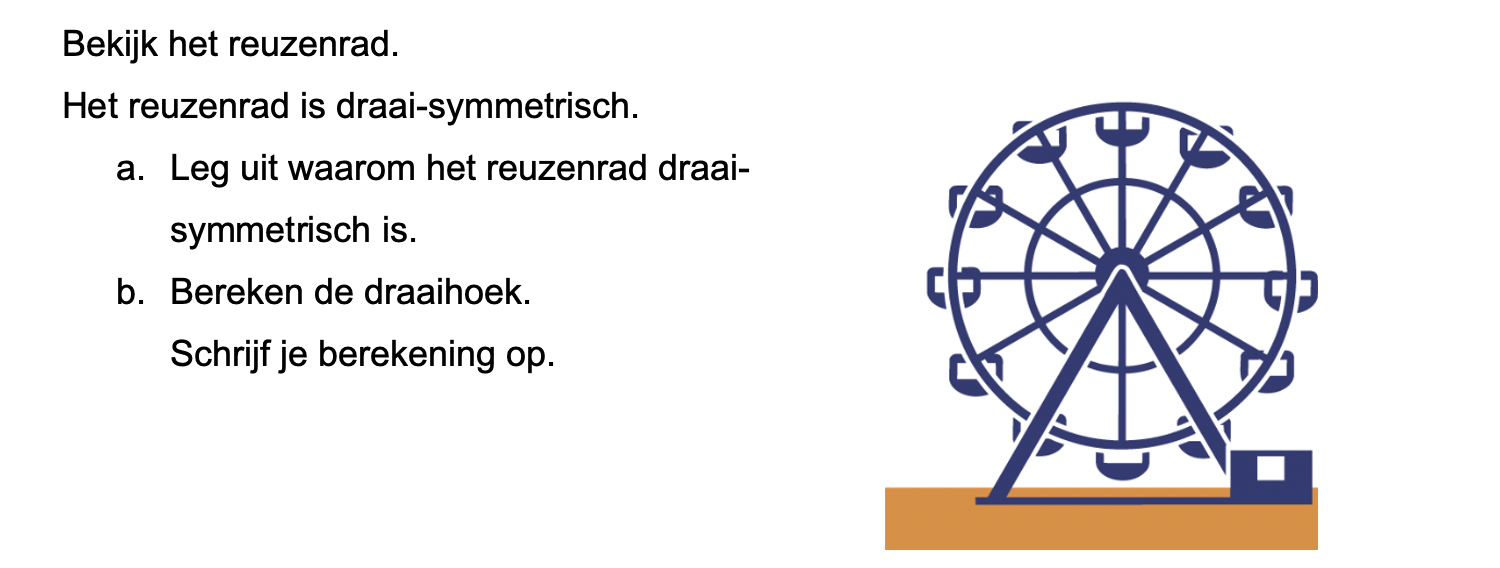






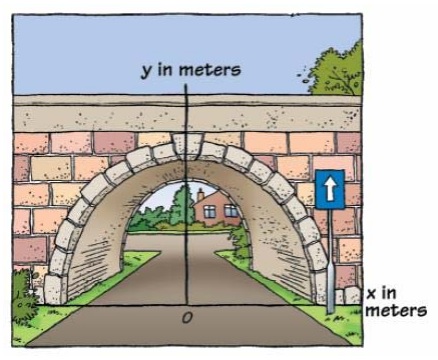
 Hoe komt het, denk je, dat veel mensen die kasteeltuinen zo mooi vinden?
Hoe komt het, denk je, dat veel mensen die kasteeltuinen zo mooi vinden?


 Nog enkele opgaven om te oefenen voor het proefwerk.
Nog enkele opgaven om te oefenen voor het proefwerk.









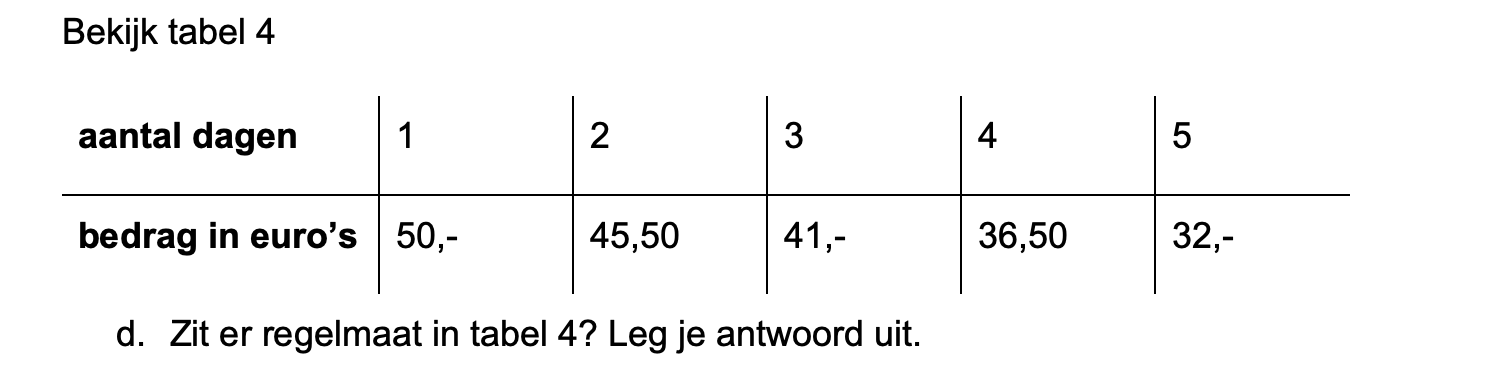
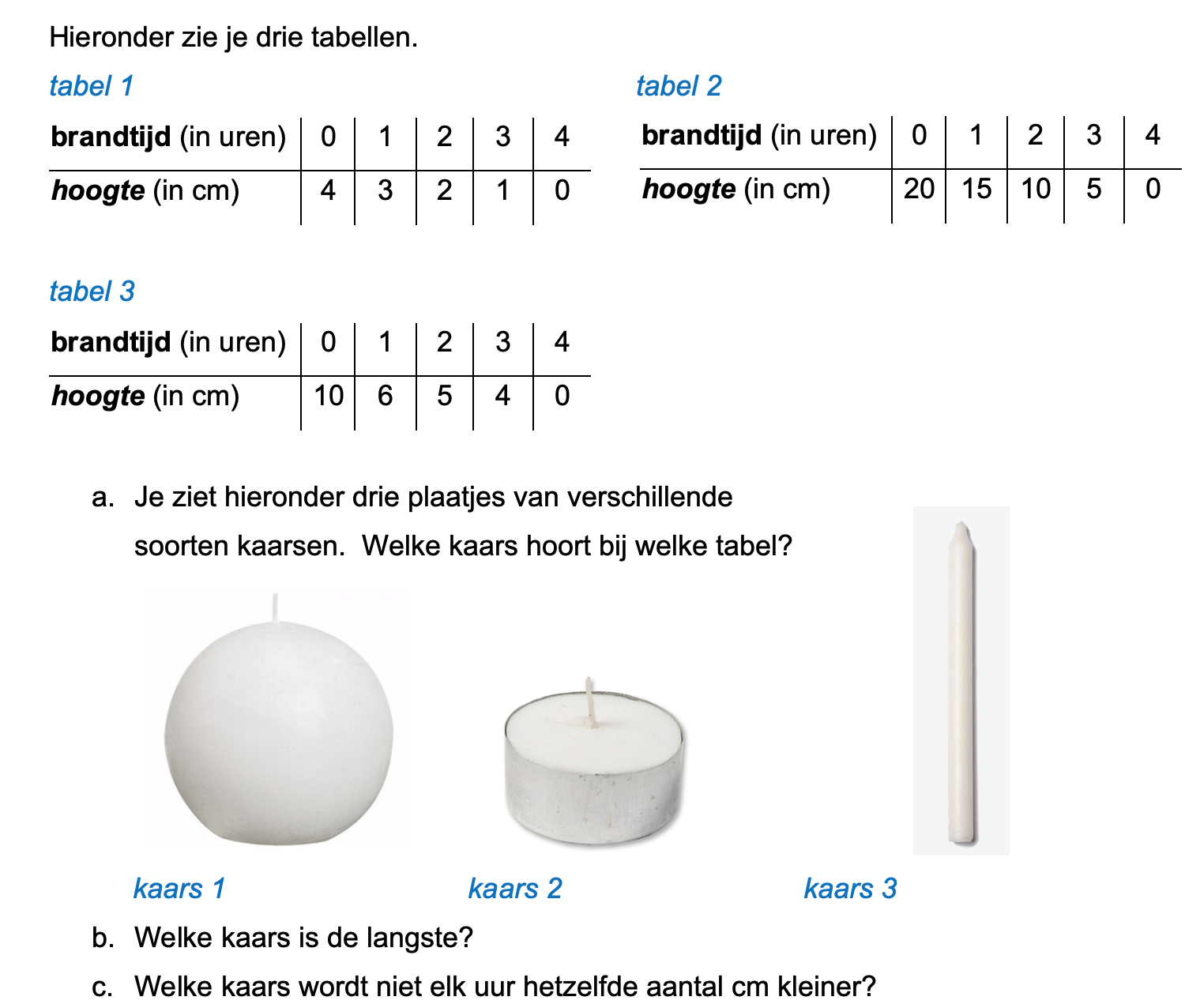





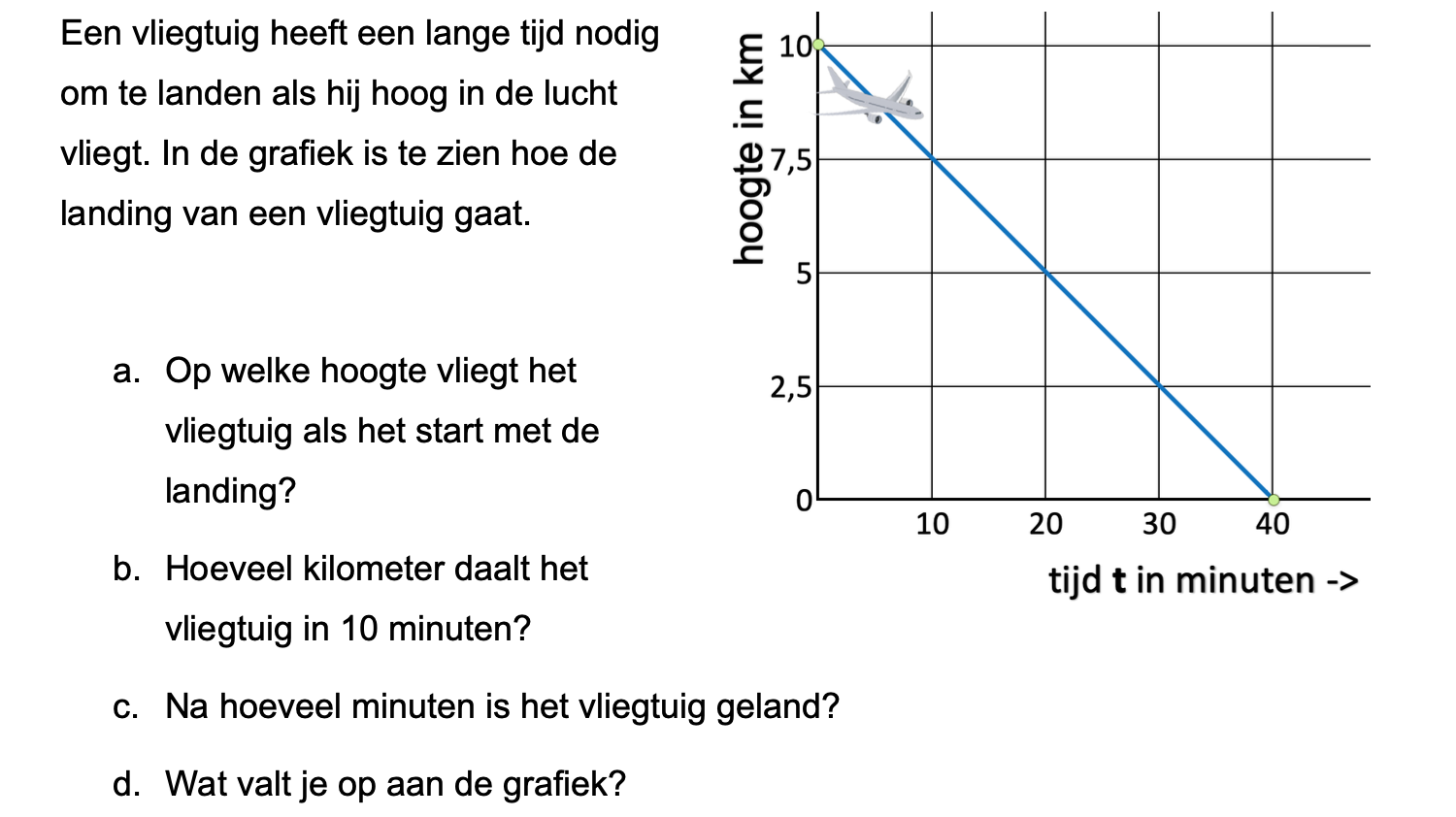
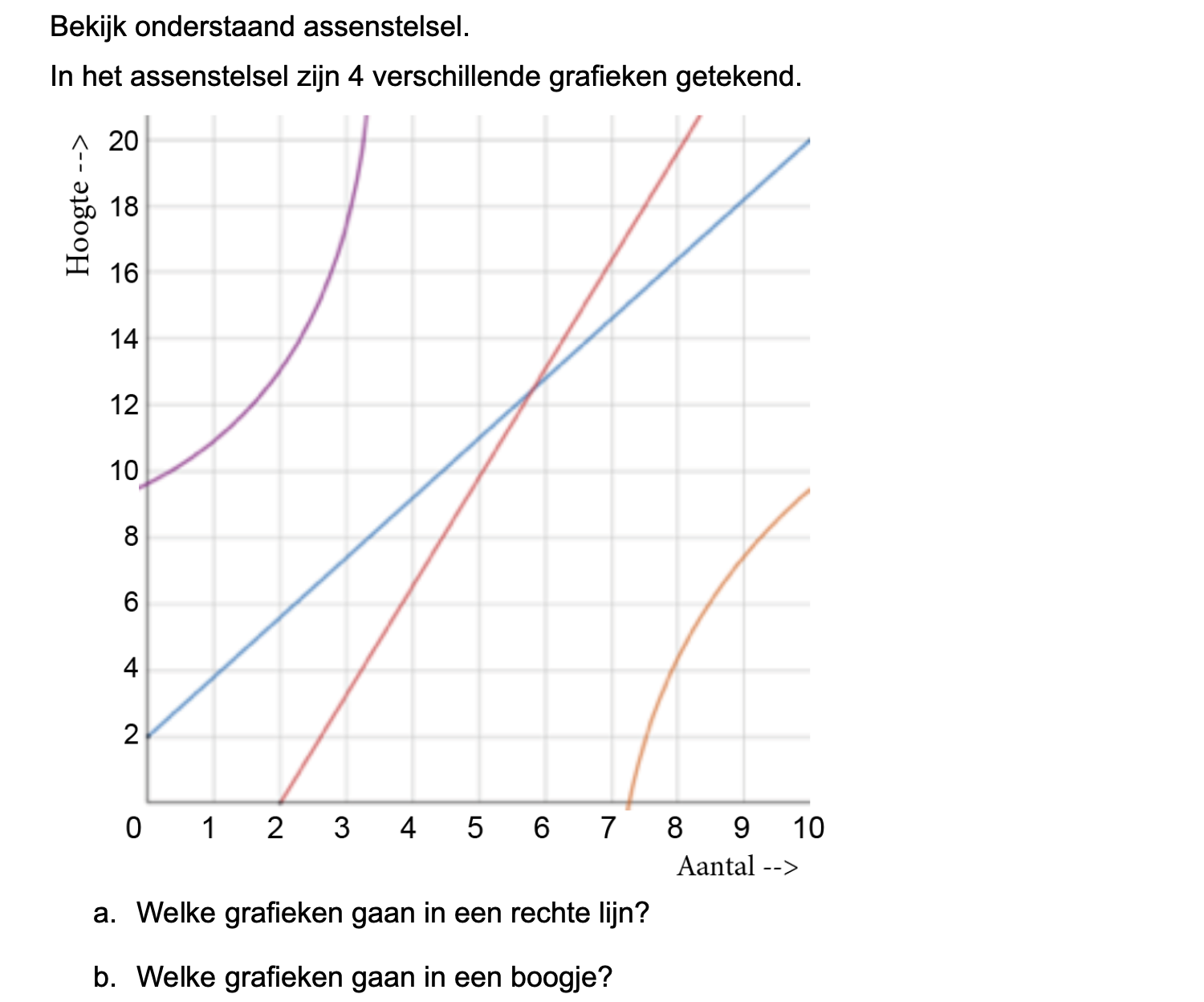






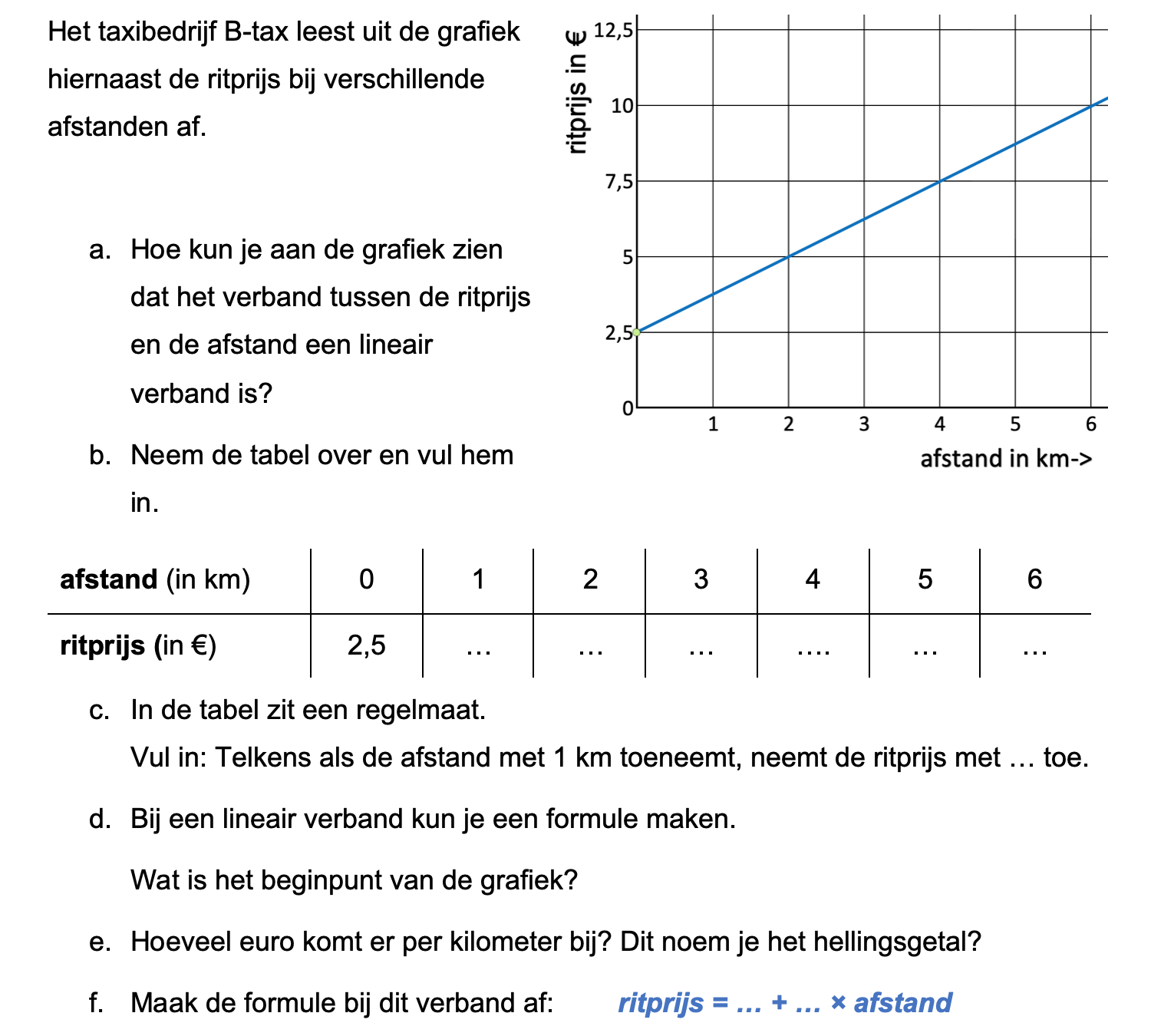

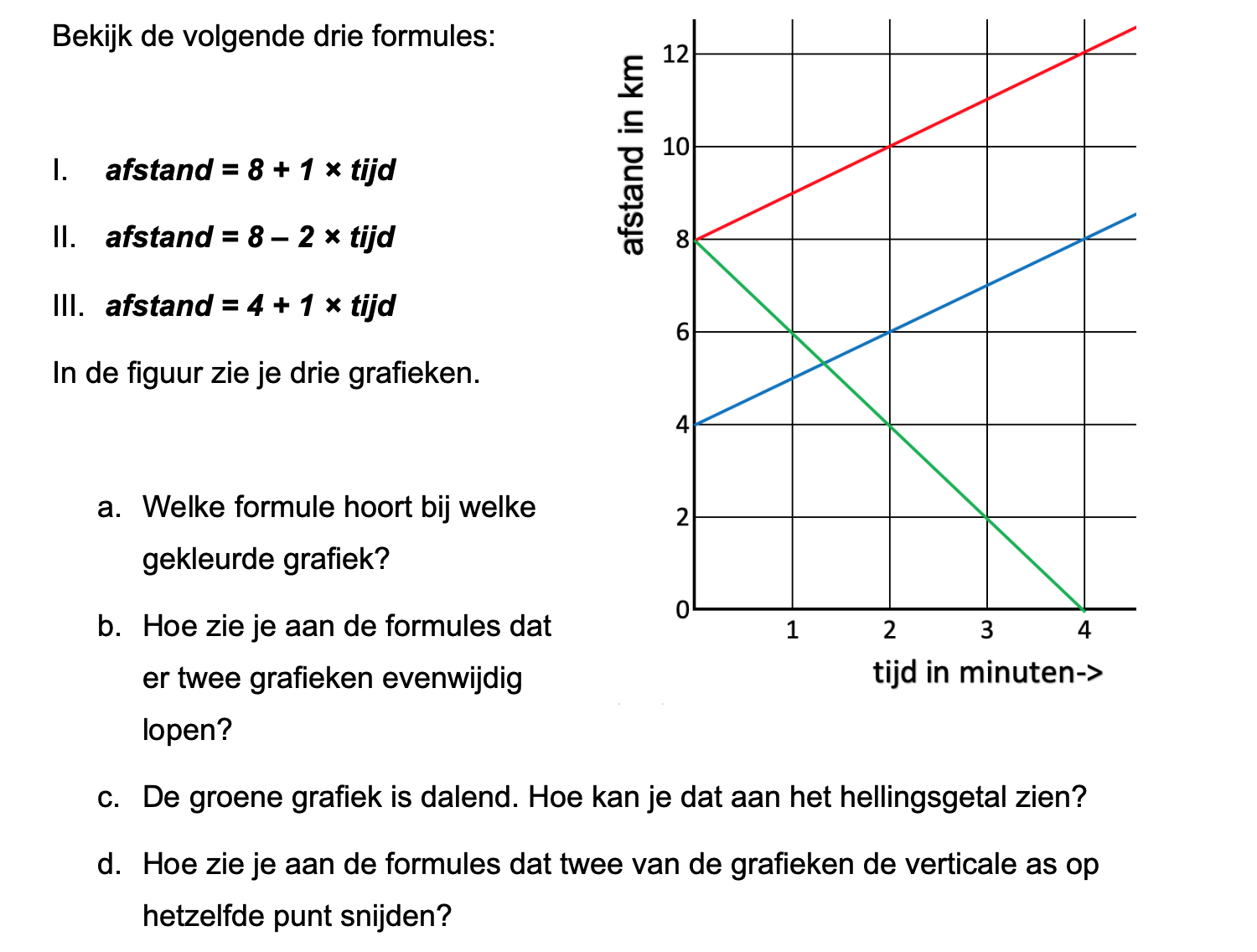



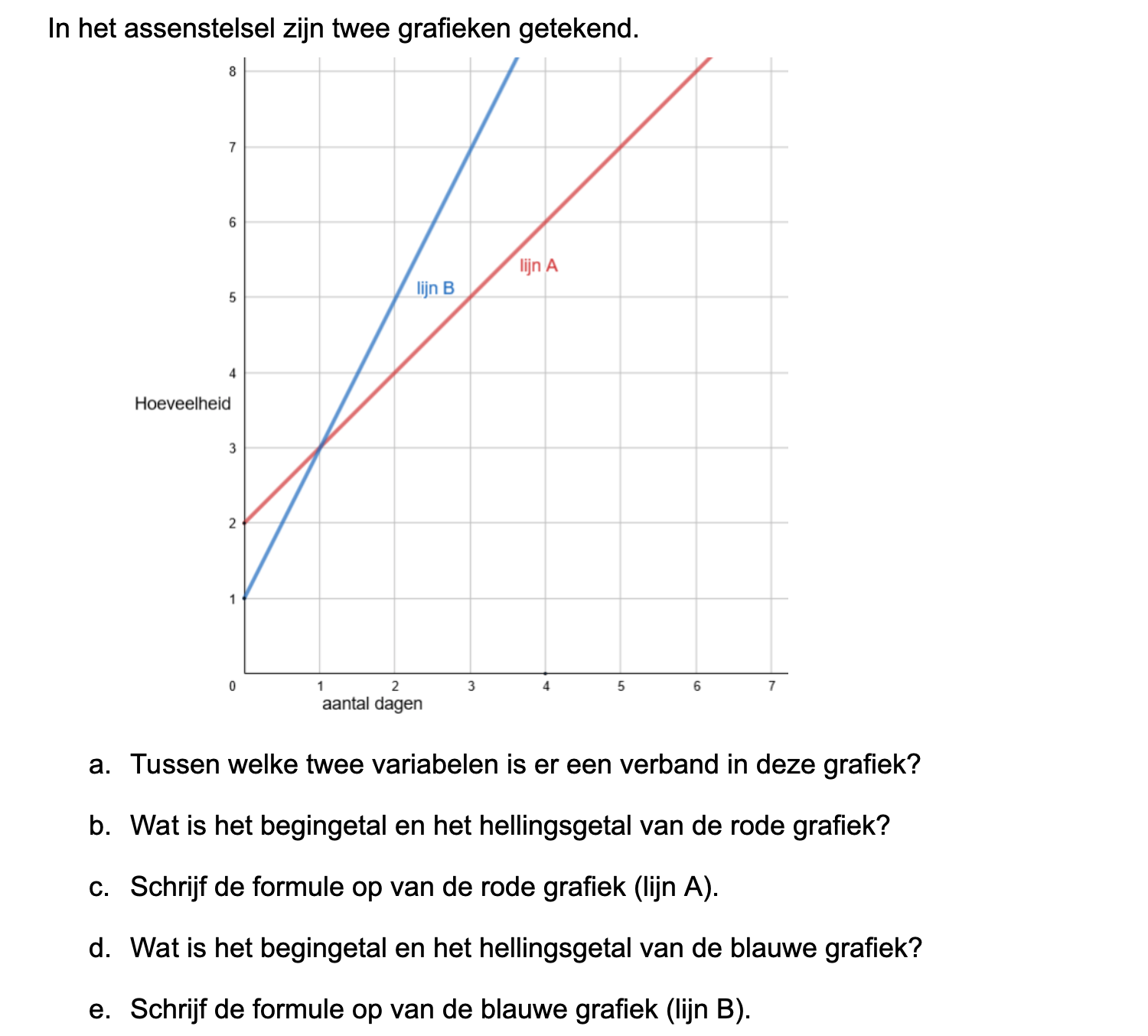
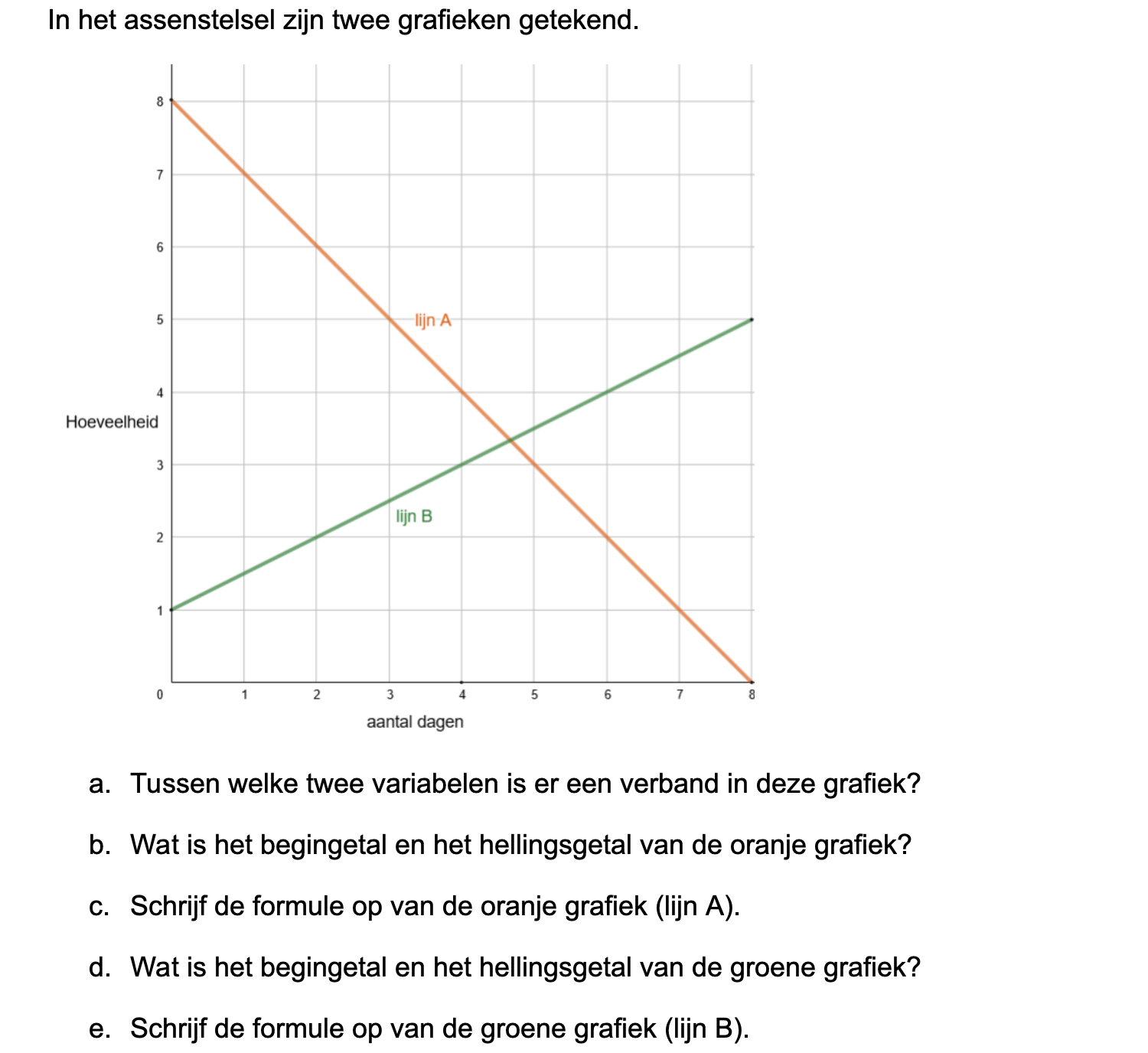
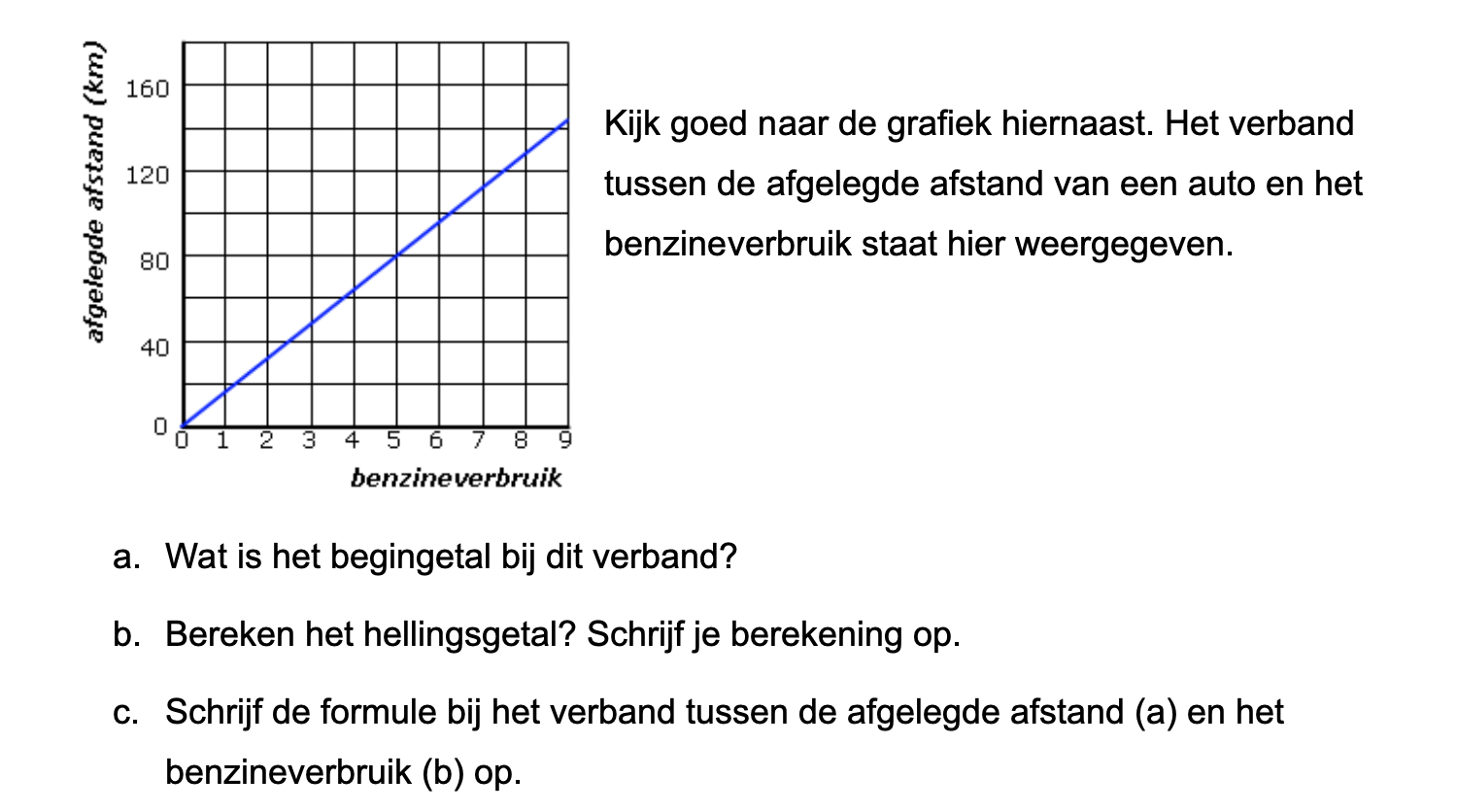
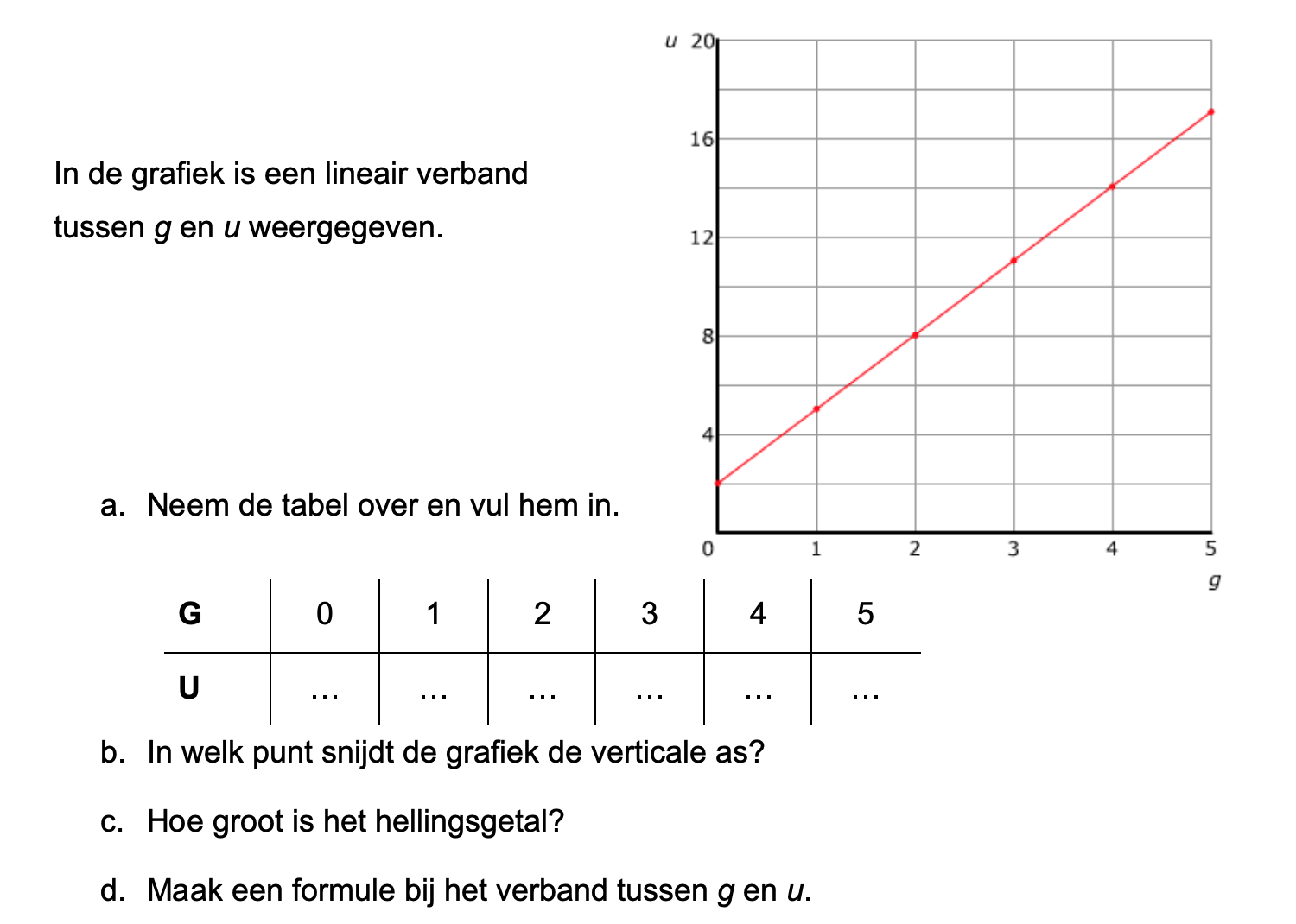


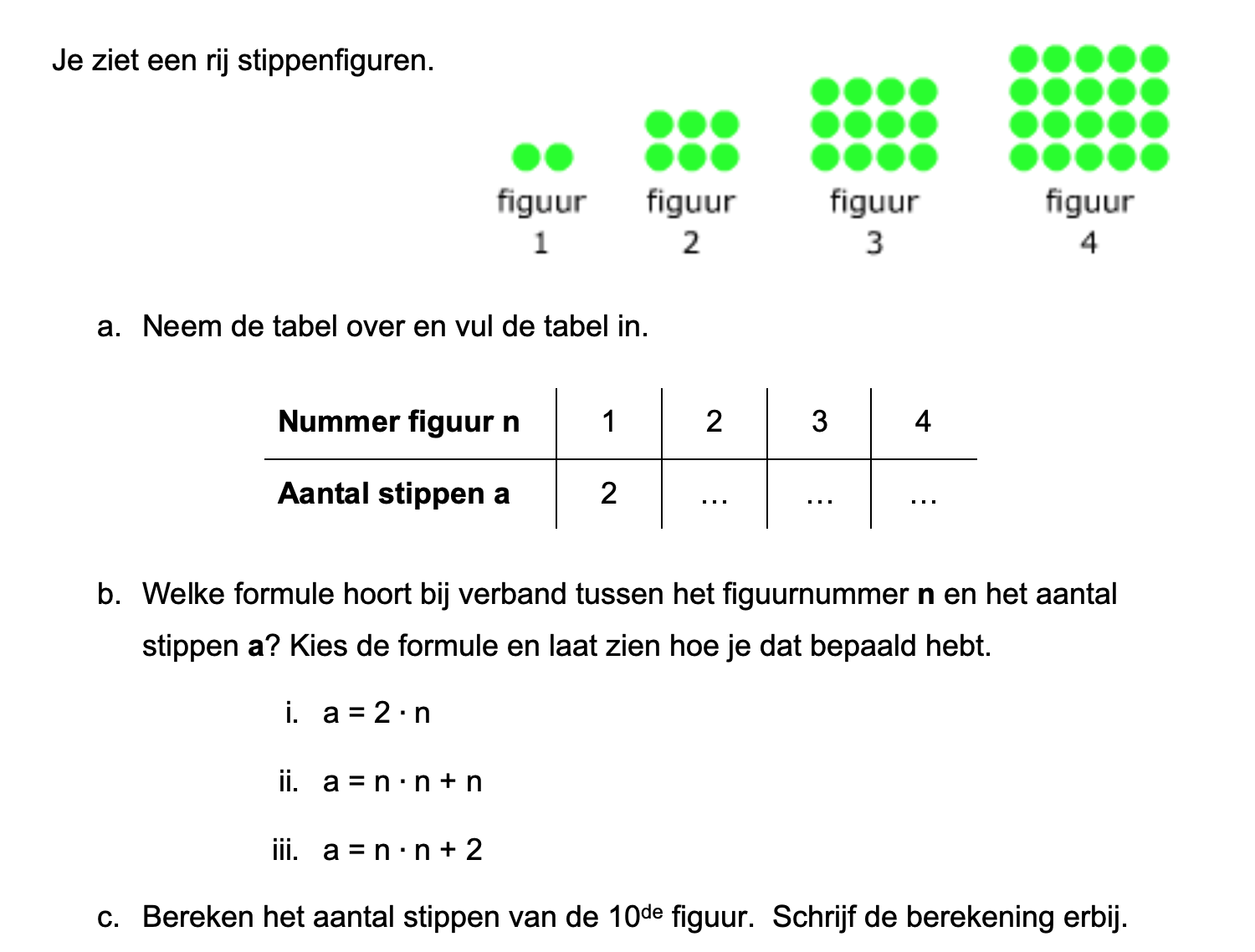
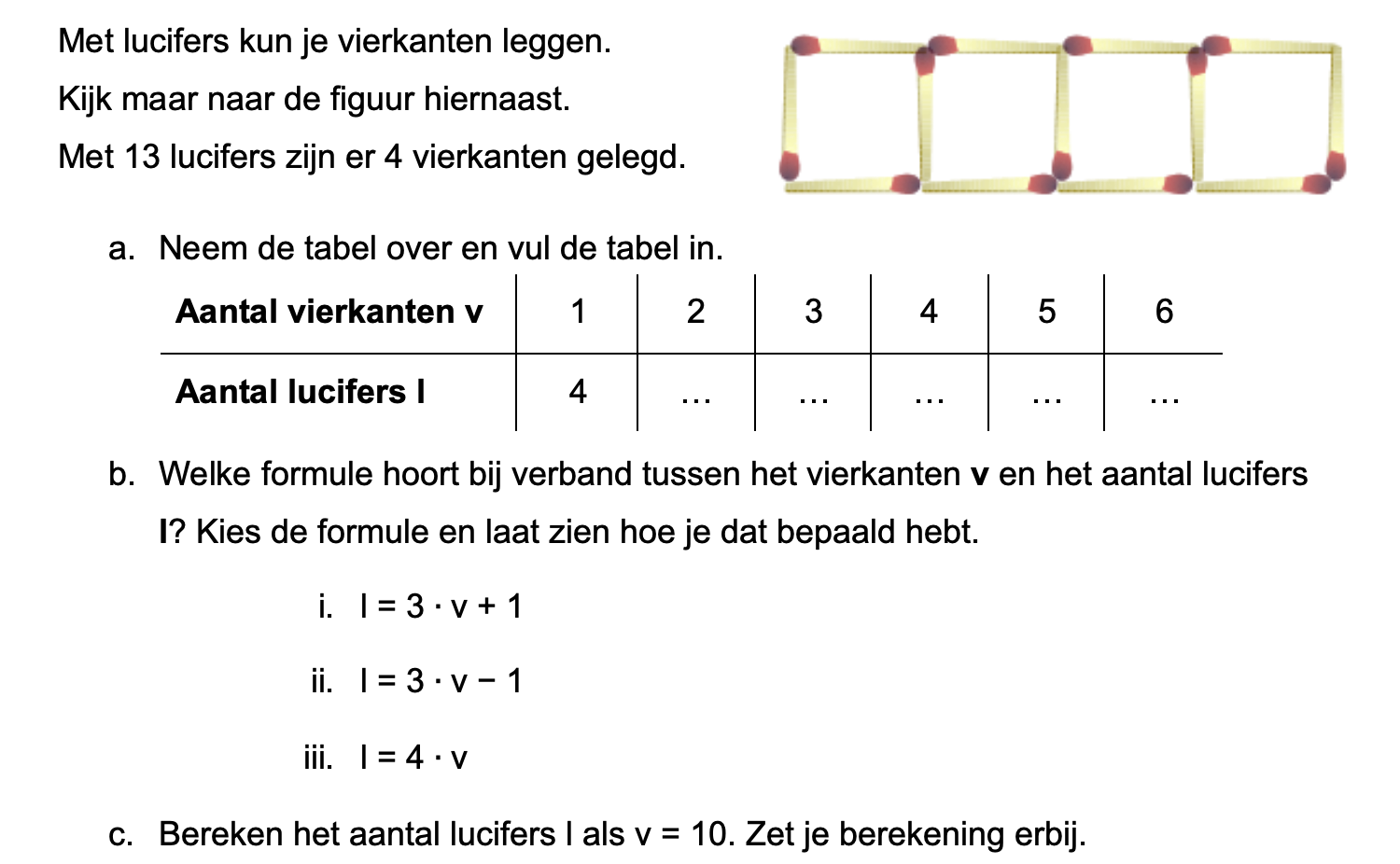









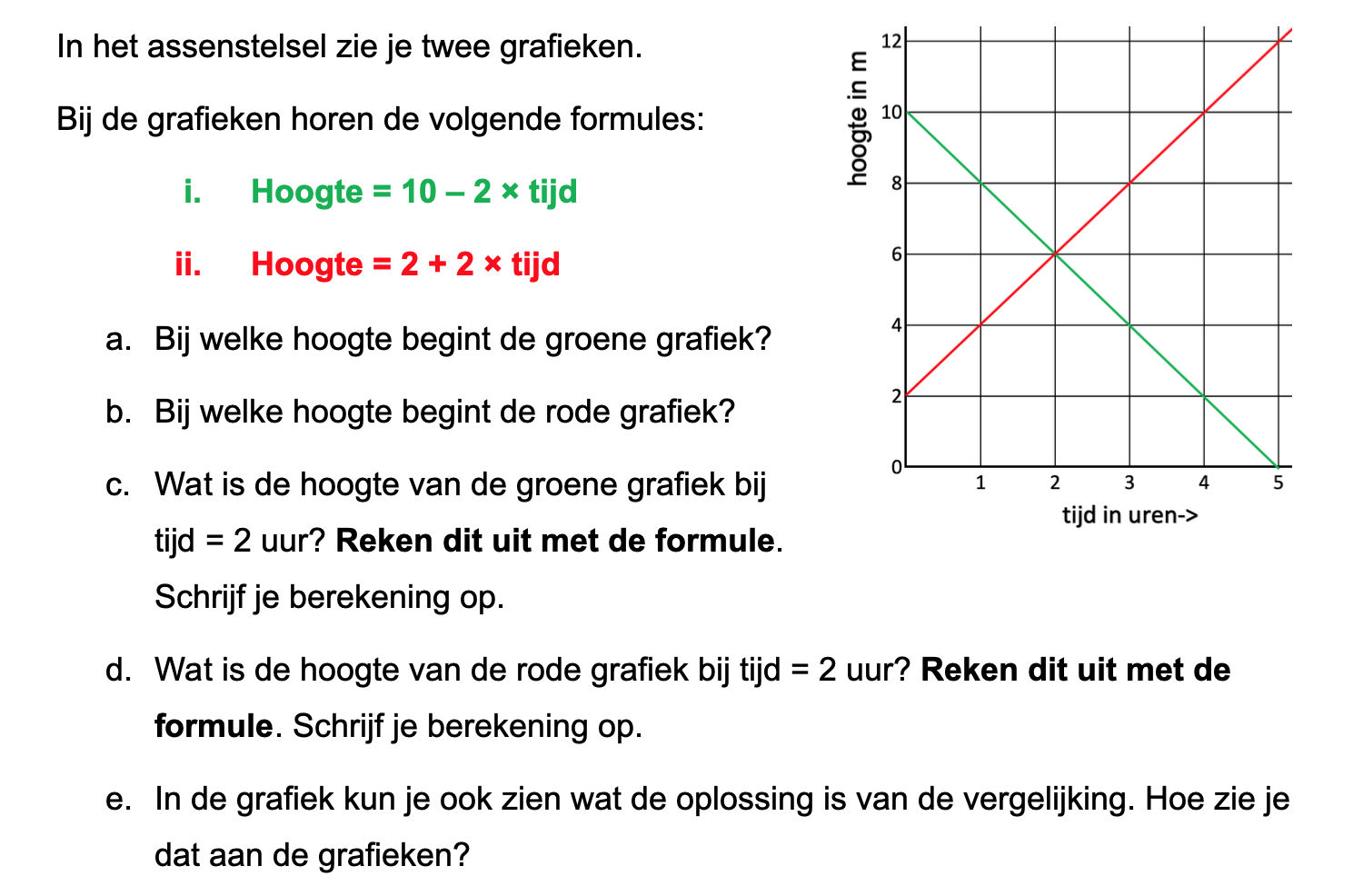

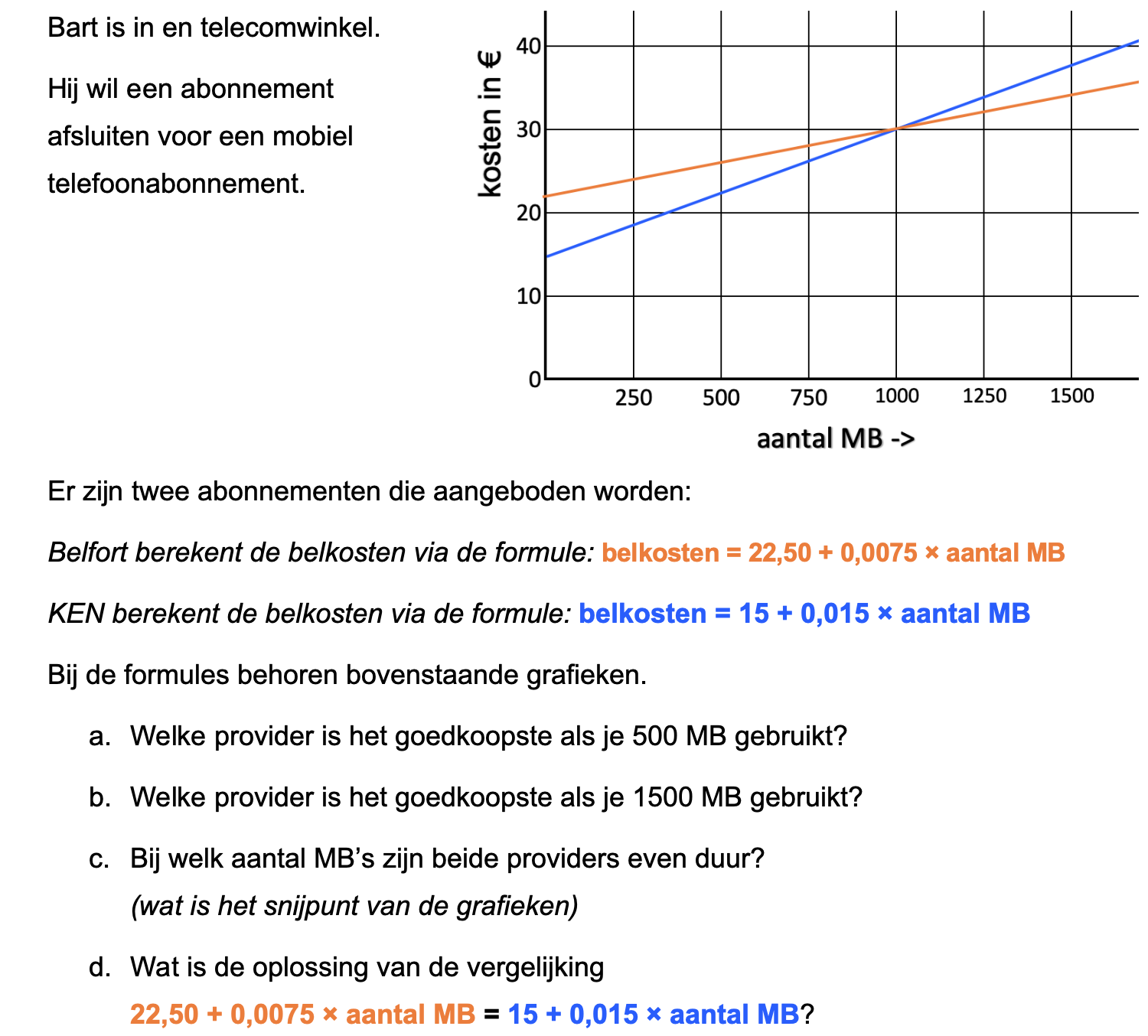
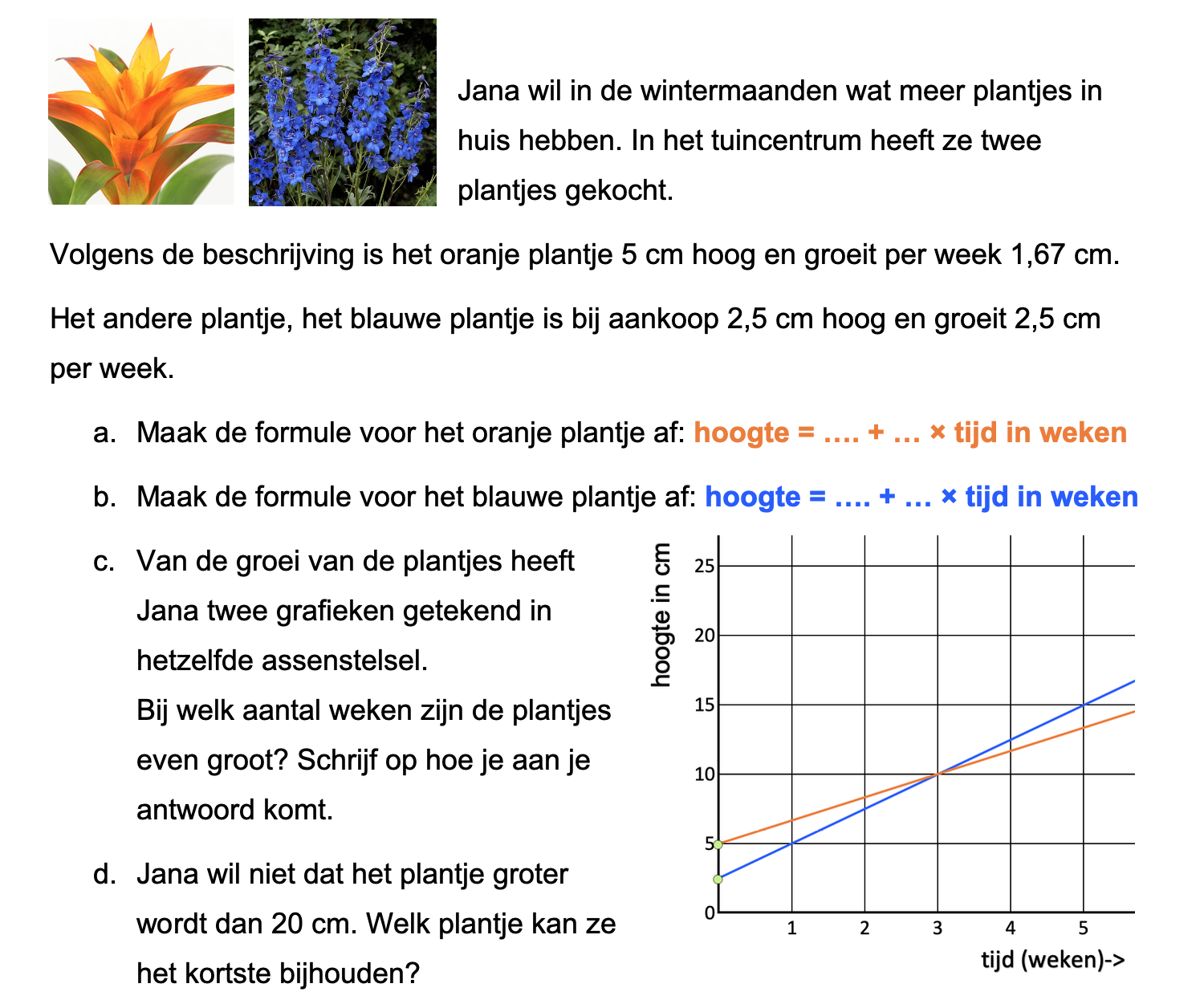

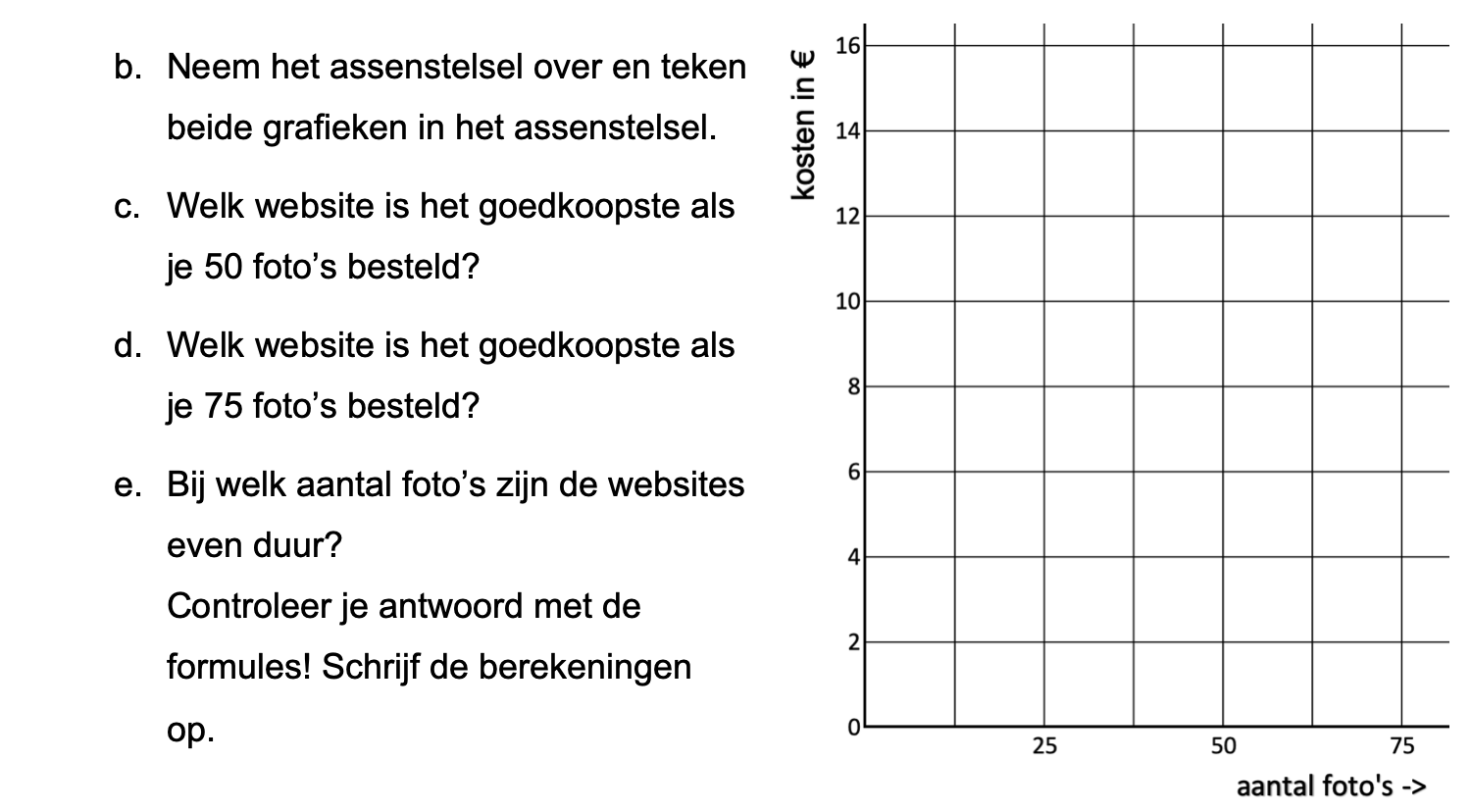
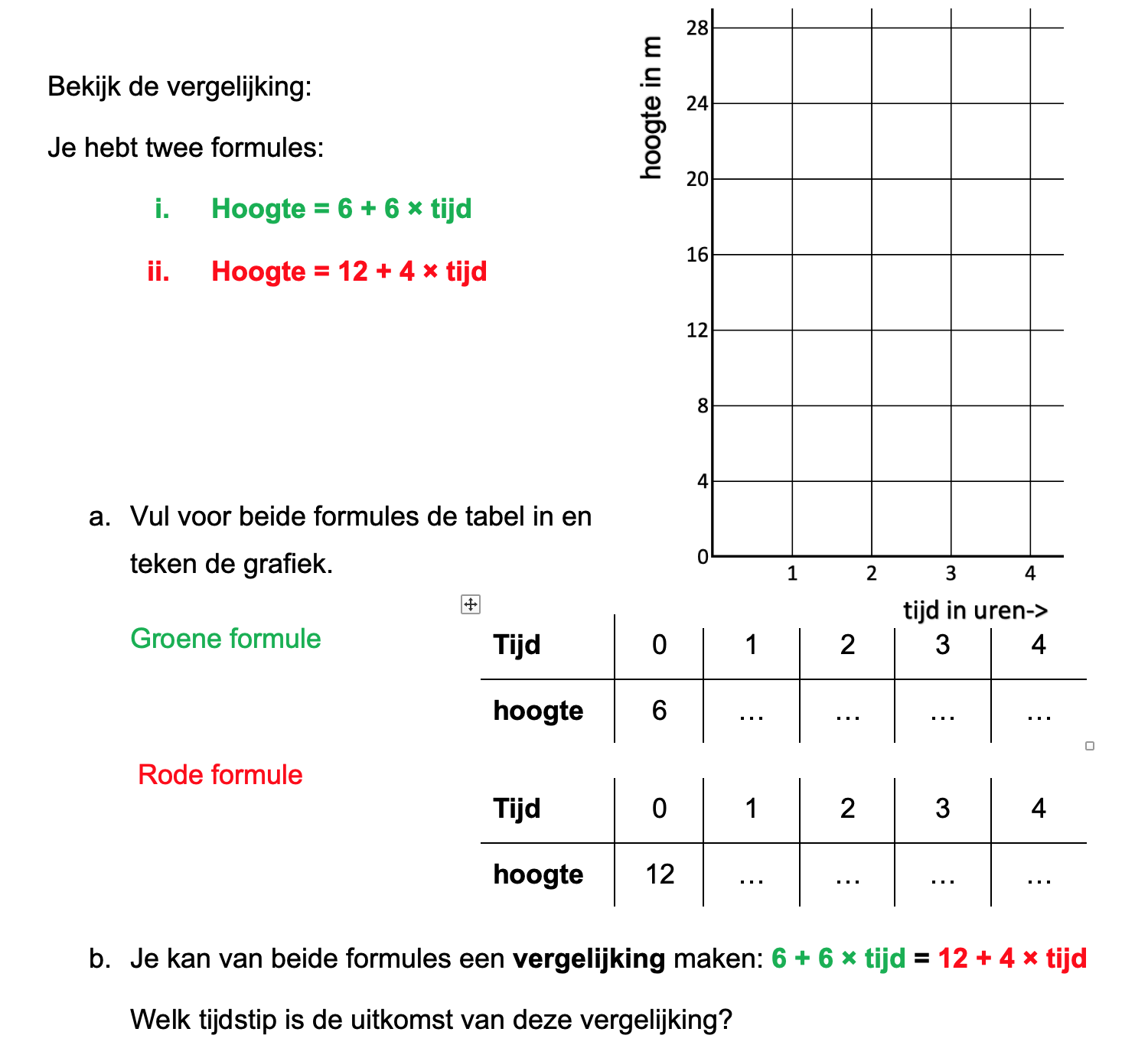

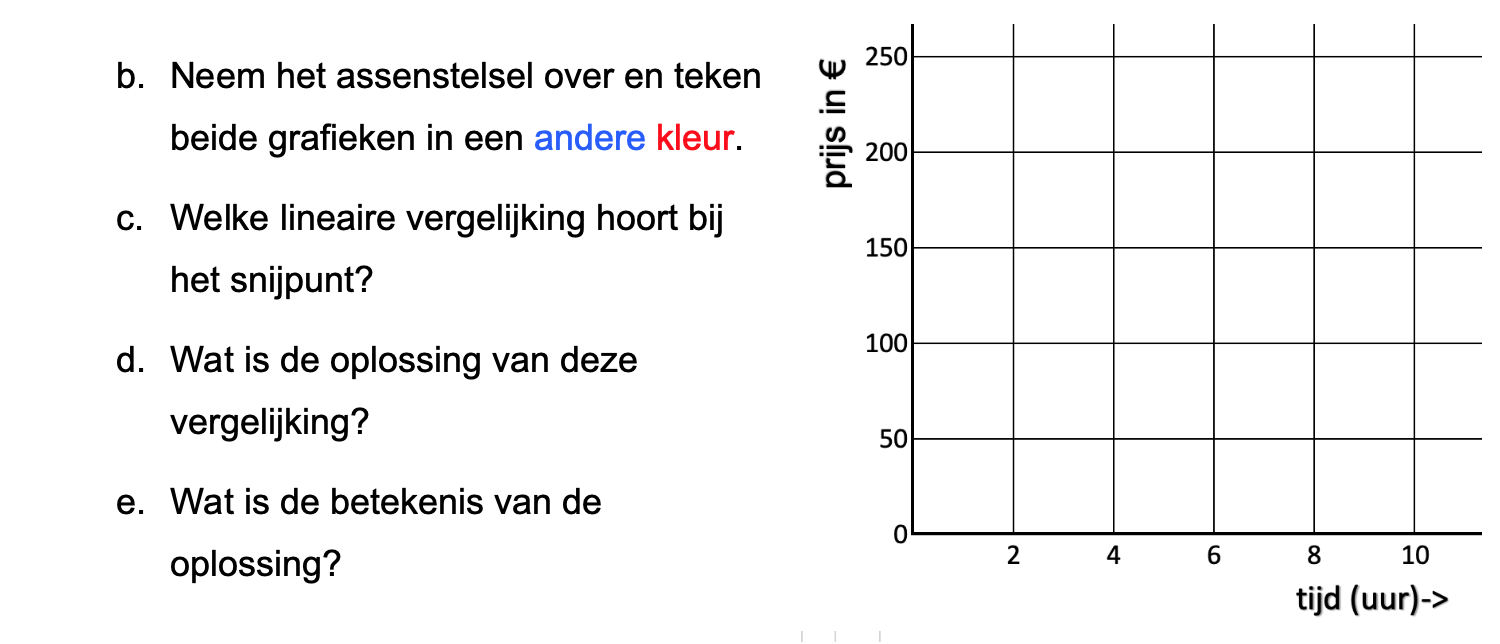


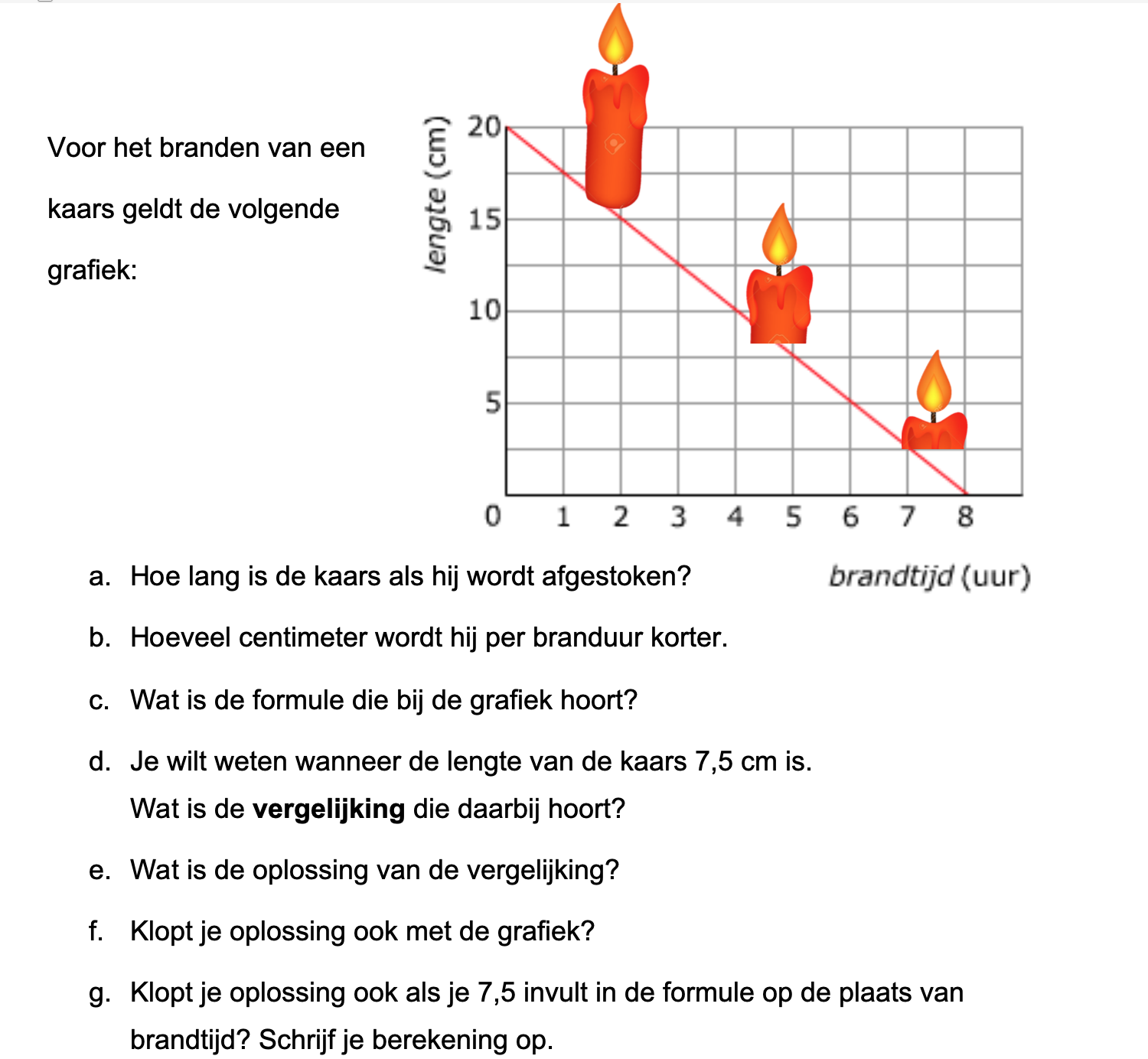





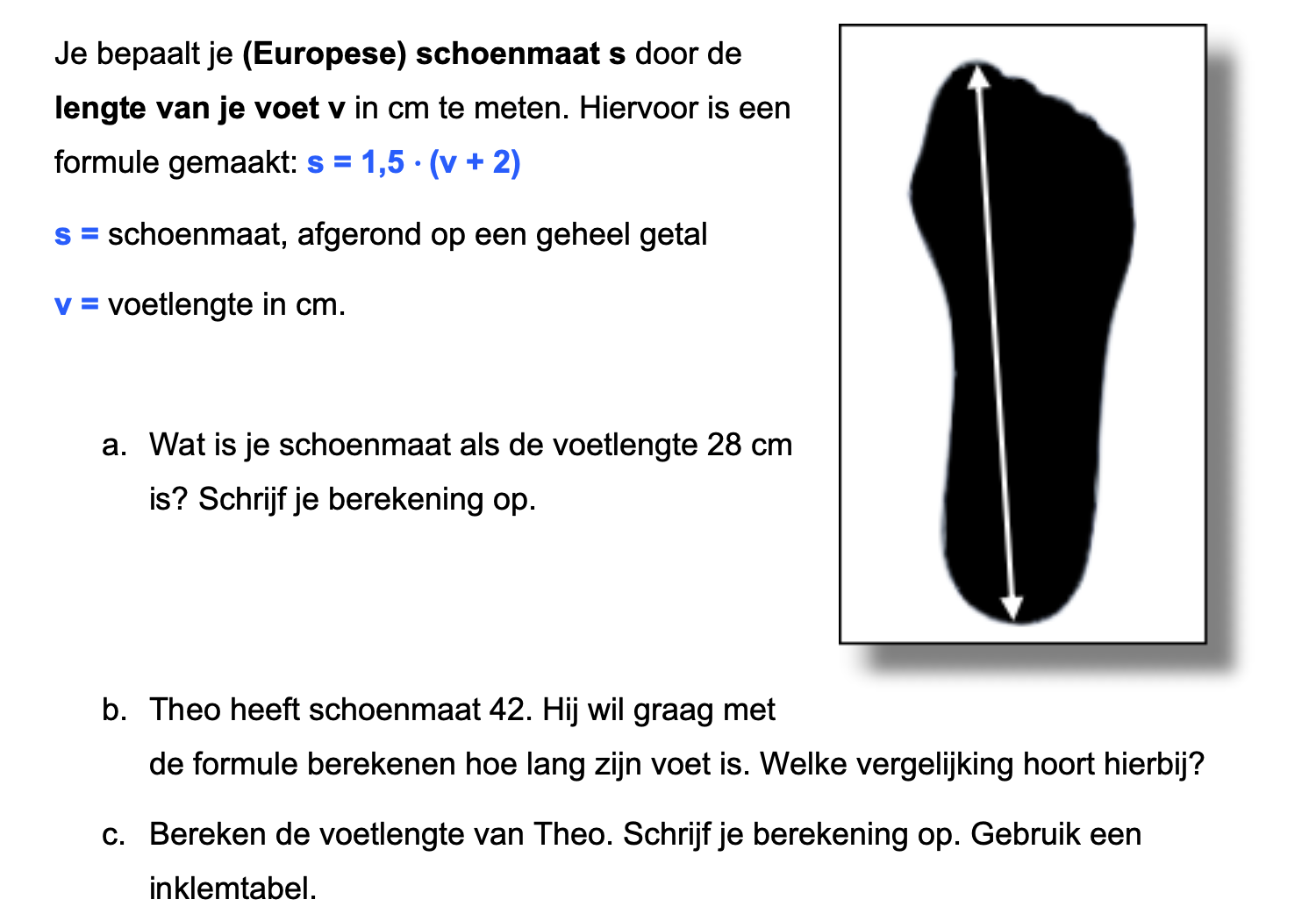
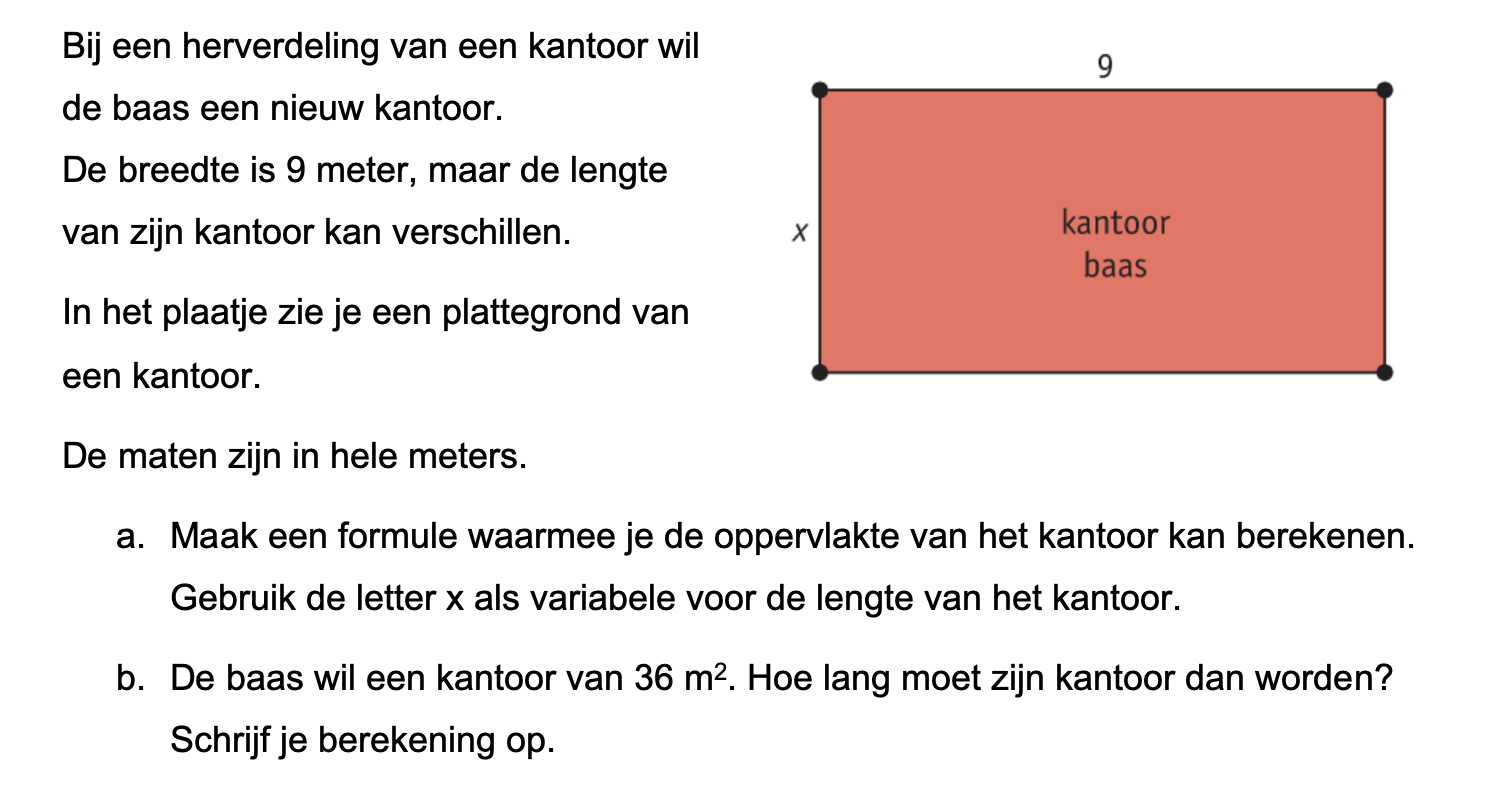





















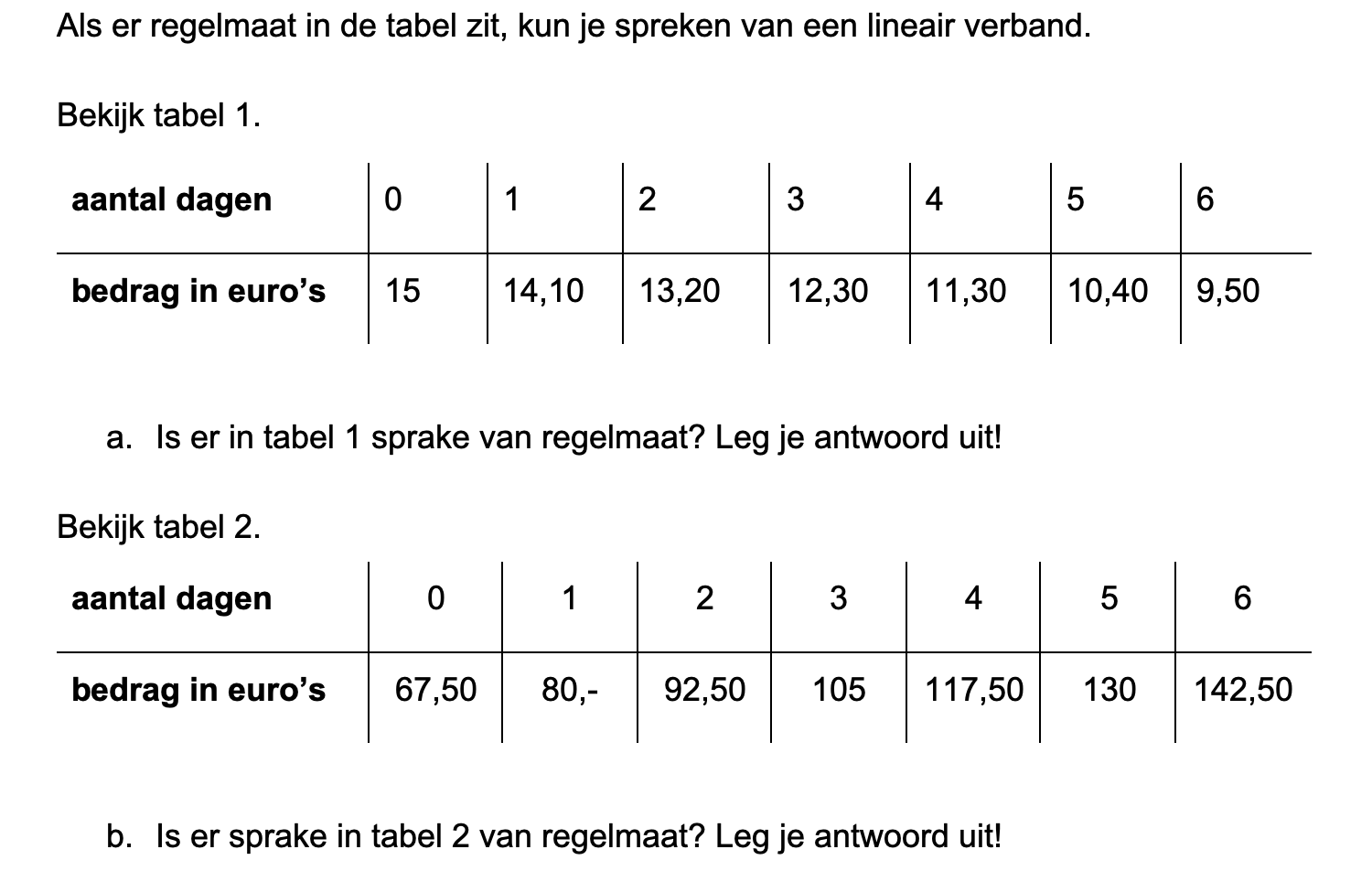
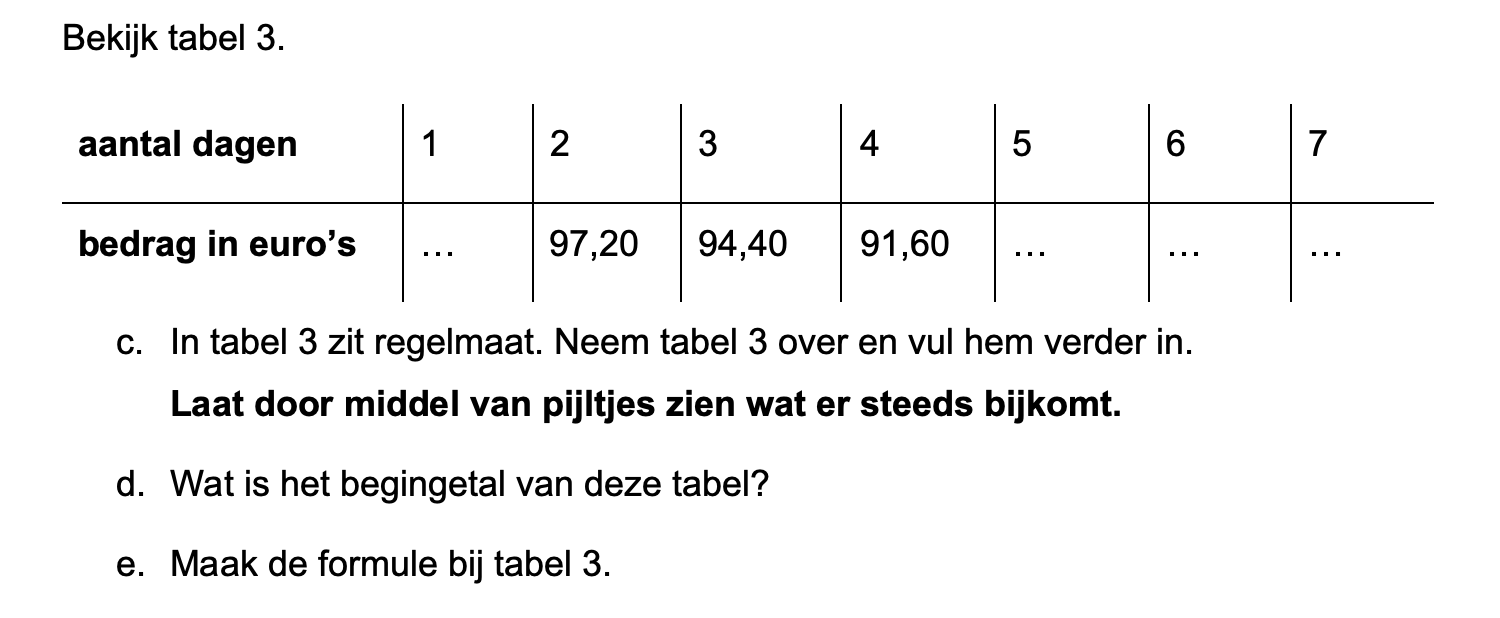
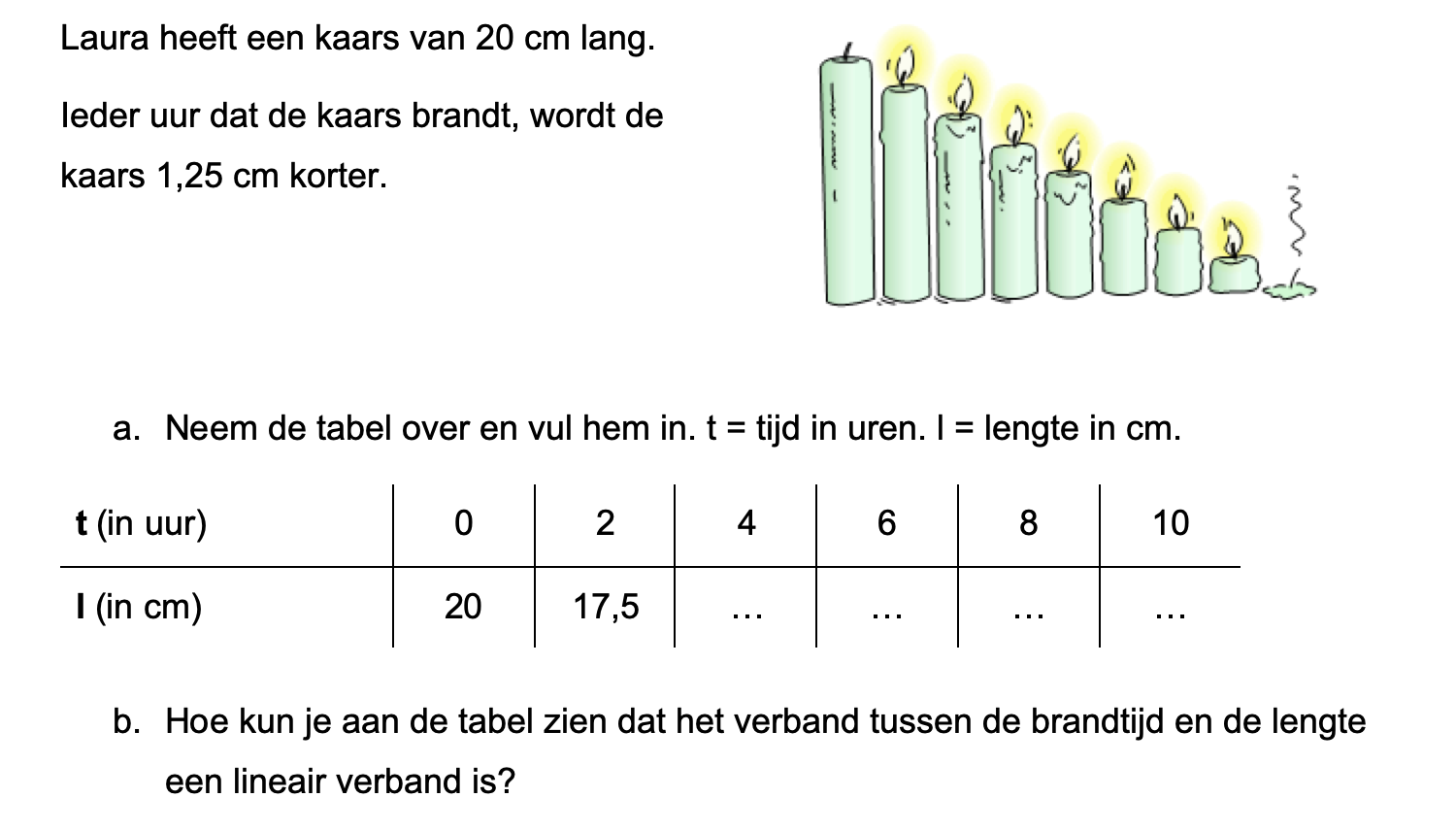
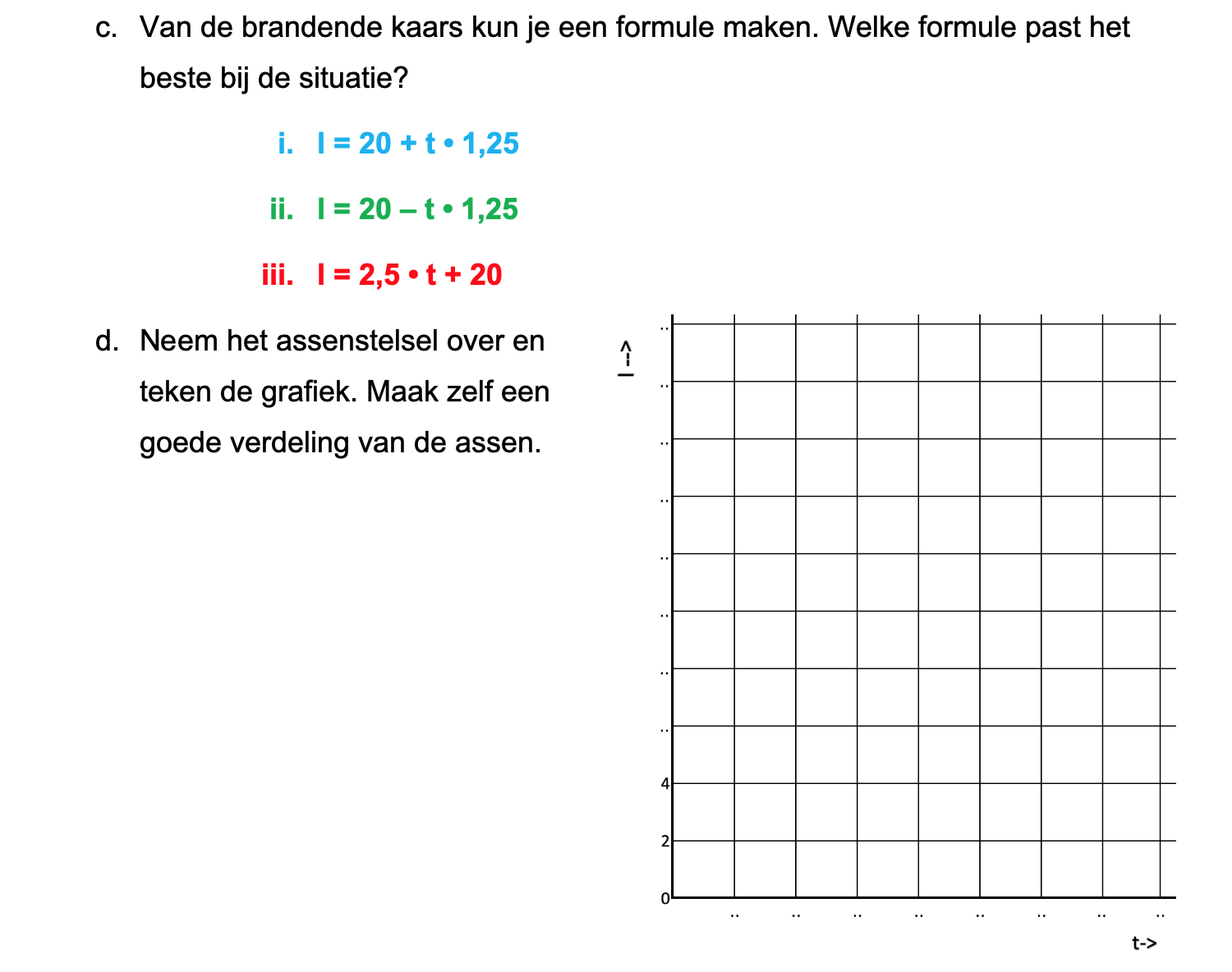
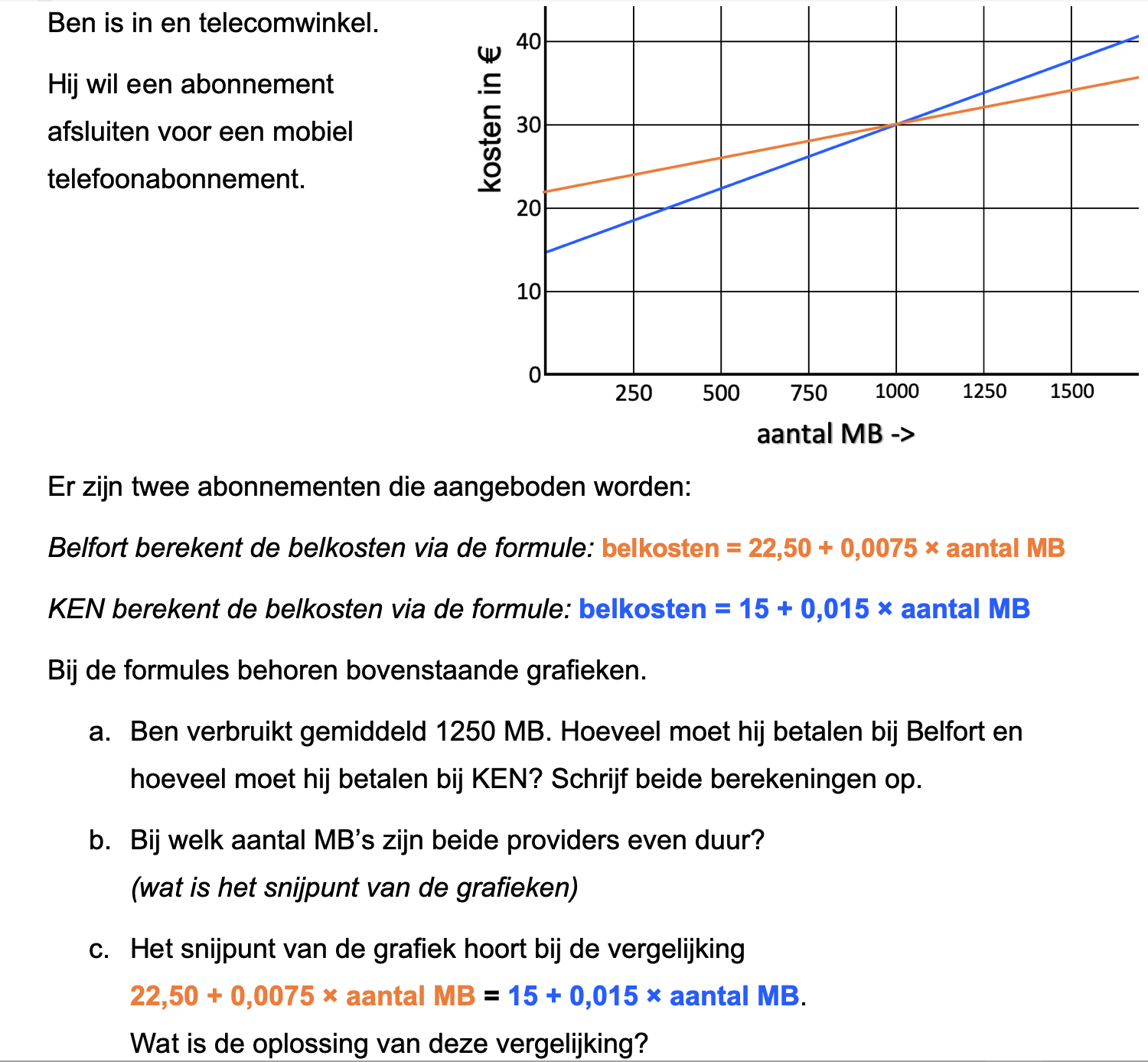
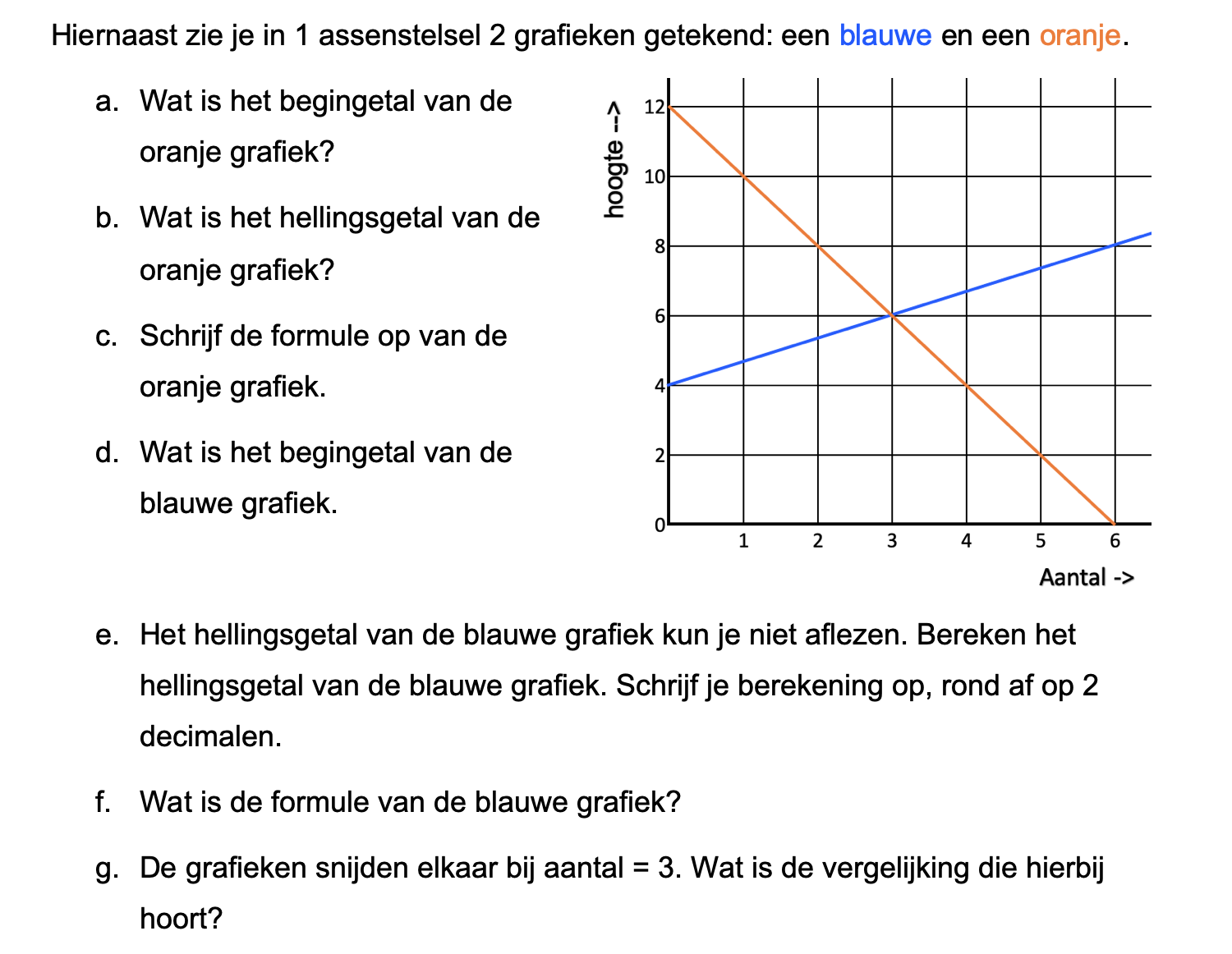



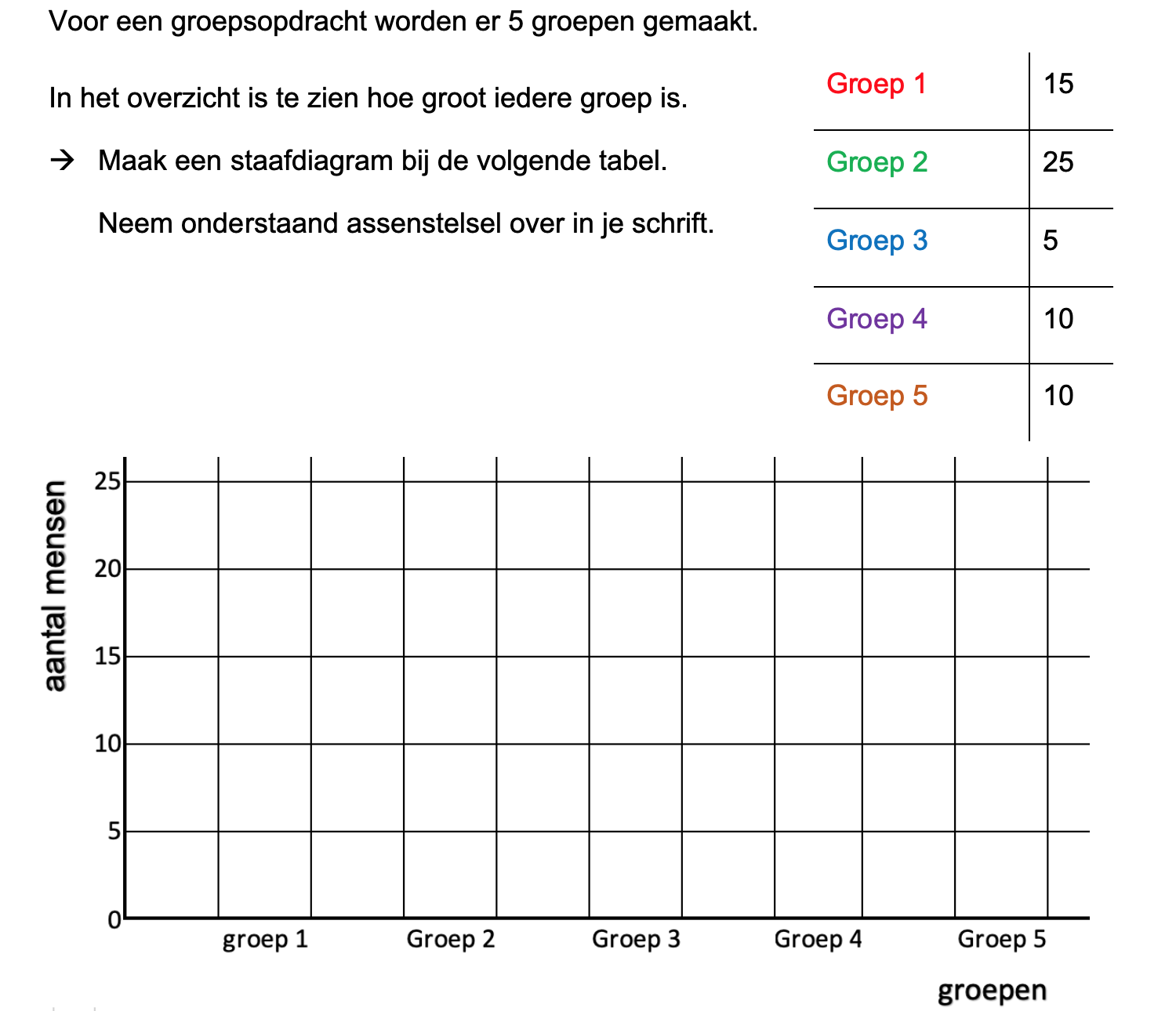
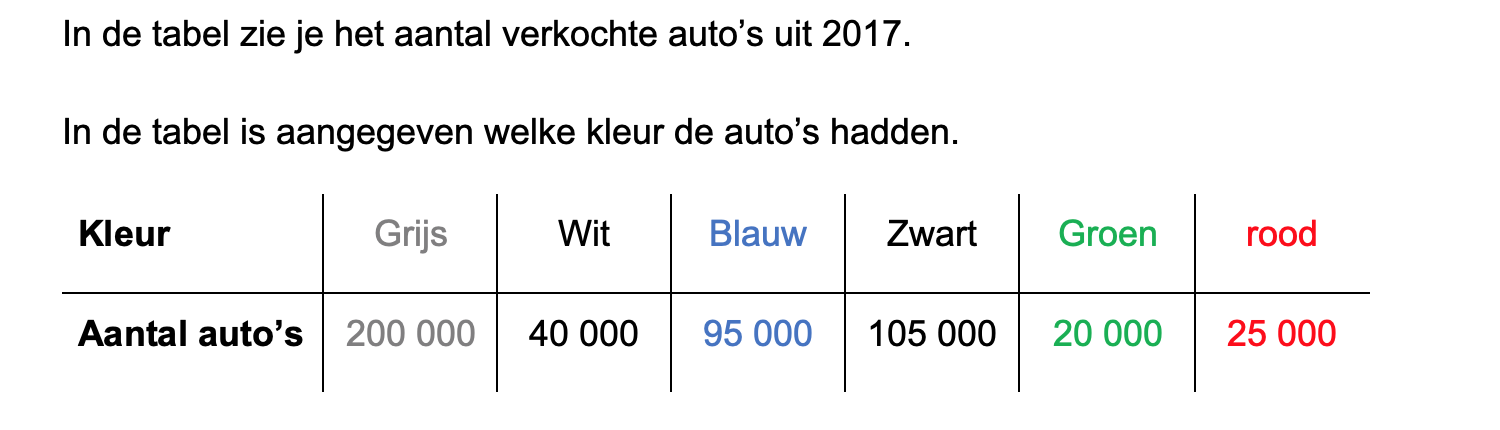
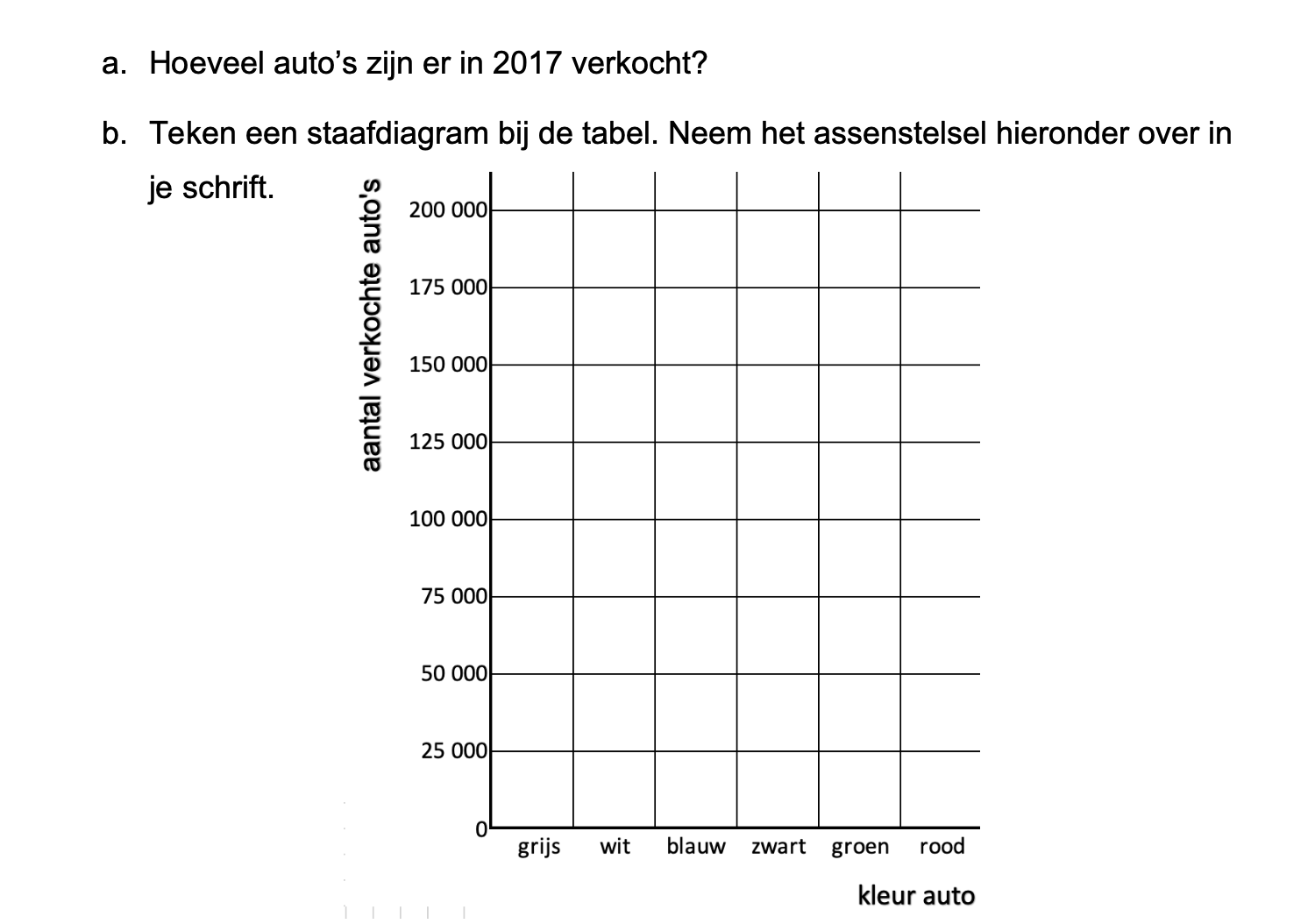
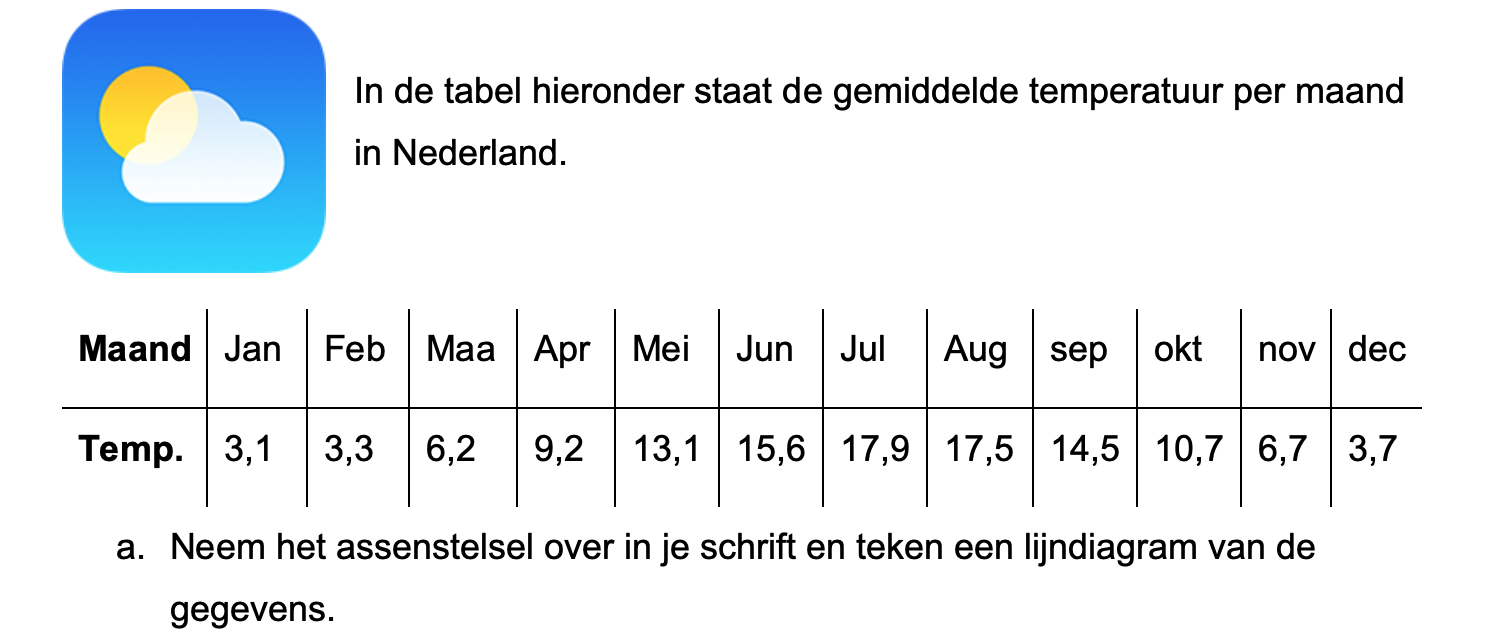
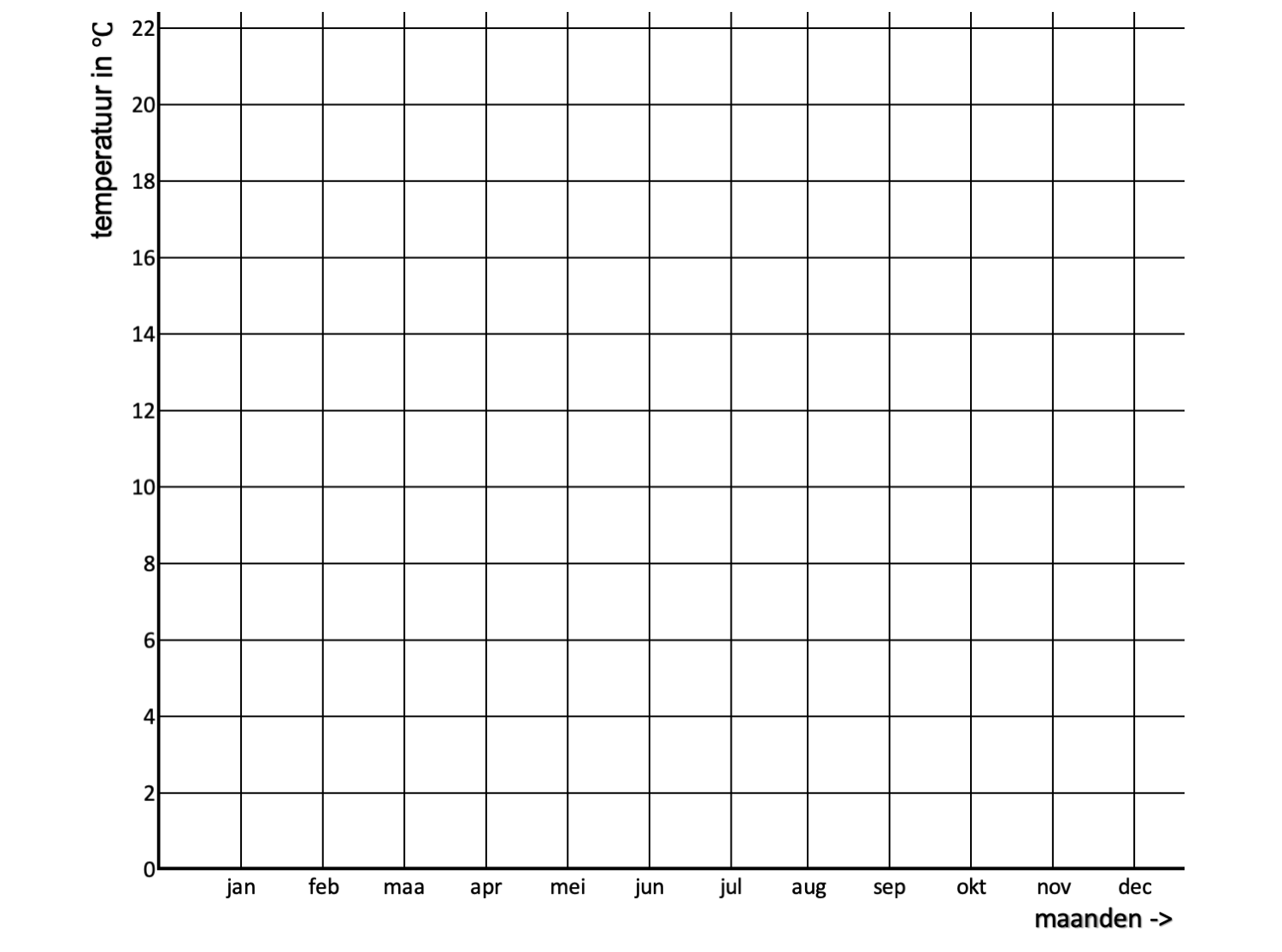
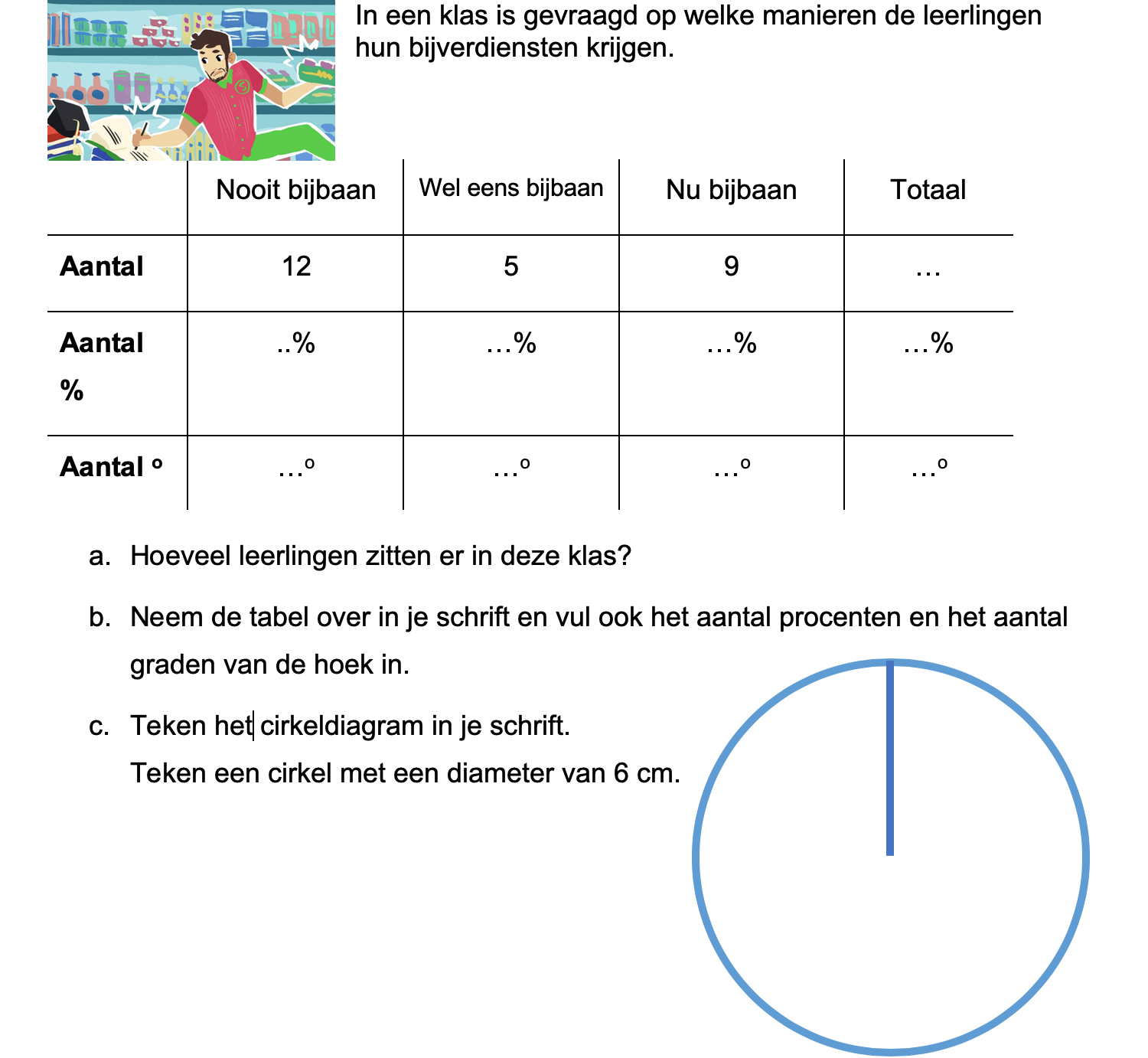
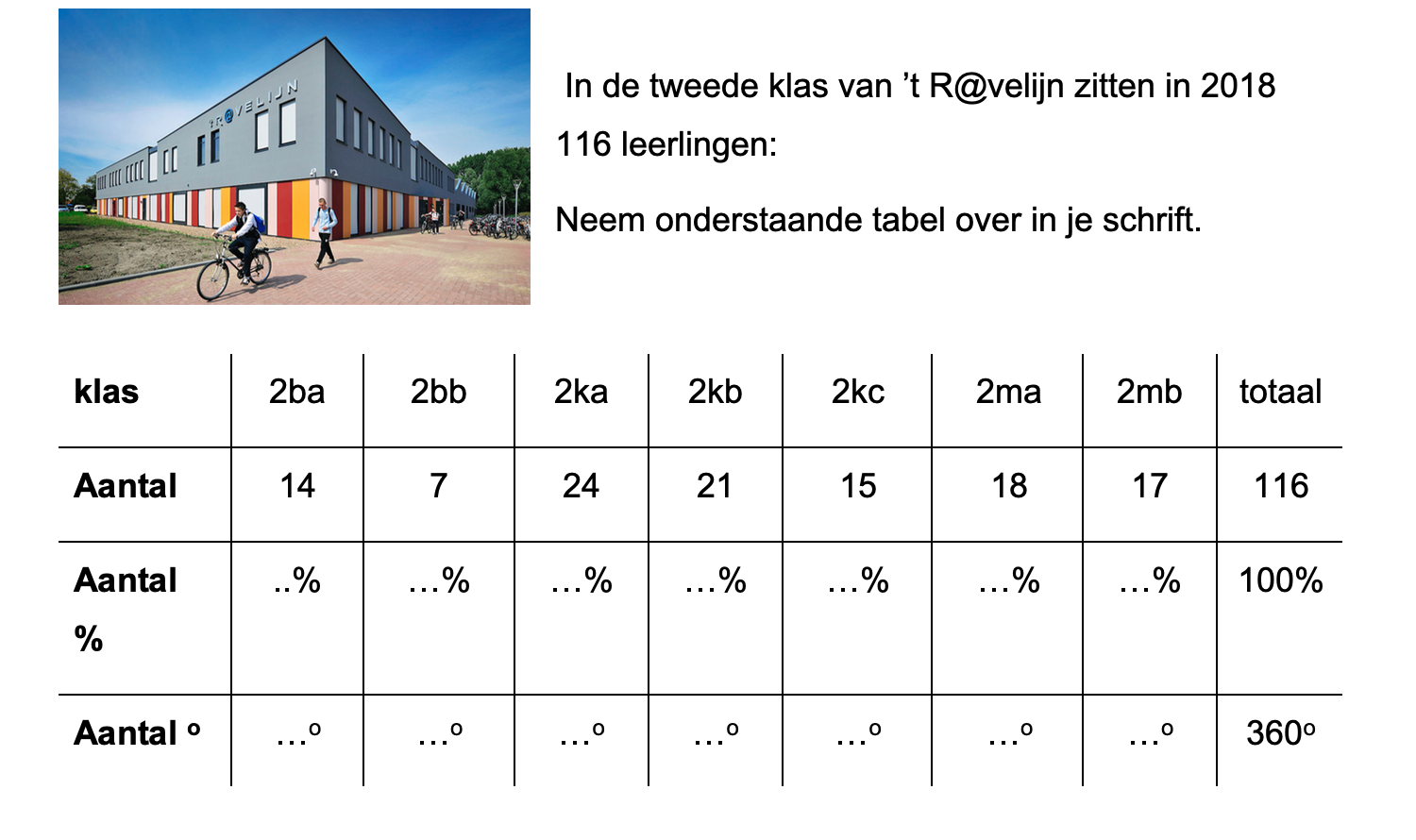
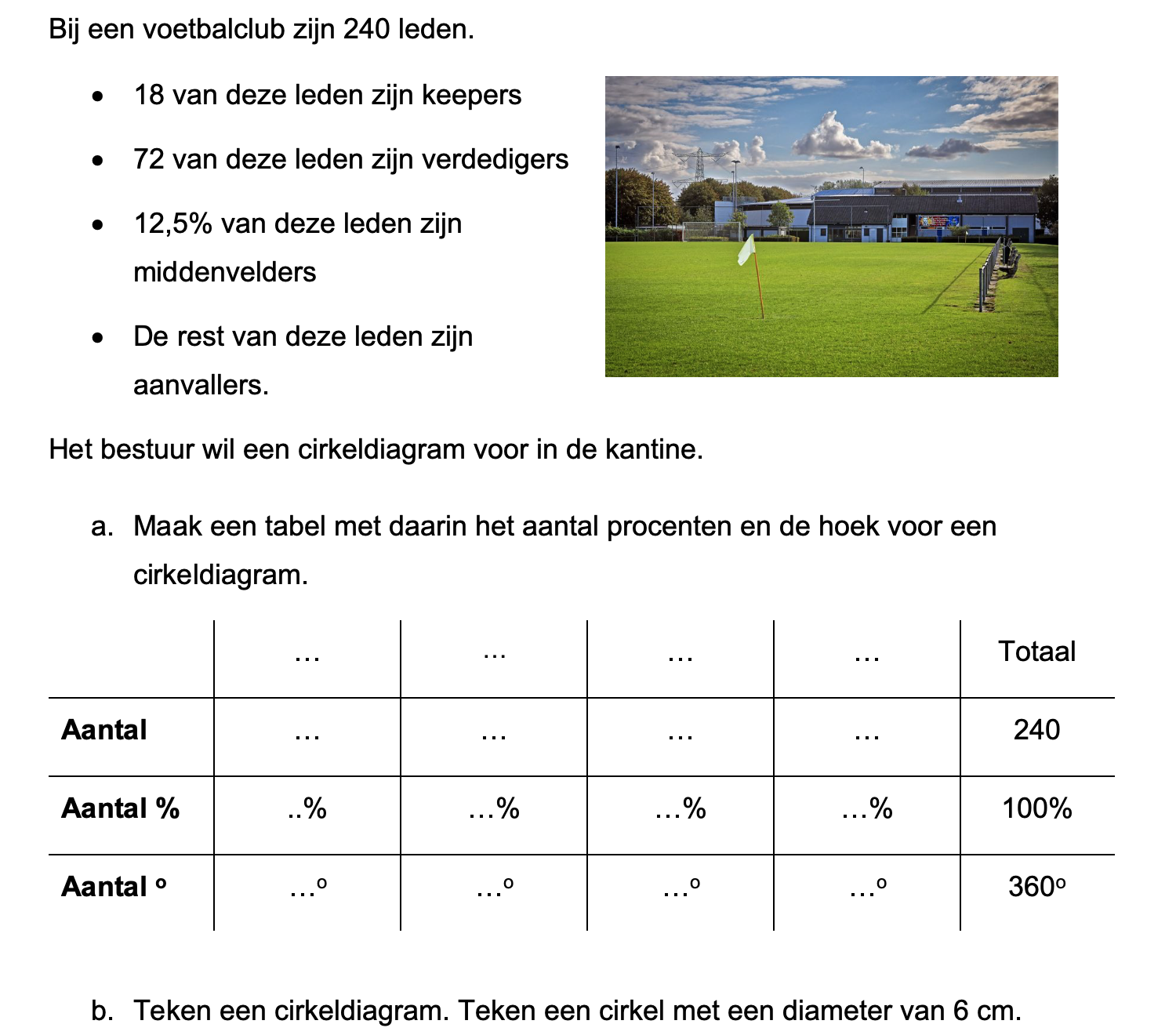
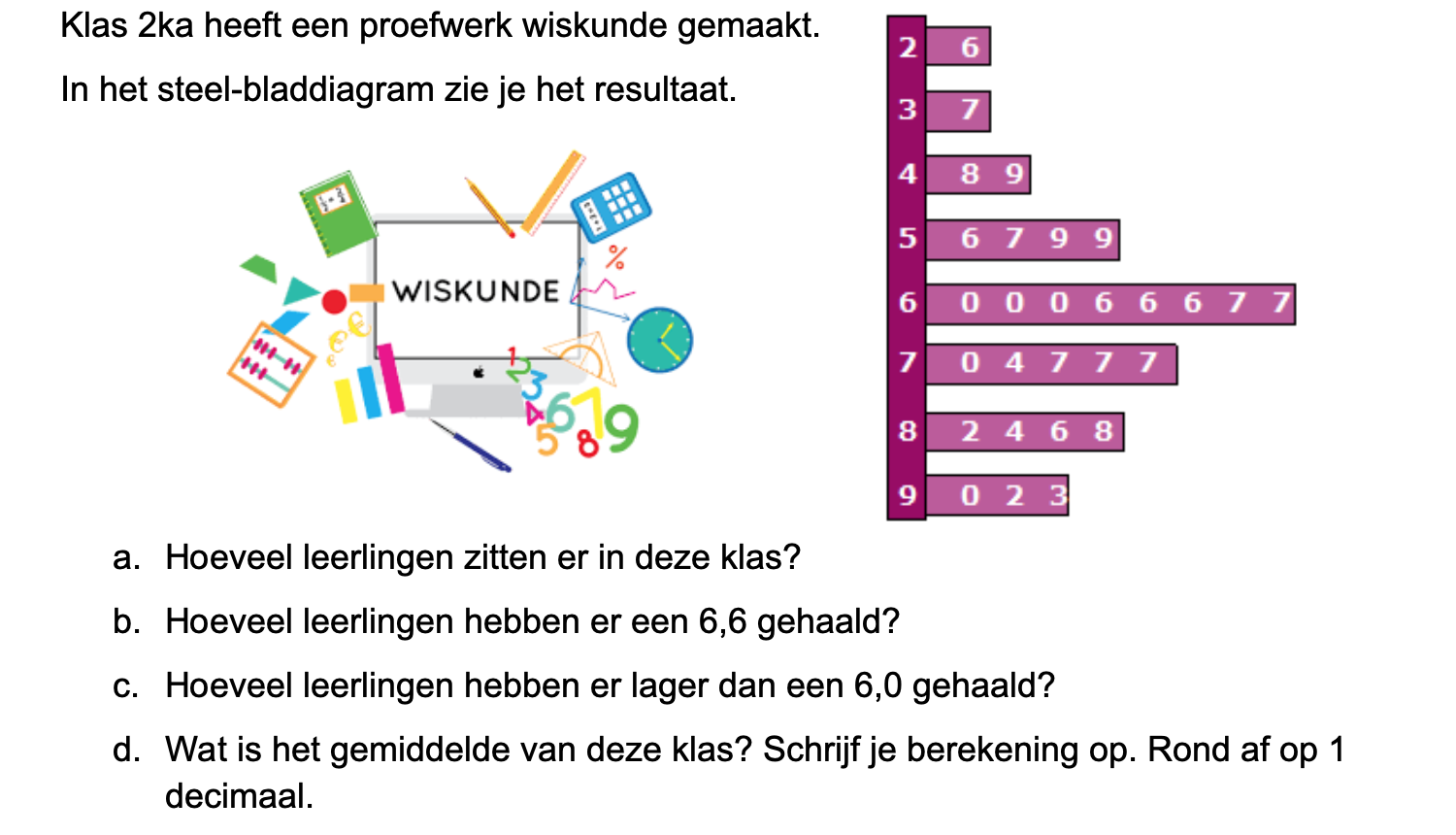
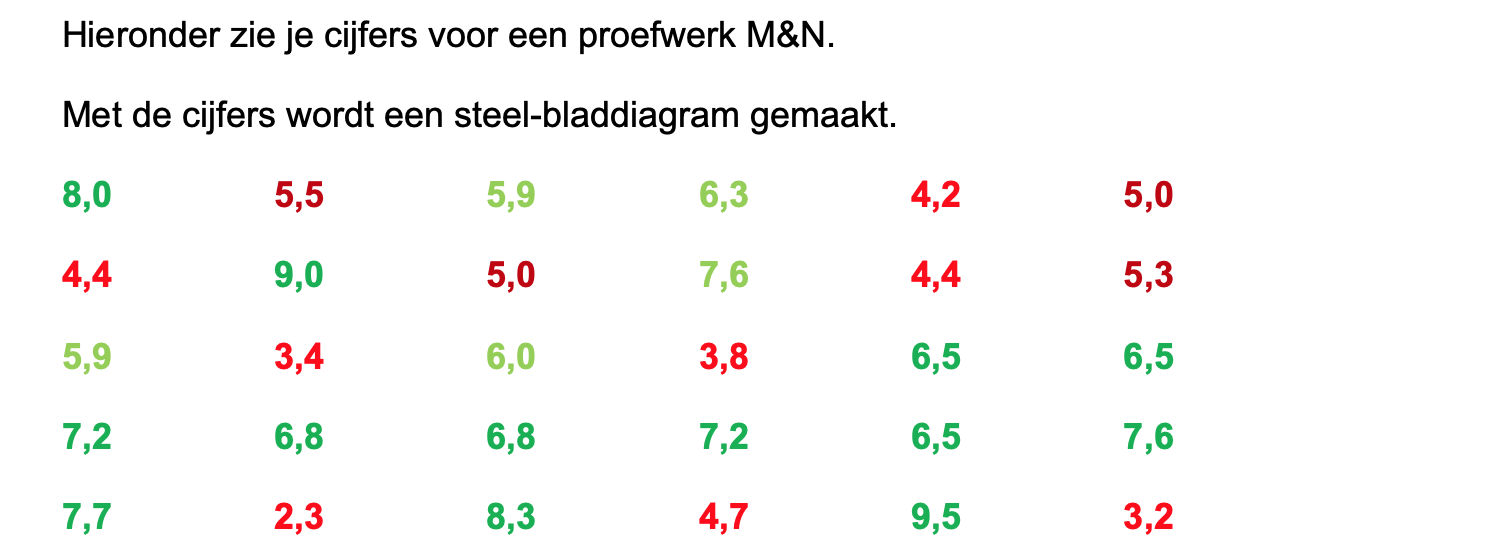
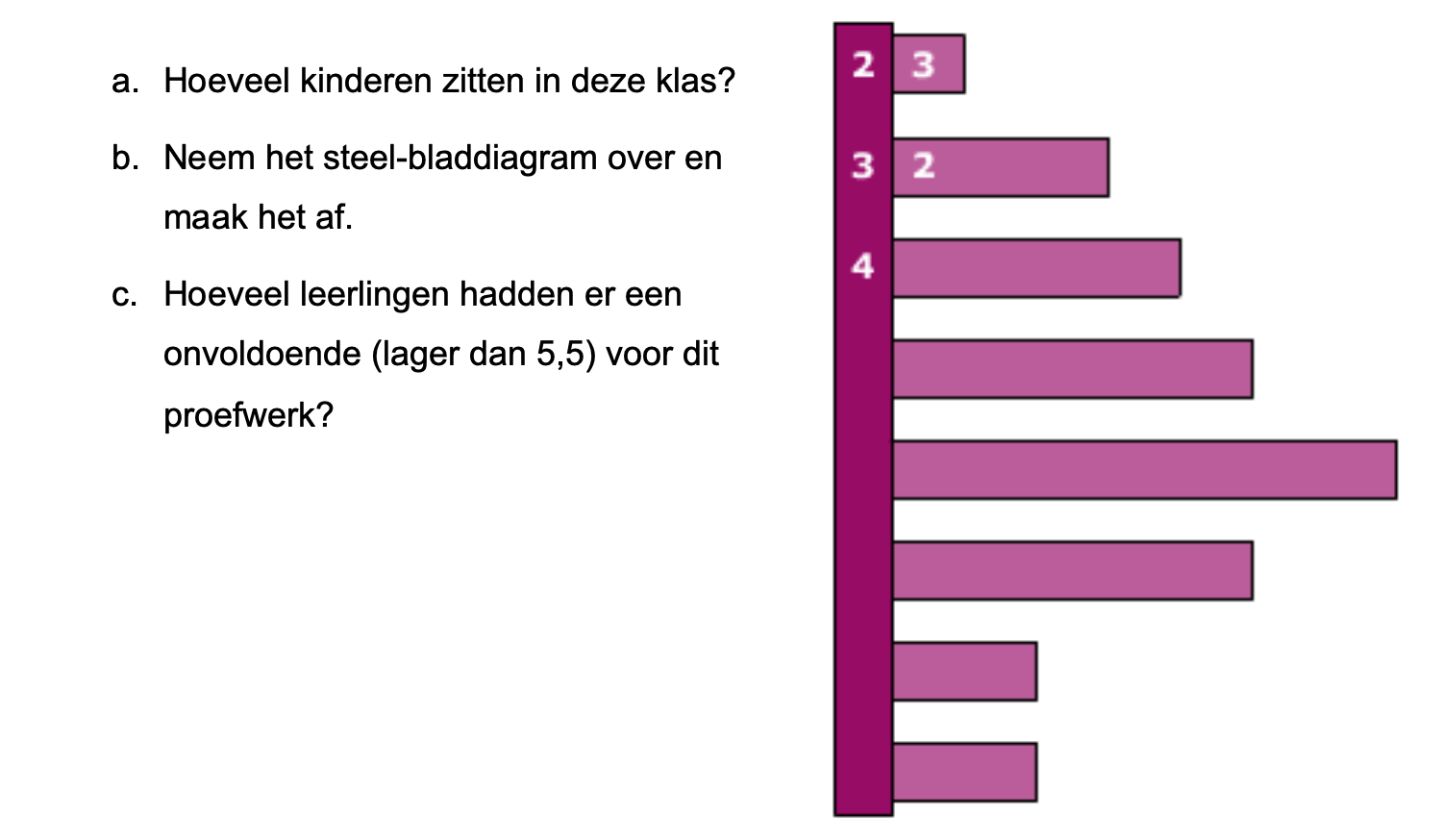
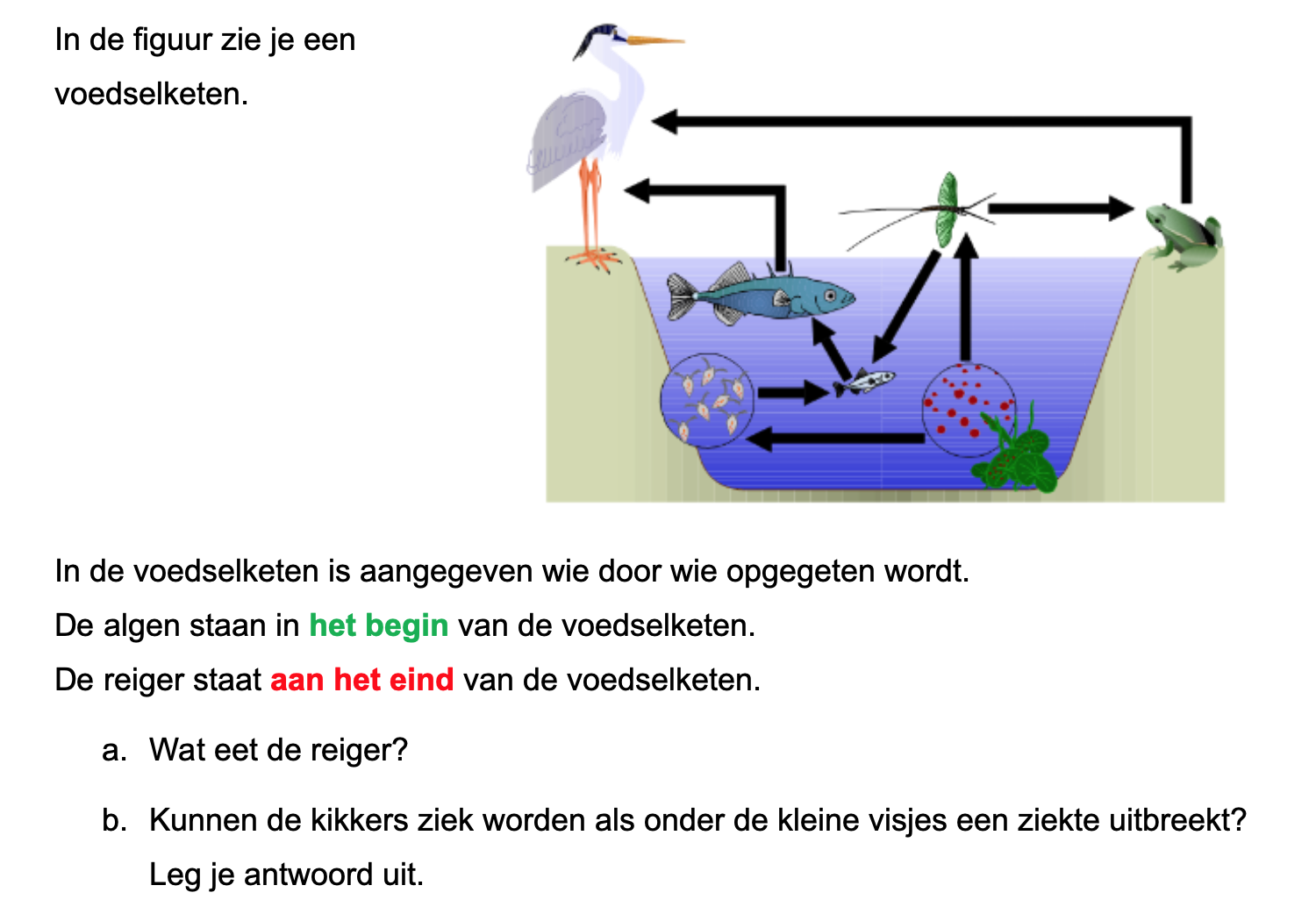
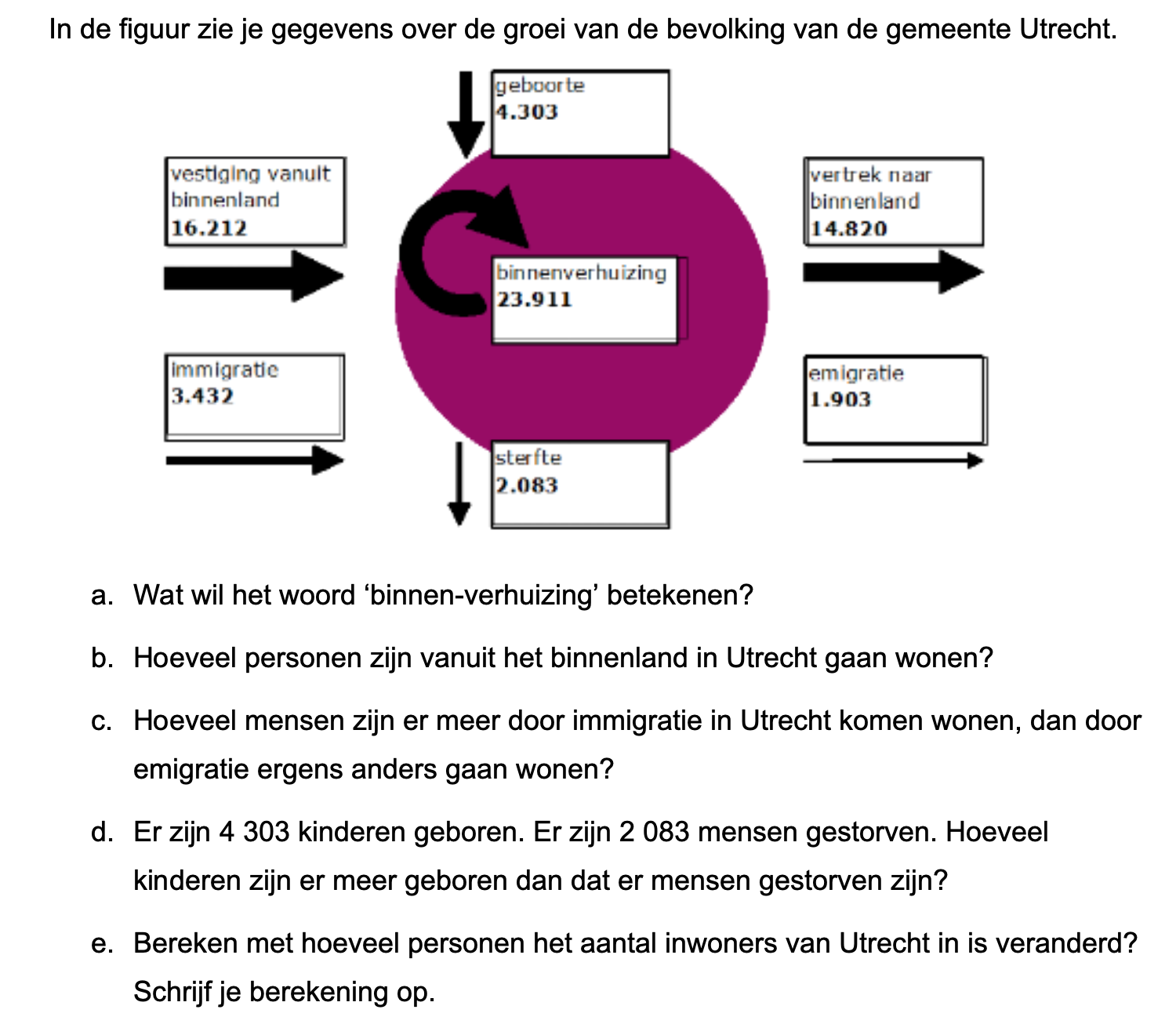
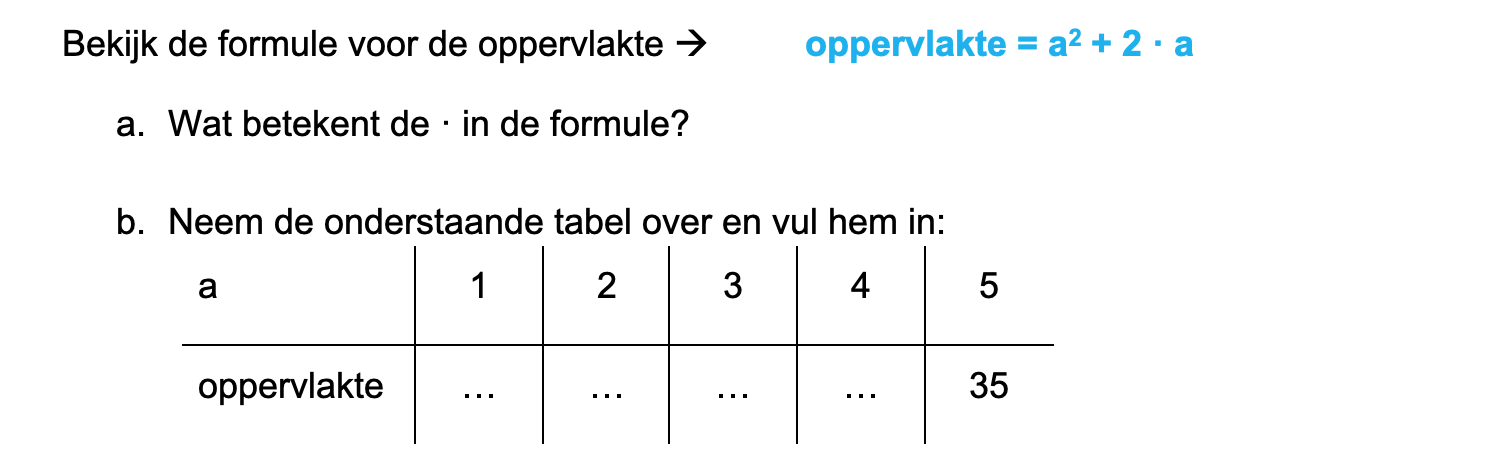
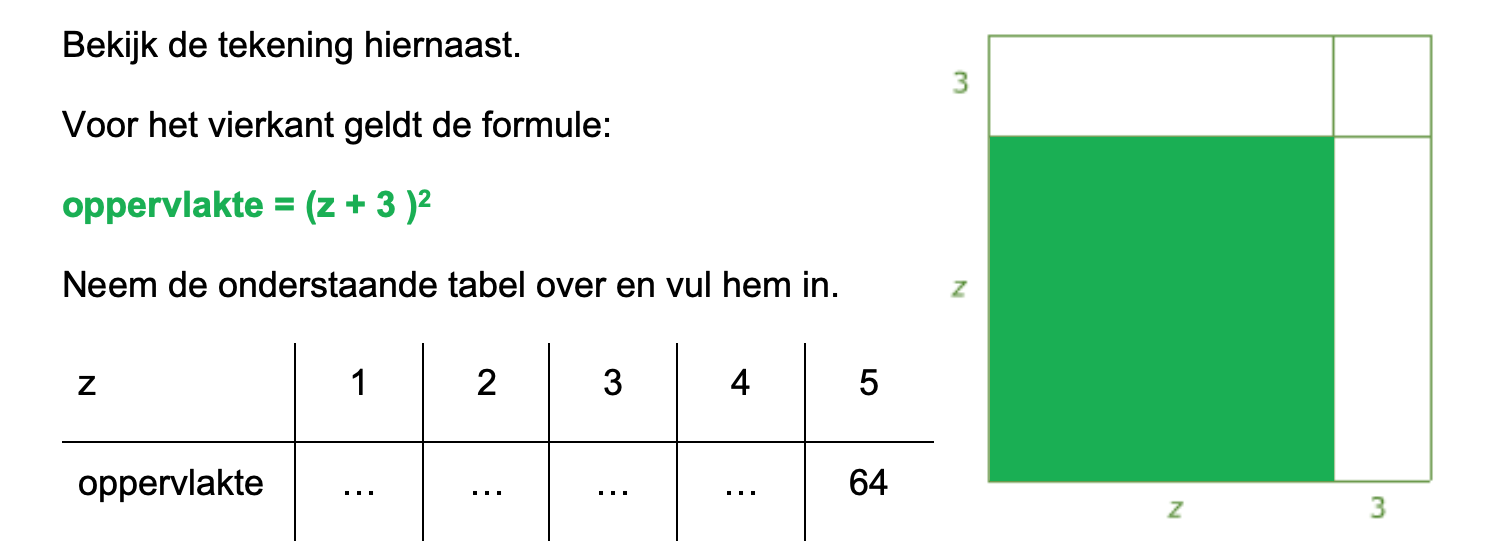
 Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:





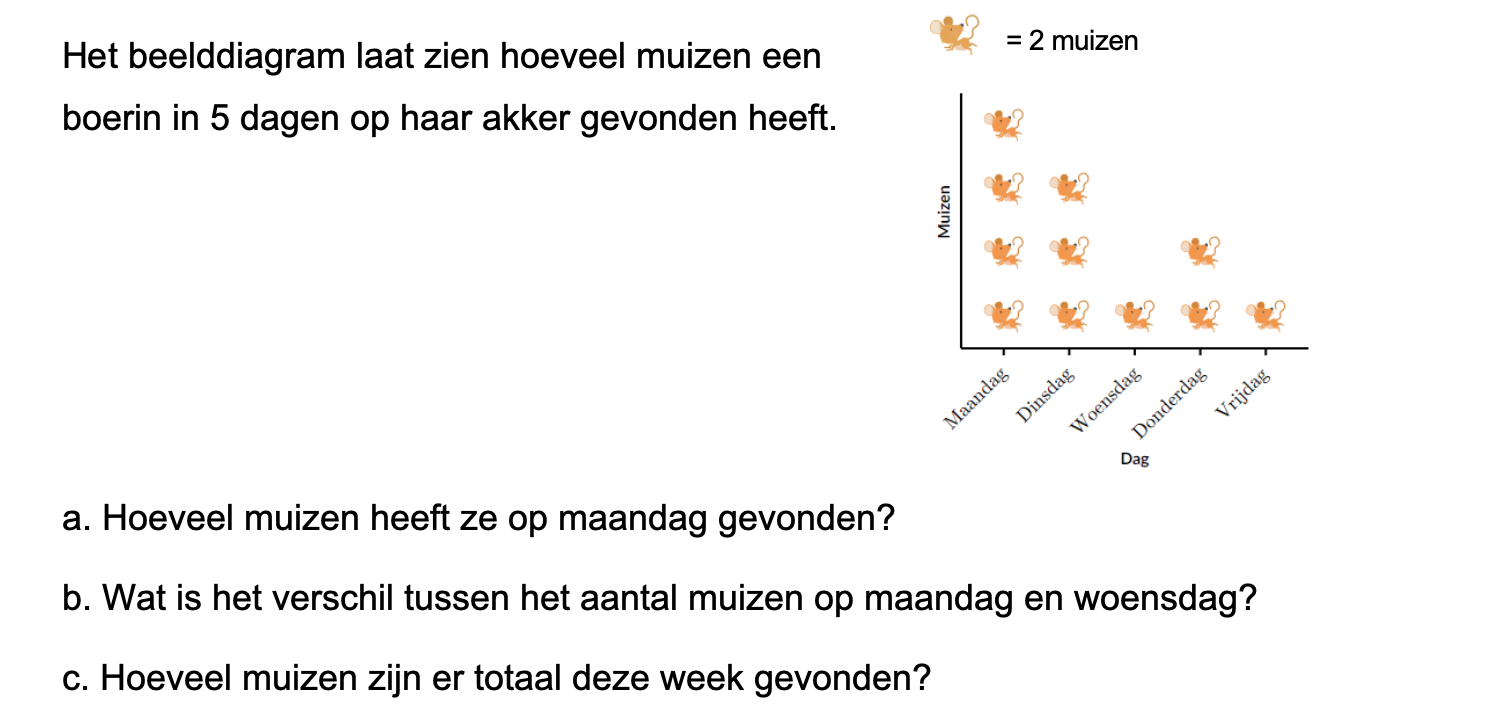





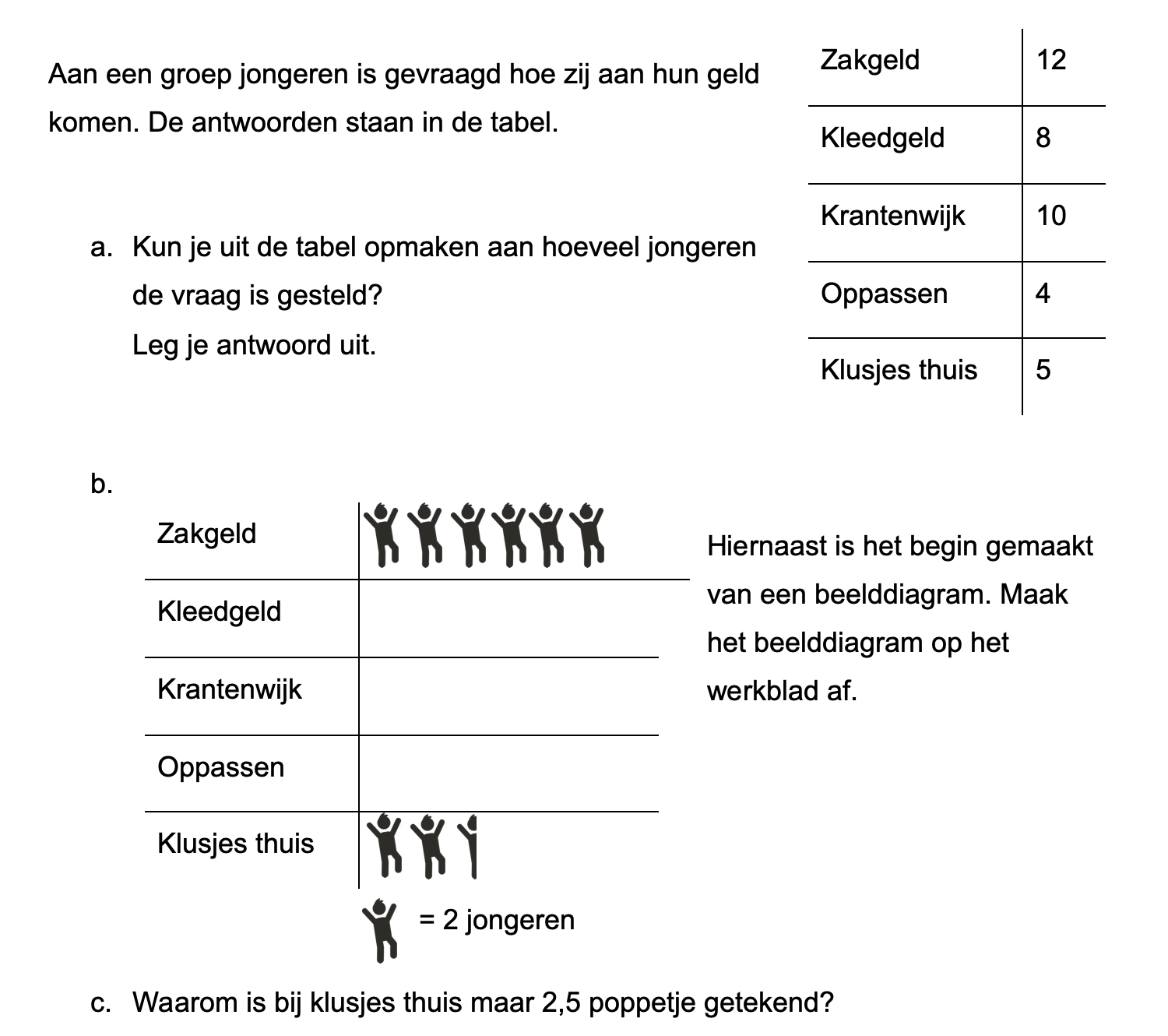
































































/f.jwwb.nl%2Fpublic%2Fg%2Fo%2Fh%2Fmichelroozen%2Fsvbfpp%2Fsamenwerken1.jpg)























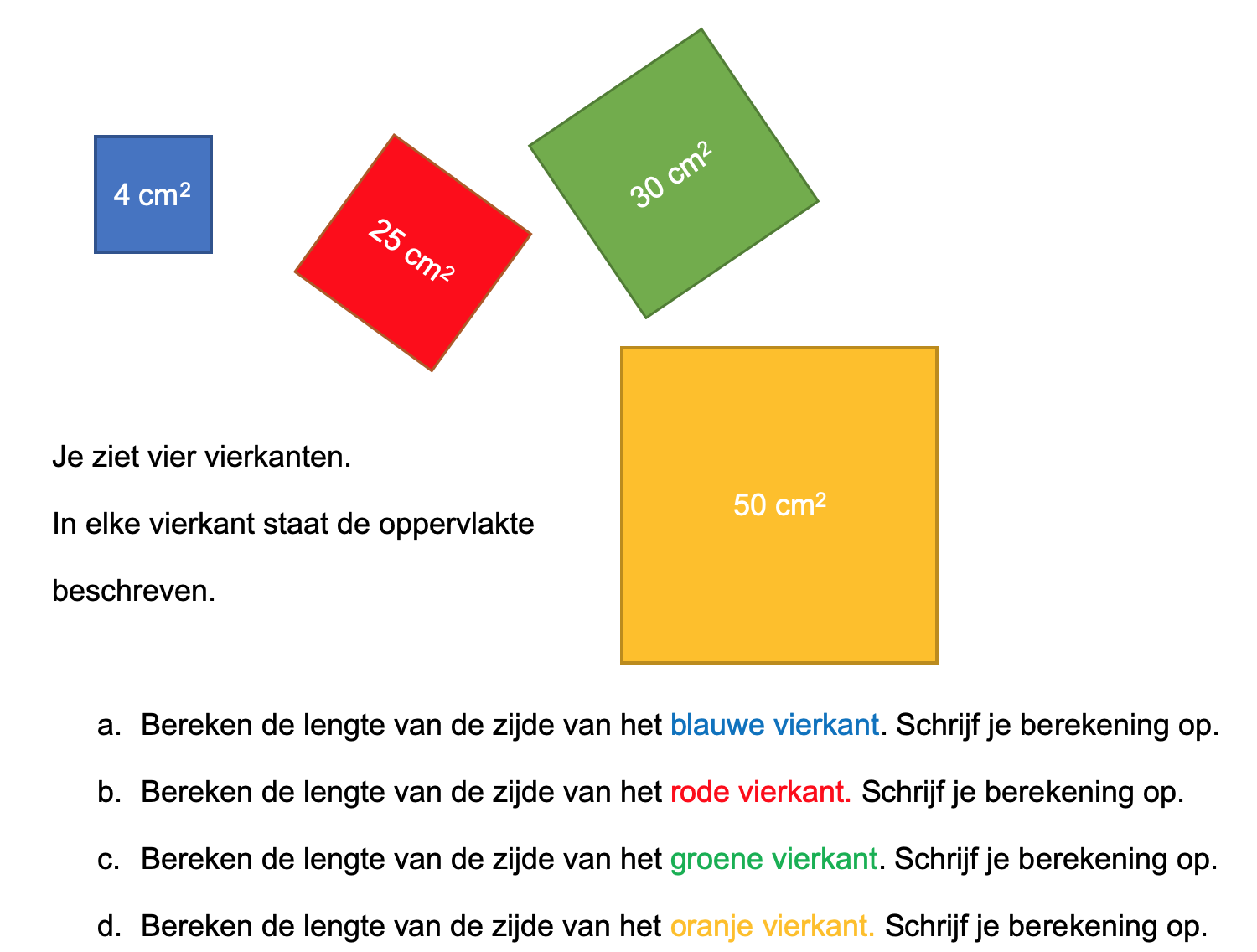








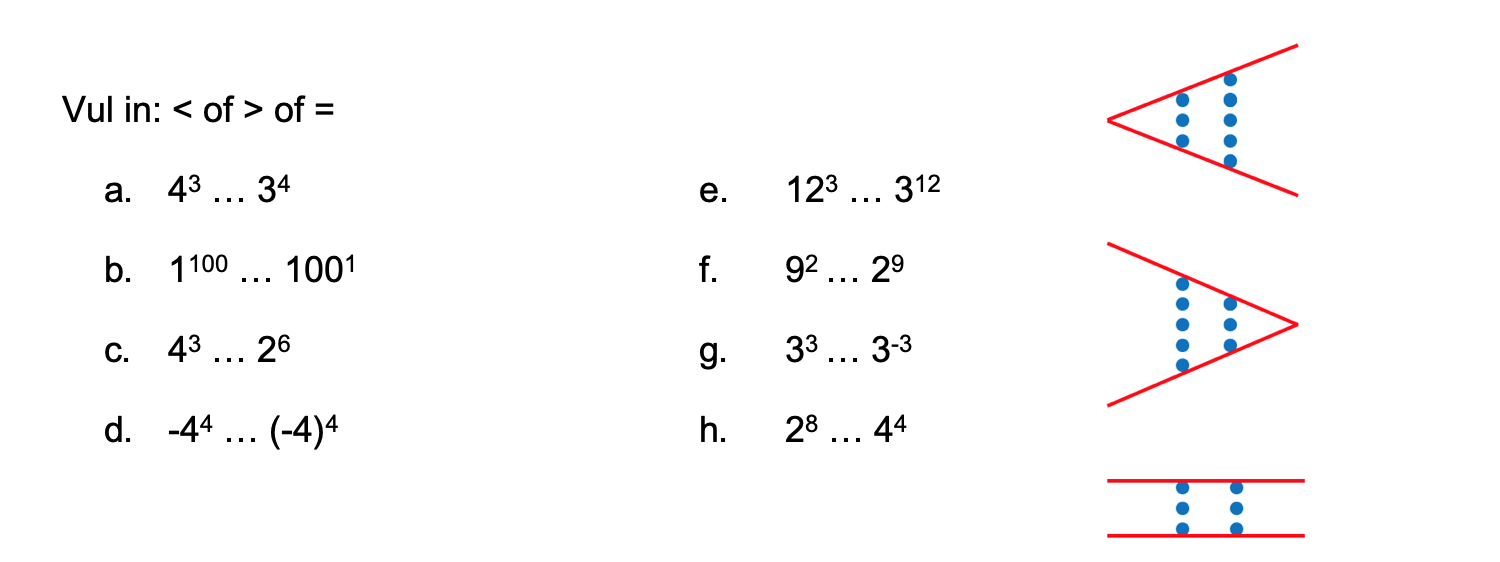
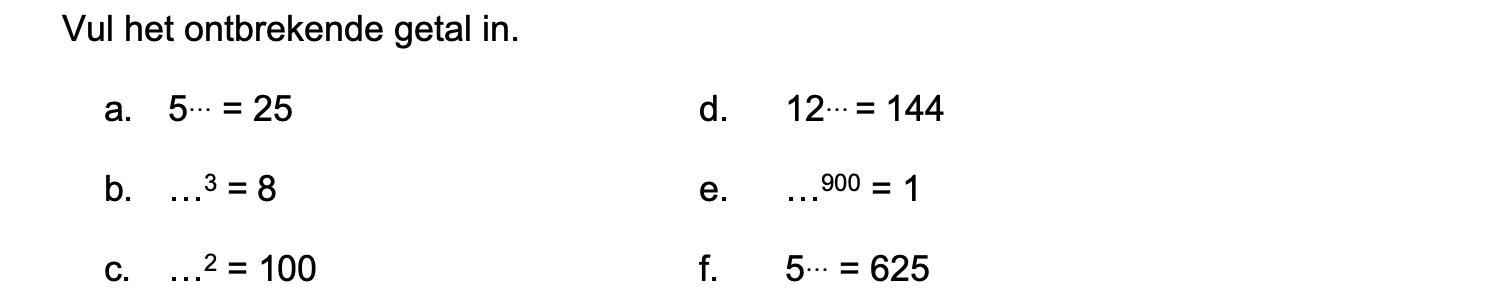


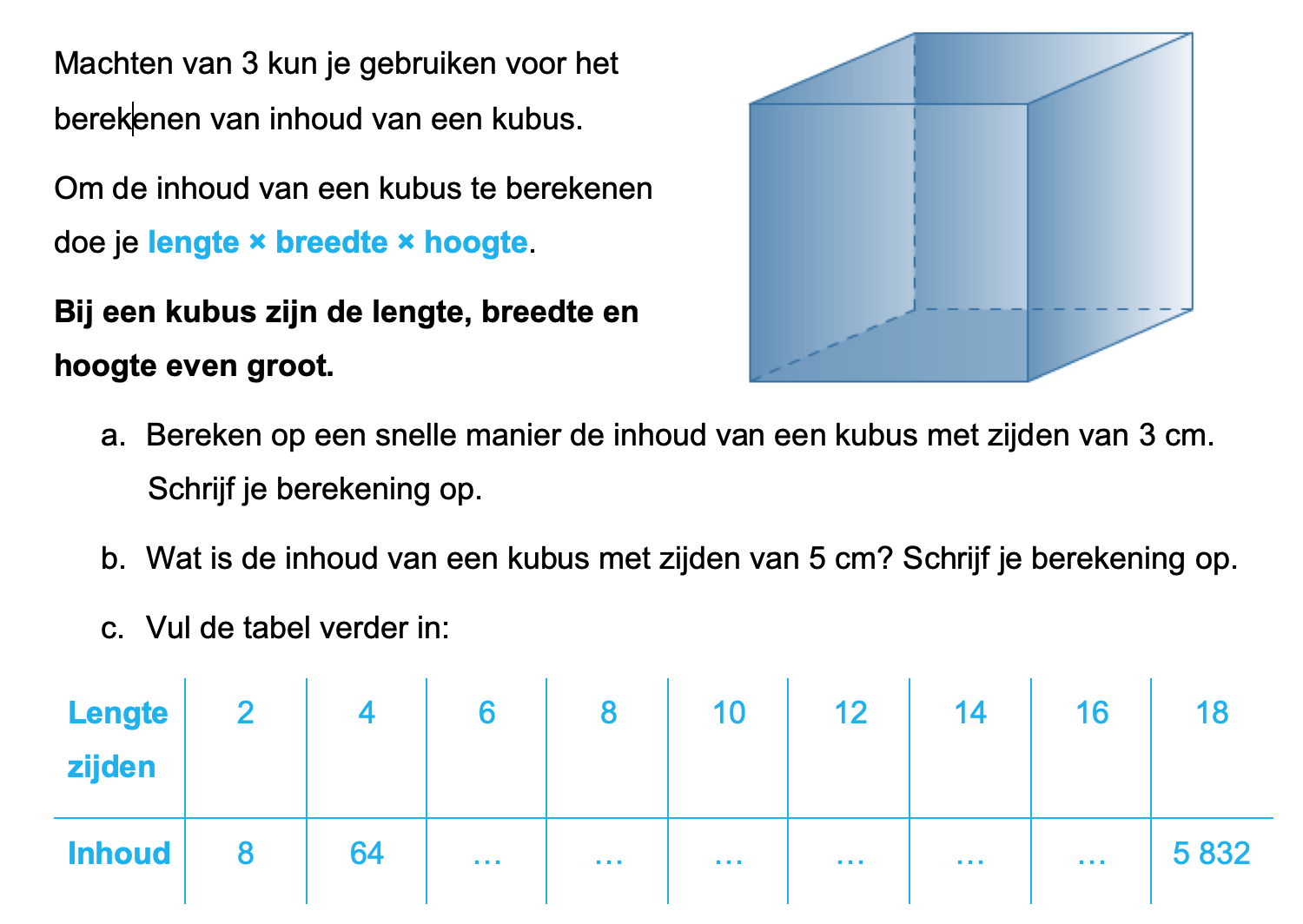

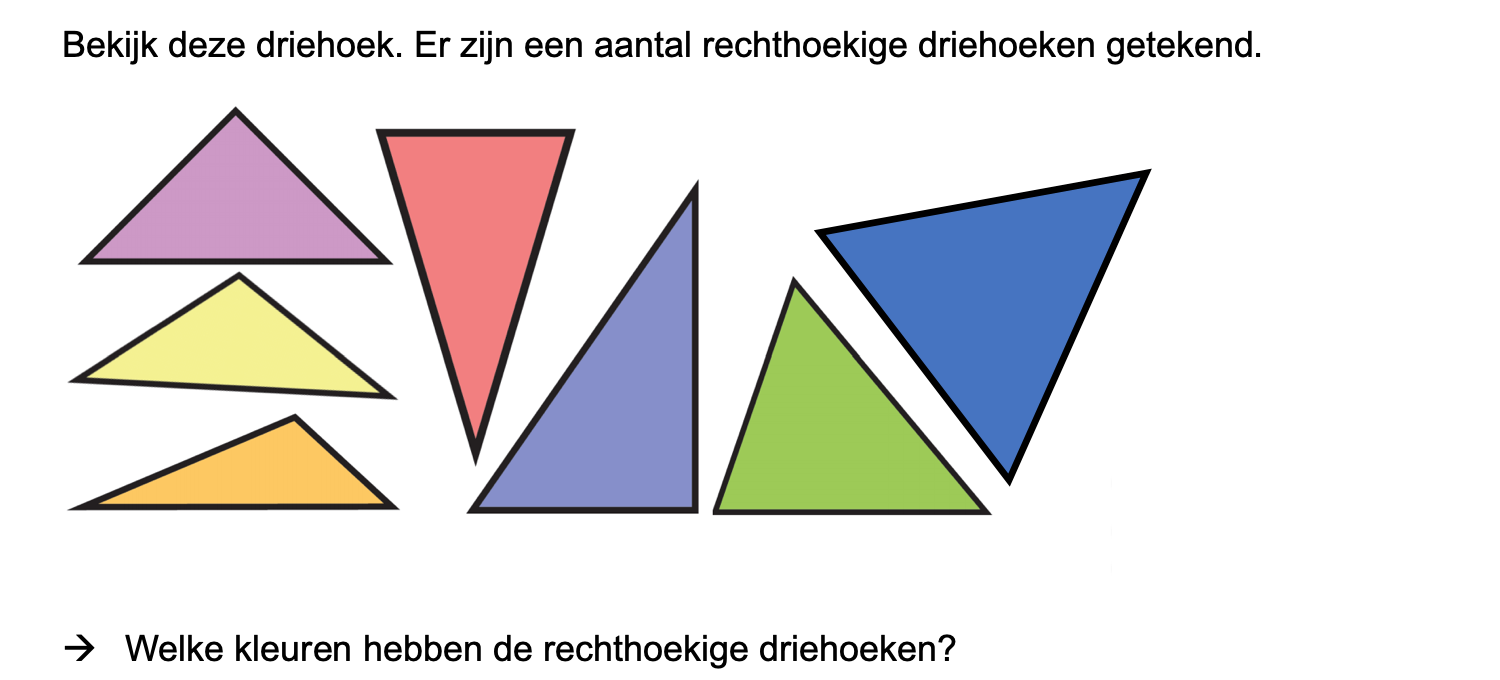
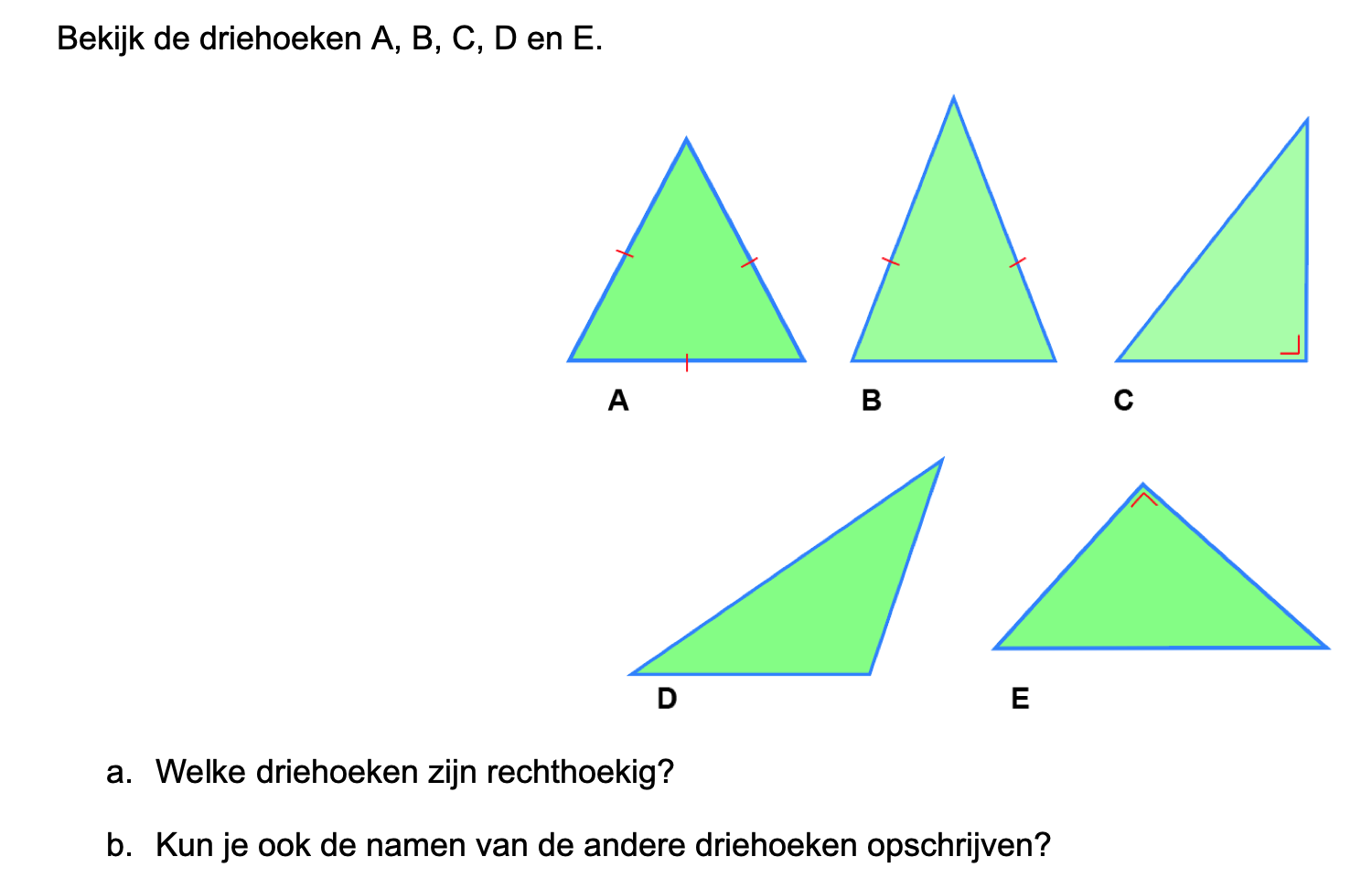

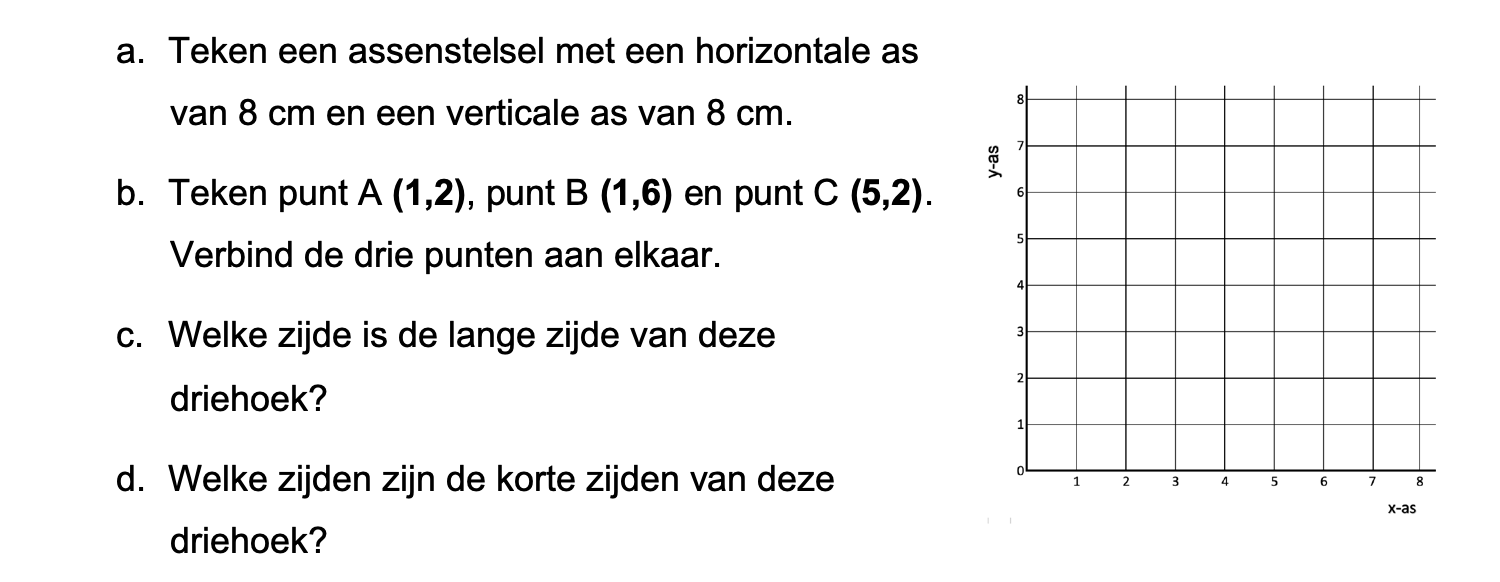


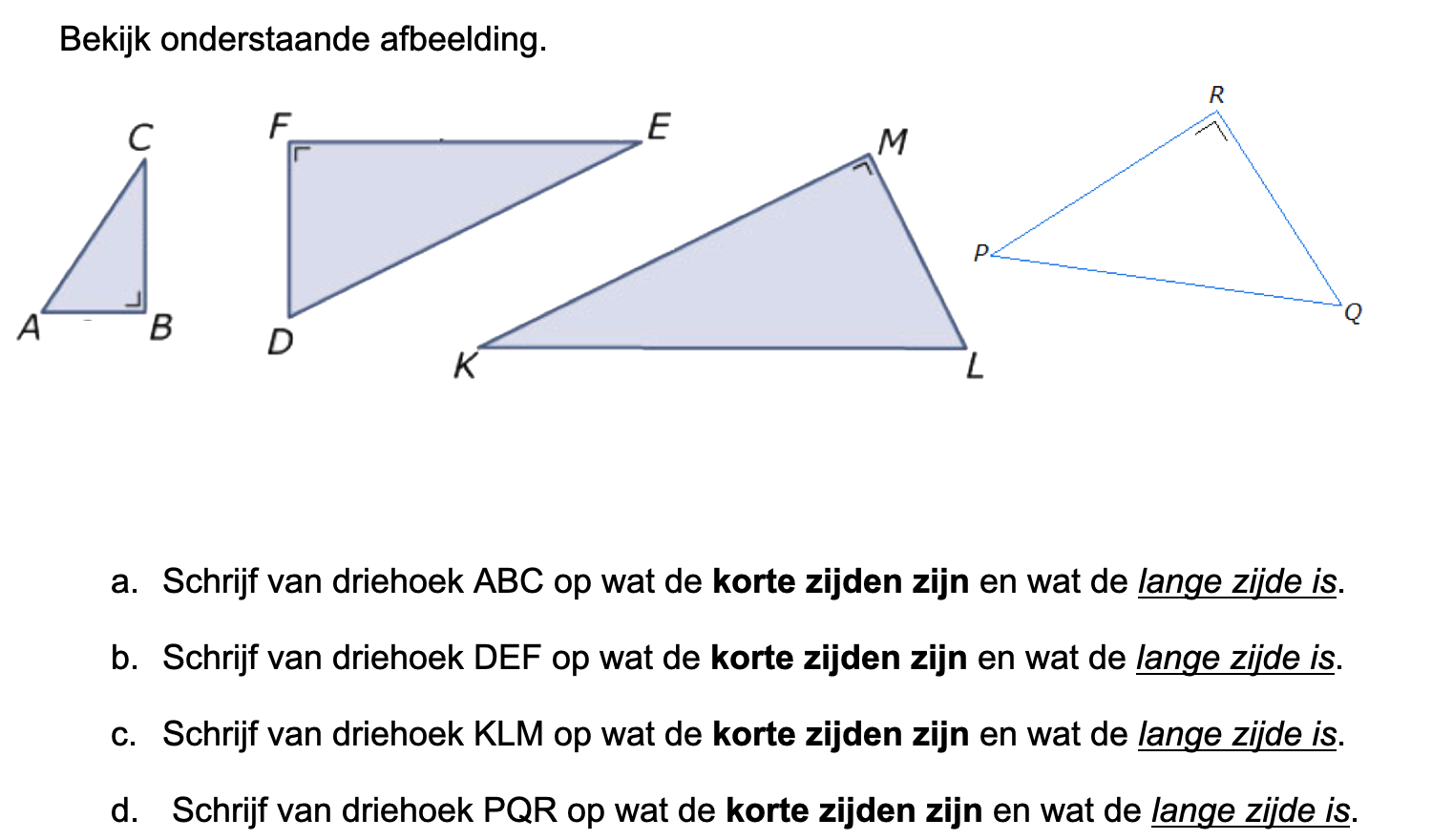
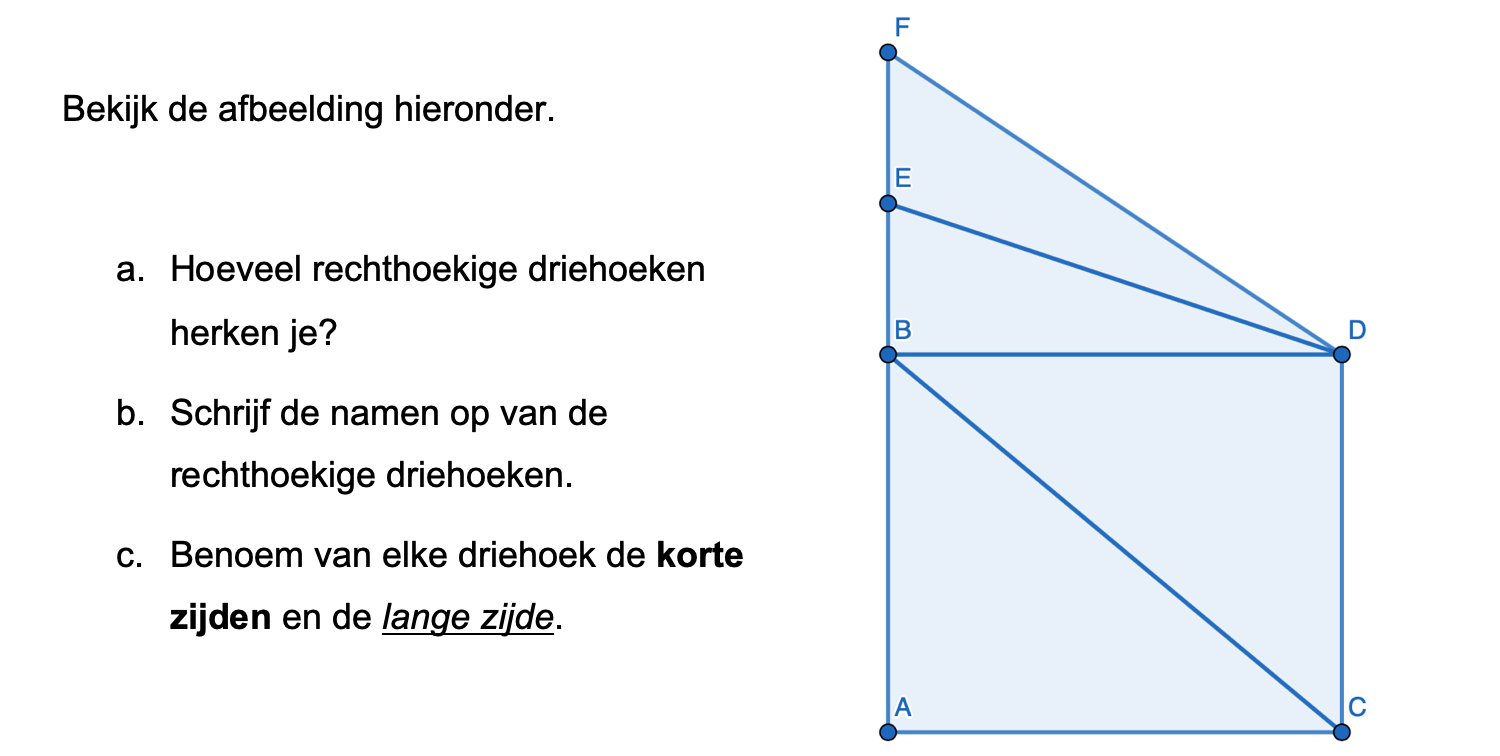


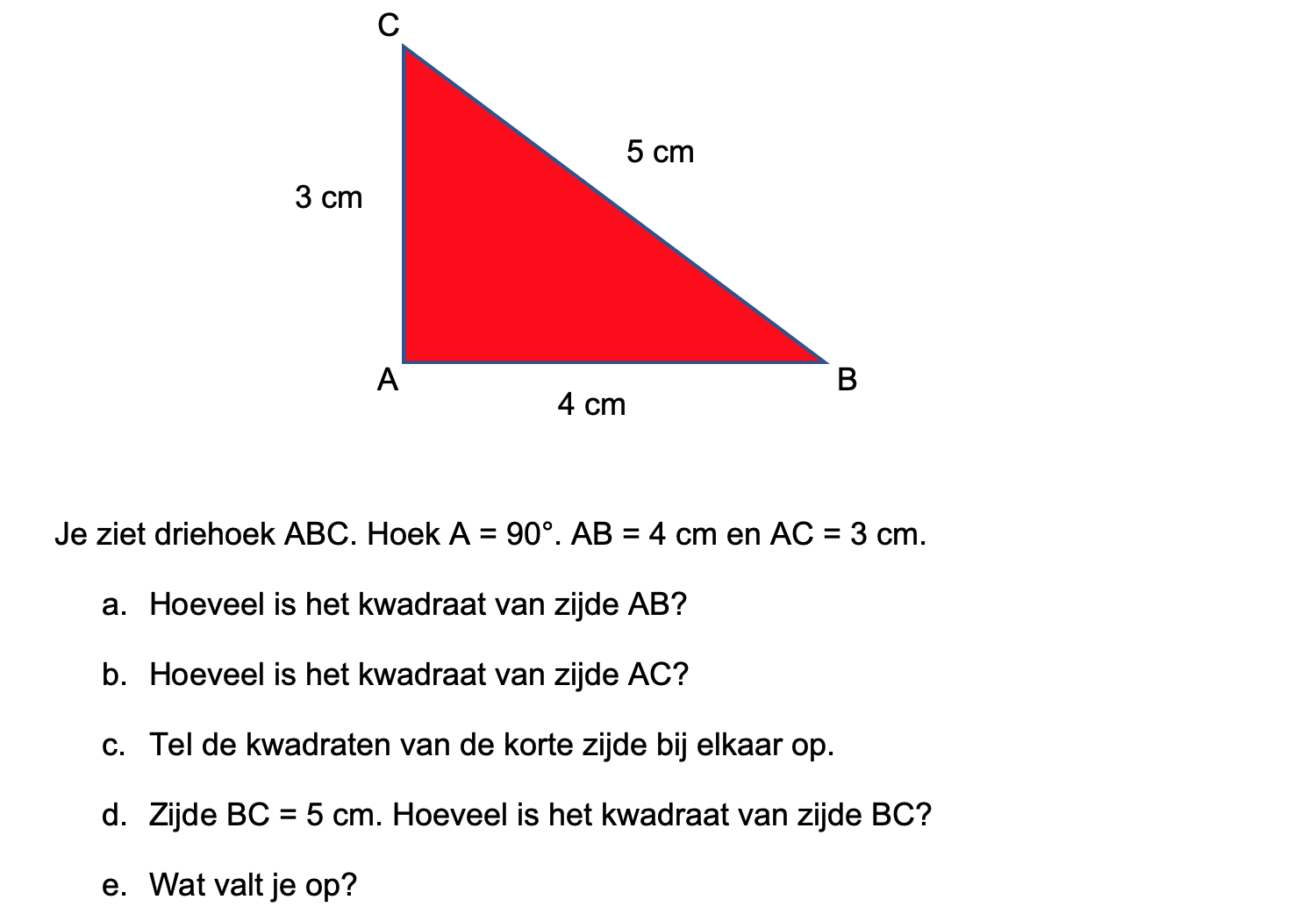
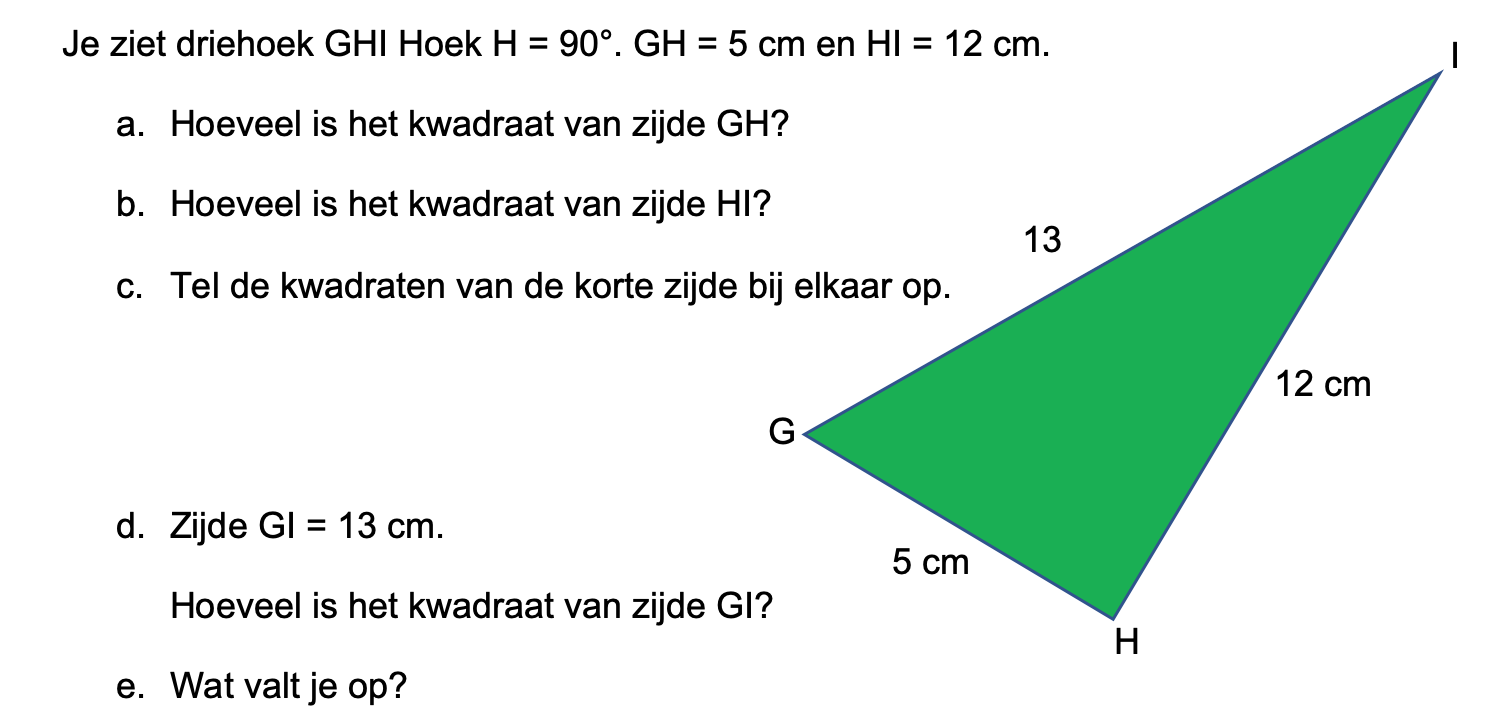
 \
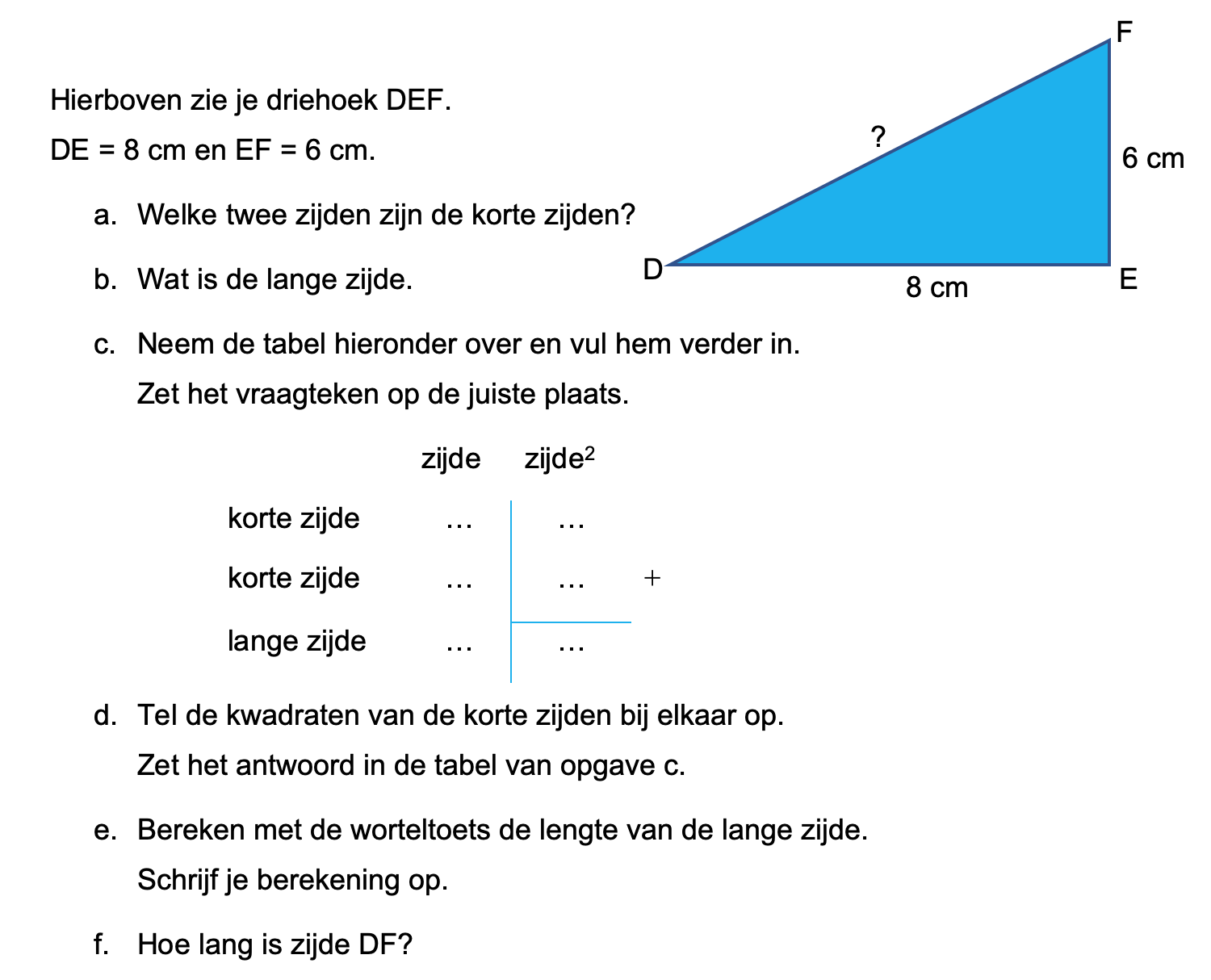
\
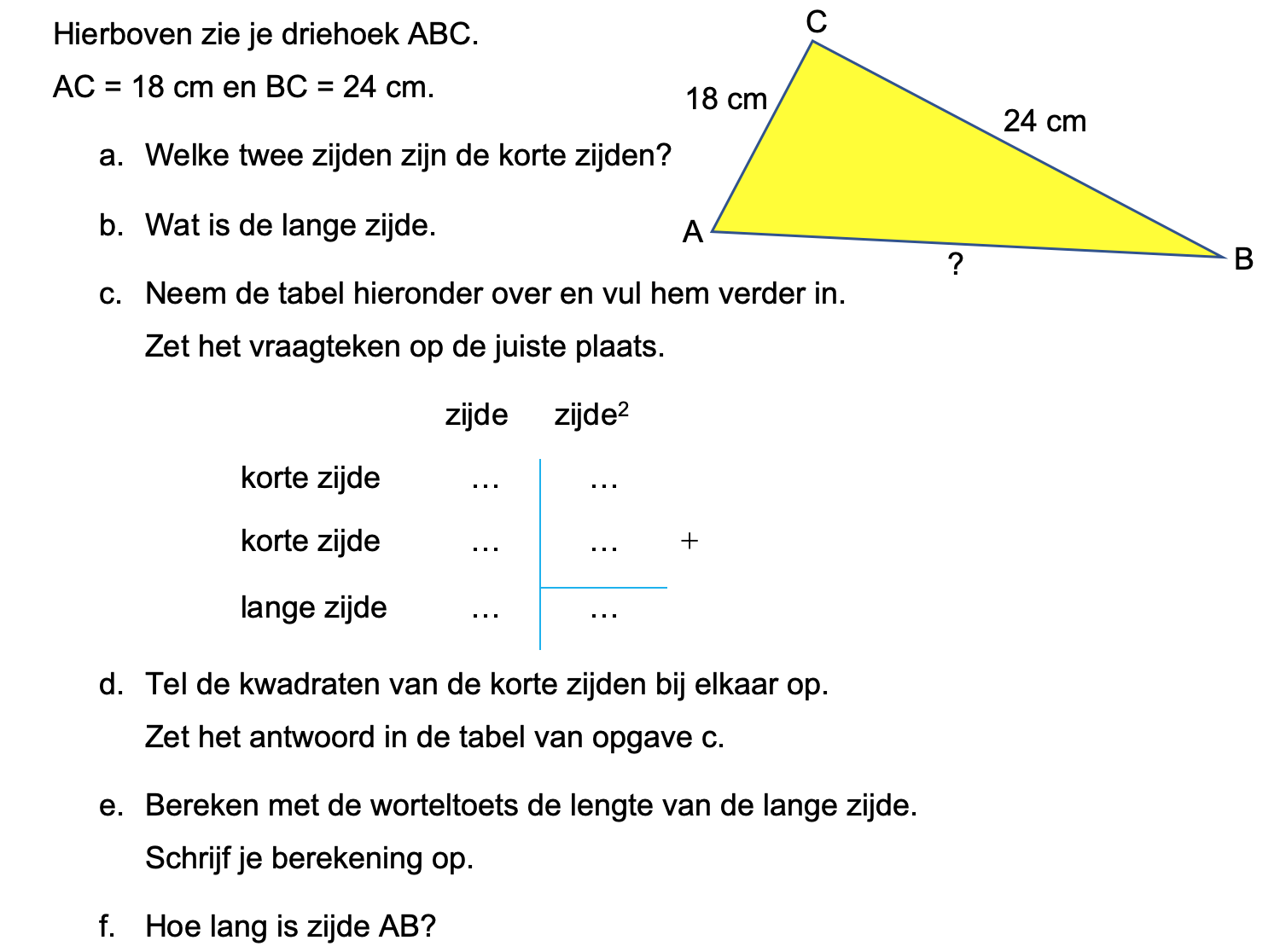

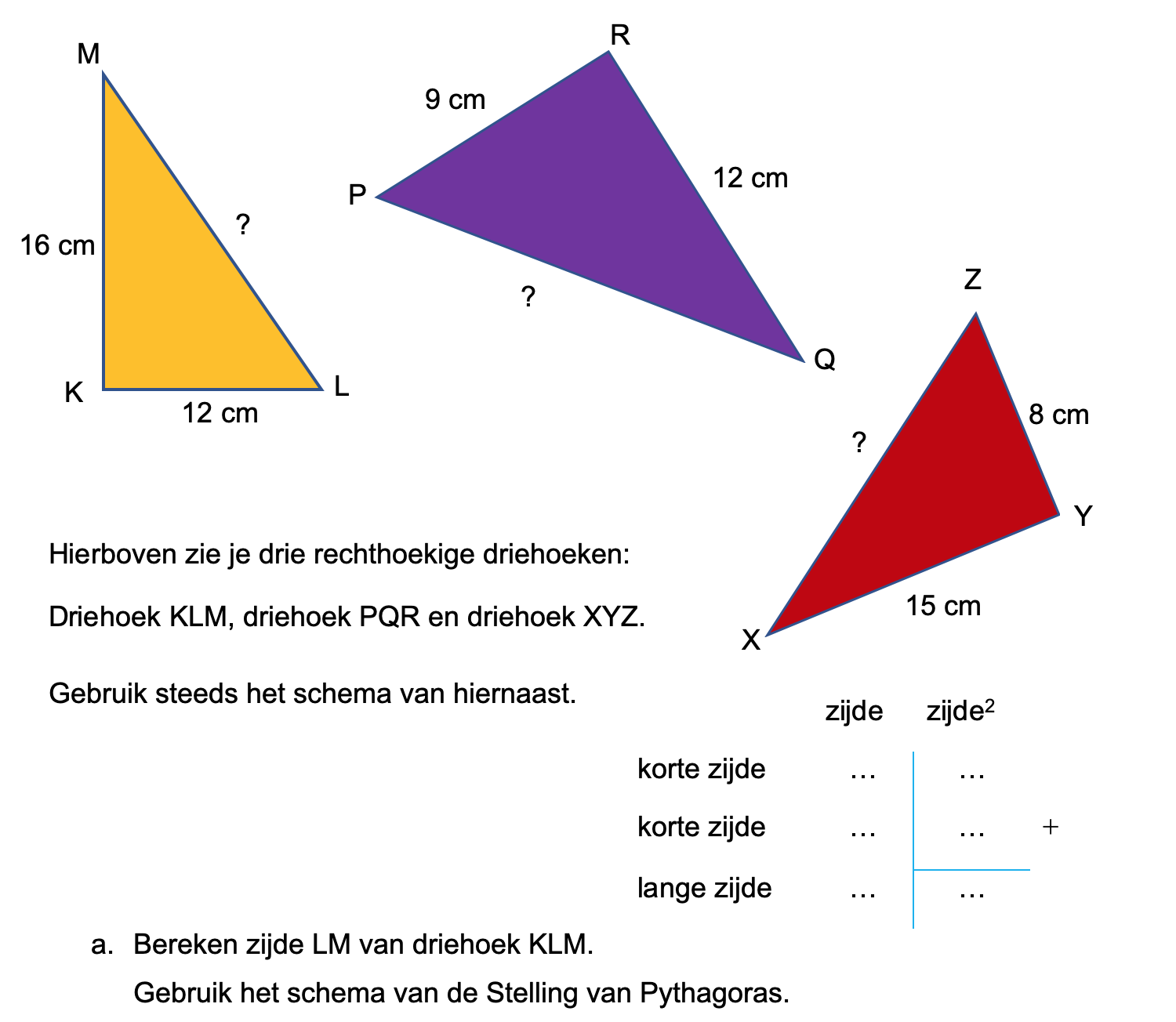

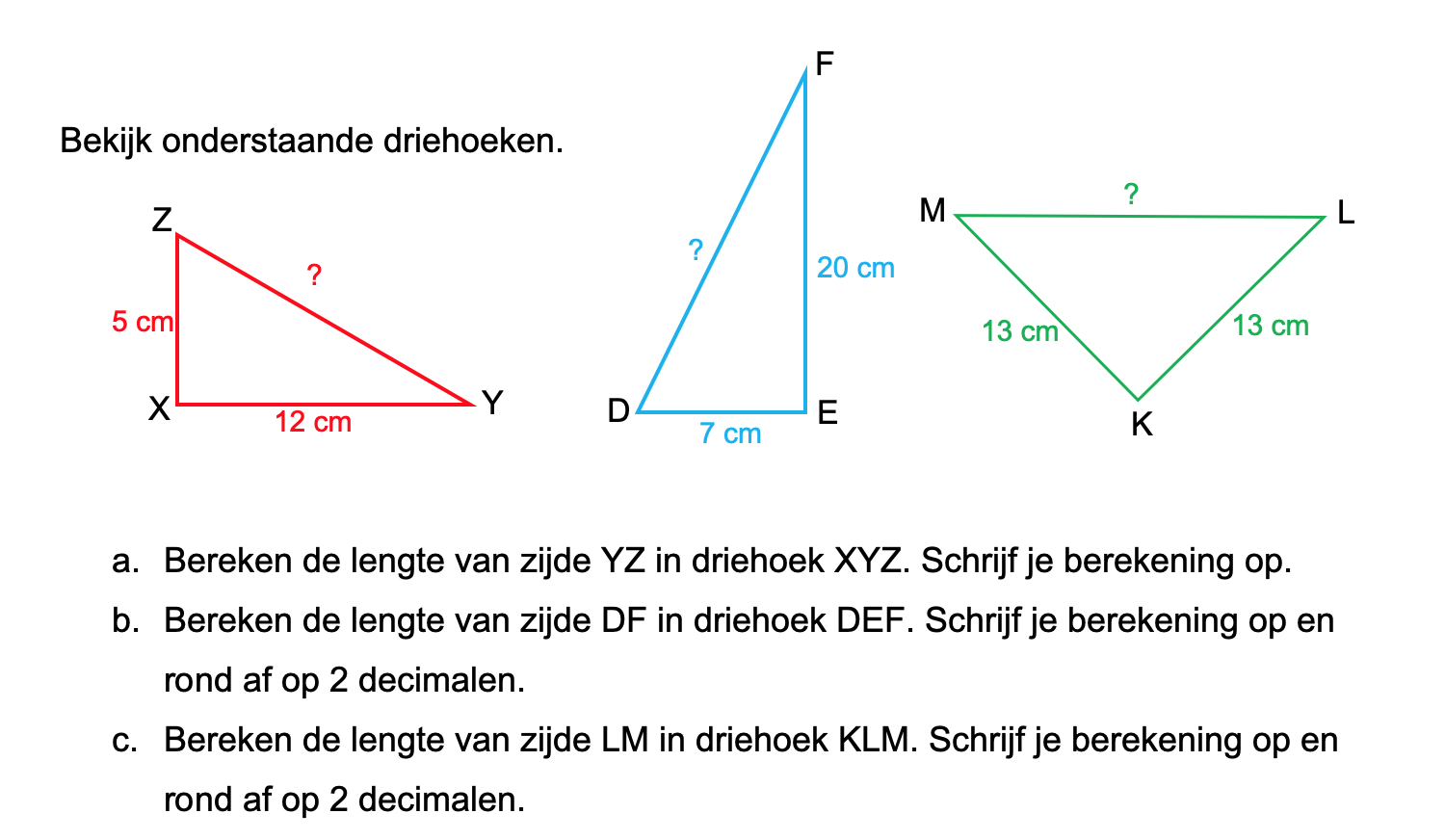
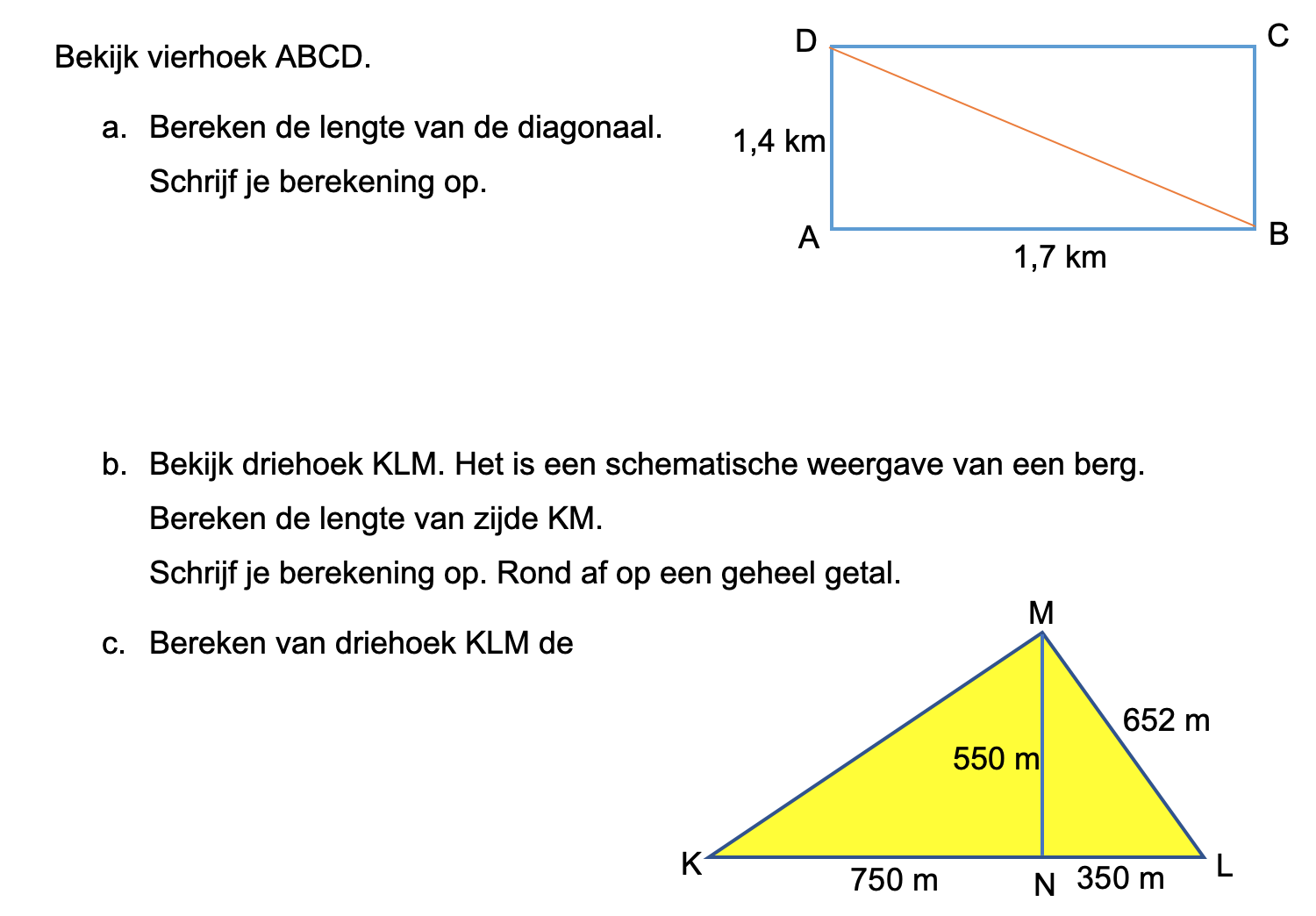





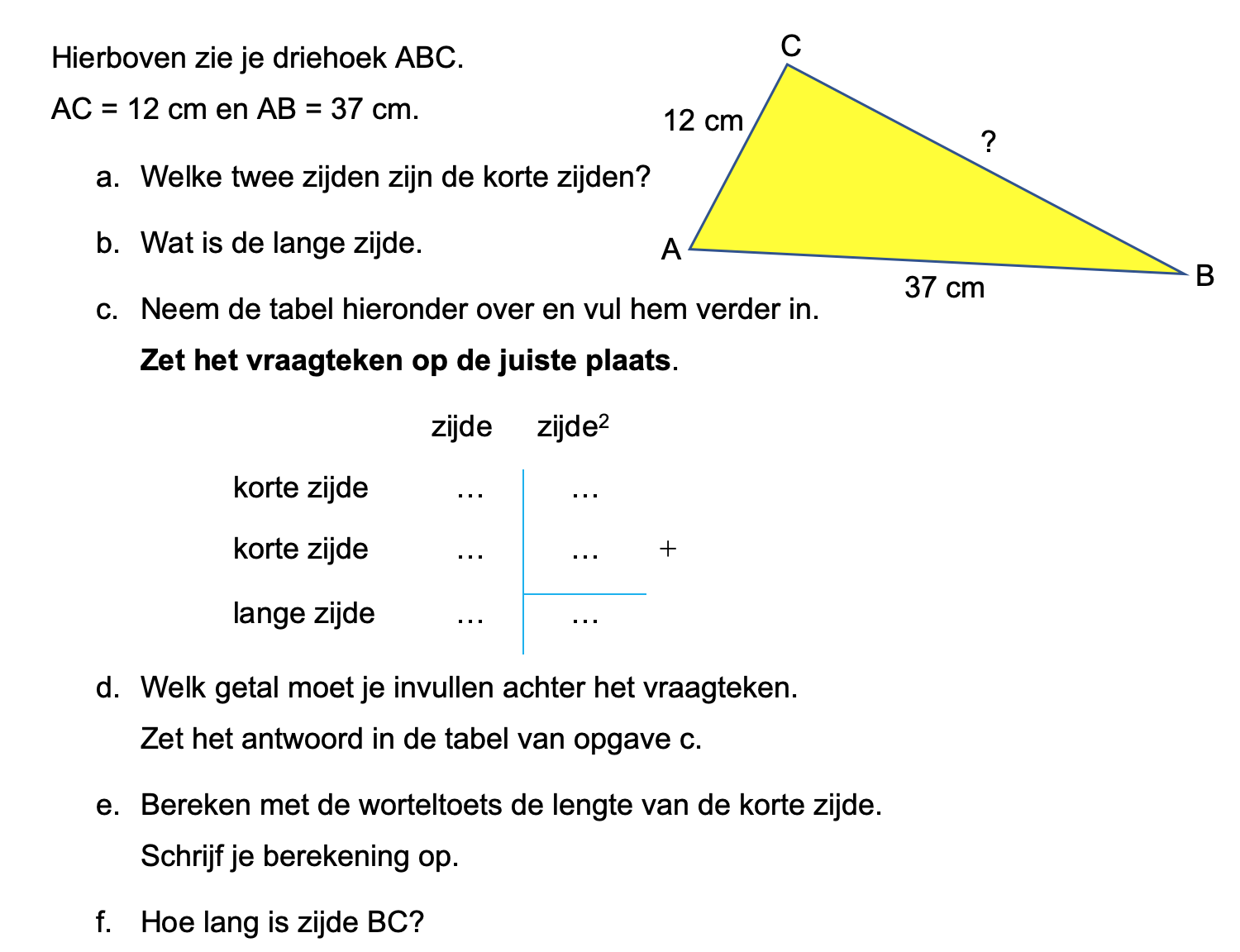
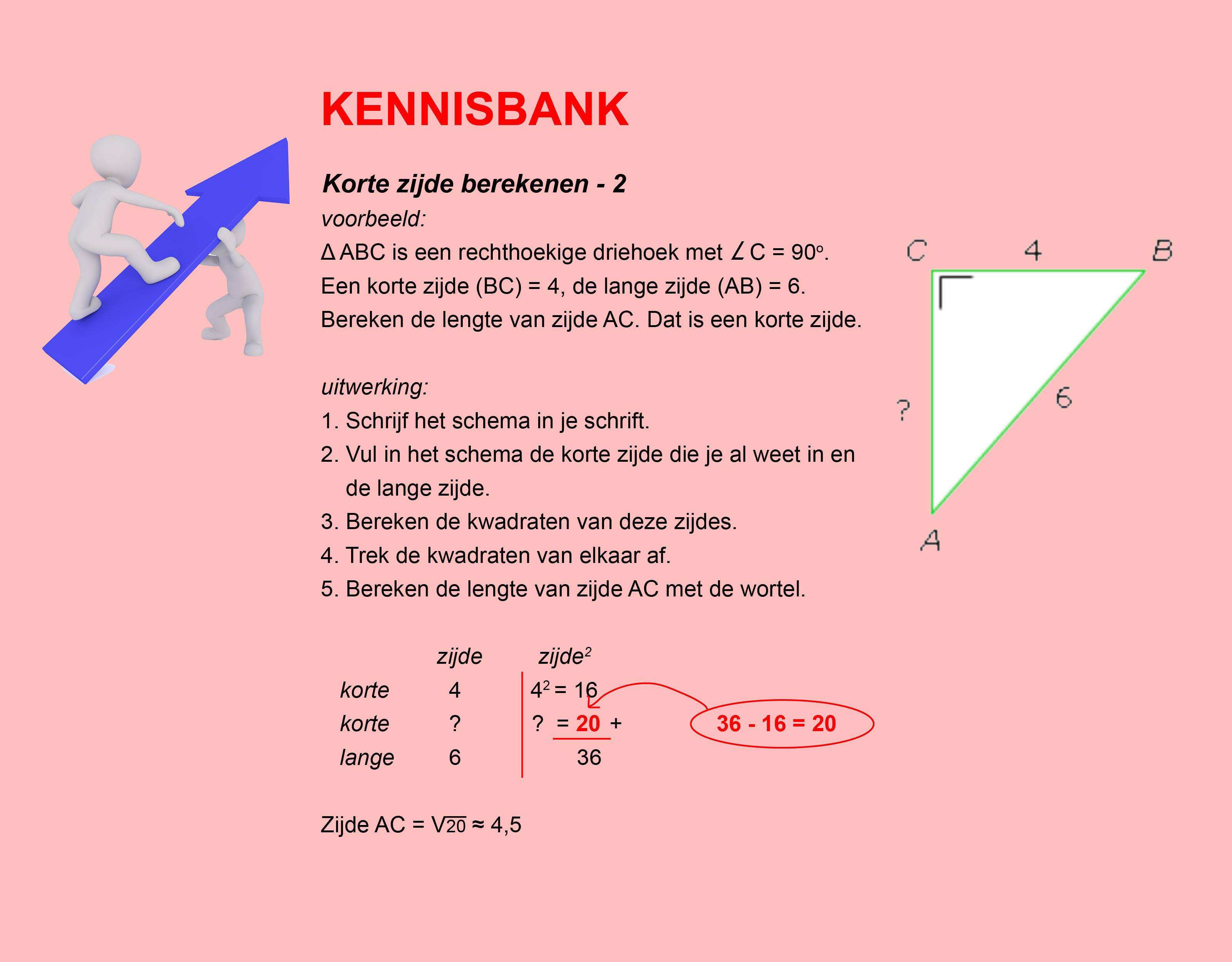
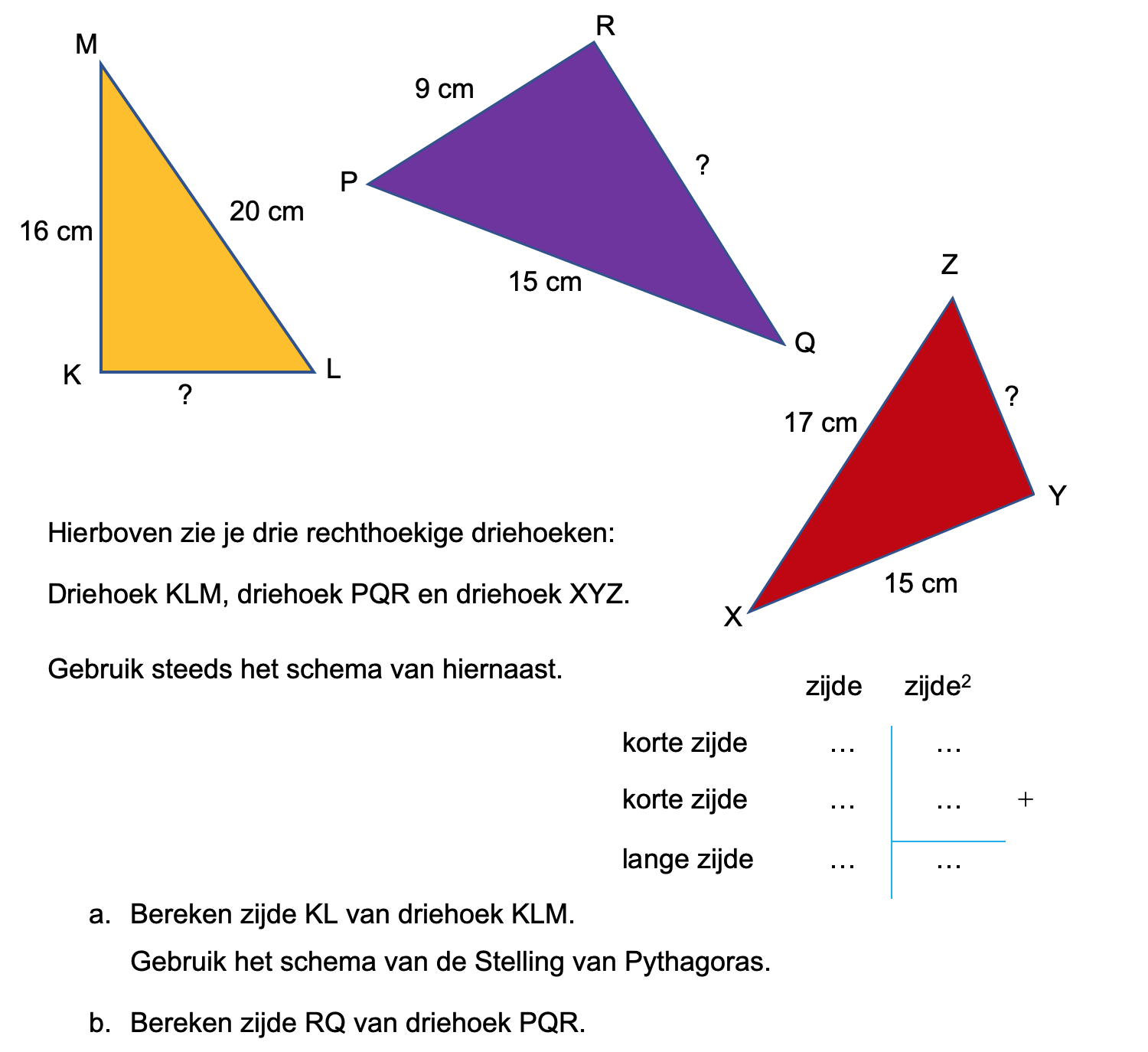

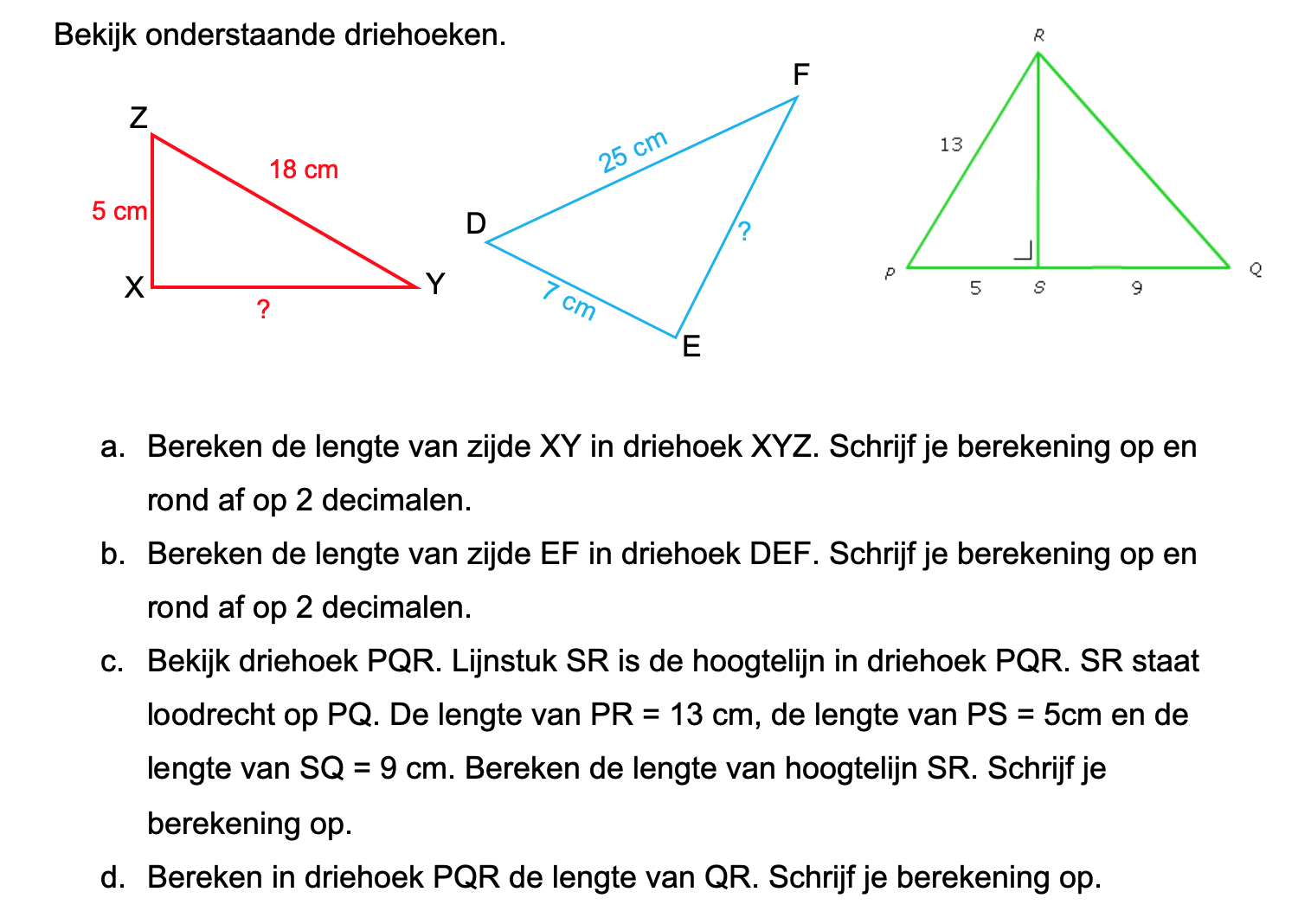
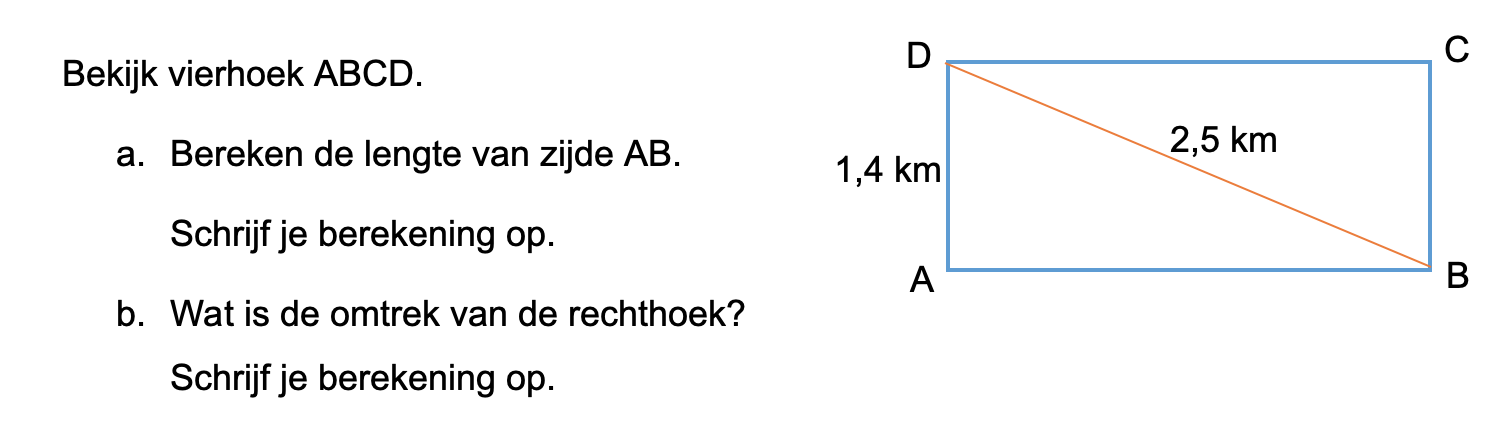
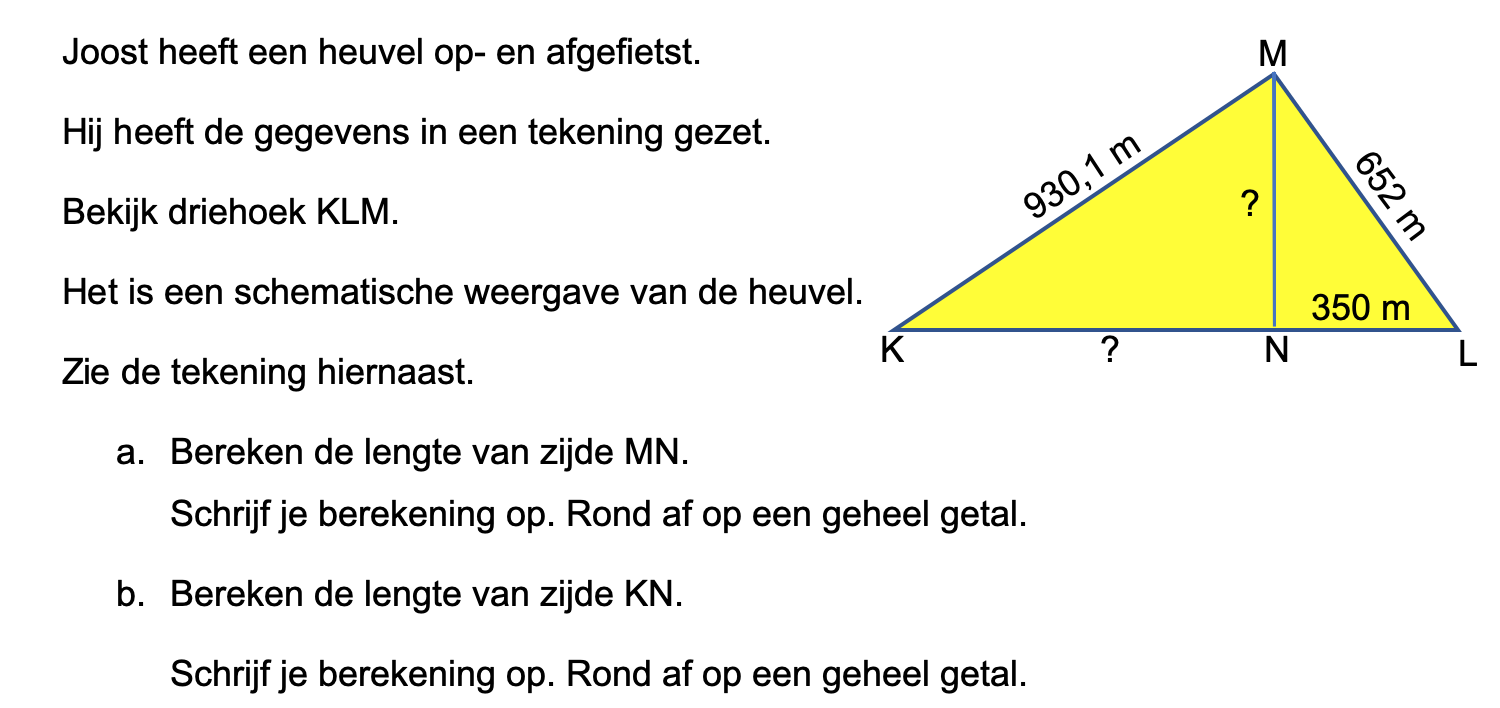


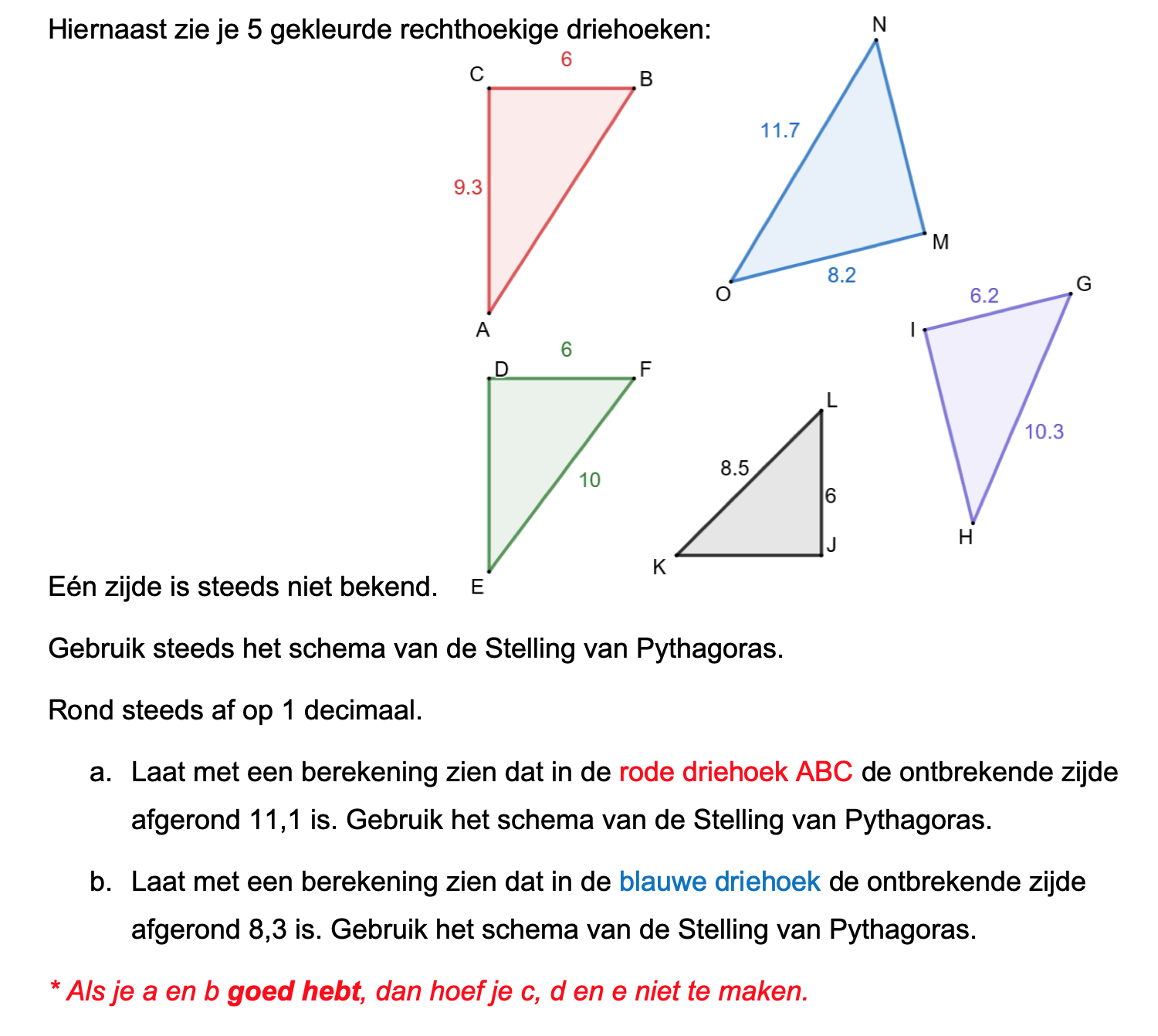



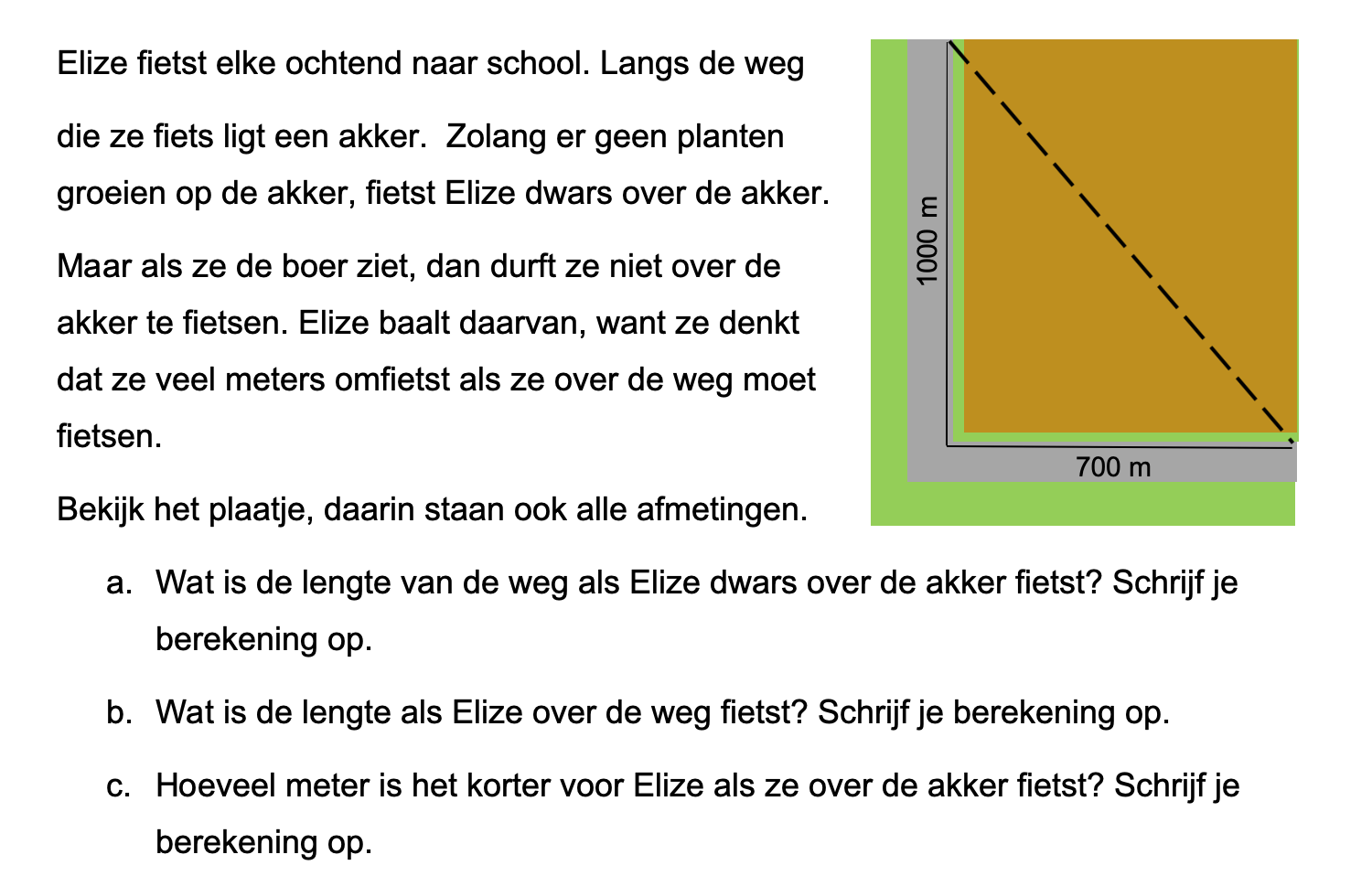




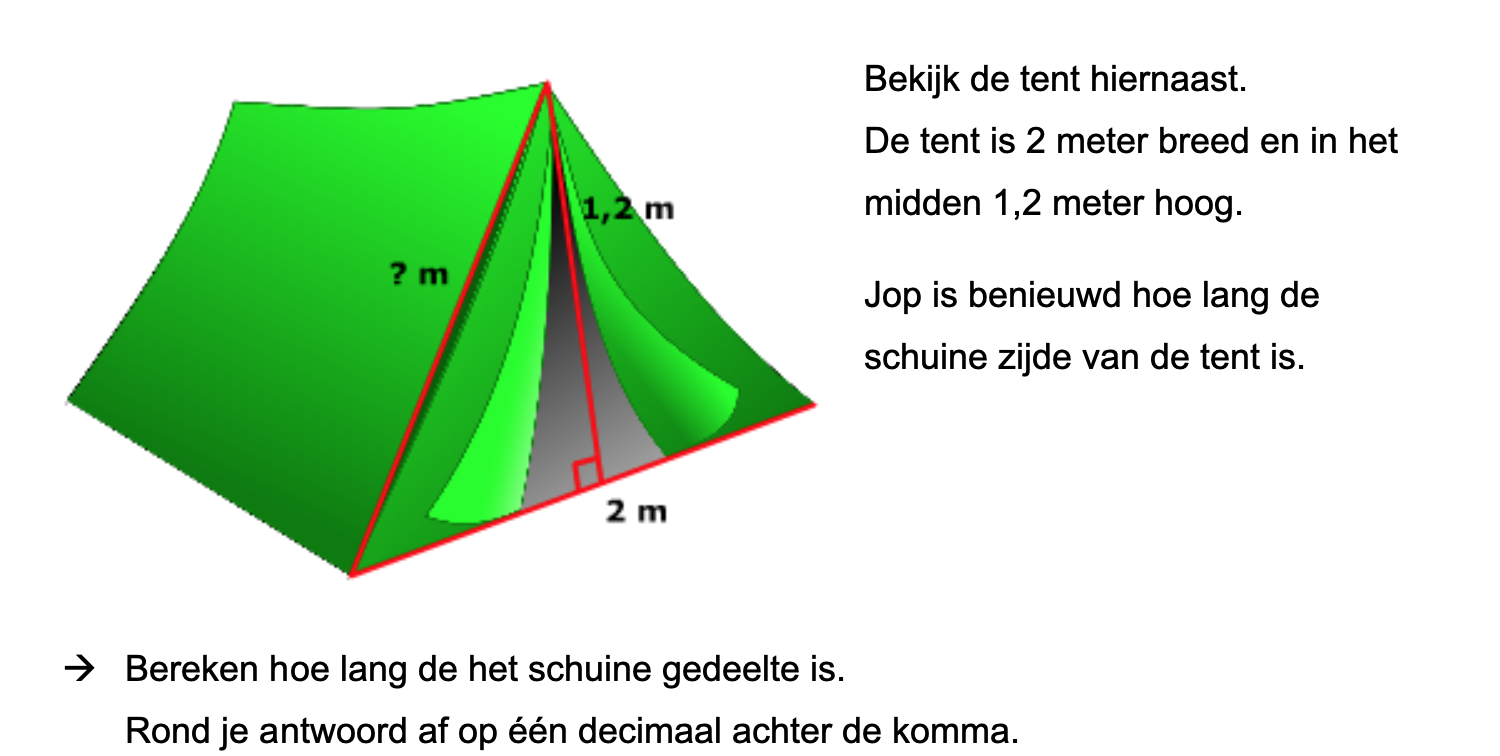

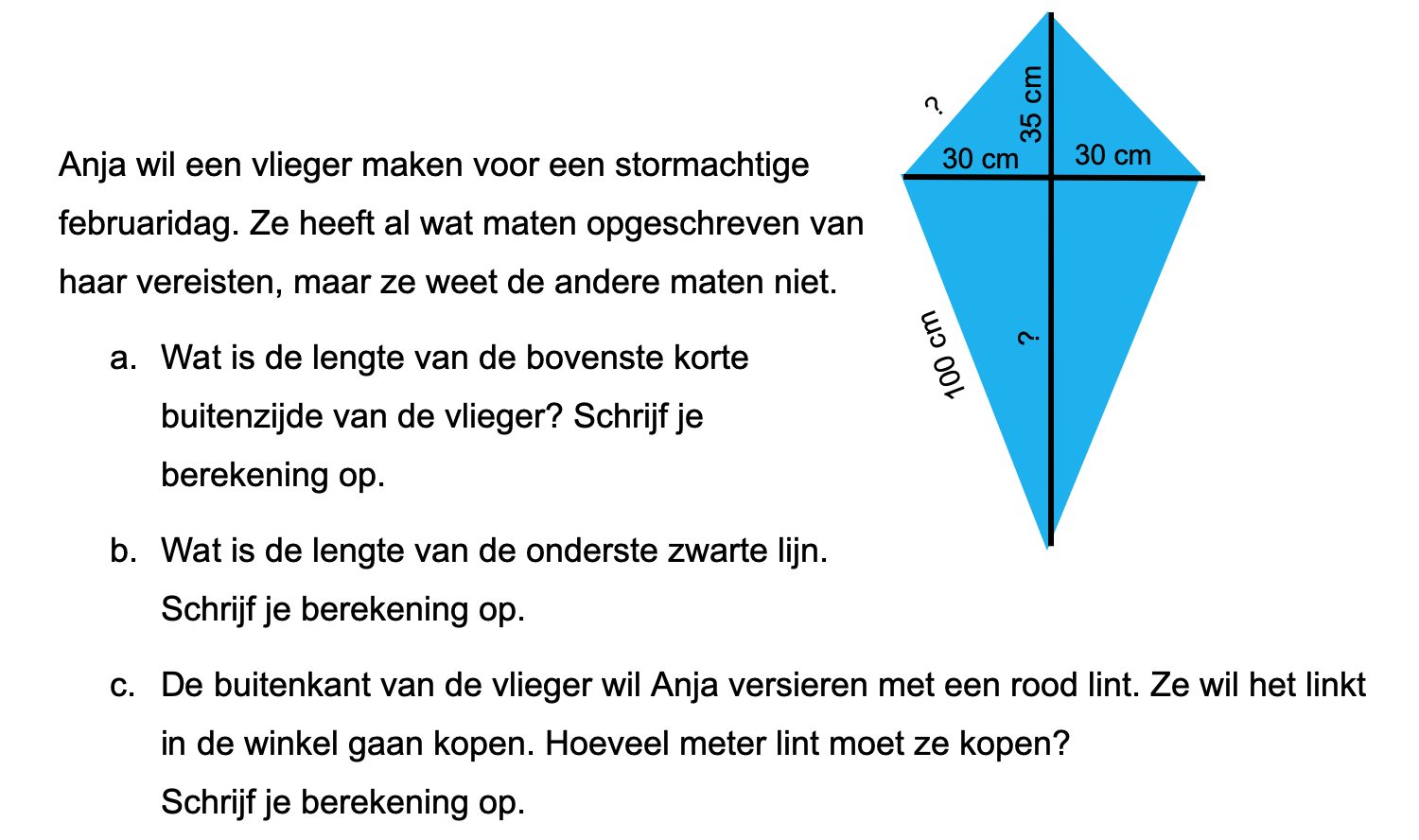










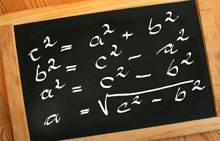 Nog enkele opgaven om te oefenen voor het proefwerk.
Nog enkele opgaven om te oefenen voor het proefwerk.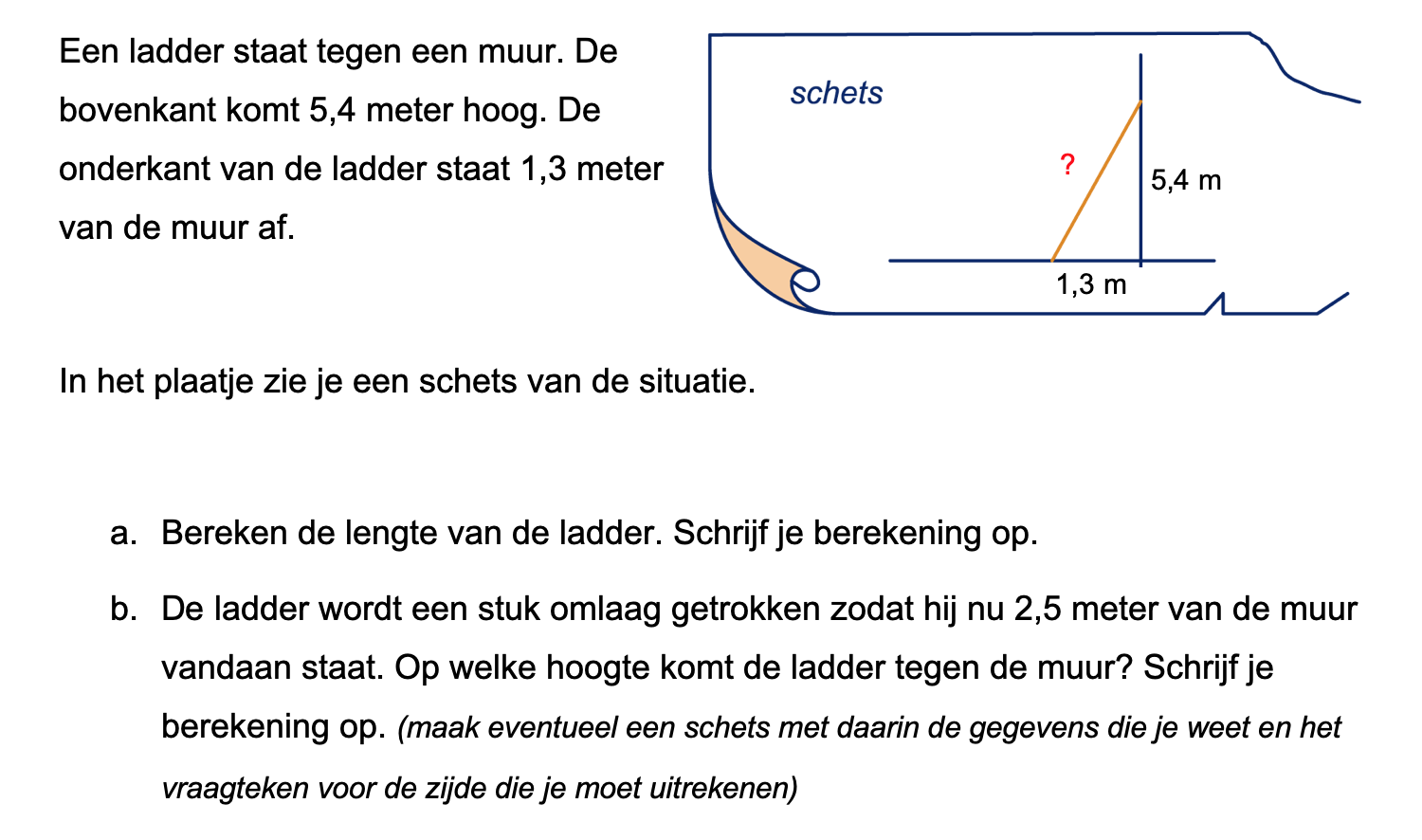
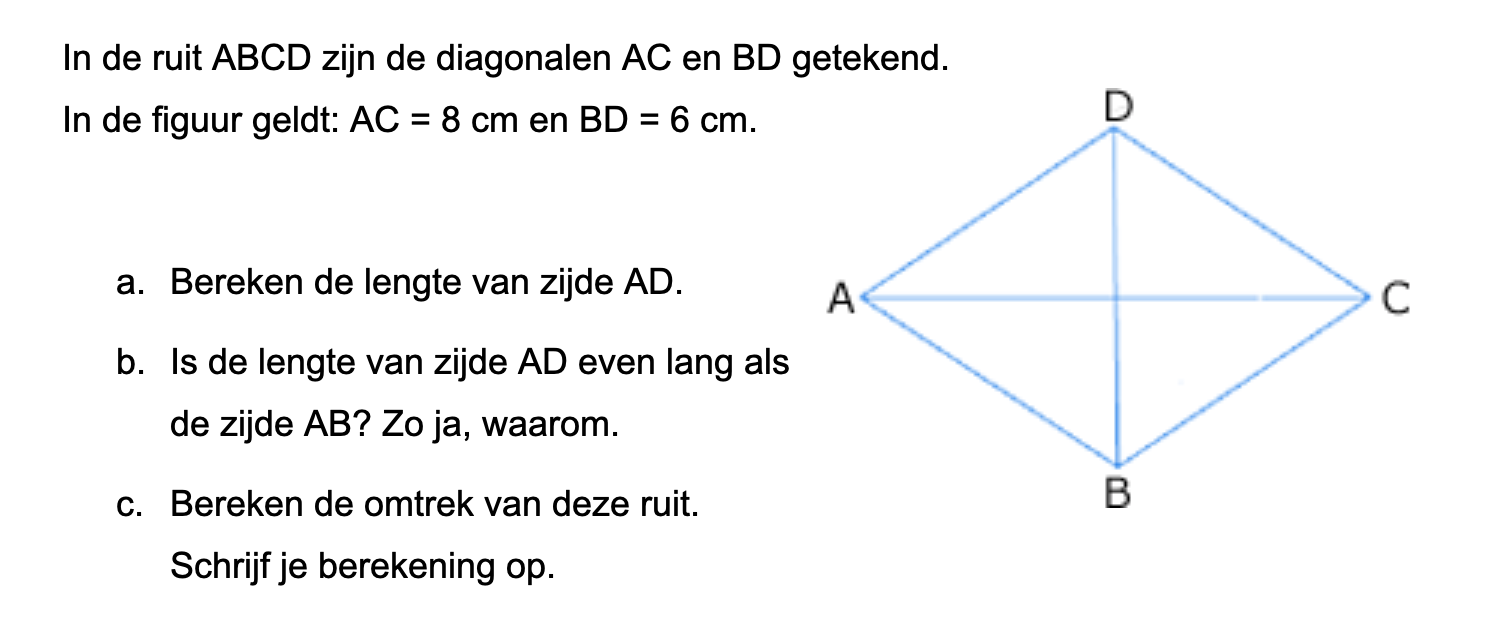



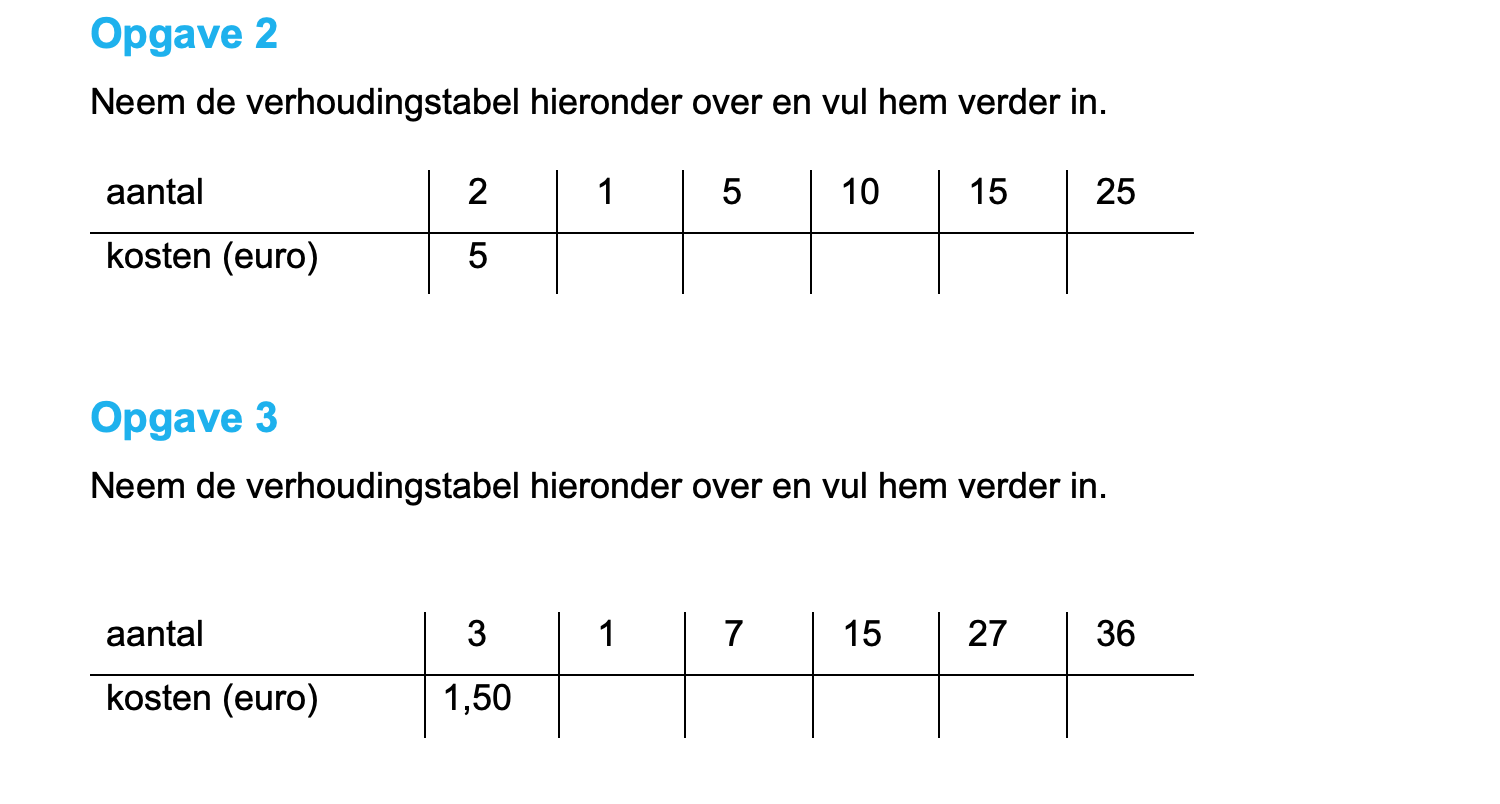
 \
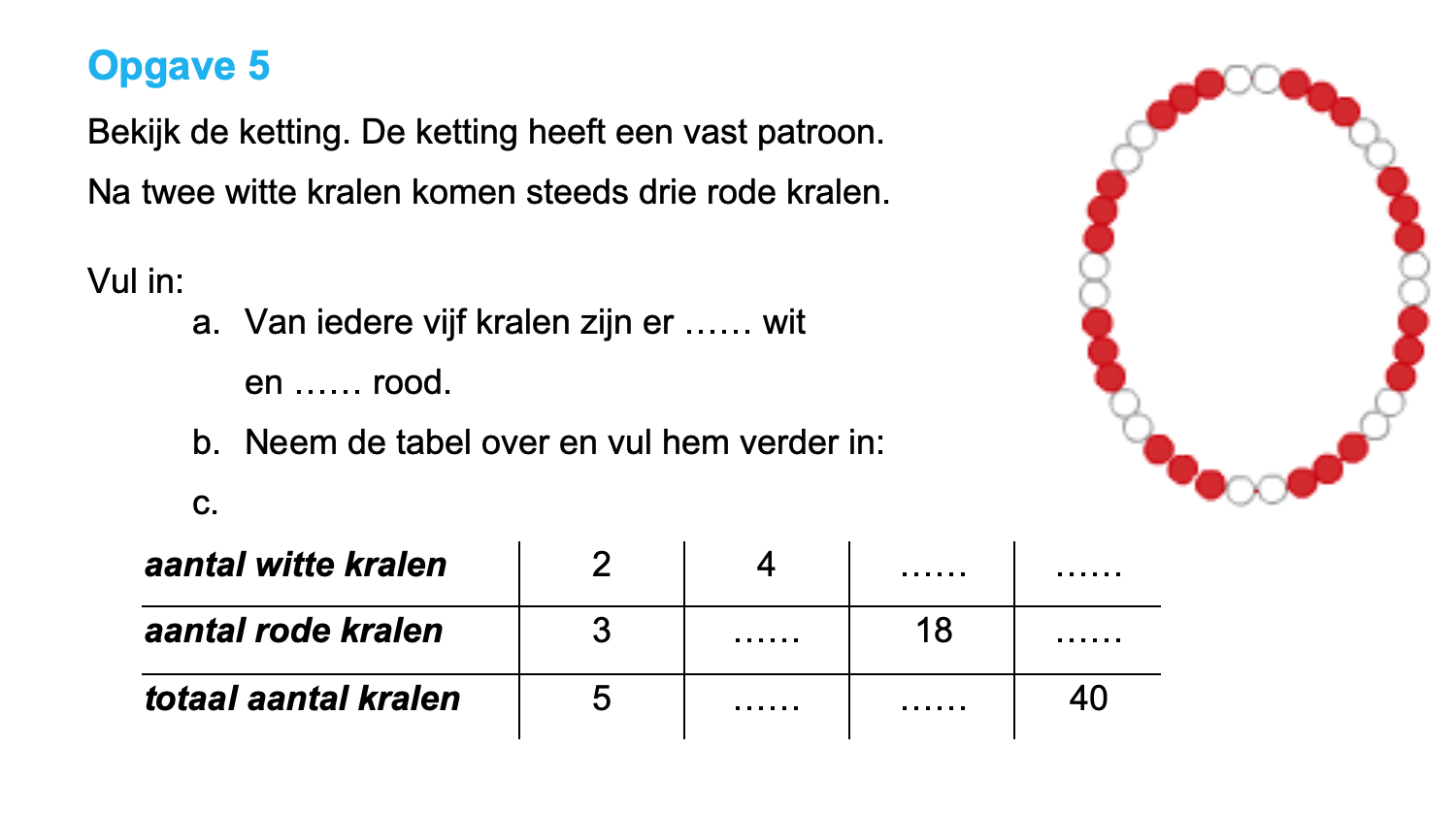
\







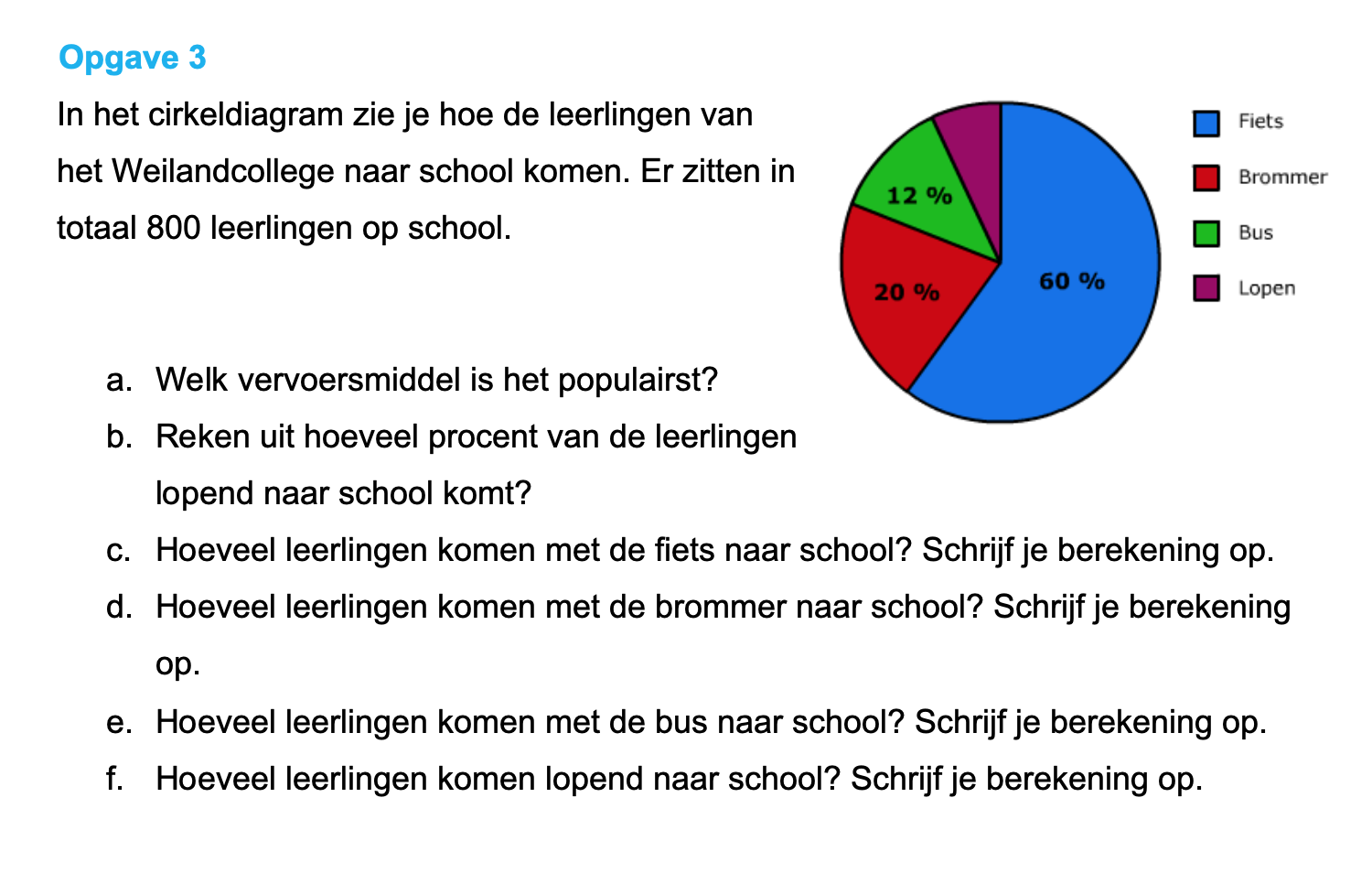


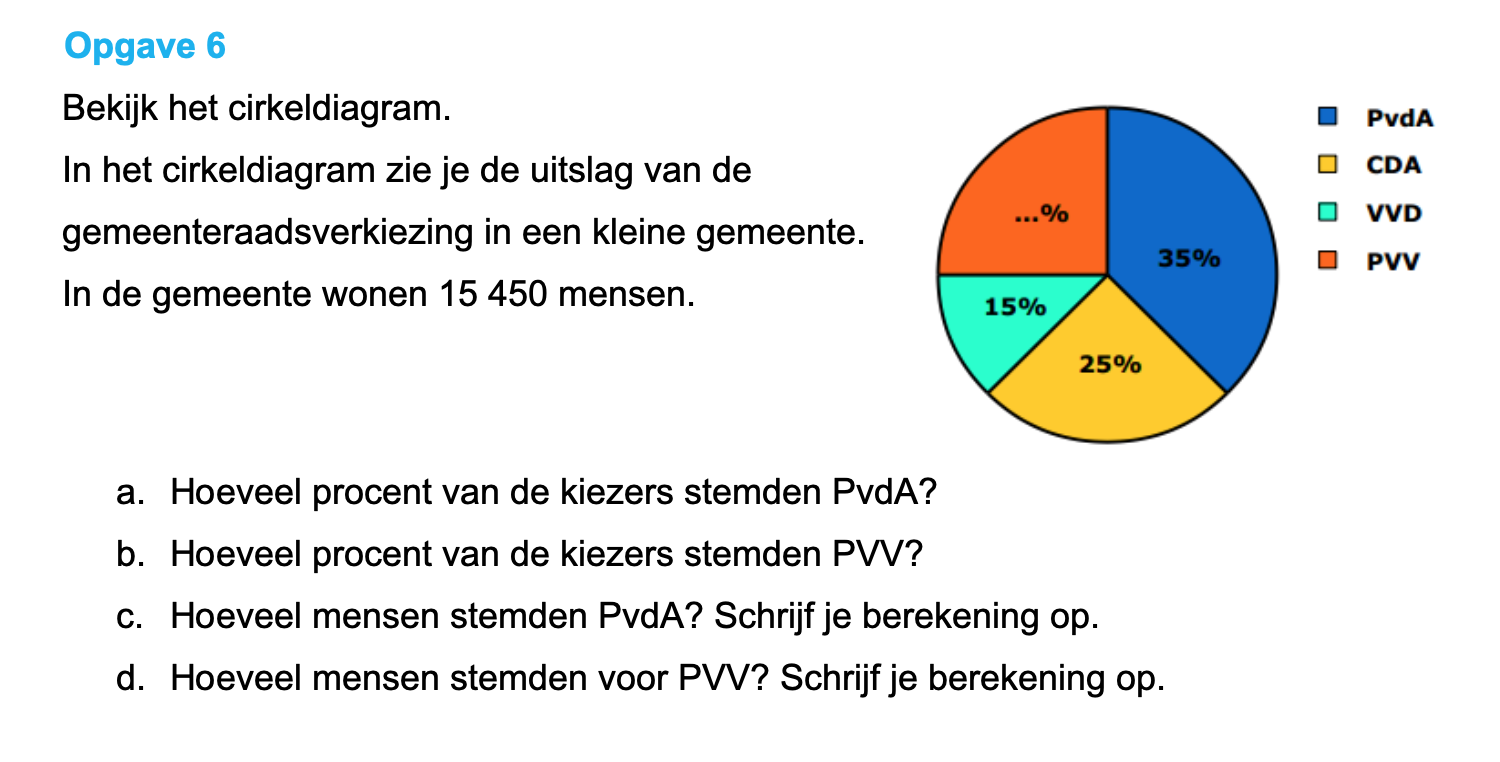



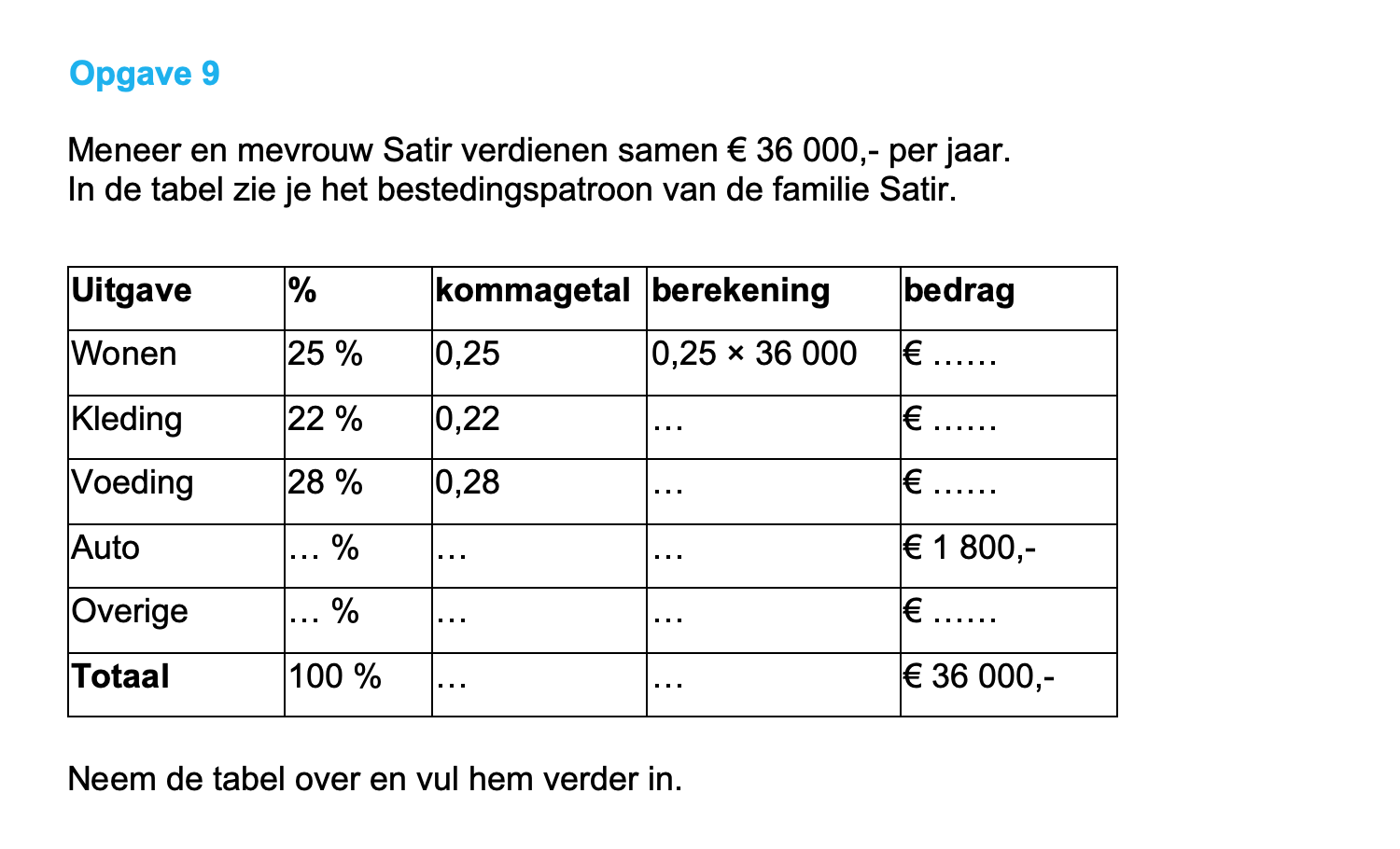




















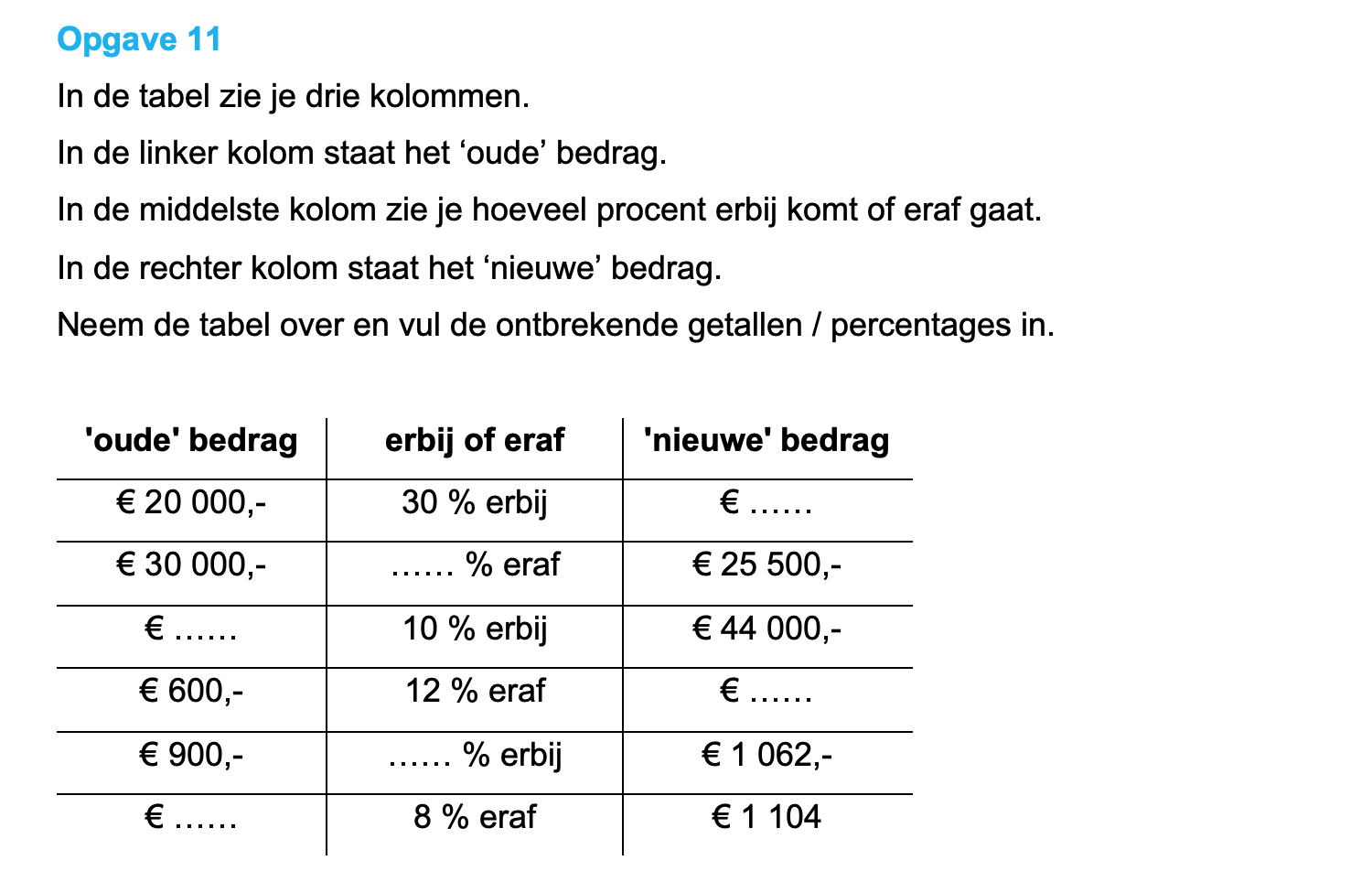










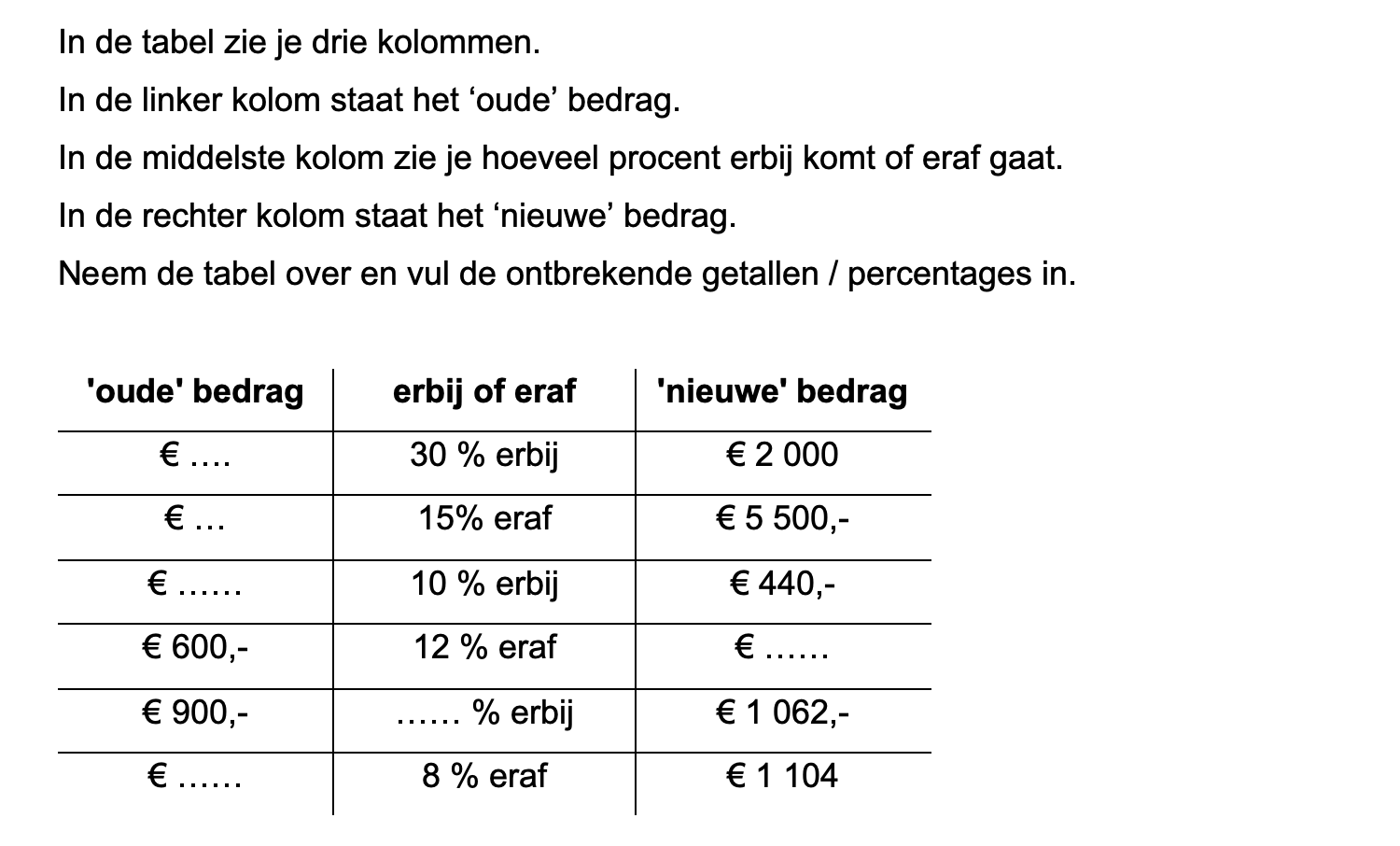










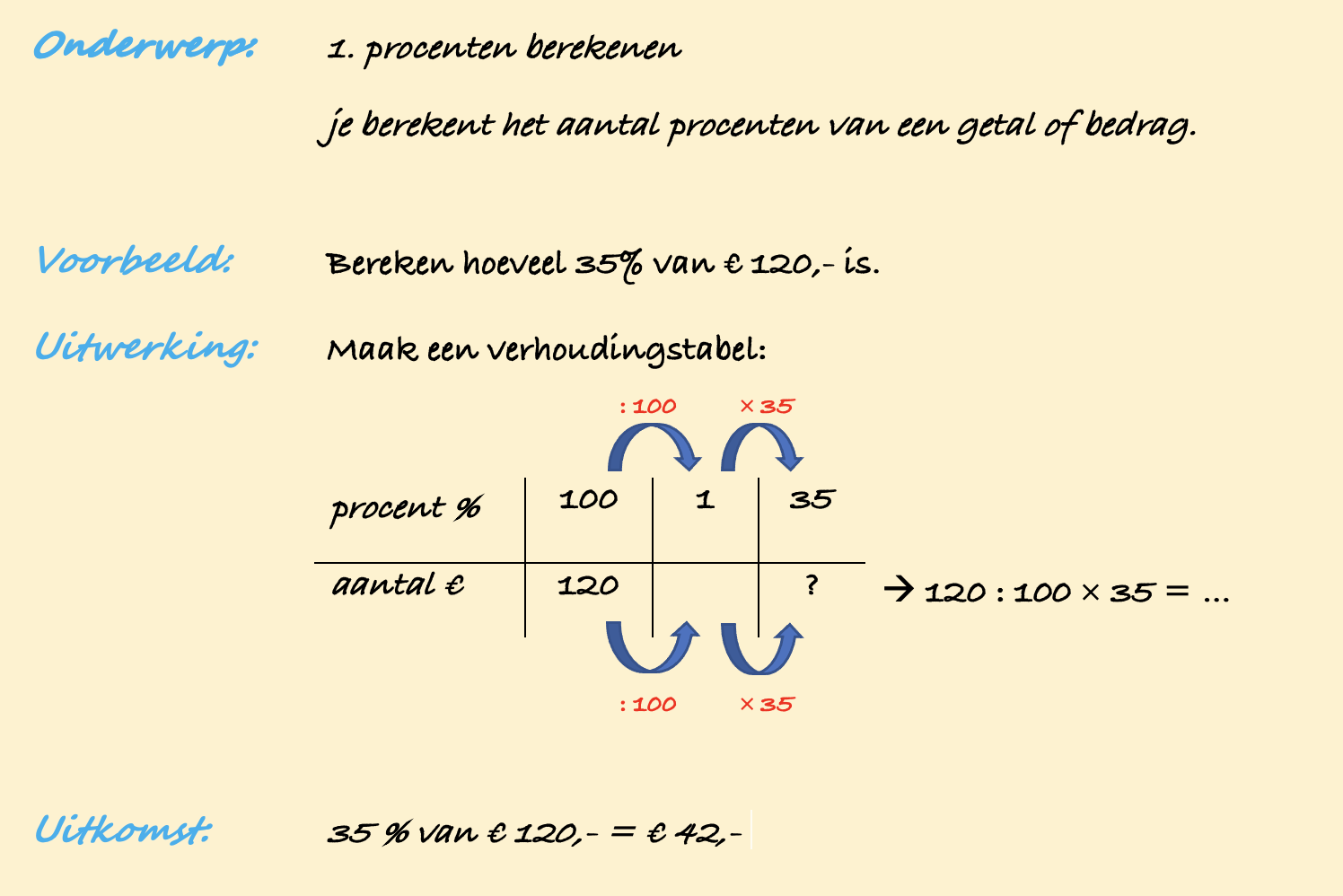
 Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven: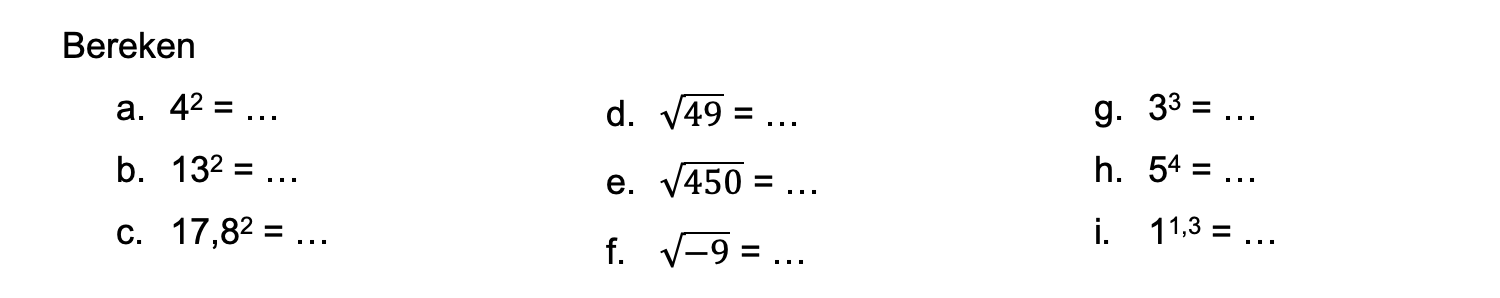
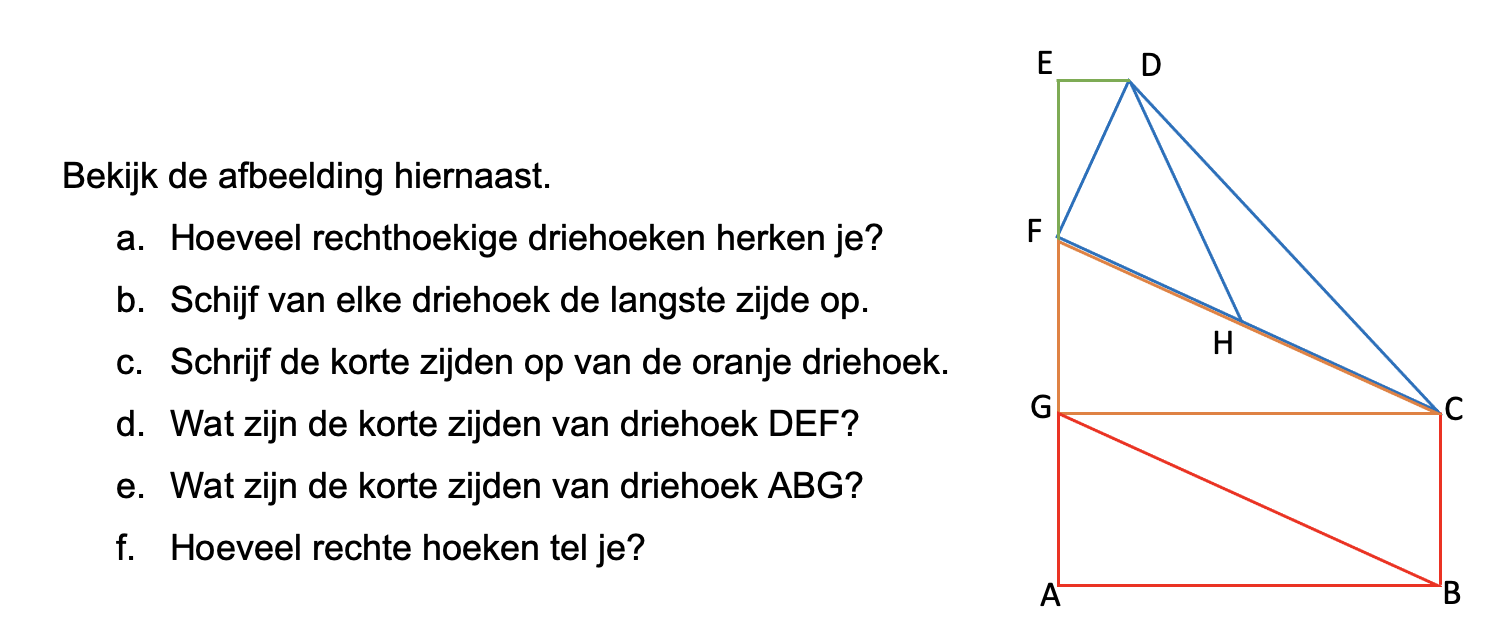

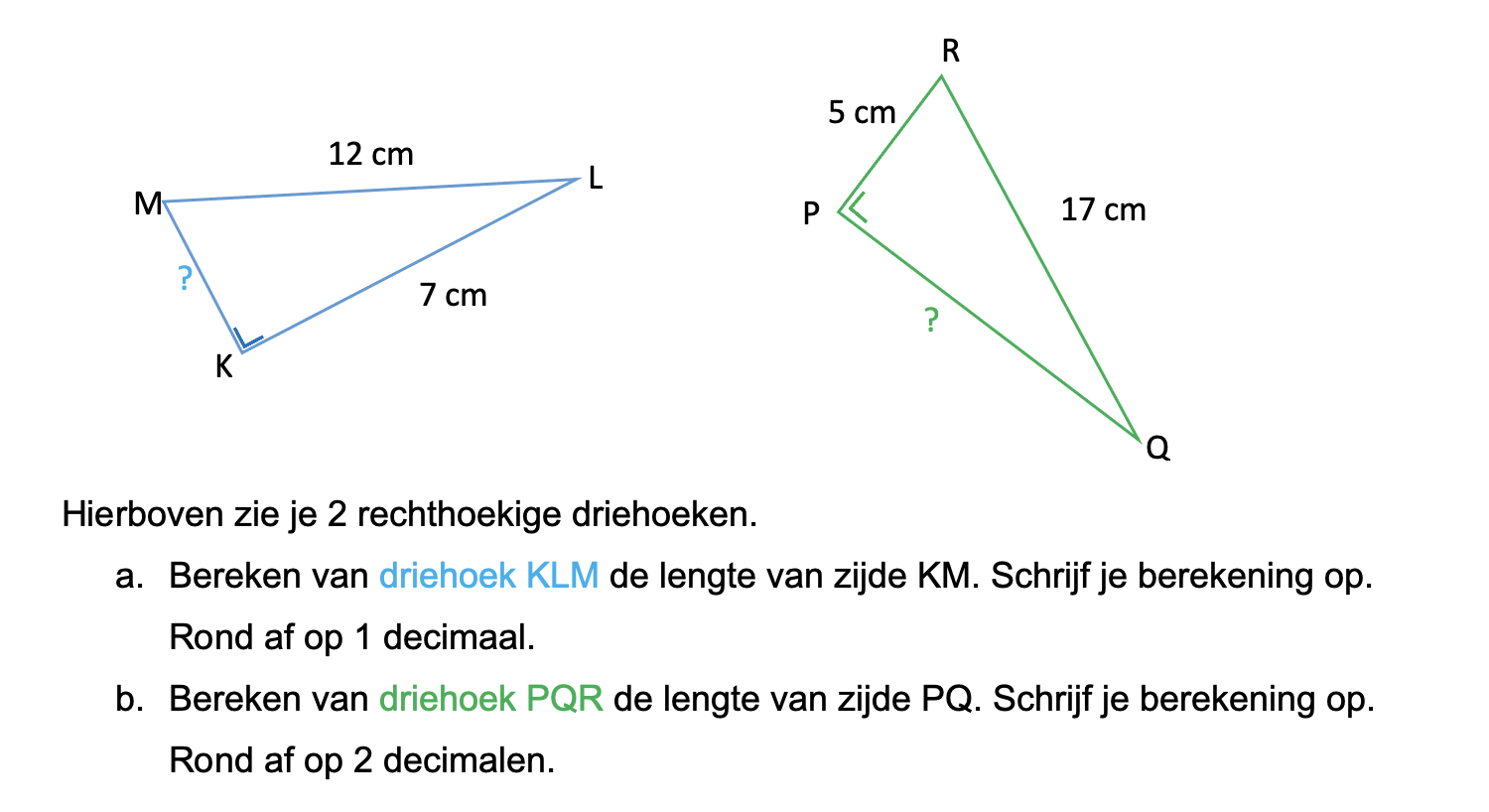
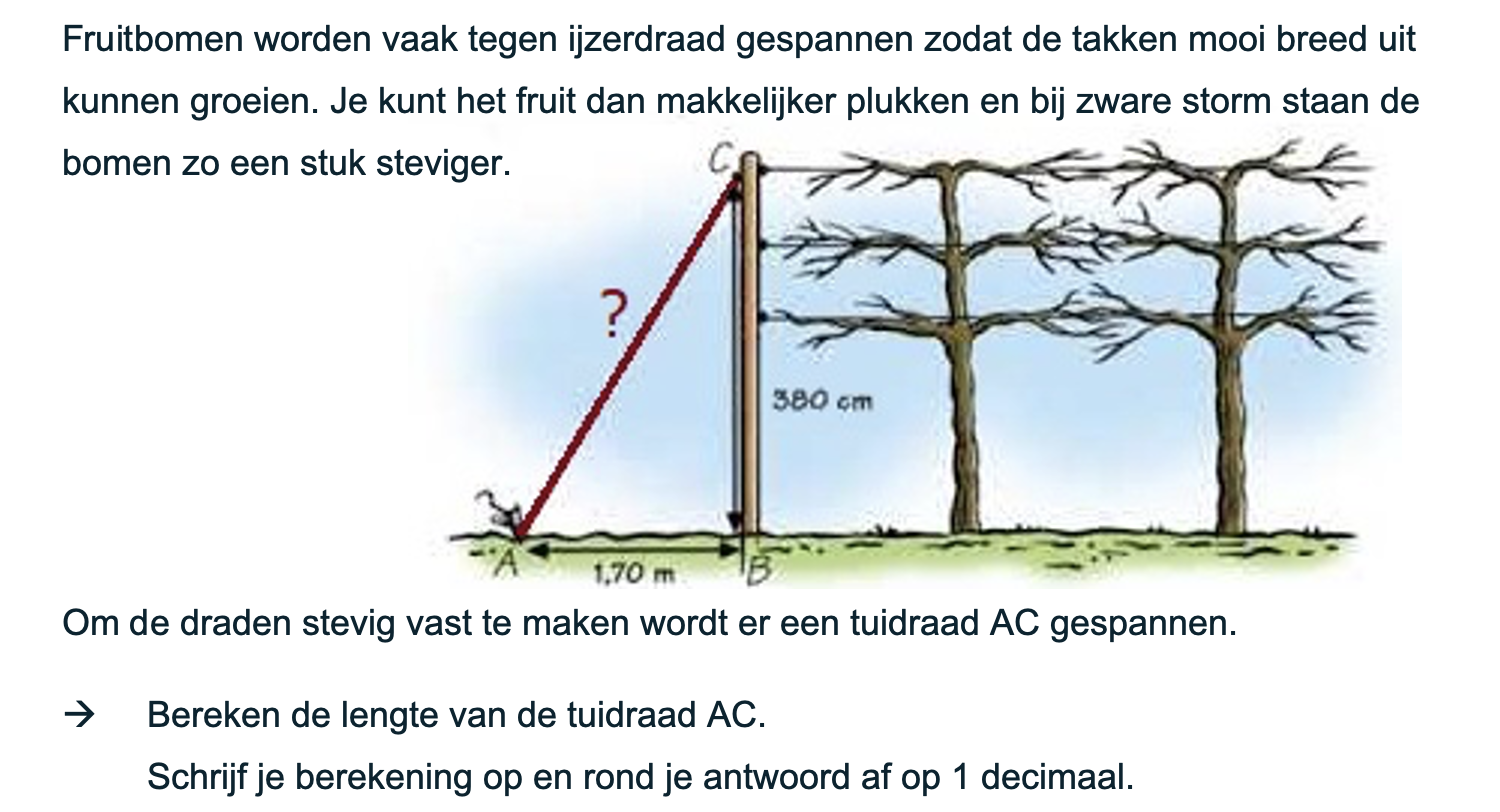

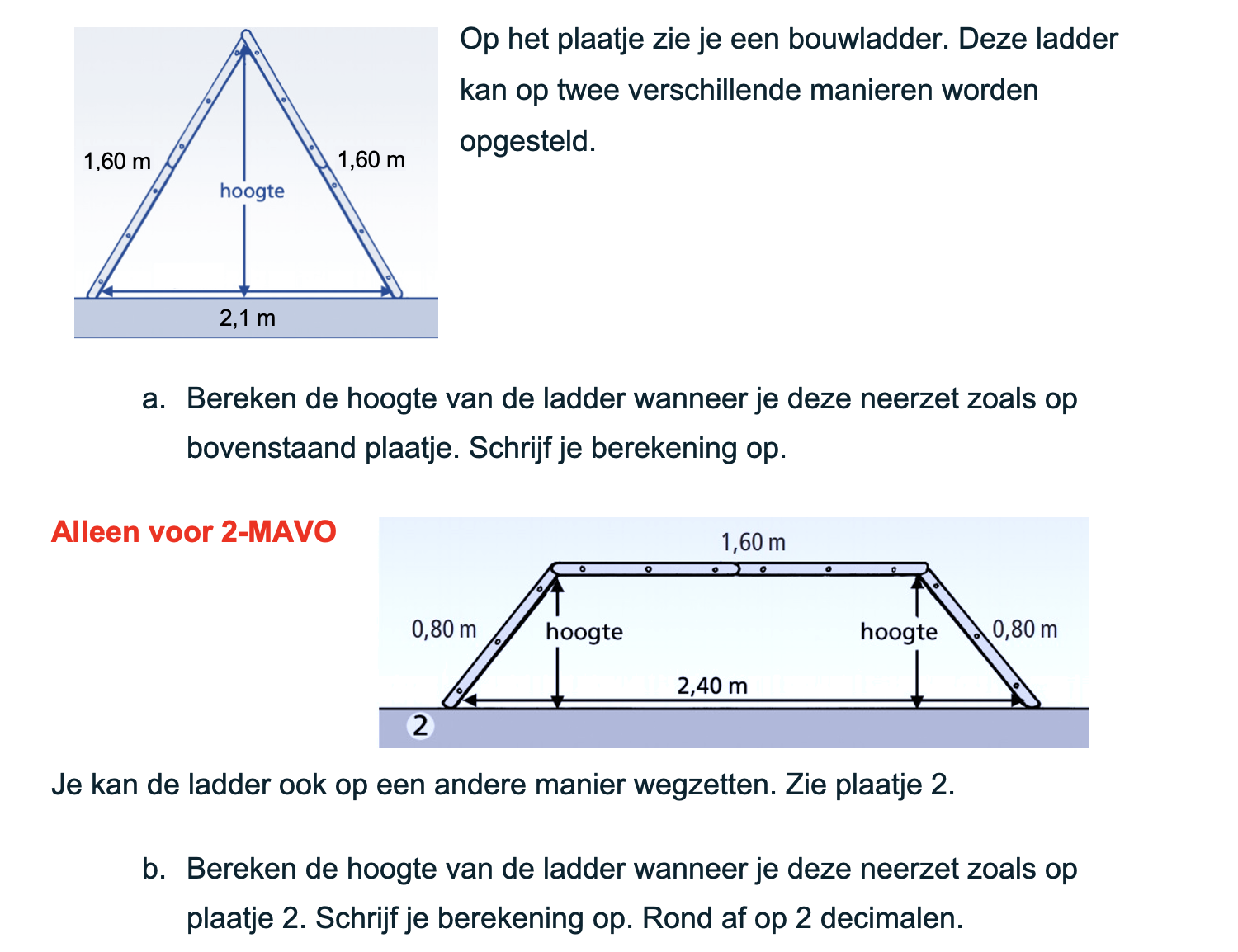









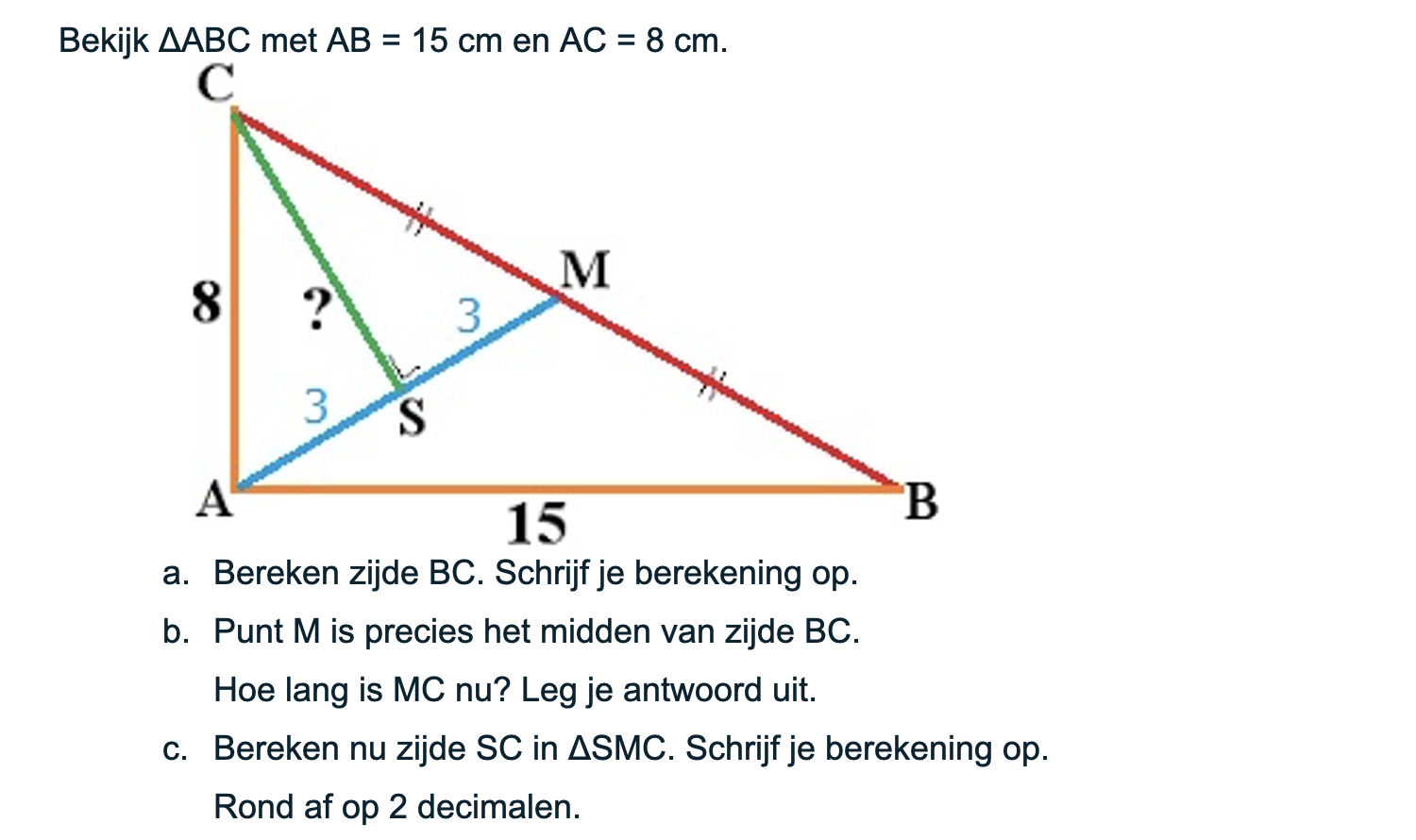
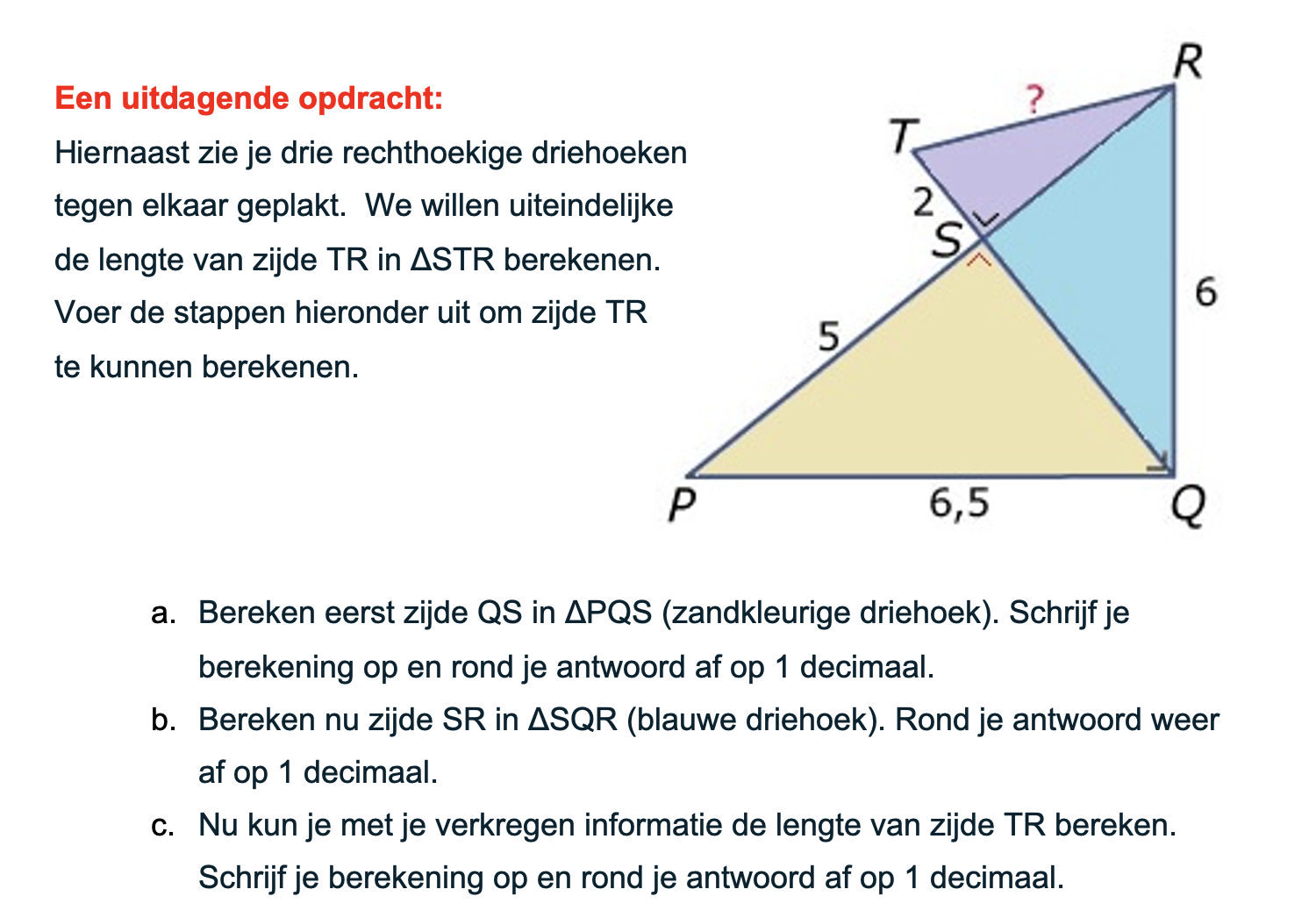

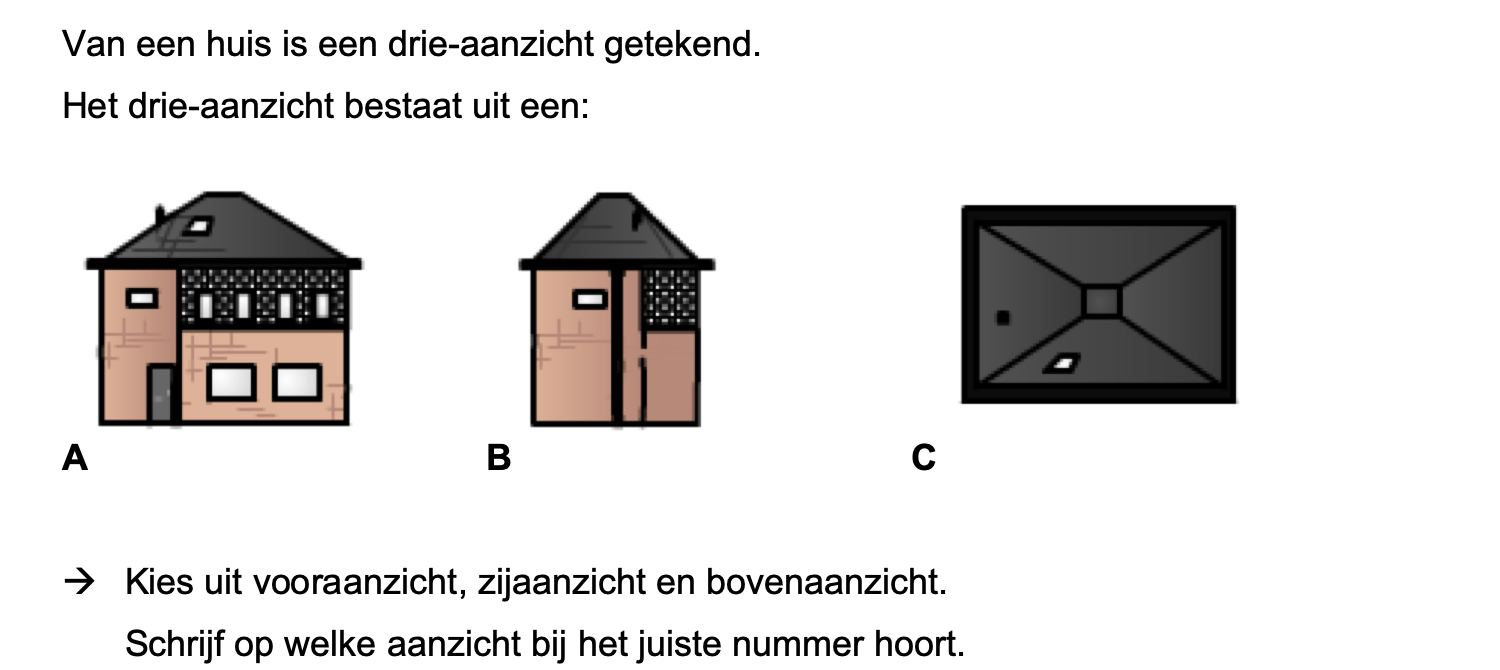

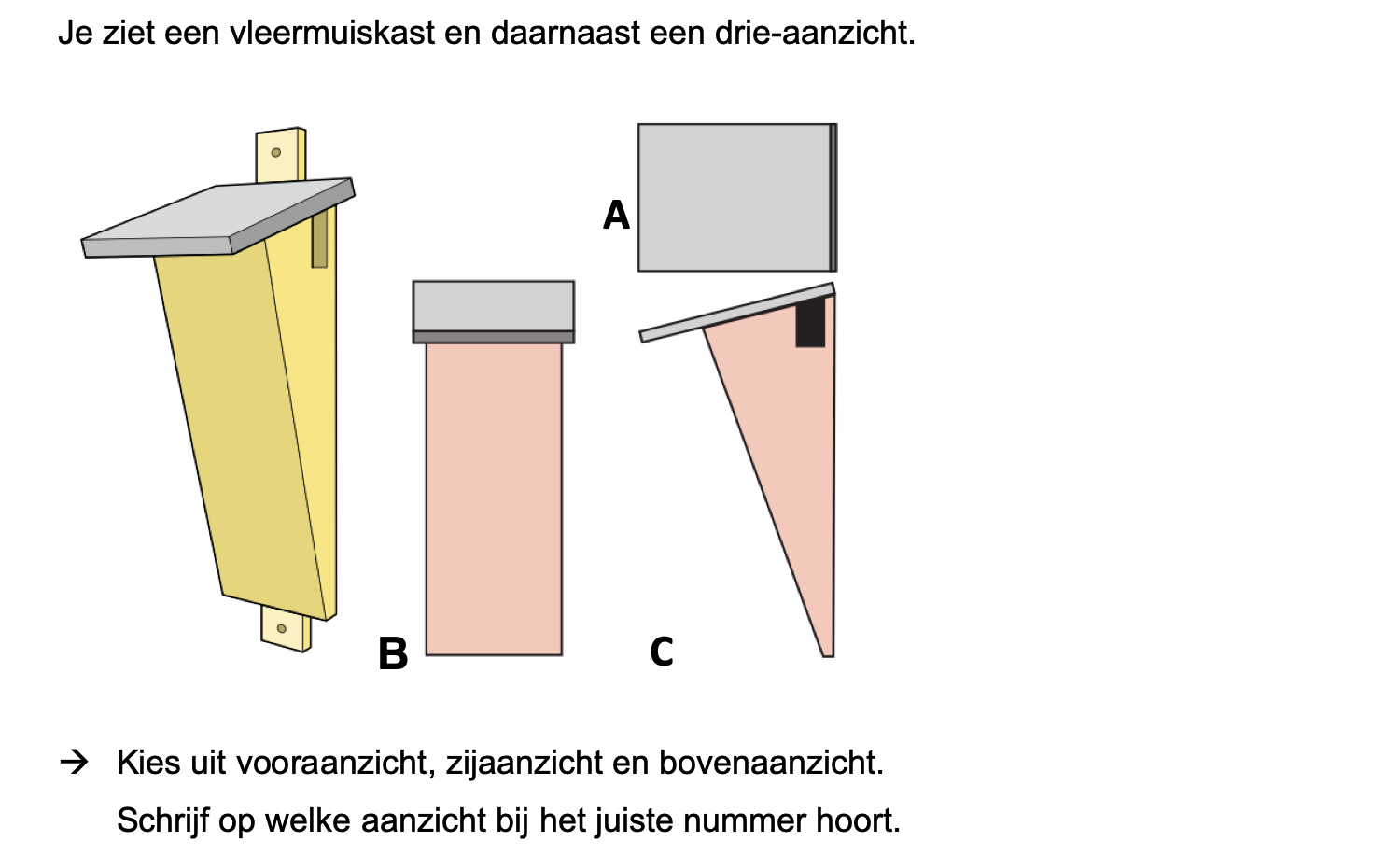
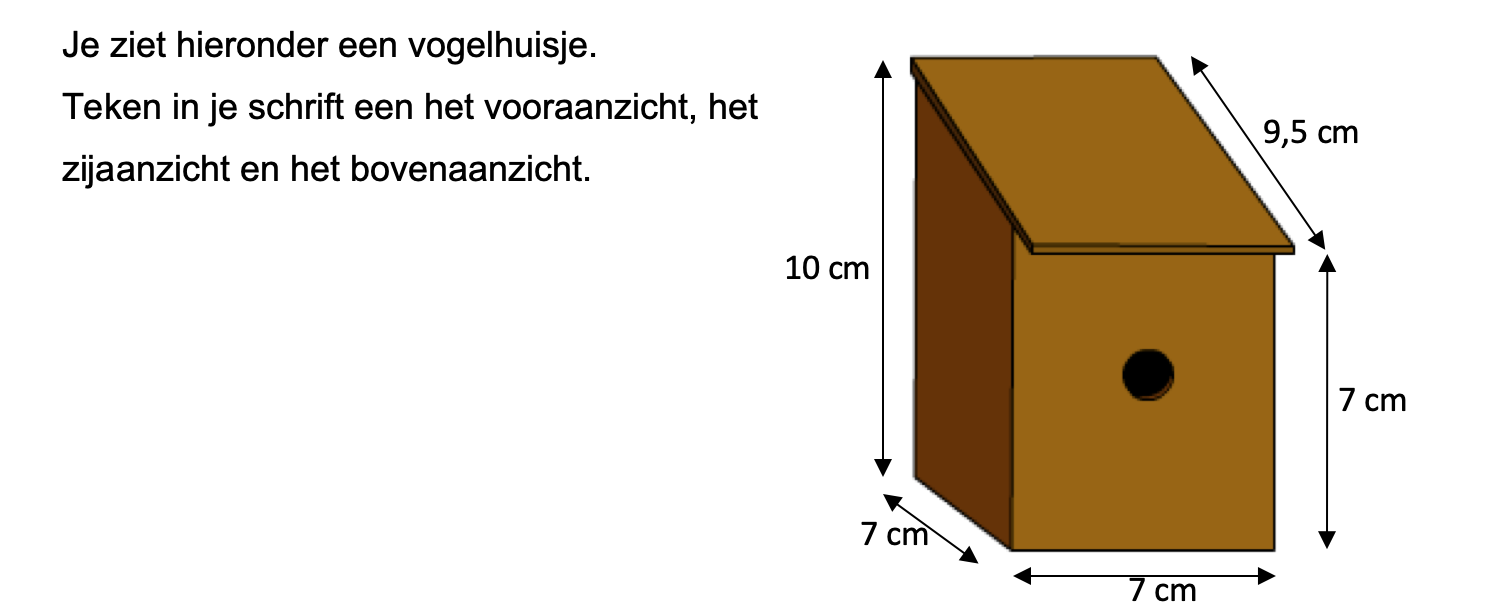


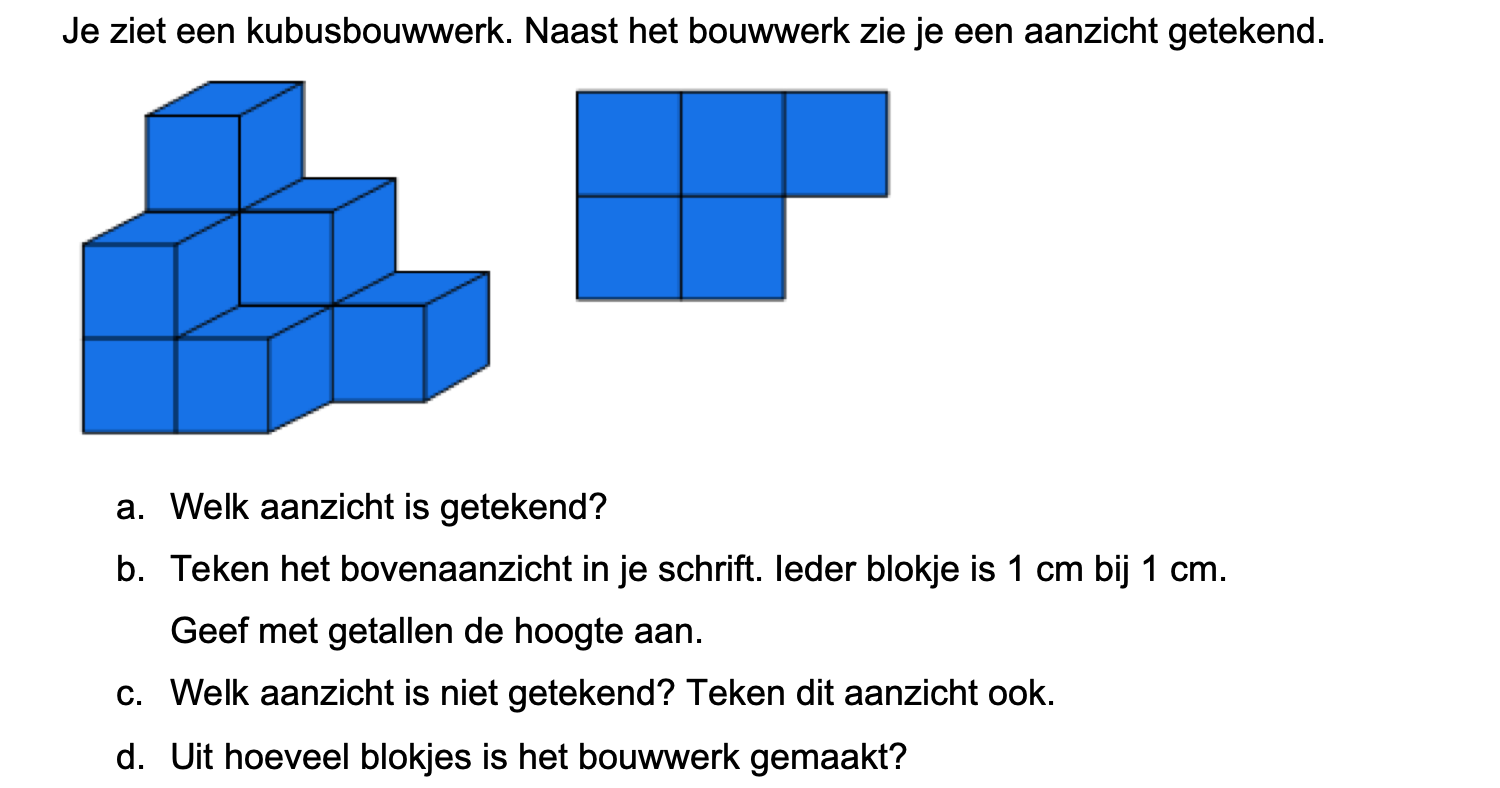
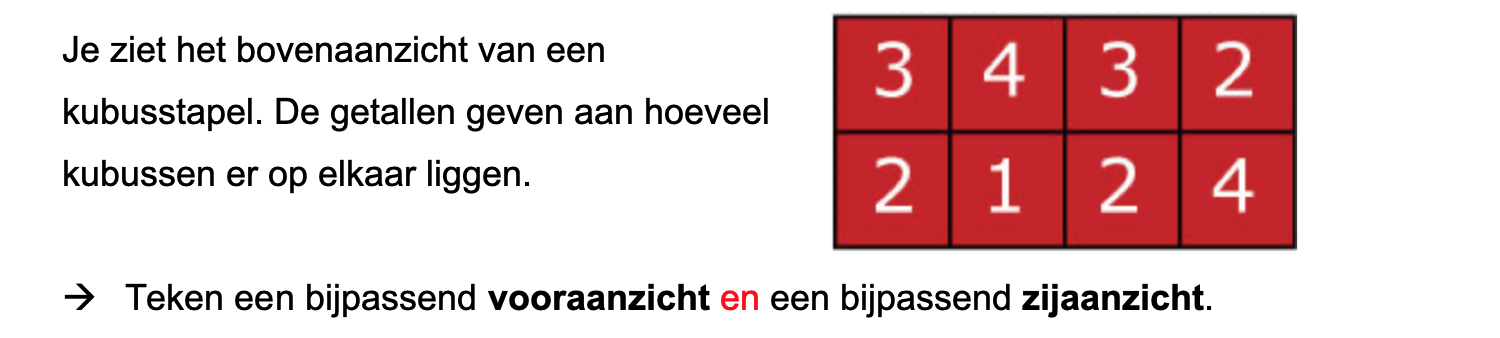
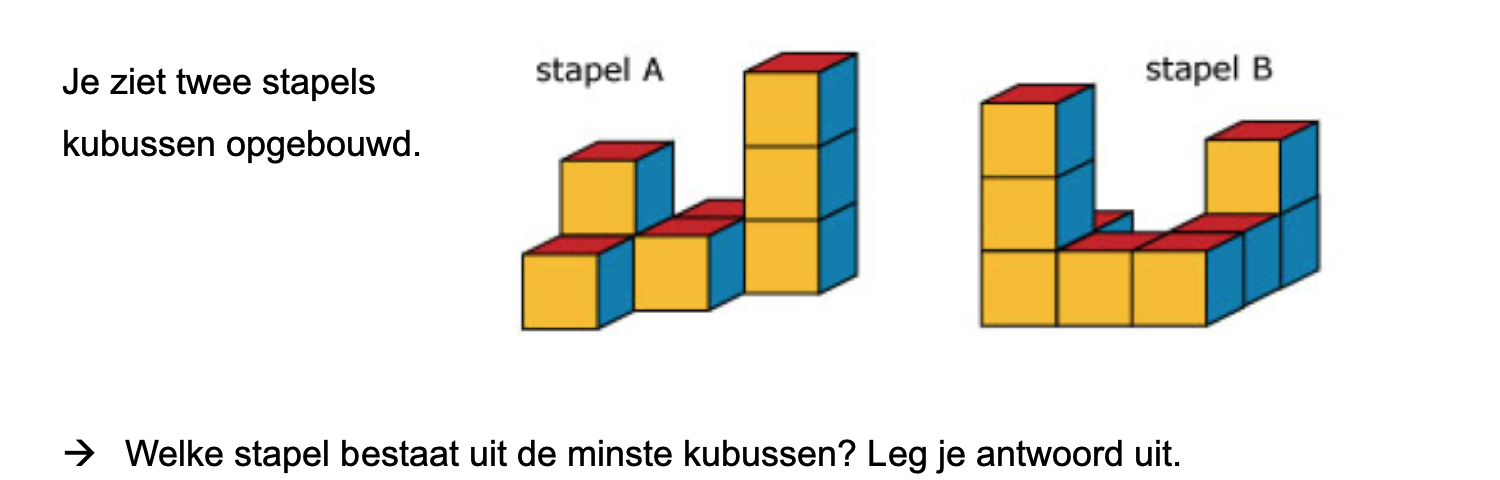
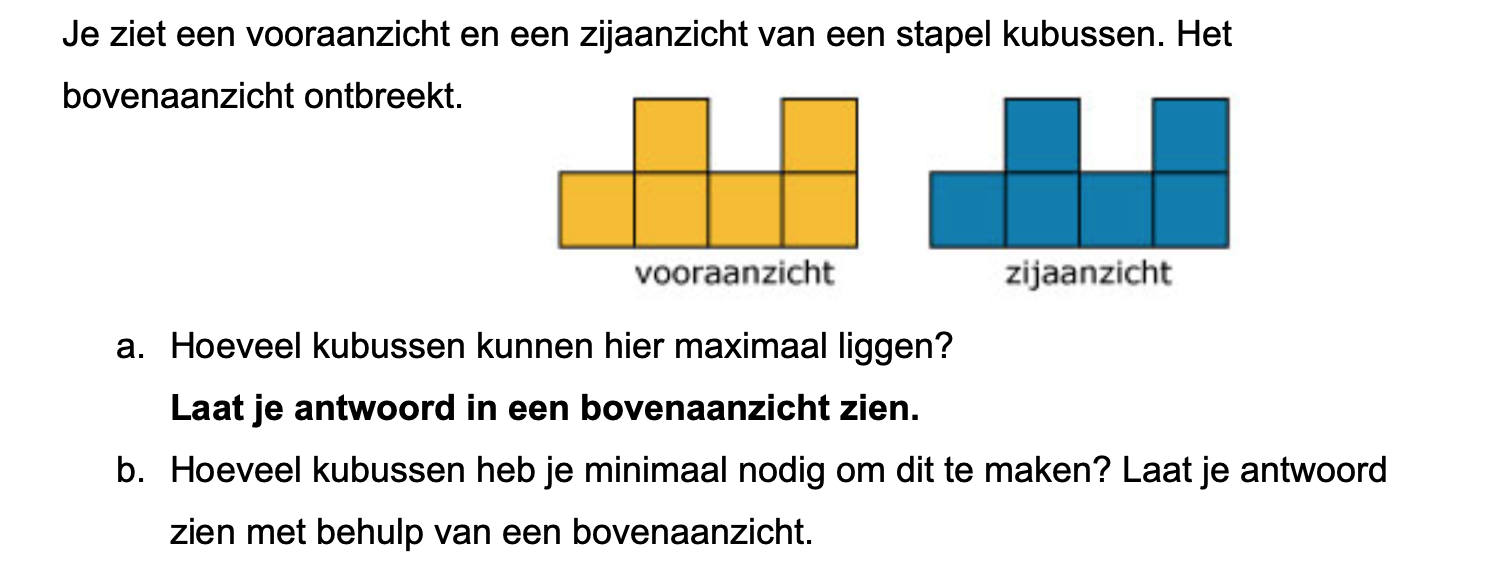
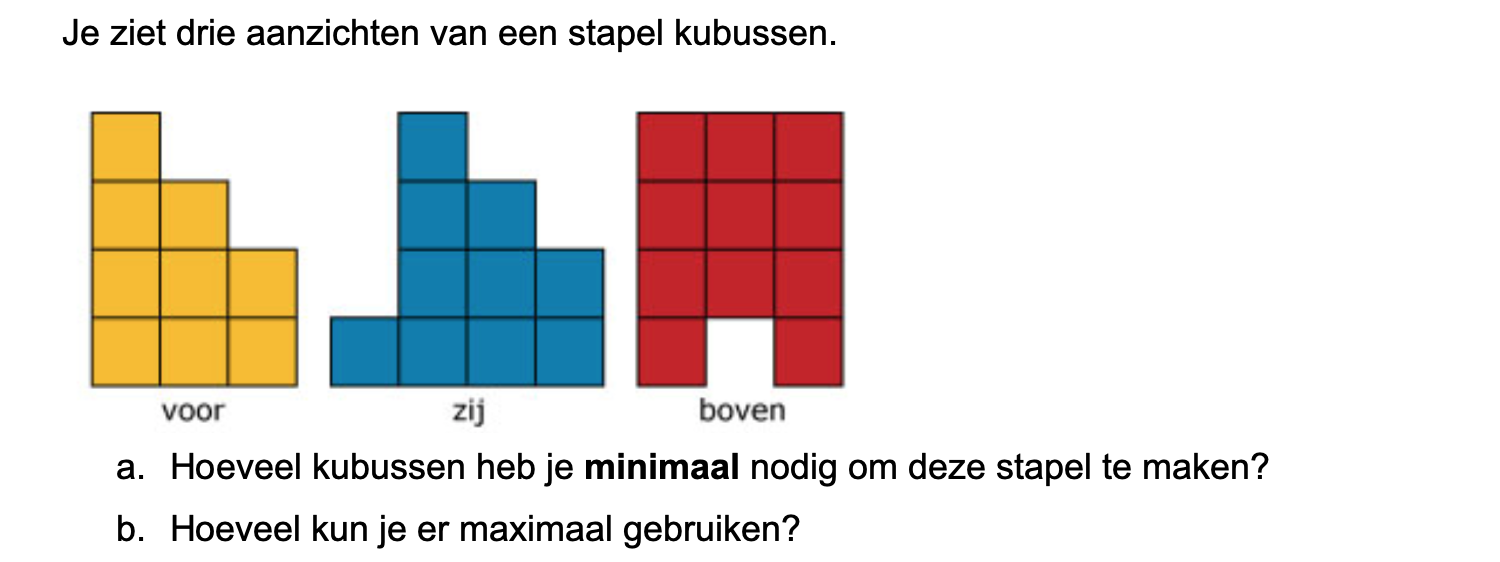
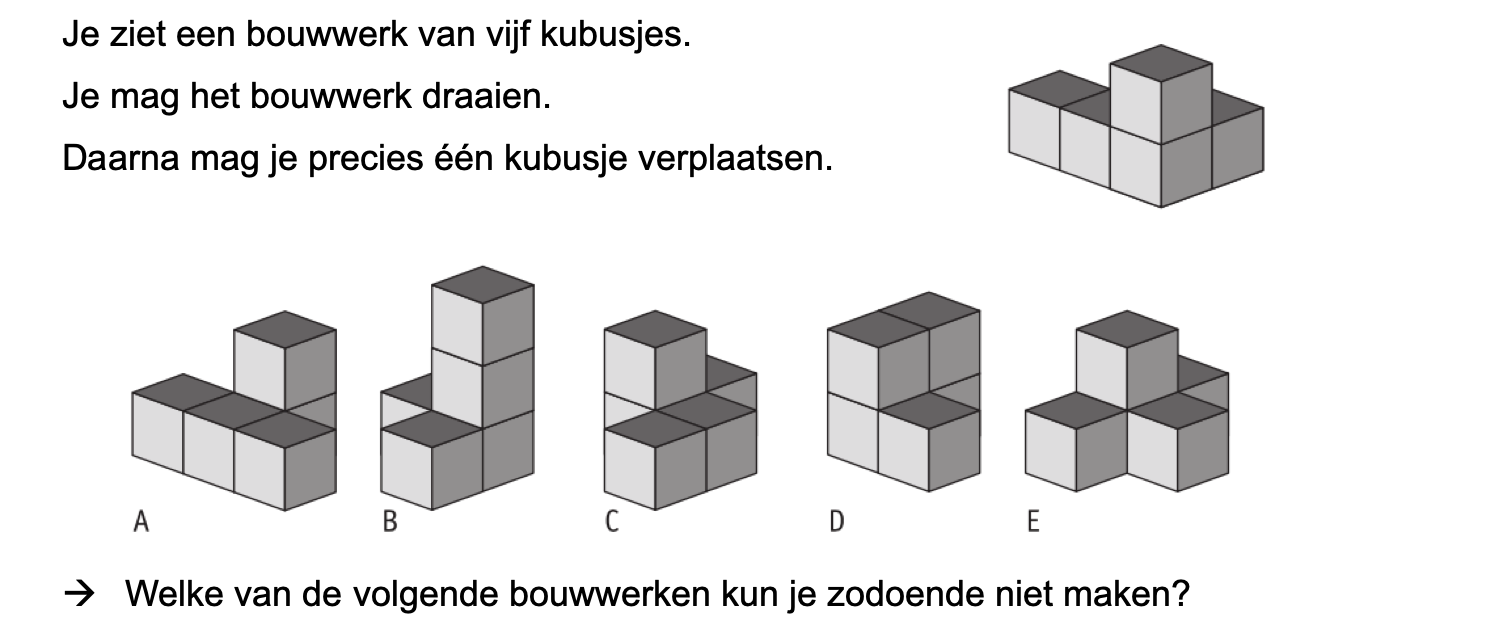



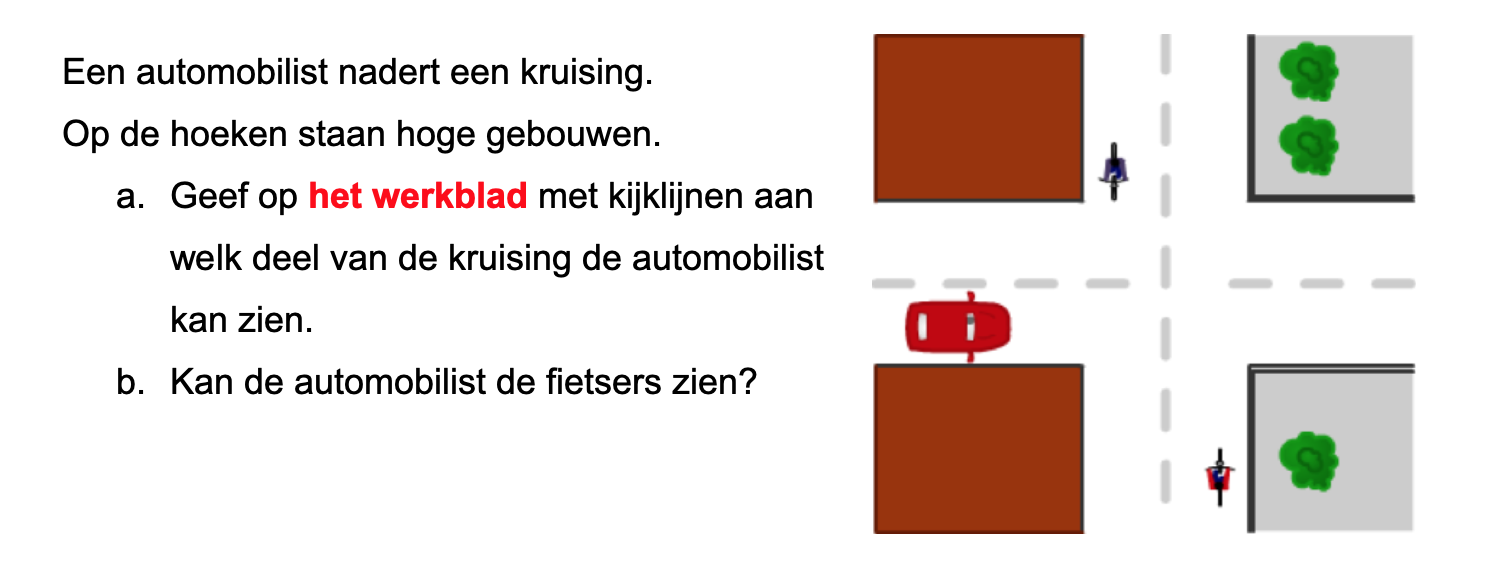
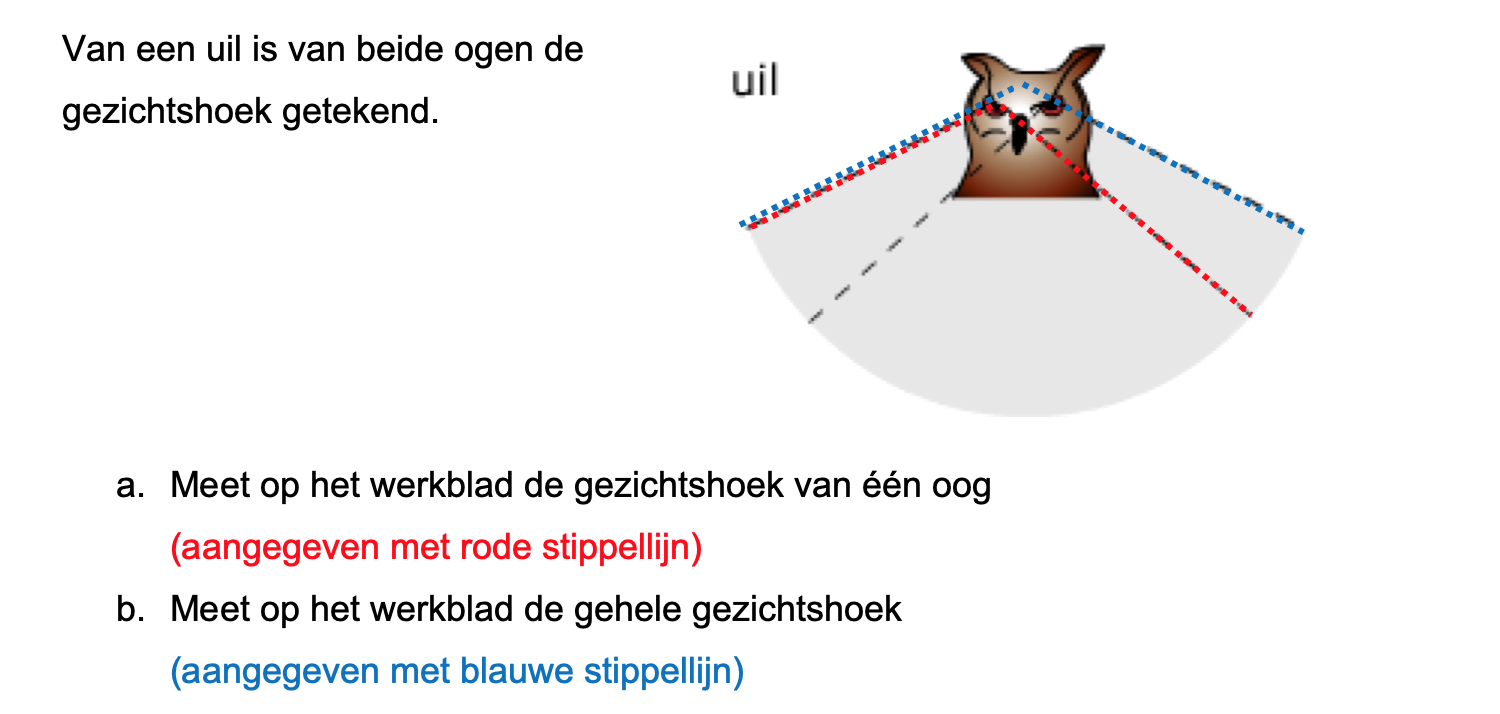
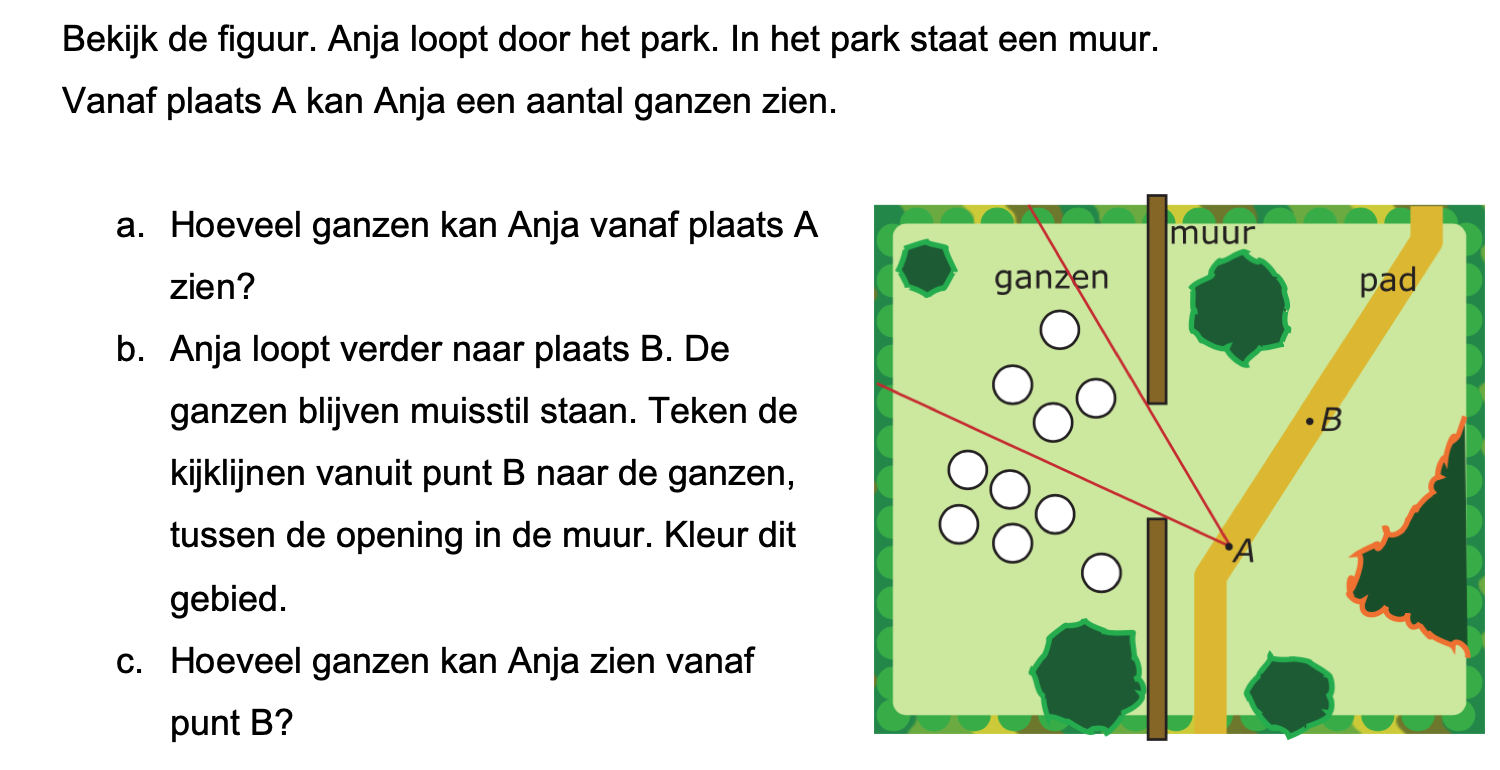
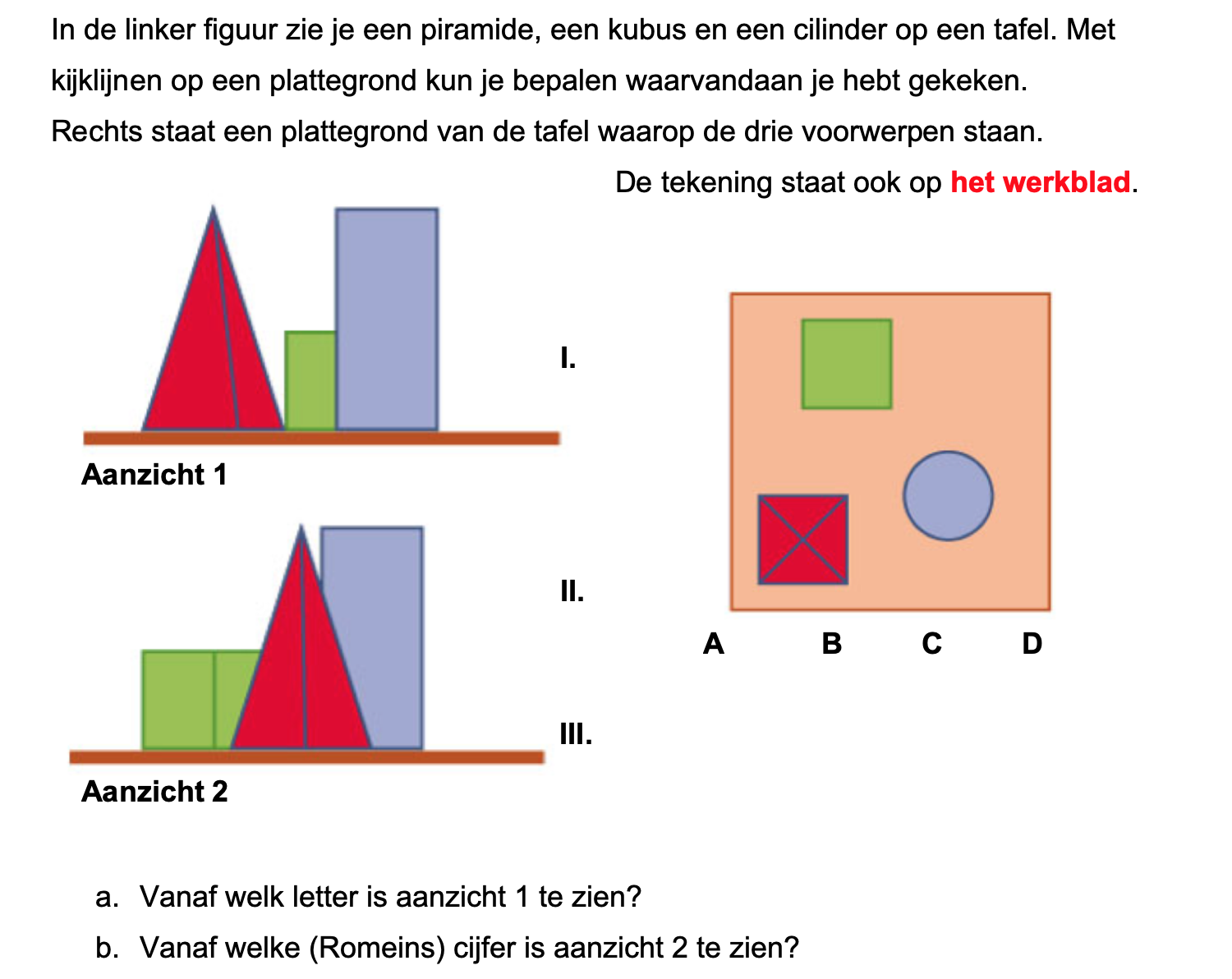






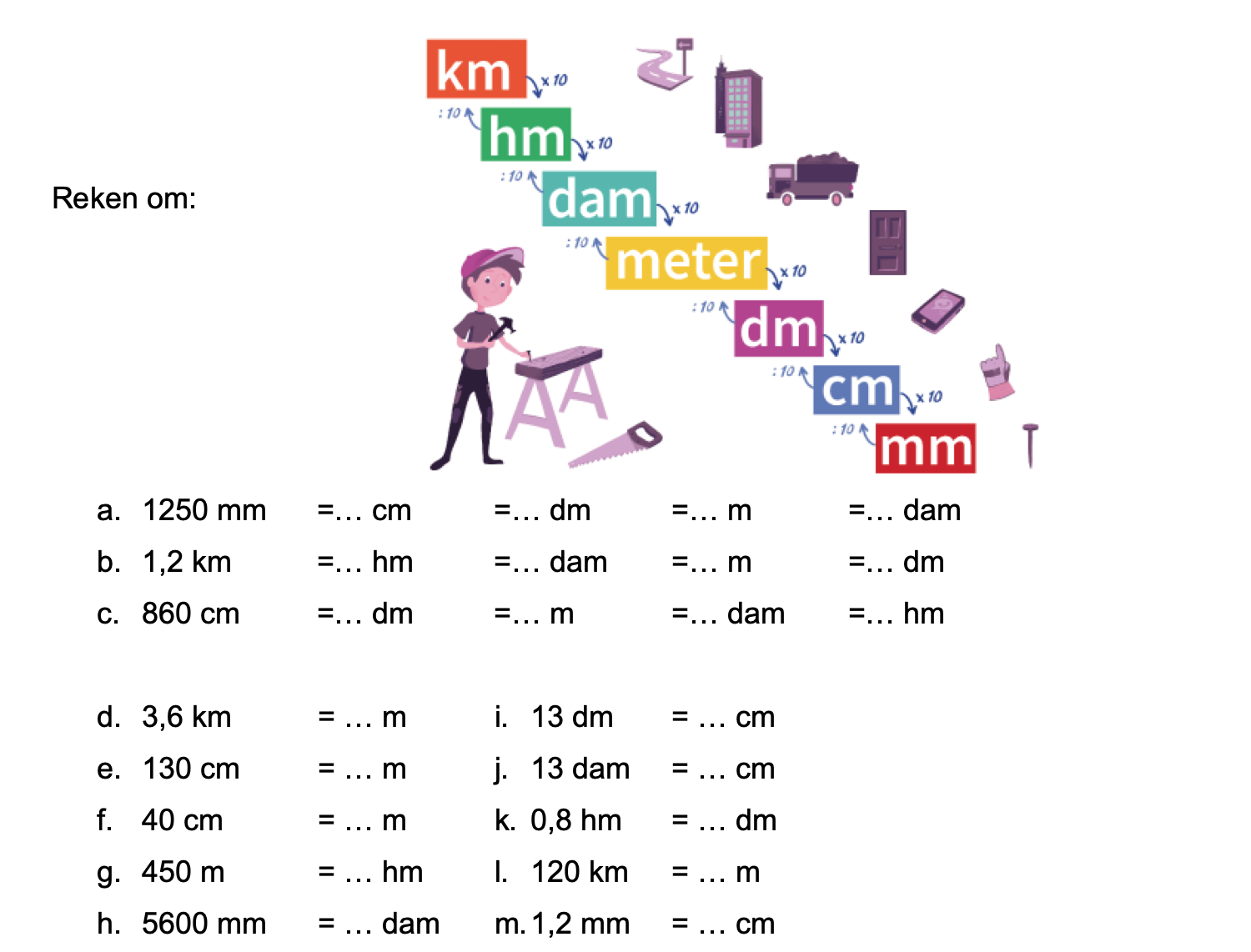




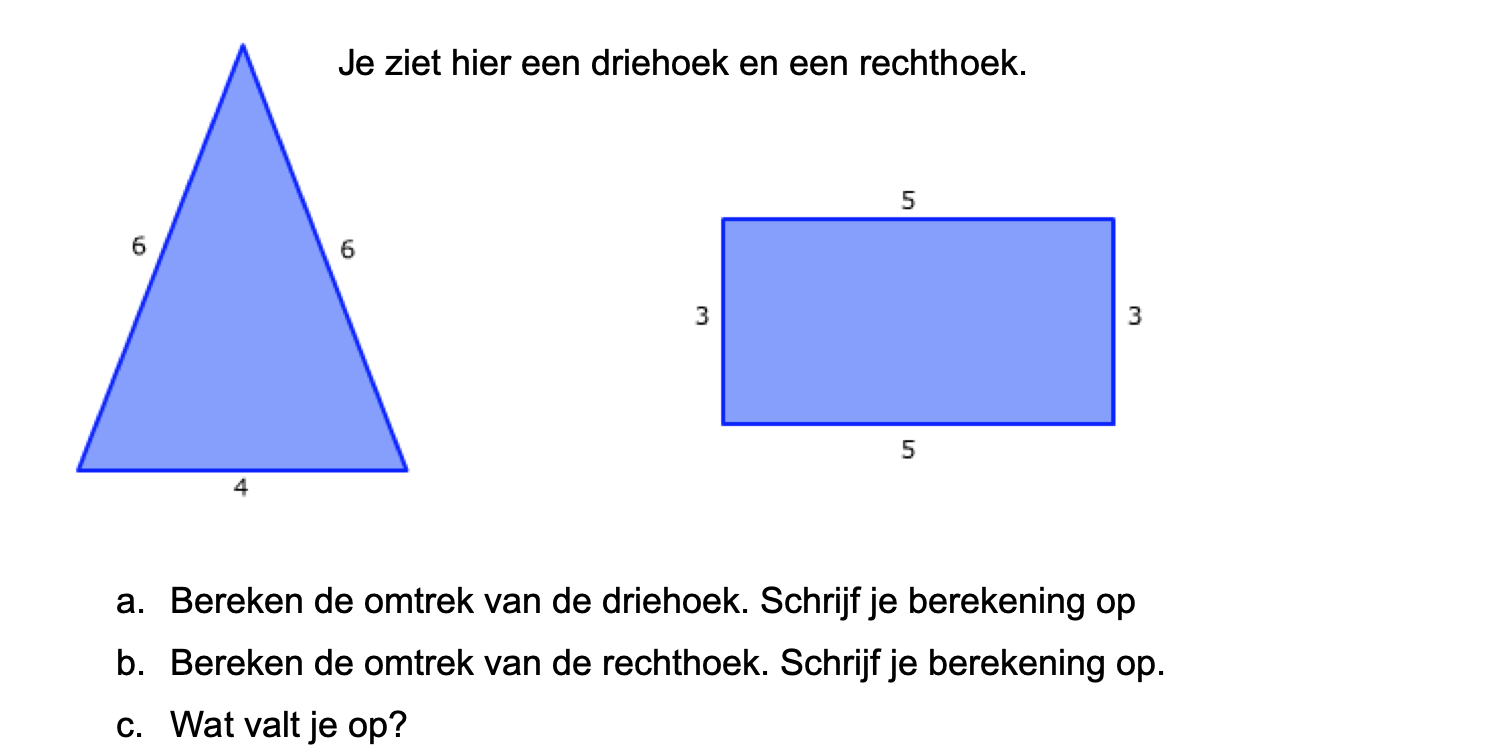
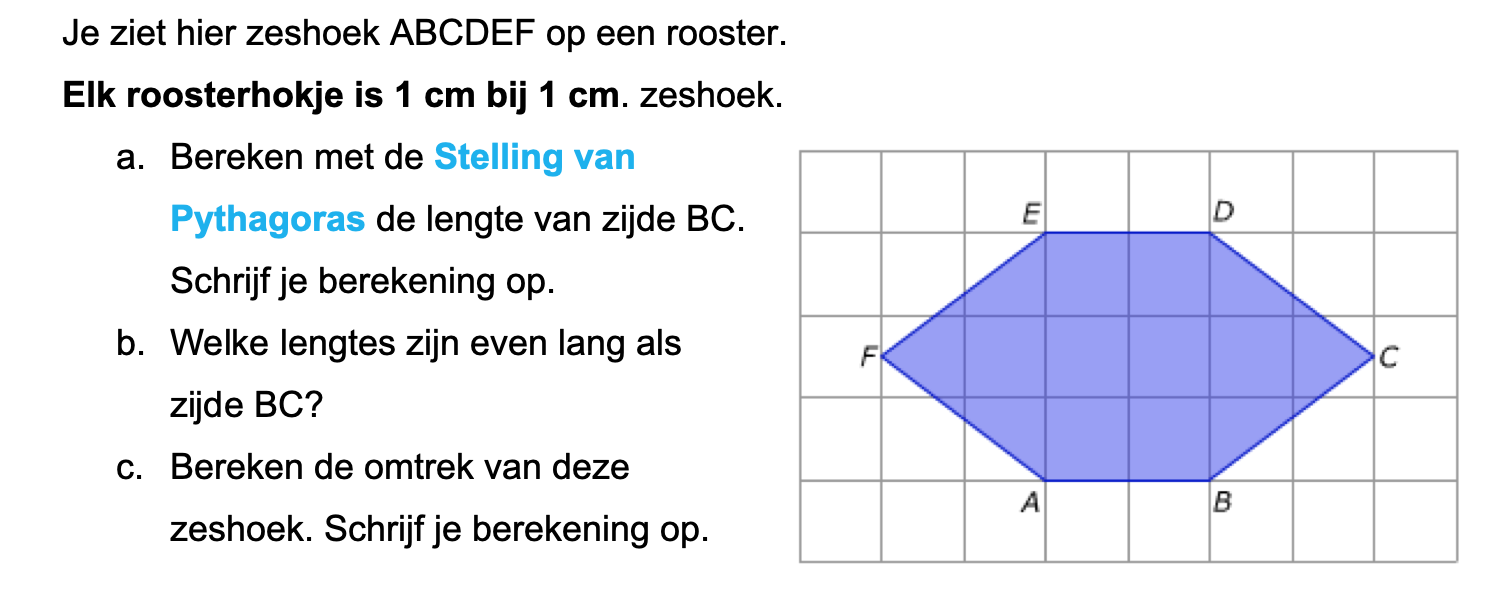
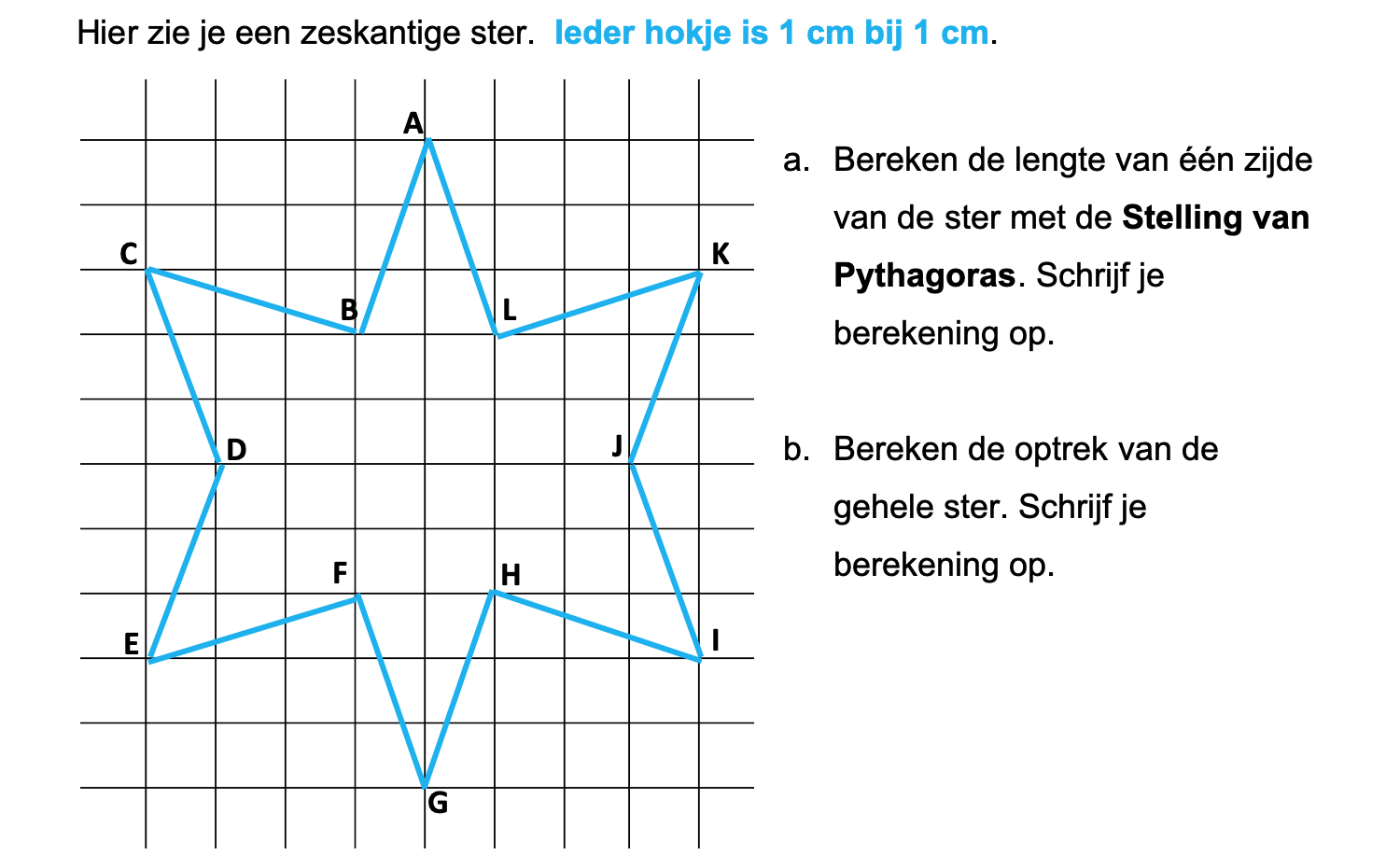



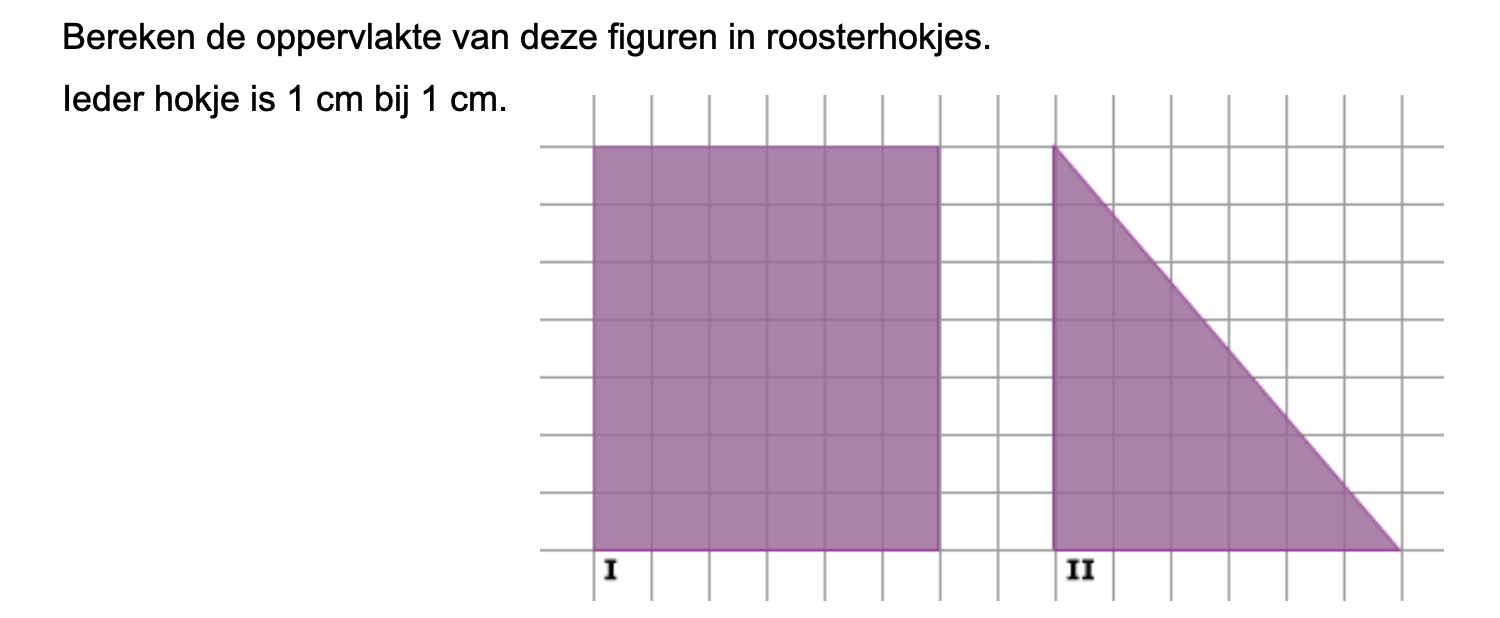





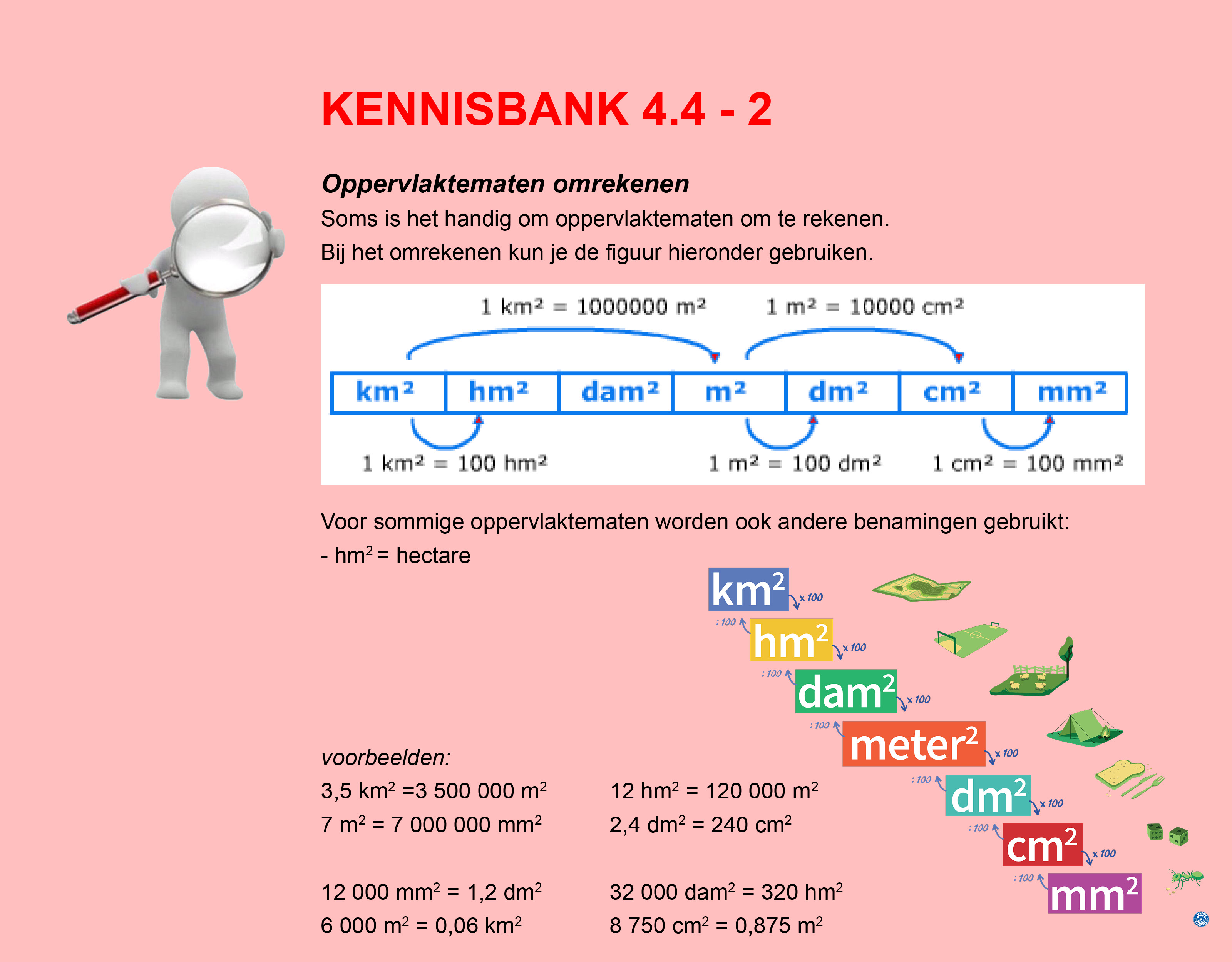



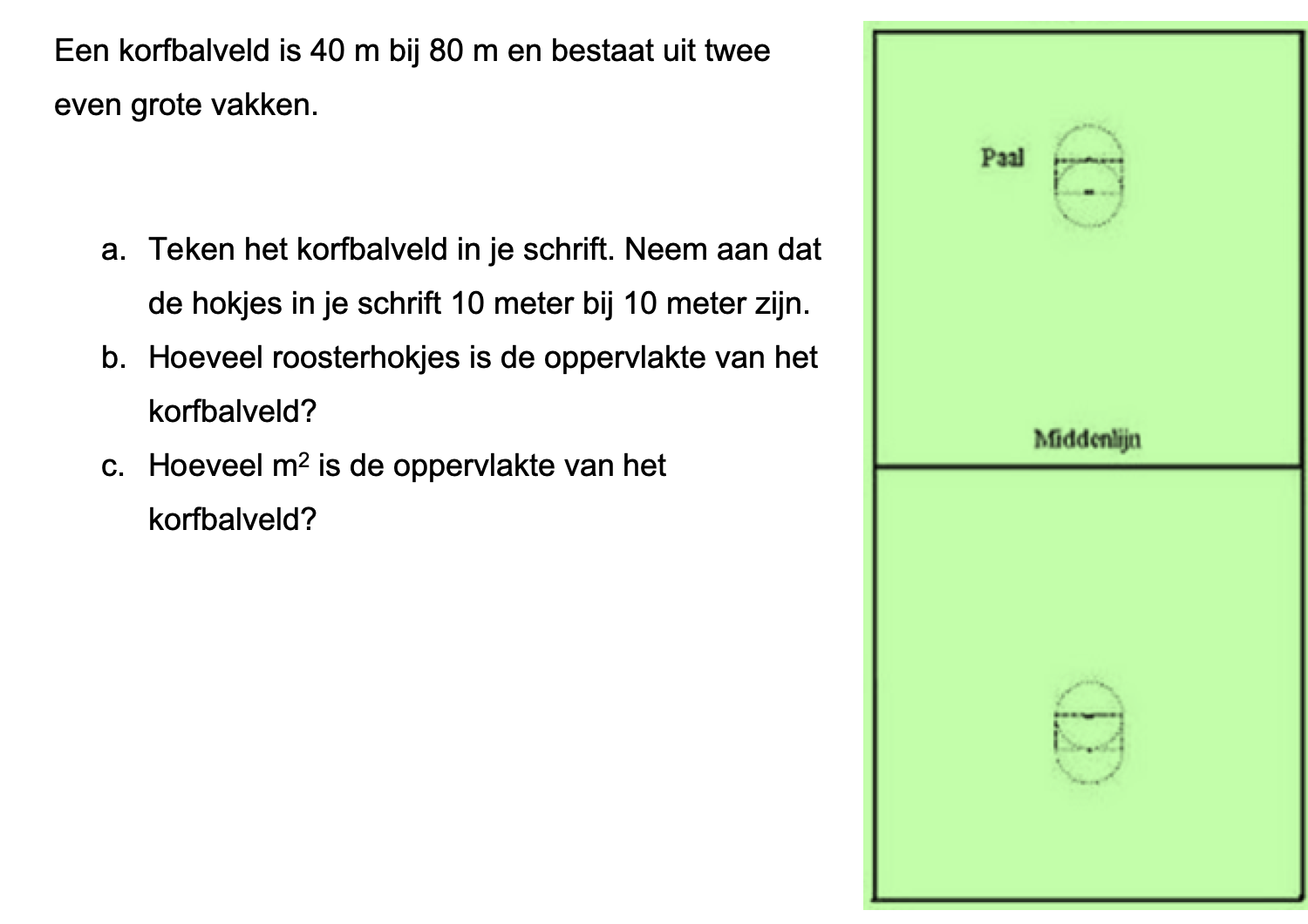


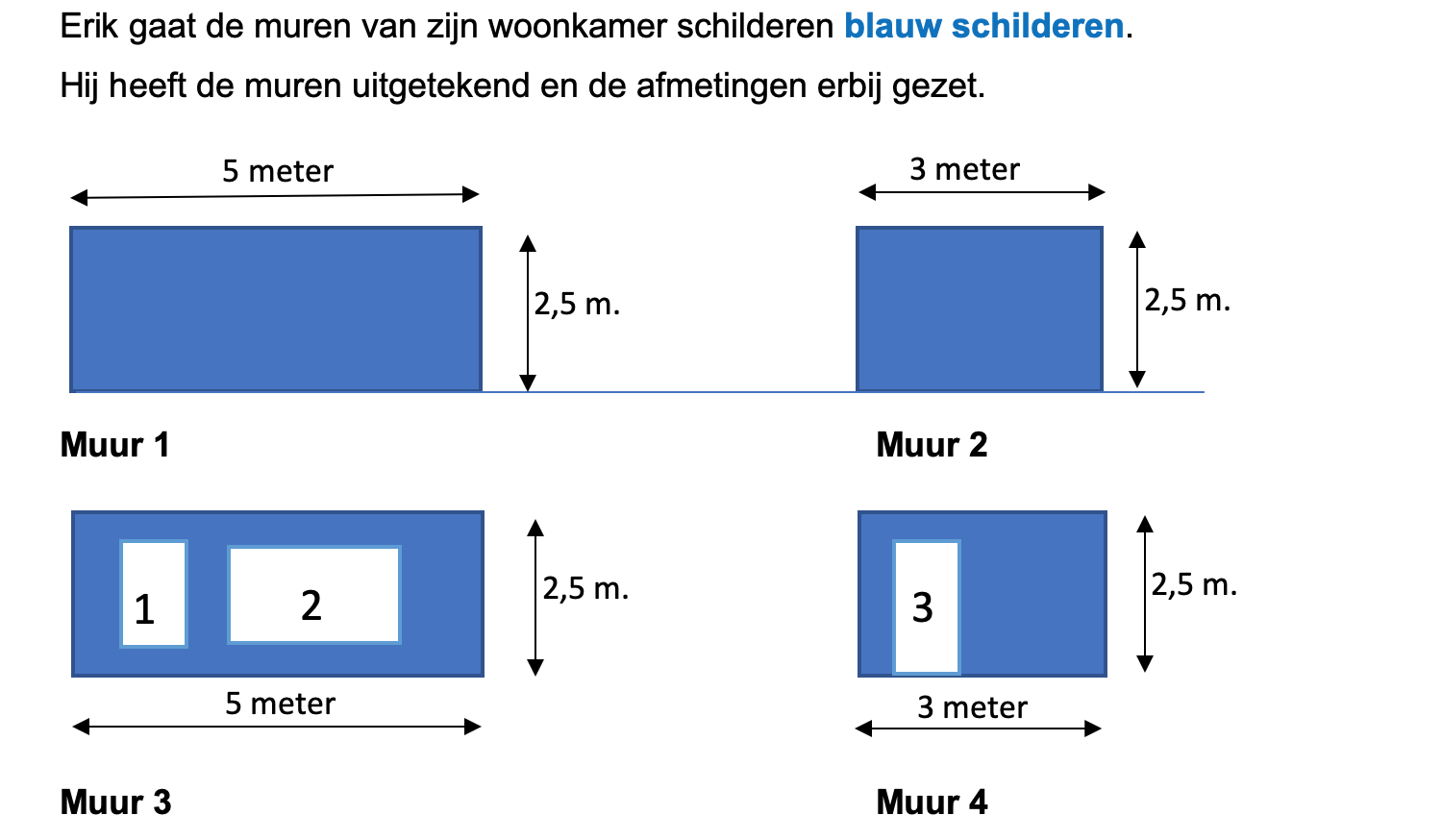


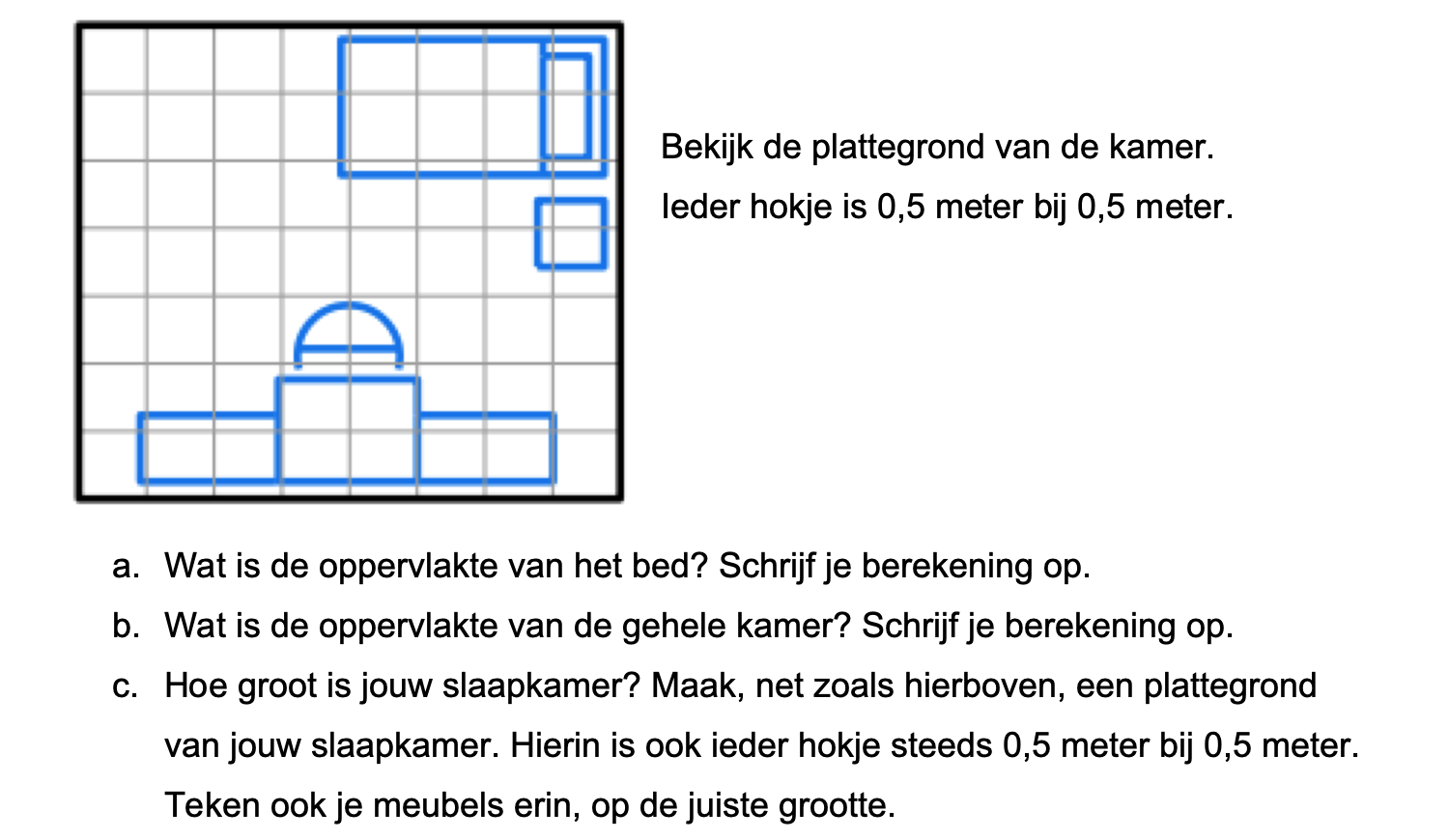
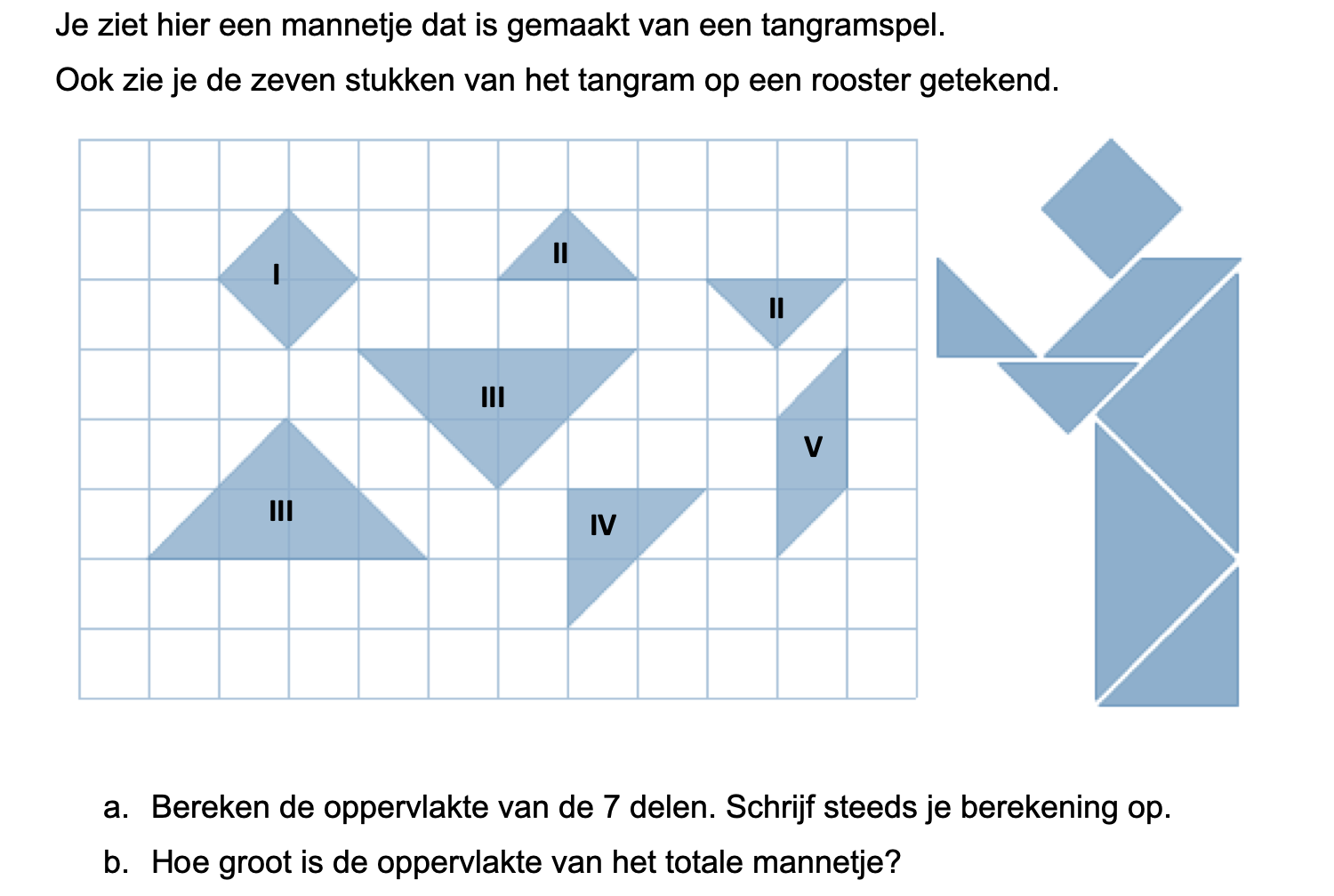




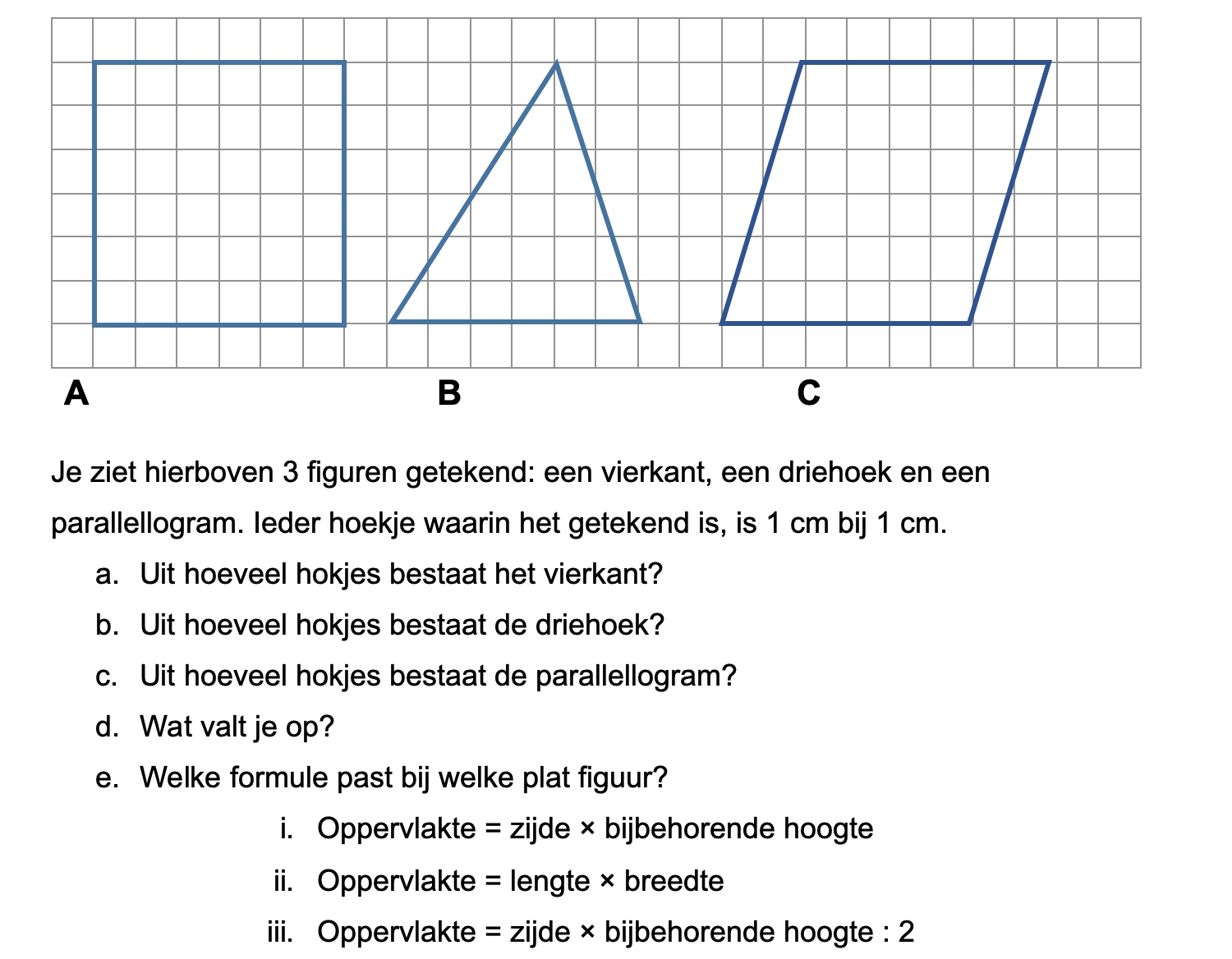

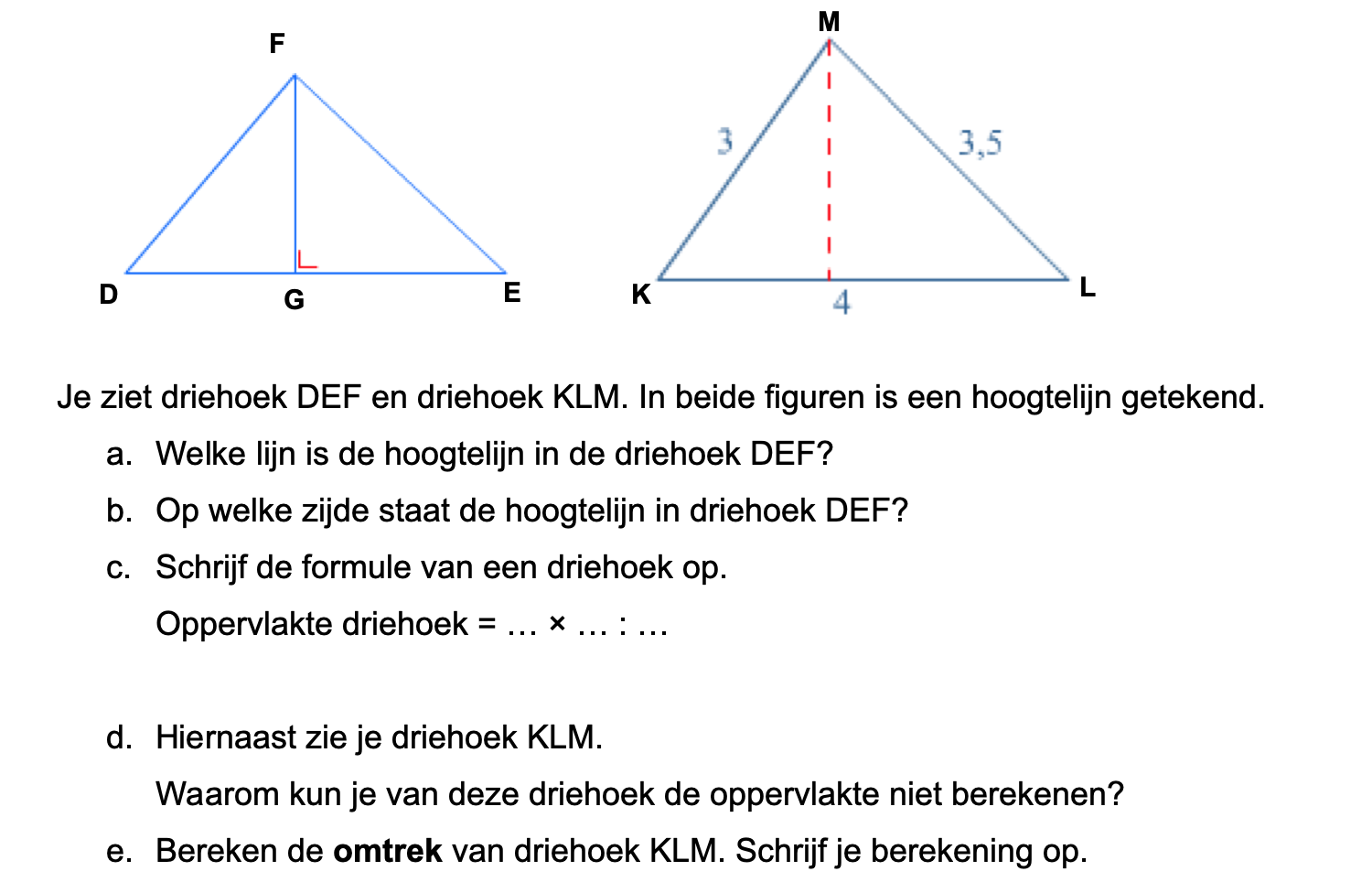
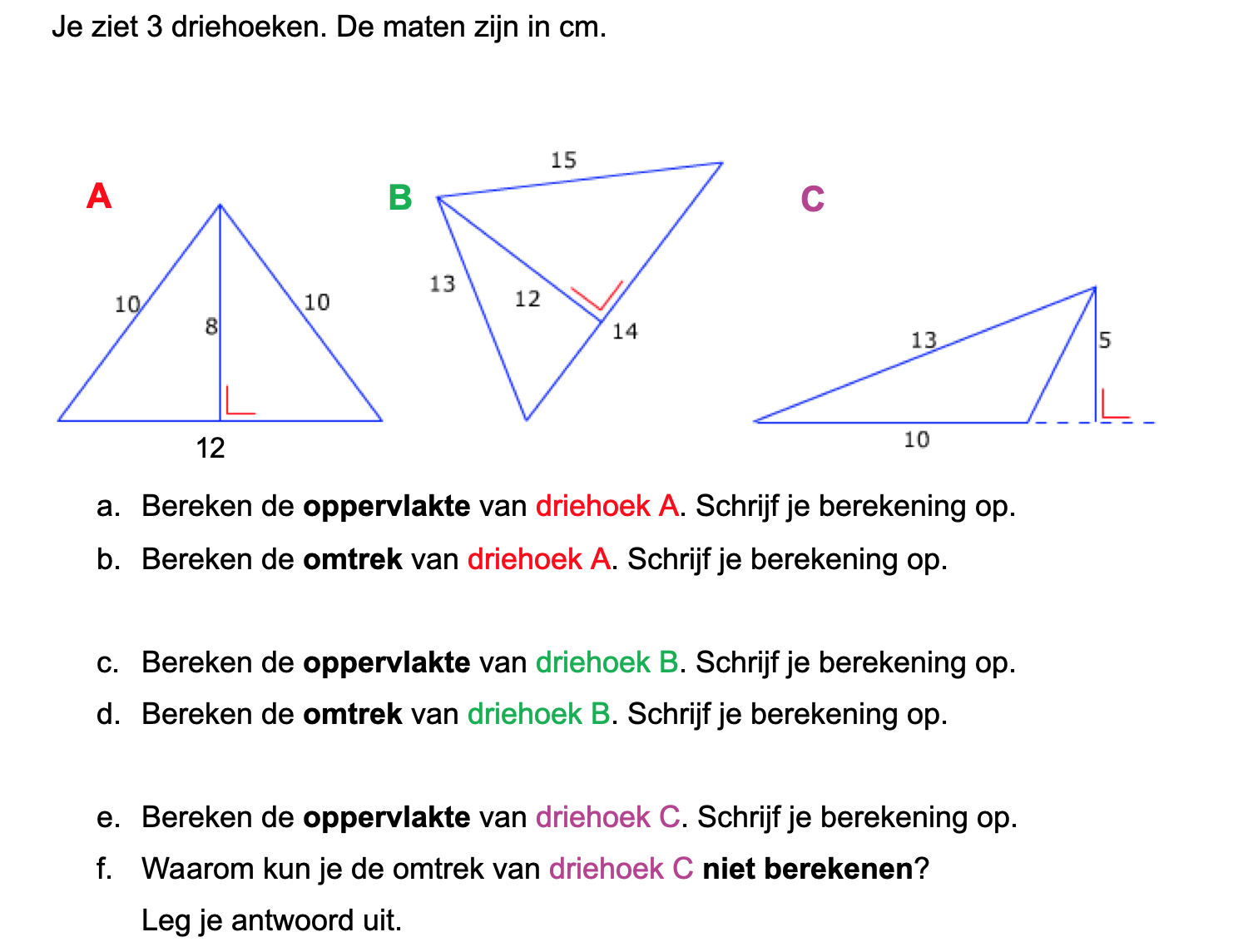
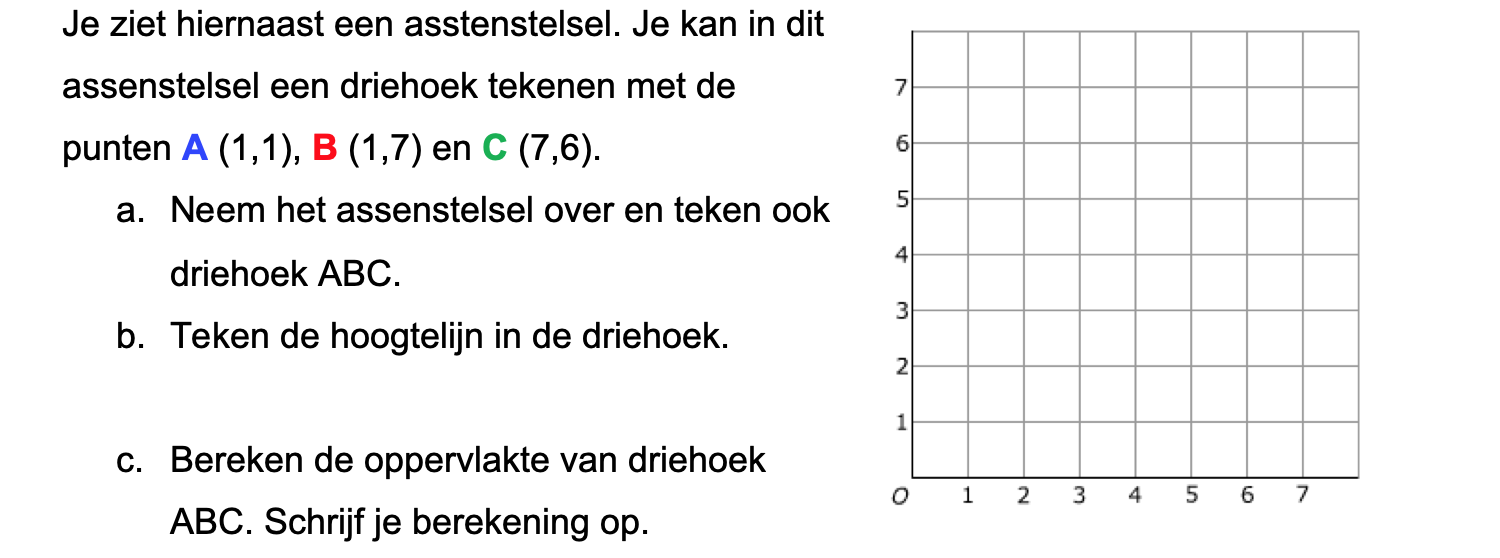


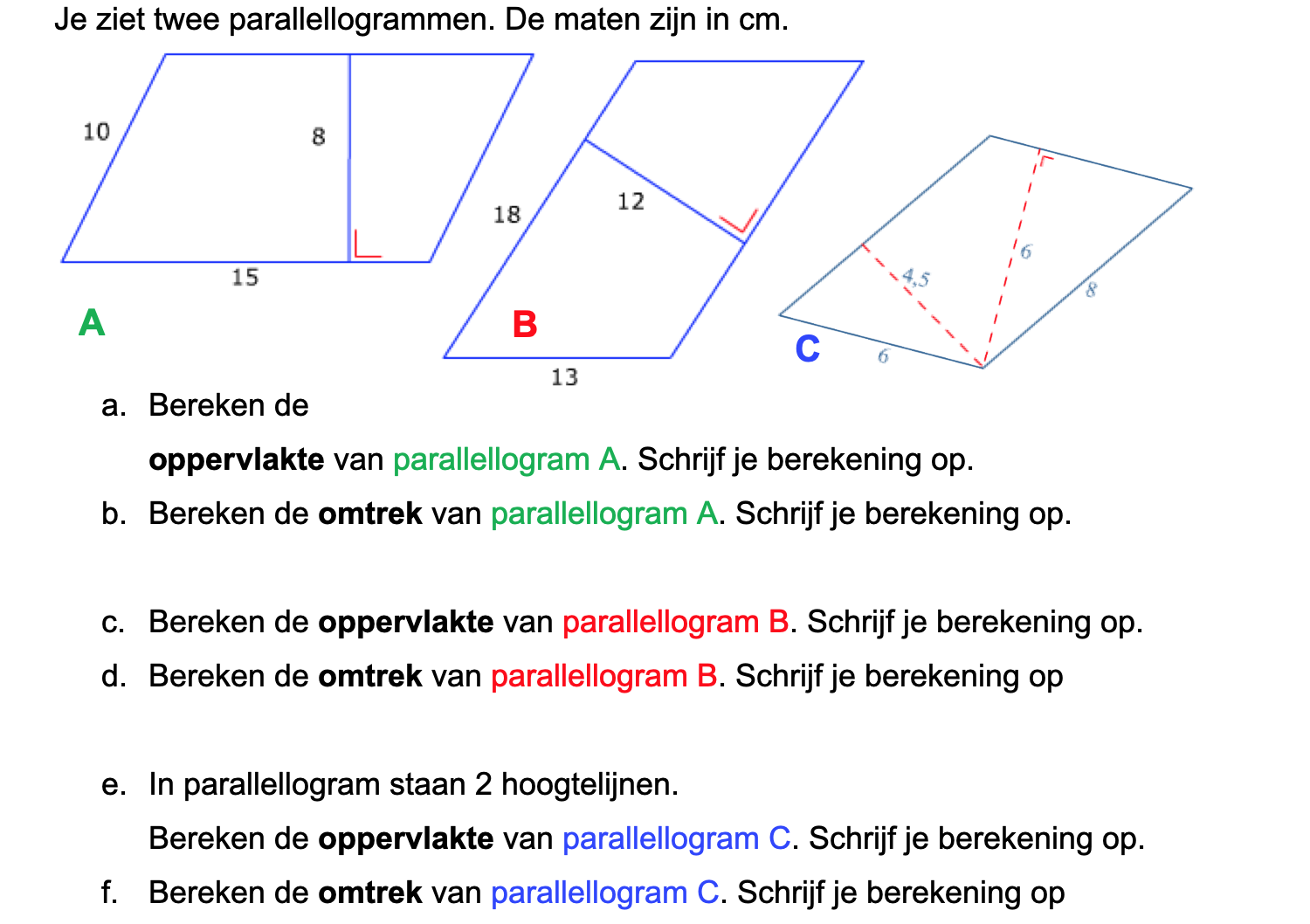
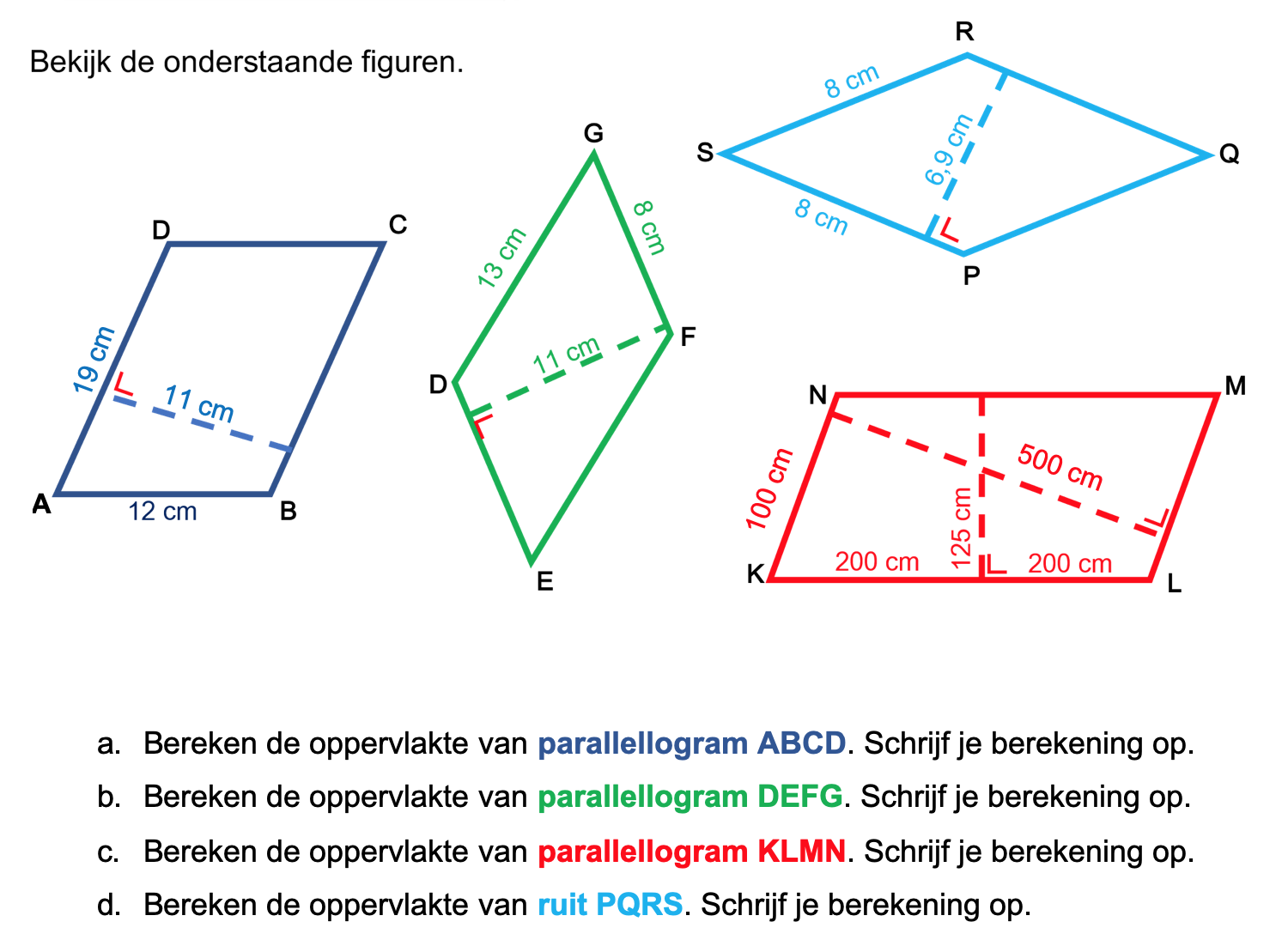
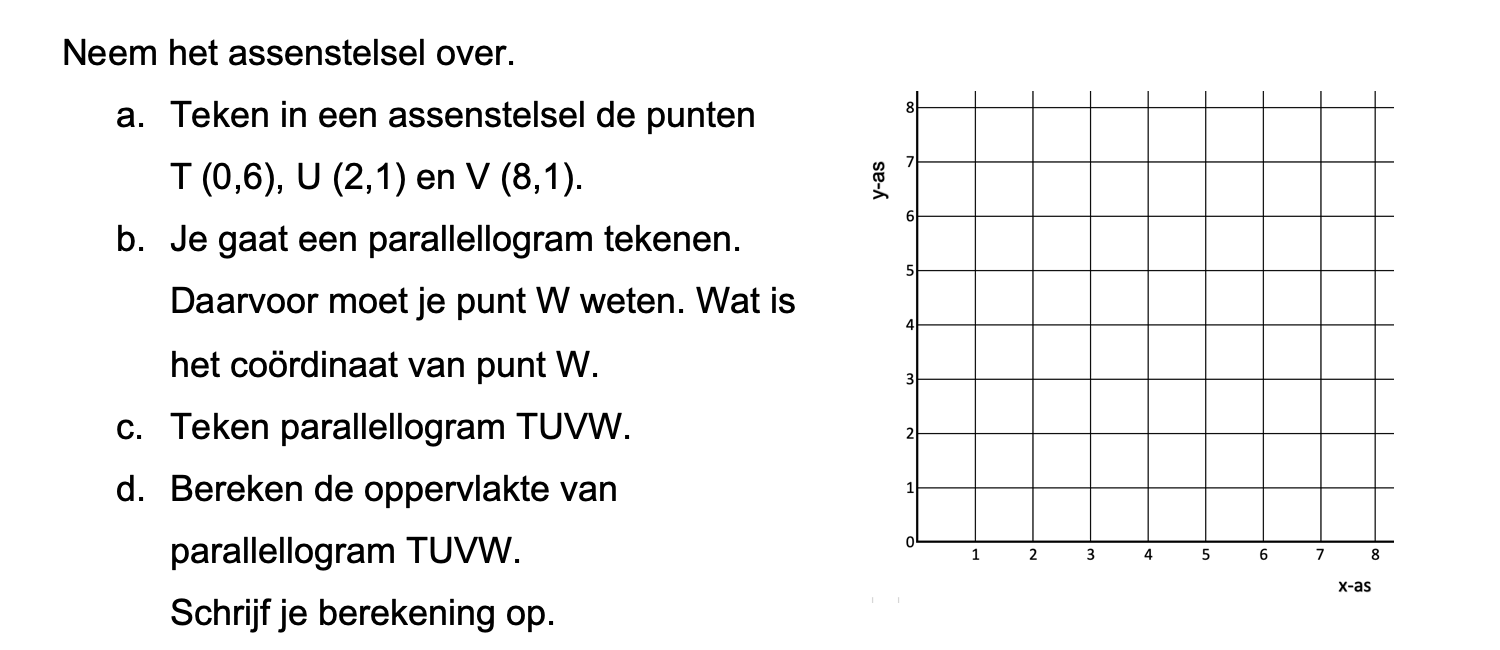
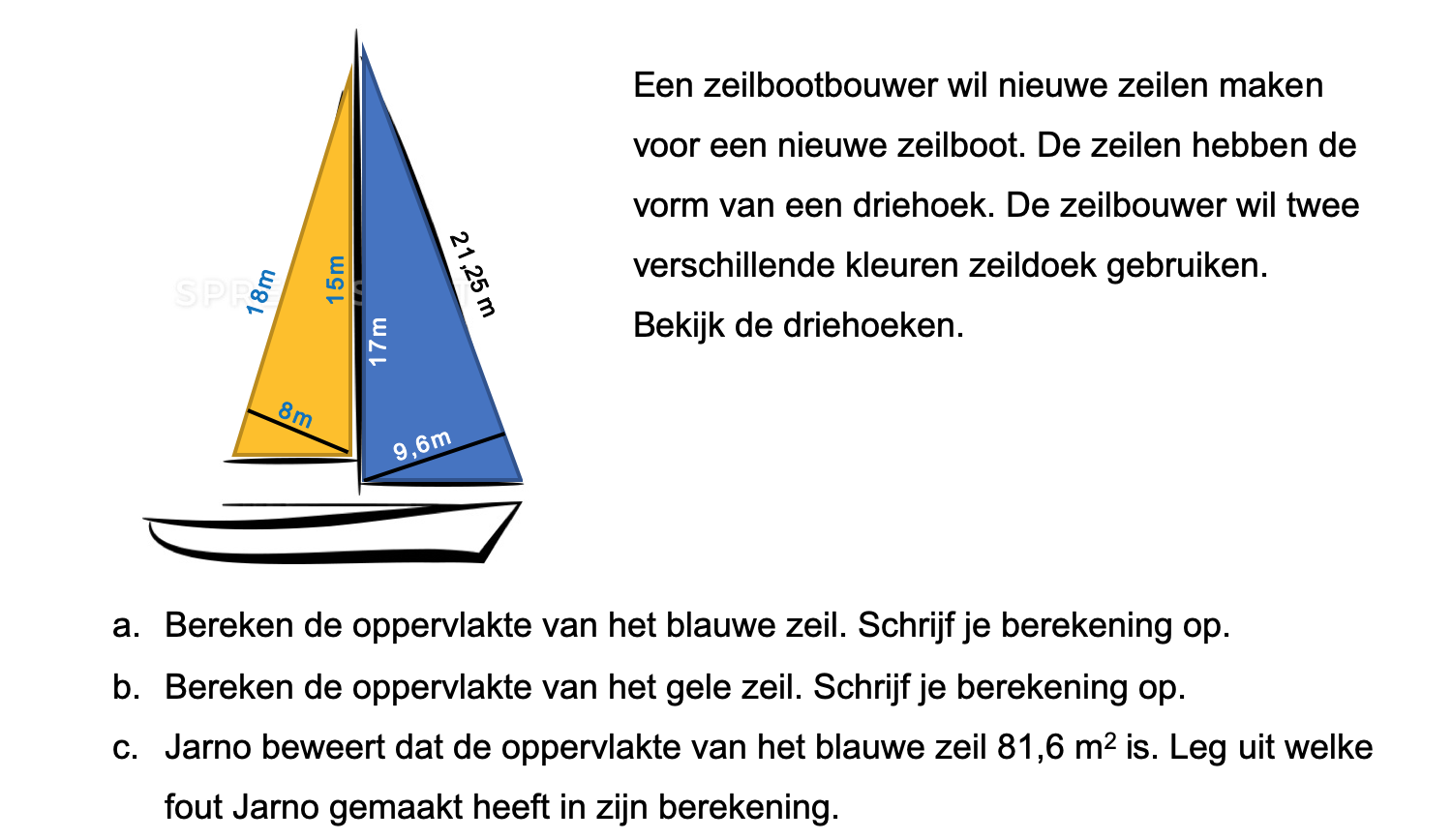





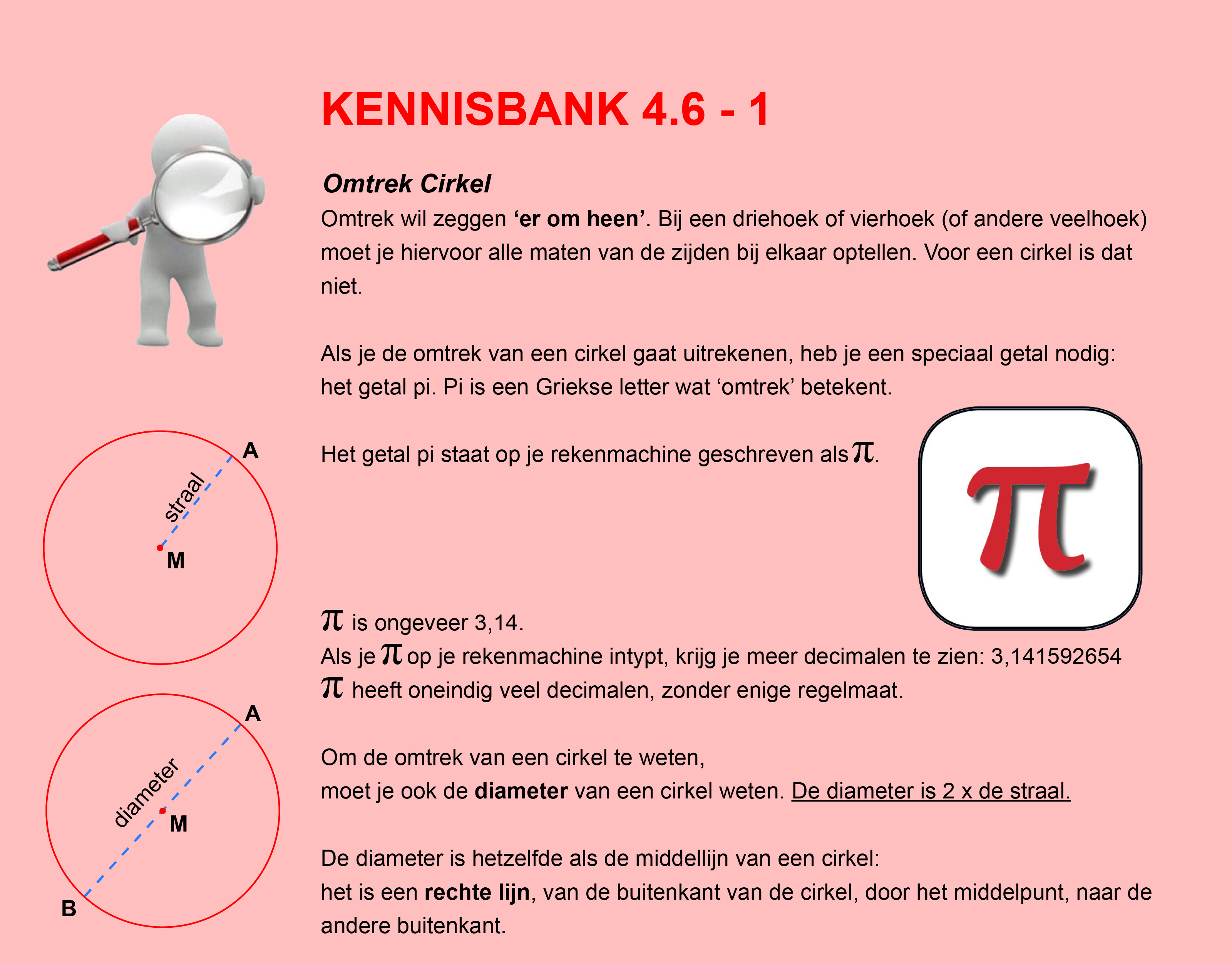


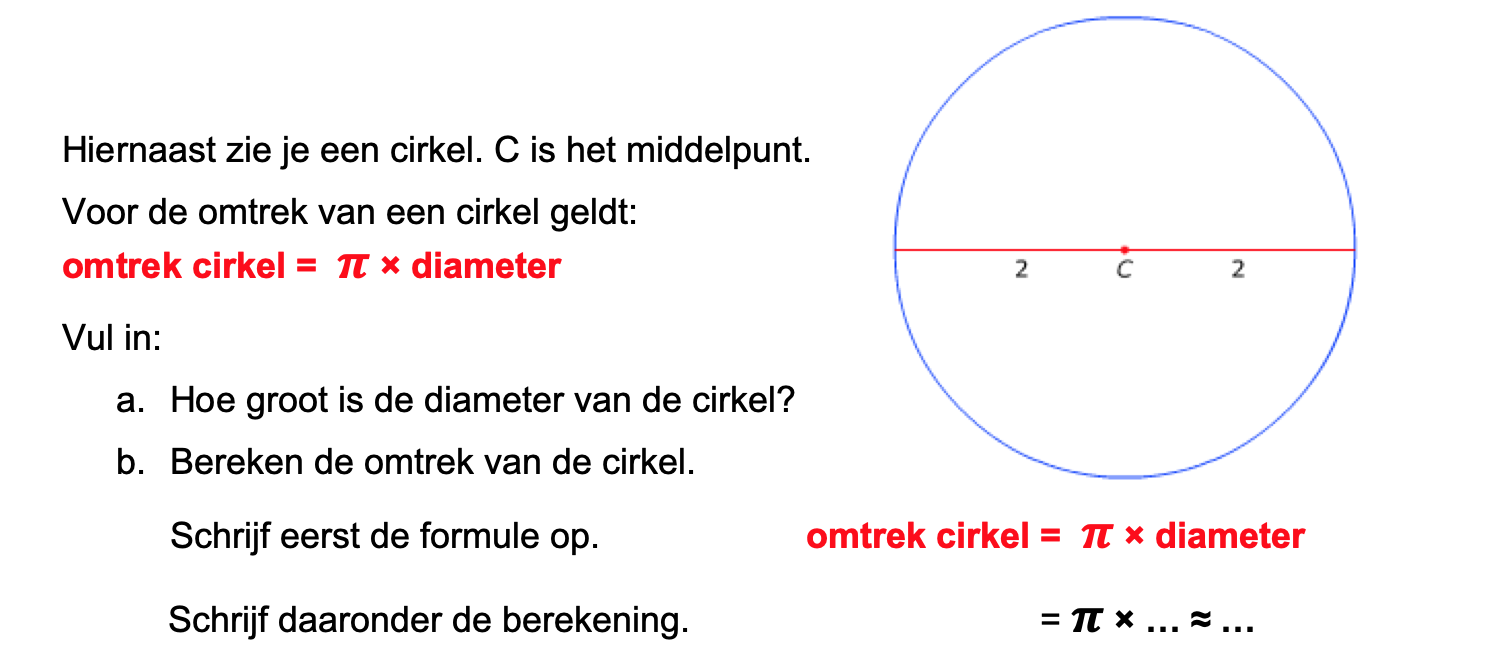

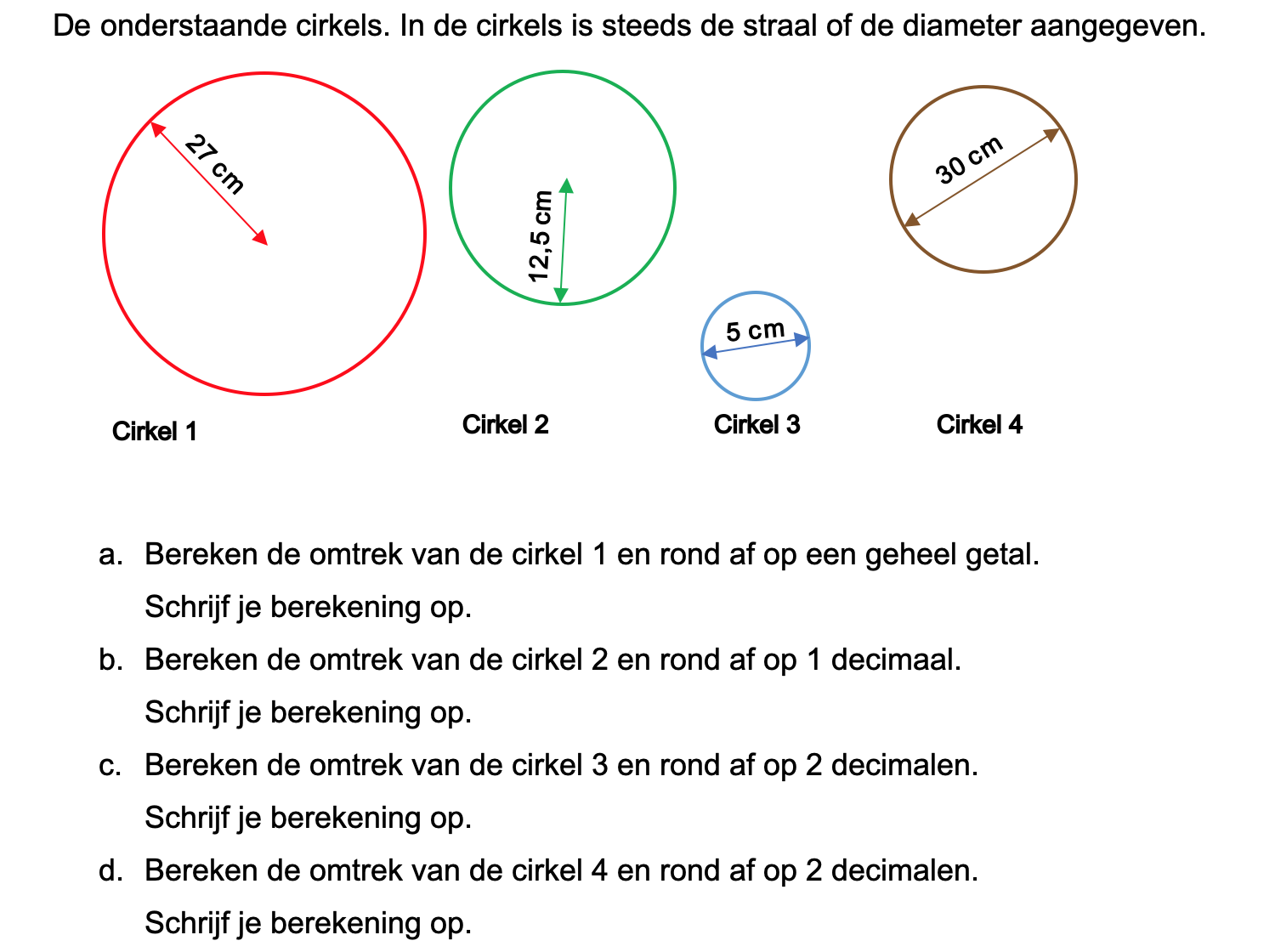
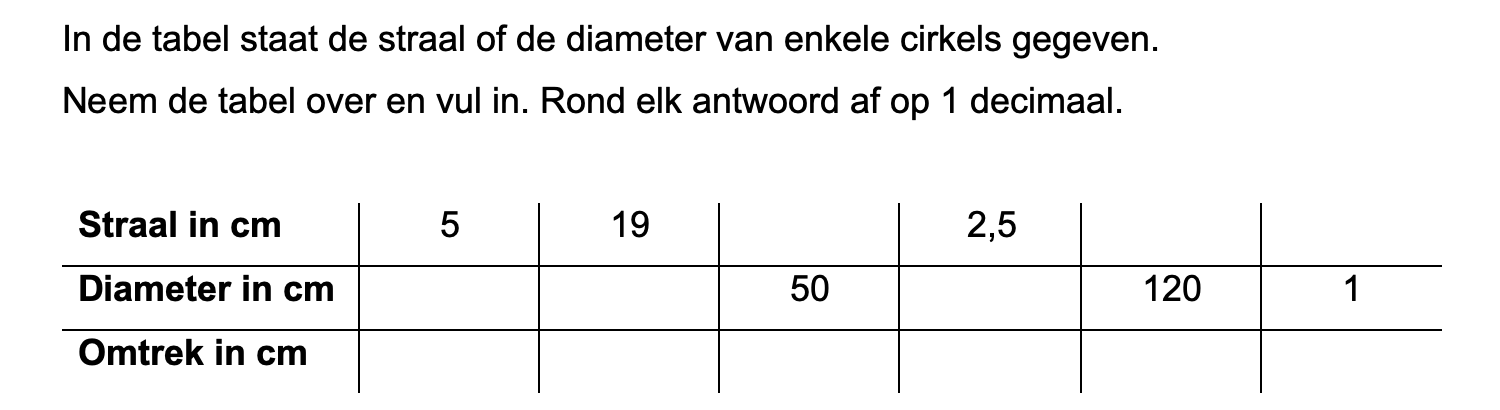



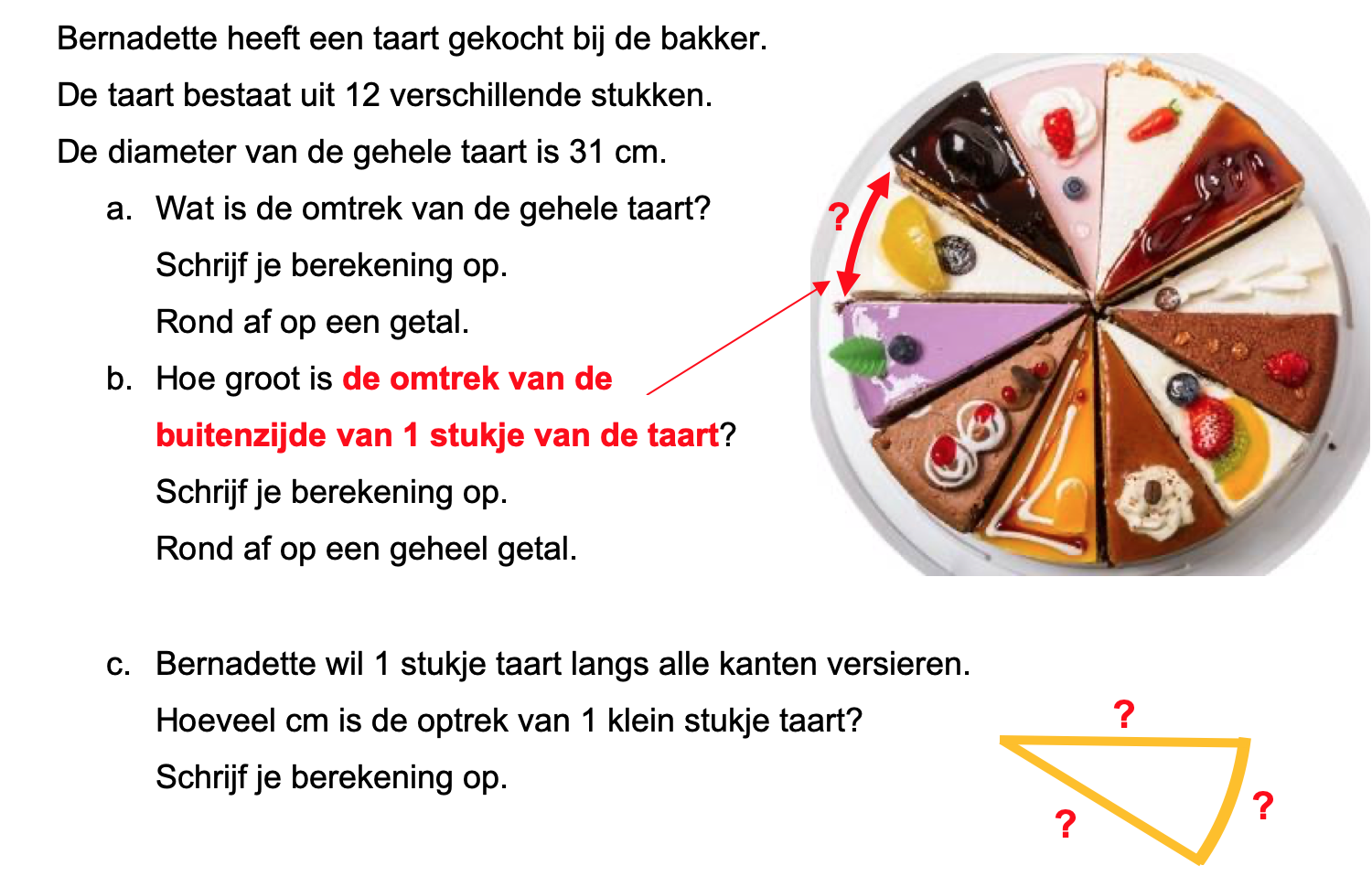




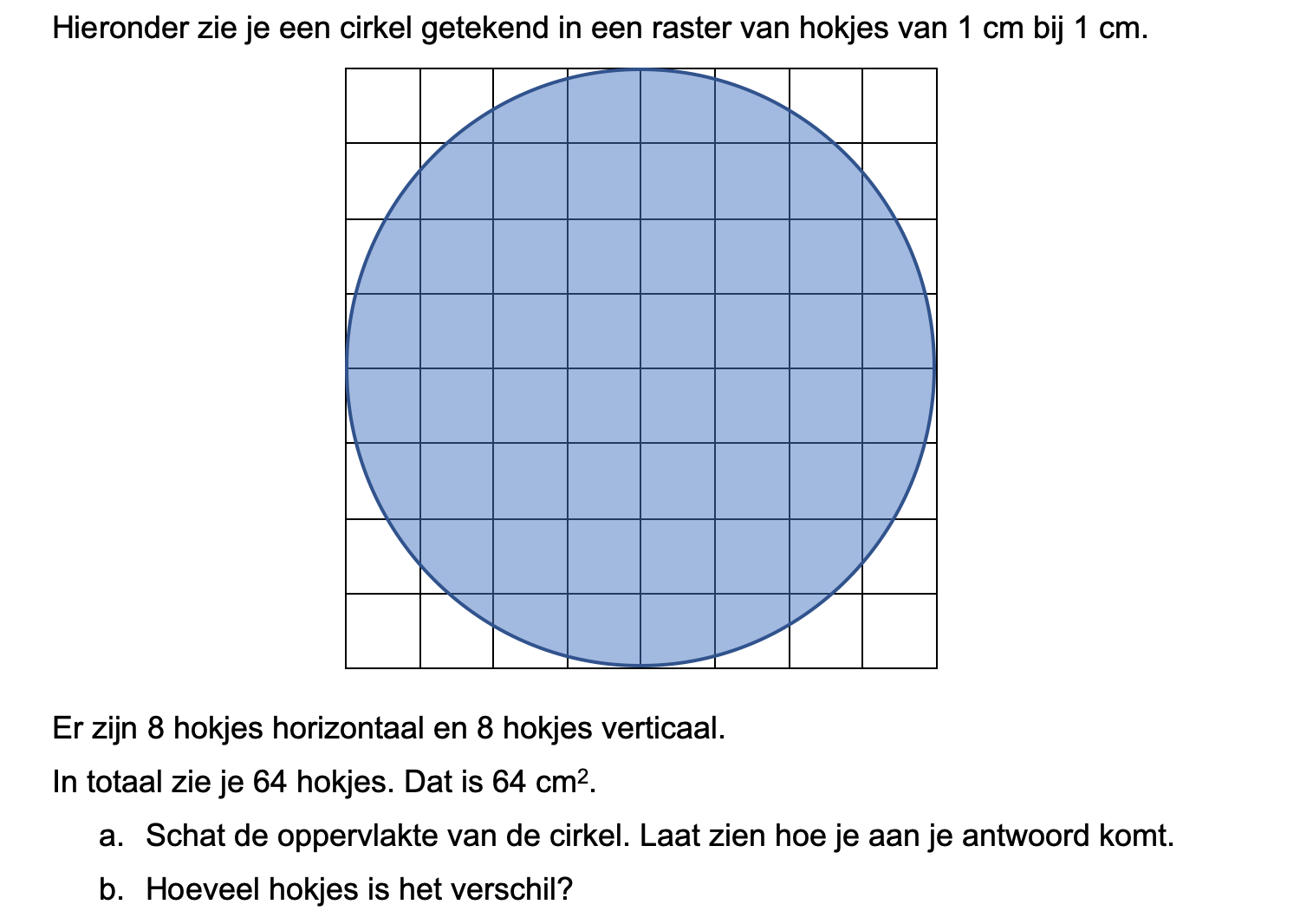
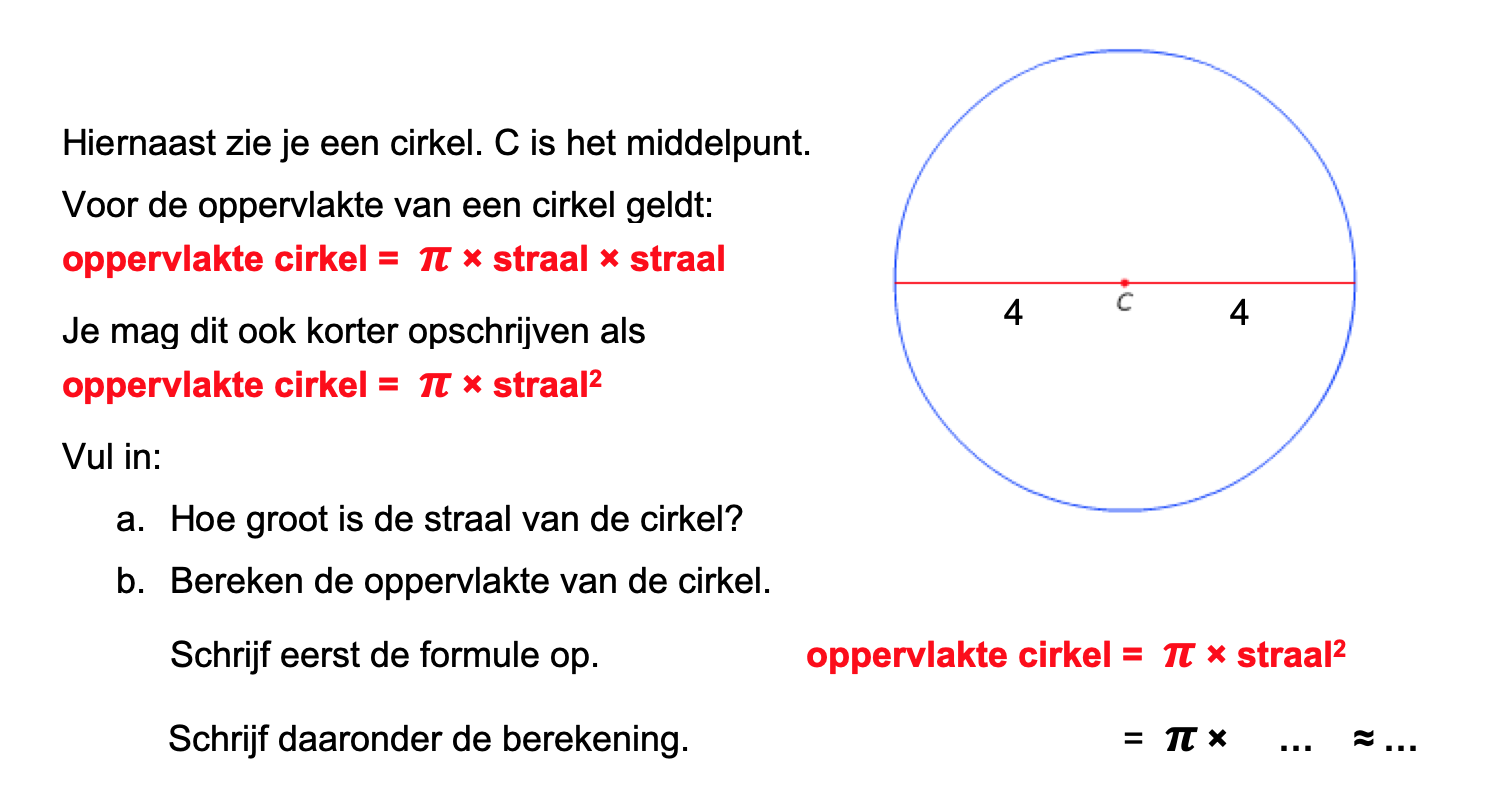

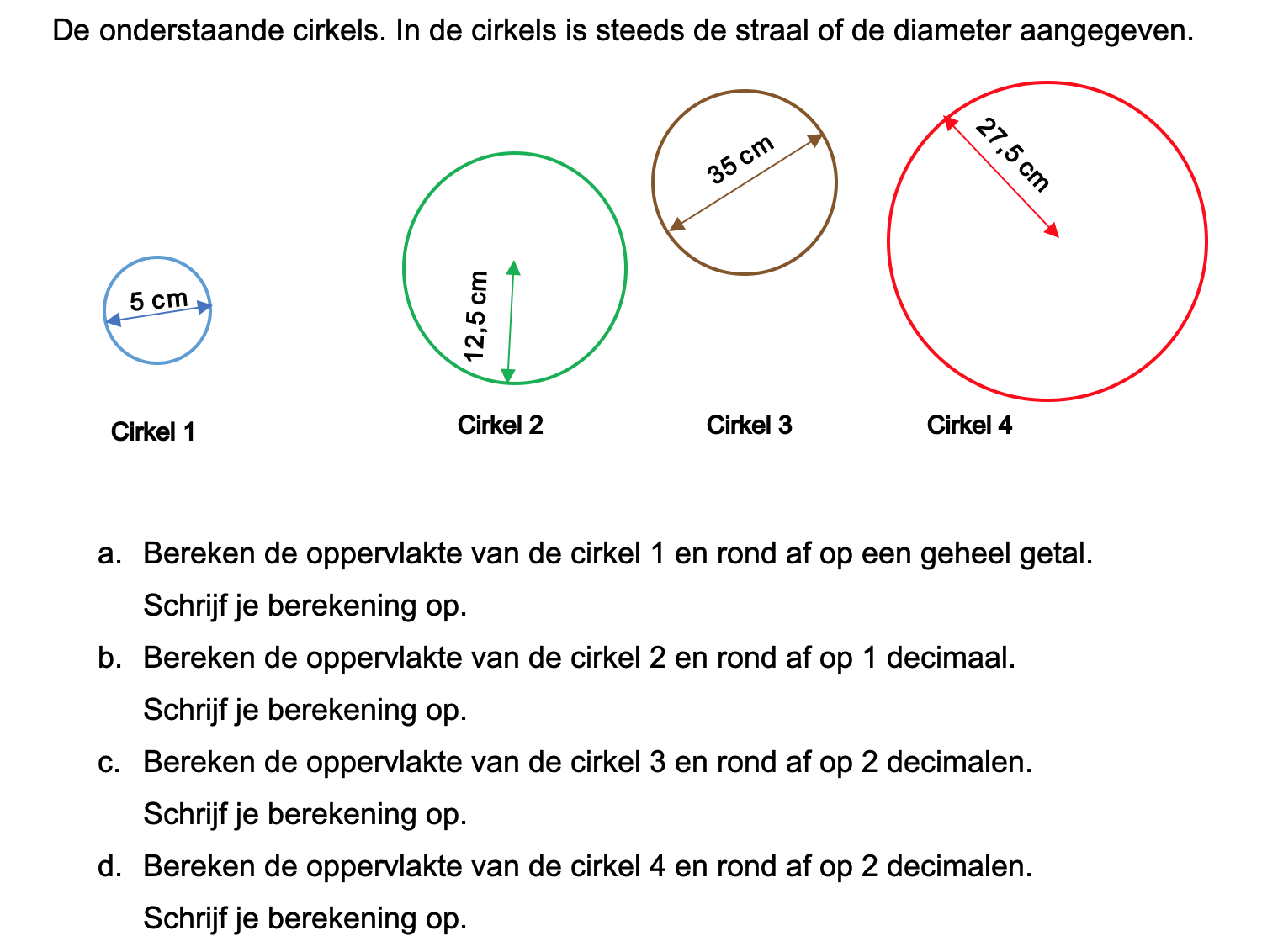




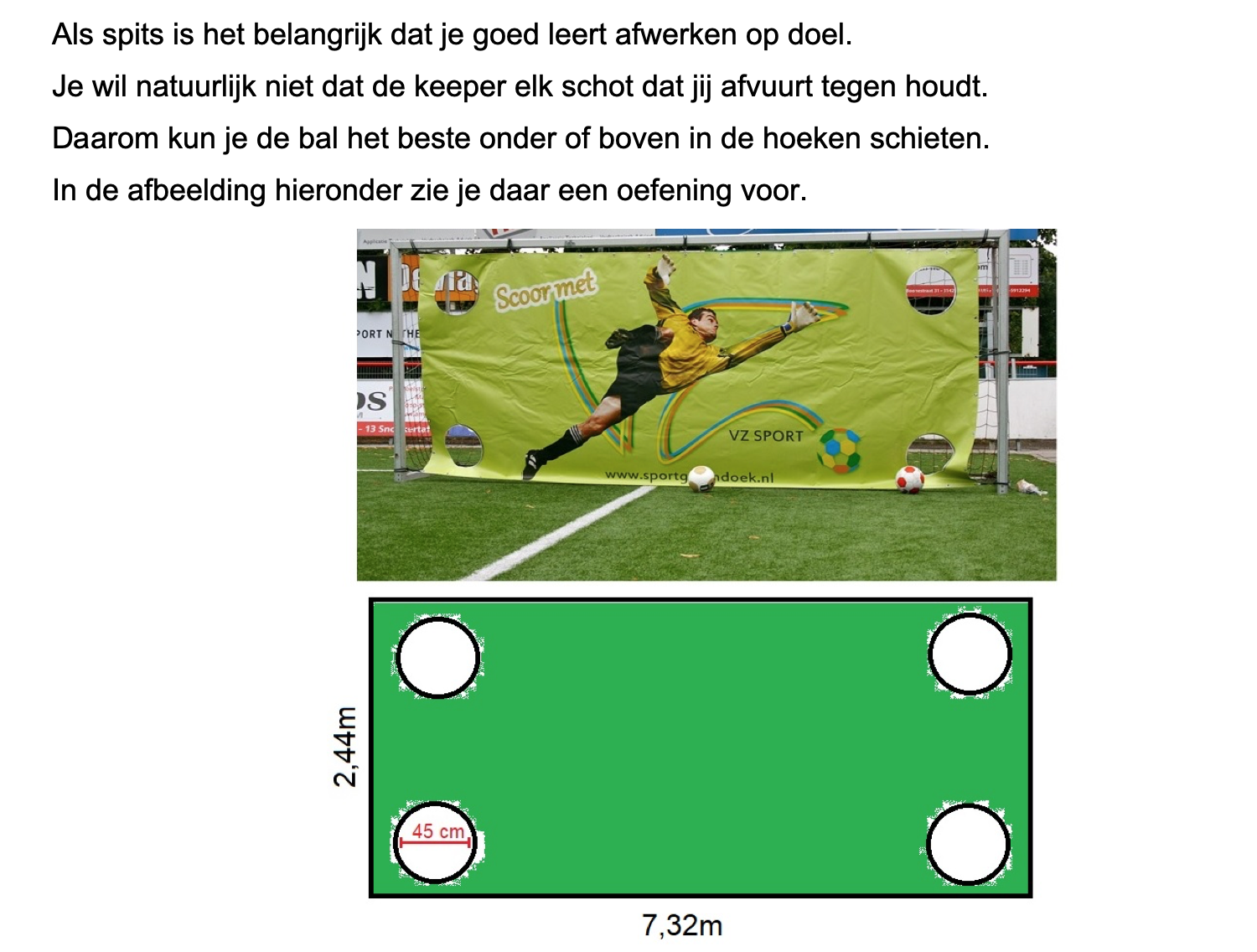





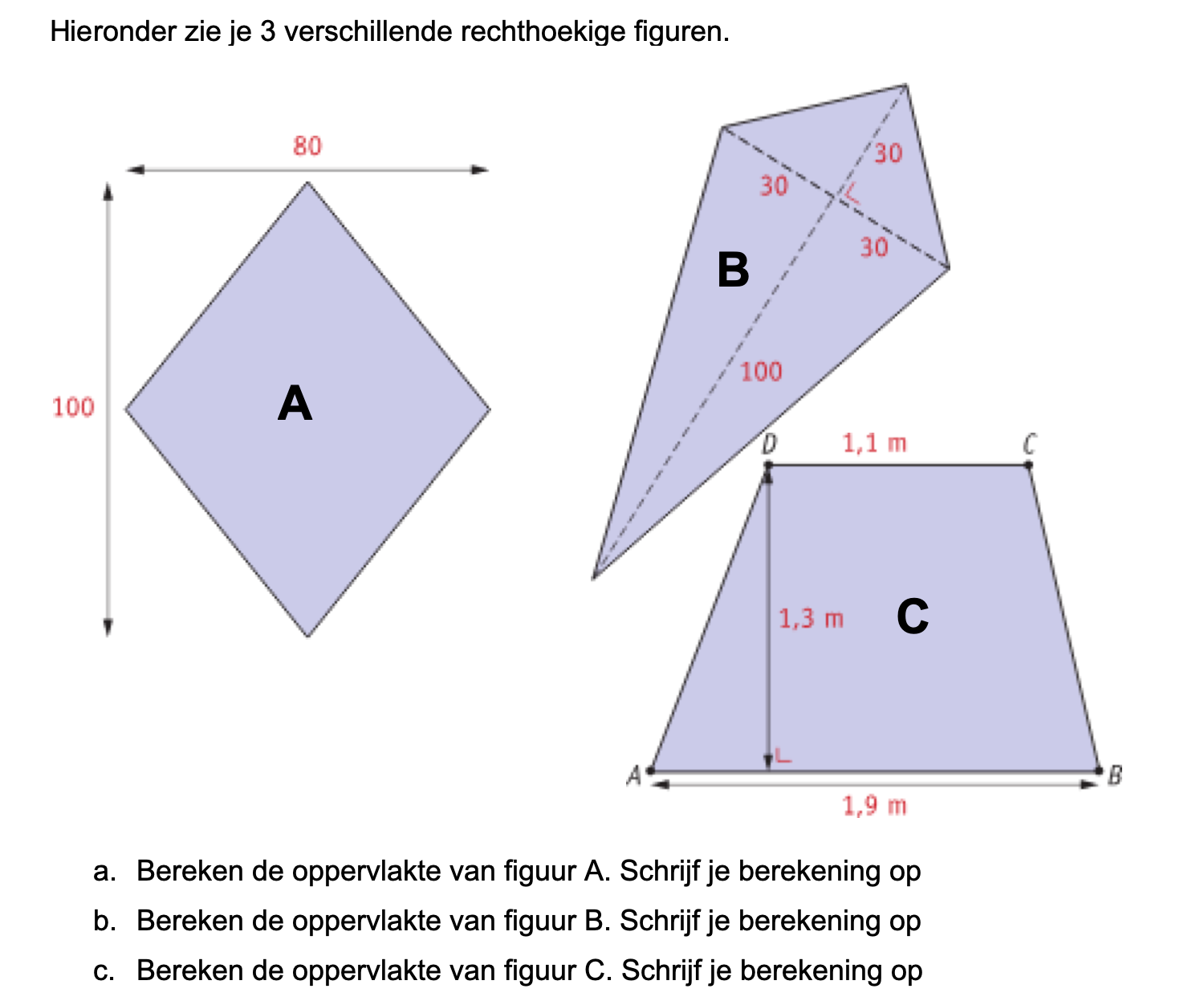
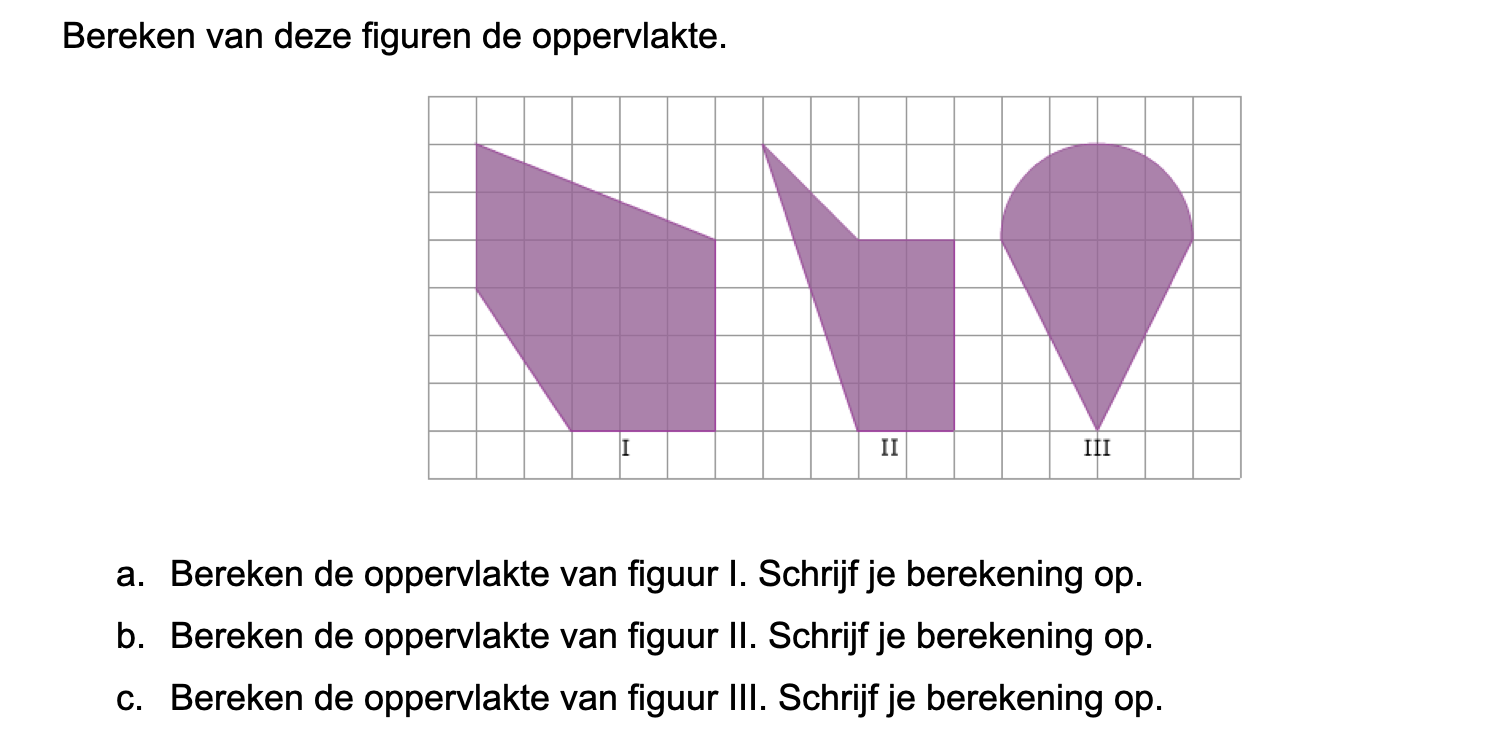
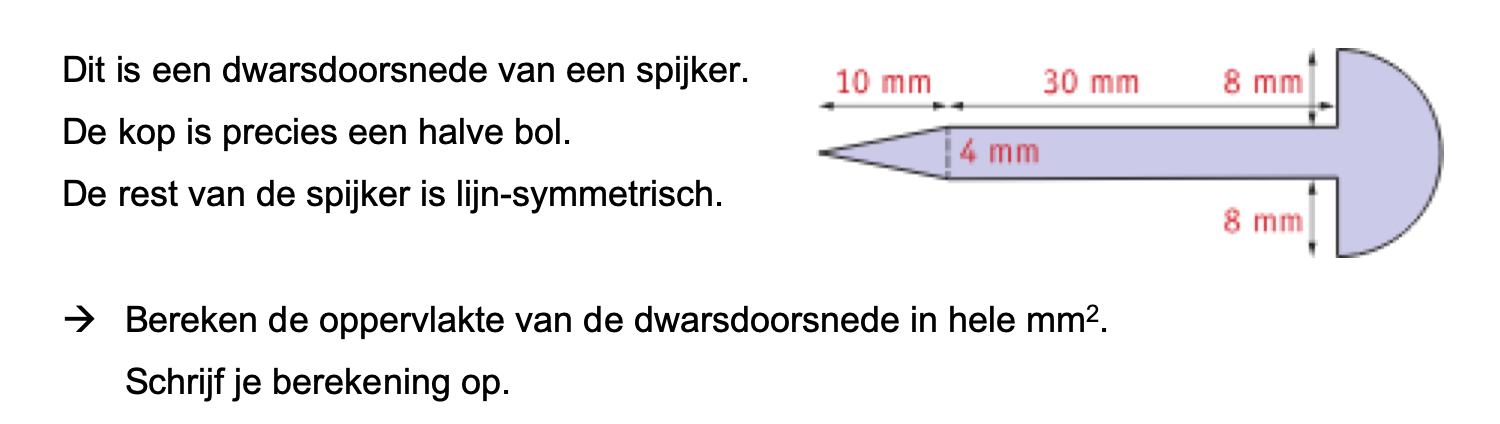















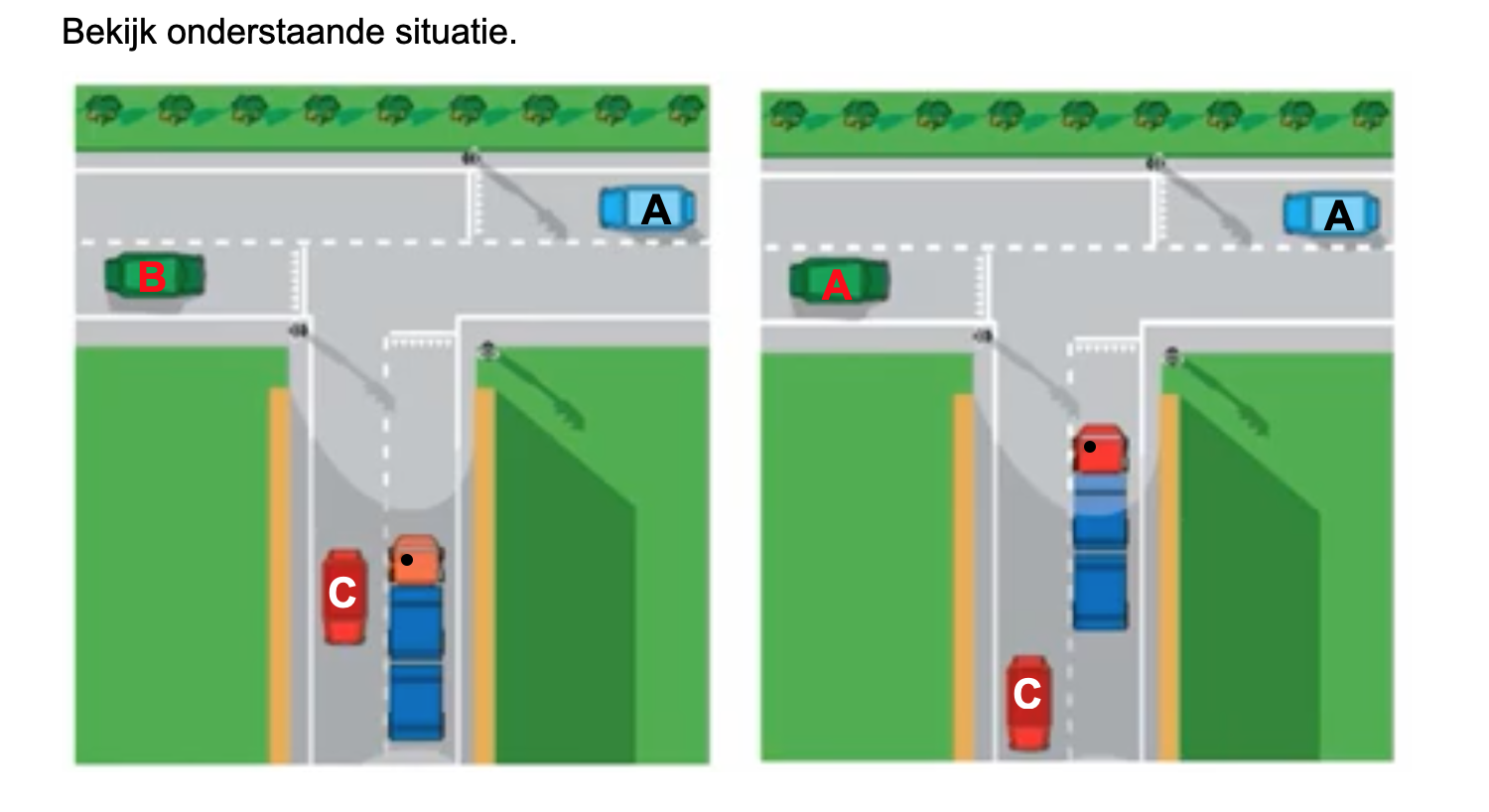

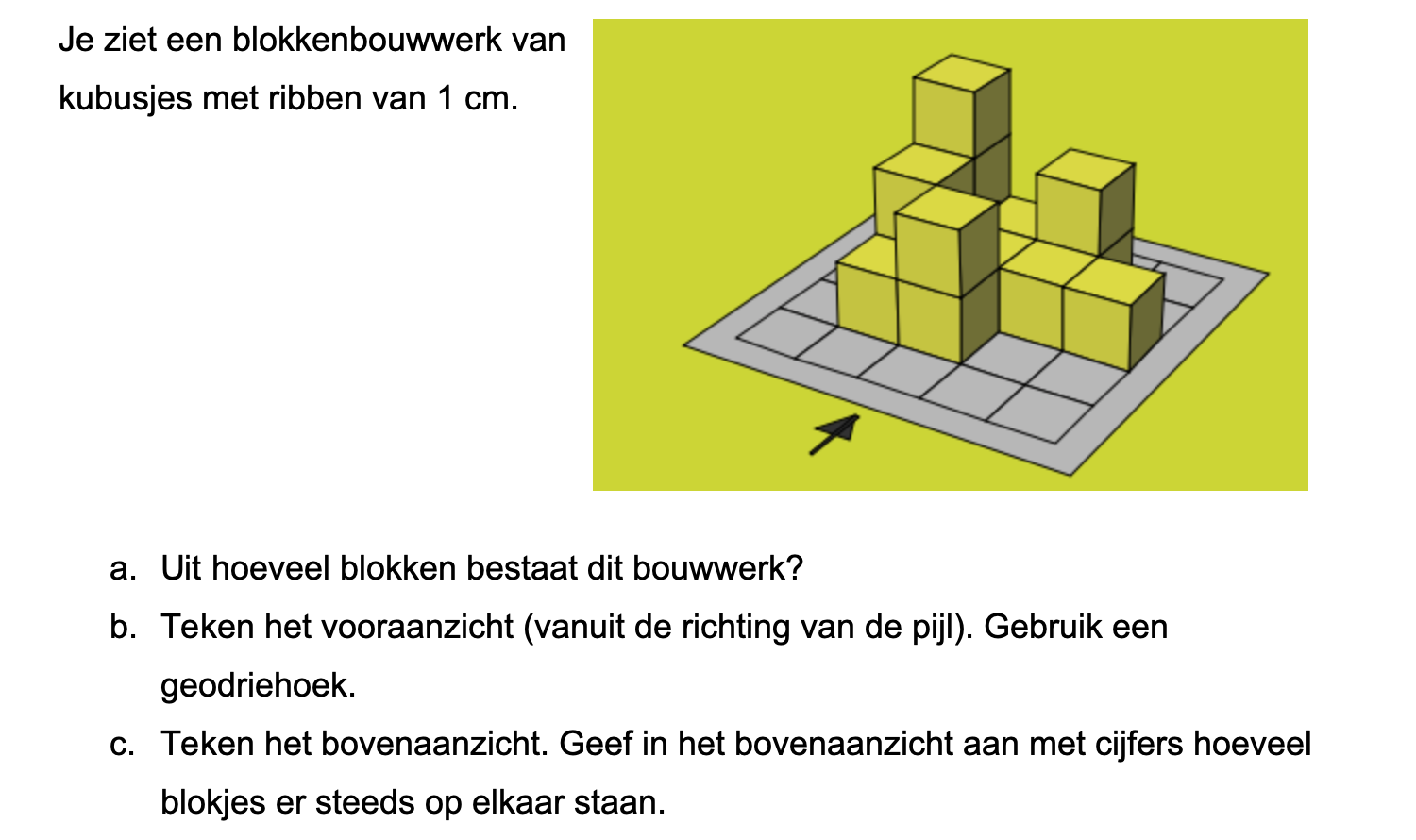


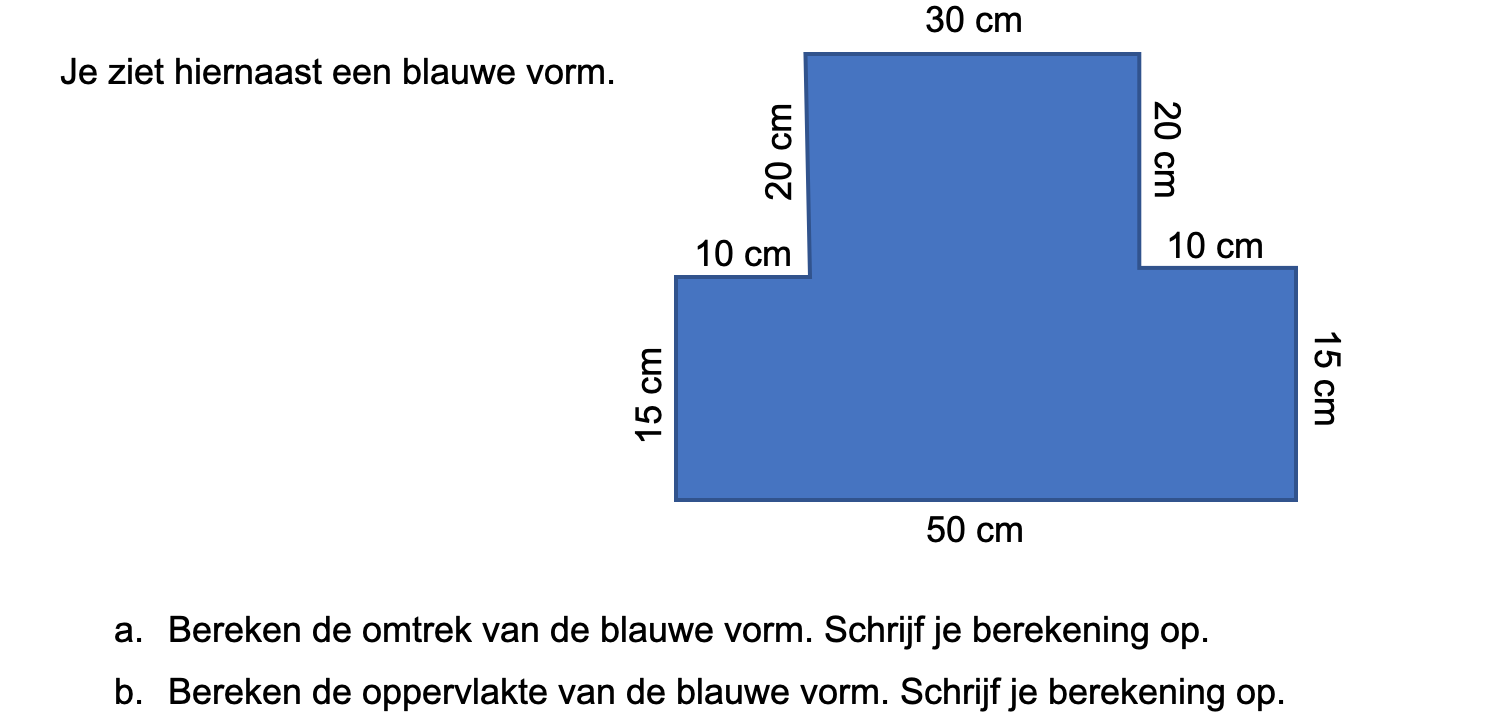
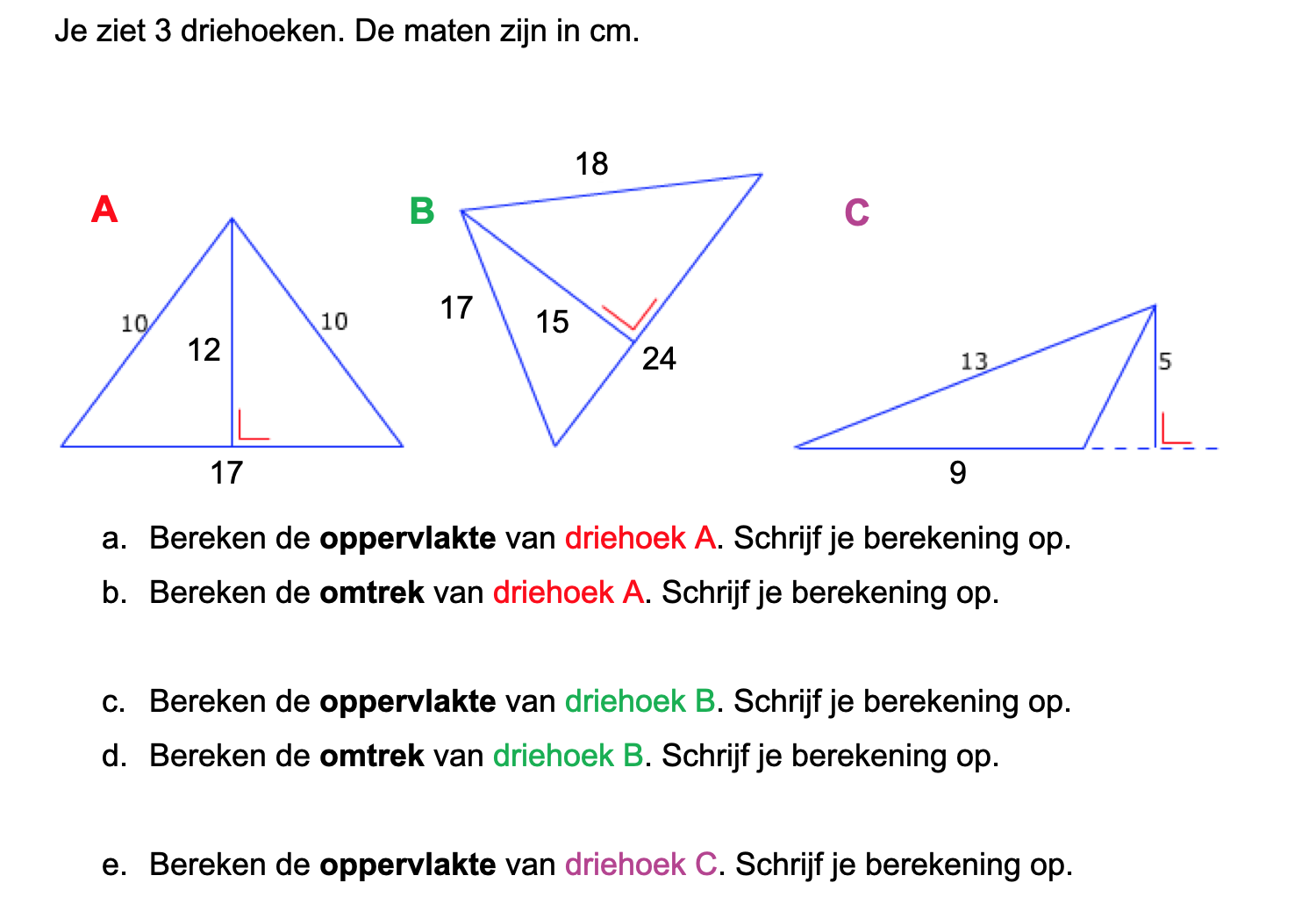
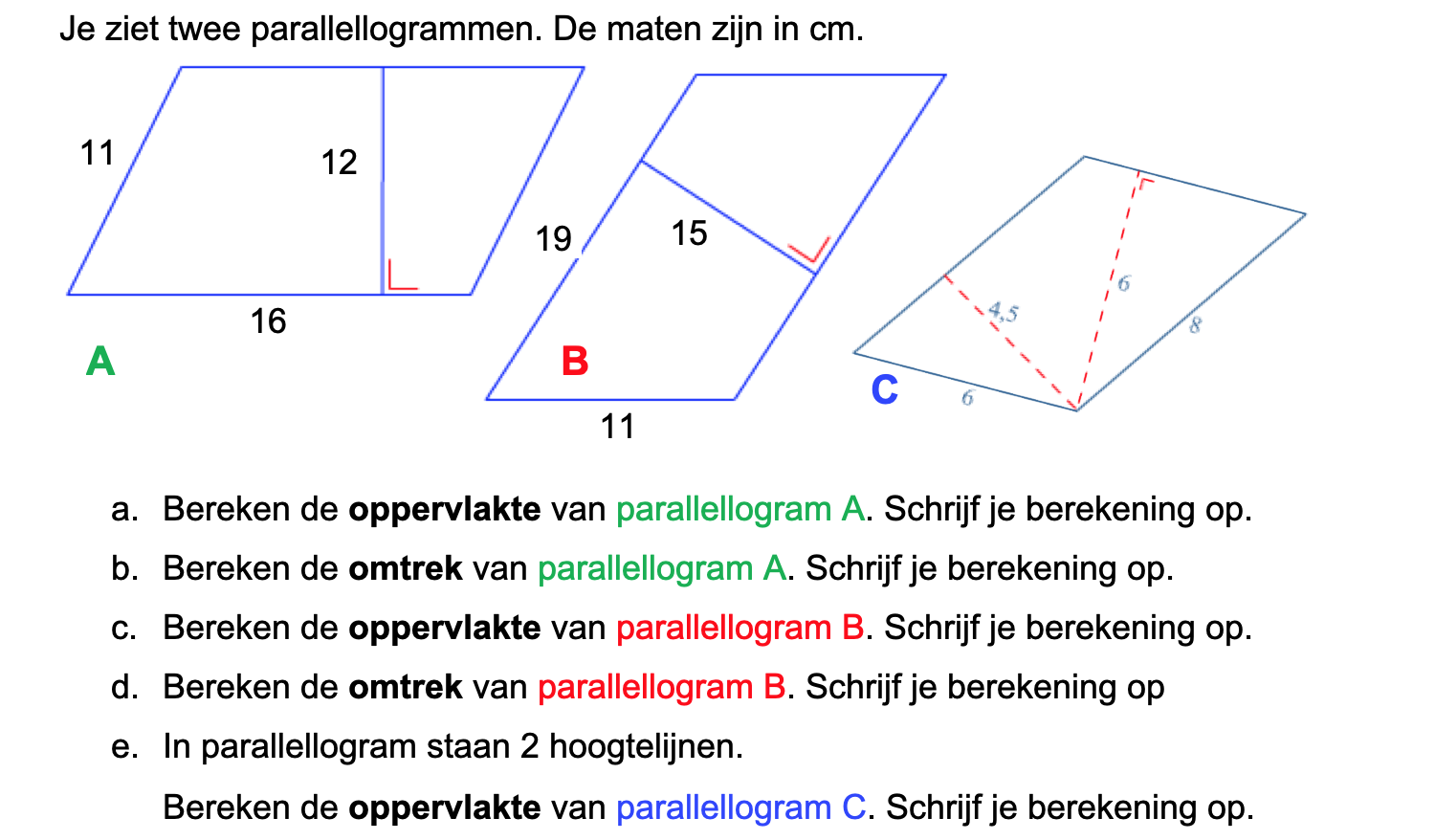





 Nog enkele opgaven om te oefenen voor het proefwerk.
Nog enkele opgaven om te oefenen voor het proefwerk.




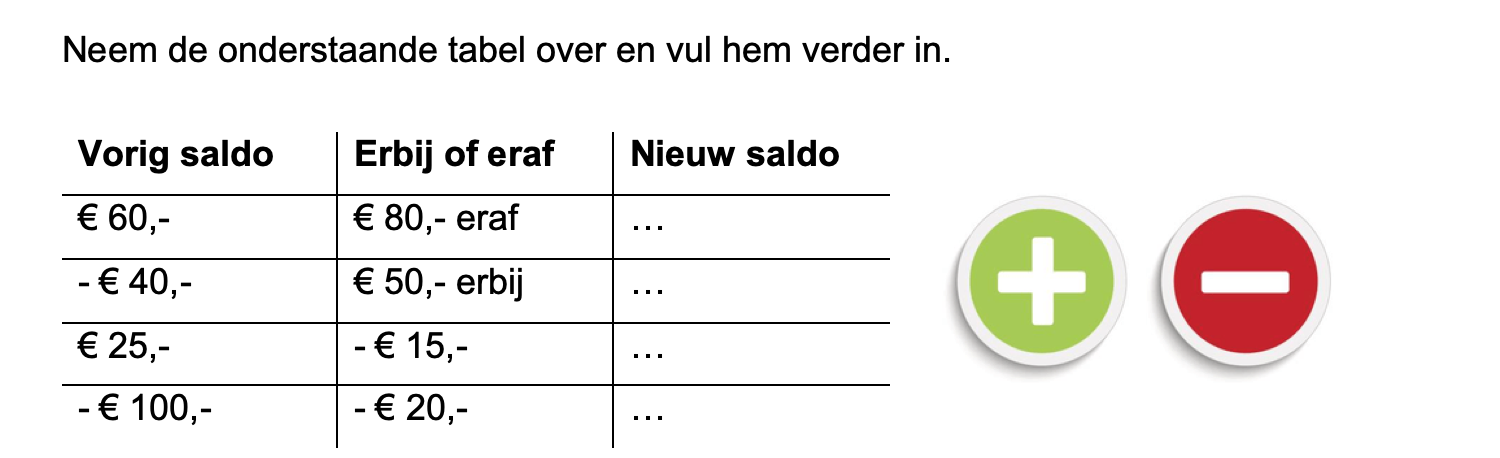


























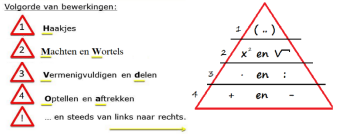 Je wist vast al dat er een bepaalde volgorde bij het berekenen van opgaven wordt gehanteerd.
Je wist vast al dat er een bepaalde volgorde bij het berekenen van opgaven wordt gehanteerd.
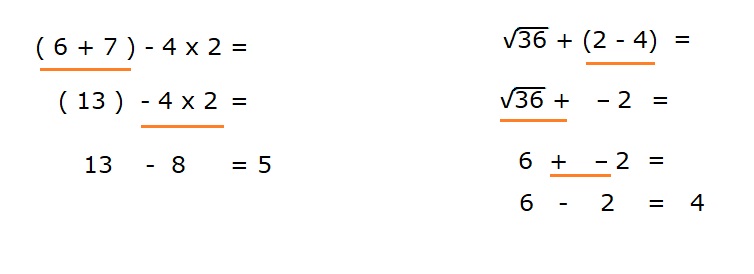
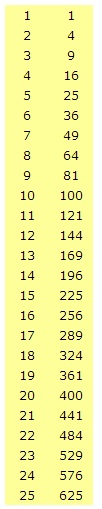 Aan het eind van deze paragraaf kan ik negatieve getallen kwadrateren.
Aan het eind van deze paragraaf kan ik negatieve getallen kwadrateren.

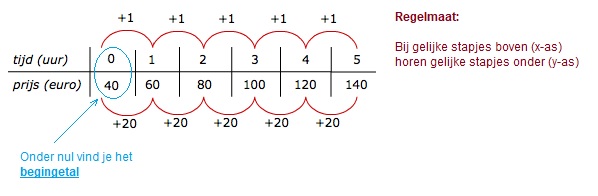
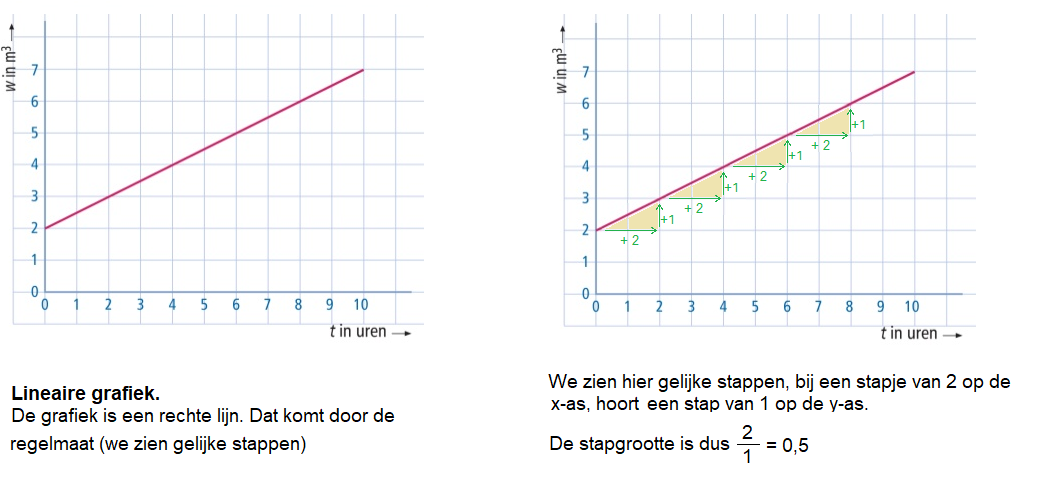
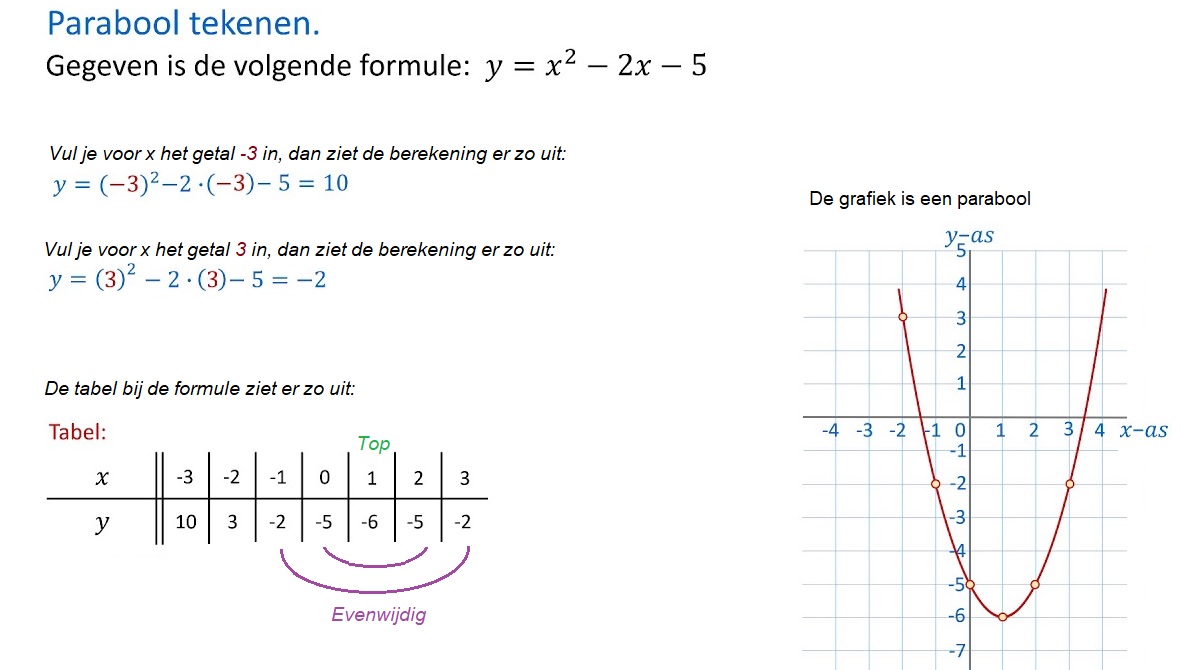
 Gegeven is de formule:
Gegeven is de formule:  Bij het branden van een cilindervormige kaars kun je ook een formule maken.
Bij het branden van een cilindervormige kaars kun je ook een formule maken.
 Kenneth is keeper van een voetbalelftal. Kenneth oefent veel op het nemen van een doeltrap zodat hij de bal met een vere trap naar de spits van het elftal kan schieten. Bij de baan die de bal aflegt wanneer je deze wegtrapt hoort een kwadratische formule.
Kenneth is keeper van een voetbalelftal. Kenneth oefent veel op het nemen van een doeltrap zodat hij de bal met een vere trap naar de spits van het elftal kan schieten. Bij de baan die de bal aflegt wanneer je deze wegtrapt hoort een kwadratische formule.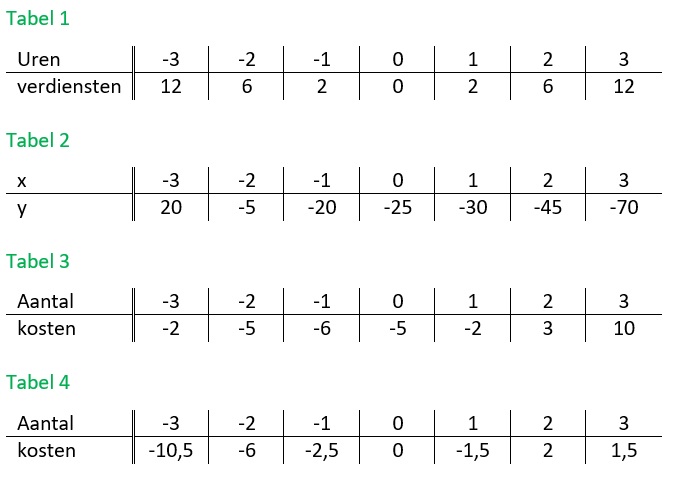
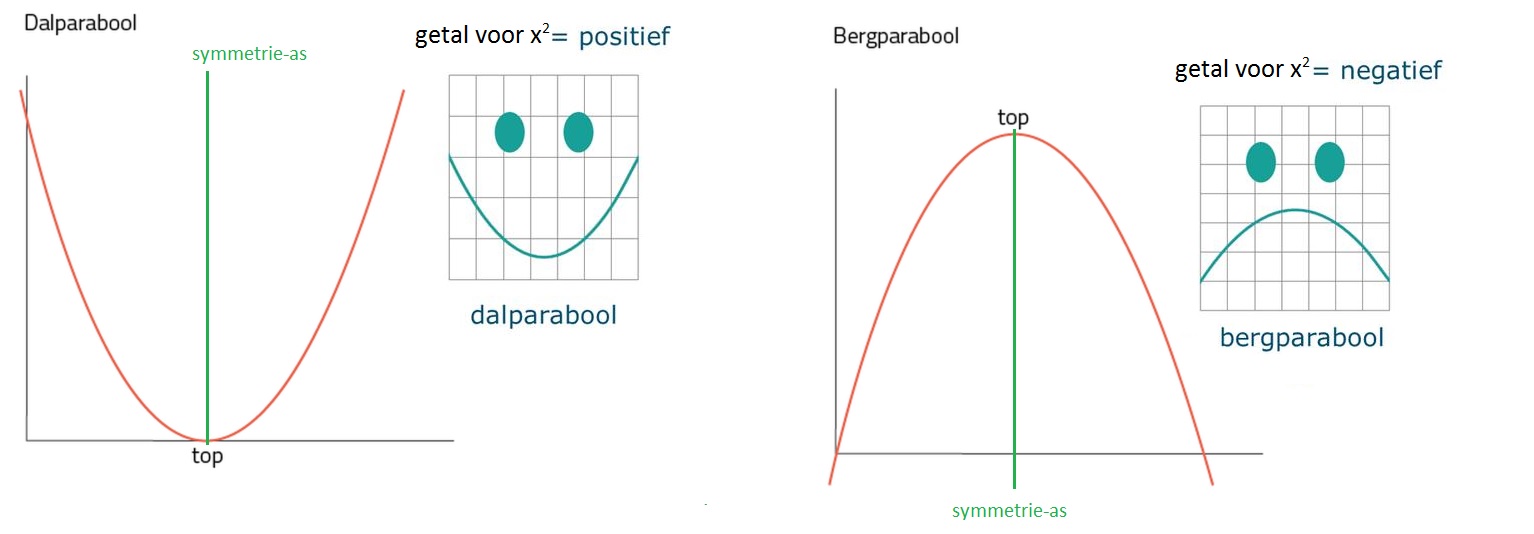



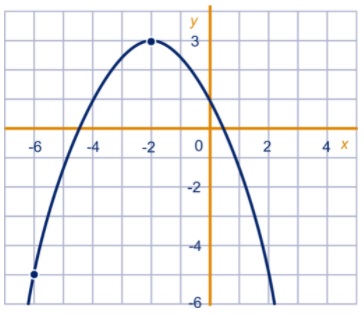
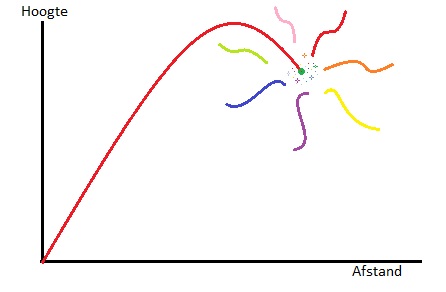 Aan het eind van de wereldhavendagen wordt er in rotterdam een grote vuurwerkshow gehouden. Bij het afschieten van een vuurpijl hoort ook een kwadratische formule. De baan van de vuurpijl heeft namelijk de vorm van een parabool.
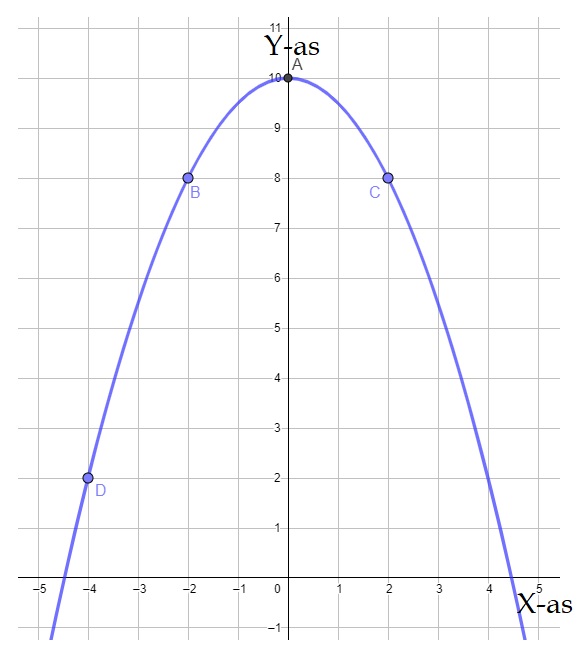
Aan het eind van de wereldhavendagen wordt er in rotterdam een grote vuurwerkshow gehouden. Bij het afschieten van een vuurpijl hoort ook een kwadratische formule. De baan van de vuurpijl heeft namelijk de vorm van een parabool.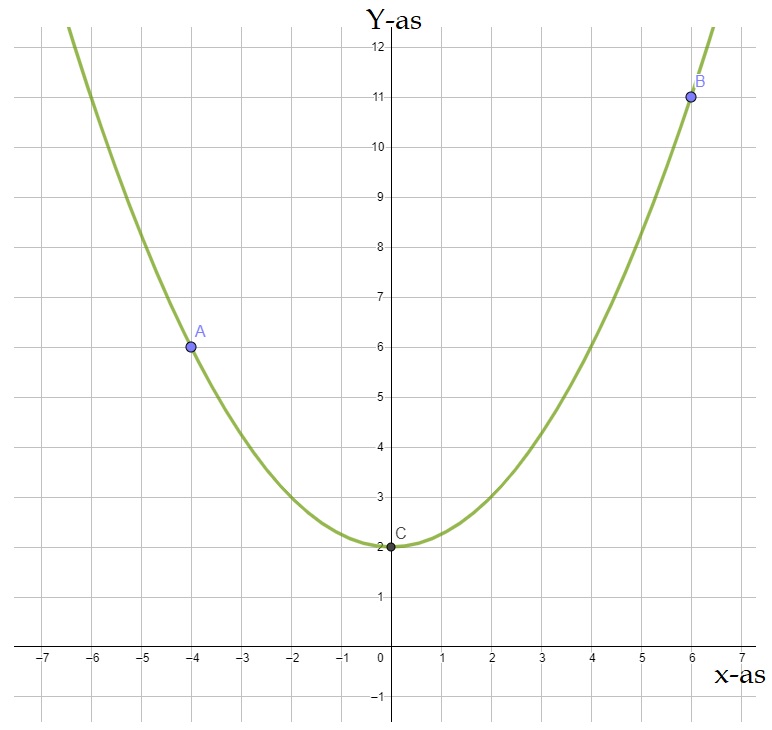
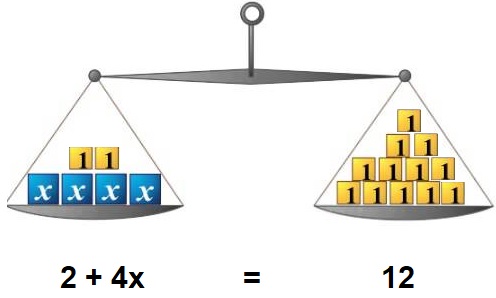
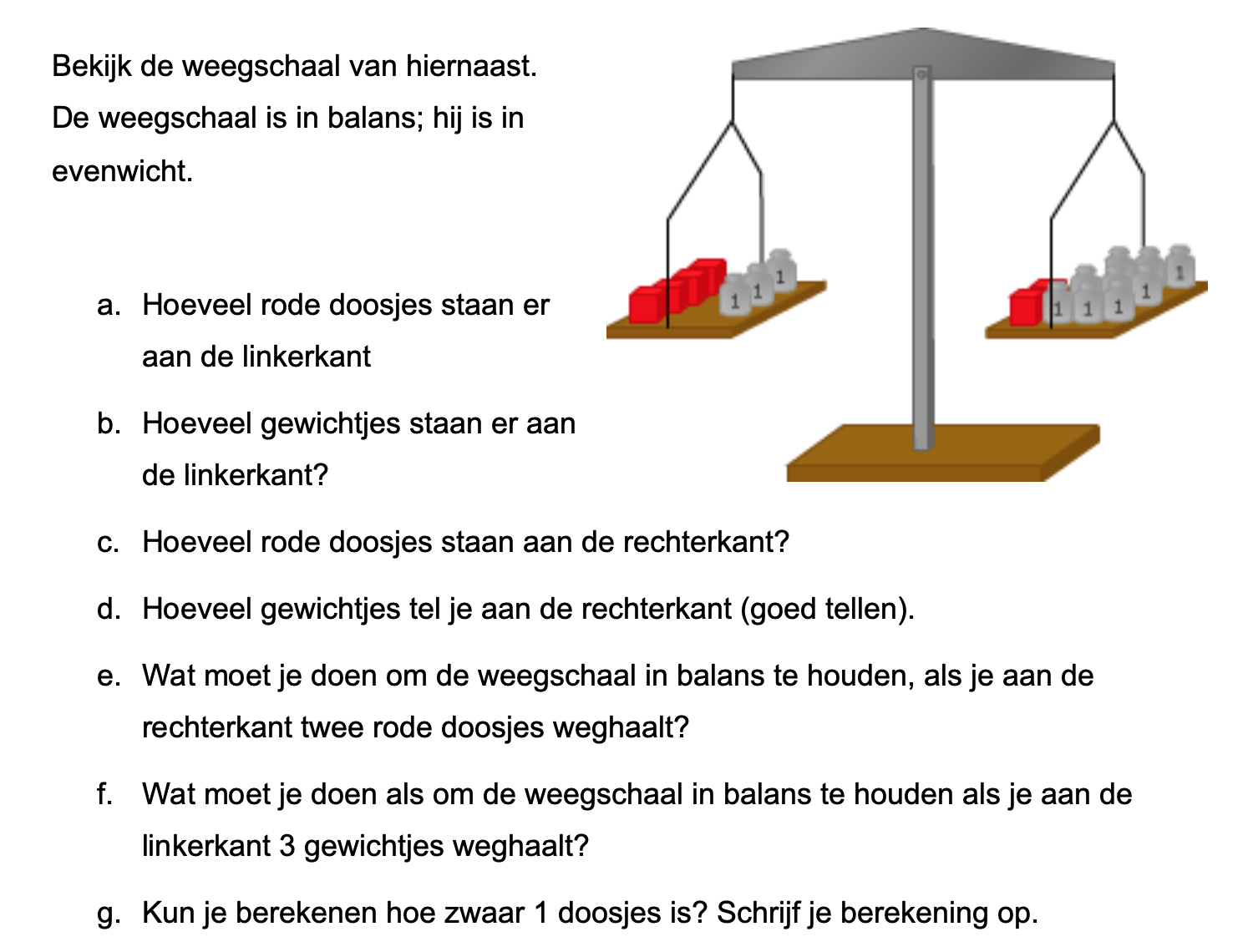
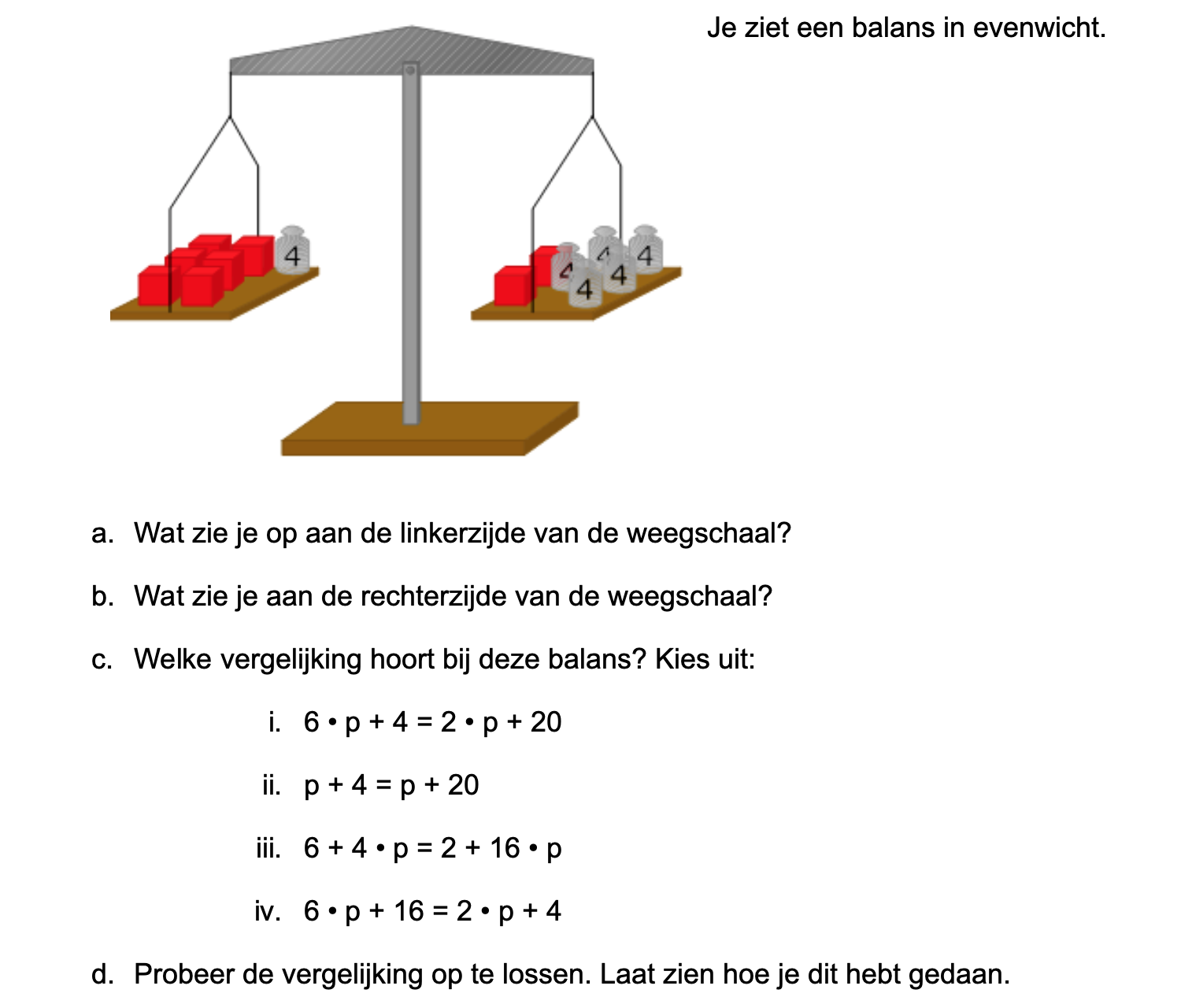
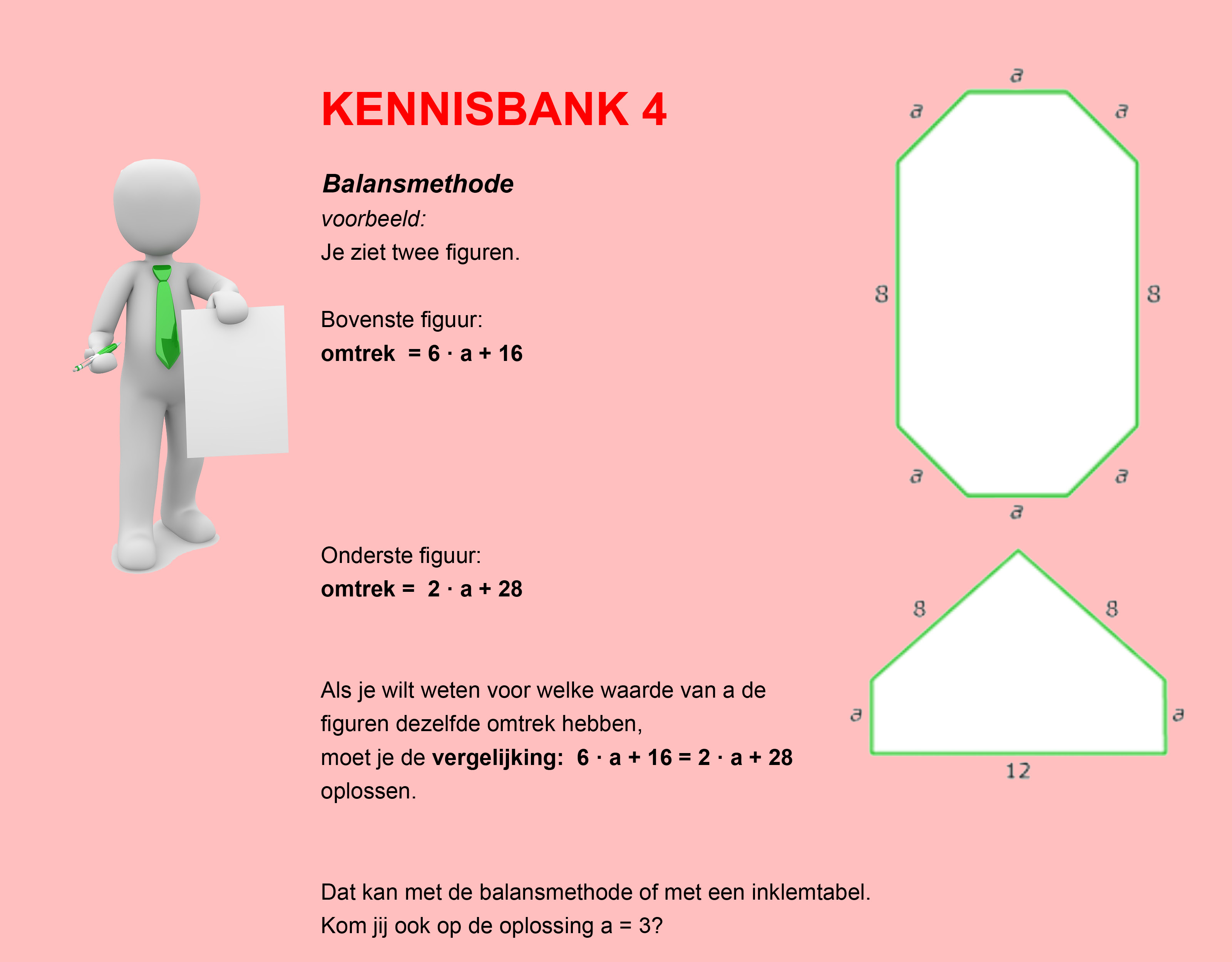
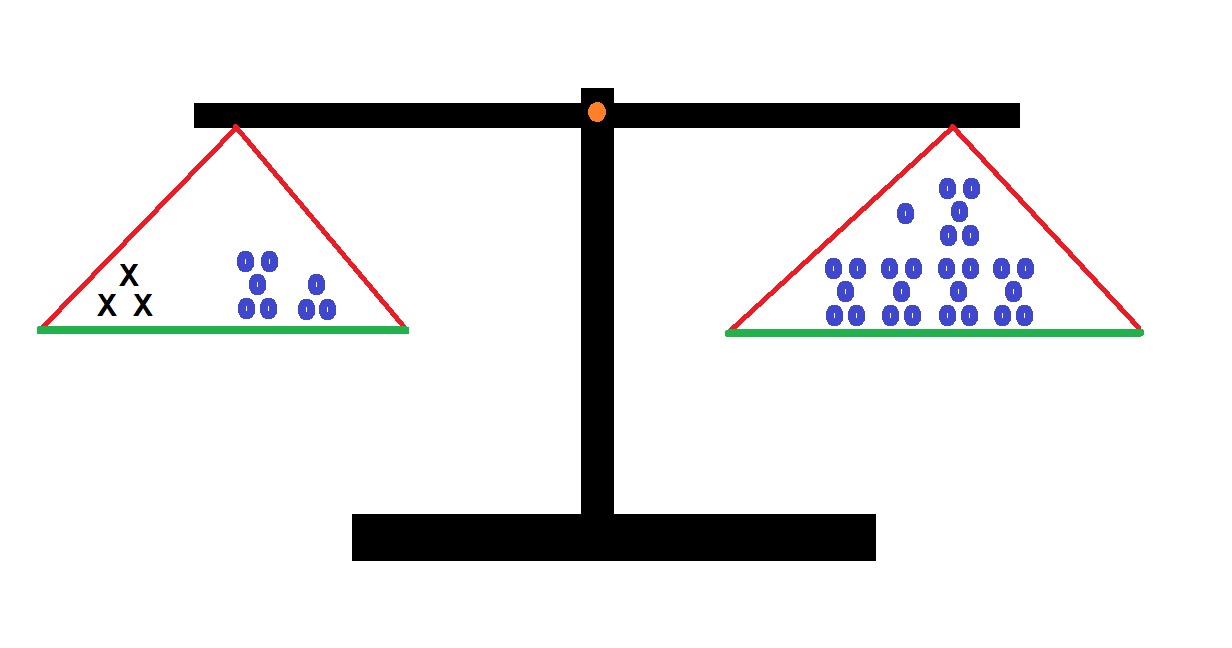 Hiernaast zie je een balans getekend.
Hiernaast zie je een balans getekend.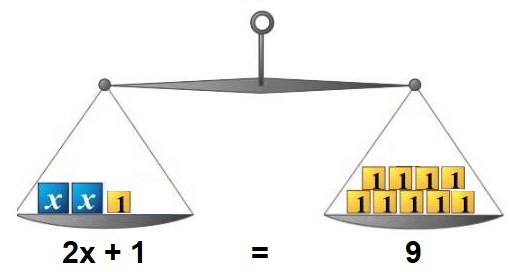
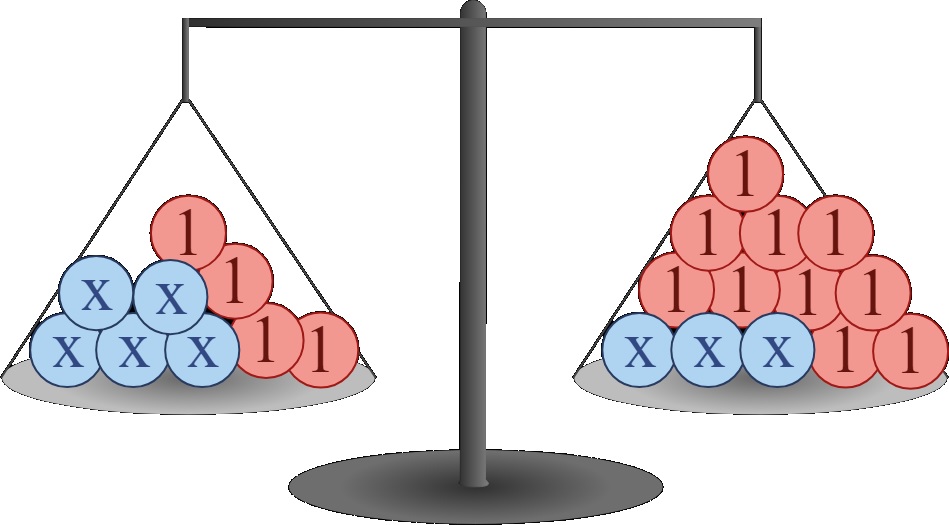
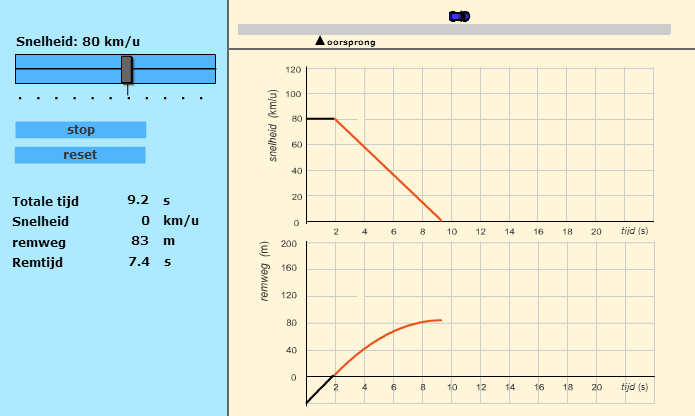
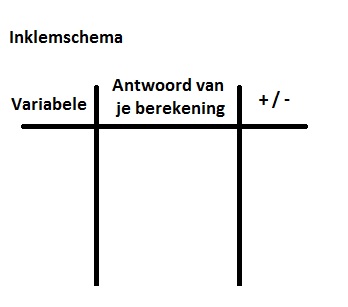 Is de formule waarmee je werkt niet-lineair, dan kun je een vergelijking oplossen met de inklem-methode. De inklem-methode is als het ware gokken. Je vult net zo lang getallen in tot je het goede antwoord hebt gevonden. Bij inklemmen houdt je in een schema bij wat je allemaal geprobeerd hebt.
Is de formule waarmee je werkt niet-lineair, dan kun je een vergelijking oplossen met de inklem-methode. De inklem-methode is als het ware gokken. Je vult net zo lang getallen in tot je het goede antwoord hebt gevonden. Bij inklemmen houdt je in een schema bij wat je allemaal geprobeerd hebt.
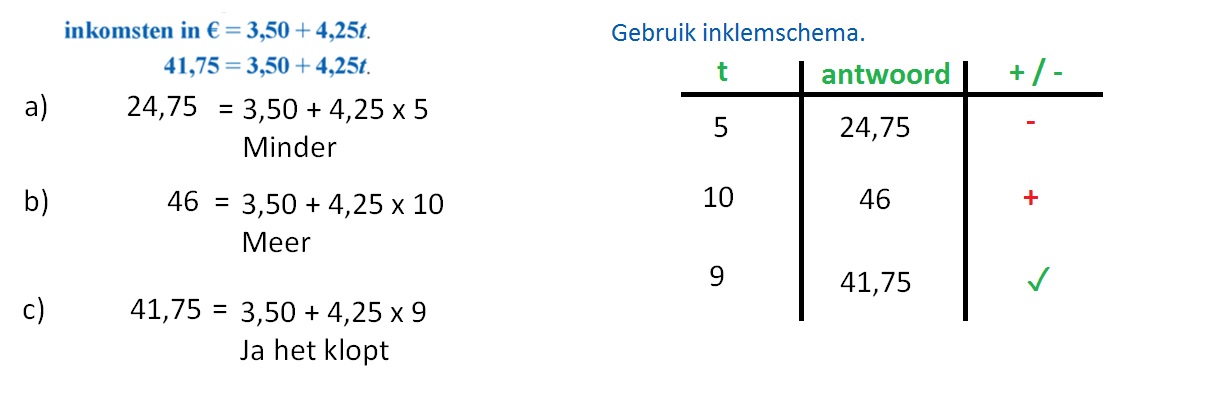
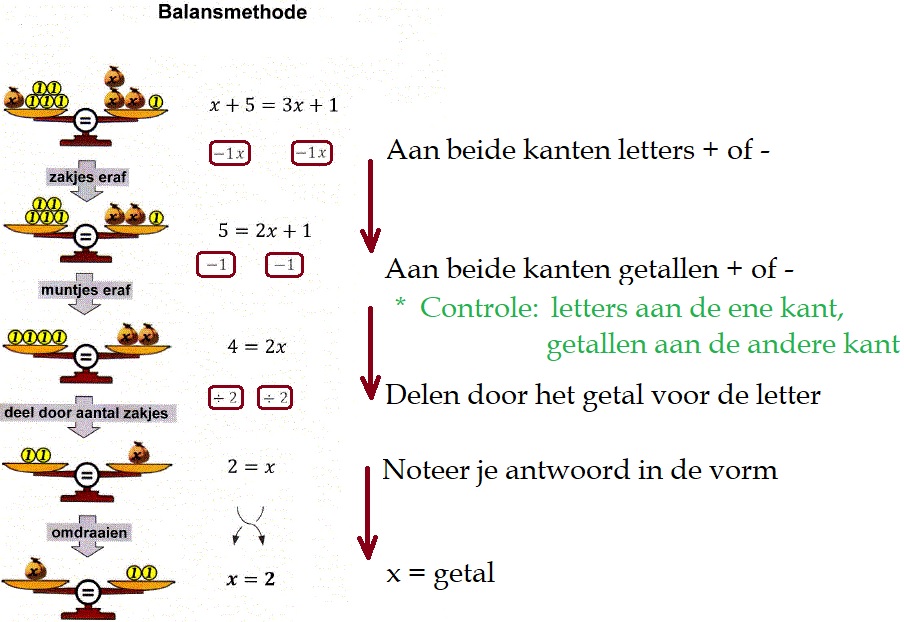
 In opgave 1 t/m 5 heb je jouw kennis over de balansmethode weer even herhaalt. Je werkte in al die opgaven met lineaire formule. Is de formule niet-lineair, dan kun je de balansmethode niet gebruiken, je gebruikt dan de inklemmethode.
In opgave 1 t/m 5 heb je jouw kennis over de balansmethode weer even herhaalt. Je werkte in al die opgaven met lineaire formule. Is de formule niet-lineair, dan kun je de balansmethode niet gebruiken, je gebruikt dan de inklemmethode.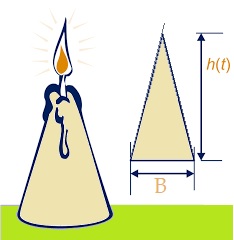 Hiernaast zie je een kaars. Een formule die ongeveer het verband tussen de hoogte van deze kaars en de brandtijd aangeeft, is:
Hiernaast zie je een kaars. Een formule die ongeveer het verband tussen de hoogte van deze kaars en de brandtijd aangeeft, is: Hiernaast zie je een foto van de Red-Bull Cliffdive competitie. Hierbij hoort een verband tussen de hoogte van het plateau en de tijdsduur van de sprong in seconden. Voor dit verband geldt de volgende formule
Hiernaast zie je een foto van de Red-Bull Cliffdive competitie. Hierbij hoort een verband tussen de hoogte van het plateau en de tijdsduur van de sprong in seconden. Voor dit verband geldt de volgende formule Sarah is bloemiste, zij heeft een eigen bloemenzaak.
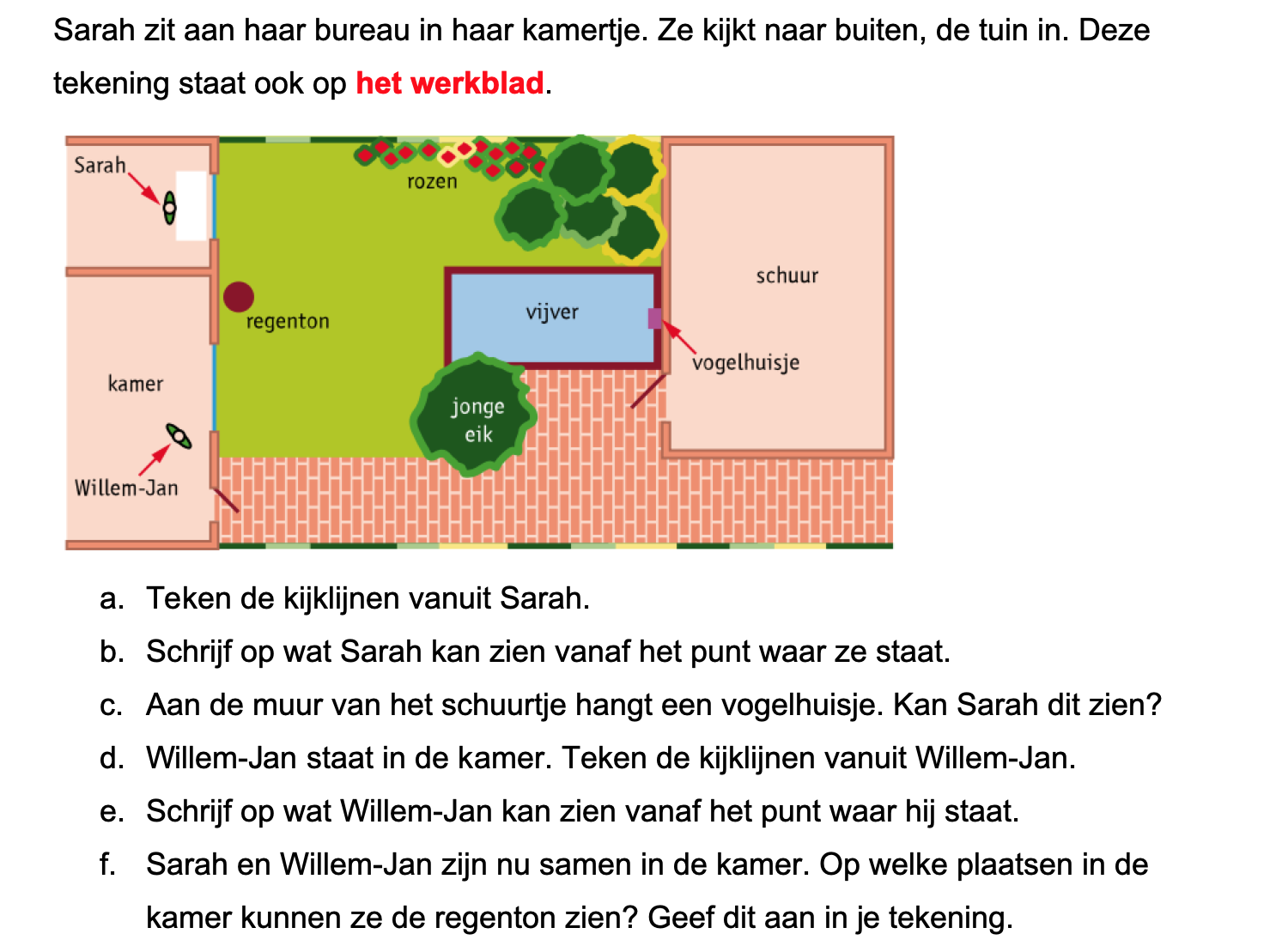
Sarah is bloemiste, zij heeft een eigen bloemenzaak.



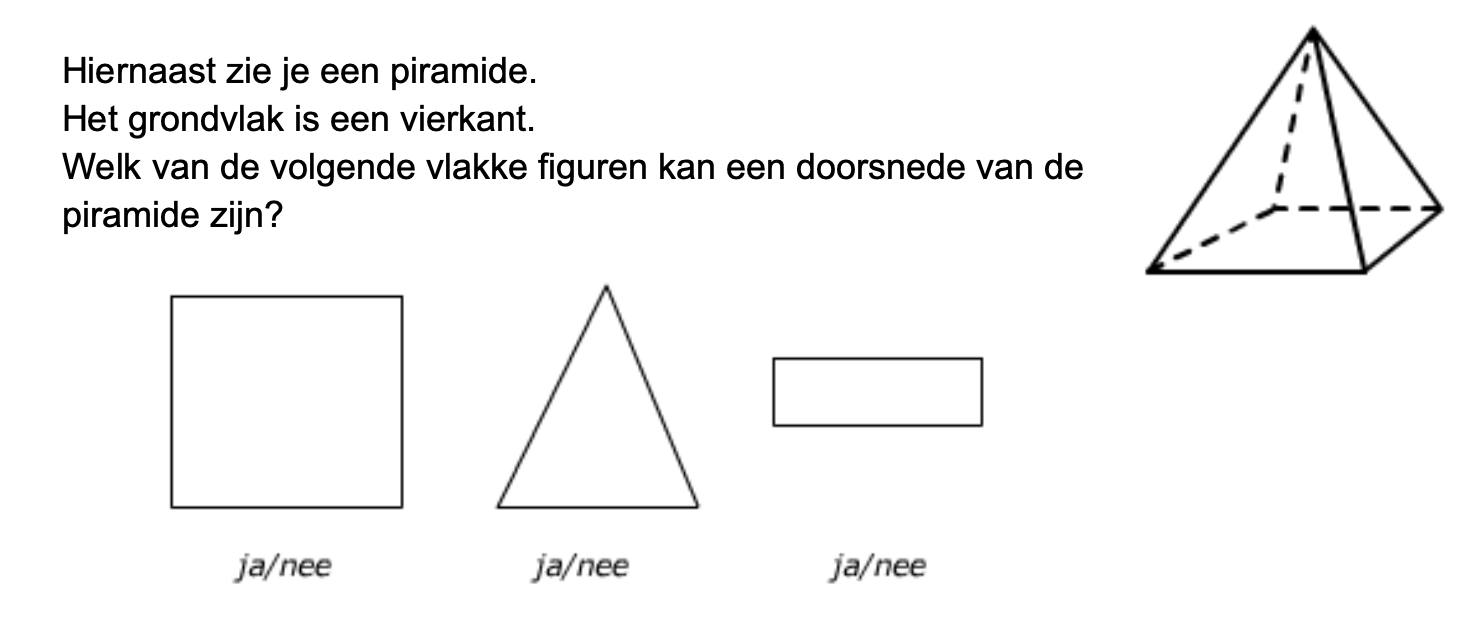

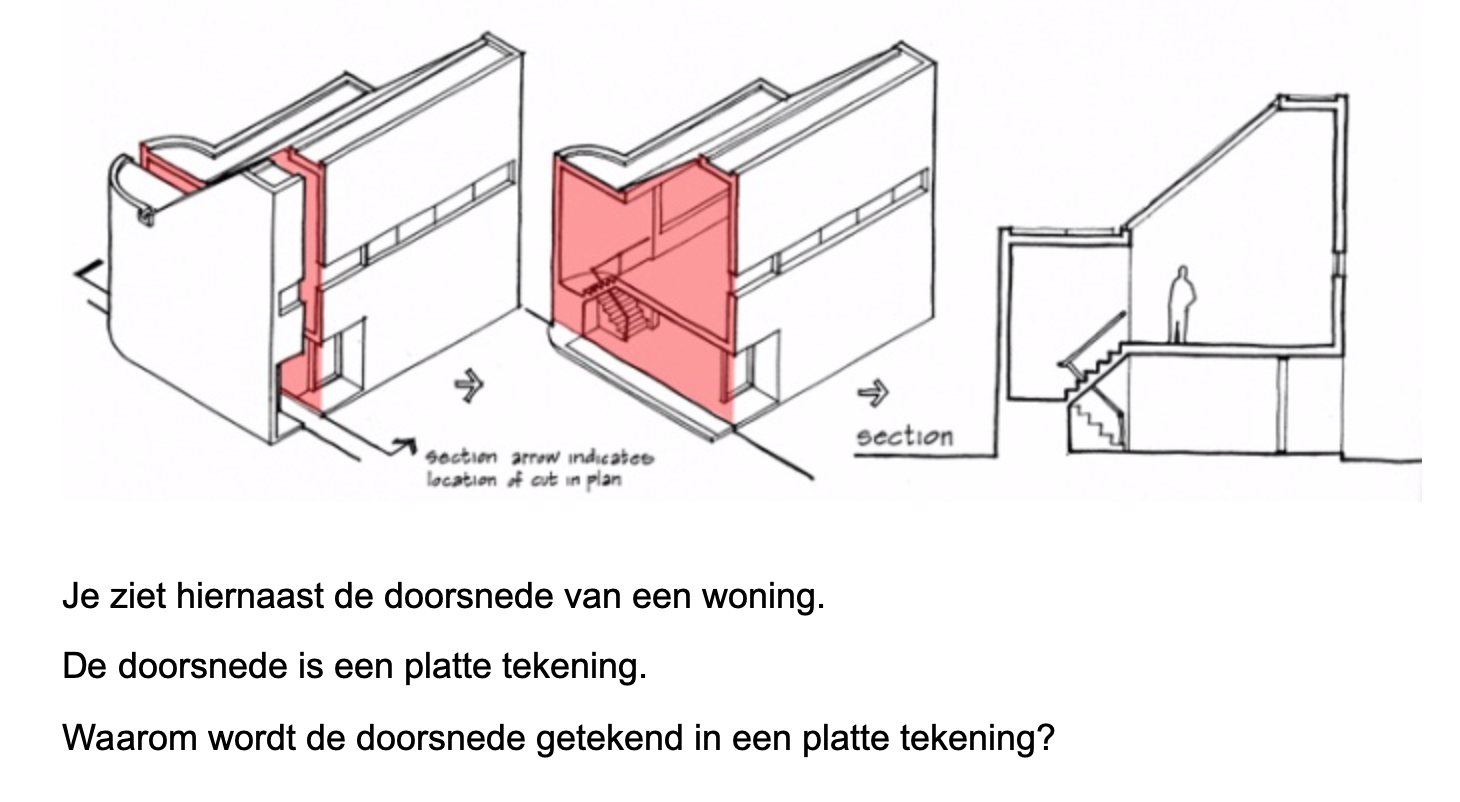

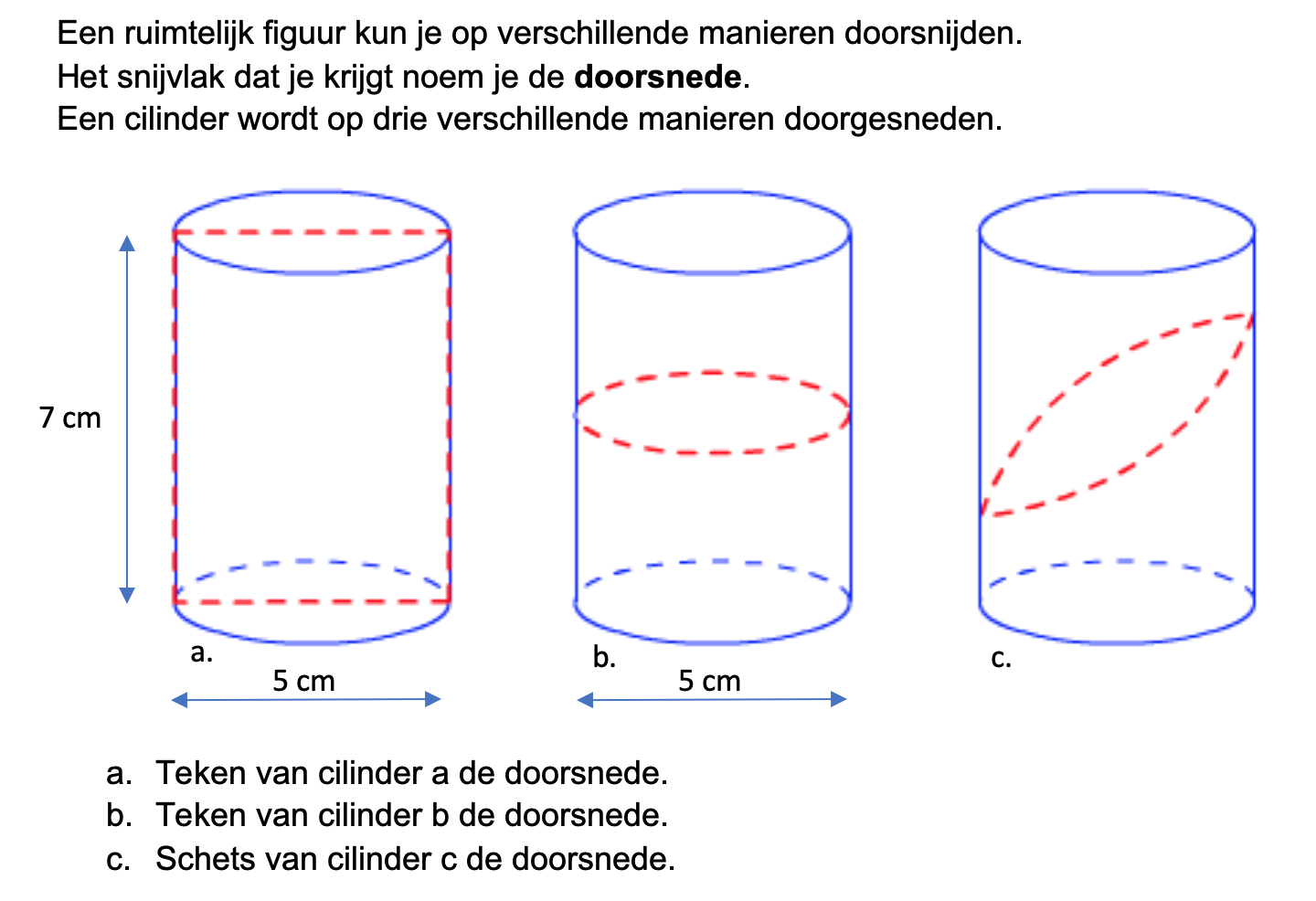
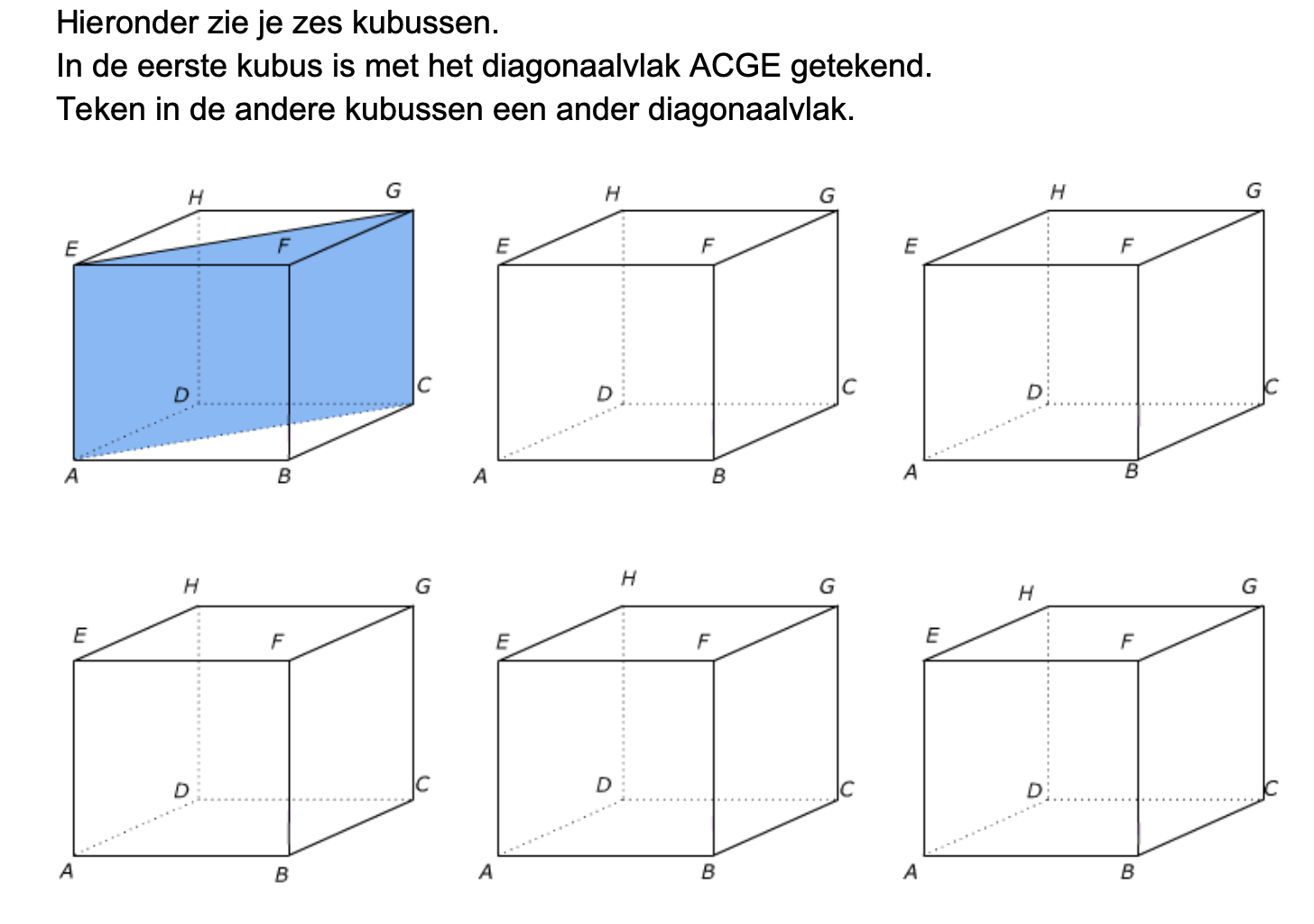
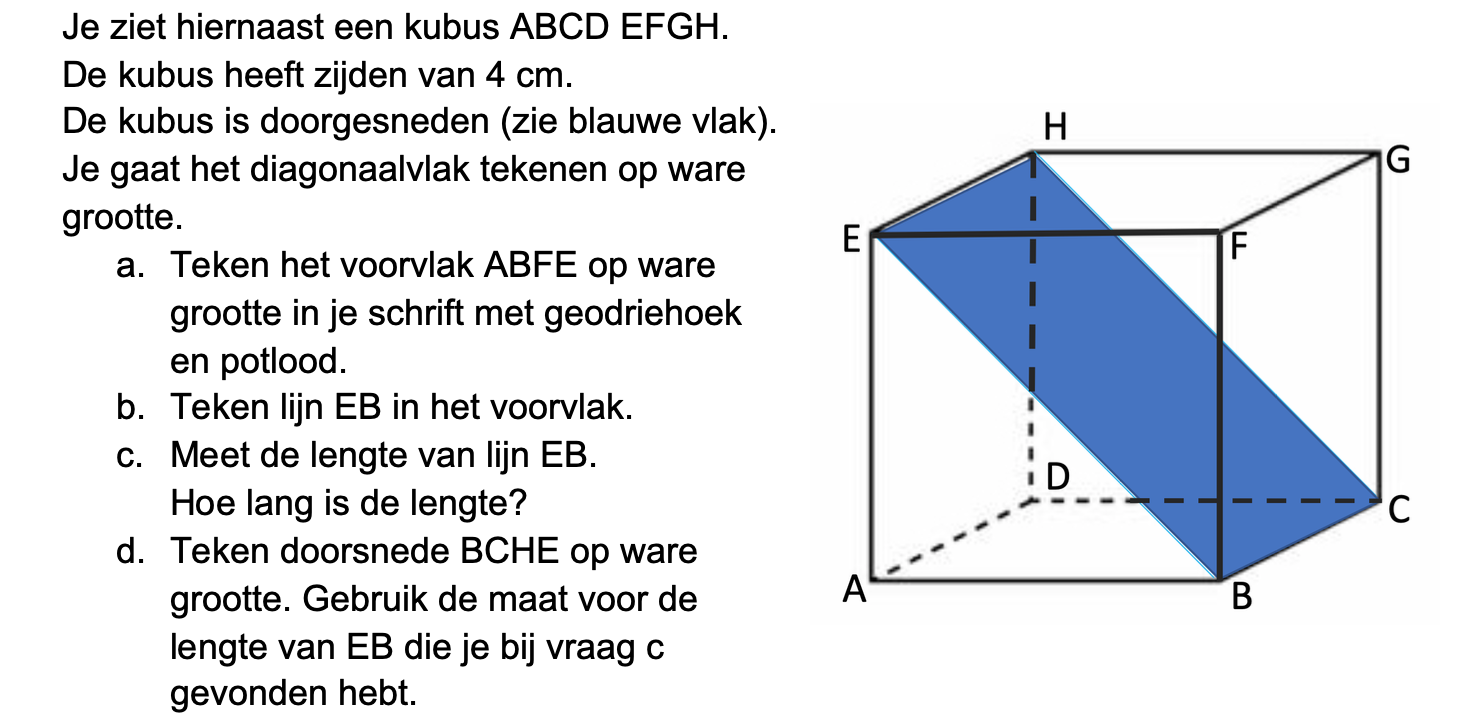
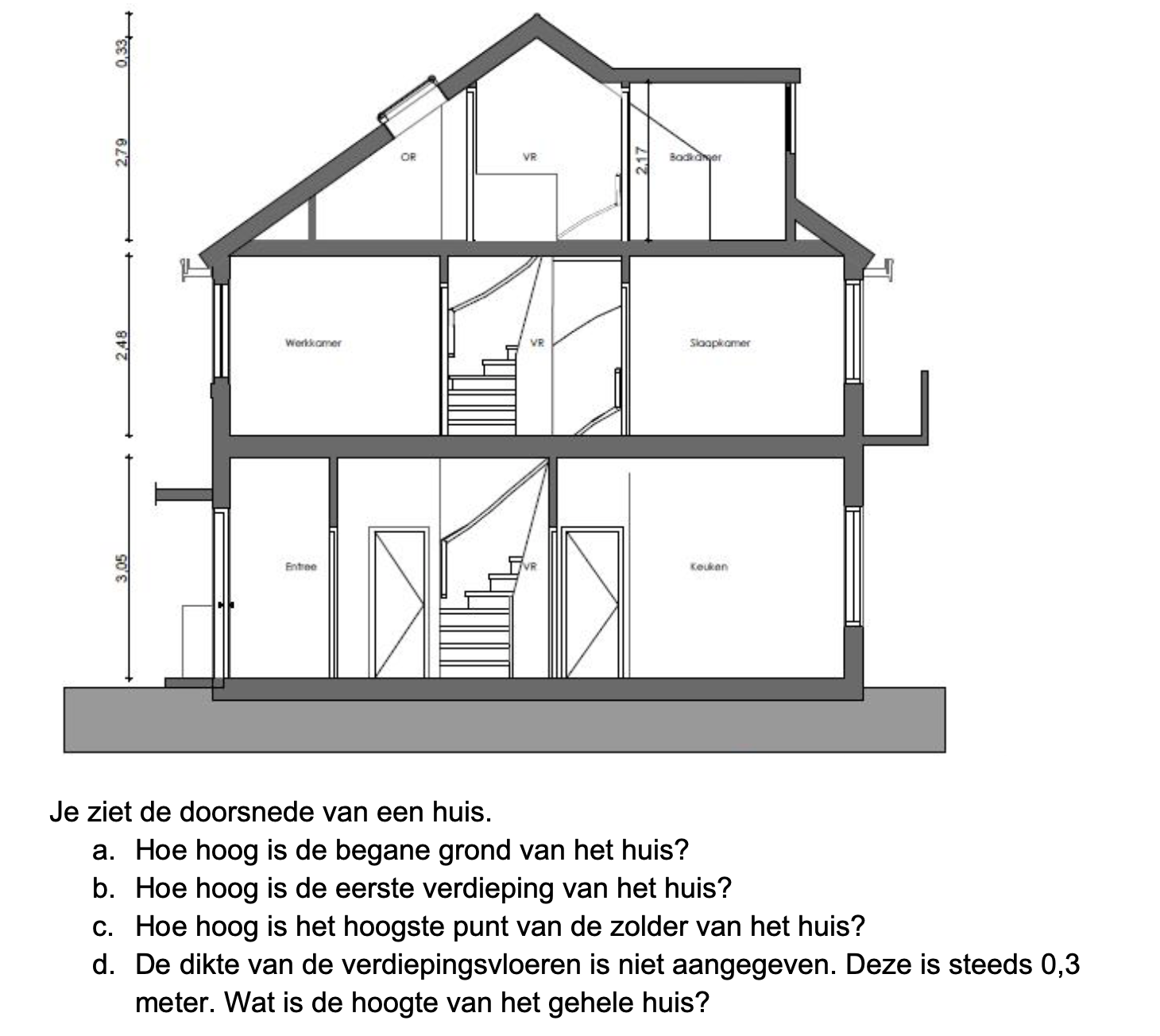
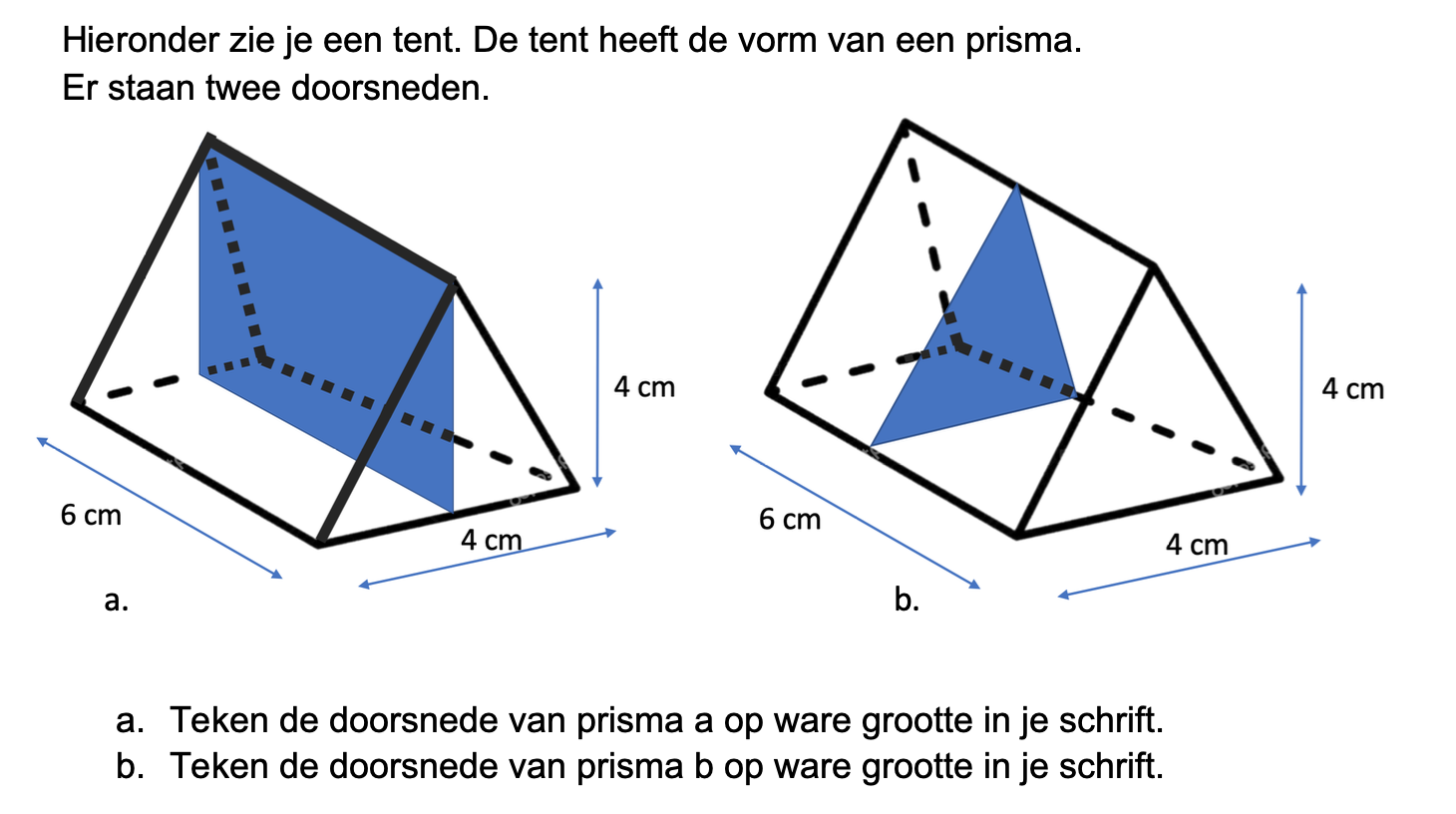


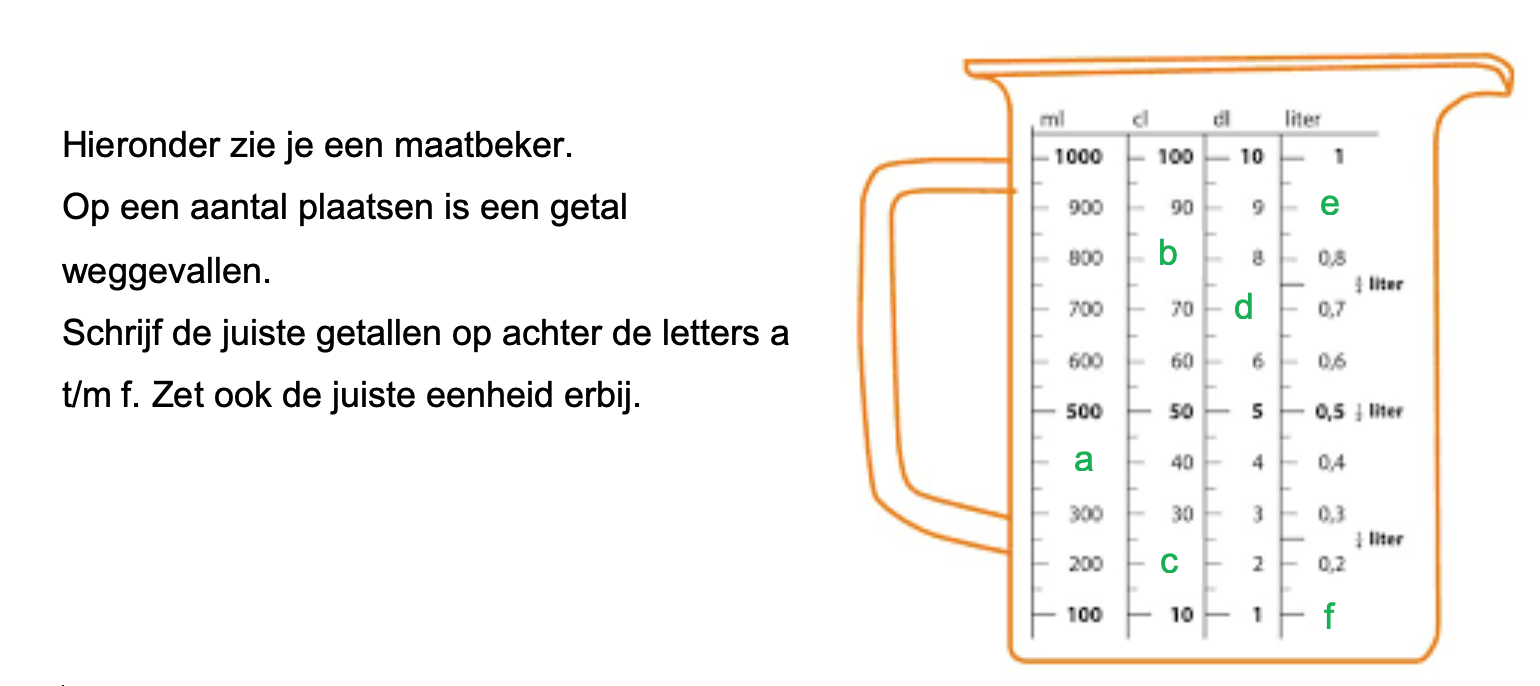





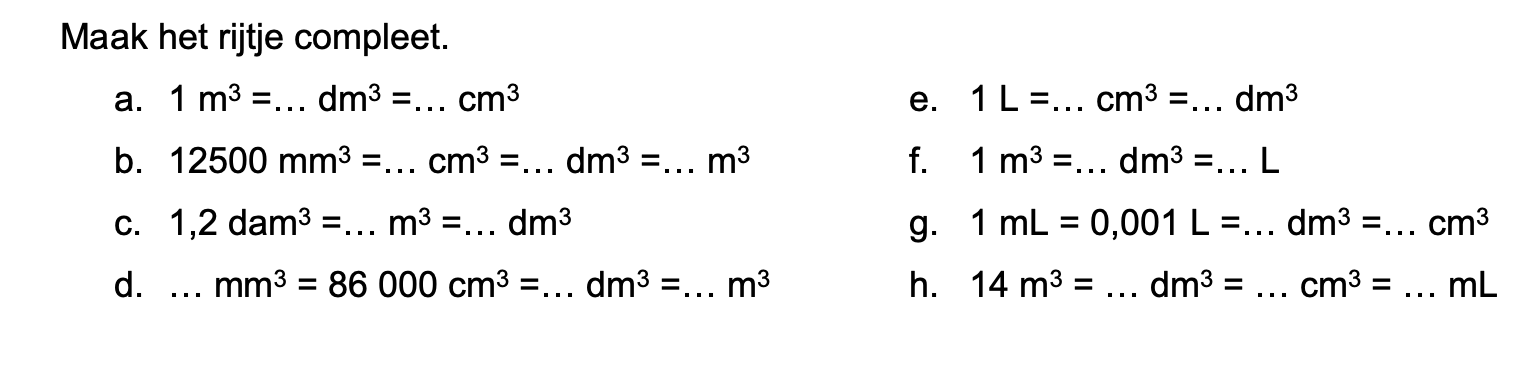


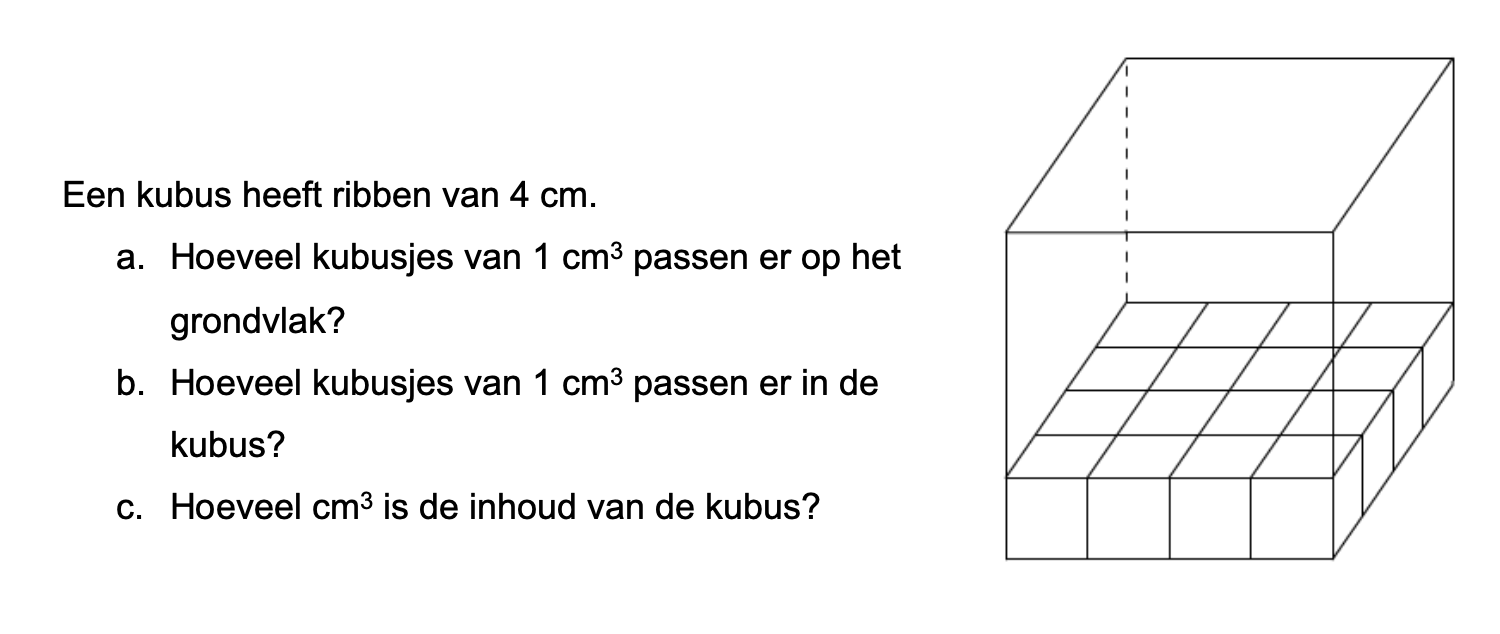

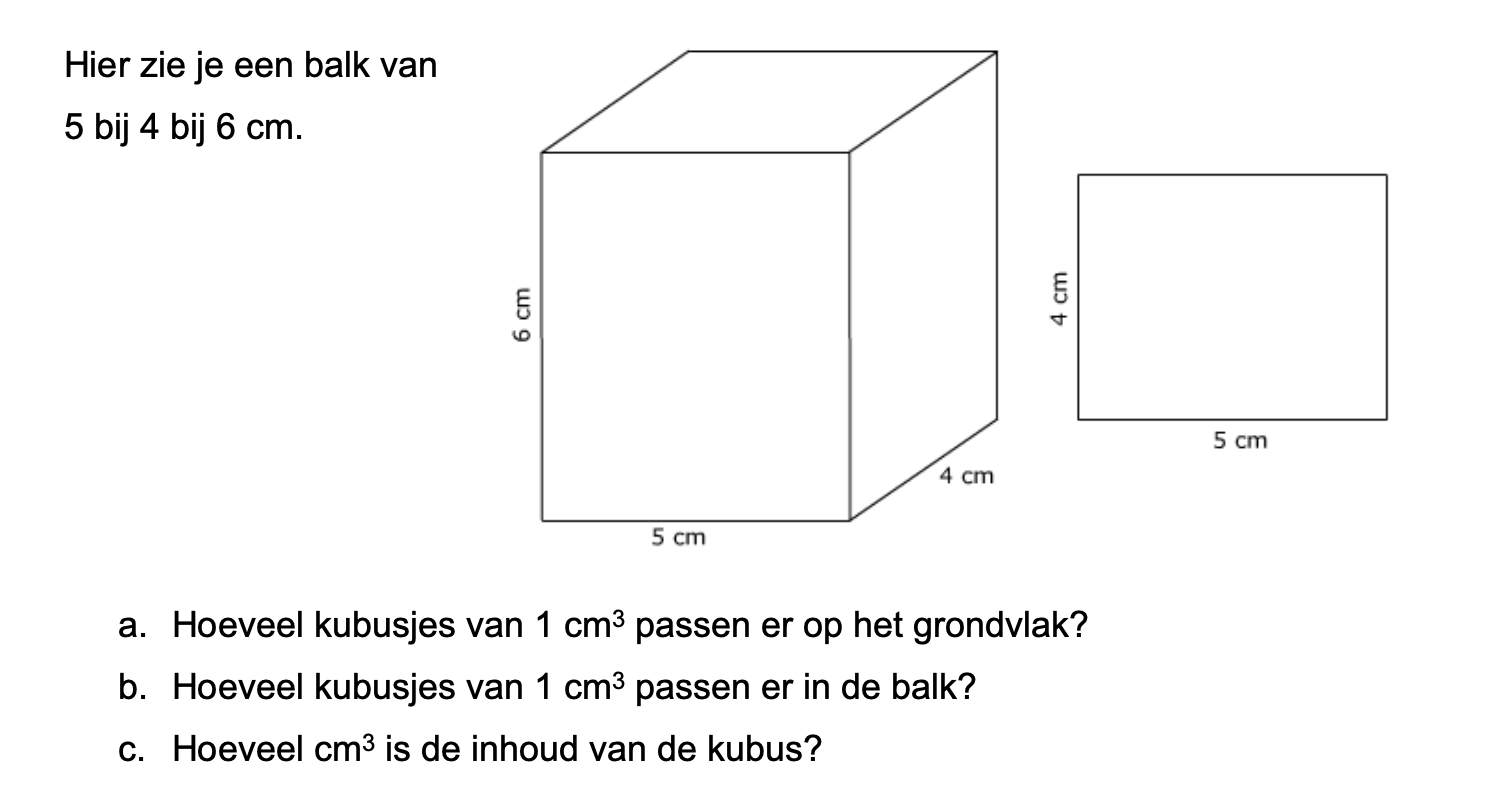
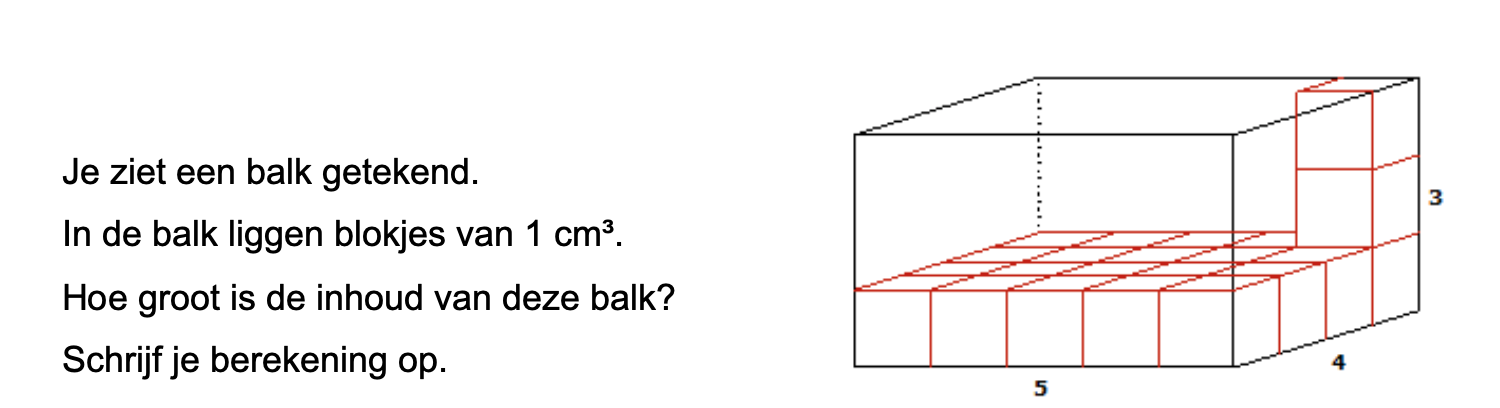

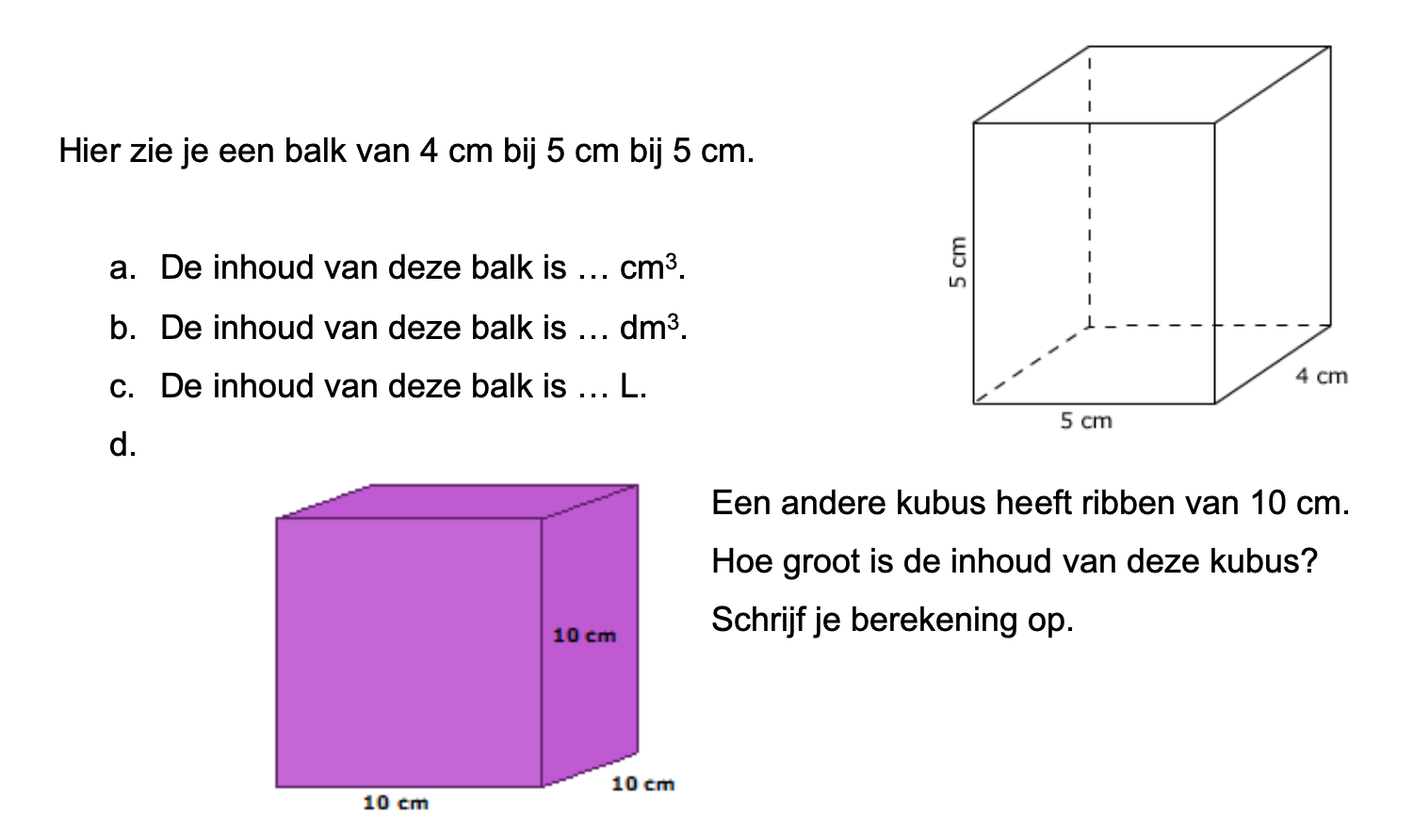


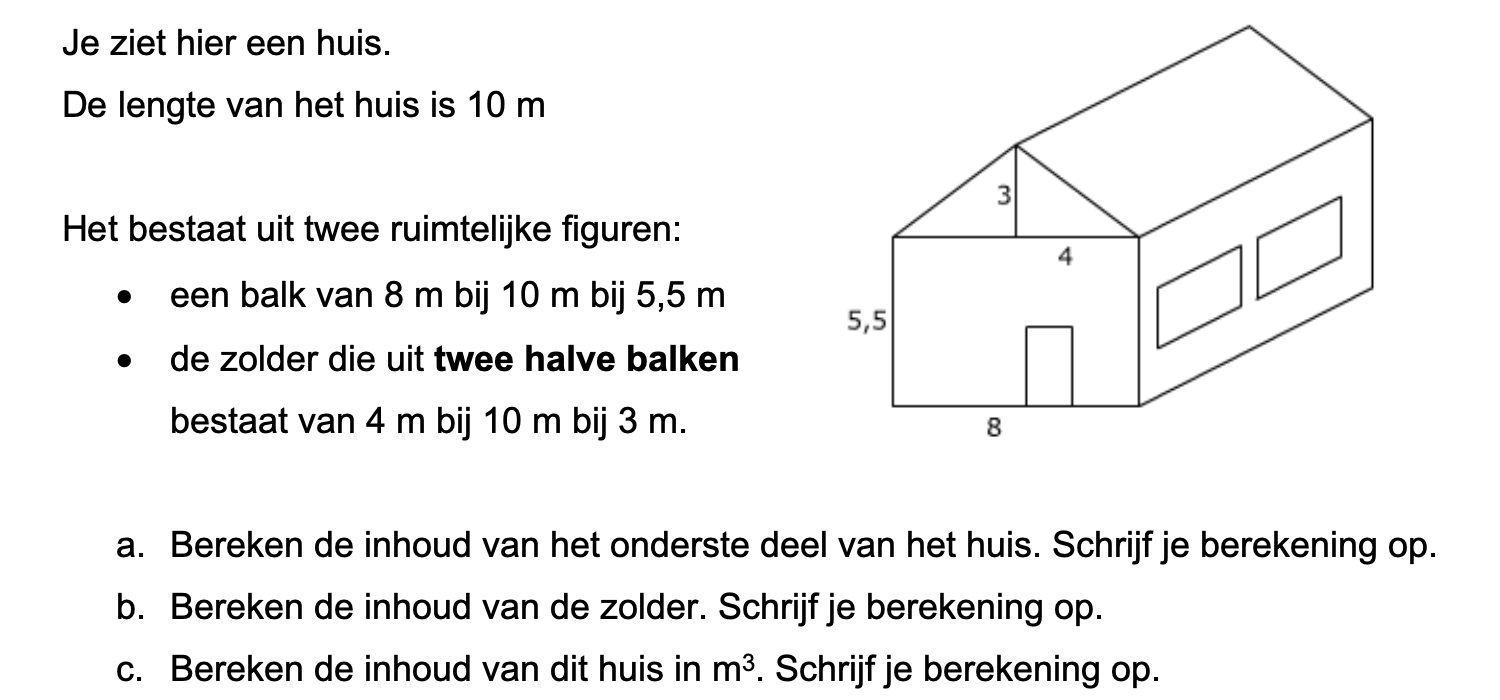


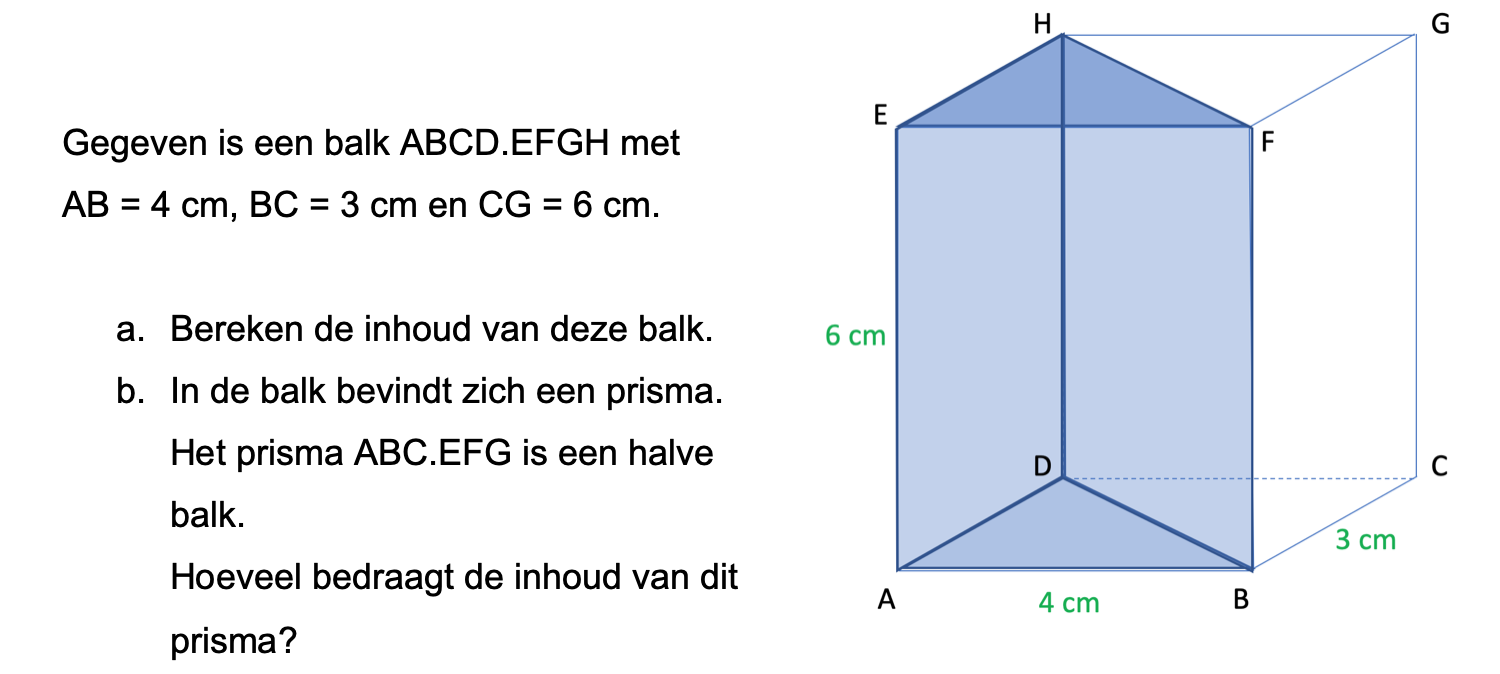












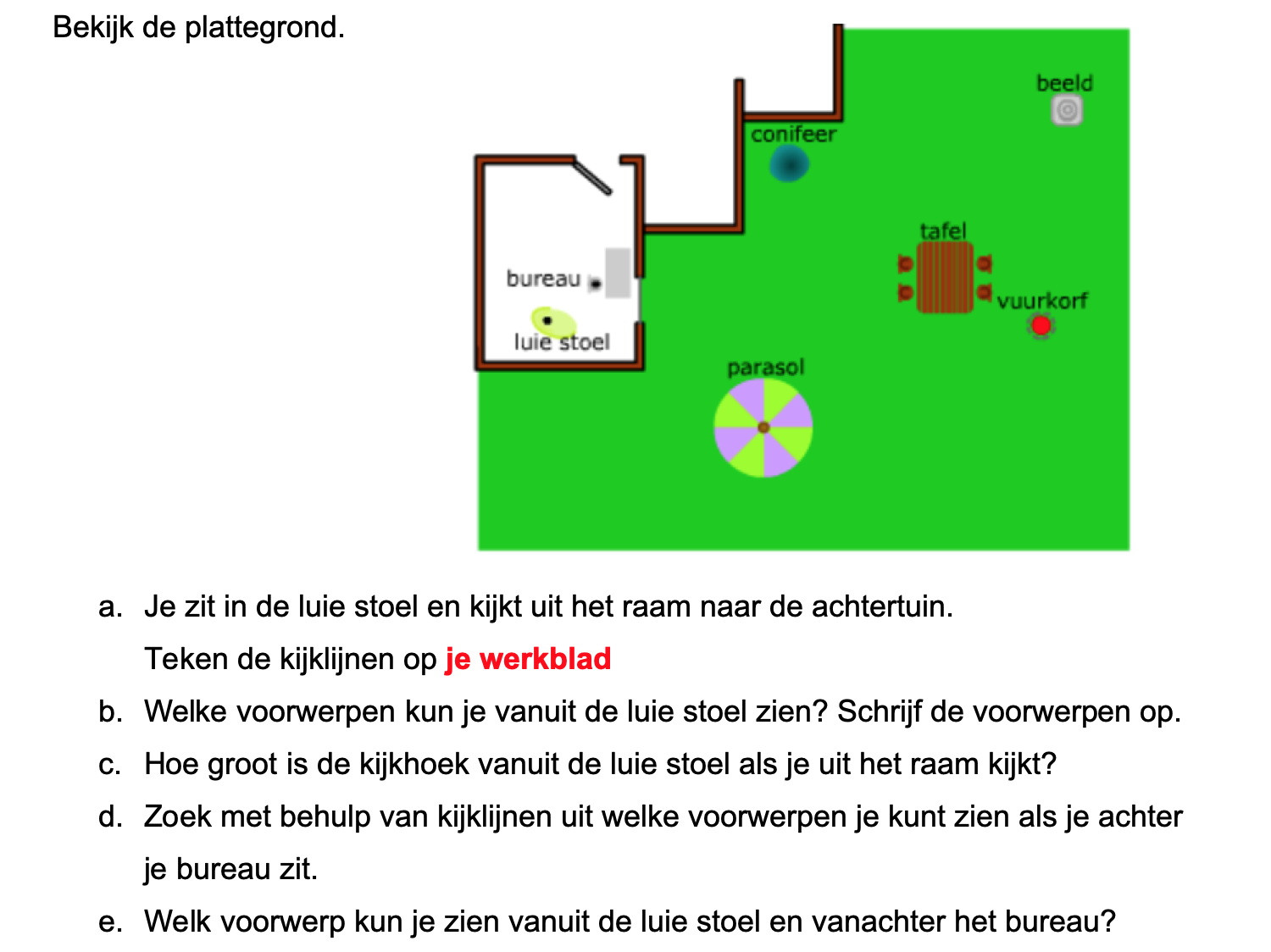
 Bij de plattegrond op werkblad
Bij de plattegrond op werkblad 




















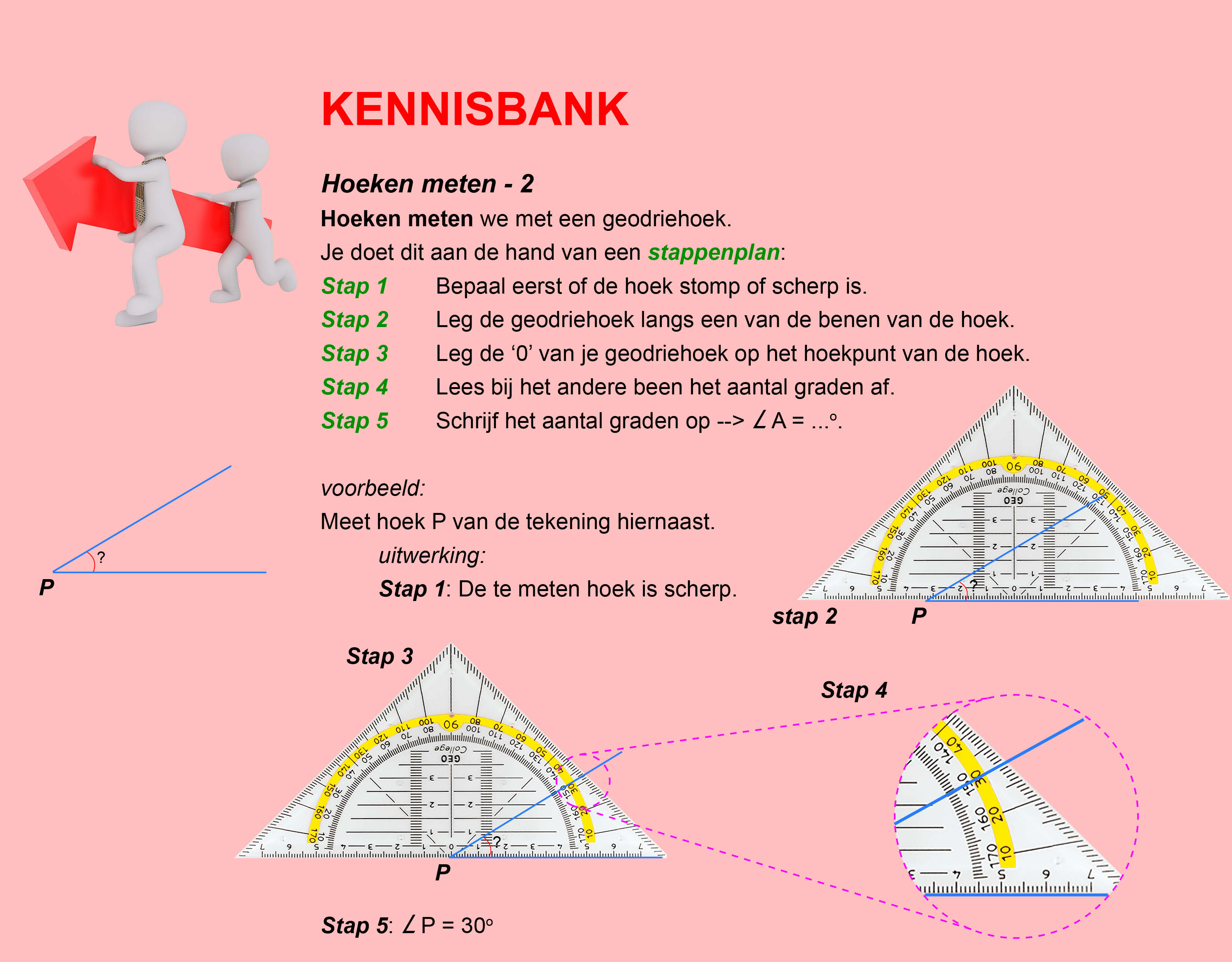
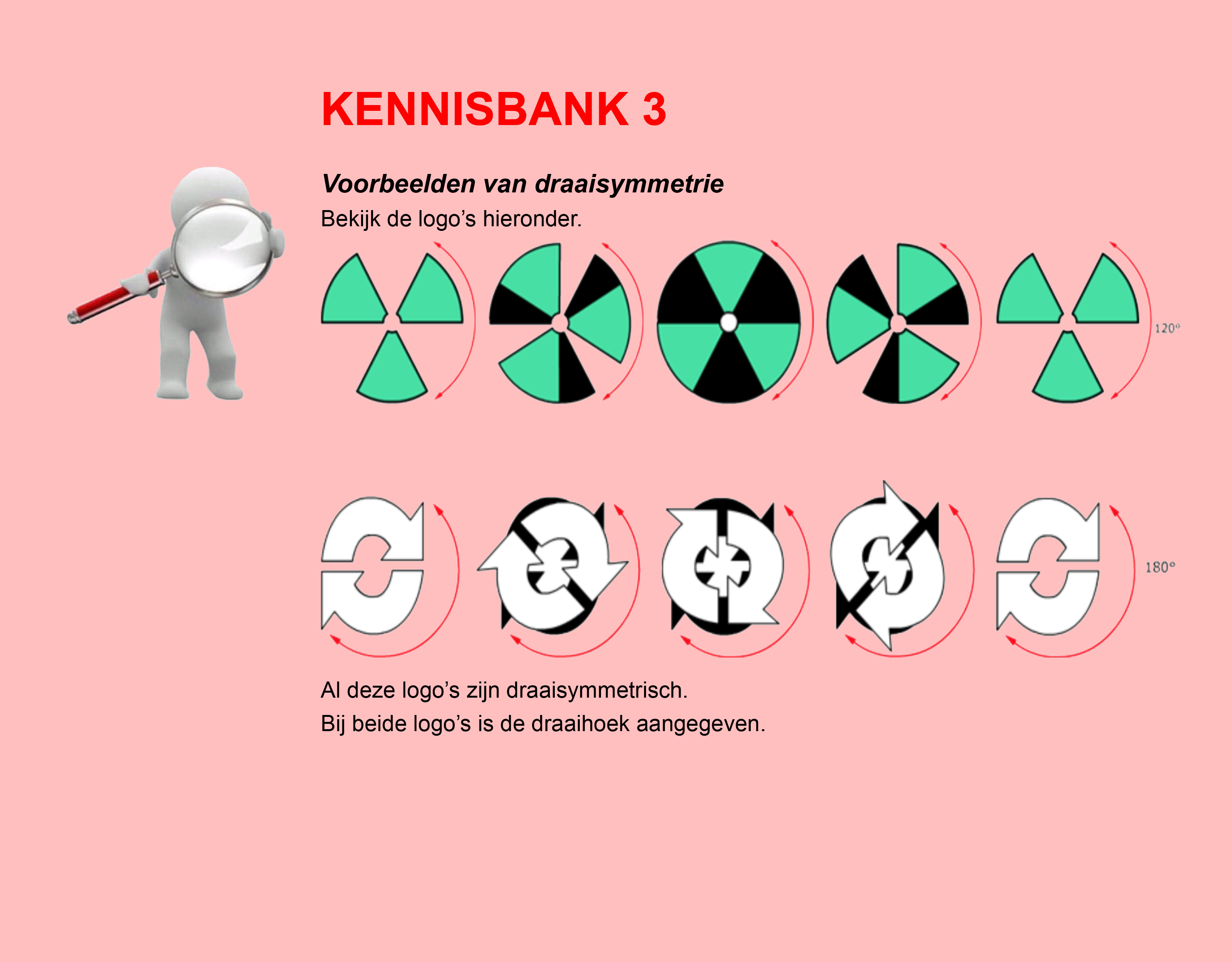
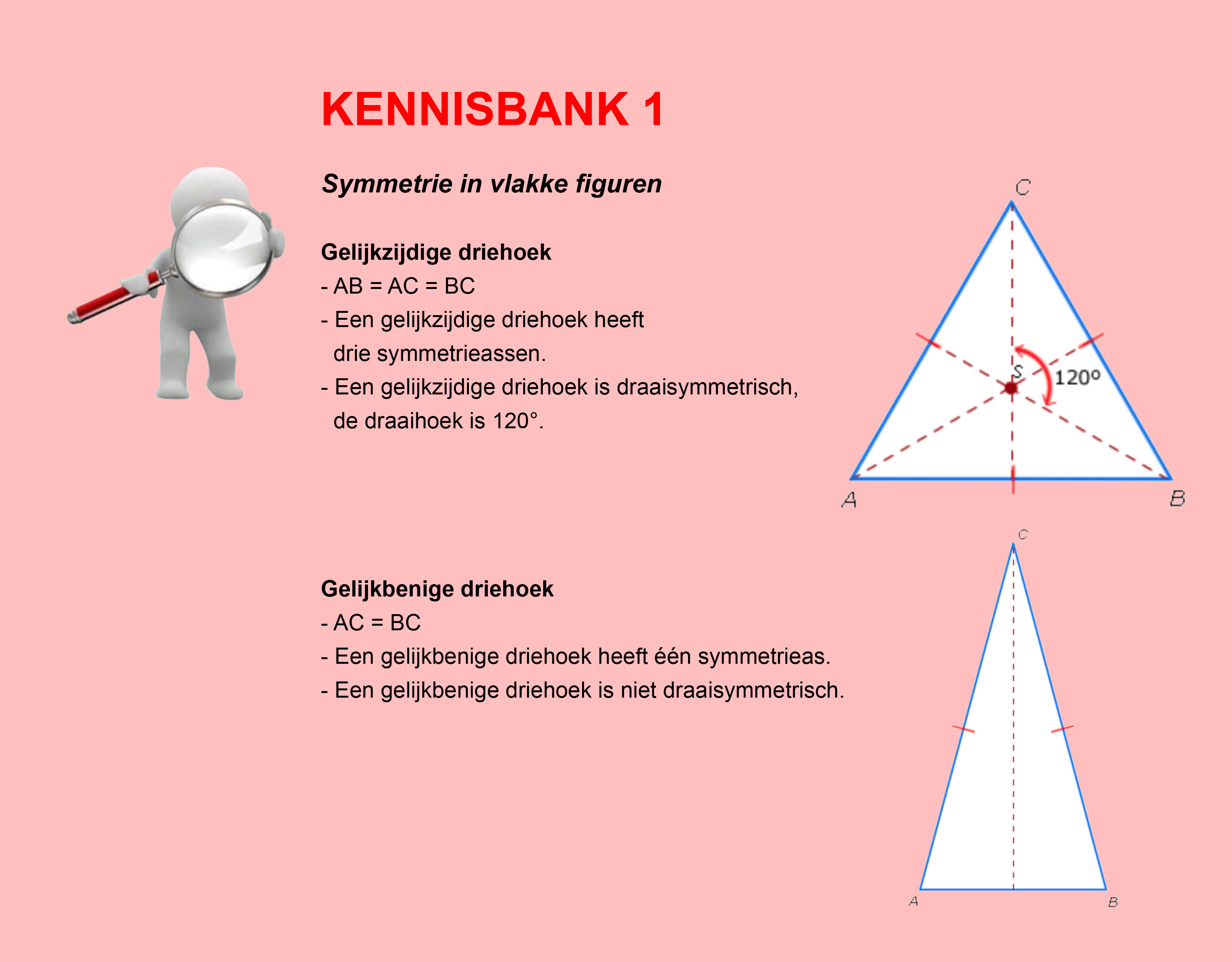
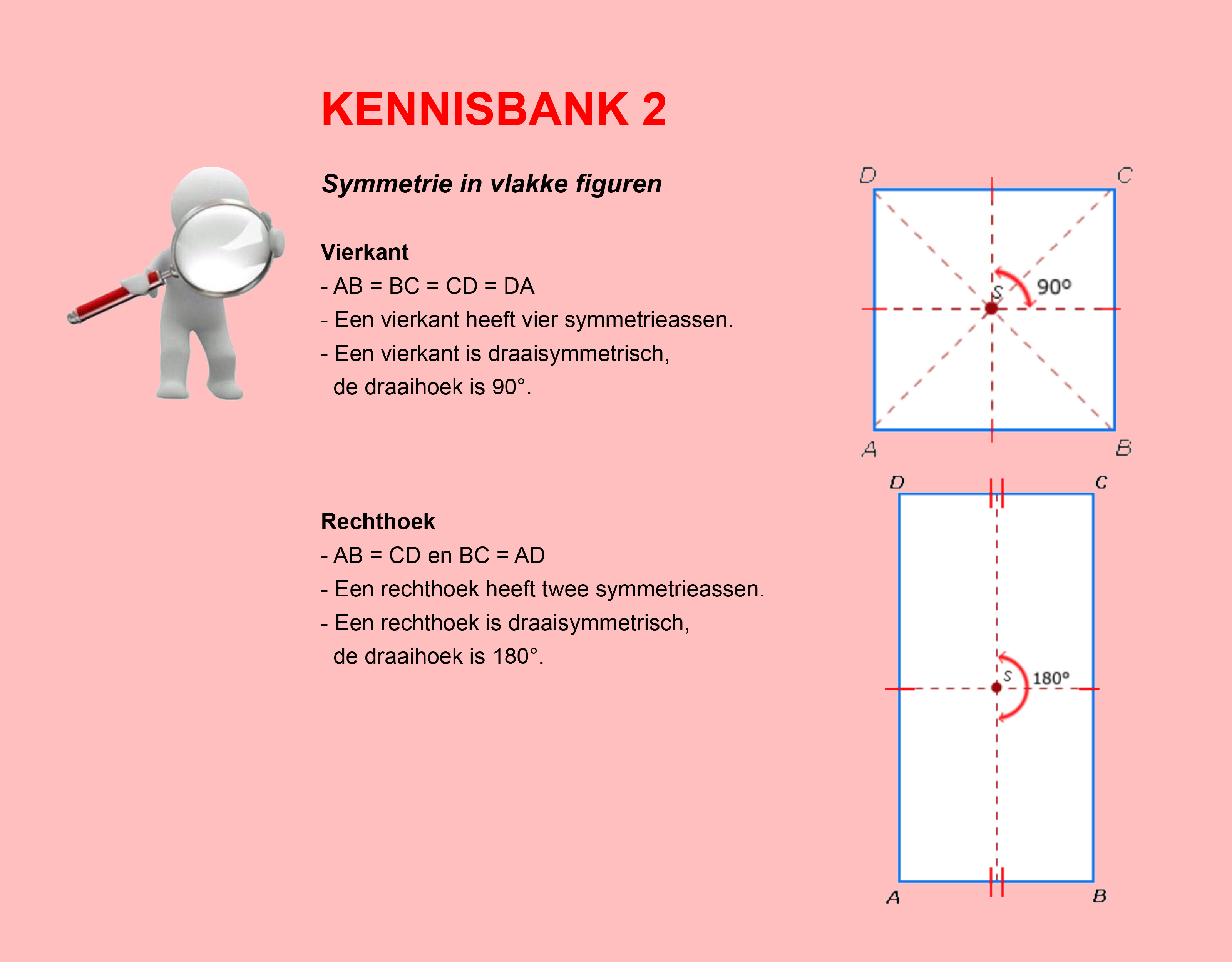
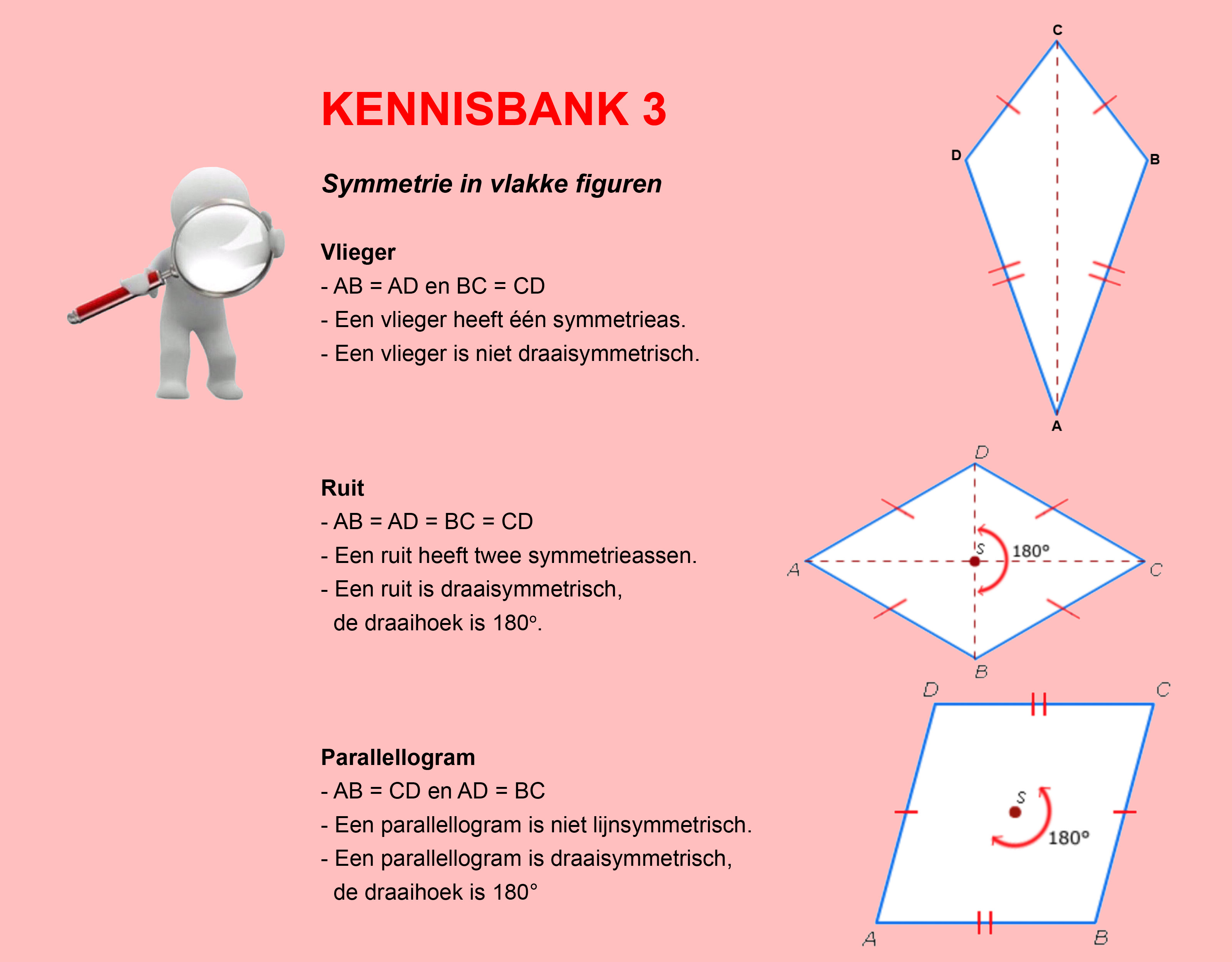
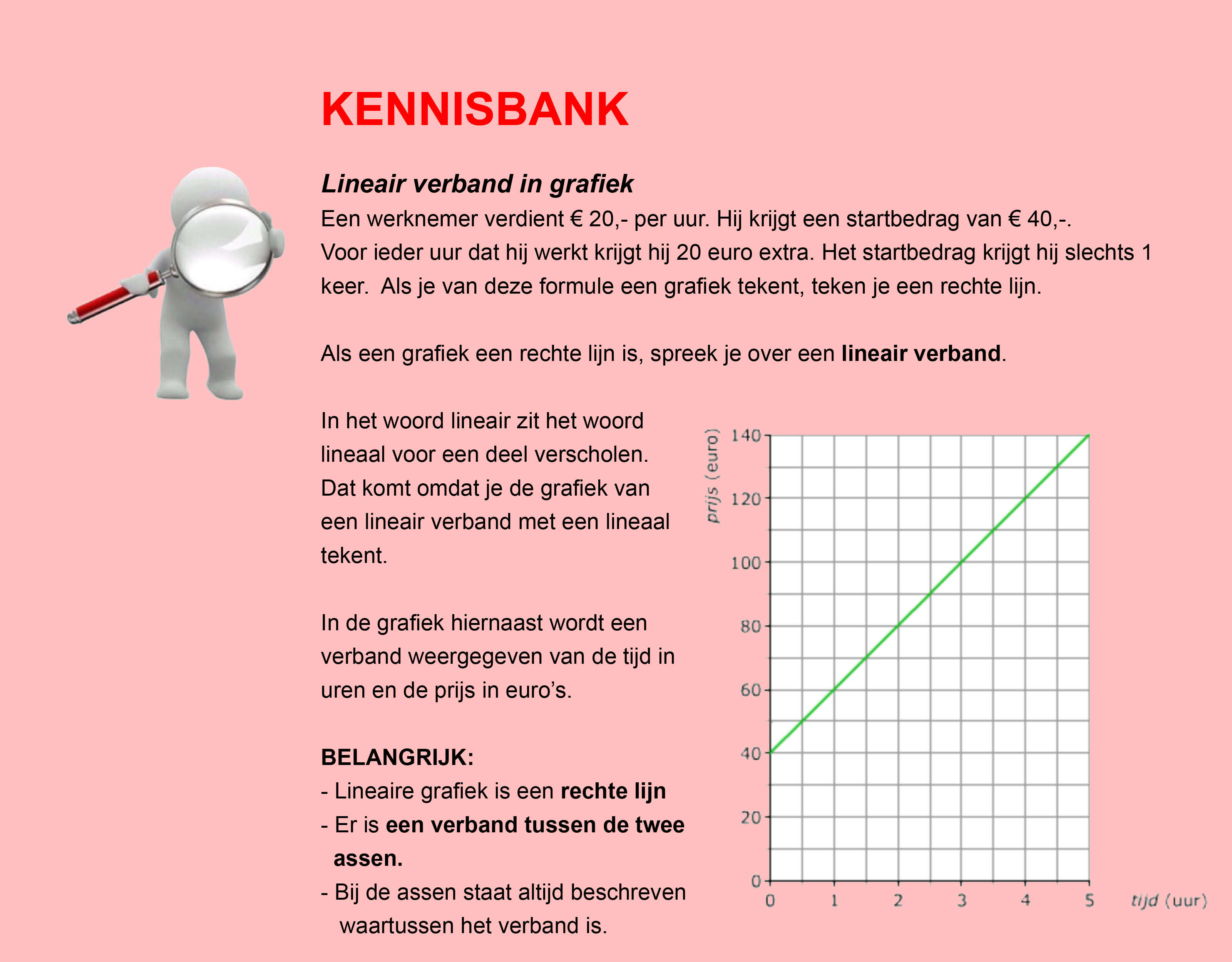
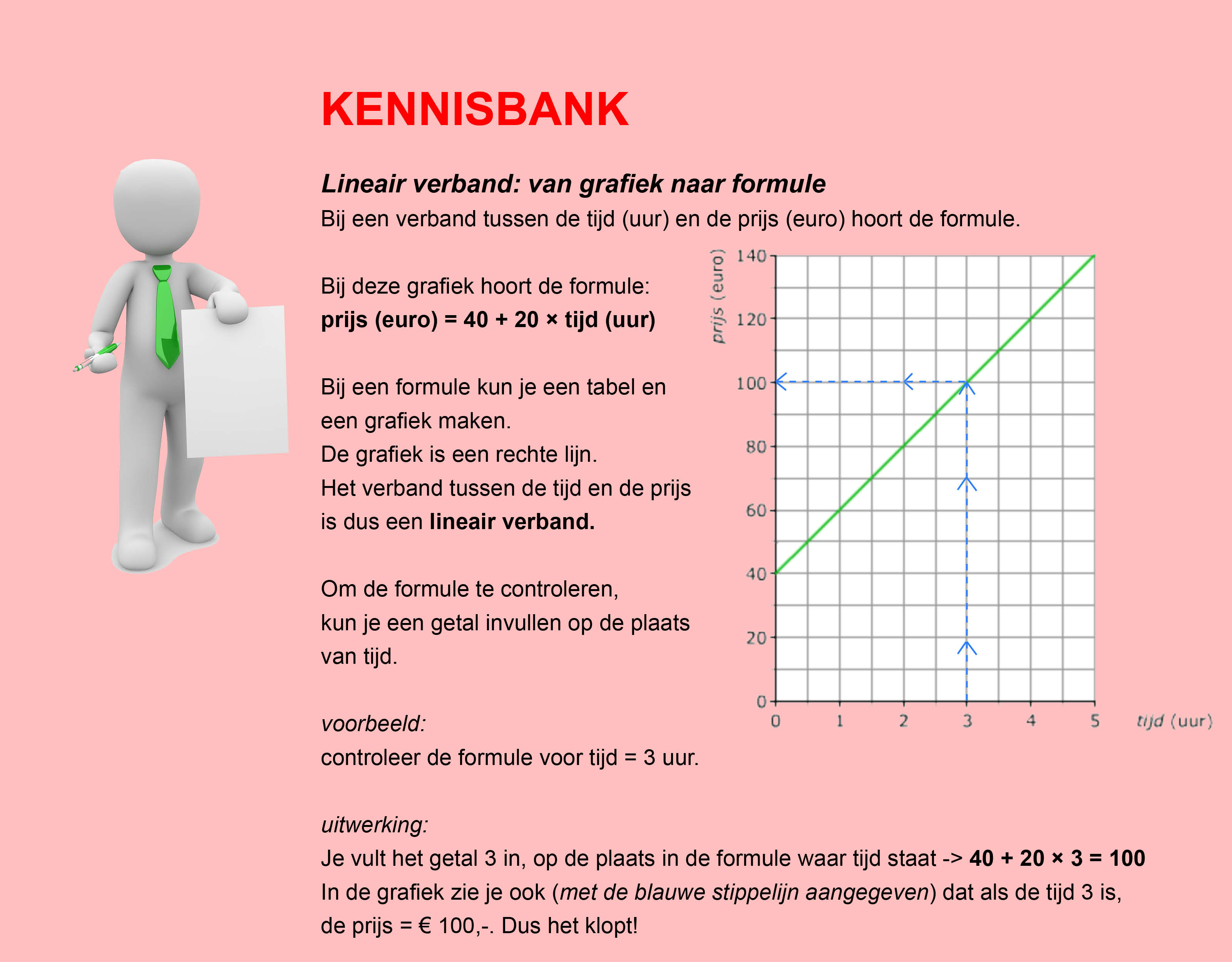
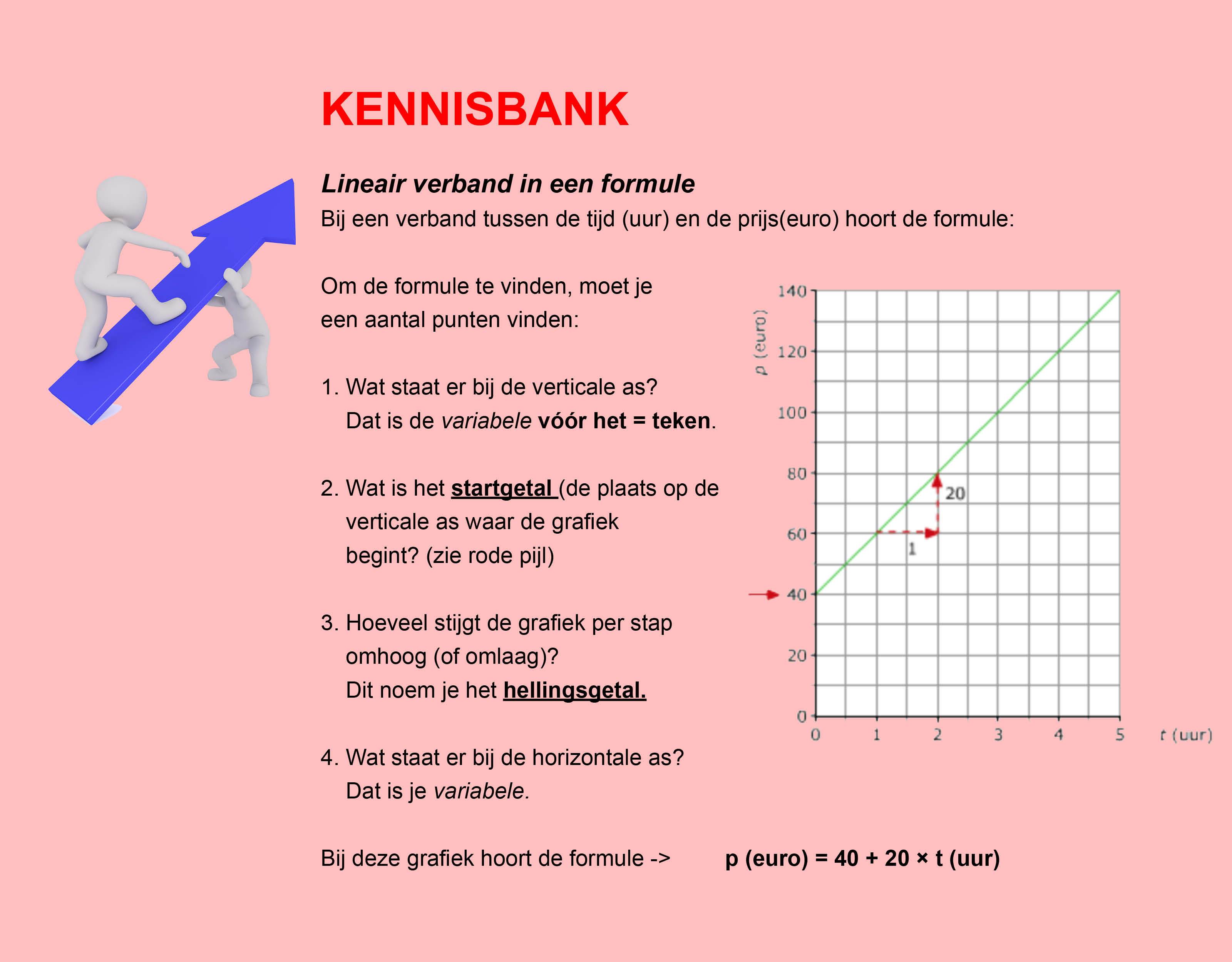
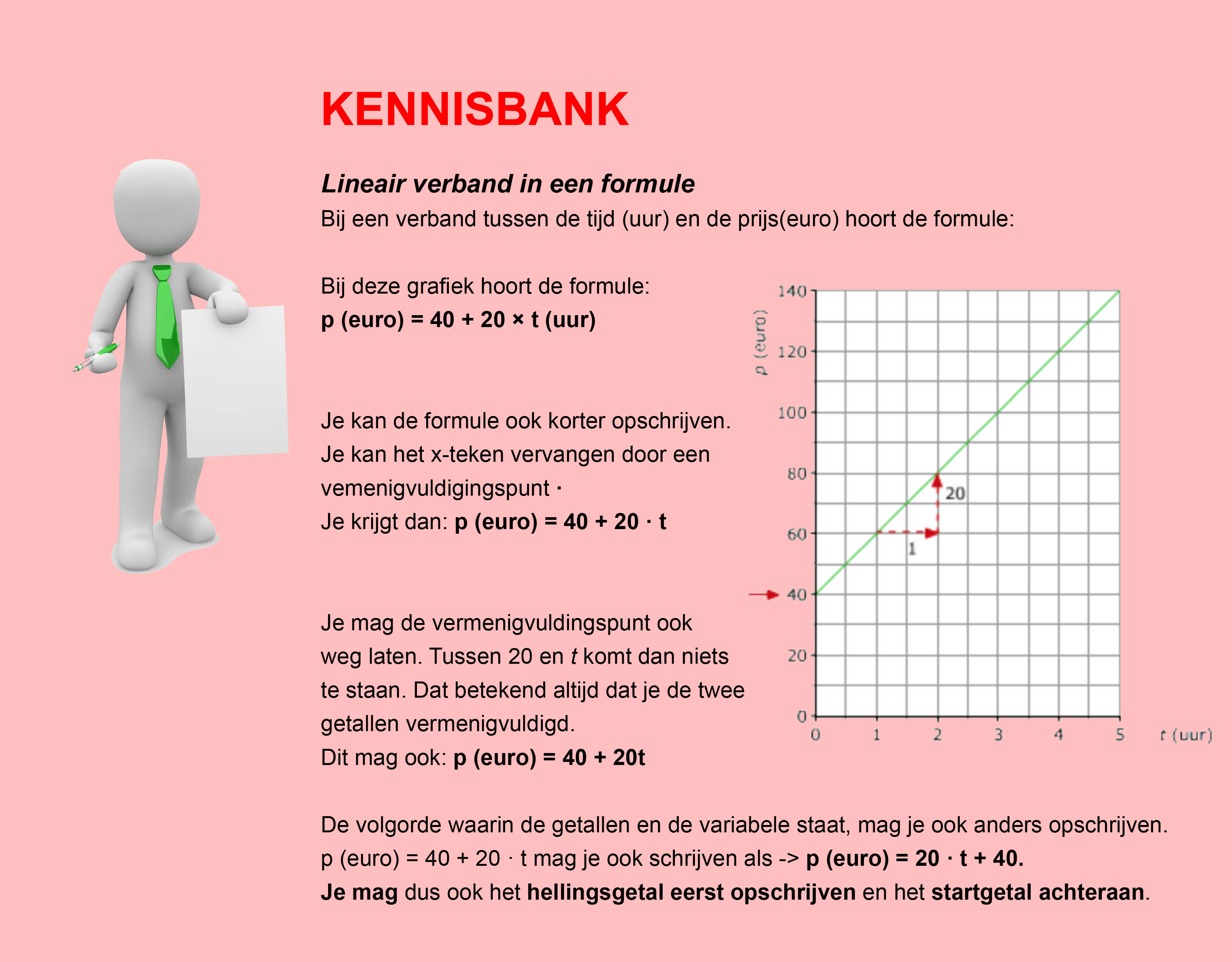
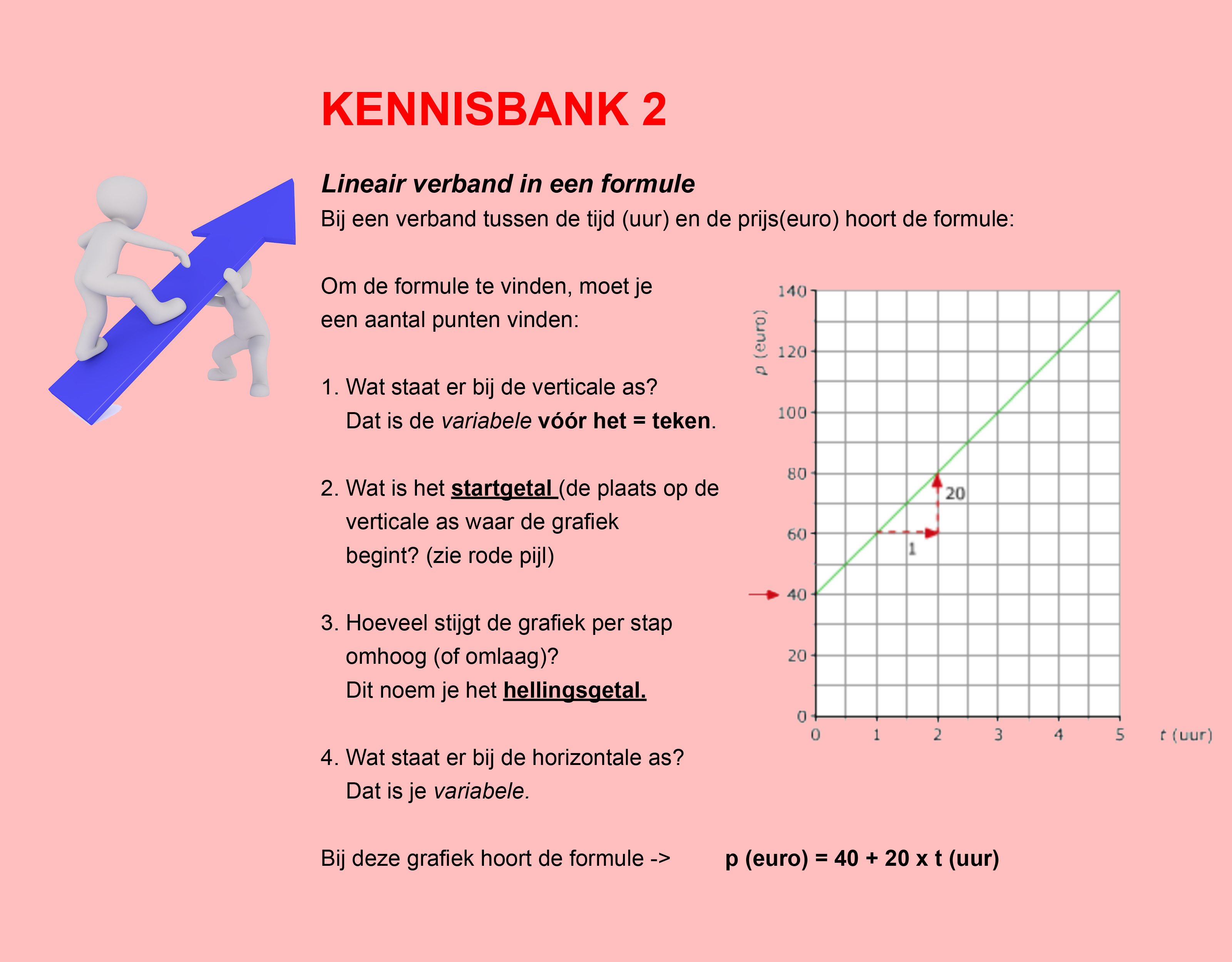
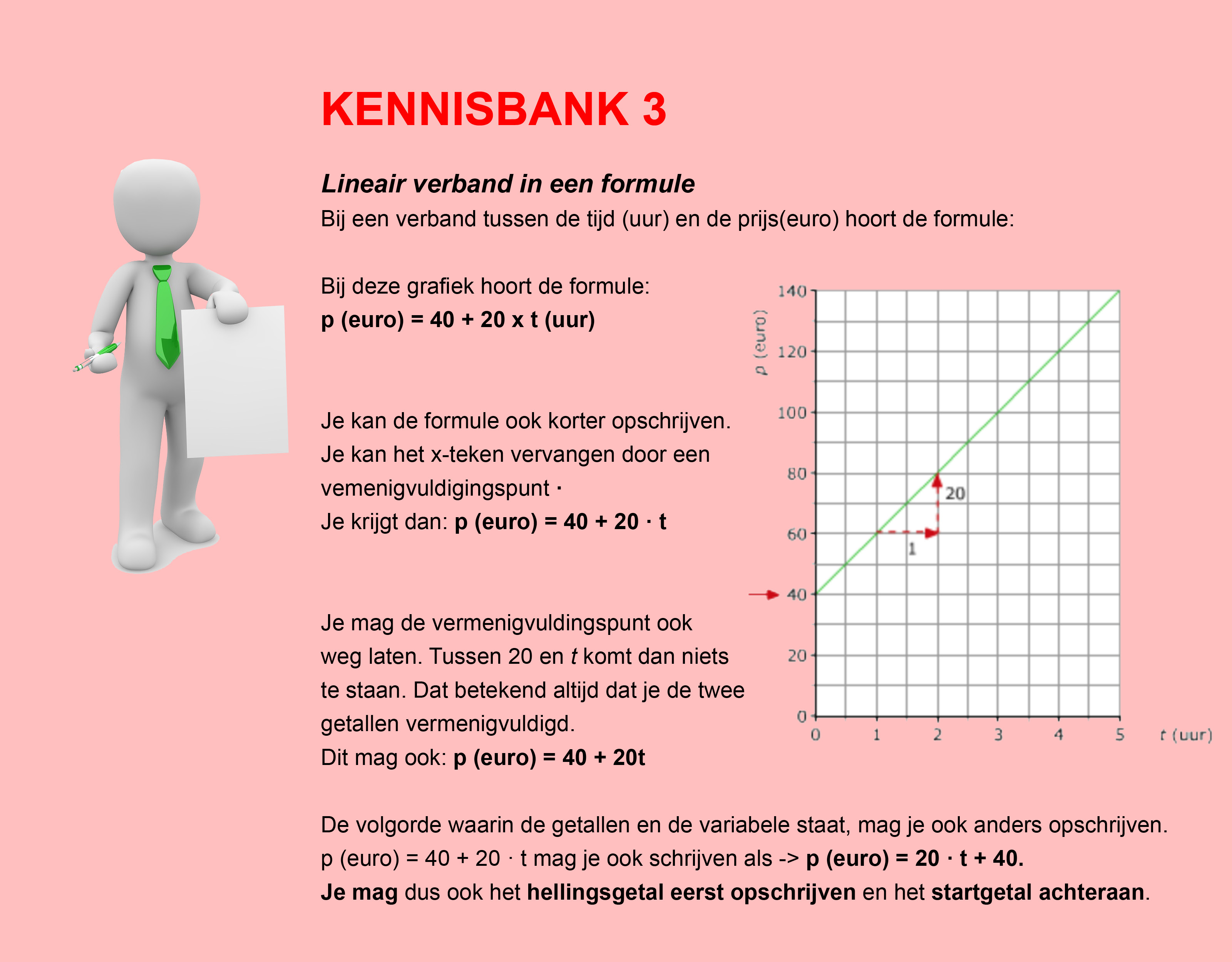
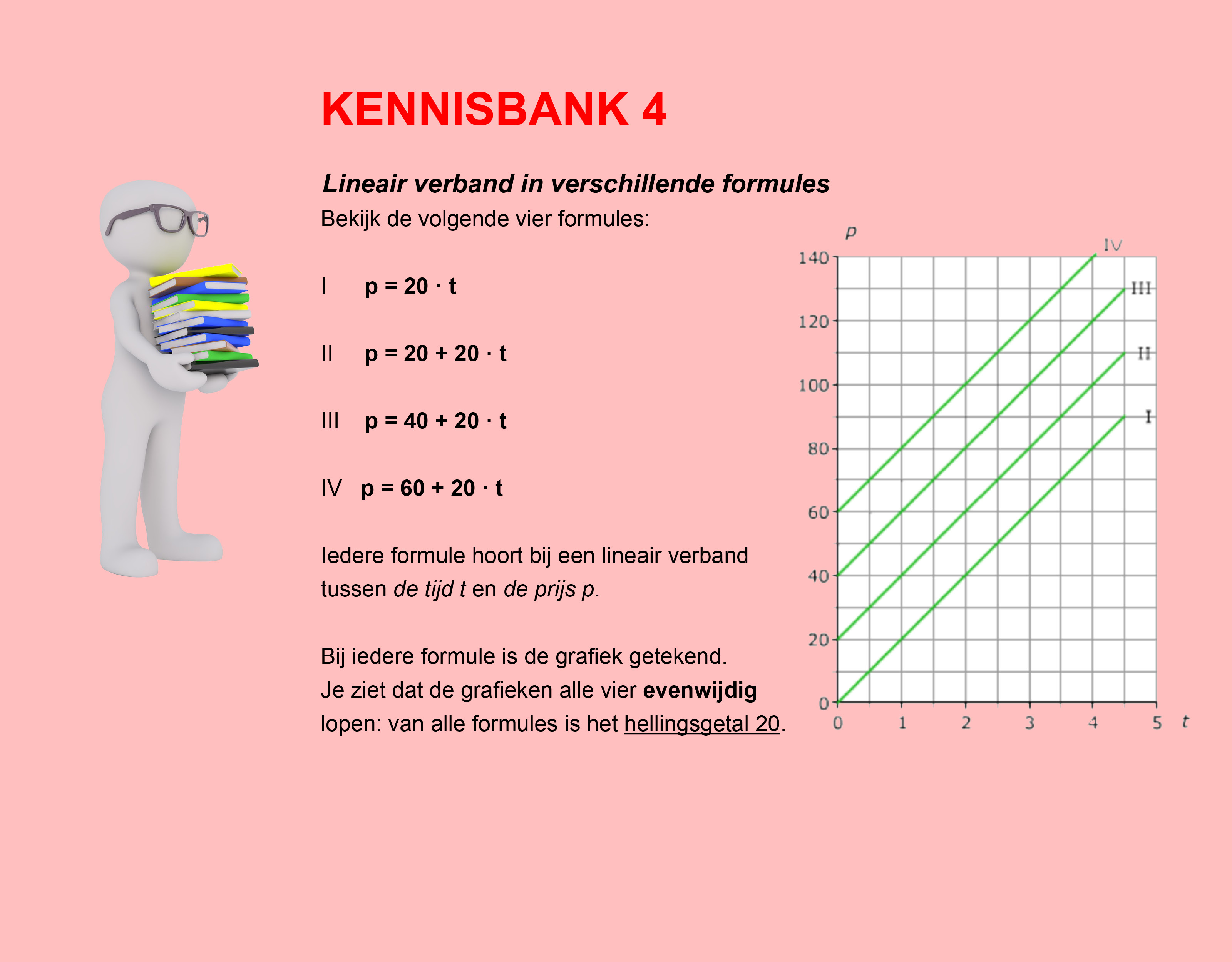
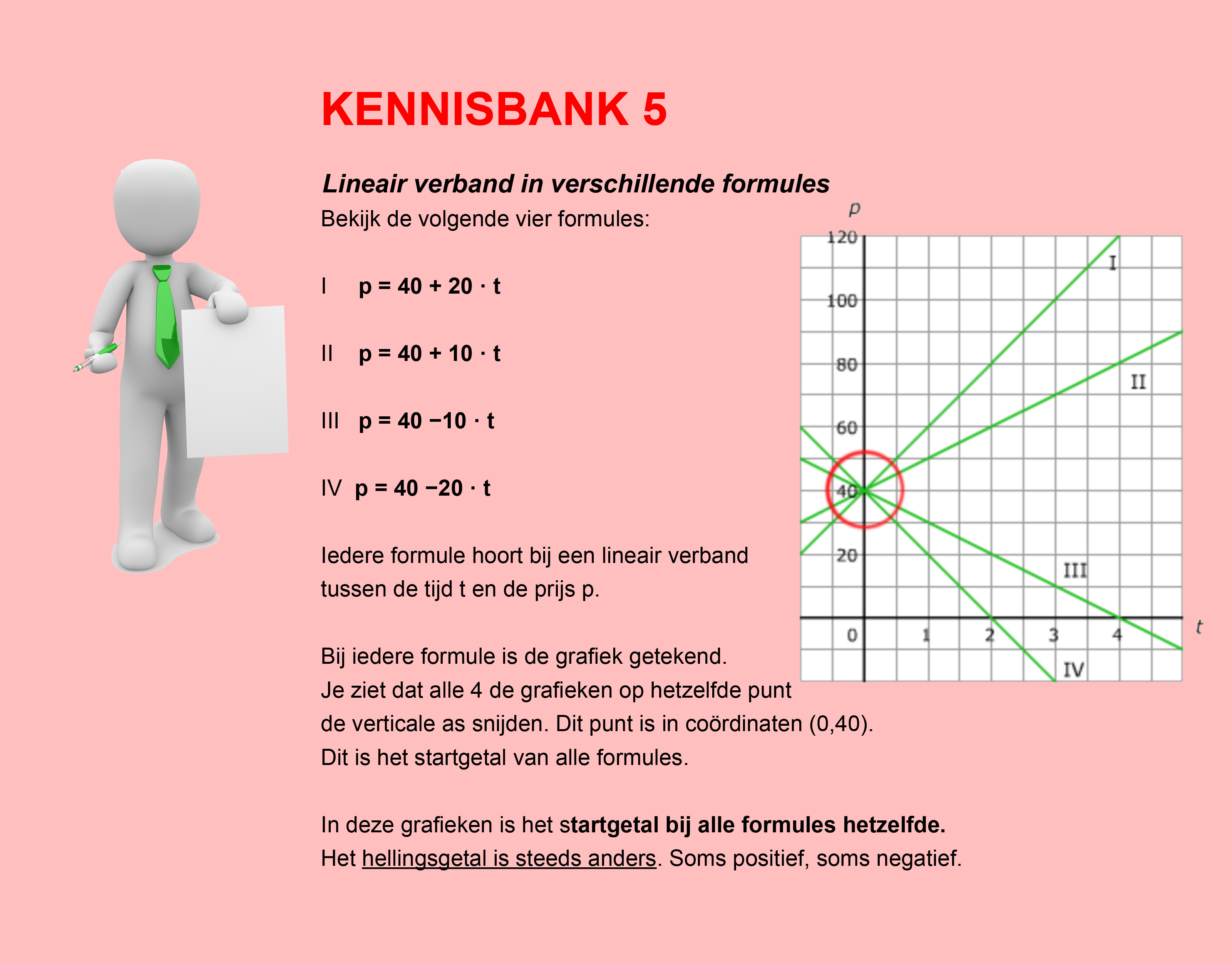
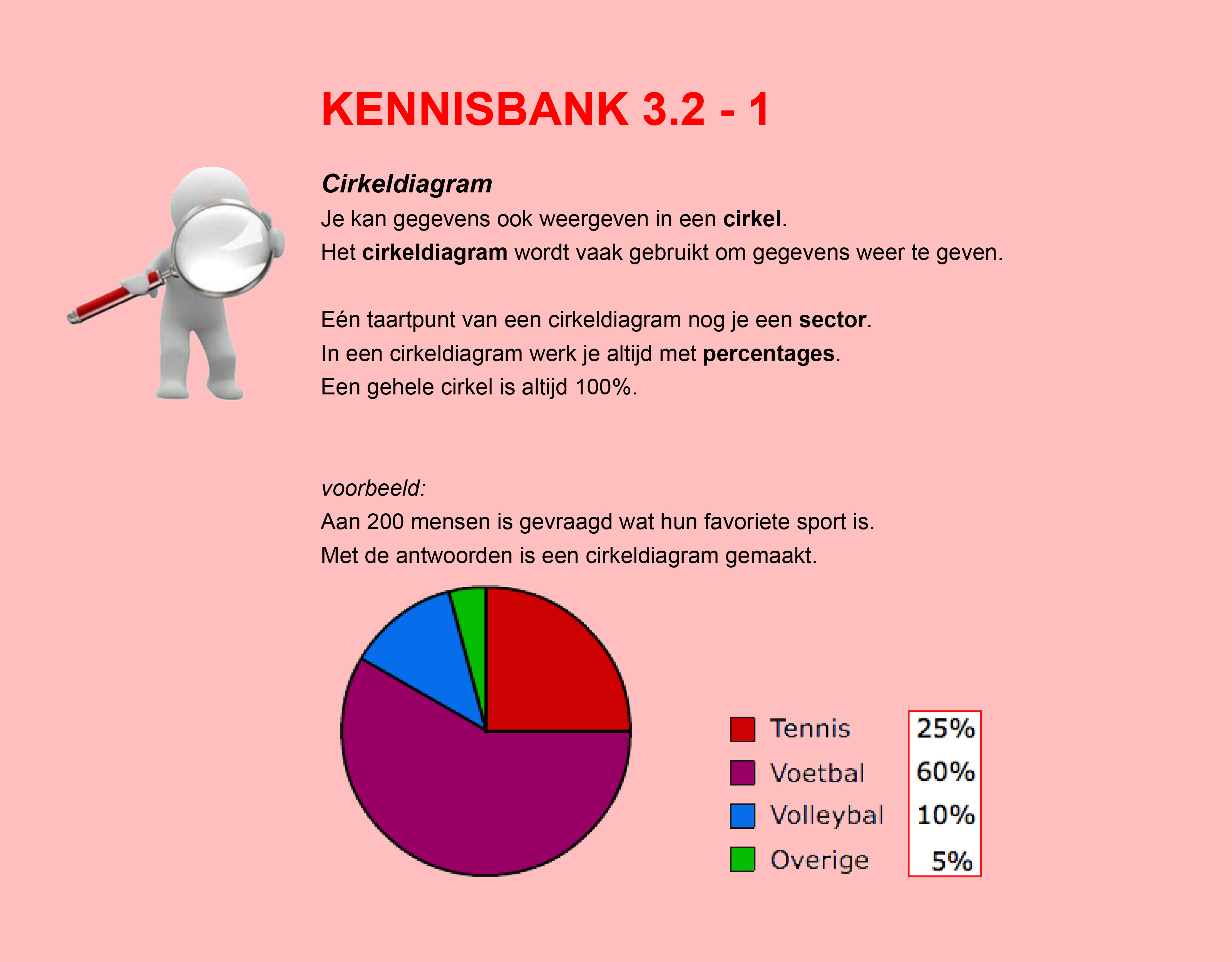
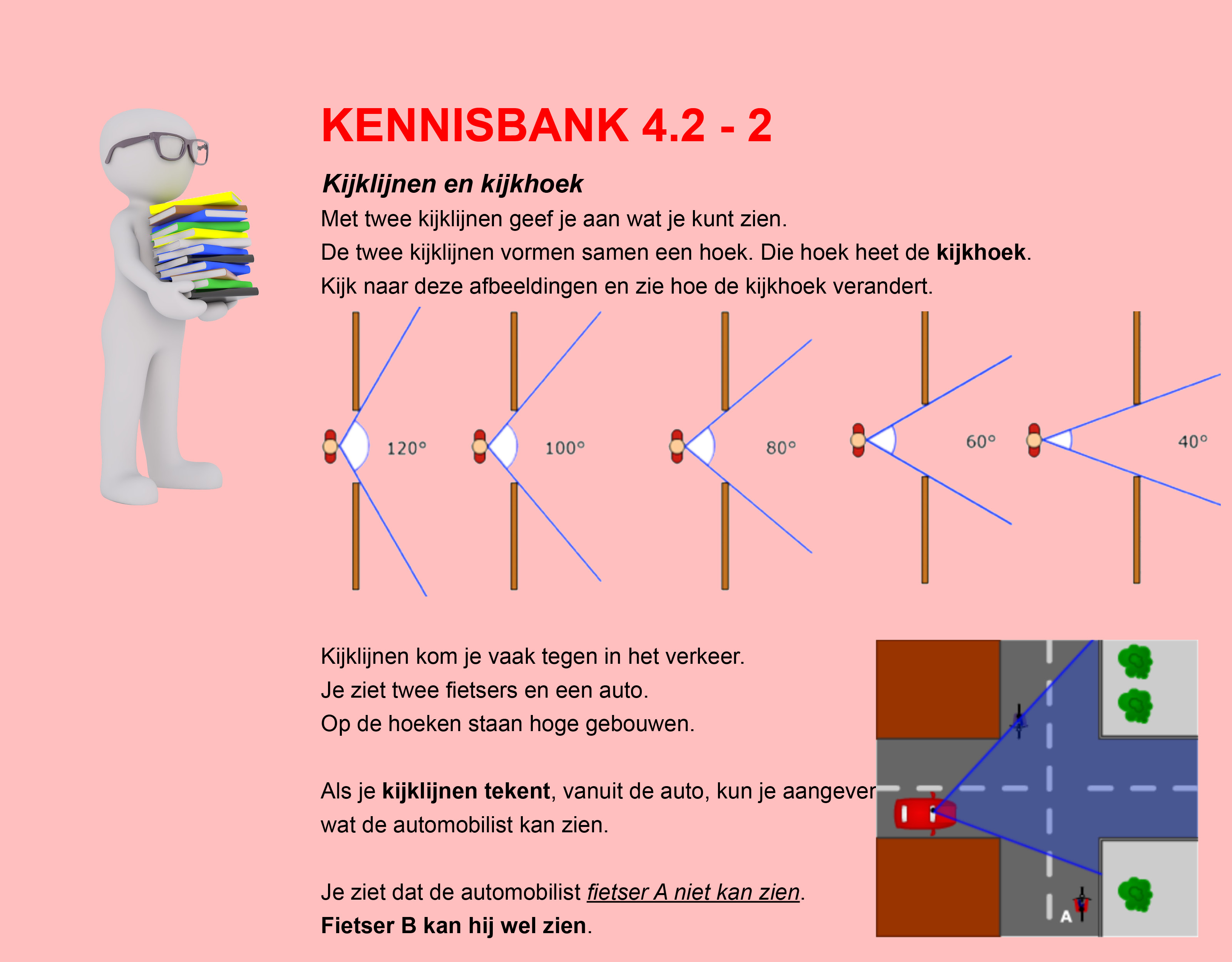
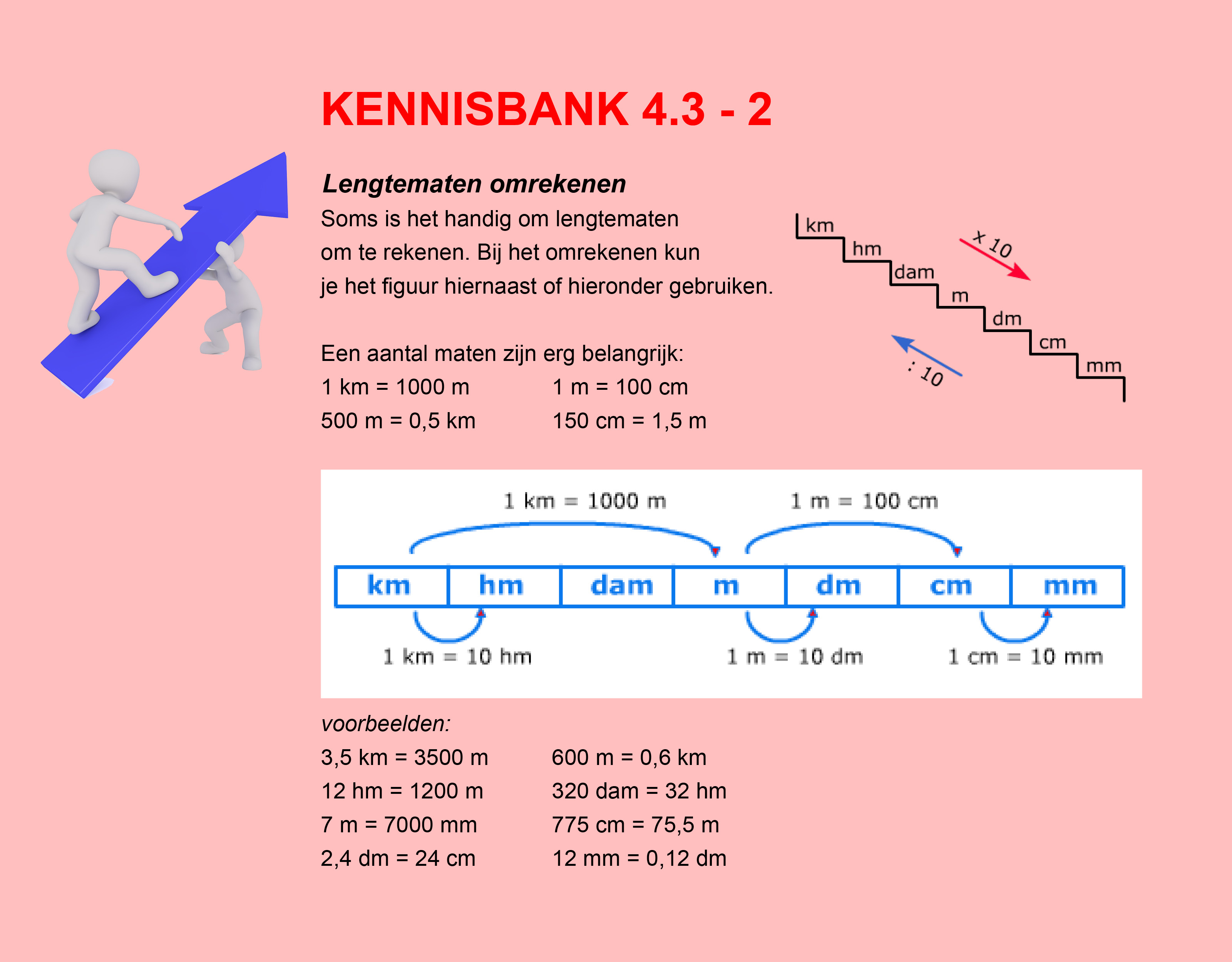
 In de thema´s/opdrachten van de Stercollecties wiskunde wordt regelmatig verwezen naar de Kennisbank wiskunde. In de Kennisbank vind je de theorie die je nodig hebt voor het beantwoorden van de vragen en het maken van de opdrachten.
In de thema´s/opdrachten van de Stercollecties wiskunde wordt regelmatig verwezen naar de Kennisbank wiskunde. In de Kennisbank vind je de theorie die je nodig hebt voor het beantwoorden van de vragen en het maken van de opdrachten.



 Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:


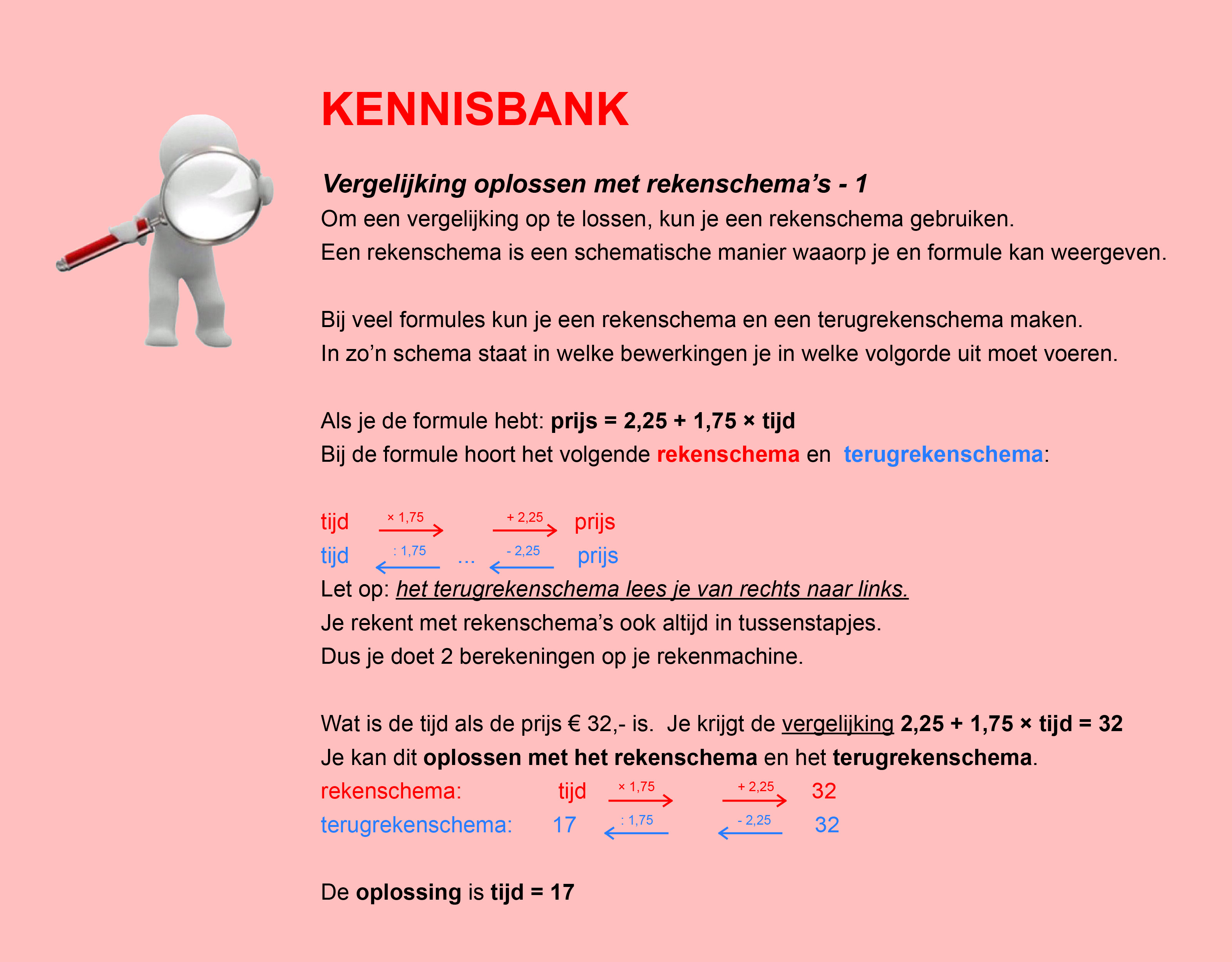
 Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
 Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
 Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven: Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven: Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer uit de Kennisbank wiskunde het onderdeel:
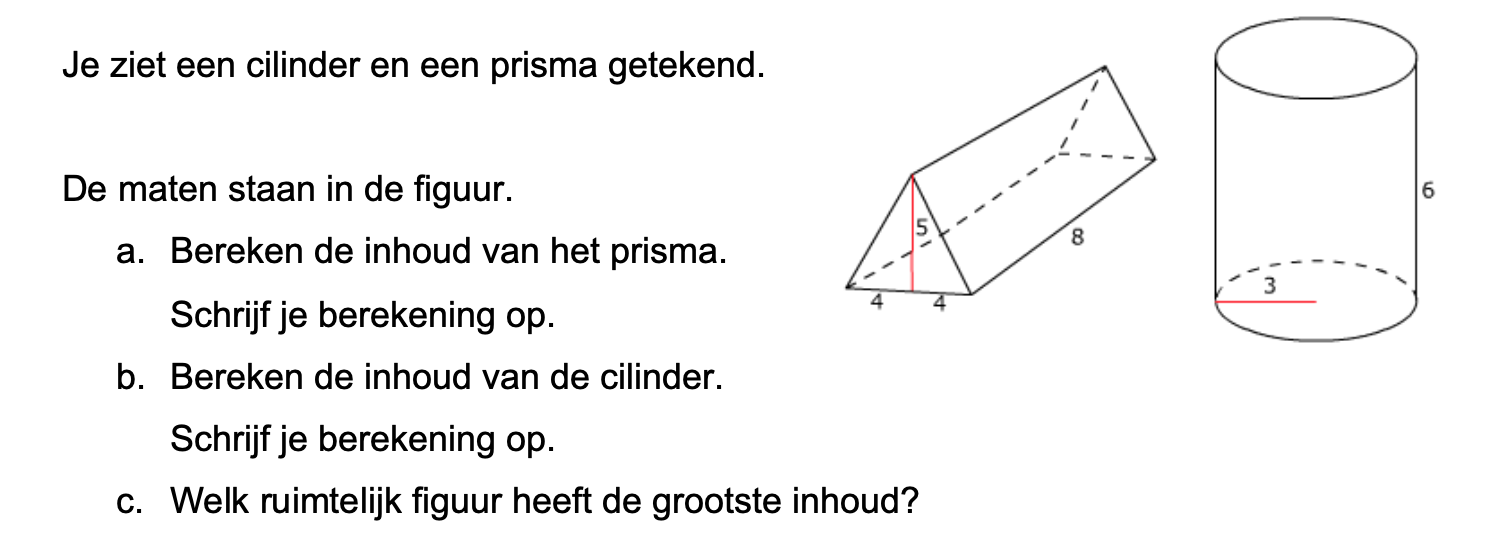
Bestudeer uit de Kennisbank wiskunde het onderdeel: Bestudeer eerst uit de Kennisbank wiskunde het onderdeel: INHOUD
Bestudeer eerst uit de Kennisbank wiskunde het onderdeel: INHOUD












 Maak de volgende opgaven als extra oefening voor de D-toets.
Maak de volgende opgaven als extra oefening voor de D-toets.
 Nog enkele opgaven om te oefenen voor het proefwerk.
Nog enkele opgaven om te oefenen voor het proefwerk.