Bij een groenteboer vraagt iemand hoe veel een zak aardappelen weegt, het is dan natuurlijk niet handig om te antwoorden met zwaar of licht. Als iemand op station vraagt hoe laat het is antwoord je ook niet met vroeg of laat.
Om duidelijk antwoord te geven op dit soort vragen moet gemeten worden. Meten is vergelijken met een afgesproken maat. Neem als afgesproken maat bijvoorbeeld een meter of kilogram.
Wat je meet is een grootheid. Er zijn verschillende grootheden, bijvoorbeeld:
Temperatuur is een maat voor hoe koud of warm iets is. Wanneer de temperatuur stijgt zet een vloeistof uit, zo kan de temperatuur gemeten worden met behulp van een vloeistofthermometer.
De vloeistof komt hoger te staan in de stijgbuis als de temperatuur hoger wordt. Op de stijgbuis staan streepjes om de temperatuur aan te geven, dit noem je een schaalverdeling.
Temperatuur kan met verschillende eenheden aangegeven worden:
In Nederland gebruiken we de graad Celsius (°C) als we het hebben over temperatuur.
De Zweed Anders Celsius (1701-1744) maakte een schaalverdeling van 0 tot 100. Met als nulpunt de temperatuur van smeltend ijs en voor de waarde 100 koos hij de temperatuur van kokende water. Hij verdeelde het gebied tussen 0 en 100 in stukjes en elk van deze 100 stukjes heet 1 graad celsius.
Fahrenheit
Ook wordt de graad Fahrenheit gebuikt als het gaat om temperatuur. Fahrenheit wordt bijvoorbeeld in Amerika gebuikt, in plaats van de graad Celsius.
De Fahrenheit is vernoemd naar de Amsterdammer Gabriël Fahrenheit (1686-1736) die de eerste betrouwbare vloeistofthermometer maakte met behulp van de vloeistof kwik.
Kwik reageert namelijk beter op temperatuurveranderingen dan bijvoorbeeld alcohol (wat eerst werd gebruikt in thermometers).
Kelvin
De grondeenheid van temperatuur is echter Kelvin (K). De Kelvin komt van de Engelse natuurwetenschapper lord Kelvin (1824-1907). De temperatuur zegt iets over de bewegingssnelheid van de moleculen. Als het warmer wordt bewegen ze harder en als het kouder wordt bewegen ze minder snel. Lord Kelvin kwam er achter dat bij -273 °C de moleculen stil stonden. Minder langzaam bewegen kan niet dus kan het ook niet kouder worden. Hij noemde dit punt 0 kelvin.
De schaalverdeling van Kelvin begint bij de laagste temperatuur die er bestaat (het absolute nulpunt), 0 K. De temperatuur 0 K is gelijk aan -273 °C. De schaalverdeling van Kelvin is in even grote stukjes verdeelt als de graden Celsius.
Ook tijd kan gemeten worden. Je zal eerst tijd moeten meten om erachter te komen hoe laat het is. Maar hoe wordt dit dan gedaan?
Een al oude manier van meten is de zonnewijzer. Met behulp van de schaduwen veroorzaakt door het licht van de zon kan opgemaakt worden welk punt van de dag het is. De Egyptenaren gebruikte deze methode 3000 jaar geleden al. Wanneer er zonlicht op een stok schijnt en de schaduw lang is, staat de zon laag, en is het dus begin of eind van de dag. Wanneer de schaduw het kortst is, staat de zon op zij hoogste punt, en is het mid-dag oftewel 12 uur.
Het uur bleef lang de meest nauwkeurige eenheid van tijd. In de Middeleeuwen rond 1100 werd pas het uur verdeeld in 60 gelijke stukjes, 60 minuten. Toen men nog nauwkeuriger kon gaan meten werd de minuut ook opgedeeld in 60 stukjes, 60 seconden.
In de 17e eeuw werd het eerste slingeruurwerk gebouwd door de Nederlandse natuurwetenschapper Christiaan Huygens. Een slingeruurwerk is een voorbeeld van een mechanische klok, deze worden tegenwoordig nog gemaakt. Ook wordt tijd nu gemeten met elektrische klokken en kwartsklokken. Voor een precieze meting van tijd wordt gebruik gemaakt van atoomklokken, deze heeft slechts een afwijking van 1 seconde in 1,7 miljoen jaar. Heel erg precies dus.
Andere oude methodes van tijd meten zijn:
De sterrenklok, waterklok, zandloper, vuurklok en de slingerklok van Huygens.
Ook wordt er gebruik gemaakt van de omwenteling van de aarde om zijn eigen as om dagen te meten. Een omwenteling van de aarde duurt 24 uur. Maar nu we nauwkeuriger de tijd kunnen meten blijkt dat een dag niet precies 24 uur duurt. Hiervoor worden regelmatig correcties gemaakt, neem bijvoorbeeld de extra dag (29 februari) in een schrikkeljaar.
Lengte
Vroeger meten de mens afstanden aan de hand van hun ledematen.
zo was er de Duim
De lengtemaat duim was zo lang als de breedte van het bovenste kootje van een duim van een volwassen man. Ook de duim was per streek verschillend.
Amsterdamse duim: 2,573 cm
Franse duim: 2,7 cm
Gelderse of Nijmeegse duim: 2,7 cm
Hondsbosse en Rijpse duim: 2,4 cm
Rijnlandse duim: 2,6 cm
Een andere bekende lengtemaat is de Voet
Ook het lichaamsdeel voet werd gebruikt om te meten. De verschillende streken hadden hun eigen definitie van een voet. Ook de verdeling duimen ten opzichte van voeten was niet overal gelijk. Soms was de voet verdeeld in 10, 11, 12 of 13 duimen. In Nederland werd de Rijnlandse voet het meest gebruikt.
De Rijnlandse voet: 0,3140 m (een Rijnlandse voet is 12 Rijnlandse duimen)
Amsterdamse voet: 0,2831 m (een Amsterdamse voet is 11 Amsterdamse duimen).
Rotterdamse voet: 0,2823 m (een Rotterdamse is 11 Rotterdamse duimen)
Blooise voet: 0,301 m
('s Hertogen)bossche voet: 0,287 m
Honsbossche en Rijpse voet: 0,285 m
Schouwse voet: 0,311 m
Dat was niet eerlijk en handdig. Daarom vond men tijdens de Franse Revolutie van 1789 dat het tijd werd om een lengte-eenheid in te voeren die voor iedereen gelijk is. Zo’n eenheid noemen we een standaardeenheid. In dit geval kreeg de Koninklijke Academie van Wetenschappen uit Parijs de opdracht zo’n eenheid voor lengte te verzinnen. Hier hebben we dan ook de eenheid meter aan te danken.
Massa wordt gebruikt om een hoeveelheid stof/materie aan te geven. Neem bijvoorbeeld een zak aardappelen van 2 kg. Massa is dus de hoeveelheid materiaal.
Eerder hebben we het gehad over de standaardmeter, vergelijkbaar is er ook de standaardkilogram. De originele standaardkilogram wordt bewaard in Parijs maar alle landen hebben hier een kopie van. Zo is de massa van de zak aardappelen van 2 kg hier in Nederland hetzelfde als in bijvoorbeeld Spanje.
In de natuurwetenschappen mag je de term gewicht echter niet gebruiken voor de massa, deze twee worden vaak met elkaar verward. De massa is dus niet het gewicht van een voorwerp. Gewicht is namelijk afhankelijk van zwaartekracht en massa niet. Om dit duidelijk te maken volgt nu een voorbeeld:
Wanneer je op een weegschaal gaat staan op de aarde zal je zwaarder wegen dan op een weegschaal op de maan. Dit komt door de grotere zwaartekracht van de aarde, in andere woorden ‘de aarde trekt je harder richting het middelpunt van de aarde’. Je gewicht op aarde is dus hoger dan je gewicht op de maan, terwijl je massa hetzelfde blijft.
Bij elke grootheid hoort een eenheid. Een eenheid is een afgesproken maat. Maar welke afspraken zijn er eigenlijk gemaakt? En welke meetinstrumenten gebruiken we hierbij?
De tijd in seconde
De temperatuur in graad Celsius of Kelvin?De lengte in meter
Wat zijn eenheden?
Een stapje verder dan de grootheid komt de eenheid. Je kunt een meter bijvoorbeeld ook 100 centimeter noemen. De maat waarin je een grootheid omschrijft is dan ook de eenheid.
Een eenheid is een afgesproken maat.
Vroeger werden eenheden als el, voet en duim gebruikt. Deze eenheden zijn afgeleid van het menselijk lichaam, wat makkelijk is want je draagt ze altijd bij je. Het tegendeel is dat niet ieders voet of duim even groot is.
Om duidelijkheid te geven over eenheden zijn er internationale afspraken gemaakt. Er is een systeem ontwikkeld waarin iedereen dezelfde eenheden gebruikt. Dit stelsel van eenheden heet het Système International, het SI.
Er zijn zeven afgesproken internationale eenheden. Met deze zeven eenheden zijn alle andere eenheden af te leiden. De zeven eenheden worden ook wel grondeenheden genoemd.
De volgende grondeenheden moet je kennen:
Grootheid
SI-eenheid
Afkorting van eenheid
Lengte
Meter
m
Tijd
Seconde
s
Temperatuur
Kelvin
K
Massa
Kilogram
kg
De overige SI-eenheden worden afgeleide eenheden genoemd.
Er zijn ook verschillende eenheden die niet in het SI staan, maar wel gebruikt worden. Een aantal hiervan zijn:
De grootte van een getal wordt aangegeven met een voorvoegsel. Zo kan een eenheid worden aangepast aan de grootte van het getal. Dit is efficiënter dan het schrijven van meerdere nullen. Neem bijvoorbeeld 0,001 s (seconde), dit is ook gelijk aan 1 ms (milliseconde).
Een aantal bekende voorvoegsels zijn hieronder weergeven:
Voorvoegsel
Afkorting
Betekenis
milli
m
0,001 (eenduizendste)
centi
c
0,01 (eenhonderdste)
deci
d
0,1 (eentiende)
kilo
k
1000 (duizend)
Voorbeelden hiervan zijn:
1 dl is 1 deciliter en betekend eentiende liter
(1 dl = 0,1 l)
1 km is 1 kilometer en betekend duizend meter
(1 km = 1000 m)
Meetinstrumenten
Om een grootheid te kunnen meten heb je een meetinstrument nodig. Per grootheid verschilt wat je meet en dus verschilt ook het meetinstrument dat hier bij nodig is. Hieronder een aantal voorbeelden:
Voor het meten lengte gebruik je een liniaal.
Voor het meten van tijd gebruik je een klok.
Voor het meten van temperatuur gebruik je een thermometer.
Daarnaast zijn er twee verschillende soorten meetinstrumenten, namelijk analoge en digitale.
Een analoog apparaat heeft een wijzer die tussen twee streepjes kan staan. Bij het aflezen van een analoog instrument maak je een schatting.
Een digitale meter heeft een schermpje met cijfers, dit is dan ook gemakkelijker en preciezer af te lezen.
Een horloge wordt gebruikt om de tijd af te lezen.
Een micrometer wordt gebruikt om kleine afstanden te meten.
In de afbeelding wordt tijd niet weergeven. Met tijd reken je op de volgende wijze:
Tijd
1 jaar = 12 maanden
1 jaar = 365 dagen
1 jaar = 52 weken
1 maand = 30 dagen
1 dag = 24 uur
1 uur = 60 minuten
1 minuut = 60 seconden
Opgaven
Maak de volgende opgaven in je schrift.
(Neem alles over en noteer daarachter het antwoord met eenheid)
Lengte
100 cm = ……………………………………………………… m
20 dam = ……………………………………………………. m
5,5 dm = …………………………………………………….. cm
4,25 m = …………………………………………………….. cm
2,75 hm = ……………………………………………………. dam
50 cm = …………………………………………………… dm
9,7 m = …………………………………………………… dam
0,75 mm = …………………………………………………… cm
120 dm = …………………………………………………… dam
4,5 hm = …………………………………………………….. km
2 m = …………………………………………………….. dm
35 cm = …………………………………………………….. mm
4 dam = …………………………………………………….. m
8,67 m = …………………………………………………….. cm
965 mm = …………………………………………………….. dm
5,45 dm = …………………………………………………….. dam
2,87 km = …………………………………………………….. dam
3,4 dam = …………………………………………………….. hm
2 dm = …………………………………………………….. hm
2 hm = …………………………………………………….. dm
4,56 km = …………………………………………………… m
9.854 dam = ………….……………………………………… cm
76 cm = …………………………………………………… hm
3,9 m = …………………………………………………… km
5,67 hm = …………………………………………………… dm
5 cm = …………………………………………………… hm
0,075 km = …………………………………………………… dm
7,6 m = …………………………………………………… cm
2 dam = …………………………………………………… km
2 dm = …………………………………………………… hm
Oppervlakte
2 cm2 = ……………………………………………… mm2
5,5 hm2 = ……………………………………………… dam2
5 dm2 = ……………………………………………… m2
9,9 cm2 = ……………………………………………… m2
5,5 km2 = ……………………………………………… dam2
2 mm2 = ……………………………………………… m2
0,078 hm2 = ……………………………………………… dam2
288 dm2 = ……………………………………………… mm2
0,0055 km2 = ……………………………………………… dam2
9,99 m2 = ……………………………………………… hm2
Tijd (rond af op 2 getallen achter de komma)
1 h = ……………………………………………… min
120 min = ……………………………………………… h
3600 s = ……………………………………………… h
25 min = ……………………………………………… u
31 h = ……………………………………………… s
2 dagen = ……………………………………………… min
1 week = ……………………………………………… h
3 maanden = ……………………………………………… jaar
0,25 week = ……………………………………………… min
1 s = …………………… dag (schrijf op als breuk)
4 Grootheden en eenheden
Grootheden afleiden
Vier grootheden en de bijbehorende SI-eenheden zijn nu uitgelegd namelijk: tijd (seconde), lengte (meter), temperatuur (kelvin) en massa (kilogram).
Deze grootheden kunnen ook nog leiden naar andere grootheden. Zo zijn de grootheden oppervlakte en volume afgeleid van de grondeenheid meter.
Oppervlakte
De eenheid van oppervlakte is afgeleid van de eenheid van lengte, de meter. Oppervlakte is eigenlijk lengte in twee richtingen: in de lengte en in de breedte.
Zo wordt de eenheid van oppervlakte: m x m = m2. Dit spreek je uit als vierkante meter.
Je kunt ook andere eenheden van oppervlakte hebben, neem bijvoorbeeld vierkante centimeter (cm2) en vierkante kilometer (km2).
Volume
Wanneer we het hebben over lengte in drie richtingen, spreken we over volume. De eenheid van volume is ook afgeleid van de eenheid van lengte. Het is eigenlijk lengte in de breedte, lengte en hoogte richting.
Dit maakt de eenheid van volume: m x m x m = m3. Dit spreek je uit als kubieke meter.
Andere eenheden van volume zijn bijvoorbeeld kubieke decimeter (dm3) en kubieke centimeter (cm3).
Daarnaast zijn bijvoorbeeld de liter (l) en milliliter (ml) eenheden van volume. Zo past er een liter water in een kubieke decimeter (dm3).
Van onregelmatige voorwerpen, zoals een steen, kun je het volume niet berekenen uit de afmetingen. Het volume moet anders bepaald worden. Hiervoor wordt de onderdompelingsmethode gebruikt.
Wanneer een maatcilinder voor een deel gevuld is met water, zal de hoogte van het water toenemen wanneer er bijvoorbeeld een steentje in wordt gegooid. De hoeveelheid die het water stijgt in de maatcilinder komt overeen met het volume van het steentje.
Stel het waterniveau in de maatcilinder ligt op 50,0 ml en je gooit er een steentje in. Nu ligt de waterhoogte op 59,0 ml. Dan is het volume van de steen het verschil tussen de twee volumes:
59,0 – 50,0 = 90 ml.
Rekenen met eenheden 2
Overzicht rekenen met eenheden:
Opgaven
Maak de volgende opgaven in je schrift.
(Neem alles over en noteer daarachter het antwoord met eenheid)
Volume
1 m3 = ……………………………………… dm3
400 cm3 = ……………………………………… dm3
5,5 km3 = ……………………………………… hm3
654,88 dam3 = ……………………………………… m3
0,5 mm3 = ……………………………………… cm3
6,66 dam3 = ……………………………………… hm3
8 dam3 = ……………………………………… km3
2 cm3 = ……………………………………… dam3
50.000 cm3 = ……………………………………… m3
0,0000086 dam3 = ……………………………………… dm3
6 L = ……………………………………… dL
9,5 mL = ……………………………………… cL
0,5 hL = ……………………………………… L
87 daL = ……………………………………… dL
9,99 L = ……………………………………… daL
55 daL = ……………………………………… L
4 dL = ……………………………………… daL
90,5 cL = ……………………………………… daL
0,09 kL = ……………………………………… L
0,00075 kL = ……………………………………… mL
6 dm3 = ……………………………………… L
9,5 cm3 = ……………………………………… mL
0,9 L = ……………………………………… dm3
5,5 daL = ……………….… L = ………………… dm3
0,5 m3 = ……………….… dm3 = ……………….… L
9 cL = ……………………………………… cm3
0,77 dL = ……………………………………… mm3
20.000 cL = ……………………………………… dam3
0,02 hL = ……………………………………… cm3
0,25 daL = ……………………………………… dam3
Massa
2 g = ……………………………………… dg
9 kg = ……………………………………… g
2.500 mg = ……………………………………… g
6,6 dag = ……………………………………… hg
9,99 cg = ……………………………………… dg
20 hg = ……………………………………… g
7,3 cg = ……………………………………… g
1.234 kg = ……………………………………… dag
9 g = ……………………………………… hg
20.000 cg = ……………………………………… hg
5 Meetresultaten en grafieken
Ordenen van meetresultaten
Bij het uitvoeren van experimenten worden veel meetresultaten verzameld. Deze resultaten kunnen op verschillende manieren verwerkt worden bijvoorbeeld in een tabel of diagram. Op deze manier worden de meetresultaten overzichtelijk weergeven.
Tabel
In een tabel kunnen twee waardes tegen elkaar uitgezet worden. In de afbeelding hierondr is een voorbeeld van een tabel te vinden.
Komkommers komen in verschillende lengtes voor. Voor elke lengte is een massa bepaald. In de tabel is te zien wat de massa is van de komkommer per lengte eenheid.
Lengte van de komkommer (cm)
Massa van de komkommer (g)
20
160
25
200
30
240
35
280
Diagram
In een tabel staan de twee gemeten getallen naast of onder elkaar. Dit is niet altijd overzichtelijk genoeg dus maken we er een plaatje van, dit heet een diagram. Een diagram heeft twee assen namelijk een horizontale en een verticale as. Hieronder een voorbeeld van een diagram.
In de diagram is te zien dat de assen elkaar snijden in de oorsprong. In de wiskunde wordt de horizontale as de x-as genoemd en de verticale as wordt de y-as genoemd. De assen van eendiagram met de bijbehorende meetgegevens heten grootheden.
In het voorbeeld van de komkommer wordt de lengte de x-as en de massa de y-as.
Grafieken tekenen
De grafiek die je in het assenstelsel tekent moet zo veel mogelijk lijken op de meetpunten die je hebt. Wanneer een rechte lijn niet past teken je een vloeiende kromme.
Verbind de punten dus niet met rechte lijntjes.
In een diagram kun je snel het verband tussen twee grootheden zien.
In de wiskunde gaat er door de punten in een diagram vaak een rechte lijn of vloeiende kromme. Bij meetresultaten is dat een ander geval. Door bijvoorbeeld niet goed af te lezen ontstaan er altijd kleine foutjes. Zo zal de grafiek niet helemaal perfect door alle gevonden punten gaan.
Soms gaat het maken van zulke foutjes onopgemerkt.
Grote meetfouten zullen opvallen in een diagram, omdat de gevonden meetwaarde ver buiten de grafiek ligt. Hieronder een voorbeeld, waarbij meetpunt 4 niet klopt.
In een grafiek kunnen de tussenliggende waarden van de meetpunten worden afgelezen. Dit kan in een tabel niet. Dit is dus een voordeel van een diagram.
Interpoleren
In een diagram is het verband tussen twee grootheden te zien. Zo kun je met een diagram ook voorspellingen doen over de niet gemeten waarden.
Het meetgebied is het gebied tussen de kleinste en grootste gemeten waarde in een diagram. Tussen de twee waarden kunnen de niet gemeten waarden op de lijn afgelezen worden. Voorspellingen kunnen dus worden gedaan binnen een meetgebied. Deze methode heet interpoleren.
Interpoleren is het aflezen van een tussenliggende waarde binnen het meetgebied.
Extrapoleren
Je kunt ook voorspellingen doen van waarden die buiten het meetgebied liggen. Deze methode noem je extrapoleren.
Bij extrapoleeren moet je de getekende lijn zo goed mogelijk doortrekken buiten het meetgebied. Dit wordt meestal gedaan met behulp van een stippellijn.
Extrapoleren is het aflezen van niet-gemeten waarden buiten het meetgebied.
Verklaren en verdiepen
Verklaren
Natuurwetenschappers hebben talloze verschijnselen onderzocht. Bij het vak mens en techniek maak je kennis met de ontdekkingen die ze hebben opgedaan en met de theorie die erbij hoort. De mensen die werken met kennis van de ontdekkingen wordt de wereld van bèta en techniek genoemd.
De wereld van bèta en techniek is meer
dan witte jassen en schroevendraaiers.
Om de hoeveelheid mogelijkheden te laten zien,
verdelen we bèta en techniek in zeven werelden.
Avonturiers, creatieve geesten, ontdekkers,
vernieuwende denkers en wereldverbeteraars,
zo is voor iedereen iets te vinden
Opdracht: powerpoint maken
Toepassingen van natuurwetenschappen of de wereld van bèta en techniek kom je overal tegen. Bij deze opdracht ga je een PowerPoint maken met informatie over zo`n toepassing.
Zoek een mooie foto van zo`n toepassing.
Zet de foto op een PowerPoint- dia en zorg ervoor dat hij de hel dia vult.
Zoek informatie over de toepassing en over de natuurwetenschappelijke kennis die je erin verwerkt. Dat kan in de vorm van plaatjes en of tekst
Rangschik de informatie die je hebt gevonden in de Powerpoint. Je docent zal je vertellen hoe je het eindproduct aan de klas gaat presenteren.
Opdracht: spel Moendoes
Speel het spel Moendoes. Je kunt bij je docent het spel ophalen. De spelregels zitten bij het spel gevoegd.
Vraag aan je docent hoe lang je hebt op het spel te spelen.
Lees de spelregels.
Verdeel de taken binnen jullie team
Zorg dat alle bronkaarten goed zichtbaar zijn voor de rest van het team (klas).
Leg alle spelkaarten op de juist manier klaar.
Start het spel en houdt de tijd in de gaten.
Verdiepen
Experimenten uitvoeren
Bij een experiment ga je op zoek naar het antwoord op een onderzoeksvraag door het uitvoeren van de werkwijze. Tijdens het uitvoeren doe je waarnemingen. Aan de hand van die waarnemingen kom je tot een conclusie.
Als je de theorie niet goed begrijpt, kun je meestal geen goed uitvoeren . Gebruik daarom je boek, je eigen aantekeningen bij de voorbereiding. Een stappenplanwerk of werkwijze helpt je om een experiment uit te voeren. Alles wat je doet, noteer je in je schrift.
Als je met iemand samenwerkt kun je goed elkaars ideeën kritisch bekijken en de taken verdelen.
a. De onderzoeksvraag
De onderzoeksvraag geeft de richting aan het onderzoek. Bij het opstellen van de onderzoeksvraag zijn de volgende punten van belang:
– Is het een vraag? (dus eindigt het met een vraagteken?)
– Past de vraag in de opdracht?
– Is het duidelijk wat voor soort antwoorden gezocht worden?
– Is de vraag met een onderzoek te beantwoorden?
Het bedenken van een goede onderzoeksvraag is moeilijker dan je denkt..
Je zult dus een zo duidelijk mogelijke en concrete vraag moet bedenken. Vaak is het doel van het experiment al gegeven. Je kunt dan het doel in een vraag omzetten. Een goede onderzoeksvraag is geen opzoekvraag. Een opzoekvraag kan je gewoon vragen of opzoeken in een boek of op het internet. Een onderzoeksvraag kan je alleen echt weten als je een experiment uitvoert.
b. het opstellen van een hypothese
Voordat een experiment wordt uitgevoerd heb jij vast al een vermoeden wat het antwoord gaat zijn op de onderzoeksvraag. Omschrijf de resultaten die jij verwacht bij het practicum en leg uit waarom jij dat denkt. Het helpt je een goed experiment uit te voeren.
Het is absoluut geen probleem als de hypothese na afloop van je onderzoek niet juist blijkt te zijn. Je moet de hypothese niet achteraf verbeteren!!
c. De werkwijze
Maak alvast de tabellen voor het noteren van de meetresultaten. Daarmee verklein je de kans dat je bij het uitvoeren van het experiment vergeet iets te meten
Begin met het bij elkaar zoeken van alle benodigdheden en het bouwen van de meetopstelling als dat nodig is. Probeer de meetopstelling uit.
Let bij het uitvoeren van de proef op de volgende punten:
Lees meetinstrumenten nauwkeurig af.!
Noteer de meetgegevens in overzichtelijke tabellen.
d. Controle en Resultaten
Je moet nu nagaan of de verzamelde informatie volledig is, of je daarmee de onderzoeksvraag kunt beantwoorden. Daarvoor moet je de meetresultaten verwerken.
Maak (indien mogelijk) van de metingen een diagram
Soms moet je daarvoor eerst nog wat berekeningen uitvoeren. Bijvoorbeeld de gemiddelde berekenen als je meerdere metingen gedaan hebt.
Bekijk je diagram, trek een conclusie over het onderzoek en geef antwoord op de onderzoeksvraag.
Vergelijk de conclusie met de hypothese. Geef aan of de verwachting wel of niet is uitgekomen.
Als de uitkomst anders is dan je in de hypothese voorspeld had, moet je een aantal zaken controleren.
- Is het onderzoek wel op de juiste manier voorbereid en uitgevoerd
- Zijn de meetresultaten wel op de juiste manier verwerkt?
Als dat inderdaad het geval is, heb je dus (voor jezelf) iets nieuws ontdekt.
Als dat niet het geval is of als de uitkomst heel anders is dan je op basis van de theorie zou verwachten, hoef je niet te wanhopen. Een mislukt experiment kan even waardevol zijn als een geslaagd experiment. Je kunt ook daarvan leren, maar geef niet te snel op en probeer na een mislukking de opzet van het experiment te verbeteren en het experiment te herhalen (als daarvoor tijd is).
e. Evaluatie
Kunnen er aan het onderzoek dingen verbeterd worden waardoor de meetresultaten nauwkeuriger en/of de conclusie betrouwbaarder zou zijn?
Ben je tijdens het onderzoek problemen tegen gekomen? Hoe heb je die problemen opgelost?.
Het beantwoorden van dit soort vragen kan helpen bij het doen van een volgend experiment. Soms kom je daarbij dezelfde of vergelijkbare problemen tegen. misschien is de oplossing die je nu voor je problemen gevonden hebt dan ook bruikbaar.
Meetverslag
Verdieping
f. Meetverslag
Van een experimenteel onderzoek maak je een verslag Je geeft daarin een beschrijving van het onderzoek.
Zo ziet een meetverslag eruit;
Jouw naam en de naam van je partner. De datum waarop je het experiment hebt uitgevoerd.
De titel van het experiment.
Een korte hypothese.
De materialen die je gebruikt bij het uitvoeren van het experiment, de werkwijze en een tekening van de opstelling of een foto van de opstelling
Je waarnemingen en resultaten.
De conclusie (Dat is altijd het antwoord op je onderzoeksvraag.)
De evaluatie
Practica
Puntmuts_Practicum
Inleiding
Hier ga je leren om een weegschaal te maken van een puntmuts , gek he!
Thermometer Ijken
Inleiding
Waarom heeft de mens eigenlijk meetinstrumenten gemaakt? Wij kunnen toch best goed inschatten hoe groot voorwerpen zijn. In dit practicum ga je onderzoeken hoe goed jij het doet als meetinstrument. Je gaat je eigen thermometer jijken.
Kubus maken
De inhoud van de kubus kan je uitrekenen door de zijde van de kubus op te meten. Als je de inhoud in cm3 weet kan je deze omrekenen in mL. Namelijk 1 cm3 is gelijk aan 1 mL.
Maar je kunt ook een kubus maken en dan te vullen met water. Zo weet je ook hoeveel ml in deze kubus past.
Je gaat een kubus maken van 10 cm bij 10 cm bij 10 cm en vult deze met water. Hoeveel water past erin deze kubus?
Hoe groot moet je kubus minimaal zijn als je er 0,5 L water in moet?
Hoeveel liter past erin een kubus van 5 cm x 6 cm x 8 cm?
Het arrangement Meet_verkenner_Ondersteunings_Materiaal is gemaakt met
Wikiwijs van
Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt,
maakt en deelt.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
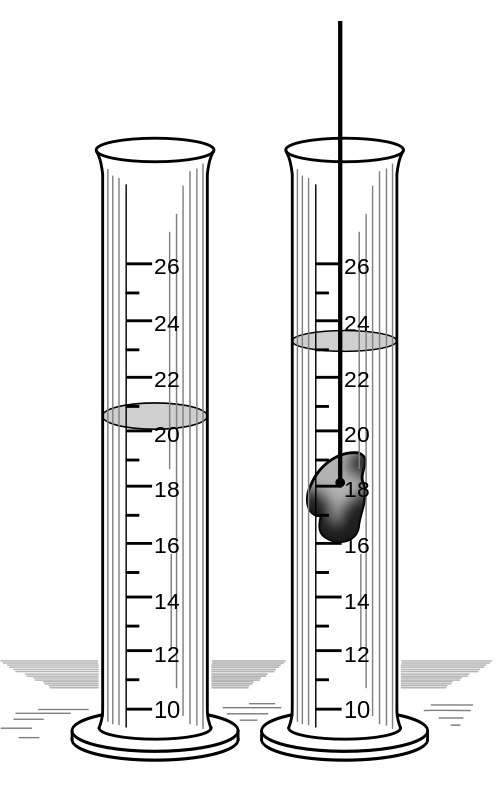
Leerlingen leren waarnemen, wat grootheden en eenheden zijn en eenheden omrekenen. Daarnaast maken ze kennis met experimenten binnen het vakgebied.
Doelgroep: brugklas (vmbo TL/havo/vwo)
Leerlingen leren waarnemen, wat grootheden en eenheden zijn en eenheden omrekenen. Daarnaast maken ze kennis met experimenten binnen het vakgebied.
Doelgroep: brugklas (vmbo TL/havo/vwo)
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
Grootheden
Temperatuur
Lengte, temperatuur, massa en tijd
Eenheden
Lees de meetinstrumenten af
grafieken
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Warmte. Bekijk de uitleg over de verschillende eenheden in temperatuur. Klik op de link.
antwoorden
Een horloge wordt gebruikt om de tijd af te lezen.
Een micrometer wordt gebruikt om kleine afstanden te meten.
In een diagram kun je snel het verband tussen twee grootheden zien.
