Het arrangement Kennisbank Wiskunde vmbo-b34 is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 07-10-2025 19:53:49
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding-GelijkDelen 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding en publicatie onder dezelfde licentie vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding-GelijkDelen 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Toelichting
- De Kennisbanken bevatten de theorie bij de opdrachten.
- Leerniveau
- VMBO kaderberoepsgerichte leerweg, 1; VMBO kaderberoepsgerichte leerweg, 2; VMBO basisberoepsgerichte leerweg, 1; VMBO basisberoepsgerichte leerweg, 2;
- Leerinhoud en doelen
- Rekenen/wiskunde;
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
- Trefwoorden
- kennisbank, leerlijn, rearrangeerbare
Gebruikte Wikiwijs Arrangementen
VO-content - Kennisbanken. (2019).
Afronden, schatten, rekenregels - geheel
https://maken.wikiwijs.nl/107407/Afronden__schatten__rekenregels___geheel
VO-content - Kennisbanken. (2019).
Centrummaten en klassen - geheel
https://maken.wikiwijs.nl/107433/Centrummaten_en_klassen___geheel
VO-content - Kennisbanken. (2017).
Diagrammen - geheel
VO-content - Kennisbanken. (2017).
Driehoeken - geheel
VO-content - Kennisbanken. (2019).
Gemiddelde en gewogen gemiddelde
https://maken.wikiwijs.nl/145662/Gemiddelde_en_gewogen_gemiddelde
VO-content - Kennisbanken. (2017).
Lineair verband - geheel
VO-content - Kennisbanken. (2019).
Nog meer procenten - geheel
https://maken.wikiwijs.nl/108040/Nog_meer_procenten___geheel
VO-content - Kennisbanken. (2019).
Nog meer verbanden 1
VO-content - Kennisbanken. (2017).
Omtrek, oppervlakte, inhoud - geheel
https://maken.wikiwijs.nl/107404/Omtrek__oppervlakte__inhoud___geheel
VO-content - Kennisbanken. (2017).
Oplossen met grafieken - geheel
https://maken.wikiwijs.nl/107427/Oplossen_met_grafieken___geheel
VO-content - Kennisbanken. (2019).
Periodiek verband
VO-content - Kennisbanken. (2019).
Procenten - geheel
VO-content - Kennisbanken. (2019).
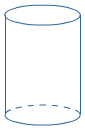
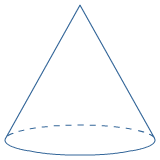
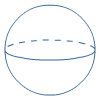
Ruimtemeetkunde - geheel
VO-content - Kennisbanken. (2017).
Tabel, grafiek, formule - geheel
https://maken.wikiwijs.nl/107426/Tabel__grafiek__formule___geheel
VO-content - Kennisbanken. (2019).
Vergelijking en oplossing - geheel
https://maken.wikiwijs.nl/108041/Vergelijking_en_oplossing___geheel
VO-content - Kennisbanken. (2019).
Vergelijkingen oplossen - geheel
https://maken.wikiwijs.nl/107429/Vergelijkingen_oplossen___geheel
VO-content - Kennisbanken. (2017).
Verhoudingen - geheel
VO-content - Kennisbanken. (2017).
Vierhoeken - geheel

 Welkom bij de Kennisbank Wiskunde onderbouw vmbo-kgt12.
Welkom bij de Kennisbank Wiskunde onderbouw vmbo-kgt12. Een verhouding kun je weergeven in een verhoudingstabel.
Een verhouding kun je weergeven in een verhoudingstabel.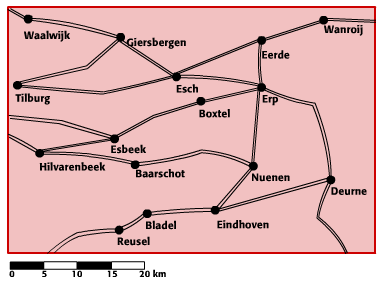



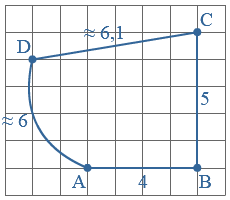 De omtrek van een figuur is de lengte van de buitenrand.
De omtrek van een figuur is de lengte van de buitenrand.
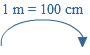
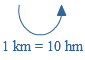
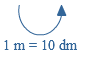
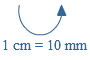
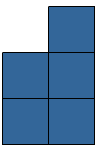
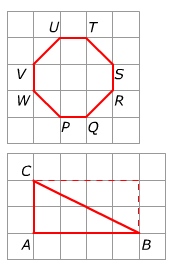 Door het aantal hokjes te tellen, reken je de oppervlakte van een figuur uit.
Door het aantal hokjes te tellen, reken je de oppervlakte van een figuur uit.
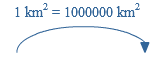
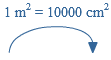
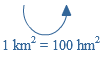
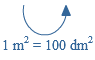
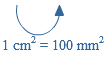
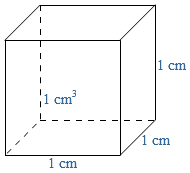
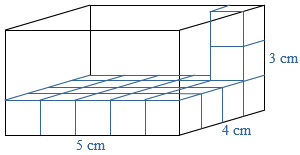
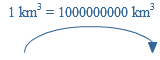
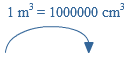
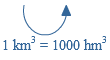
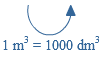
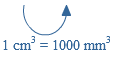
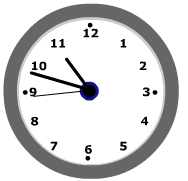 Als eenheid van tijd gebruik je seconde (s), minuut (min) of uur.
Als eenheid van tijd gebruik je seconde (s), minuut (min) of uur. De massa van een voorwerp meet je met een weegschaal.
De massa van een voorwerp meet je met een weegschaal. 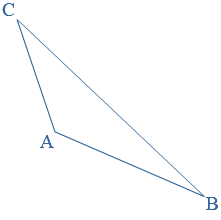 Een driehoek is een vlak figuur met drie hoeken en drie zijden.
Een driehoek is een vlak figuur met drie hoeken en drie zijden. Een gelijkbenige driehoek is een driehoek met:
Een gelijkbenige driehoek is een driehoek met:
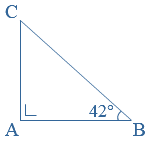
 Voor de oppervlakte van een driehoek geldt:
Voor de oppervlakte van een driehoek geldt: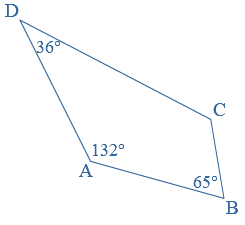 Een vierhoek is een vlak figuur met vier hoeken en vier zijden.
Een vierhoek is een vlak figuur met vier hoeken en vier zijden.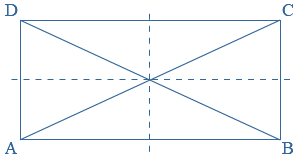
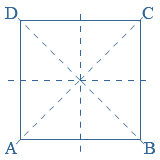
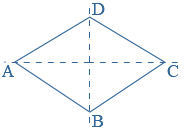
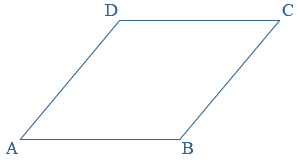
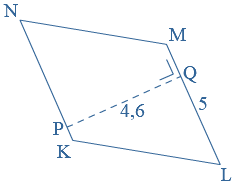
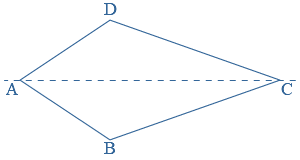 Vierhoek
Vierhoek 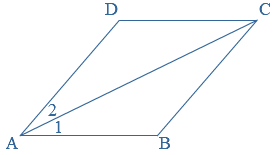 ls er bij een punt meerdere hoeken zijn, gebruik je meestal cijfertjes om de hoeken van elkaar te onderscheiden.
ls er bij een punt meerdere hoeken zijn, gebruik je meestal cijfertjes om de hoeken van elkaar te onderscheiden.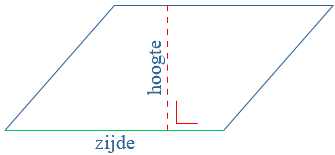
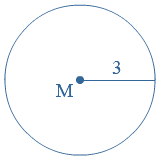 Voor de
Voor de 
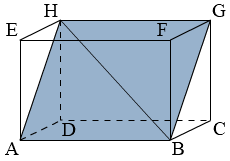
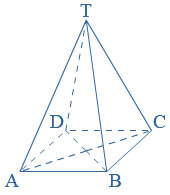
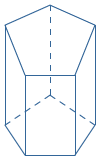
 Voorbeeld
Voorbeeld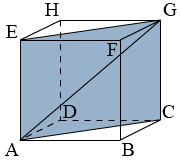


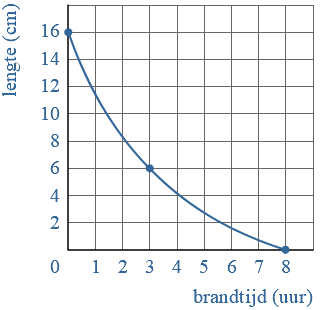
 Een verband tussen twee variabelen kun je soms weergeven in een formule.
Een verband tussen twee variabelen kun je soms weergeven in een formule.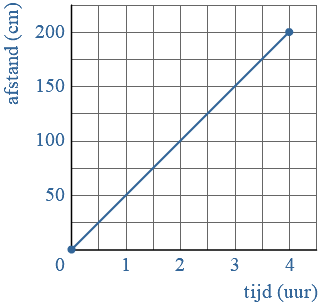
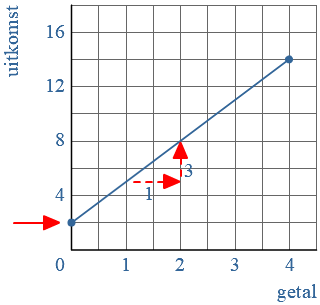 In de grafiek is het verband tussen een
In de grafiek is het verband tussen een 
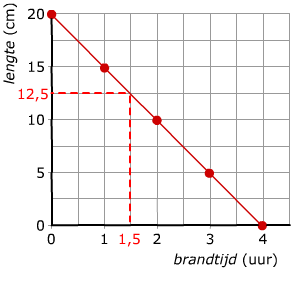
 Bij de volgende formule is een grafiek getekend:
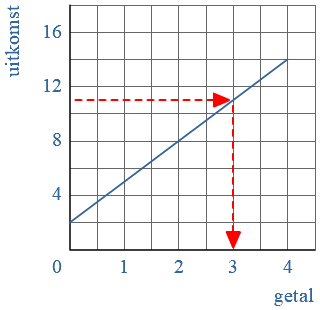
Bij de volgende formule is een grafiek getekend: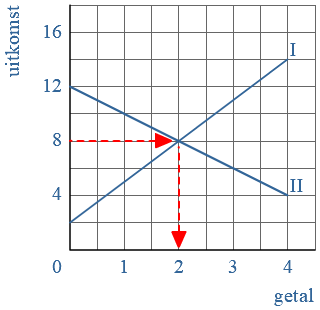 Bij de grafieken hiernaast horen de formules:
Bij de grafieken hiernaast horen de formules: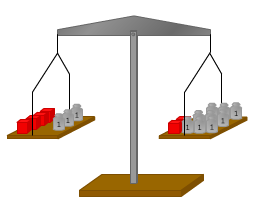 Soms kun een vergelijking oplossen door aan een balans te denken.
Soms kun een vergelijking oplossen door aan een balans te denken.
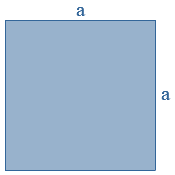 In een formule kan een variabele twee keer voorkomen.
In een formule kan een variabele twee keer voorkomen.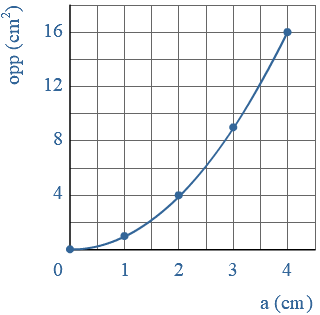
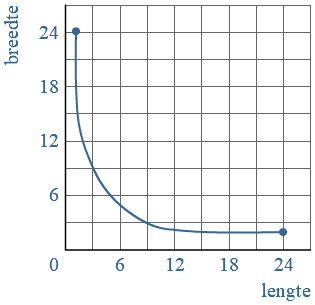
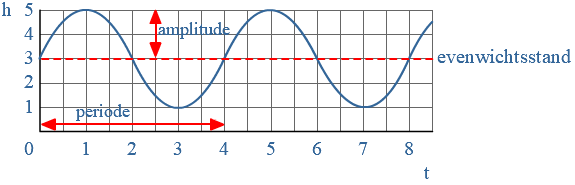

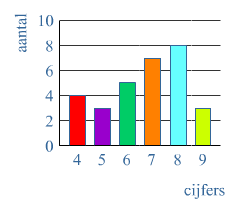
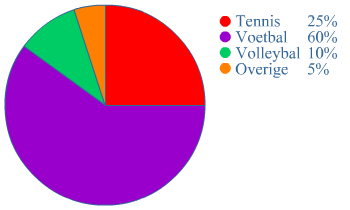 Ook een cirkeldiagram wordt regelmatig gebruikt om gegevens weer te geven. Een cirkeldiagram bestaat uit verschillende sectoren.
Ook een cirkeldiagram wordt regelmatig gebruikt om gegevens weer te geven. Een cirkeldiagram bestaat uit verschillende sectoren.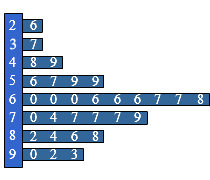 Zijn je gegevens getallen, dan kun je de gegevens soms ook weergeven in een
Zijn je gegevens getallen, dan kun je de gegevens soms ook weergeven in een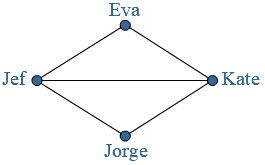 Voorbeeld
Voorbeeld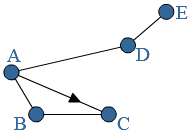
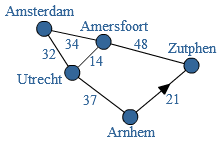
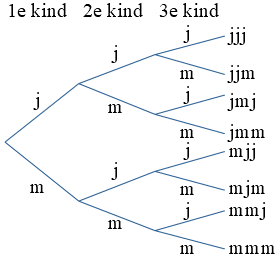
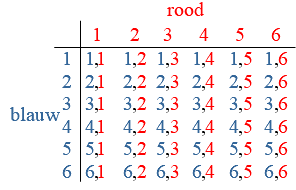
 Soms is een wegendiagram een handig hulpmiddel bij het tellen van de mogelijkheden.
Soms is een wegendiagram een handig hulpmiddel bij het tellen van de mogelijkheden.