Elke ochtend kijk je vast even in de spiegel. Je bent dan met symmetrie bezig zonder dat je het door hebt. Of knipt jou vader of moeder de heg in de tuin ook altijd zo netjes? Ook dan ben je met symmetrie bezig.
In de kunst of in de mode wereld kom je ook heel veel symmetrie tegen, maar ook iemand die de glazen van je bril maakt werkt veel met symmetrie. Symmetrie kom je dus heel veel tegen. Had je dat zelf ook al ontdekt?
Leerdoelen:
Aan het eind van dit hoofdstuk kan ik:
Ik kan in een figuur lijnsymmetrie herkennen.
Ik kan t de symmetrieas aanwijzenen tekenen in een figuur.
Ik kan een figuur spiegelen in een lijn.
Ik herken een draaisymmetrische figuur.
Ik kan de kleinste draaihoek van een draaisymmetrische figuur berekenen.
Ik weet dat overstaande hoeken even groot zijn.
Ik kan hoeken berekenen met overstaande hoeken.
Ik kan een puntsymmetrische figuur tekenen.
Ik kan de eigenschappen van een gelijkbenige driehoek benoemen.
Ik kan de tophoek en basishoeken van een gelijkbenige driehoek aanwijzen.
Ik kan symmetrieassen tekenen in gelijkbenige en gelijkzijdige driehoeken.
Ik kan de eigenschappen van een gelijkzijdige driehoek benoemen.
Werkbladen.
Aan het eind van dit hoofdstuk kan ik:
Na het maken en leren van §1:
Ik kan in een figuur lijnsymmetrie herkennen.
Ik kan t de symmetrieas aanwijzenen tekenen in een figuur.
Ik kan een figuur spiegelen in een lijn.
Na het maken en leren van §2:
Ik herken een draaisymmetrische figuur.
Ik kan de kleinste draaihoek van een draaisymmetrische figuur berekenen.
Ik weet dat overstaande hoeken even groot zijn.
Ik kan hoeken berekenen met overstaande hoeken.
Ik kan een puntsymmetrische figuur tekenen.
Na het maken en leren van §3:
Ik kan uitleggen wanneer twee figuren gelijkvormig zijn.
Ik herken gelijkvormigheid in driehoeken.
Ik kan bij twee gelijkvormige figuren een verhoudingstabel invullen.
Na het maken en leren van §4:
Ik kan de eigenschappen van een gelijkbenige driehoek benoemen.
Ik kan de tophoek en basishoeken van een gelijkbenige driehoek aanwijzen.
Ik kan symmetrieassen tekenen in gelijkbenige en gelijkzijdige driehoeken.
Ik kan de eigenschappen van een gelijkzijdige driehoek benoemen.
1.2 Lijnsymmetrie
Bestudeer eerst uit de Kennisbank wiskunde het onderdeel: Lijnsymmetrie
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staan een paar video's die goed passen bij dit thema.
Bekijk de video's. Kun je de video's goed volgen?
Bespreek de inhoud van de video's met een klasgenoot. Lijnsymmetrie Draaisymmetrie
Let op:
Als je een video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
1.4 Draaisymmetrie
Wat ga je in deze paragraaf leren?
- Wat is lijnsymmetrie
- Hoe kan ik een symmetrie as tekenen
- Hoe herken ik of een figuur lijnsymmetrisch is
* Bij deze paragraaf behoort een werkblad. Vraag dat aan je docent.
1.2 opgave 1
kennisbank
1.2 opgave 2
1.2 opgave 3
kennisbank
1.2 opgave 4
bekijk het filmpje
1.2 opgave 5
1.2 opgave 6
1.2 opgave 7
1.2 opgave 8
De antwoorden en uitwerkingen komen in de leertaak.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Draaisymmetrie
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Hieronder vind je een aantal vragen om te oefenen voor de toets van het hoofdstuk.
Je kan hiermee meten of je de vragen al onder de knie hebt of niet.
Heb je van een bepaald onderdeel de lesstof nog niet helemaal onder de knie, kijk dan opnieuw naar de vragen van deze paragraaf en stel vragen aan de docent tijdens het instructiemoment!
Kijk ook goed in je leertaak.
Je kan hierin afvinken welke onderdelen je al goed kan!
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Vergelijkingen oplossen
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
06 Kijkmeetkunde
07 Getallen en grafieken
04 Stelling van Pythagoras
Leerdoelen
Aan het eind van dit thema:
kun je het kwadraat van een getal uitrekenen;
weet je dat bij het rekenen kwadrateren voor vermenigvuldigen, delen, optellen en aftrekken gaat;
kun je de wortel uit een getal uitrekenen;
kun je vermenigvuldigen met negatieve getallen;
weet je wat machtsverheffen is.
Paragrafen:
Kwadraten
Wortels
Machten
Stelling van Pythagoras
4.1 Kwadraten
Wat ga je in deze paragraaf leren:
- Wat is een kwadraat
- Hoe reken je het kwadraat uit
- Hoe reken je met een kwadraat in een som
- Hoe reken je met een kwadraat in een formule
4.1 opgave 1
kennisbank
4.1 opgave 2
4.1 opgave 3
4.1 opgave 4
bekijk het filmpje
4.1 opgave 5
4.1 opgave 6
4.1 opgave 7
kennisbank
4.1 opgave 8
4.1 opgave 9
4.1 opgave 10
4.1 opgave 11
DE VOLGENDE OPGAVEN ZIJN ALLEEN VOOR 2-MAVO
kennisbank
4.1 opgave 12
4.1 opgave 13
4.1 opgave 14
4.1 opgave 15
Antwoorde en uitwerkingen komen in de leertaak.
Opgaven: Kwadraten
0%
Maak voor jezelf aantekeningen van de leeerstof
Als je iets niet begrijpt? Zet dan een * in de kantlijn en vraag het in de les.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Kwadraat
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
4.2 Wortels
In deze paragraaf ga je leren:
- wat is een wiskundige wortel
- hoe reken je met een wortel op je rekenmachine
- hoe reken je de zijde van een vierkant uit, als je de oppervlakte weet
- waarom kun je geen wortel berekenen van een negatief getal
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Opgaven:Machten en wortels, Stelling van Pythagoras
Wat moet je vooraf weten
Leerdoelen
Aan het eind van dit thema:
weet je wat lettervariabelen zijn en weet je hoe je lettervariabelen kunt gebruiken in een formule;
weet je wat een vergelijking is;
weet je wat wordt bedoeld met de oplossing van een vergelijking en weet je hoe je kunt controleren of een getal de oplossing van een vergelijking is;
weet je wat een rekenschema is en kun je rekenschema's gebruiken bij het oplossen van vergelijkingen.
Paragrafen:
Lettervariabelen 1 en 2
Vergelijkingen oplossen
Rekenstappen in schema
oplossen door inklemmen
7.1 Rekenen met negatieve getallen
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
KENNISBANK:
FILMPJE:
OPDRACHTEN:
Opgaven: Lettervariabelen
0%
Je hebt de kennisbankjes door genomen.
Aantekeningen gemaakt.
Je weet wat een variabele is en wat bedoeld wordt met een lettervariabele
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
KENNISBANK:
FILMPJE:
OPDRACHTEN:
Opgaven: Rekenen met lettervariabelen
0%
Je weet gelijke variabelen kun je optellen
het x teken kan in de schrijfwijze 4 x avervangen worden door een . (punt) 4.a bv en ook weggelakten worden in bv 4a
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in.
Als je nog wat meer uitleg wil kun je het filmpje bekijken.
Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Terugrekenschema
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in. Als je nog wat meer uitleg wil kun je het filmpje bekijken. Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in. Als je nog wat meer uitleg wil kun je het filmpje bekijken. Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in. Als je nog wat meer uitleg wil kun je het filmpje bekijken. Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Inhoud balk
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
6.2 Kijklijnen en kijkhoeken
In deze paragraaf ga je leren:
- wat zijn kijklijnen
- hoe kun je met kijklijnen bepalen wat je wel kan zien
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Inhoud balk
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
19.2 Doorsnede en inhoud
Bestudeer uit de Kennisbank wiskunde het onderdeel:
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Inhoudsmaten
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Korting berekenen
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
Leerdoelen
Aan het eind van dit thema:
kun je de oppervlakte van een parallellogram en een driehoek uitrekenen;
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Oppervlakte parallellogram Oppervlakte driehoek
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
6.6 Omtrek cirkel
In deze paragraaf ga je leren:
- Hoe je de omtrek van een cirkel berekent.
- Hoe je de diameter berekent als je de omtrek weet.
- Hoe je de straal berekent als je de omtrek weet.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Leerlingen voor leerlingen
Op de website www.lvoorl.nl vind je verschillende video's die door leerlingen voor leerlingen zijn gemaakt.
Hieronder staat een video die goed past bij dit thema.
Bekijk de video. Kun je de video goed volgen?
Bespreek de inhoud van de video met een klasgenoot. Oppervlakte cirkel
Let op:
Als je de video wilt stoppen, druk dan eerst op de stopknop en klik dan de popup weg.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
De onderstaande antwoorden moet je zelf nakijken; vergelijk jouw antwoorden met de goede
antwoorden, en geef aan in welke mate jouw antwoorden correct zijn.
Papier en (kleur)potloden, stiften, schaar, lijm, karton, plakband, ... voor het maken van de folder.
Stap 1
Download de vier werkbladen/werktekeningen en print de bladen ook uit.
Pak werkblad \(\small{1}\). Op werkblad \(\small{1}\) zie je een plattegrond van de omgeving van het plaatsje Opperdam.
Opperdam ligt aan de rivier de "Opper".
Ten oosten van Opperdam ligt het gehucht Vierhuizen.
De weg die van Opperdam naar Vierhuizen loopt, heet de Molenweg.
Ten zuiden van de Molenweg ligt een terrein dat is bestemd voor de bouw van de vakantiehuisjes. Daar komt vakantiepark 'Heideheuvel'.
Geef op de kaart aan waar het noorden is.
Zet op de kaart de volgende namen op de goede plaats: 'Opperdam', de rivier 'de Opper', 'Vierhuizen', 'Molenweg' en 'Heideheuvel'.
Stap 2
Op de kaart zie je vier dikke stippen. De stippen zijn vier gebouwen. In het midden van Opperdam staat een kerk met een hoge toren. Aan de rand van Opperdam staat een molen. De brandtoren staat in het Oppersebos. In Vierhuizen staat ook een kerk.
Zet de namen van de gebouwen op de kaart.
Je ziet hiernaast twee vergezichten van Opperdam. Op de vergezichten kun je kerktoren en de molen herkennen.
Welk vergezicht is vanaf Vierhuizen te zien?
Welk vergezicht is vanaf de brandtoren te zien?
Thema-opdracht 1
Bij de plattegrond op werkblad \(\small{1}\) zie je een schaallijn getekend.
Hoe groot is de afstand tussen de twee kerktorens hemelsbreed?
Schat de oppervlakte het dorp Opperdam in m2 en in km2.
Pak werkblad \(\small{2}\). Op werkblad \(\small{2}\) zie een plattegrond van het vakantiepark 'Heideheuvel'. Op het park
is ruimte voor \(\small{12}\) huisjes. \(\small{1}\) cm op de kaart is in werkelijkheid \(\small{10}\) m.
Bepaal zo nauwkeurig mogelijk de werkelijke oppervlakte van de kavels \(\small{5}\), \(\small{11}\) en \(\small{12}\)?
Stap 4
De prijs van de kavels is verschillend:
Kavel \(\small{5}\) kost € \(\small{22.000},-\)
Kavel \(\small{11}\) kost € \(\small{18.500},-\)
Kavel \(\small{12}\) kost € \(\small{17.800},-\).
Welk kavel is per vierkante meter het duurst? Waarom zijn de prijzen per m² verschillend, denk je?
Hiernaast zie je tekening van een vakantiehuisje. Je ziet het huisje schuin van achteren. Je hebt bouwtekeningen geprint. Pak ze er bij. De schaal van de tekeningen is \(\small{1}\):\(\small{100}\). Dat wil zeggen dat \(\small{1}\) cm op de tekening in werkelijkheid \(\small{100}\) cm is.
Gebruik alle tekeningen.
Hoeveel ramen heeft het huisje, volgens jou?
Stap 5
Gebruik de plattegrond van de begane grond.
Hoeveel m2 is de grondoppervlakte van het huisje?
Gebruik de tekening van de voorgevel.
Hoeveel m is de hoogte van het huisje?
Maak een schatting van de inhoud van de begane grond m3.
Maak ook een schatting van de inhoud van de verdieping (zonder de dakconstructie).
Kijk goed naar de dakconstructie
Uit hoeveel (bijna) driehoeken is het dak opgebouwd?
Stap 6
Jullie hebben nu al de nodige informatie verzameld. Informatie over Opperdam en omgeving, over de ligging van het vakantiepark en over de vakantiehuisjes.
Maak met deze informatie de folder voor het bouwbedrijf. Bedenk dat het bouwbedrijf de folder gaat gebruiken om mensen over te halen om een vakantiehuisje te kopen. De folder moet daarom zeer wervend zijn.
Als jullie straks ook een begroting hebben gemaakt, moet de prijs van het huisje nog in de folder worden ingevoegd.
Thema-opdr: maquette
Thema-opdracht 2
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor het maken van de maquette heb je ongeveer \(\small{2}\) lesuren nodig. Je maakt de maquette samen met een klasgenoot.
Papier en (kleur)potloden, stiften, schaar, lijm, karton, plakband, ... voor het maken van de maquette.
Stap 1
Pak de twee bouwtekeningen. Teken op stevig karton alle gevels op een schaal van \(\small{1}\) : \(\small{50}\). Dus elke meter in werkelijkheid wordt in de tekening \(\small{2}\) cm.
Teken nu ook de dakdelen en de schoorsteen op dezelfde schaal. Om de buitenkant compleet te maken, teken je ook de vloer. Gebruik een schaar of stanleymes om alle onderdelen uit karton te knippen/snijden. Maak nu ook de vloer van de verdieping, de binnenmuren en de trap. Hoe meer er af is, hoe mooier het resultaat.
Als jullie alle onderdelen hebben, zetten jullie de maquette in elkaar. Het is leuk als één van de dakdelen afneembaar is, dan is het mogelijk binnenin te kijken.
Thema-opdr: begroting
Thema-opdracht 3
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor het maken van de begroting heb je ongeveer \(\small{2}\) lesuren nodig. Je maakt de begroting samen met een klasgenoot.
Je krijgt een lijst met materialen die nodig zijn om het huisje te bouwen. Door te meten en te rekenen met de plattegronden en aan de maquette, moeten jullie zelf bepalen hoeveel je van alles nodig hebt. Verdeel de klus. Zorg dat alle gegevens in het werkblad in Excel worden ingevoerd. Excel rekent de totale kosten uit.
Betonwerk
Gewapend betonnen vloer onder de gehele begane grond, behalve onder de natte ruimten.
Systeemvloer onder alle natte ruimten op de begane grond.
Stap 2
Metselwerk
betonsteen (\(\small{49}\) stuks per m2): al het gevelmetselwerk.
gebakken metselsteen (\(\small{75}\) stuks per m2): alle binnenmuren op de begane grond.
Dakafwerking buiten
Drie laagse mastiekbedekking: hele dakoppervlakte.
Timmerwerk
hardhouten kozijnen alle raamkozijnen, terraskozijn en buitendeurkozijnen.
buitendeur en terrasdeur met raam.
binnendeuren van kunstof.
multiplexplaten: alle binnenwanden verdieping.
Stap 3
Plafondafwerking
Kunststof plafonddelen in alle natte ruimten op de begane grond.
Grenenhouten lattenplafonds in alle overige ruimten op de begane grond.
Glaswerk
blank vensterglas in alle raamkozijnen en in de terrasdeur.
Stelposten
dakconstructie, vloer van de verdieping, loodgieterswerk, elektra, hang en sluitwerk, keuken, trap, schoorsteen, ...
Hoeveel uur zullen ze bezig zijn met het bouwen van zo'n huisje? Maak de begroting in Excel af door achter arbeidsloon het aantal uur in te vullen. Druk de begroting af. Neem de prijs die het bouwbedrijf voor het huisje gaat rekenen op in je folder.
Stap 4
Afronding
Jullie zijn klaar met het maken van de folder, de maquette en de begroting.
Ziet de folder er netjes uit?
Is de maquette volledig en kloppen de de maten?
Is het Excelblad volledig ingevuld?
Tevreden? Laat alle drie de eindproducten beoordelen door jullie docent.
Thema-opdr: Ganzenbord
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je ongeveer \(\small{2}\) lesuren nodig. Je maakt het eindproduct samen met een klasgenoot.
Benodigheden
(Kleur)potloden, stiften, schaar, lijm, karton, plakband, ... voor het maken van het ganzenbord.
Stap 1
Stap 1
Je gaat samen met een klasgenoot aan de slag met het maken van het GROTE FORMULE GANZENBORD.
Klik voor dat jullie beginnen eerst op de volgende link en lees wat er over het maken van een spel staat in de gereedschapskist: spel.
Bedenk nu eerst hoeveel hokjes jullie ganzenbord gaat krijgen. Bedenk vervolgens welke formules jullie willen gaan gebruiken. Natuurlijk hoef je niet voor ieder hokje een nieuwe formule te bedenken. Wordt het spel straks met één of met twee dobbelstenen gespeeld? Bedenk bij iedere formule welke uitkomsten je kunt krijgen.
Stap 2
Stap 2
Maak nu het speelbord van het ganzenbord. Schrijf/teken de formules op het bord. Controleer of je daadwerkelijk op de finish kunt komen. Zorg er ook voor dat je niet 'onder de finish' uit kunt komen.
Schrijf een korte handleiding bij het spel. In de handleiding leggen jullie eerst kort (maximaal \(\small{100}\) woorden) uit wat het spel met vergelijkingen te maken heeft. In de handleiding komen ook de spelregels.
Speel het spel dan een aantal keer. Laat het spel ook door een aantal klasgenoten spelen. Vraag om commentaar. Natuurlijk spelen jullie ook het spel van jullie klasgenoten. Geef op een goede manier feedback.
Pas het spel eventueel nog iets aan.
Tevreden? Laat het spel dan beoordelen door je docent.
THEMA OPDRACHTEN
Thema-opdracht 5
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je 2 lesuren nodig. Je maakt samen met een klasgenoot een ontwerp voor een symmetrisch terras. Jullie berekenen ook de oppervlakte van het terras.
Stap 1
Bekijk het volgende filmpje uit de serie 'Wat en waar is wiskunde?'.
In het filmpje zie je hoe ze een symmetrische versie van het beroemde schilderij de 'Mona Lisa' maken.
Je kunt ook zelf een symmetrisch portret maken. Dat kan bijvoorbeeld in het computerprogramma Paint.
Bekijk onderstaand filmpje:
Natuurlijk mag je met een foto van je eigen gezicht in Paint een mooi kunstwerkje maken.
Stap 2
Stap 2
Jullie gaan beginnen met het maken van het eindproduct: een symmetrisch terras rond een vijver in de kasteeltuin. Download het lege ontwerp voor een terras. Op het lege ontwerp staat een plattegrond van een vijver. De ruimte er omheen kun je gebruiken voor het terras.
Voor het ontwerp mogen jullie verschillende soorten tegels gebruiken (vierkant, rechthoek, driehoek, parallellogram, ruit, vlieger). Jullie mogen ook verschillende kleuren gebruiken (grijs, zwart, rood, beige).
Natuurlijk zorgen jullie er voor dat het terras symmetrisch blijft!
Stap 3
Stap 2
Jullie moeten ook de oppervlakte van het terras uitrekenen. Bepaal van alle verschillende tegels die jullie hebben gebruikt de oppervlakte. Bepaal ook de oppervlakte van het hele terras. Schrijf de berekening van de oppervlakte van het terras op jullie ontwerp (eventueel op de achterkant).
Klaar en tevreden?
Laat het ontwerp van het terras en de berekening van de oppervlakte beoordelen door jullie docent.
Thema-opdr: Getallenraadsel
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je \(\small{1}\) lesuur nodig. Je maakt het eindproduct alleen.
Benodigheden
Geen bijzonderheden.
Thema-opdracht 6
Stap 1
In de inleiding stond het volgende getallen'raadsel'.
Neem een getal in gedachte.
Tel er 4 bij op.
Verdubbel het antwoord.
Trek het begingetal er af.
Trek er 7 van af.
Trek nogmaals het begingetal er af.
Wat is de uitkomst?
Welk begingetal je ook in gedachte neemt, je krijgt altijd \(\small{1}\) als uitkomst. Je kunt dit uitleggen door te werken met lucifers en luciferdoosjes. Bekijk het schema hiernaast.
Het begingetal is het aantal lucifers in het luciferdoosje. Tel er \(\small{4}\) bij op betekent \(\small{4}\) lucifers er bij tekenen.
Verdubbelen betekent \(\small{2}\) keer zoveel luciferdoosjes én \(\small{2}\) keer zoveel lucifers. Trek het beginggetal er af betekent een luciferdoosje weghalen.
Je ziet dat je uiteindelijk één lucifer overhoudt.
Het maakt niet uit met welk getal je bent begonnen.
Stap 2
Stap 2
Je kunt het raadsel uit stap \(\small{1}\) ook met variabelen opschrijven.
Neem voor het getal dat je in gedachte neemt bijvoorbeeld de letter g.
Je krijgt dan:
Stap 3
Je gaat aan de slag met het eindproduct: je maakt zelf een getallenraadsel zoals in de inleiding van dit thema. Zorg dat je bij ieder begingetal dezelfde uitkomst krijgt. De uitkomst hoeft natuurlijk niet \(\small{1}\) te zijn.
Maak ook een schema waarin je met lucifers en luciferdoosjes zichtbaar maakt hoe het raadsel werkt.
Laat ook zien hoe je het raadsel met variabelen op kunt schrijven.
Klaar? Probeer samen met een klasgenoot of het raadsel werkt. Kijk of je klasgenoot het raadsel met variabelen op kan schrijven. Natuurlijk kijken jullie ook zijn/haar raadsel werkt.
Tevreden? Laat het raadsel beoordelen door je docent.
Thema-opdr: Collage/puzzel
Thema-opdracht 7
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je \(\small{1}\) lesuur nodig. Het eindproduct maak je samen met een klasgenoot.
Benodigheden
(Kleur)potloden, stiften, schaar, lijm, karton, plakband, ... voor het maken van het eindproduct.
Stap 1
Stap 1
In de inleiding heb je het verhaal over de uitvinding van het schaakbord gelezen. Lees het verhaal eventueel nog een keertje. In de tabel hieronder zie hoeveel graankorrels op de de eerste zes velden komen.
Reken nu ook uit hoeveel graankorrels er op het zevende veld komen. En op het achtste veld. En op het negende en tiende veld. Reken ook eens uit hoeveel graankorrels er op het \(\small{20}\)ste veld komen. Kun je dat getal uitspreken?
Stap 1
Het aantal graankorrels dat op het 64ste veld van het schaakbord komt, is een getal van \(\small{20}\) cijfers. Zoveel graankorrels zitten er niet in één zakje graan.
Het verhaal over de uitvinding van het schaakspel liep niet goed af voor de uitvinder van het spel. Toen de koning hoorde wat de uitvinder wilde hebben, lachte hij nog en zei hij: 'Is dat echt alles wat je wilt hebben?' Maar toen bleek dat de koning niet genoeg graan had om Sissa Ben Dahir te betalen, werd hij heel boos. Hij werd zo boos dat hij Sissa Ben Dahir in de gevangenis liet gooien om hem er nooit meer uit te laten......
Stap 2
Stap 2
Je gaat aan de slag met het maken van het eindproduct. Je mag samen met een klasgenoot een eindproduct bedenken. Natuurlijk moeten machten en/of wortels een rol spelen in het eindproduct.
Tip:
Zoek op internet allerlei afbeeldingen waarin machten en wortels voorkomen. Maak met deze afbeeldingen een collage met als titel 'Machten en wortels'.
Tip:
Maak een kruiswoordraadsel. De omschrijvingen zijn sommen waarin machten en wortels voorkomen. De antwoorden moet je invullen.
Zijn jullie klaar met het eindproduct?
Laat het eindproduct dan beoordelen door jullie docent.
Thema-opdr: Filmpje
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je \(\small{2}\) lesuren nodig. Je maakt samen met een klasgenoot een filmpje van ongeveer twee minuten.
Benodigheden
Een filmcamera of een mobiele telefoon met camera.
Thema-opdracht 8
Stap 1
Op YouTube kun je heel wat filmpjes vinden waarin wiskunde wordt uitgelegd. Kijk maar eens naar het volgende filmpje.
Bespreek samen wat jullie goed en wat jullie minder goed vinden aan het filmpje.
Zoek nu zelf nog eens twee of drie uitlegfilmpjes op YouTube op. Bespreek per filmpje wat jullie goed en wat jullie minder goed aan het filmpje vinden. Bedenk steeds wat jullie anders zouden doen.
Thema-opdracht 9
Stap 2
Jullie gaan beginnen met het maken van het eindproduct. Jullie maken samen een filmpje van ongeveer twee minuten.
In het filmpje beantwoord je één van de vier volgende vragen:
Hoe bereken je de oppervlakte van een parallellogram?
Hoe bereken je de oppervlakte van een driehoek?
Hoe bereken je de omtrek van een cirkel?
Hoe bereken je de oppervlakte van een cirkel?
> Overleg met jullie docent welke vraag jullie gaan beantwoorden.
> Bepaal dan eerst welke informatie jullie willen vertellen. Maak het niet te ingewikkeld.
> Schrijf een 'script' voor het filmpje. Schrijf de teksten die gezegd moeten worden helemaal uit.
> Oefen een of twee keer zonder camera.
Stap 3
Stap 3
Jullie zijn klaar om het filmpje ook echt te gaan opnemen.
> Vraag jullie docent om een filmcamera of gebruik je mobiel.
> Neem het filmpje op.
Klaar?
> Laat jullie filmpje zien aan jullie klasgenoten. Vraag om commentaar. Natuurlijk bekijken jullie ook de filmpjes die door jullie klasgenoten zijn gemaakt. Geef op een goede manier commentaar.
> Als er nog tijd voor is, verwerk dan het commentaar dat jullie hebben gekregen.
> Laat het filmpje nu beoordelen door jullie docent.
> Zijn jullie tevreden over het resultaat en het cijfer? Plaats het filmpje dan op YouTube.
Thema-opdr: Mobieltje
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je \(\small{1}\) lesuur nodig. Je maakt het eindproduct alleen.
Stap 1
Yorrick mag een nieuwe mobiele telefoon kopen. Hij zoekt eerst uit welke mobiele telefoon het goedkoopst is. Er zijn verschillende aanbieders. Maar voor alle aanbieders geldt: 'hoe meer minuten je belt, hoe meer je betaalt'. Er is een verband tussen de beltijd en de belkosten: Hoe groter de beltijd, hoe hoger de belkosten.
Op internet heeft Yorrick de gegevens van Flexi-Bel gevonden. Die gegevens zie je hiernaast.
Beantwoord de volgende vragen op het werkblad Lineaire verbanden
Hoeveel betaal je bij Flexi-Bel per maand als je \(\small{100}\) minuten belt? En hoeveel als je \(\small{300}\) minuten belt?
Het verband tussen de beltijd en de belkosten is een lineair verband. Maak een formule bij dit verband.
Teken een grafiek bij de formule.
Stap 2
Stap 2
Een tweede aanbieder waarvan Yorrick de gegevens op internet heeft gevonden is Profile. Die gegevens zie je hiernaast.
Beantwoord de volgende vragen op het werkblad:
Welke maatschappij is duurder als je per maand \(\small{100}\) minuten belt? En welke maatschappij is duurder \(\small{300}\) minuten belt?
Het verband tussen de beltijd en de belkosten is ook bij Profile een lineair verband. Maak een formule voor Profile.
Teken, in het assenstelsel waarin de grafiek van Flexi-Bel staat, ook de grafiek van Profile.
Vergelijk de twee bedrijven.
Hoe zie je dat je bij Profile altijd duurder uit bent dan bij Flexi-Bel?
Yorrick zal dus in ieder geval niet voor Profile kiezen.
Stap 3
Stap 3
Yorrick vindt ook de gegevens van Premium op internet.
Beantwoord de volgende vragen op het werkblad:
Welke maatschappij, Flexi-Bel of Premium, is duurder als je per maand \(\small{100}\) minuten belt? En welke maatschappij is duurder \(\small{300}\) minuten belt?
Het verband tussen de beltijd en de belkosten is ook bij Premium een lineair verband. Maak een formule voor Premium.
Teken in hetzelfde assenstelsel nu ook de grafiek van Premium.
Vergelijk Premium met Flexi-Bel. Hoe zie je dat je bij Premium altijd duurder uit bent dan bij Flexi-Bel?
Yorrick zal dus in ieder geval ook niet voor Premium kiezen.
Stap 4
Stap 4
Tot nu toe is Flexi-Bel als voordeligste uit de bus gekomen. Maar Yorrick geeft nog niet op. Hij vergelijkt Flexi-Bel met nog een aanbieder: Custom.
Beantwoord de volgende vragen op het werkblad:
Welke maatschappij, Flexi-Bel of Custom, is duurder als je per maand \(\small{100}\) minuten belt? En welke maatschappij is duurder \(\small{300}\) minuten belt?
Het verband tussen de beltijd en de belkosten is ook bij Custom een lineair verband. Maak een formule voor Custom.
Teken in hetzelfde assenstelsel nu ook de grafiek van Custom.
Vergelijk Custom met Flexi-Bel. Bij welke beltijd zijn beide bedrijven even duur? Bij welke beltijd is Flexi-Bel voordeliger? En bij welke beltijd is Custom voordeliger?
Stap 5
Stap 5
Yorrick heeft vier aanbieders van abonnementen voor mobiele telefoons met elkaar vergeleken. Voor welke aanbieder zal Yorrick uiteindelijk kiezen? Licht het antwoord op de vraag toe op het werkblad.
Heb je alle vragen op het werkblad ingevuld?
Heb je alle grafieken getekend?
Heb je de conclusie ingevuld?
Ja? Laat het werkblad beoordelen door je docent.
Thema-opdracht 10
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je ongeveer \(\small{2}\) lesuren nodig. De afsluiting van het thema doe je alleen. Je maakt het eindproduct alleen.
Hoe hoog is de verkoopprijs van één liter euro \(\small{95}\) (Shell)?
De eerste drie onderdelen vormen samen de 'kale prijs'. Volgens de afbeelding is de 'kale prijs' afgerond \(\small{34}\%\). Ga na of dit klopt.
Volgens de afbeelding is de BTW afgerond \(\small{25}\) cent. Ga met een berekening na of dat klopt.
Stap 2
Stap 2
Gebruik bij de volgende vragen de afbeelding hiernaast.
Stel dat de overheid besluit de Accijnzen met \(\small{20}\) cent te verhogen. De kostprijs voor het maken van een liter benzine, de opbrengst voor de pomphouder en de opbrengst voor het olieconcern veranderen niet.
Laat met een berekening zien dat de nieuwe verkoopprijs dan afgerond € \(\small{1},{83}\) wordt.
Bereken welk percentage van de verkoopprijs bij de nieuwe verkoopprijs wordt bepaald door belastingen.
Leg uit waarom de overheid 'dubbel verdient' als ze de accijnzen verhoogd.
Stap 3
Stap 3
In de afbeelding hiernaast zie je hoe de prijs van een liter diesel is opgebouwd. Je ziet dezelfde vijf onderdelen. De prijs van een liter diesel was in \(\small{2011}\) gemiddeld € \(\small{1},{35}\).
Laat met een berekening zien dat de BTW per liter afgerond \(\small{22}\) cent bedraagt.
Stap 4
Stap 4
In de krant wordt vaak geschreven over de hoge benzineprijs. Veel auteurs vinden dat de overheid te veel verdient aan benzine en pleiten voor lagere accijns. Maar er zijn ook auteurs die het daar niet mee eens zijn. Eén van die auteurs geeft aan dat de beninzeprijs kan stijgen tot € \(\small{2},{48}\).
Hoezo dure benzine?
Door: Vincent van de Vinne
AMSTERDAM - Bijna dagelijks wordt geschreven over de stijgende olieprijs en de oplopende kosten van benzine en diesel. Maar eigenlijk moet je helemaal niet kijken naar de prijs aan de pomp. Het gaat om de brandstofkosten in relatie tot het inkomen. In \(\small{1973}\) kostte een liter benzine \(\small{45}\) eurocent. Het modale inkomen bedroeg 660 euro per maand. Gemiddeld reed men in dit tijd ongeveer \(\small{1300}\) km per maand. Een auto had een gebruik van \(\small{1}\) op \(\small{12}\). Dus om \(\small{1300}\) km te rijden verbruikte iemand ongeveer \(\small{108}\) liter benzine. Dat kostte hem dus iets minder dan \(\small{50}\) euro. Hetgeen neerkomt op ongeveer \(\small{7},{5}\%\) van zijn maandinkomen.
Uitgaande van een huidige benzineprijs van \(\small{1},{70}\) euro per liter en hetzelfde aantal kilometer per maand en een gemiddeld brandstofgebruik van \(\small{1}\) op \(\small{16}\). Is men nu \(\small{142}\) euro per maand kwijt aan benzine. Bij een modaal maandinkomen van \(\small{2700}\) euro is dat iets meer dan \(\small{5},{2}\%\) van het modale maandinkomen.
Zou ook nu \(\small{7},{5}\%\) van het maandinkomen uitgegeven moeten worden aan benzine dan kom je uit op een benzineprijs van \(\small{2},{48}\) euro!!
Bespreek het bovenstaande artikel met een klasgenoot.
Kloppen de berekeningen?
Snappen jullie de redenatie van Vincent van de Vinne?
Stap 5
Stap 5
Wat vind jij? Vind je de benzineprijs te hoog of juist te laag? Schrijf het antwoord op deze vraag op het werkblad. Natuurlijk geef je ook argumenten voor je keuze.
Heb je alle vragen op het werkblad ingevuld?
Ja? Laat het werkblad beoordelen door je docent.
Thema-opdracht 11
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je ongeveer \(\small{2}\) lesuren nodig. Je maakt het eindproduct samen met een klasgenoot.
Benodigheden
Geen bijzonderheden.
Stap 1
Stap 1
Op school krijg je veel cijfers. Je houdt die cijfers natuurlijk nauwkeurig bij. Bijvoorbeeld in je agenda. Een aantal keer per jaar krijg je een rapport. Rapportcijfers zijn meestal gehele getallen. Een rapportcijfer is een gewogen gemiddelde van je cijfers voor overhoringen, proefwerken, spreekbeurten, enzovoorts. Bij het berekenen van het gemiddelde tellen meestal niet alle cijfers even zwaar.
Voor Nederlands heeft een klasgenoot van je de volgende cijfers gehaald: \(\small{6}\), \(\small{6}\), \(\small{5}\), \(\small{7}\), \(\small{4}\) en \(\small{6}\).
Bespreek met een klasgenoot de antwoorden op de volgende vragen:
Welk cijfer krijgt je klasgenoot op zijn rapport als alle cijfers even zwaar tellen?
Leg met een berekening uit dat het kan dat je klasgenoot met deze cijfers een \(\small{5}\) op zijn rapport krijgt.
Stap 2
Stap 2
Klas \(\small{2}\)A en klas \(\small{2}\)B heben allebei een proefwerk Frans gemaakt. De leraar heeft van allebei de klassen het gemiddelde cijfer uitgerekend. Het gemiddelde cijfer in klas \(\small{2}\)A was een \(\small{6},{2}\) en het gemiddelde cijfer in klas \(\small{2}\)B was een \(\small{6},{4}\).
Bespreek samen het antwoord op de volgende vragen:
Hebben alle leerlingen in klas \(\small{2}\)B het proefwerk beter gemaakt dan de leerlingen uit klas \(\small{2}\)A? Licht jullie antwoord toe.
Wat zou de leraar nog kunnen doen om de klassen beter met elkaar te kunnen vergelijken?
Stap 3
Stap 3
Voor morgen heb je veel huiswerk voor aardrijkskunde. Een aantal van je klasgenoten denkt dat je morgen een overhoring krijgt. Inge zegt: "Ik schat de kans op een overhoring op \(\small{90}\%\)."
Bespreek samen het antwoord op de volgende vragen:
Wat wordt bedoeld met een kans van \(\small{90}\%\)?
Hoe groot is, volgens Inge, de kans dat je morgen geen overhoring krijgt?
"Volgende week geef ik een overhoring", zegt je lerares Engels. Je hebt op maandag, woensdag en vrijdag Engels. Er zijn dus drie mogelijkheden.
Bespreek samen het antwoord op de volgende vragen:
Wat is de kans dat je maandag een overhoring krijgt?
De maandag is voorbij je hebt geen overhoring Engels gekregen. Nu blijven woensdag en vrijdag nog over. Hoe groot is nu de kans dat je op woensdag een overhoring krijgt?
Stap 4
Stap 4
Je bent een proefwerk biologie aan het maken. Aan het einde van het proefwerk staan drie meerkeuzevragen. Bij iedere vraag kun je kiezen uit antwoord A, B, C of D. Je snapt niets van de vragen, dus je gokt de antwoorden. Je gokt AAB of CBA of ... .
Bespreek samen het antwoord op de volgende vragen:
Hoeveel mogelijkheden zijn er?
Welk soort diagram kun je gebruiken om de mogelijkheden in beeld te brengen?
Hoe groot is de kans dat je alle drie de vragen goed hebt?
Stap 5
Stap 5
Jullie gaan aan de slag met het eindproduct. Jullie maken een toets die bestaat uit minimaal vijf vragen. In de vragen komen alle leerdoelen van dit thema aan de orde.
Jullie maken bij de toets ook een correctiemodel. In het correctiemodel komen de goede antwoorden. Ook geven jullie in het correctiemodel aan hoeveel punten je per goed antwoord kunt krijgen en hoe je het cijfer voor de toets kunt uitrekenen.
Is de toets klaar? Laat de toets dan maken door twee andere klasgenoten. Vraag om commentaar. Natuurlijk maken jullie ook hun toets. Geef op een goede manier commentaar. Pas de toets eventueel nog iets aan. Laat de toets vervolgens beoordelen door jullie docent.
Thema-opdracht 12
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je \(\small{2}\) lesuren nodig.
In de inleiding van dit thema heb je kennisgemaakt met de kubuswoningen in Rotterdam. Hiernaast zie je een bouwtekening van zo'n kubuswoning. In de tekening zie je dat de kubuswoning meerdere verdiepingen heeft.
Download het werkblad kubuswoningen Op het werkblad zie je vier keer twee kubussen getekend. In een kubus kun je op verschillende plaatsen een doorsnede tekenen.
Teken in de eerste twee kubussen een doorsnede die de vorm heeft van een driehoek. De doorsnede hoeft niet horizontaal te lopen.
Teken in de tweede twee kubussen een doorsnede die de vorm heeft van een vierkant.
Teken in de derde twee kubussen een doorsnede die de vorm heeft van een rechthoek waarvan niet alle zijden even lang zijn.
Kun je een doorsnede tekenen in de vorm van een vijfhoek of een zeshoek? Zo ja, doe dat in de twee onderste kubussen.
Stap 2
Op de site www.kubuswoning.nl vind je allerlei extra informatie over deze kubuswoningen.
Op deze site staan onder andere de volgende gegevens
> Ga met een berekening na of het klopt dat een kubus met ribben van \(\small{7},{5}\) m een inhoud van \(\small{422}\) m3 heeft?
> Wat zal bedoeld worden met bruto inhoud?
Stap 3
Bekijk het filmpje nog eens:
Schrijf nu samen met een klasgenoot een artikel met als titel 'Wonen in een kubuswoning'. In het artikel beschrijven jullie wat de voor- en de nadelen zijn van het wonen in een kubuswoning. Illustreer het artikel met minstens vier afbeeldingen.
Klaar en tevreden?
Laat het artikel beoordelen door jullie docent.
Thema-opdracht
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je ongeveer \(\small{2}\) lesuren nodig. Je maakt een verslag van een onderzoekje naar de relatie tussen de snelheid van een auto en de remweg. Dat verslag maak je samen met een klasgenoot.
Stap 1
Je gaat op computer onderzoeken wat het verband is tussen de snelheid van een auto op het moment van remmen en de remweg. Van dat onderzoekje maak je een verslag.
Download en open nu eerst de lege opzet voor het verslag.
Het verslag begint met de de onderzoeksvraag. Schrijf onder het kopje onderzoeksvraag de hoofdvraag van jullie onderzoekje op.
Als jullie straks alle stappen hebben doorlopen, kunnen jullie deze tekst natuurlijk nog best een beetje aanpassen.
Stap 2
Stap 2
Open de applet remweg . Indien de applet niet werkt, gebruik de screenshots.
Lees de tekst hieronder nauwkeurig door.
Stel de snelheid in op \(\small{60}\) km/u en druk op start.
Controleer of het klopt dat:
de remweg 46,8 meter is;
de remtijd 5,5 sec is.
Stap 2
Druk op reset.
Stel de snelheid in op \(\small{80}\) km/u en druk op start.
Controleer of het klopt dat:
de remweg 83 meter is;
de remtijd 7,4 sec is.
Stap 3
Stap 3
In het verslag zie je onder het kopje 'Onderzoeksresultaten' een lege tabel. Gebruik de applet om de tabel in te vullen.
Werkt de applet niet, overleg dan met de docent.
Je ziet in het verslag ook twee lege assenstelsels. Gebruik het eerste lege assenstelsel om het verband tussen de snelheid (horizontale as) en de remweg weer te geven. Is het verband tussen de snelheid en de remweg een lineair verband?
Gebruik het tweede lege assenstelsel om het verband tussen de snelheid (horizontale as) en de remtijd weer te geven. Is het verband tussen de snelheid en de remtijd een lineair verband?
Stap 4
Stap 4
Jullie gaan het verslag afmaken.
Zorg dat de ingevulde tabel en de grafiek een plaatsje kunnen krijgen onder het kopje 'Onderzoeksresultaten'.
Wat is de conclusie van jullie onderzoekje? Wat is het verband tussen de snelheid van een auto en de remweg? Schrijf jullie conclusie in het verslag onder het kopje conclusie. Zorg dat de conclusie past bij de resultaten in de tabel en de grafiek.
Lees het verslag nog één keer helemaal door. Zorg dat er geen taalfouten in het verslag zitten. Print het verslag en lever het verslag in bij jullie docent.
Extra opgaven
Thema-opdracht 14
Vooraf
Lees voor je begint de werkwijzer een keer helemaal door.
Tijd
Voor de afronding van het thema heb je \(\small{1}\) lesuur de tijd. Je beantwoordt de vragen samen met een klasgenoot.
Benodigheden
Computer met tekstverwerker
Papier, pen en (kleur)potloden.
Stap 1
Stap 1
Geef antwoord op de volgende vragen.
1
Een rechthoekig raam is \(\small{1},{20}\) m bij \(\small{1},{60}\) m. Bereken de lengte van de diagonaal. Kan een plank van \(\small{1},{80}\) meter bij \(\small{3}\) meter door het raam naar binnen? Welke afmeting van de plank heeft geen invloed op je antwoord?
De breedte van een rechthoekig raam is \(\small{1},{20}\) m. Je weet niet hoe hoog het raam is. Bereken hoe hoog het raam minimaal moet zijn, zodat een plank van \(\small{1},{80}\) meter bij \(\small{3}\) meter door het raam naar binnen kan. Rond je antwoord af op twee cijfers achter de komma.
Stap 2
Stap 2
Geef nu ook antwoord op de volgende vraag.
2
Je ziet hieronder drie 'ramen' met dezelfde omtrek. Ga na of dat klopt. Zoek eens uit door welk raam de grootste plank naar binnen kan.
Stap 3
Stap 3
Geef nu ook antwoord op de volgende vraag.
3
Je hebt een plank van \(\small{1},{80}\) meter bij \(\small{3}\) meter. De plank moet door een vierkant raam. Welke afmetingen moet het raam minimaal hebben zodat de plank door het raam kan.
Stap 4
Stap 4
In de praktijk worden er niet vaak platte planken verhuisd, maar bijvoorbeeld een piano of een bed. Bij het bepalen of bijvoorbeeld een bed wel of niet door een raam kan, moet je ook rekening houden met de hoogte van het bed.
4
Een tweepersoonsbed is \(\small{1},{80}\) m breed, \(\small{2}\) m lang en \(\small{0},{4}\) m hoog. Zoek eens uit of het bed door een rechthoekig raam van \(\small{1},{20}\) m bij \(\small{1},{60}\) m kan. Maak eerst tekening op schaal.
Andere leerjaren
Alle leerjaren en niveaus werken op 't Ravelijn met een online methode.
In de thema´s/opdrachten van de Stercollecties wiskunde wordt regelmatig verwezen naar de Kennisbank wiskunde. In de Kennisbank vind je de theorie die je nodig hebt voor het beantwoorden van de vragen en het maken van de opdrachten.
Bestudeer eerst de kennisbank hieronder, daar staat de uitleg in. Als je nog wat meer uitleg wil kun je het filmpje bekijken. Maak daarna de opdrachten, schrijf deze in je schrift en kijk ze na.
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
voor alle doeleinden, inclusief commerciële doeleinden.
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
Toelichting
Rearrangeerbare stercollectie wiskunde voor leerjaar 1 en 2 VMBO KGT van Stichting VO-content. De stercollectie is ontwikkeld op basis van de kerndoelen basisvorming en de door de SLO ontwikkelde inhoud- en leerdoelspecificaties voor het vak wiskunde. Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO.
Rearrangeerbare stercollectie wiskunde voor leerjaar 1 en 2 VMBO KGT van Stichting VO-content. De stercollectie is ontwikkeld op basis van de kerndoelen basisvorming en de door de SLO ontwikkelde inhoud- en leerdoelspecificaties voor het vak wiskunde. Een Stercollectie wordt onderhouden en geactualiseerd volgens een kwaliteitszorgsysteem van SLO.
Leeromgevingen die gebruik maken van LTI kunnen Wikiwijs arrangementen en toetsen afspelen en resultaten
terugkoppelen. Hiervoor moet de leeromgeving wel bij Wikiwijs aangemeld zijn. Wil je gebruik maken van de LTI
koppeling? Meld je aan via info@wikiwijs.nl met het verzoek om een LTI
koppeling aan te gaan.
Maak je al gebruik van LTI? Gebruik dan de onderstaande Launch URL’s.
Arrangement
Oefeningen en toetsen
toets/oefening
Lijnsymmetrie
Draaisymmetrie
Draaisymmetrie
Vlakke figuren en symmetrie
Vlakke figuren en symmetrie
Symmetrie
Symmetrie
Gemiddelde
Gemiddelde
Steel- en bladdiagram
Steel- en bladdiagram
Kansen
Kansen
Statistiek
Statistiek en kans
Lineair verband
Lineair verband 1
Lineair verband
Lineair verband 2
Lineaire vergelijking
Lineaire vergelijkingen
Balansmethode
Balansmethode
Lineaire verbanden
Lineaire verbanden
Kwadraten
Kwadraten
Wortels
Wortels
Machten
Machten
Machten en wortels + Stelling van Pythagoras
Stelling van Pythagoras
Gemengde opdrachten Stelling van Pythagoras
Stelling van Pythagoras
Stelling van Pythagoras
Machten en wortels, Stelling van Pythagoras
Lettervariabelen
Lettervariabelen
Rekenen met lettervariabelen
Rekenen met lettervariabelen
Variabelen
Variabelen
Vergelijking en oplossing
Vergelijking en oplossing
Rekenstappen in schema
Rekenschema in stappen
Rekenstappen in schema 2
oplossen door inklemmen
Vergelijkingen
Vergelijkingen
Lengtematen
Oppervlaktematen
Schaallijnen
Uitslagen
Inhoud
Inhoud
Kijklijnen en kijkhoeken
Kijklijnen en kijkhoeken
Aanzichten
Aanzichten
Kijkmeetkunde
Kijkmeetkunde
Inhoud
Inhoud
Doorsnede
Doorsnede
Inhoud
Inhoud 2
Doorsnede en inhoud
Doorsnede en inhoud
Verhoudingstabellen
Verhoudingstabellen
Procenten
Procenten
Rekenen met procenten
Rekenen met procenten
Rekenen met procenten
Procenten erbij of eraf
Procenten erbij of eraf
Nog meer procenten
Nog meer procenten
Verhoudingen en procenten
Verhoudingen en procenten
Verhoudingen en procenten
Omtrek
Omtrek
Lengtematen
Lengtematen
Oppervlakte
Oppervlakte
Oppervlaktematen
Oppervlaktematen
Oppervlakte parallellogram en driehoek
Oppervlakte parallellogram en driehoek
Omtrek cirkel - Deel 2
Omtrek cirkel
Oppervlakte cirkel
Oppervlakte cirkel
Omtrek en oppervlakte
Omtrek en oppervlakte
Niet-lineaire verbanden
Niet-lineaire verbanden
Niet-lineaire verbanden
IMSCC package
Wil je de Launch URL’s niet los kopiëren, maar in één keer downloaden? Download dan de IMSCC package.
Oefeningen en toetsen van dit arrangement kun je ook downloaden als QTI. Dit bestaat uit een ZIP bestand dat
alle
informatie bevat over de specifieke oefening of toets; volgorde van de vragen, afbeeldingen, te behalen
punten,
etc. Omgevingen met een QTI player kunnen QTI afspelen.
Wikiwijs lesmateriaal kan worden gebruikt in een externe leeromgeving. Er kunnen koppelingen worden gemaakt en
het lesmateriaal kan op verschillende manieren worden geëxporteerd. Meer informatie hierover kun je vinden op
onze Developers Wiki.
Aan het eind van dit hoofdstuk kan ik:
Bestudeer eerst uit de Kennisbank wiskunde het onderdeel: Lijnsymmetrie
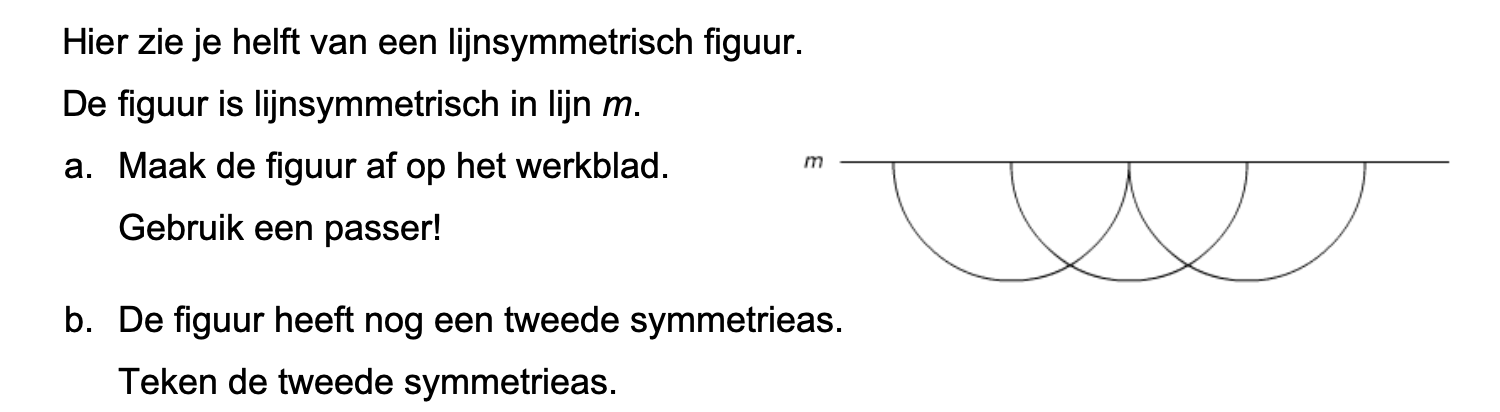
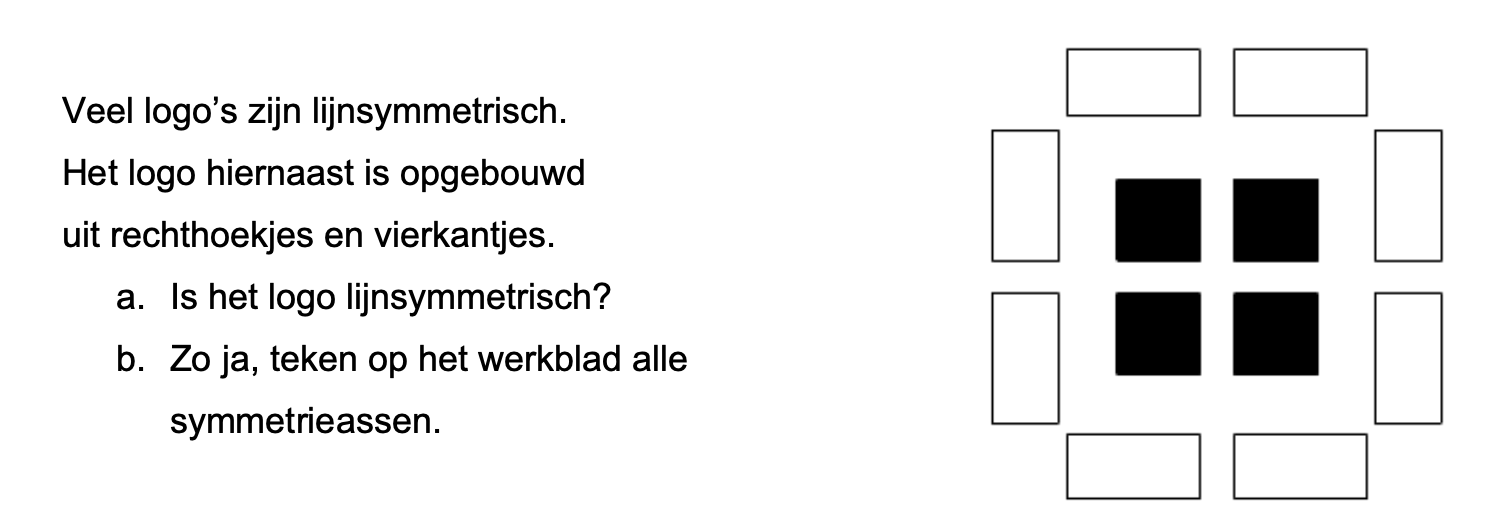
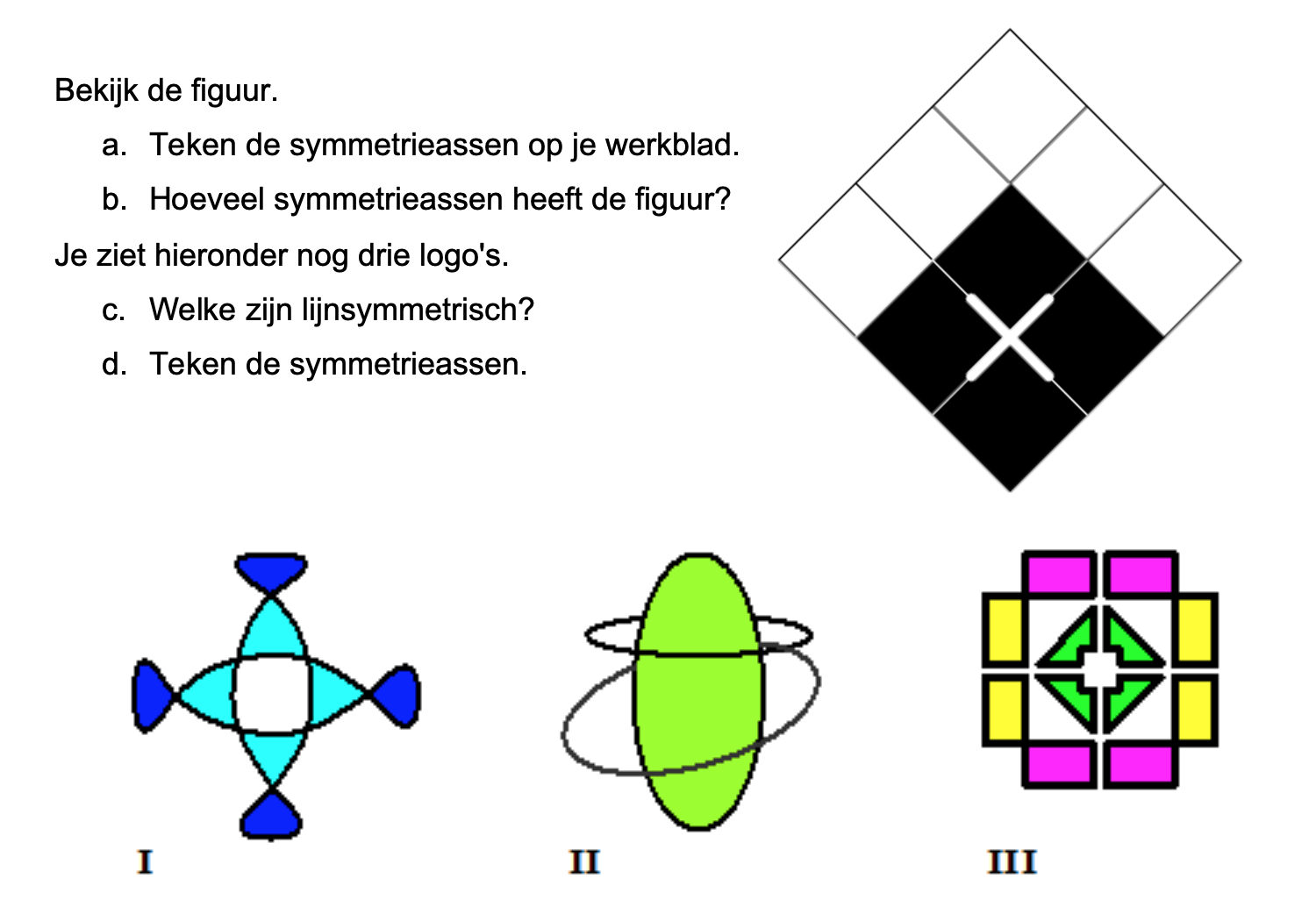
Nog enkele opgaven om te oefenen voor het proefwerk.
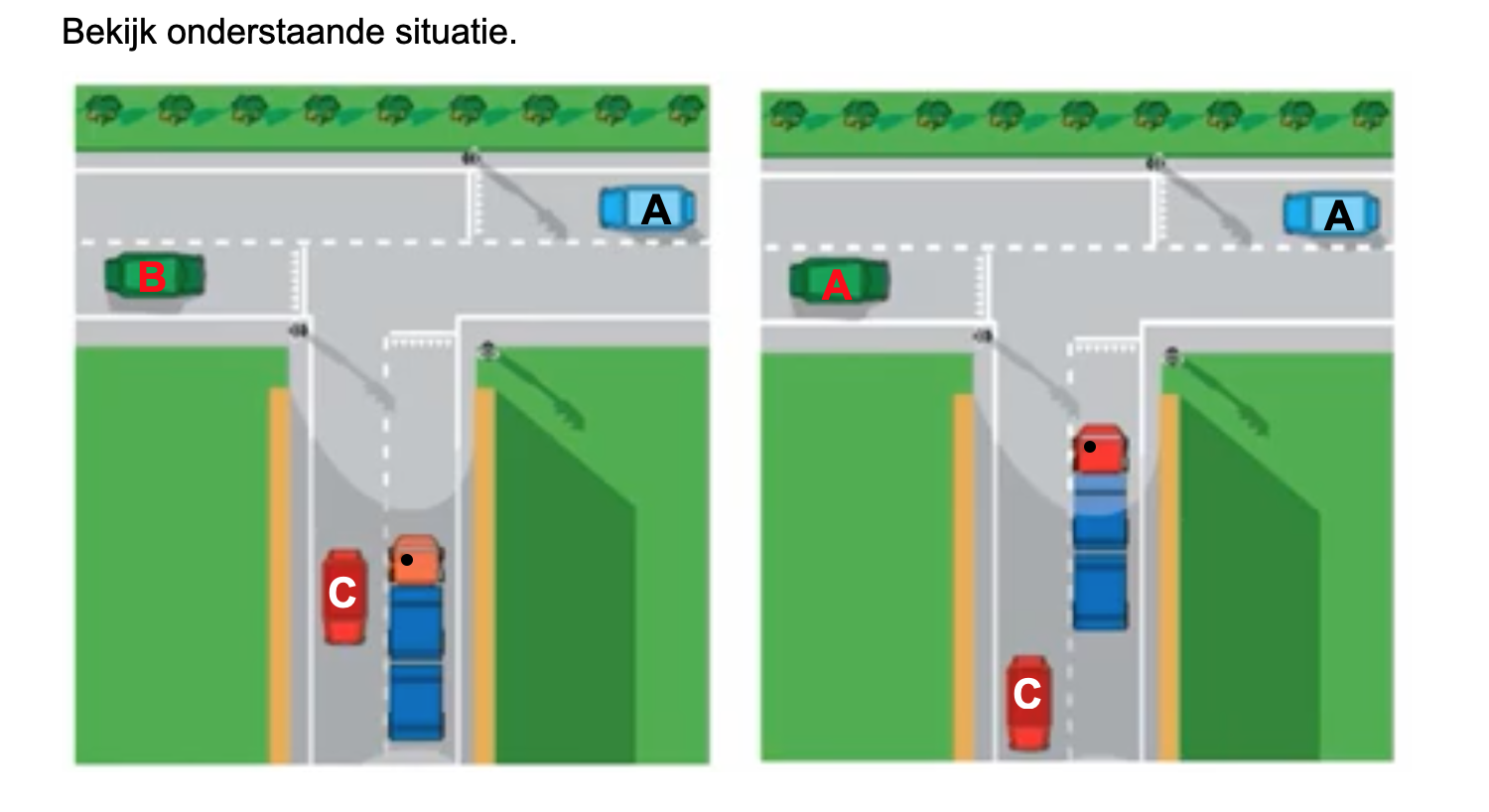
Bekijk de afbeelding hiernaast. Deze staat ook op je werkblad.
De driehoek die je hiernaast getekend ziet staat ook op je werkblad.
Bekijk de verkeersborden hiernaast. Deze staan ook op je werkblad.
Kleur in het patroon op je werkblad één motief.
Je ziet hier een plaatje van een kralenketting.
Wat is het motief in de ketting die hiernaast is afgebeeld?
en 
.
In de tekening is / S1 = 40o.
Zet sterretjes in alle hoeken die even groot zijn als de hoek met het sterretje *.
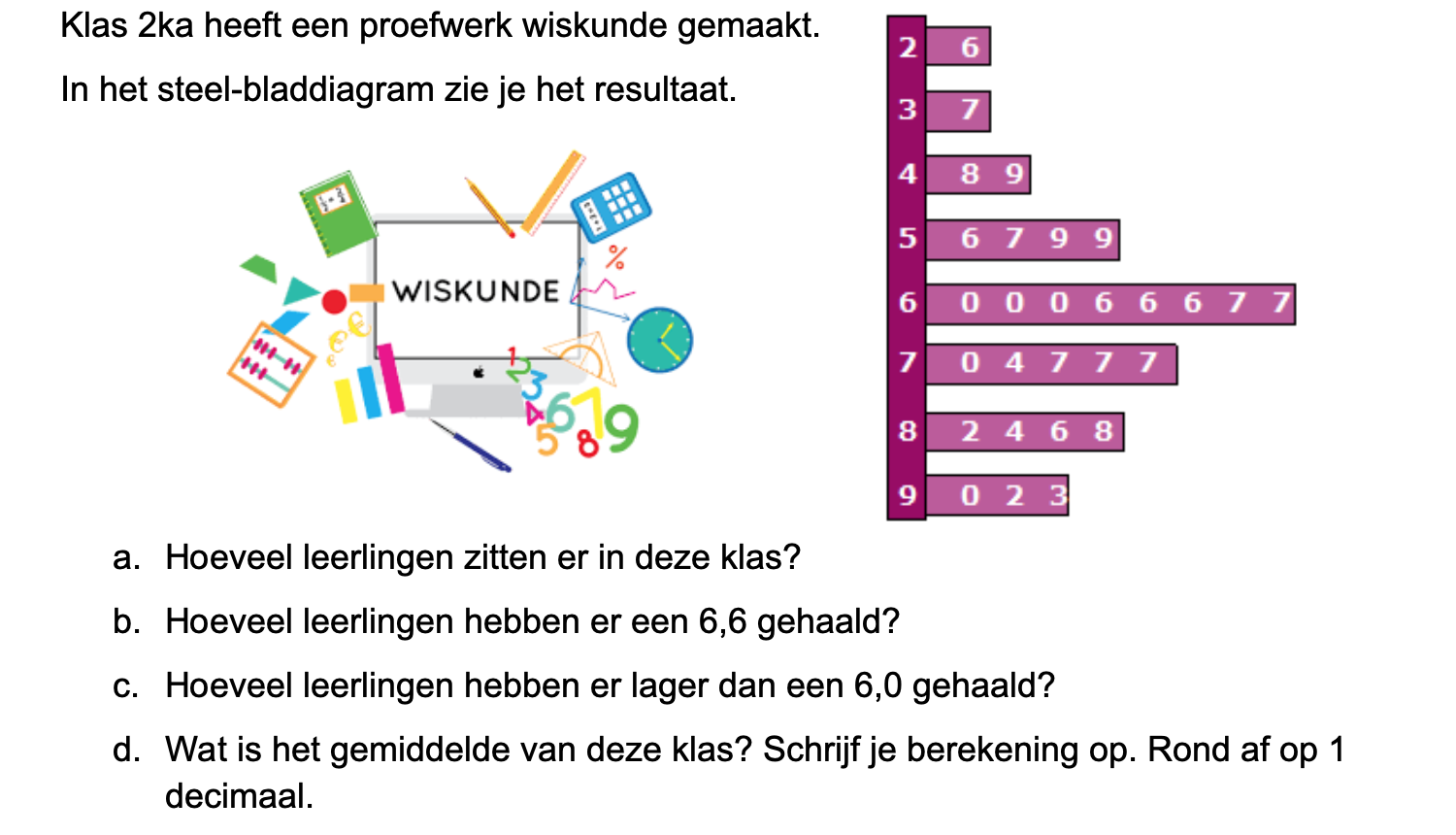
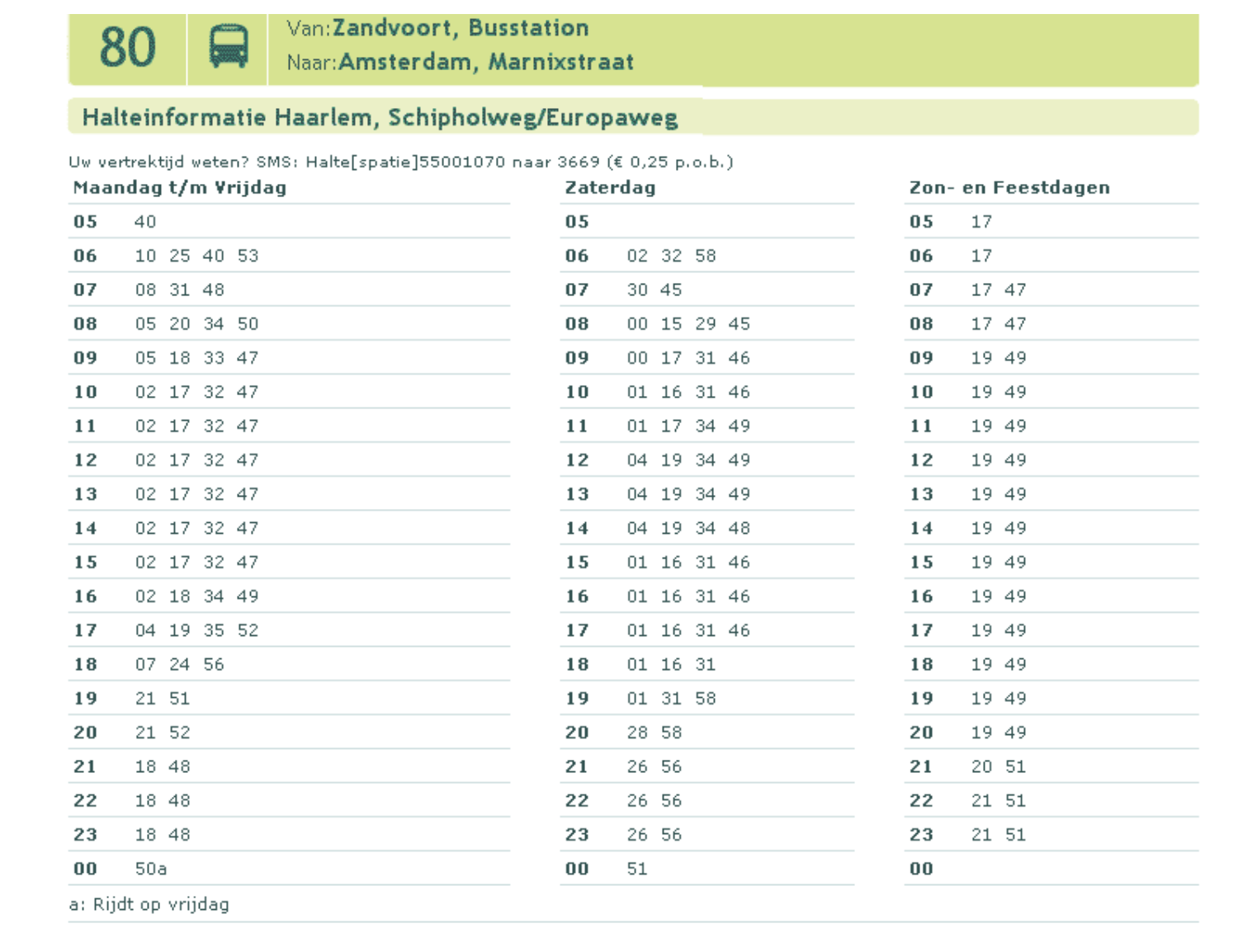
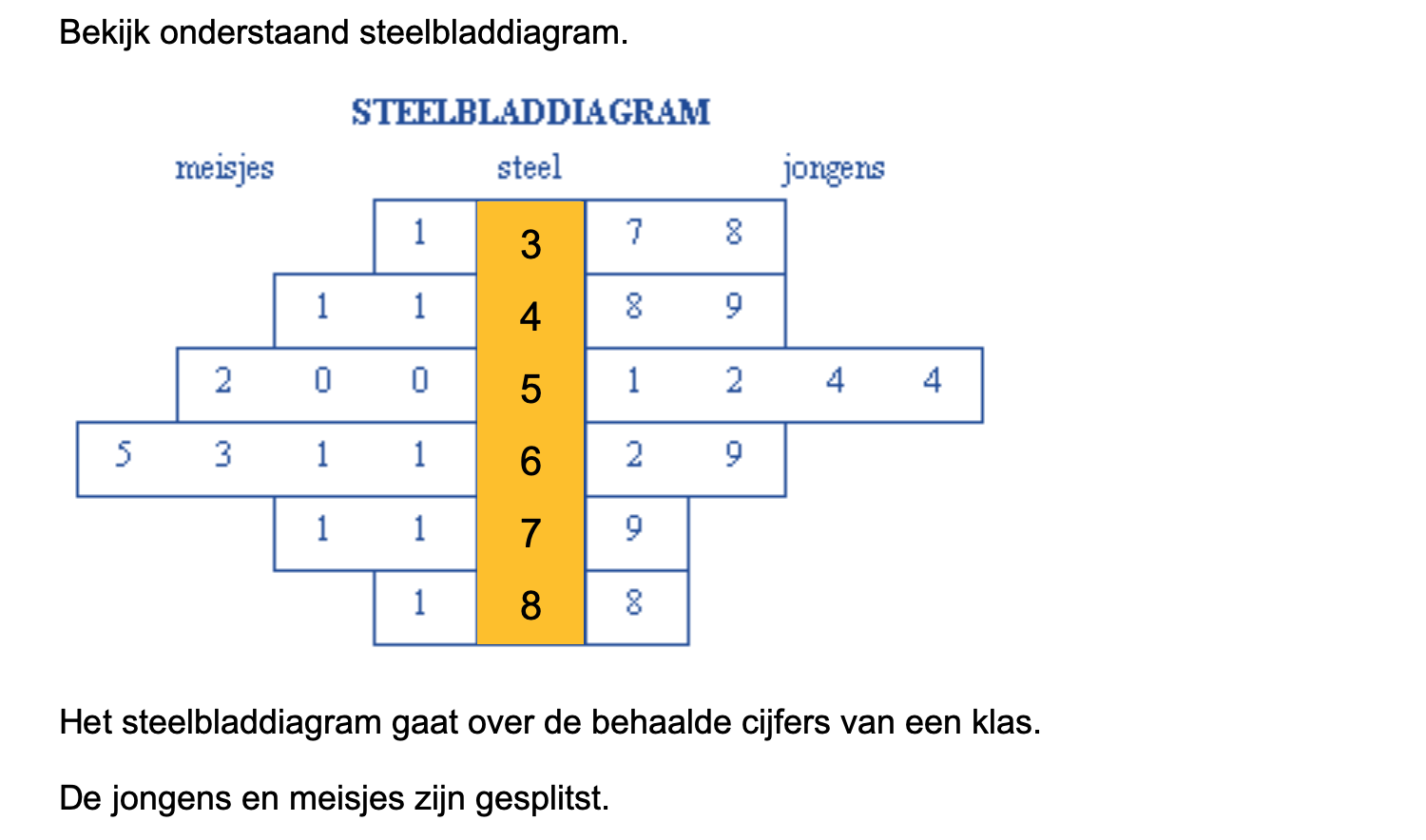
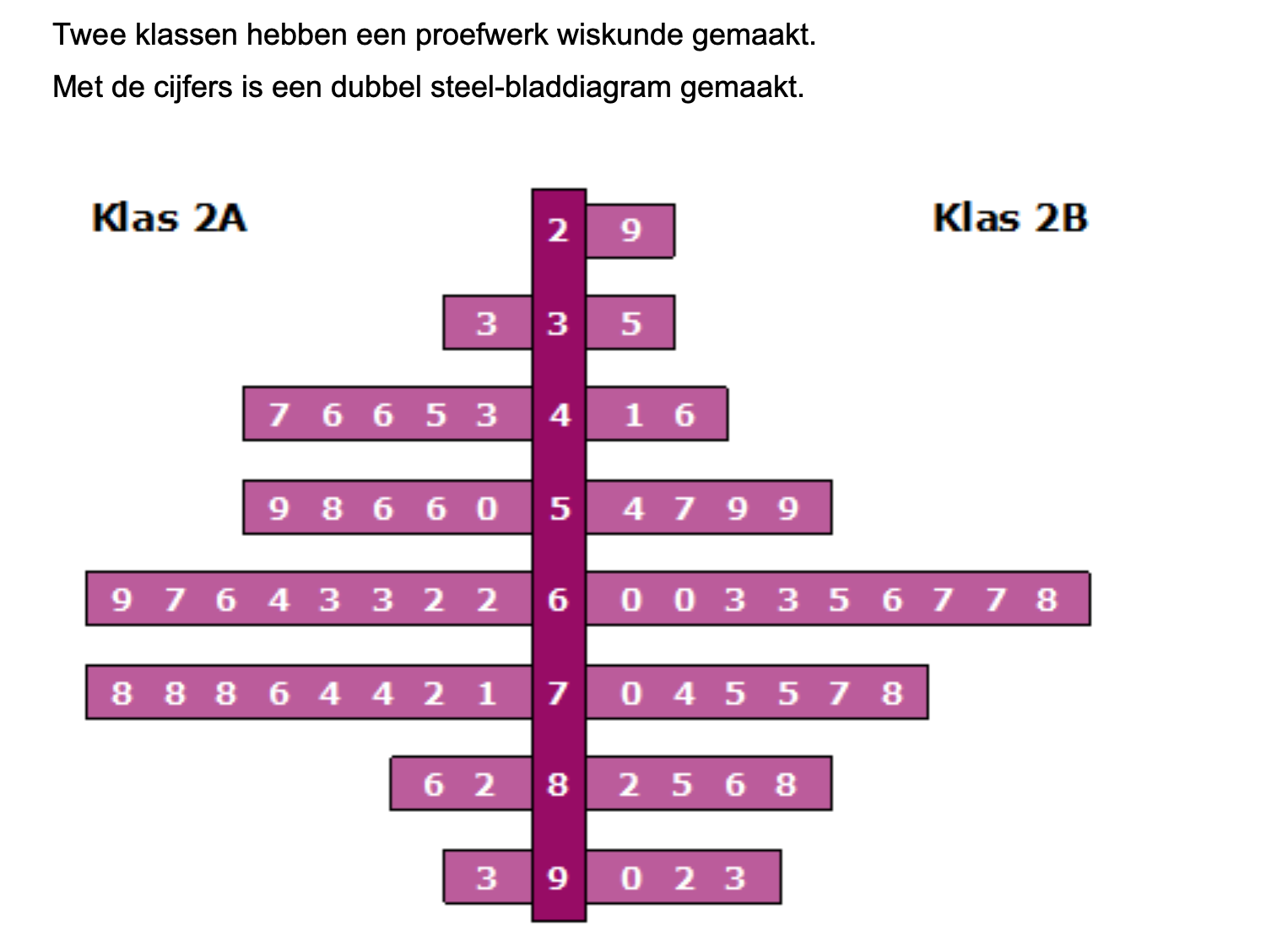
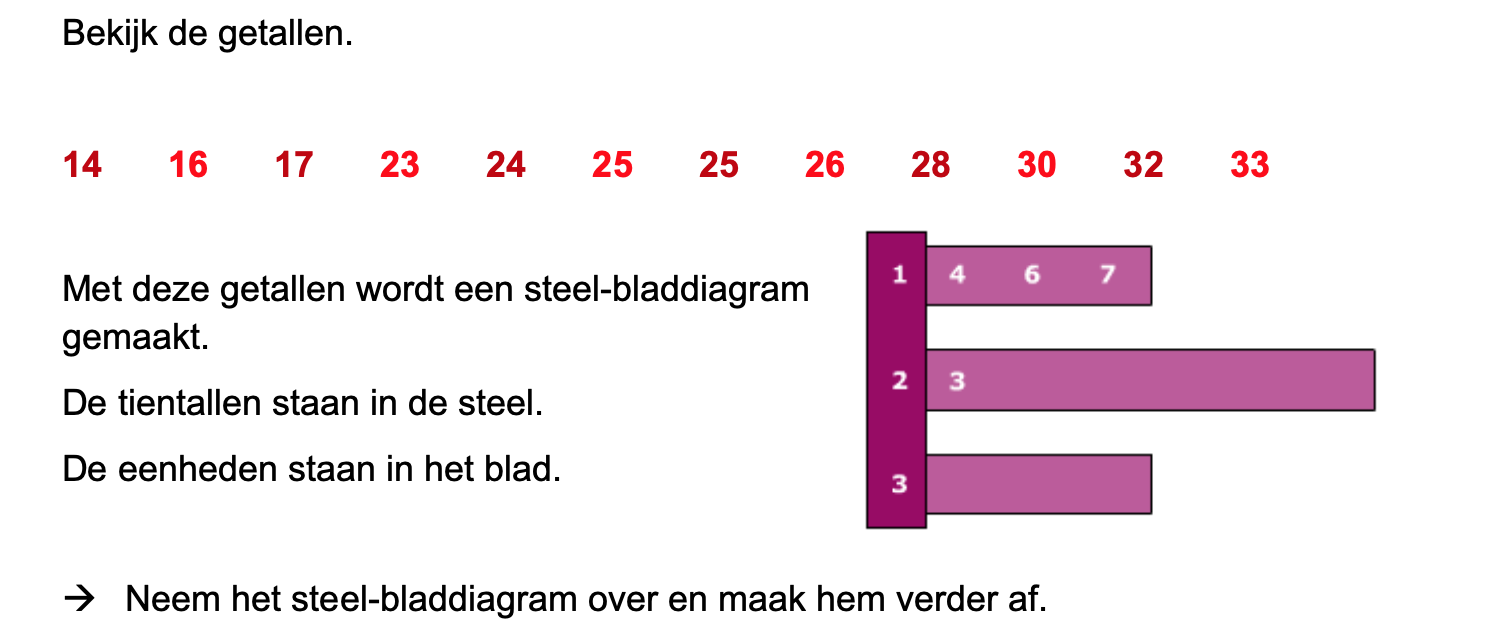
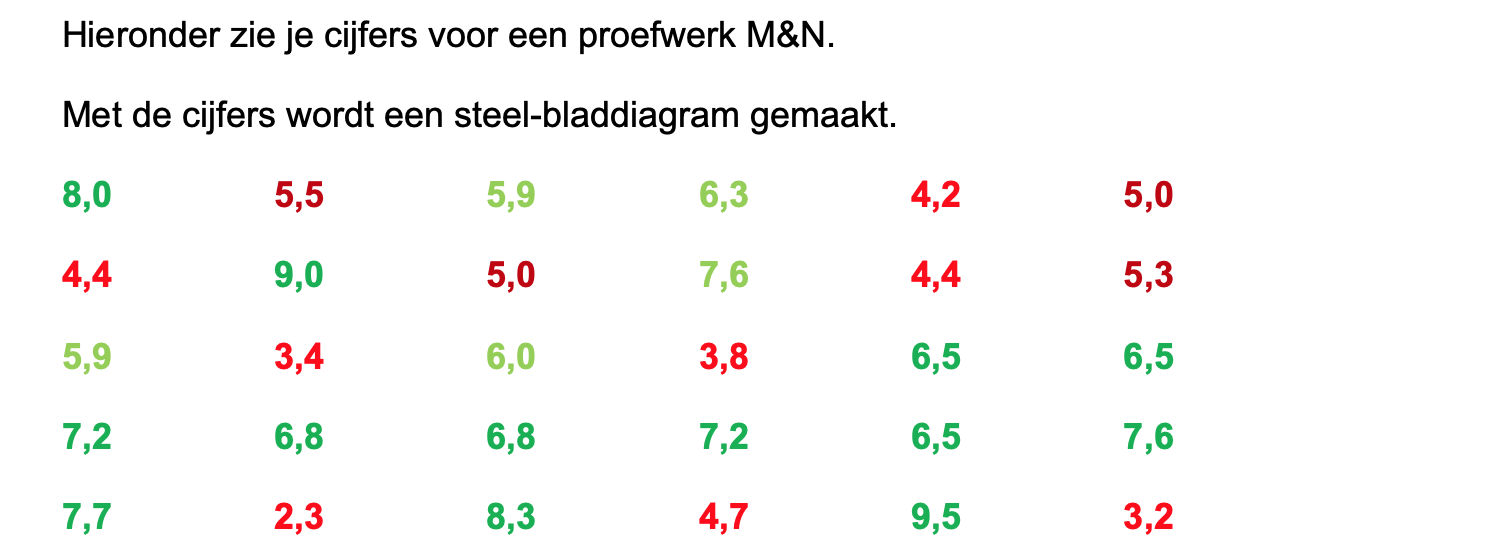
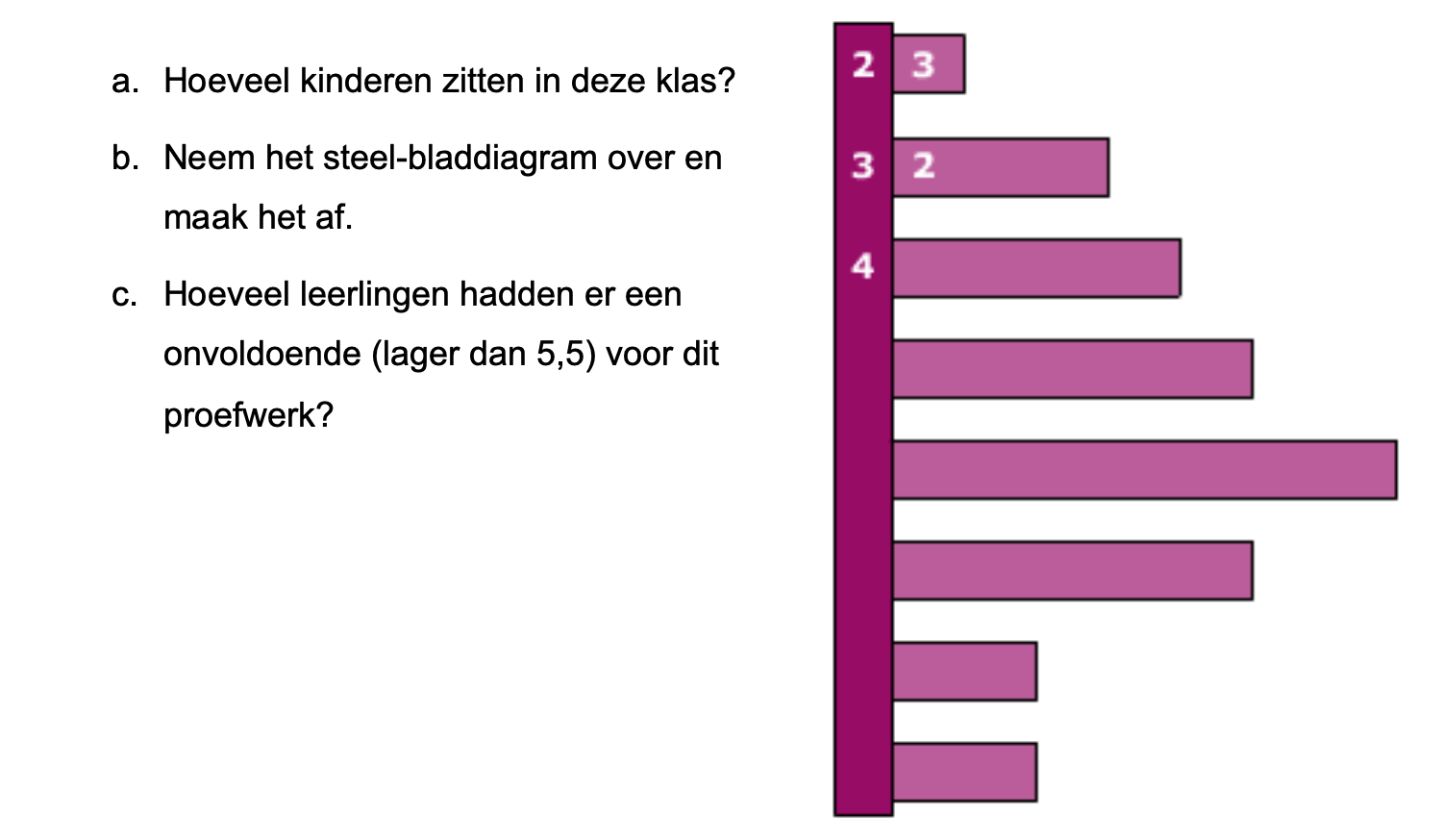
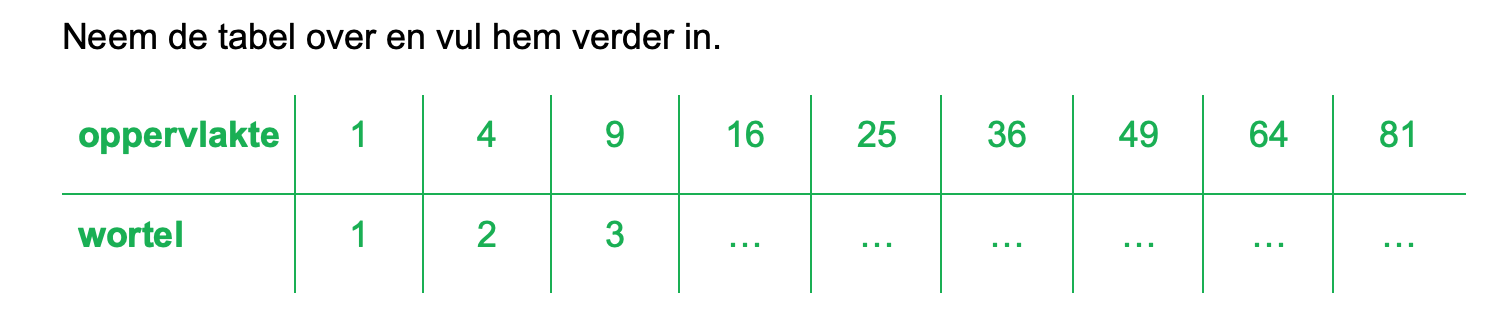
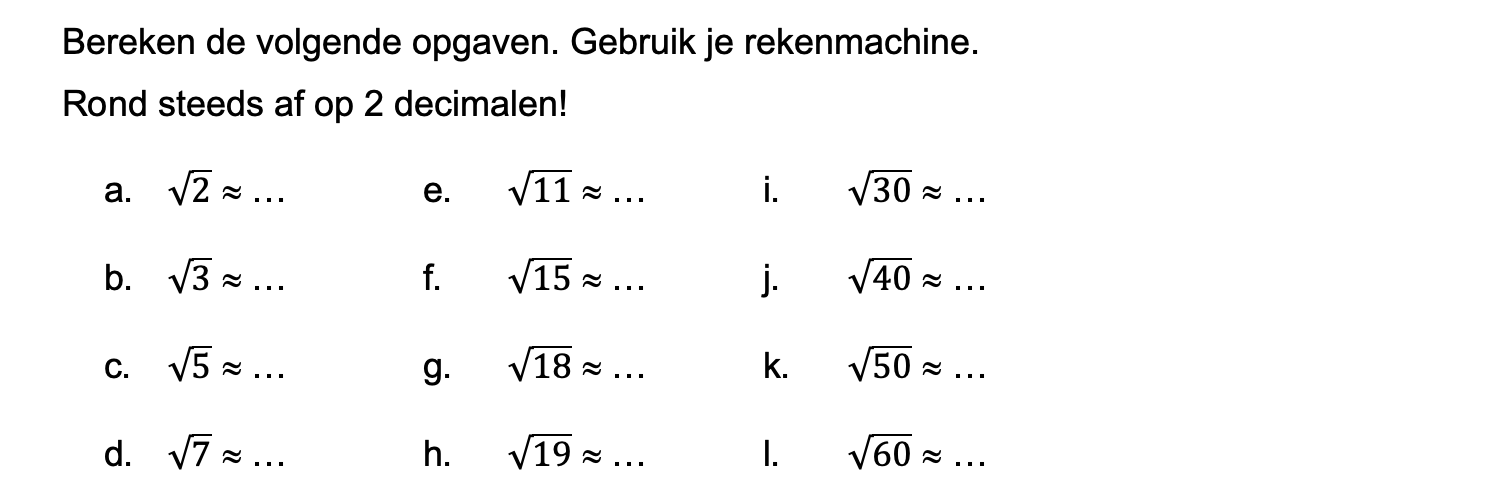
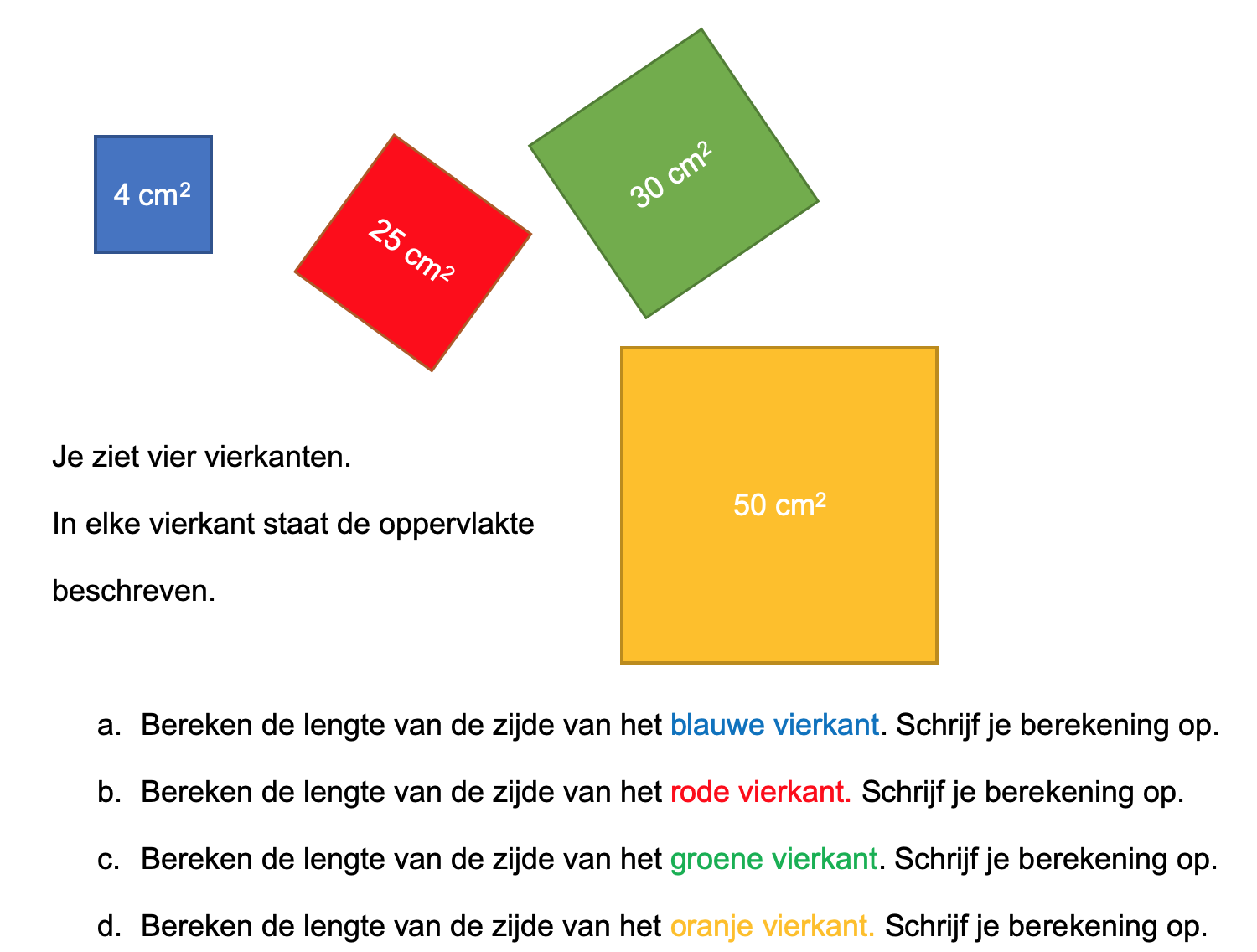
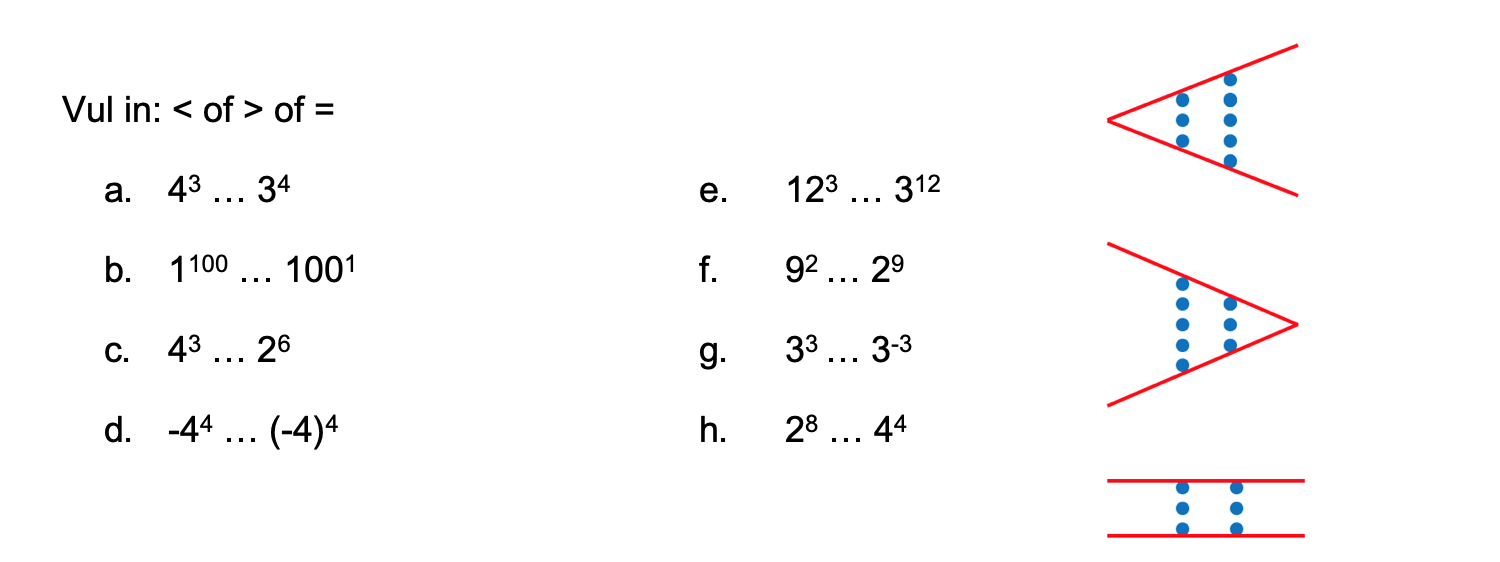
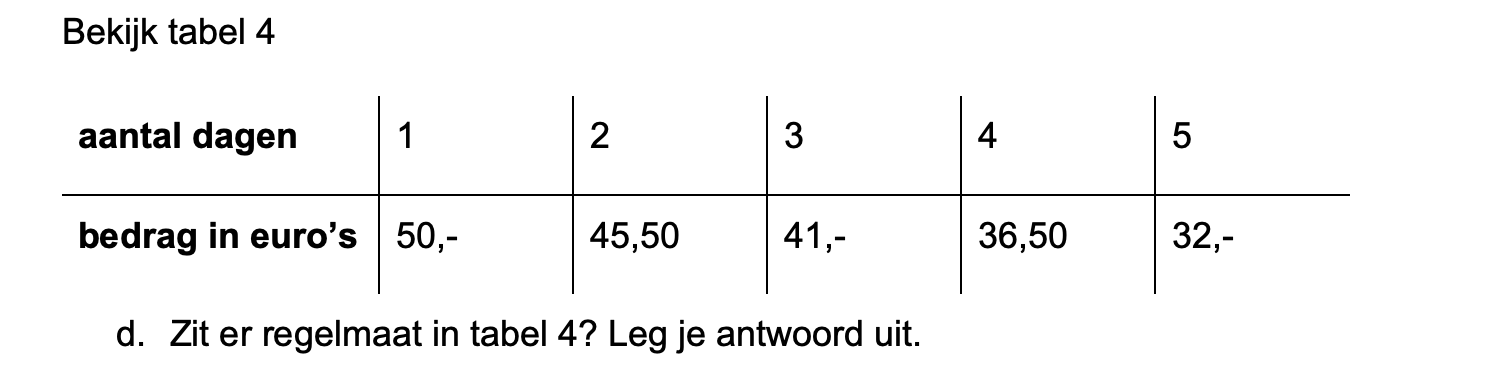
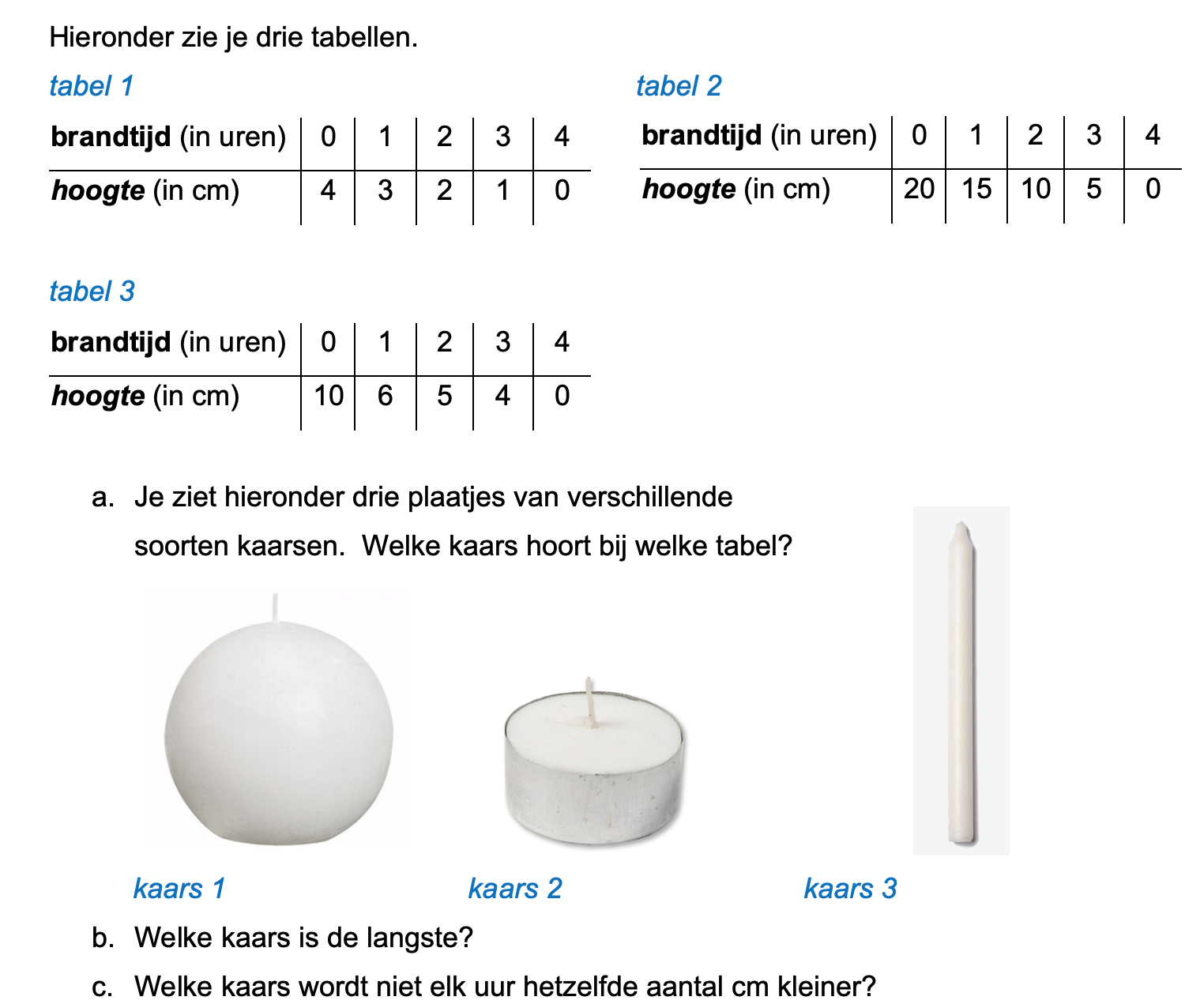
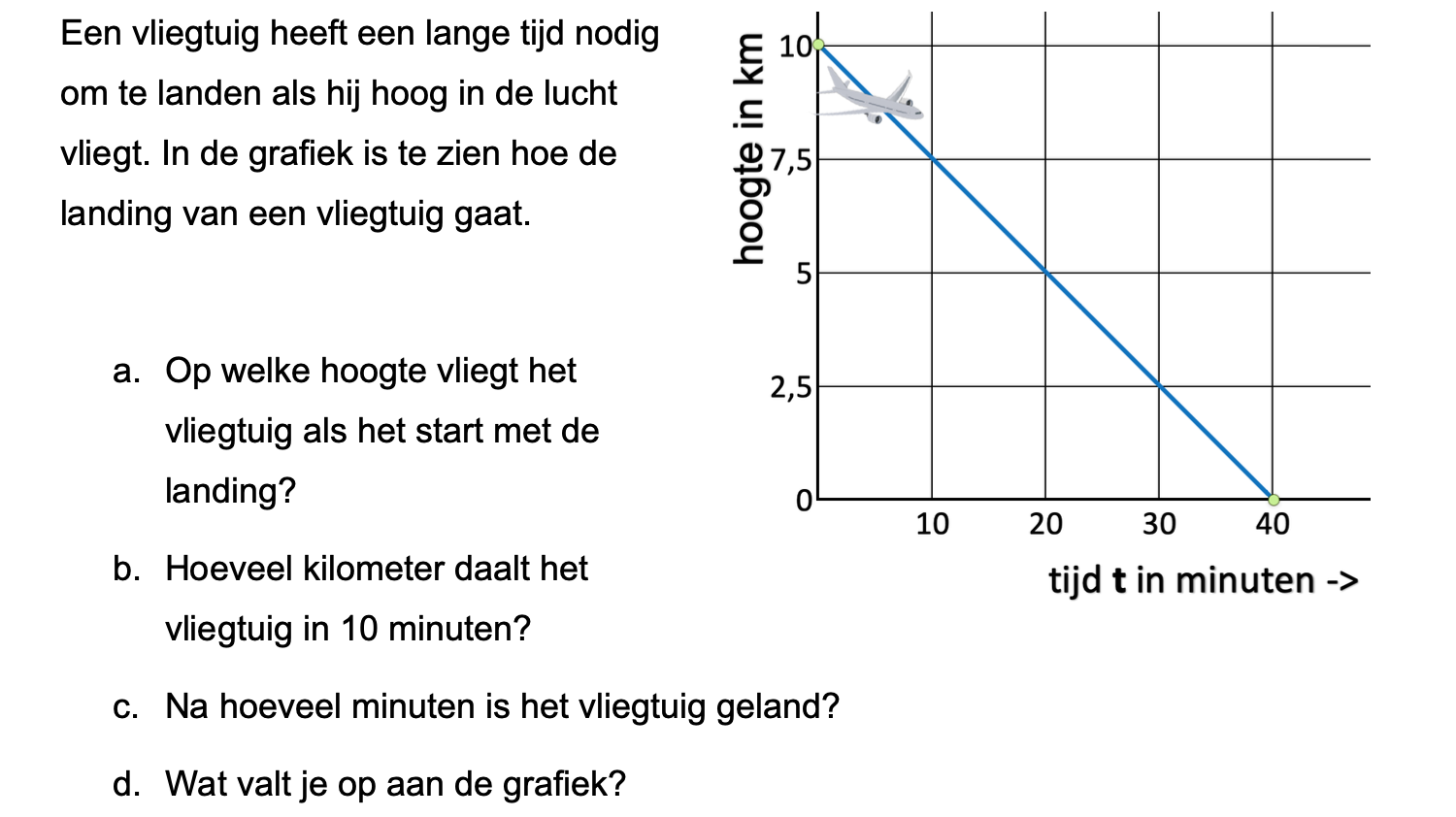
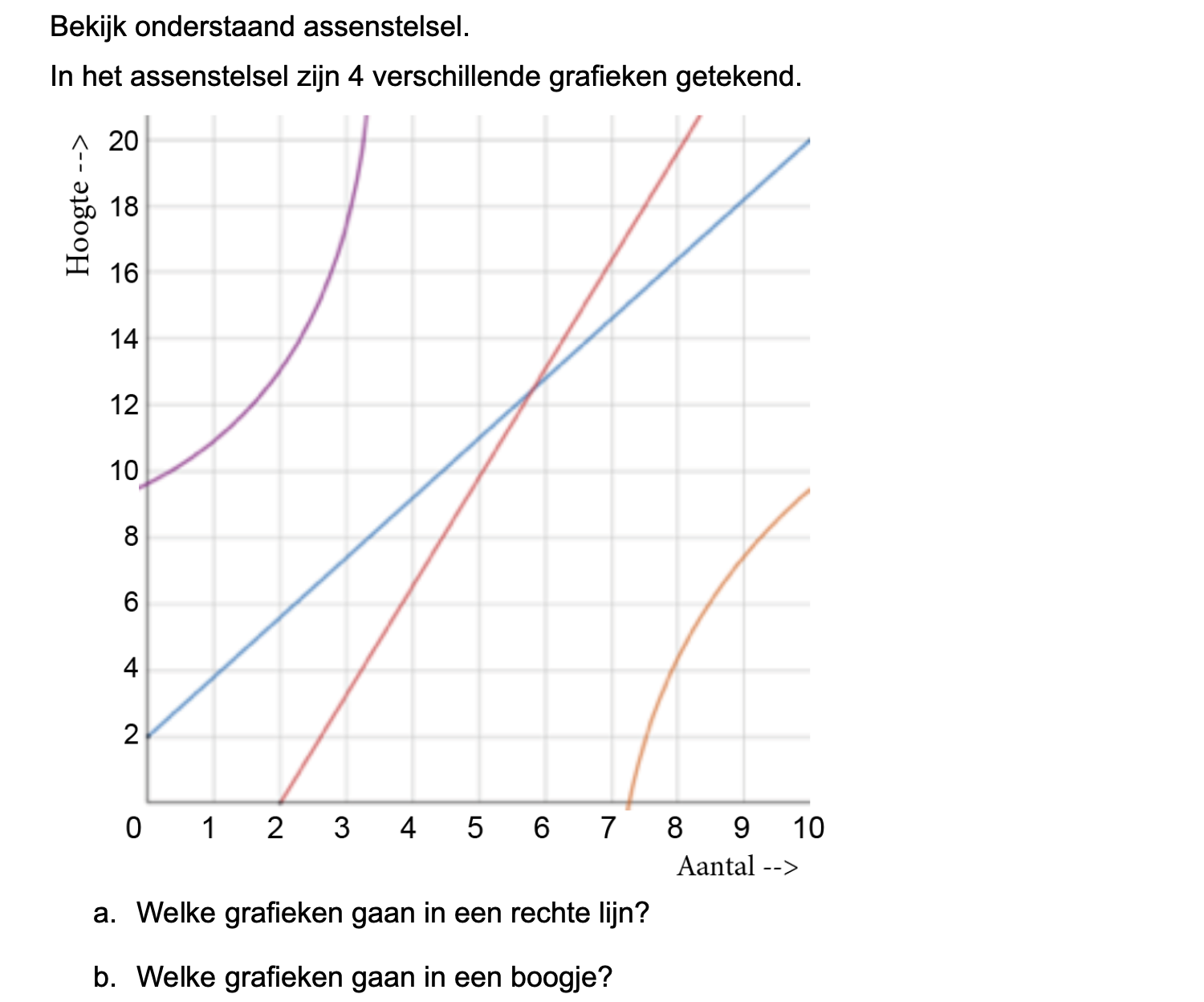
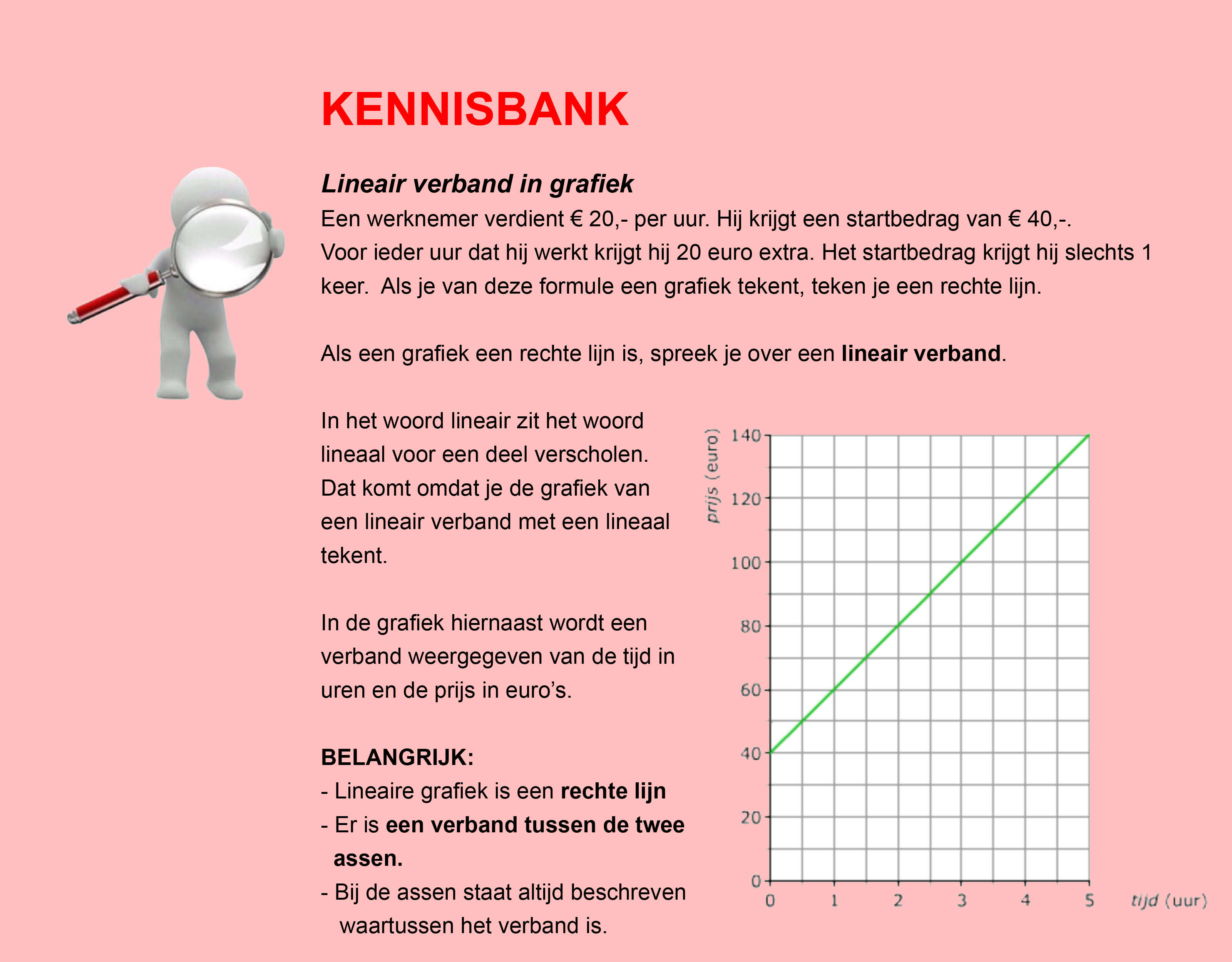
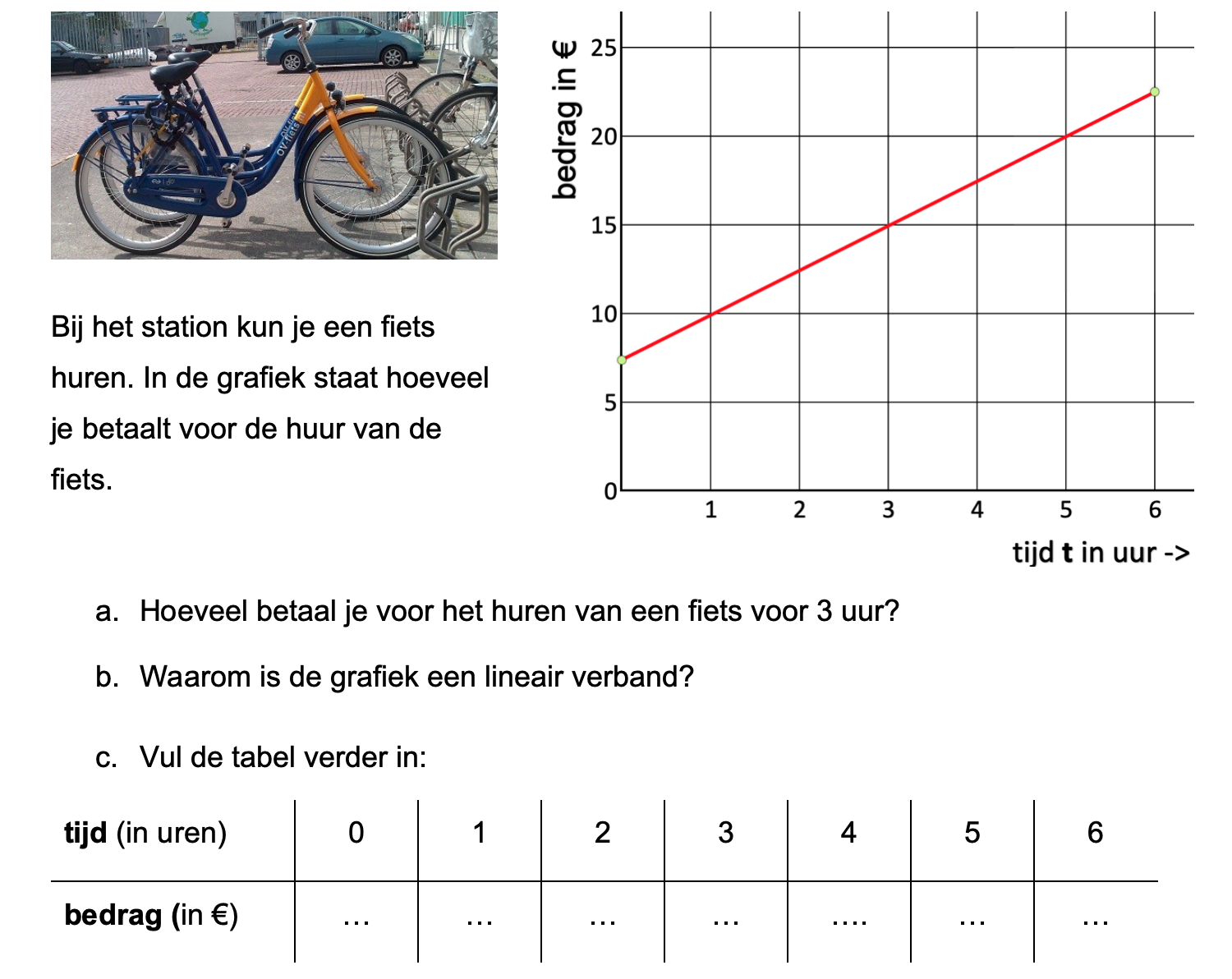
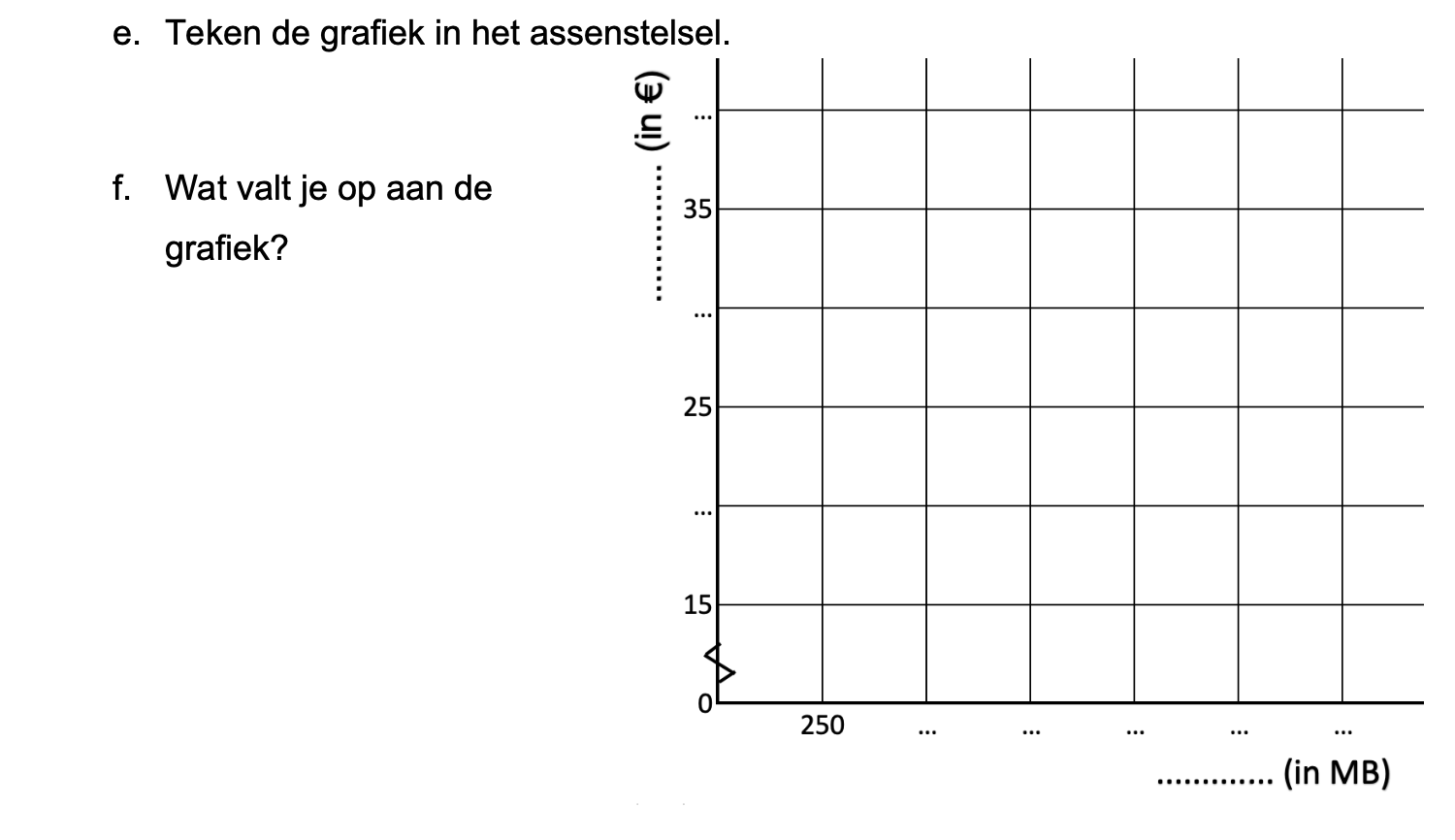
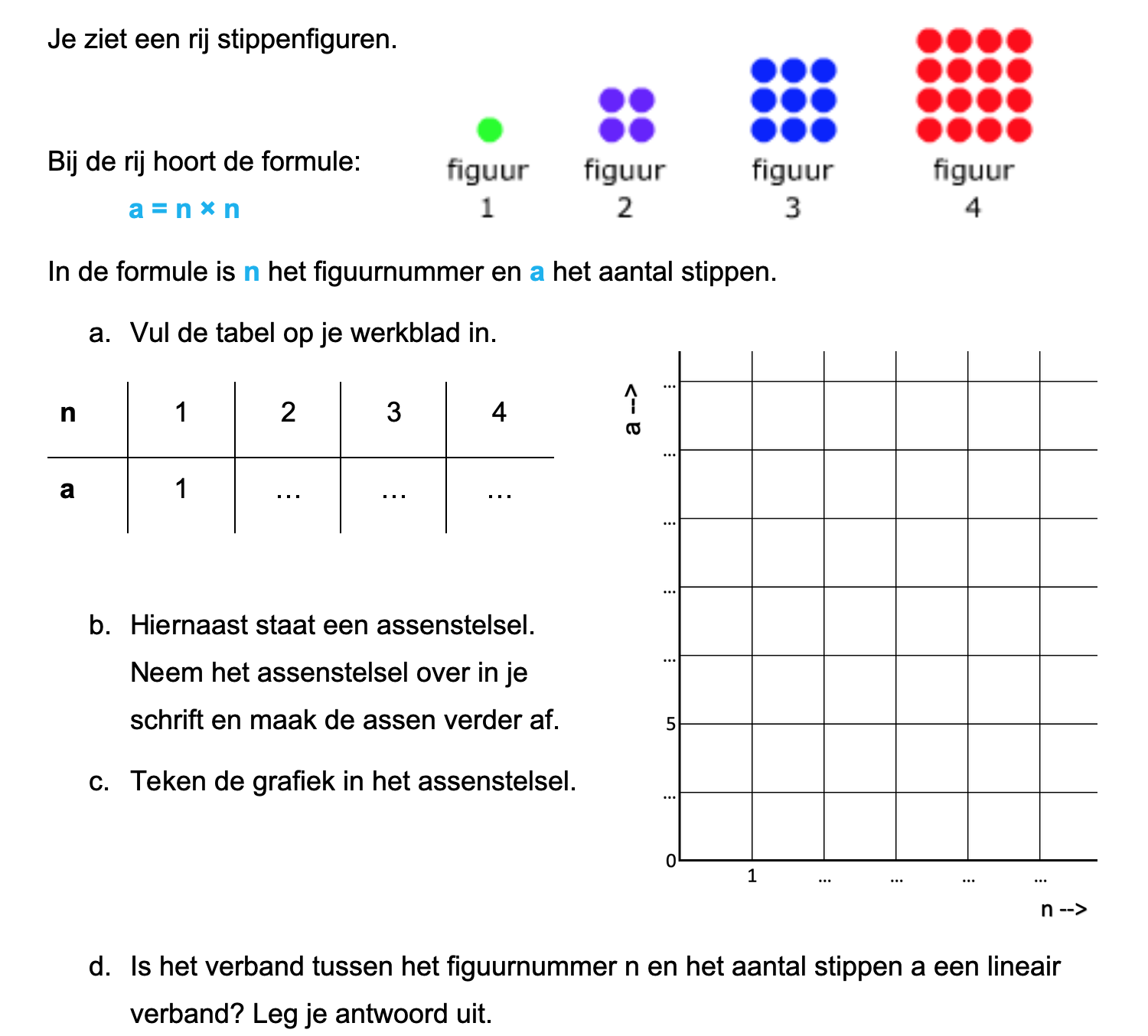
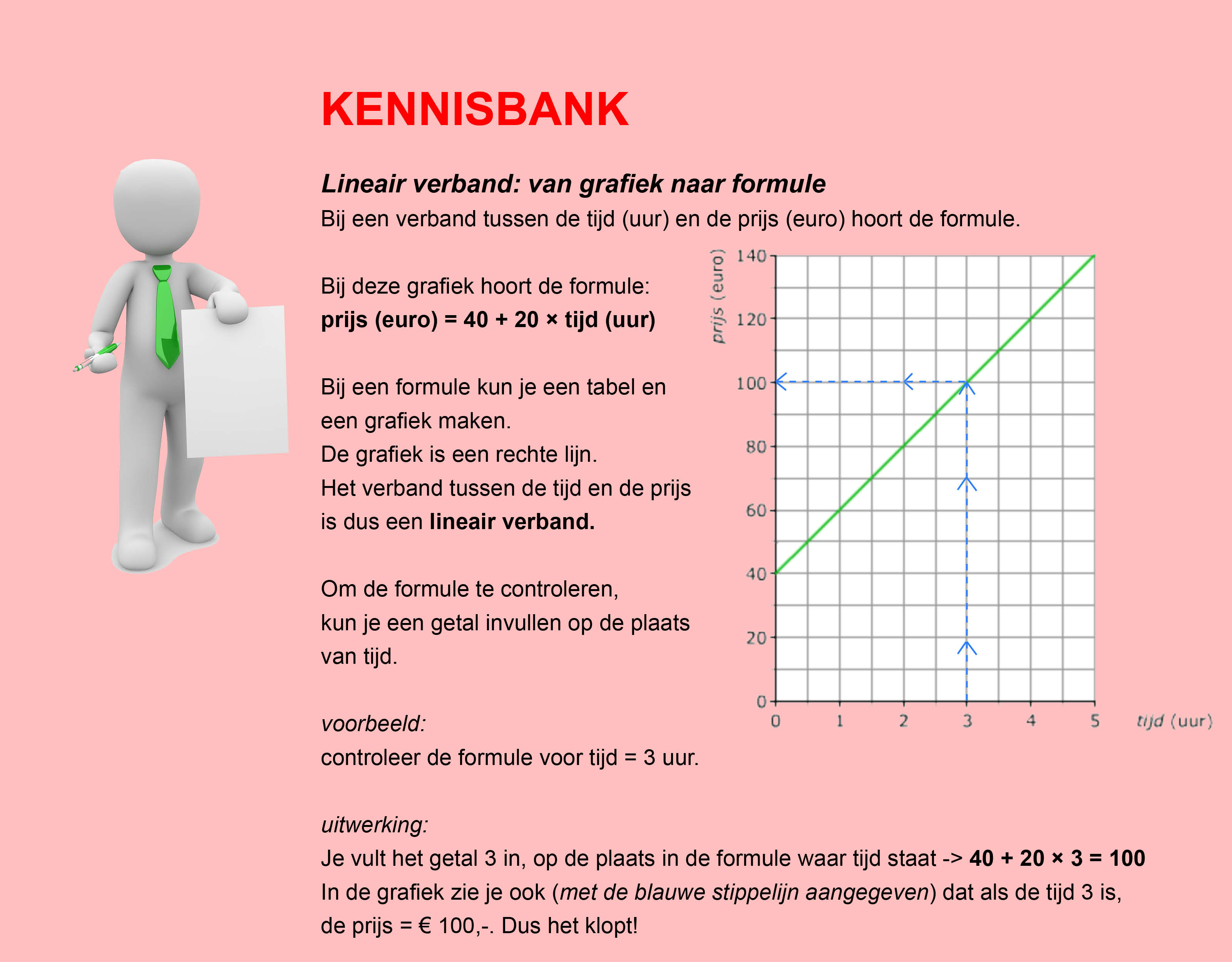
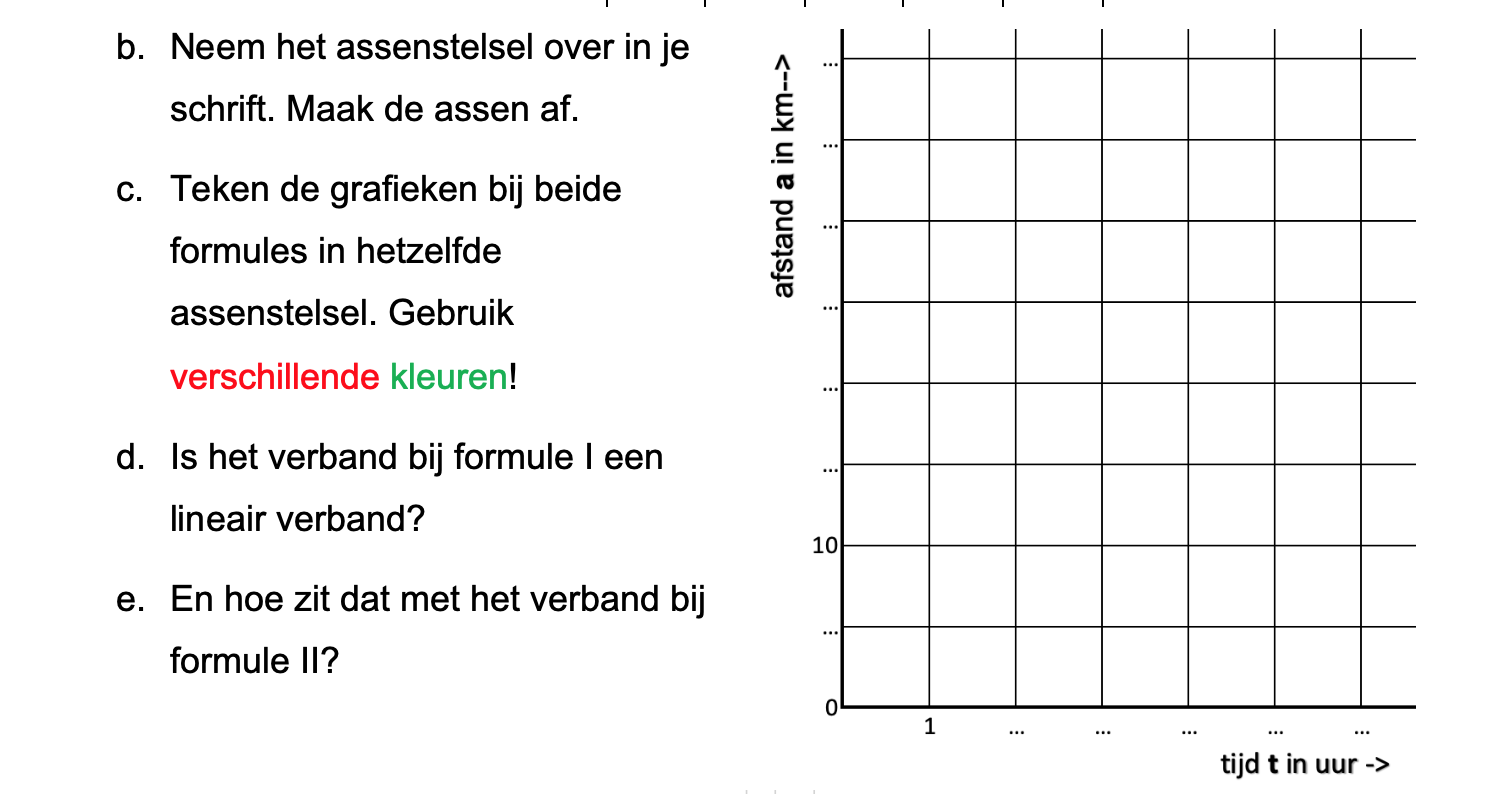
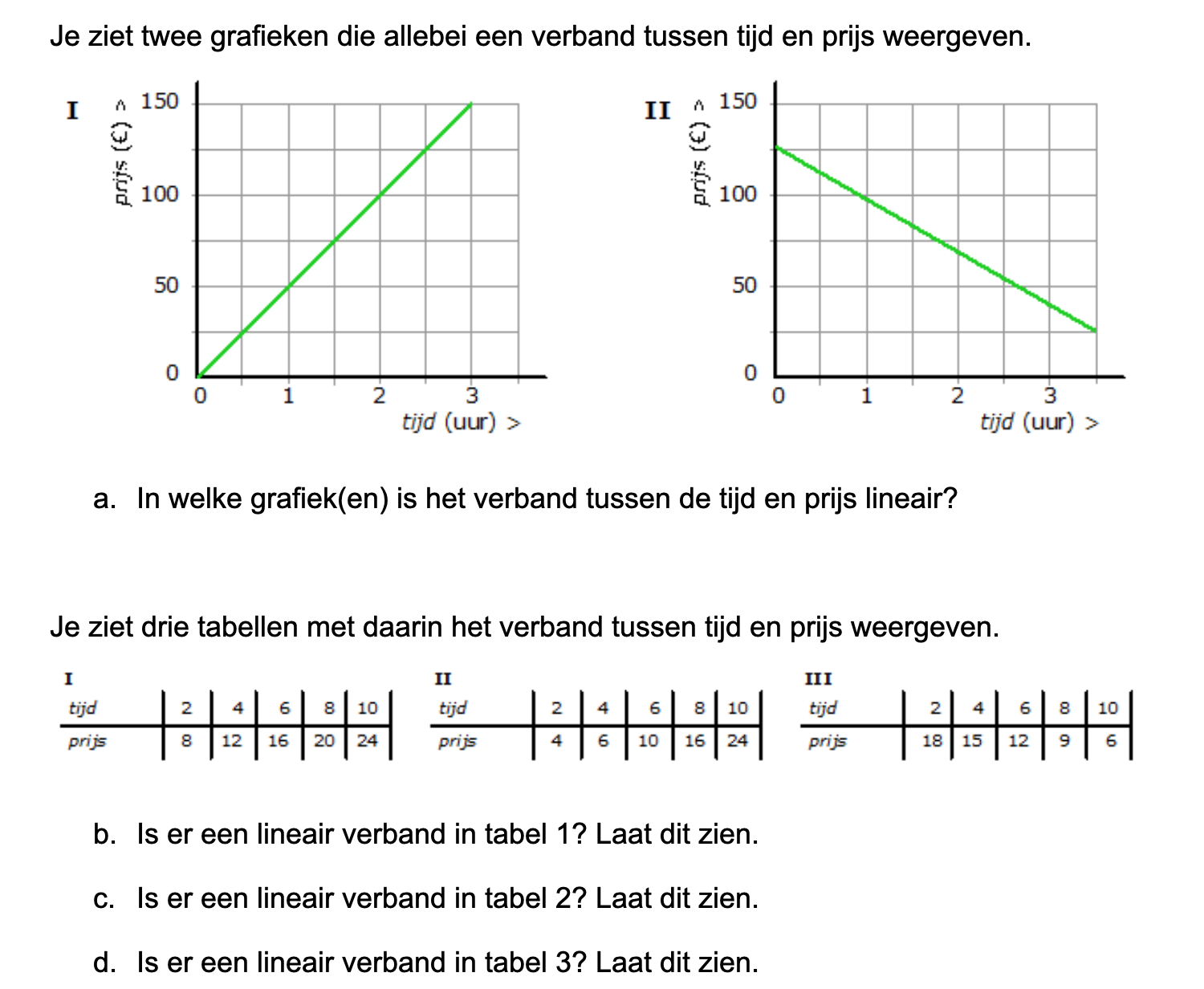
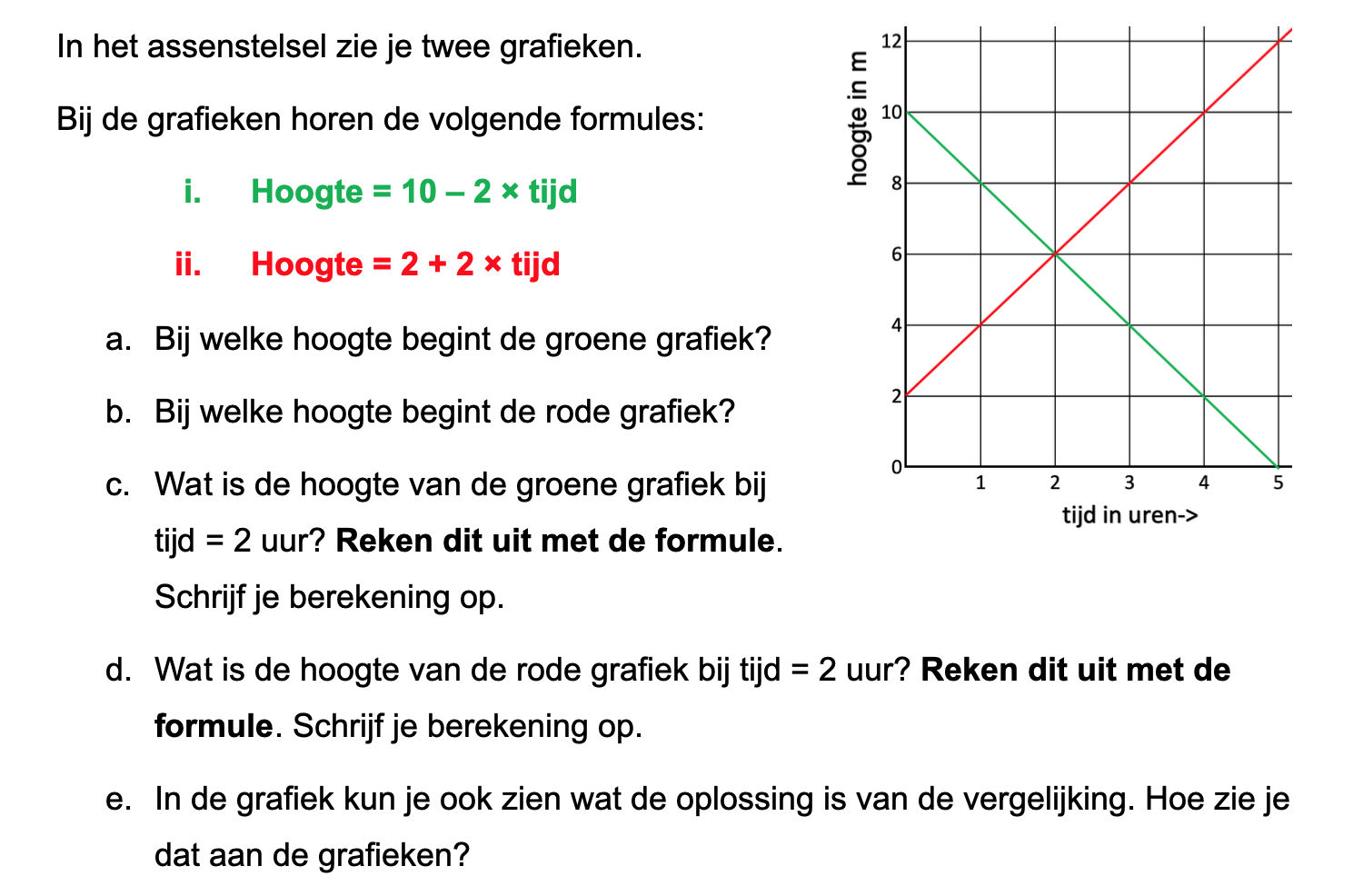
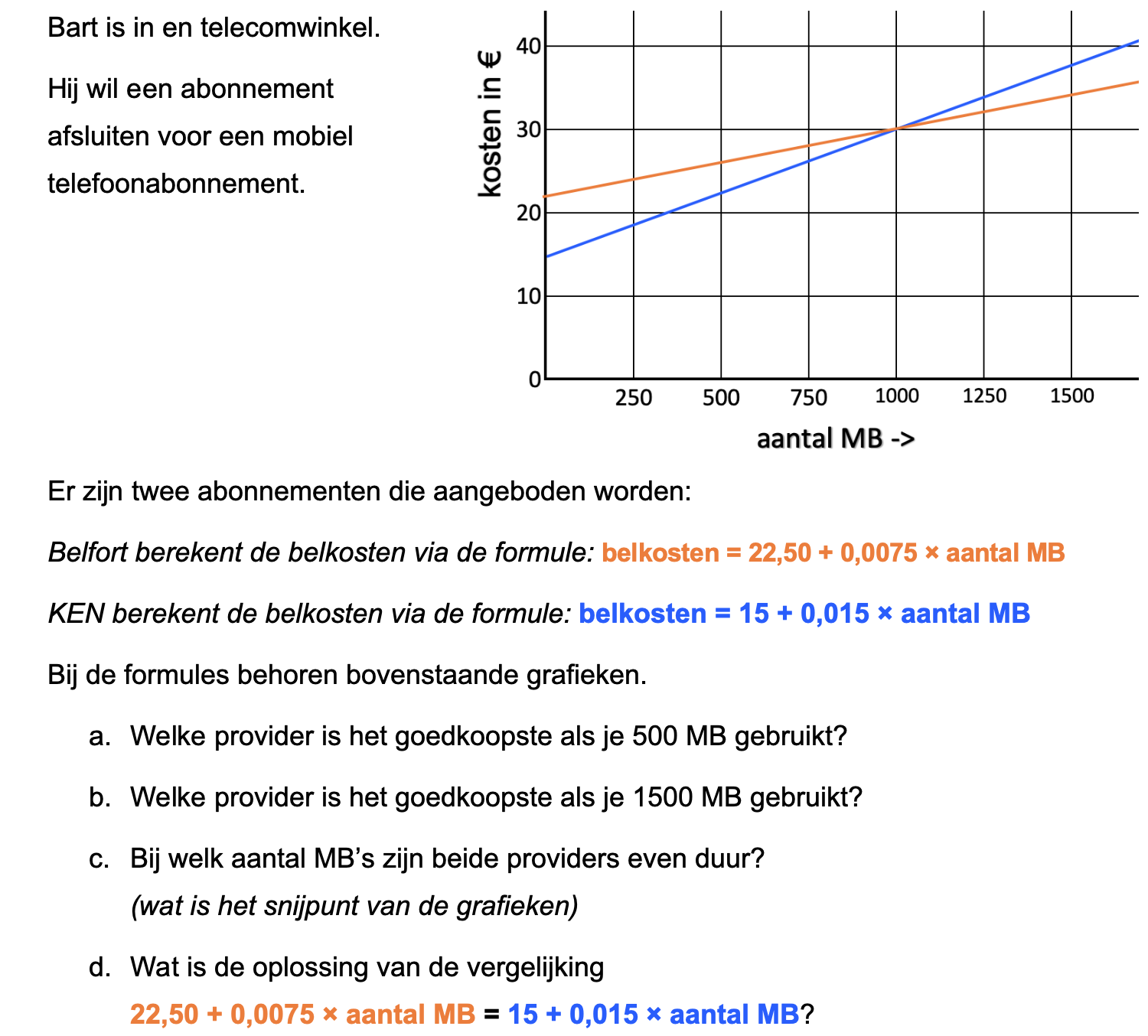
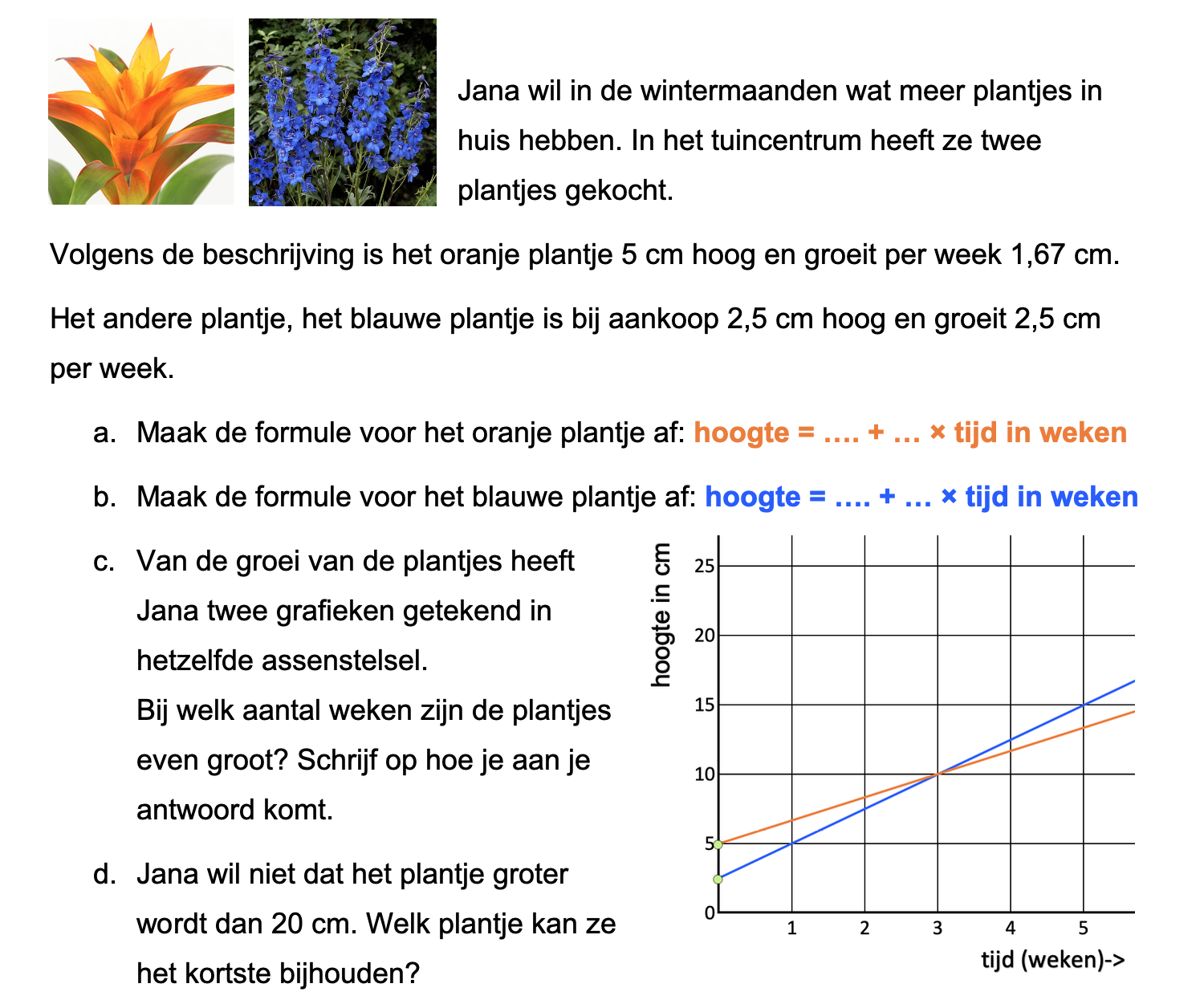
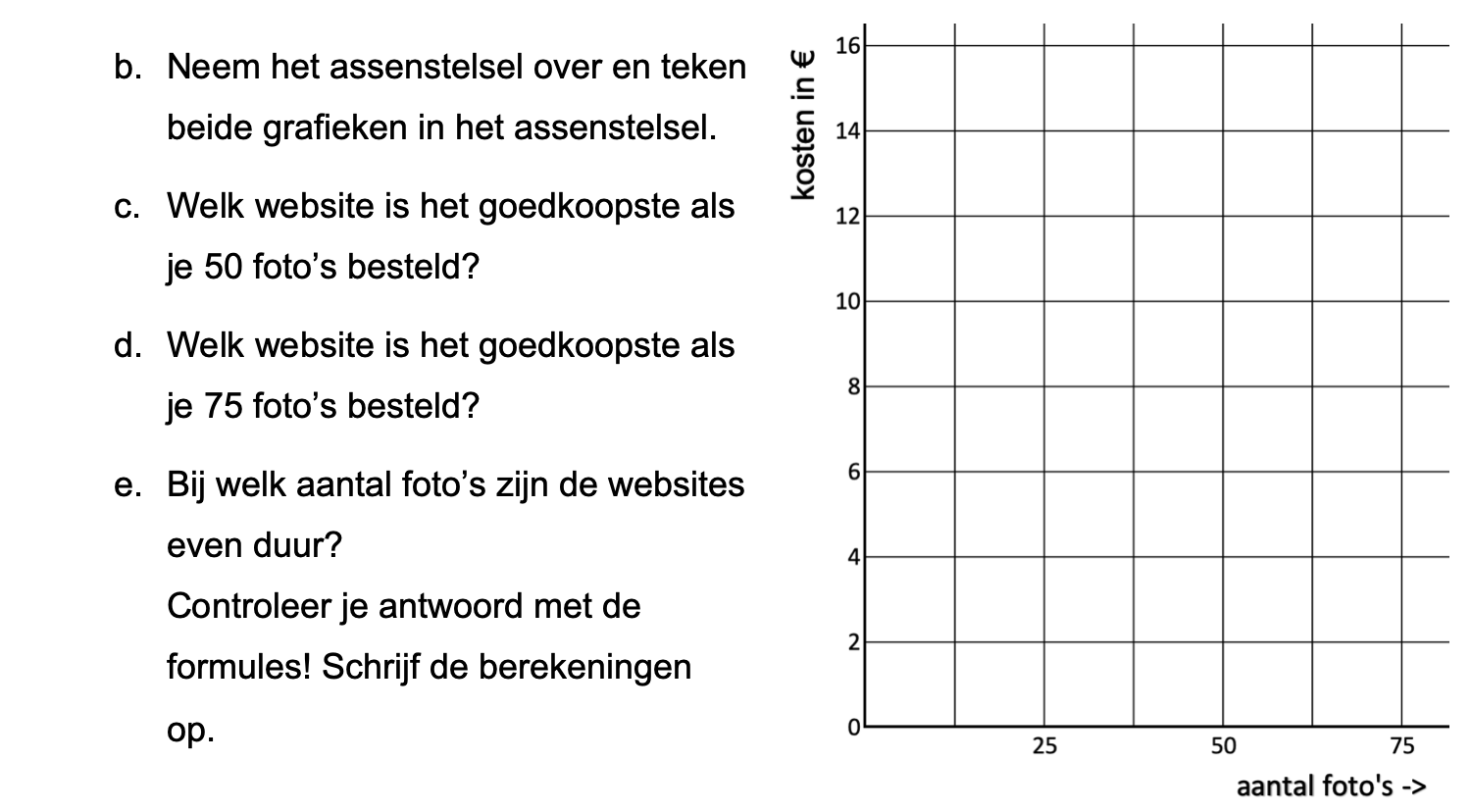
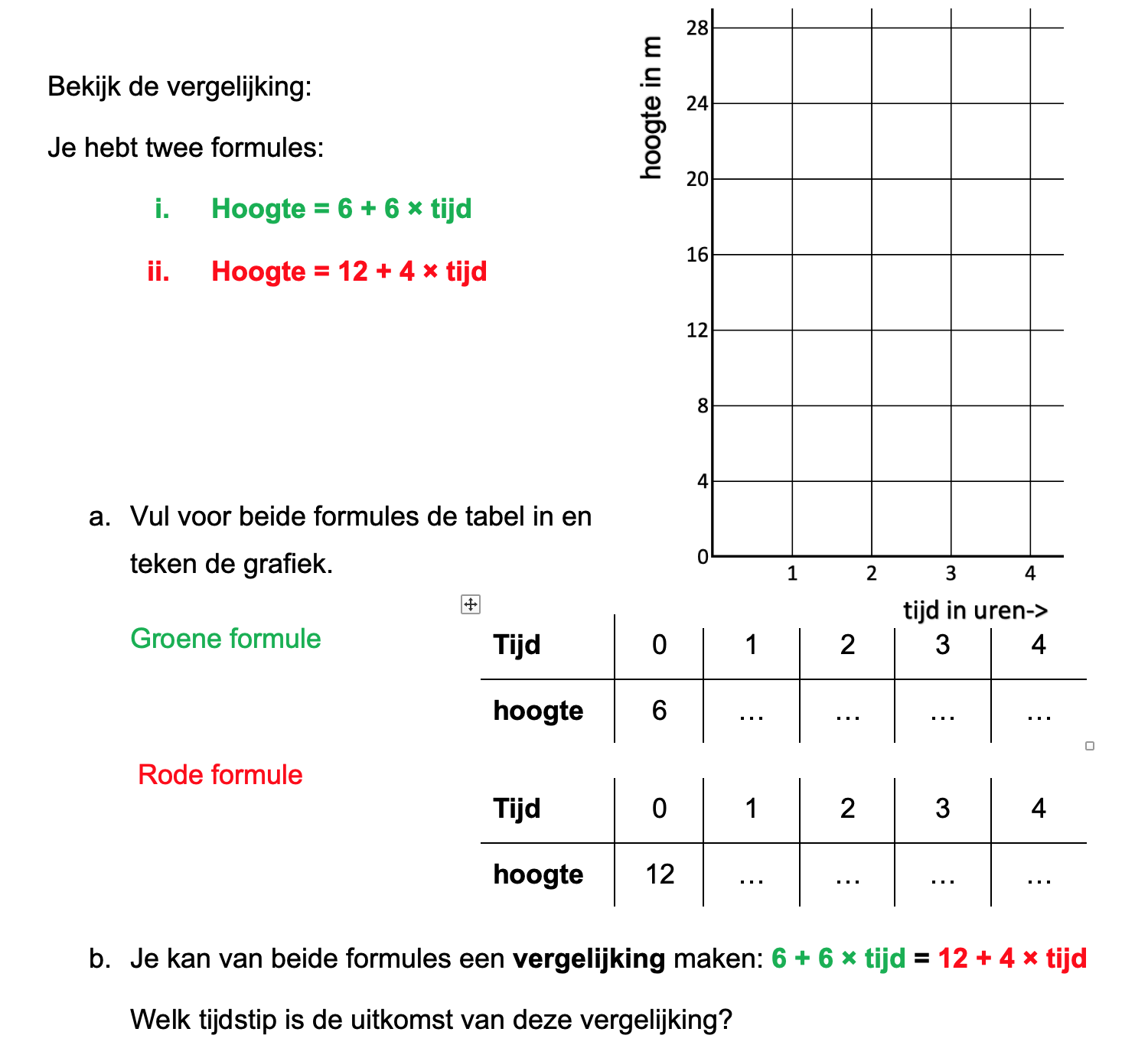
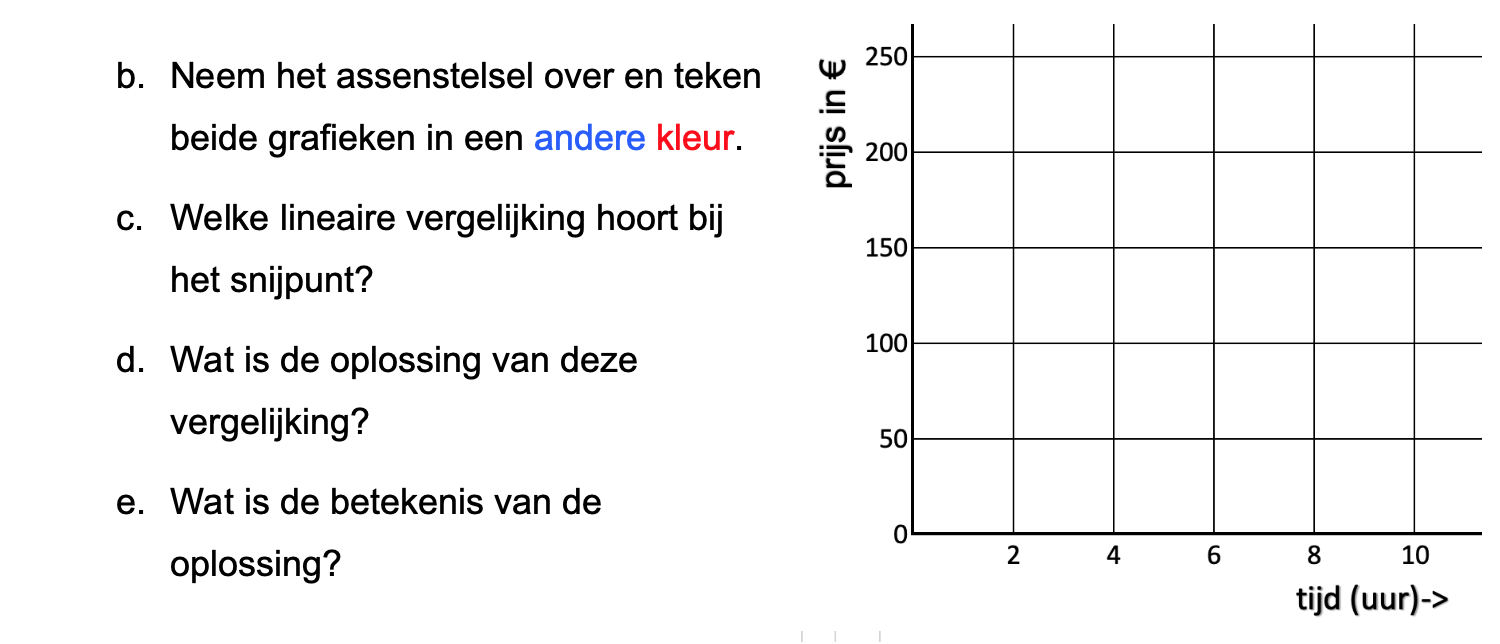
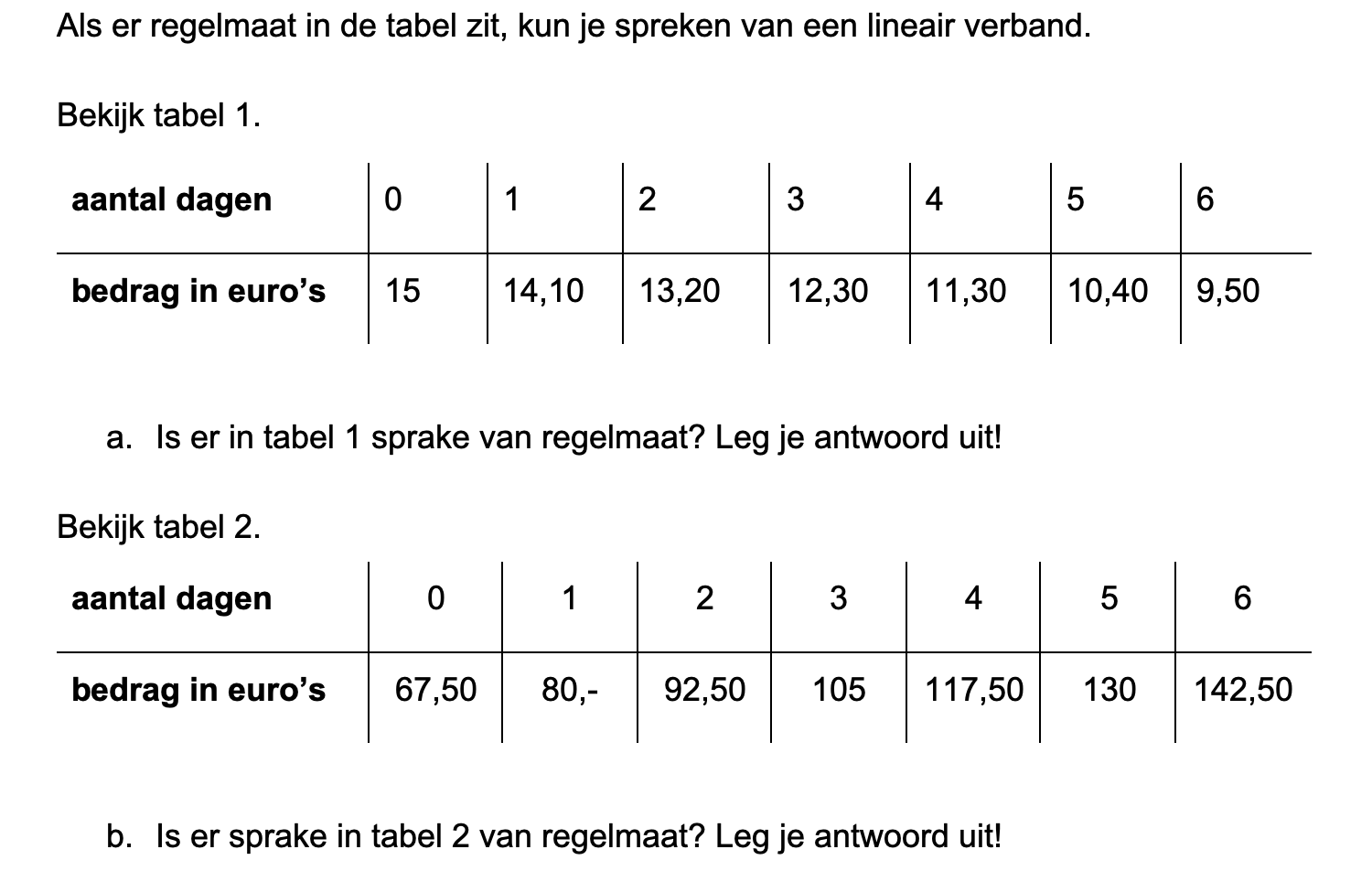
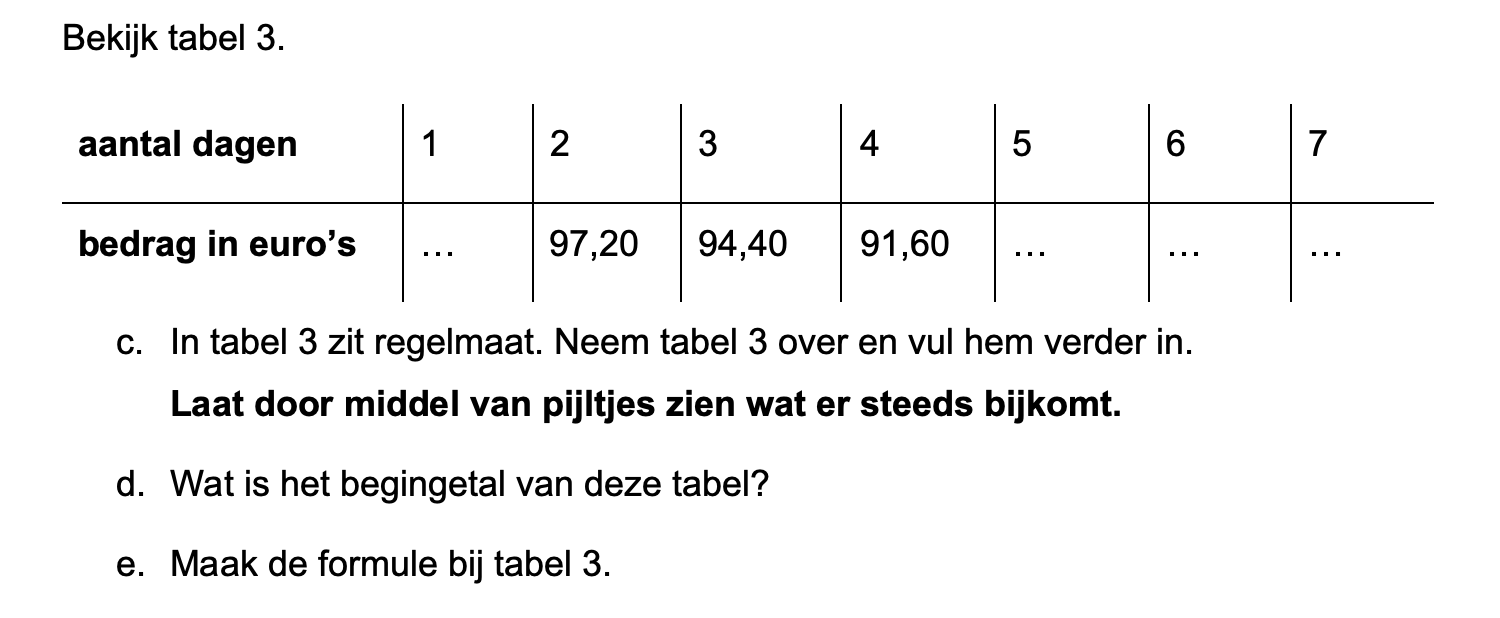
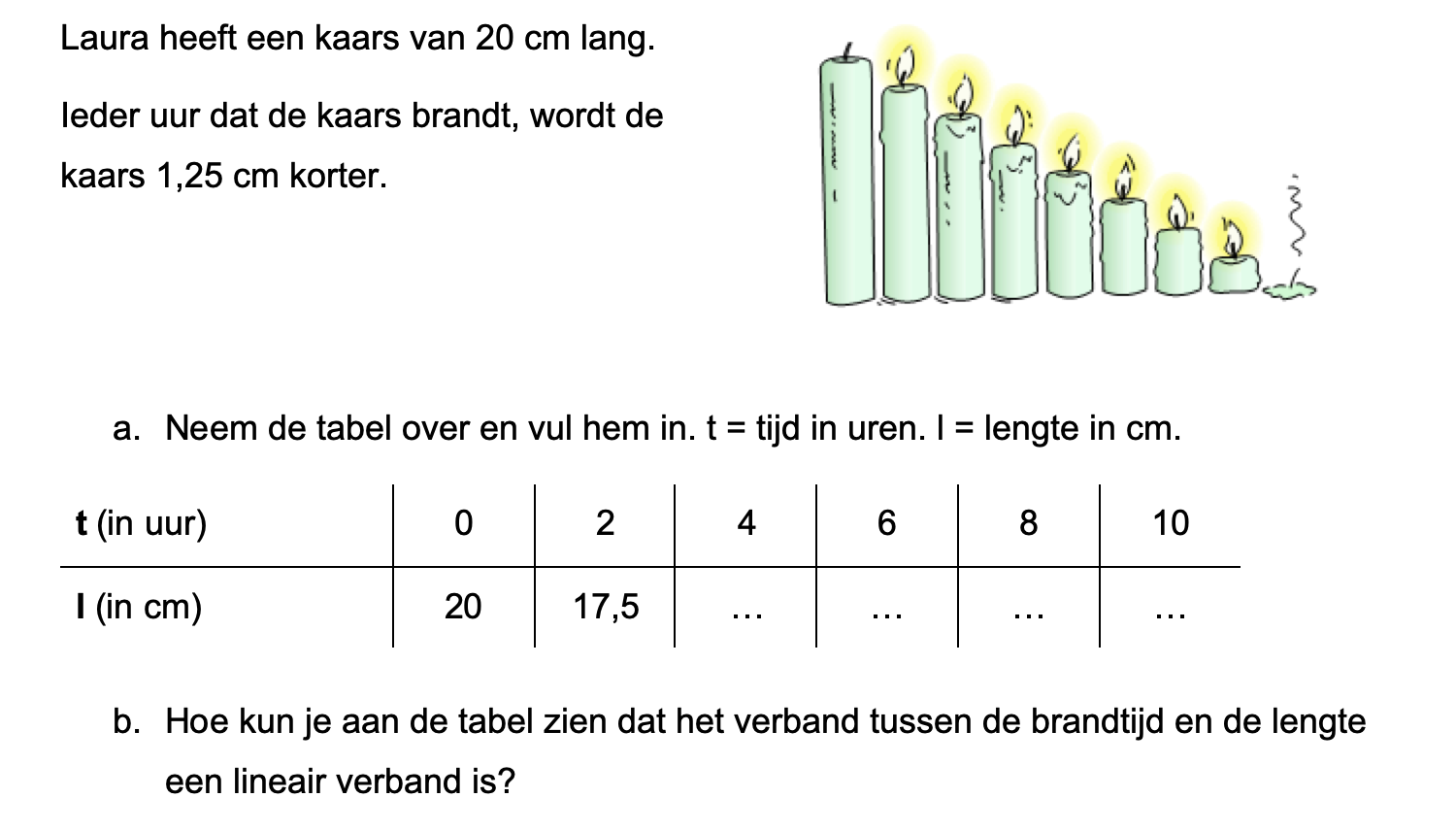
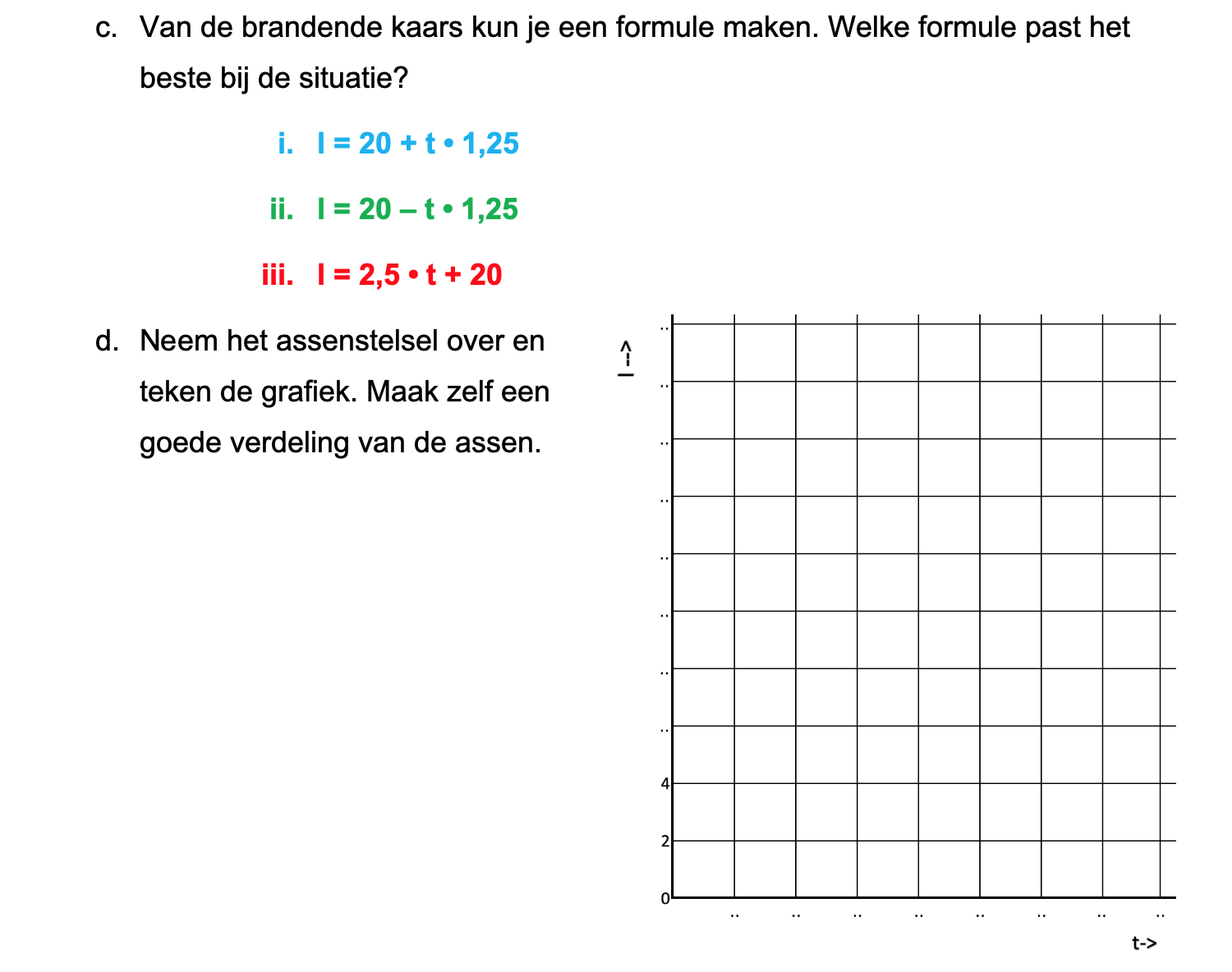
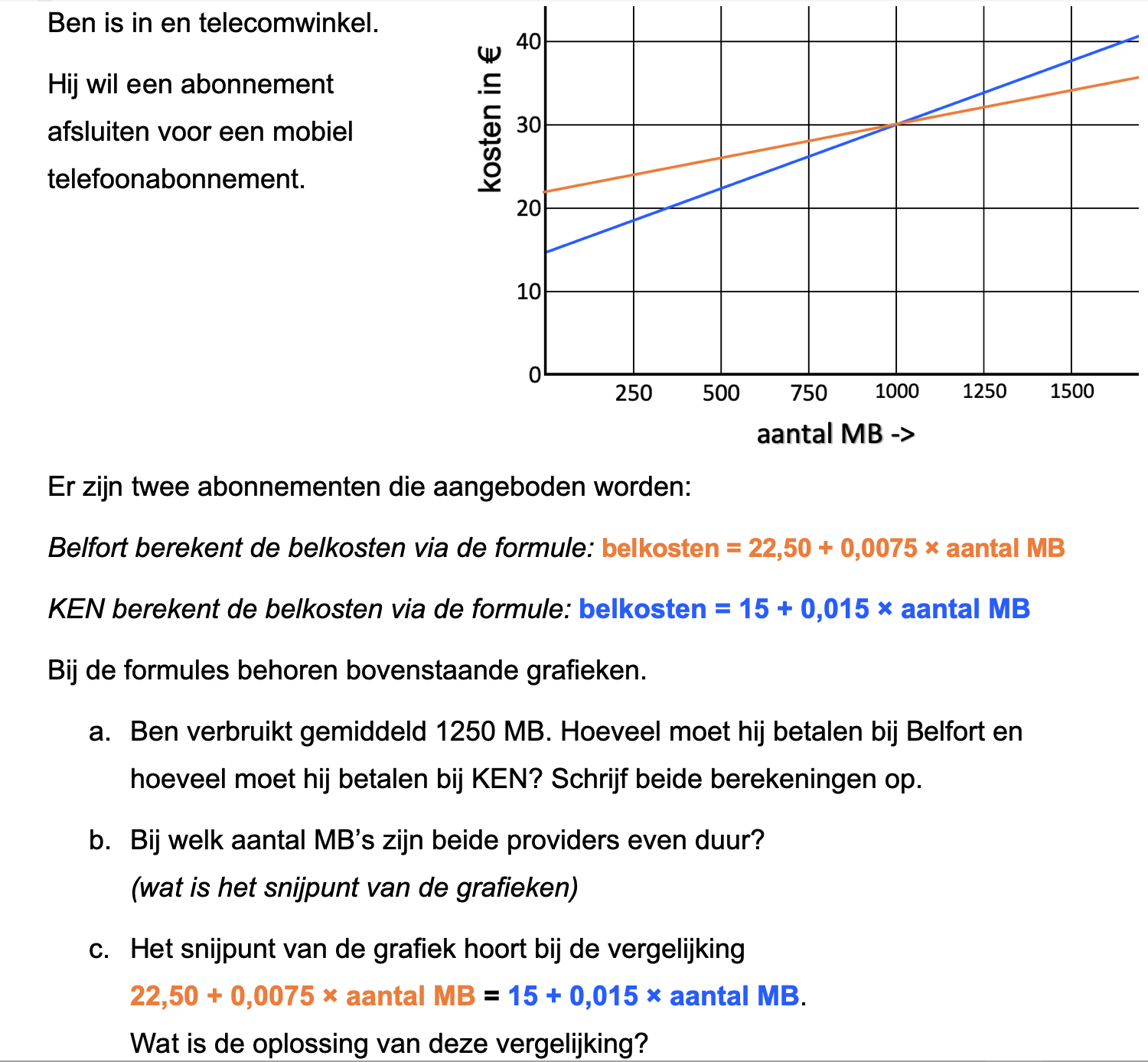
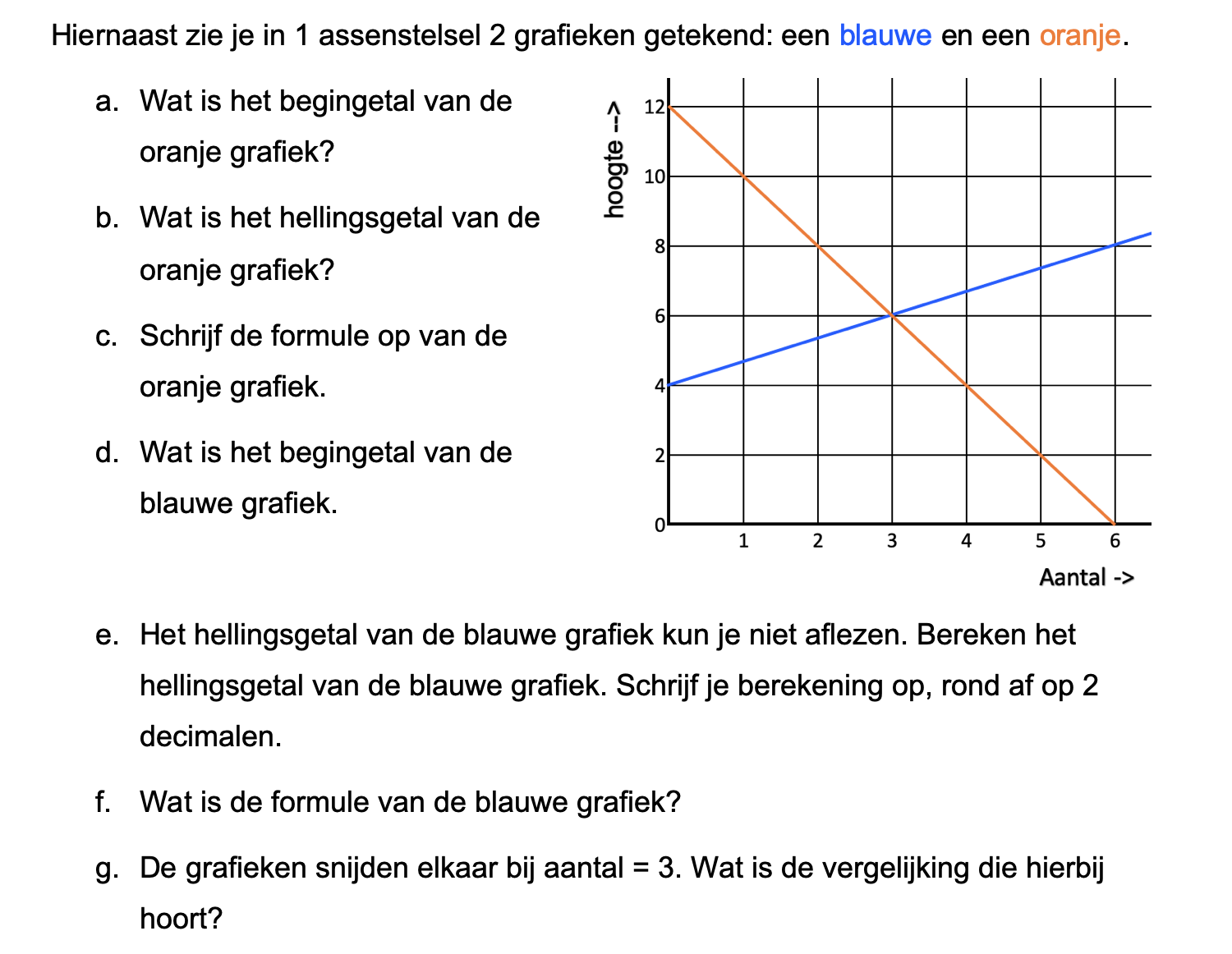
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
\
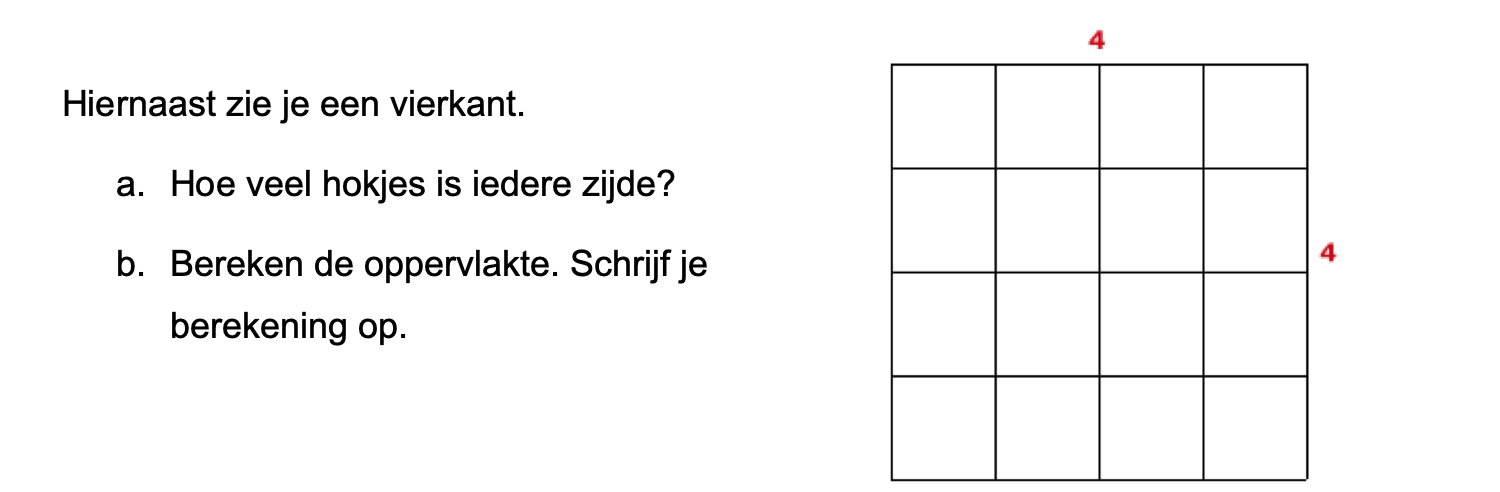
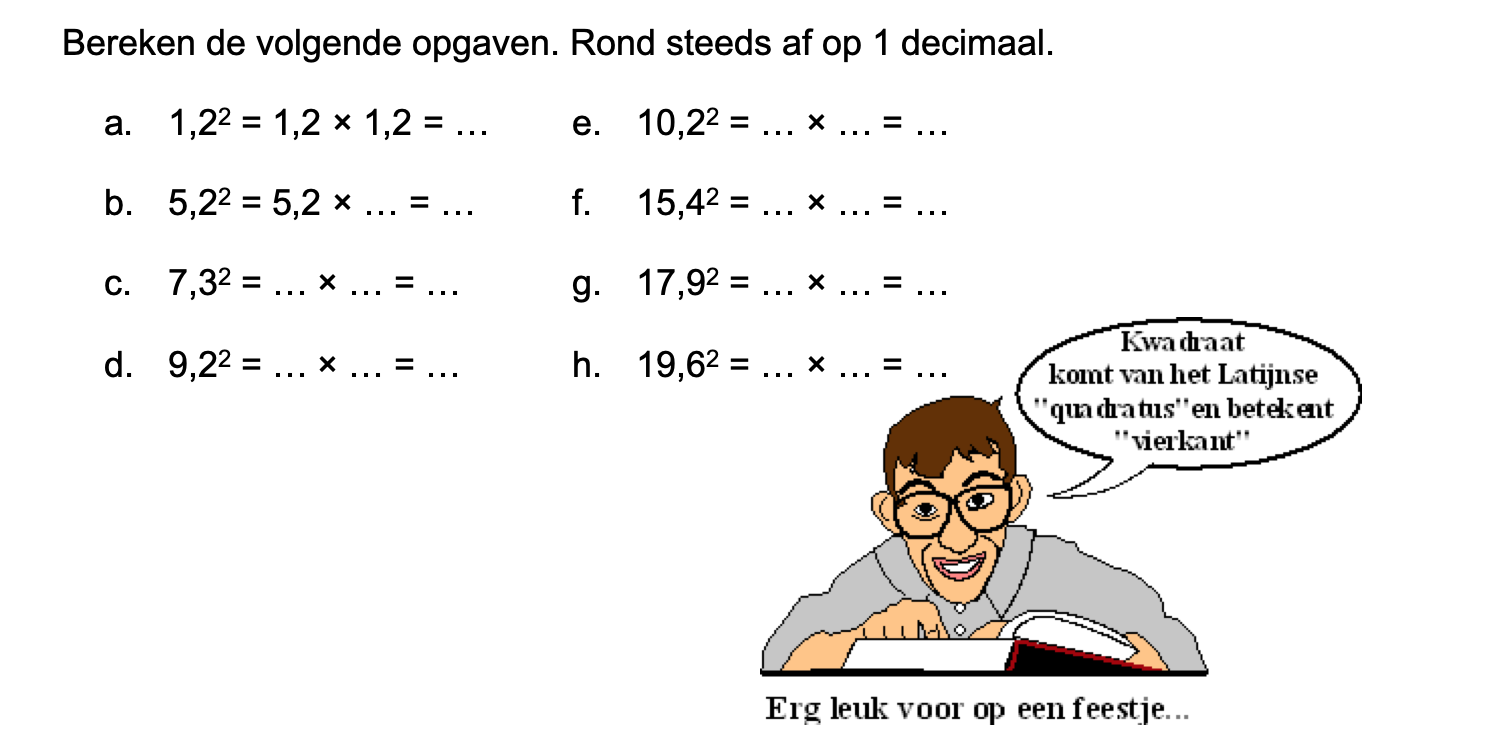
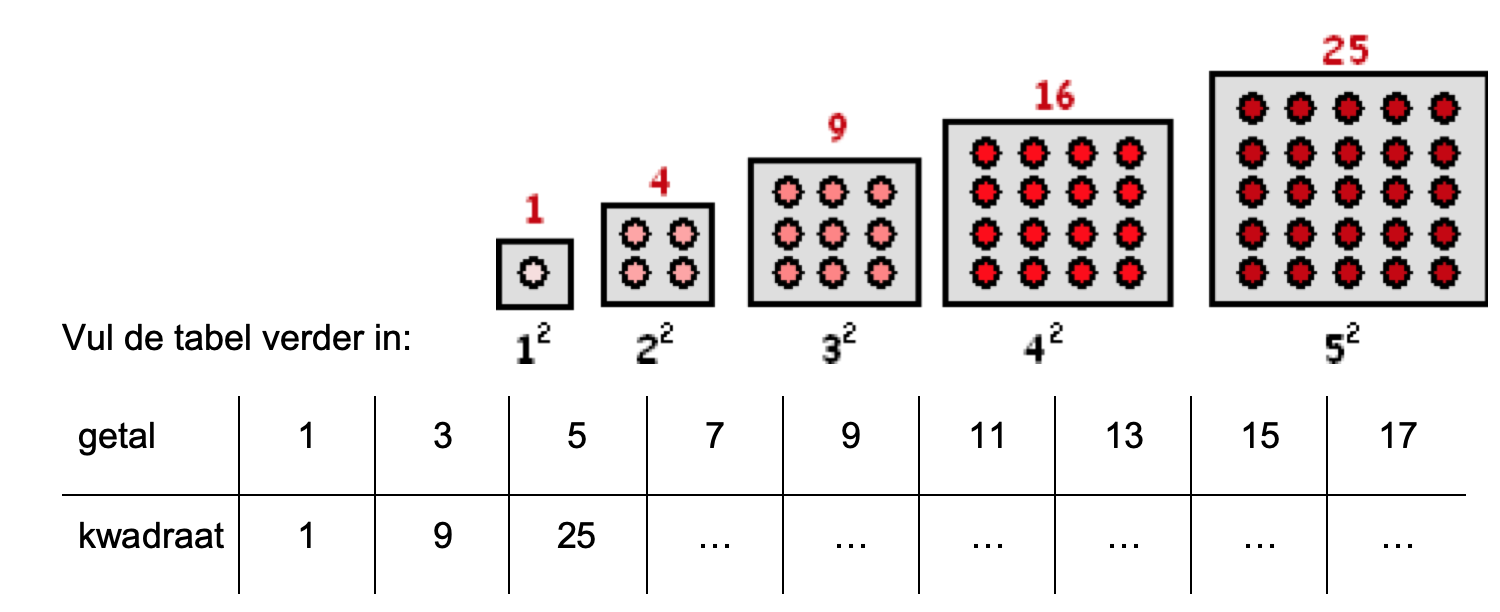
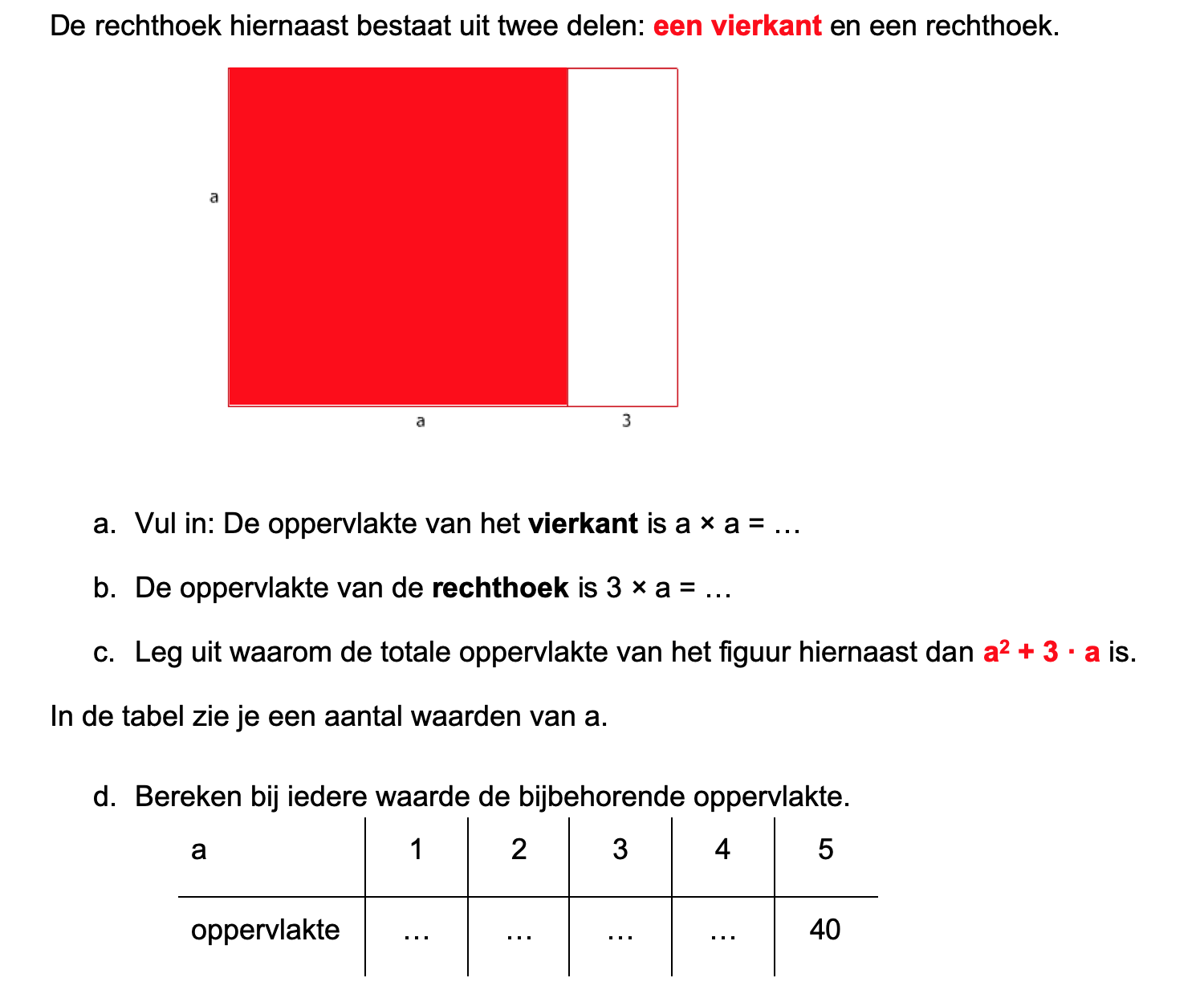
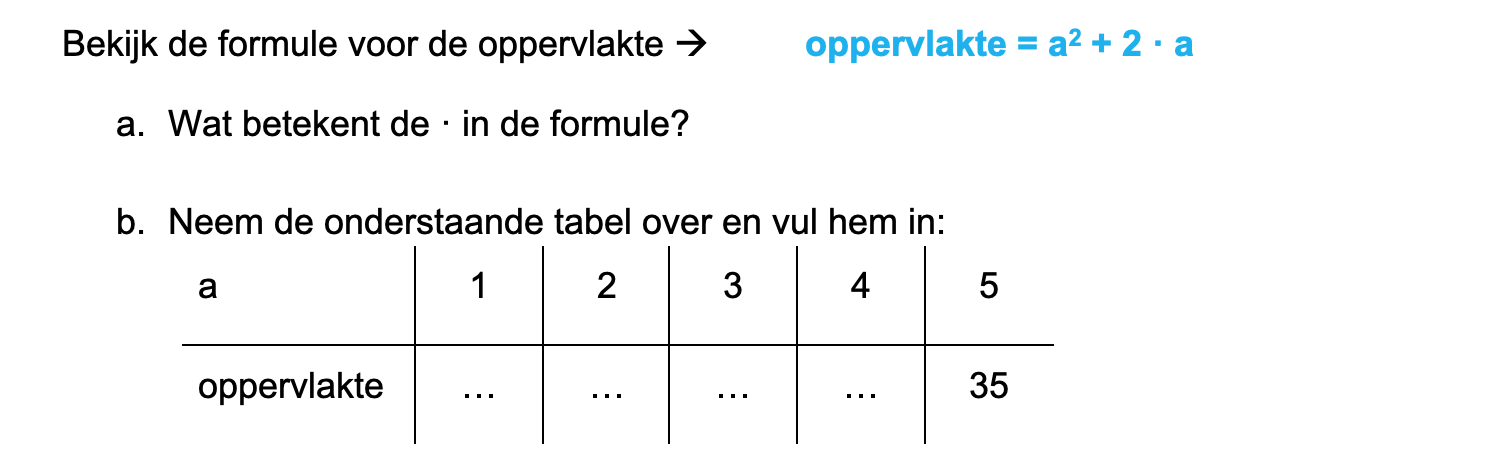
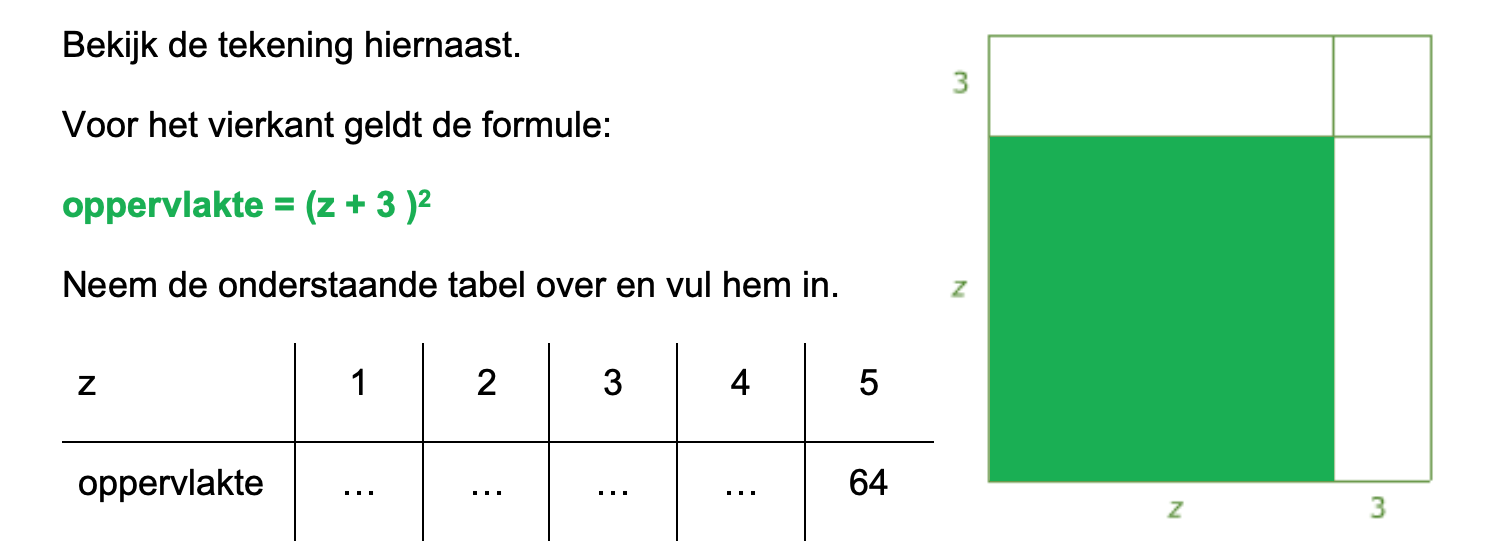
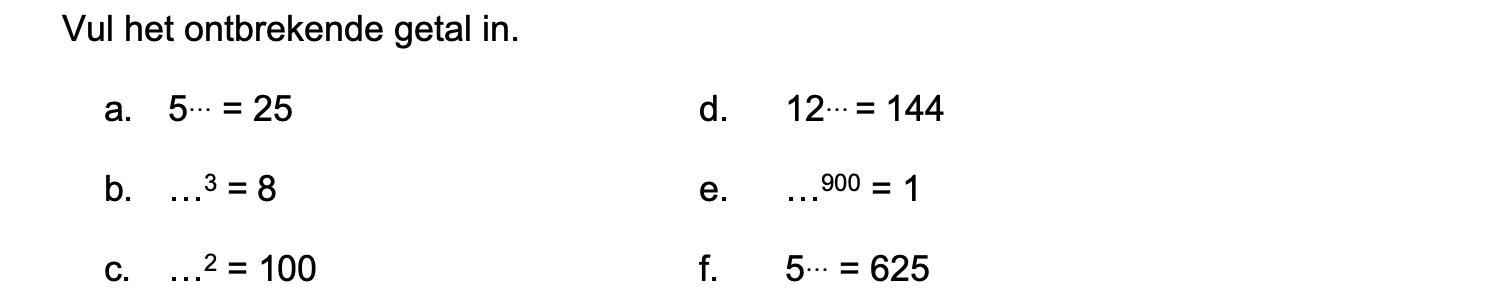
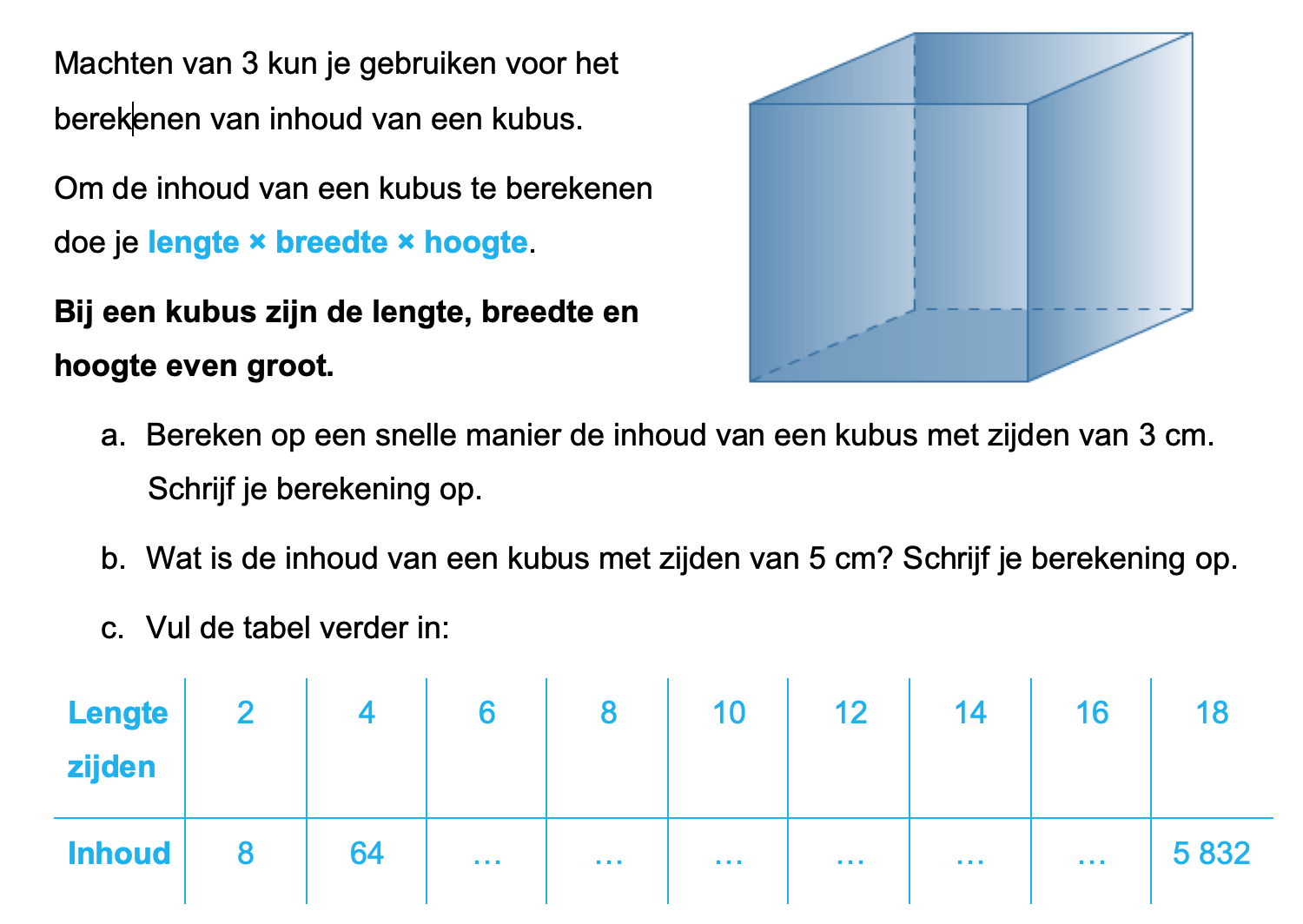
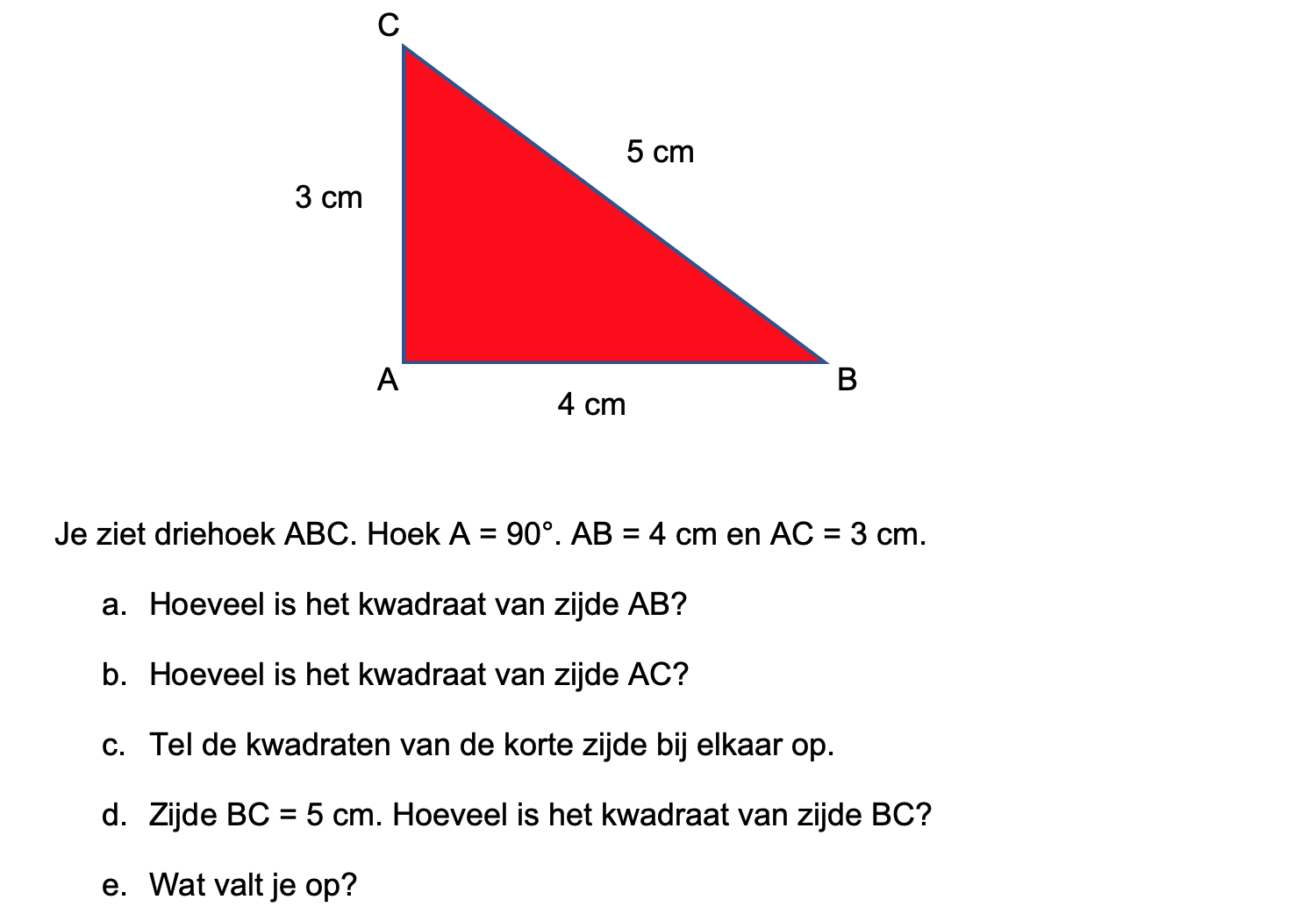
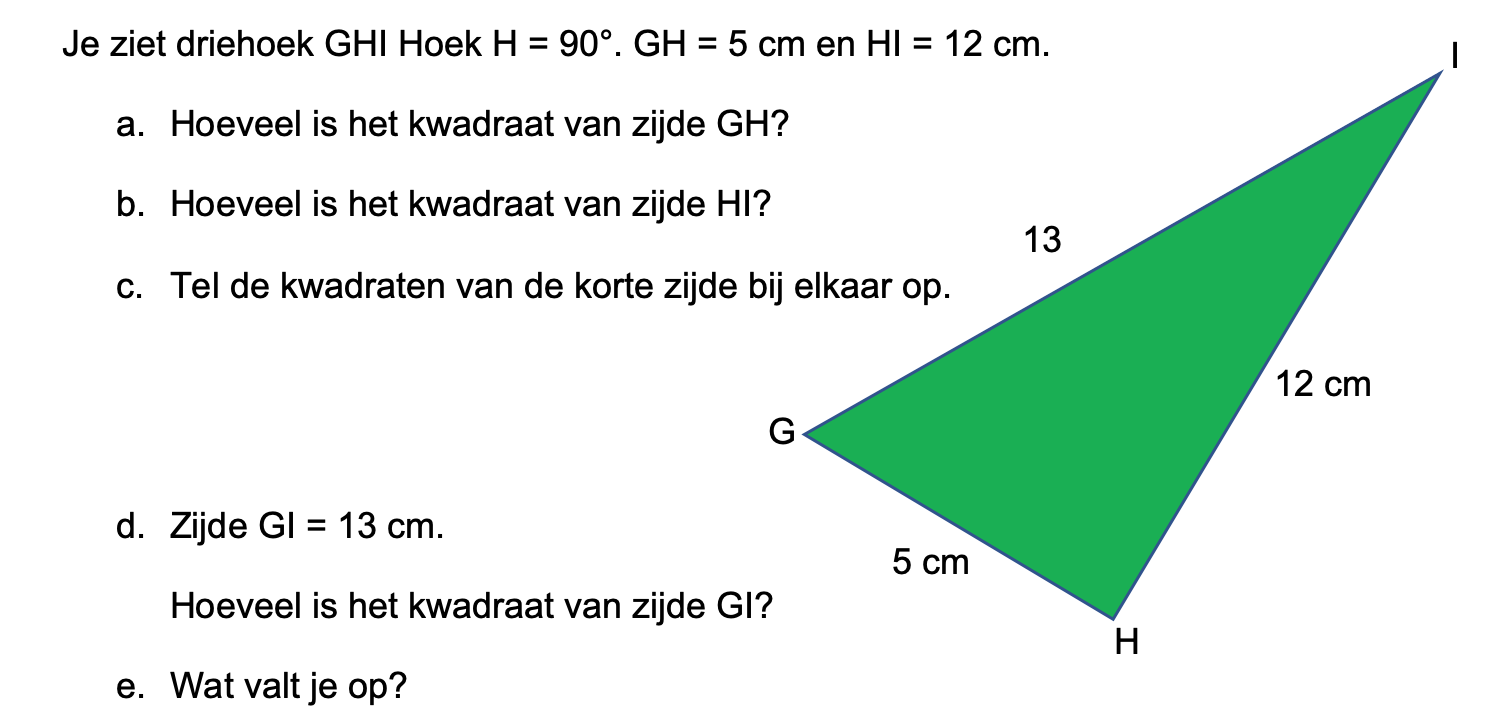
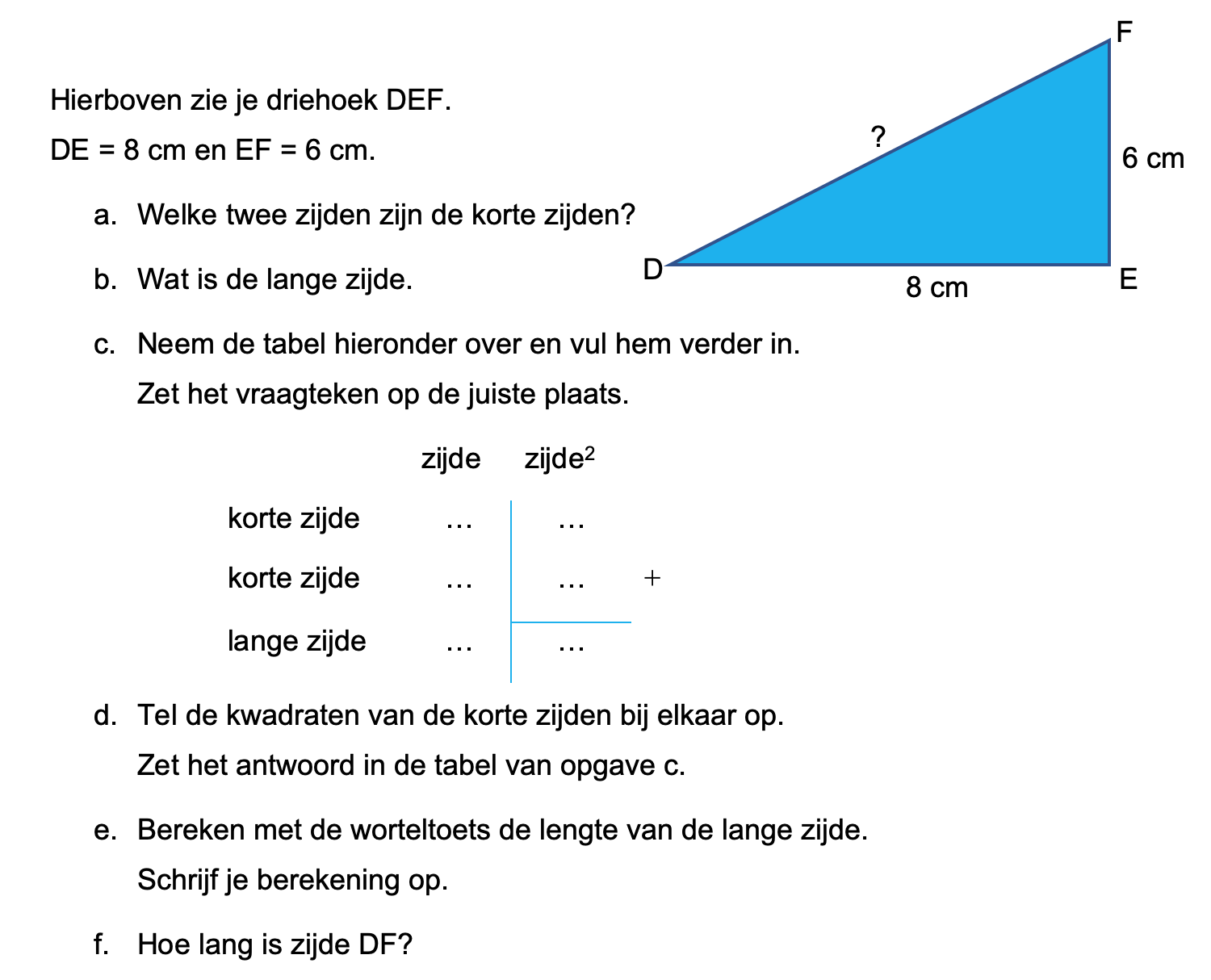
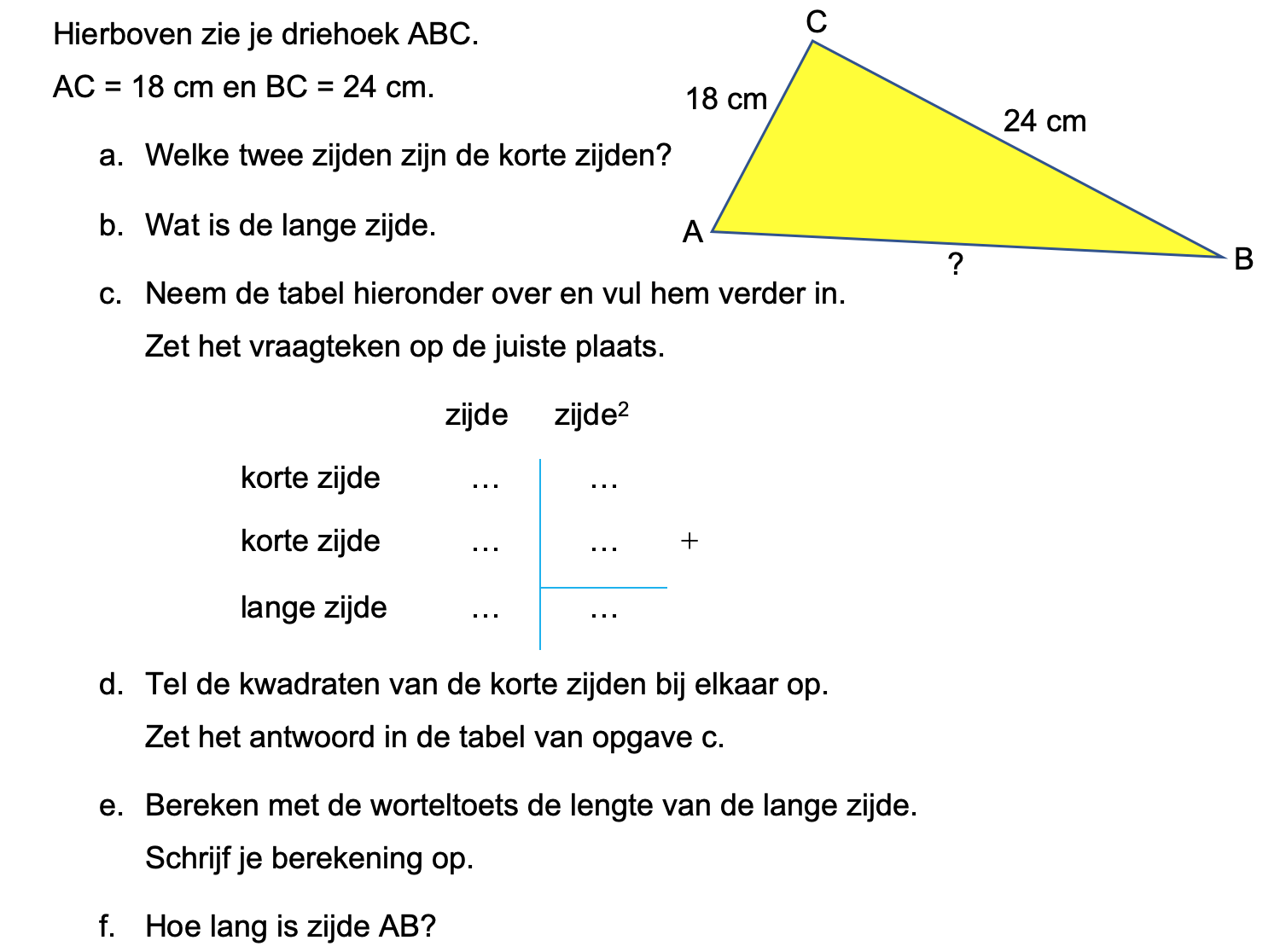
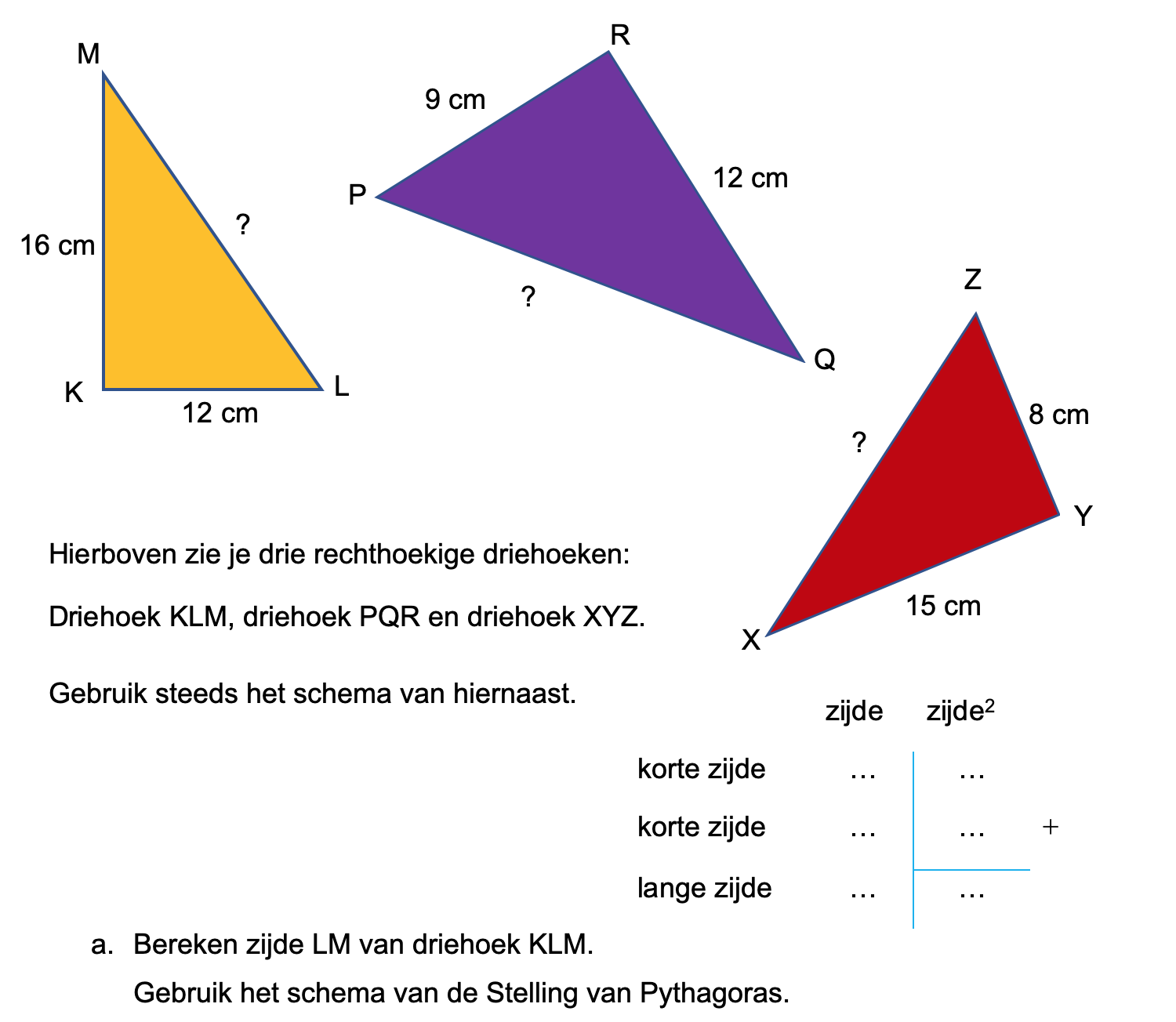
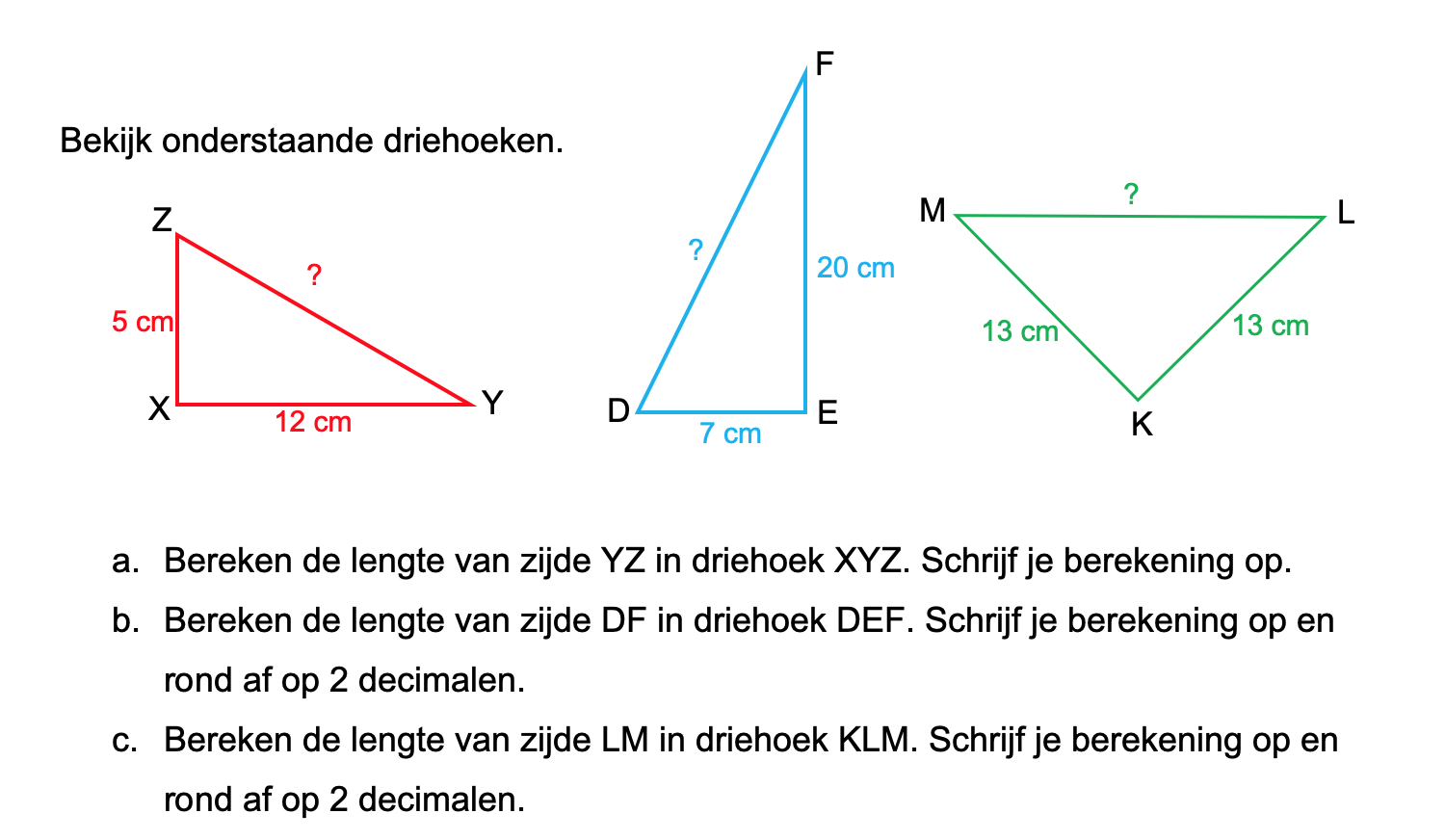
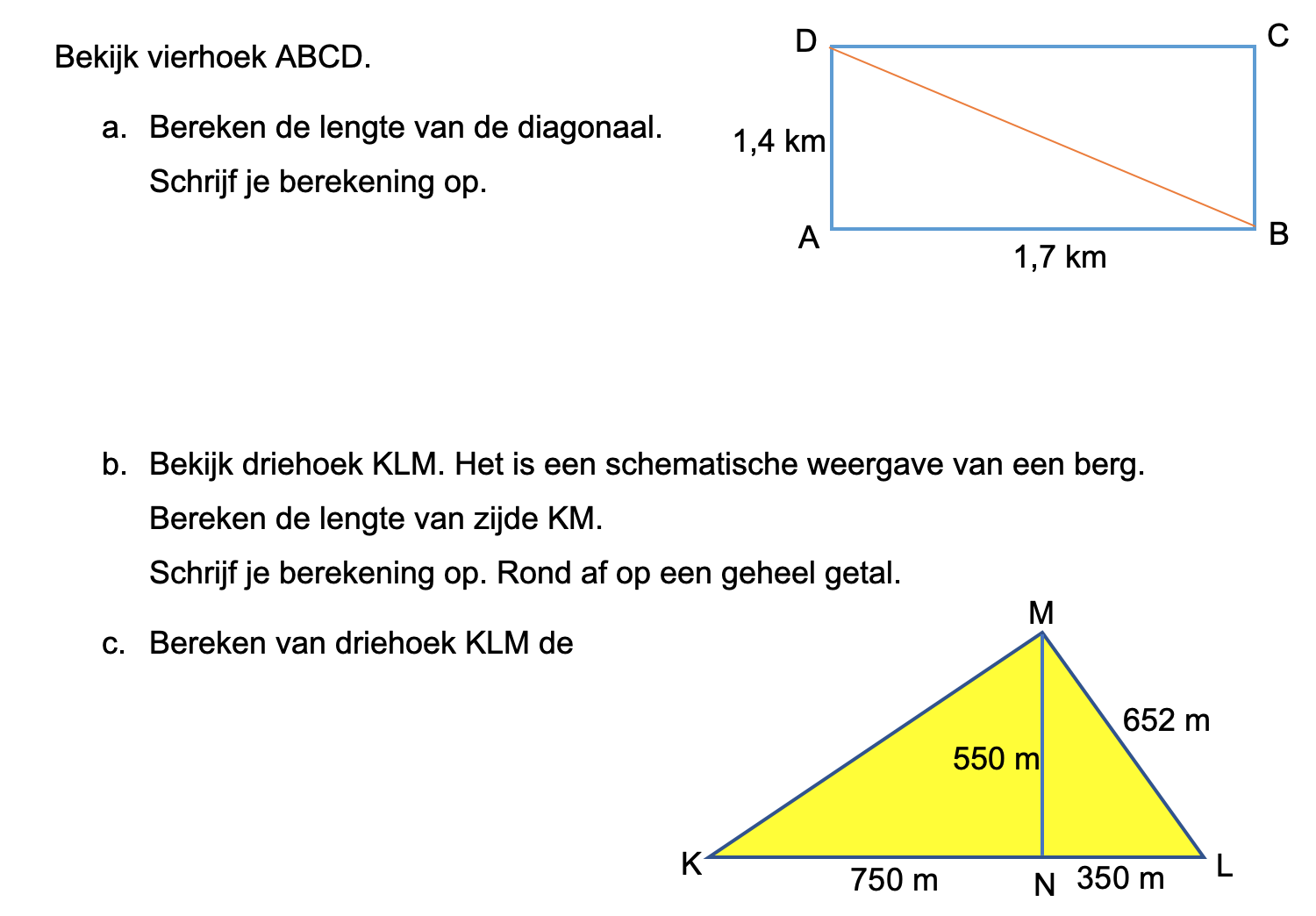
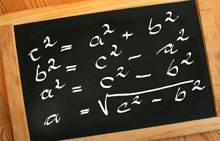Nog enkele opgaven om te oefenen voor het proefwerk.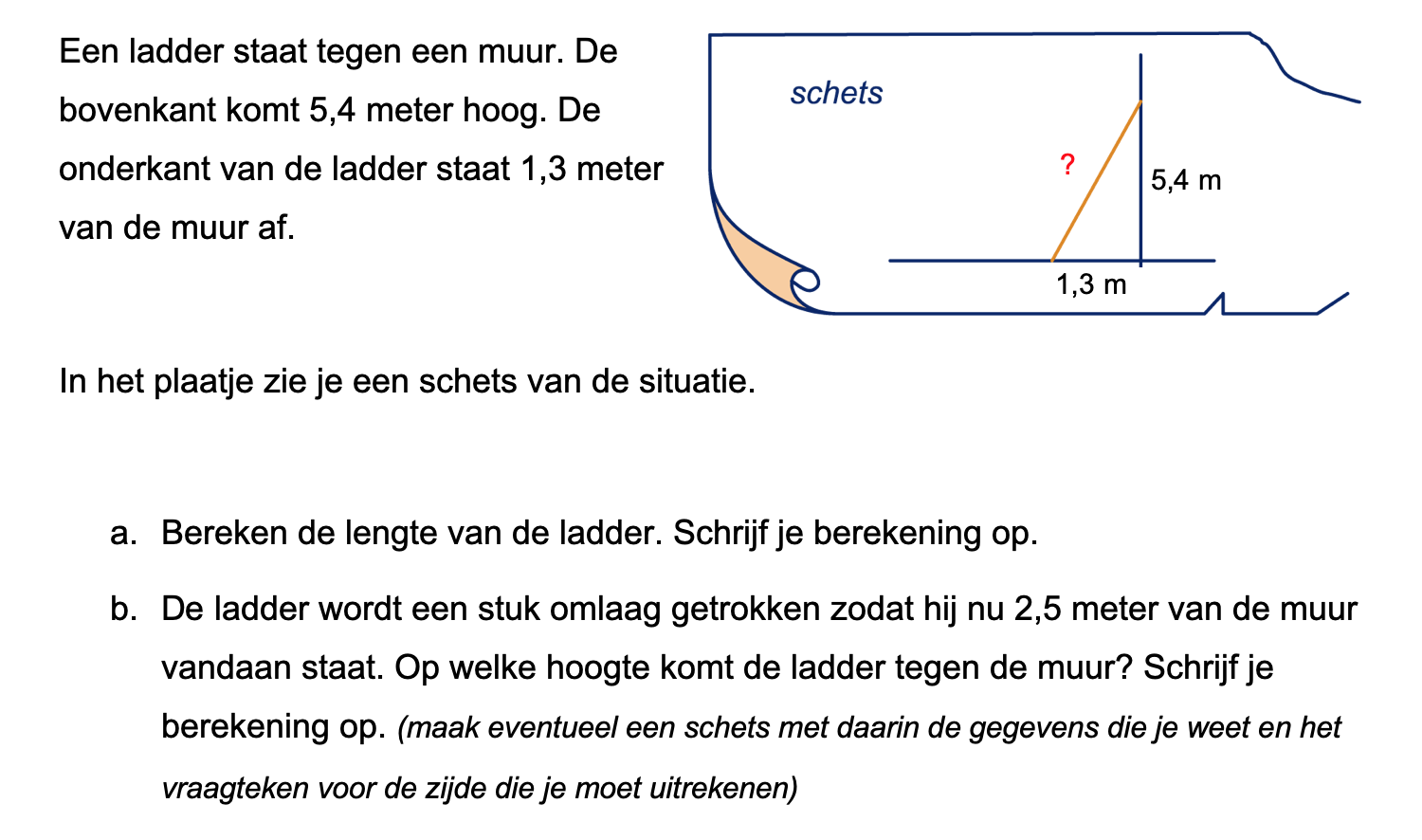
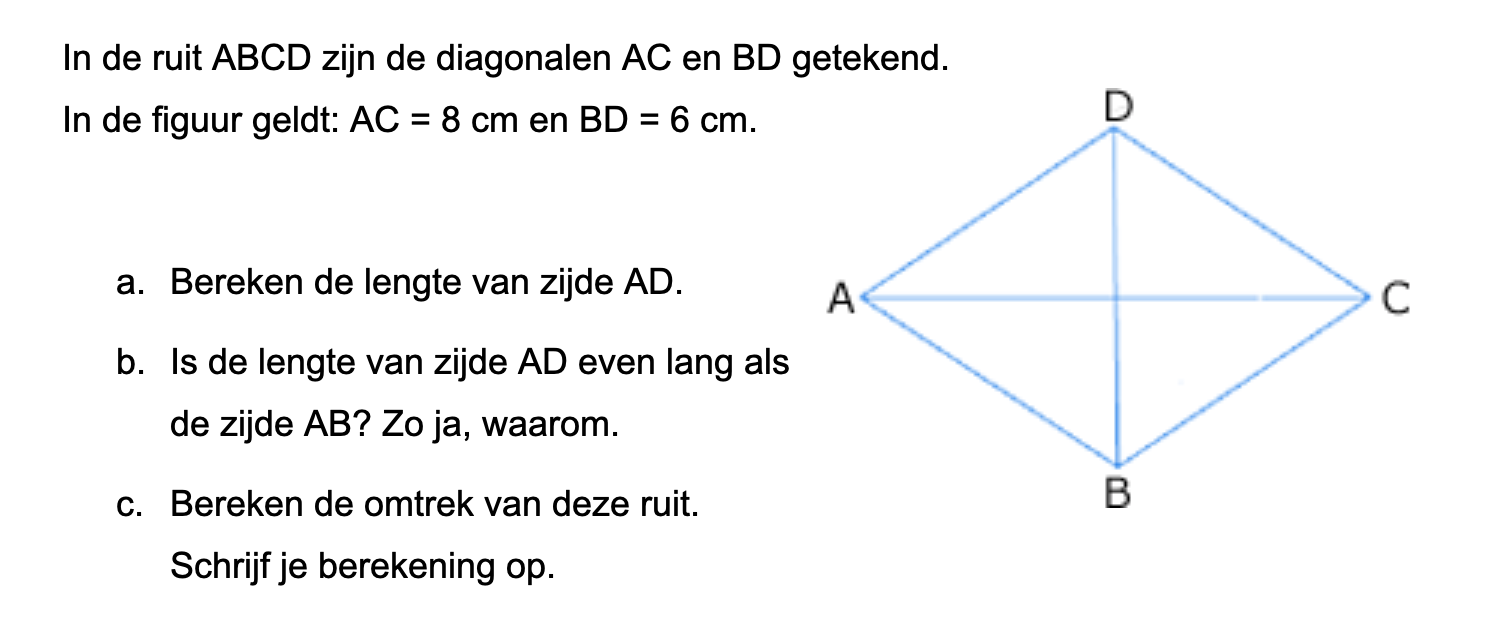
Maak de volgende opgaven als extra oefening voor de D-toets.
Nog enkele opgaven om te oefenen voor het proefwerk.
Bestudeer uit de Kennisbank wiskunde het onderdeel: Uitslagen
Bestudeer eerst uit de Kennisbank wiskunde het onderdeel: INHOUD
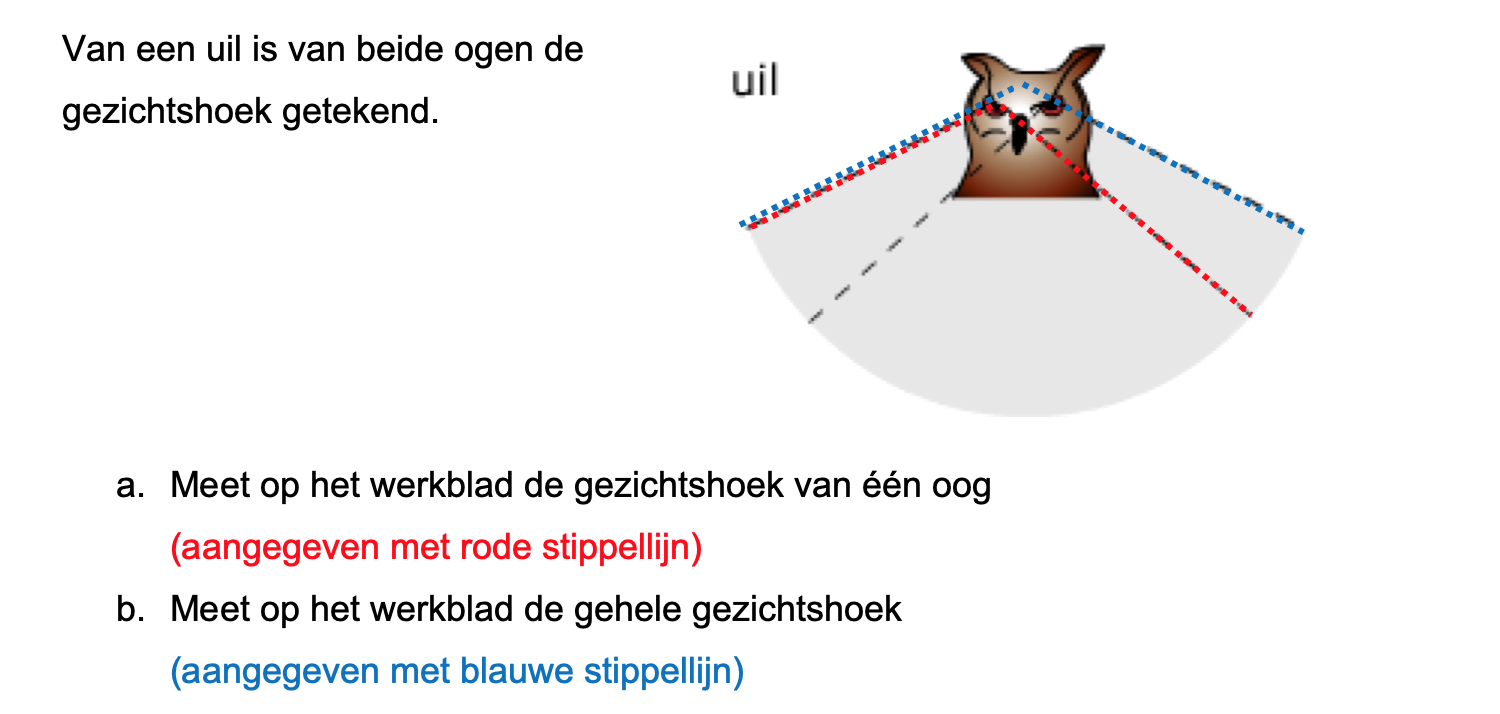
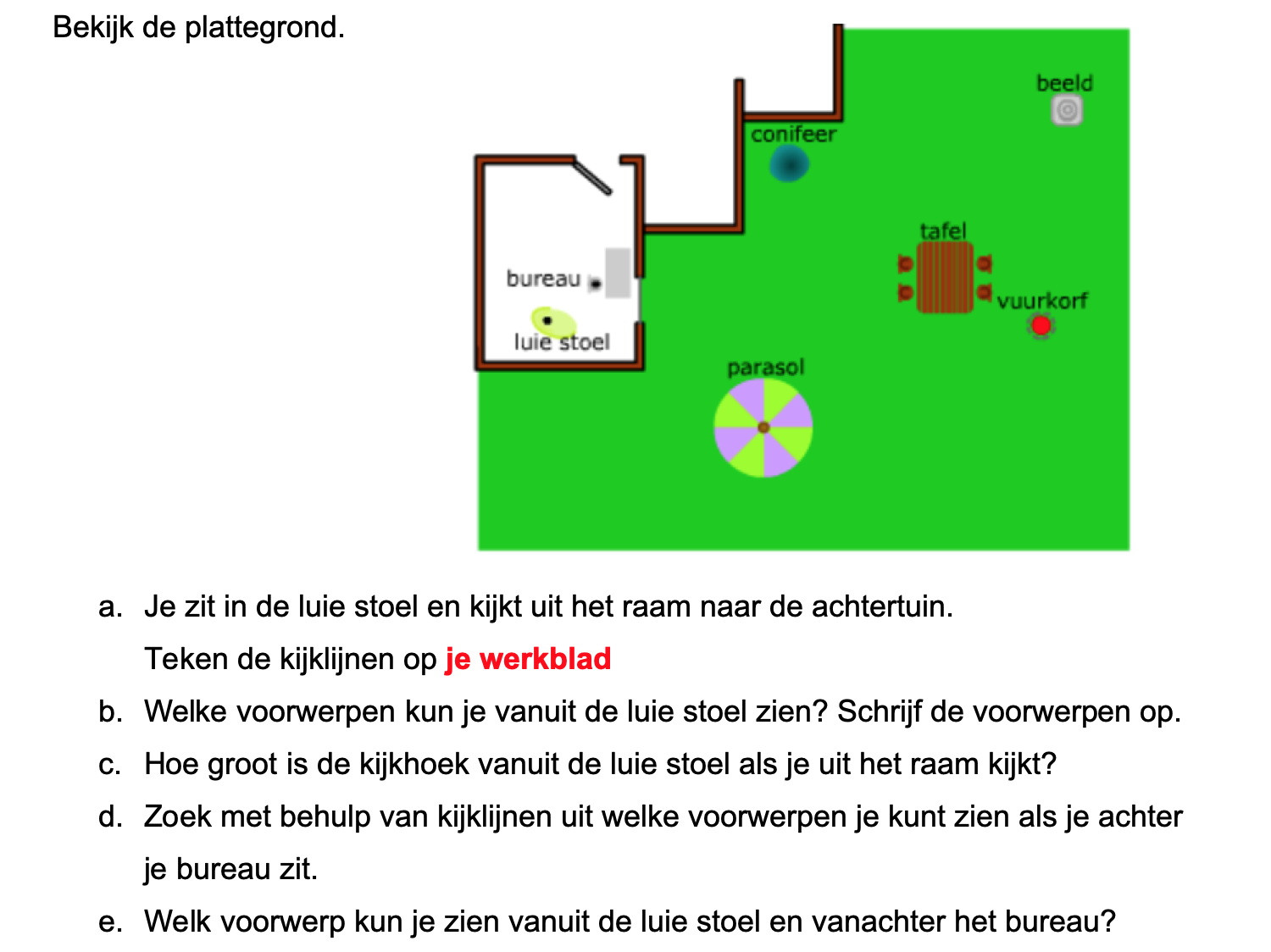
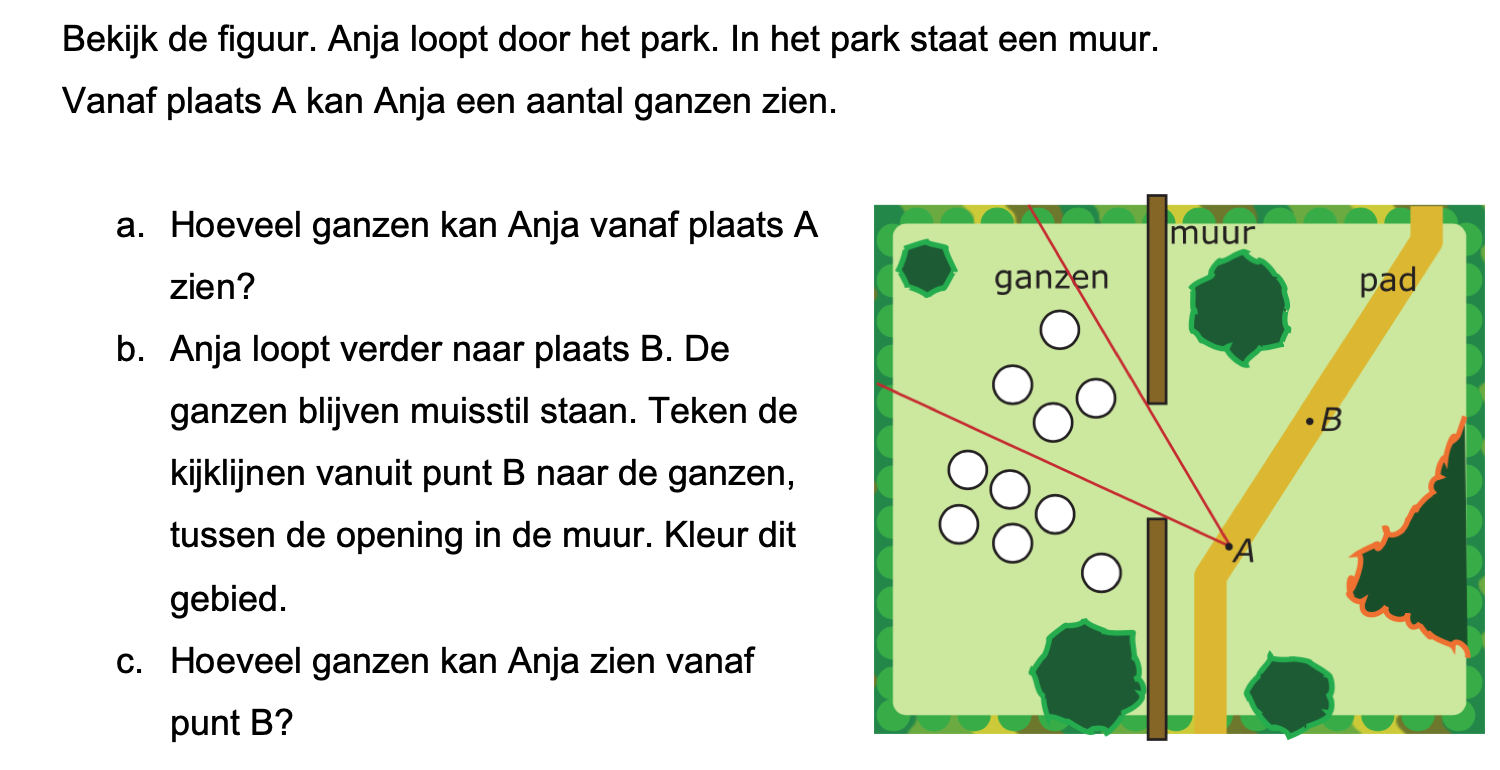
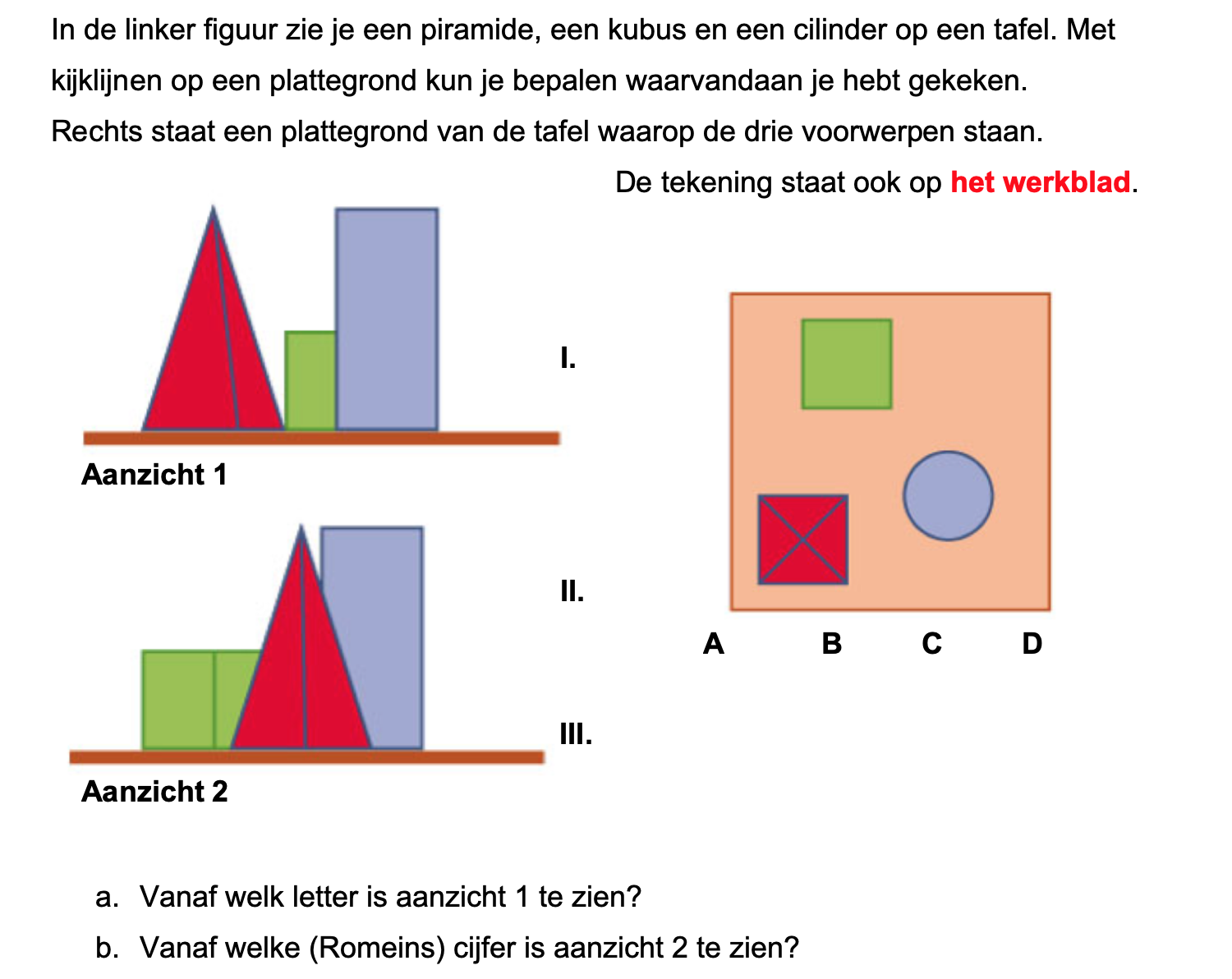
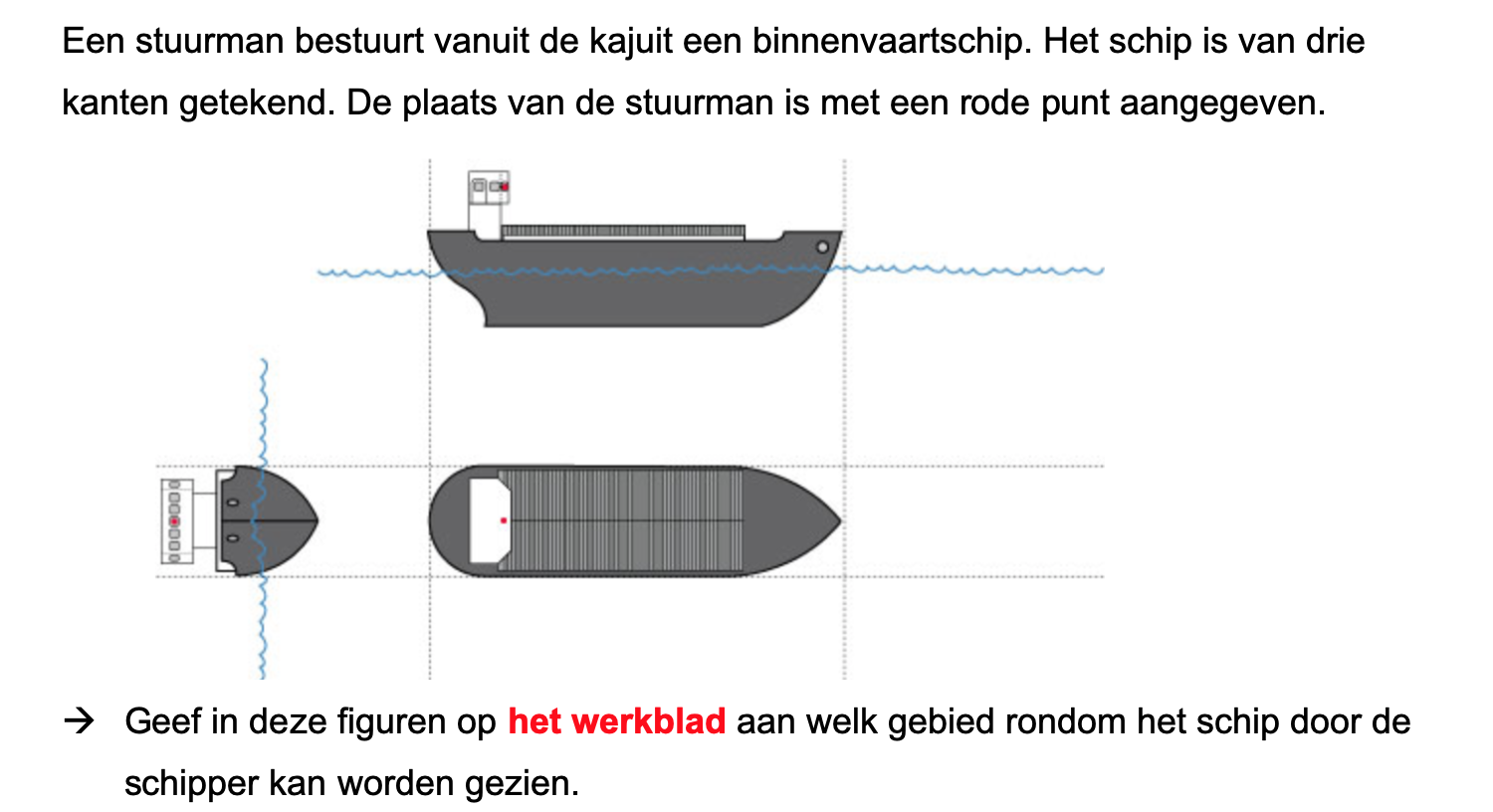
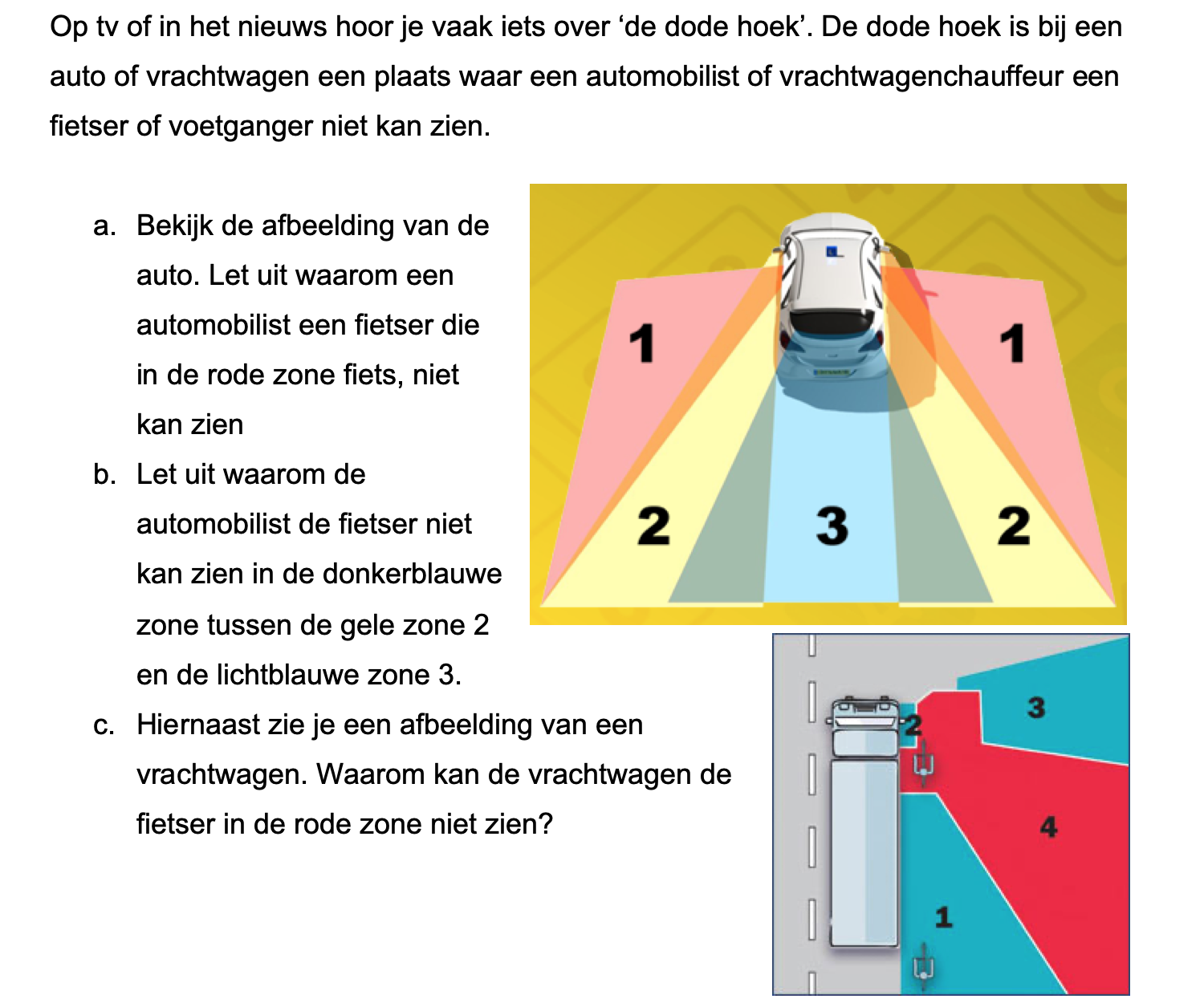
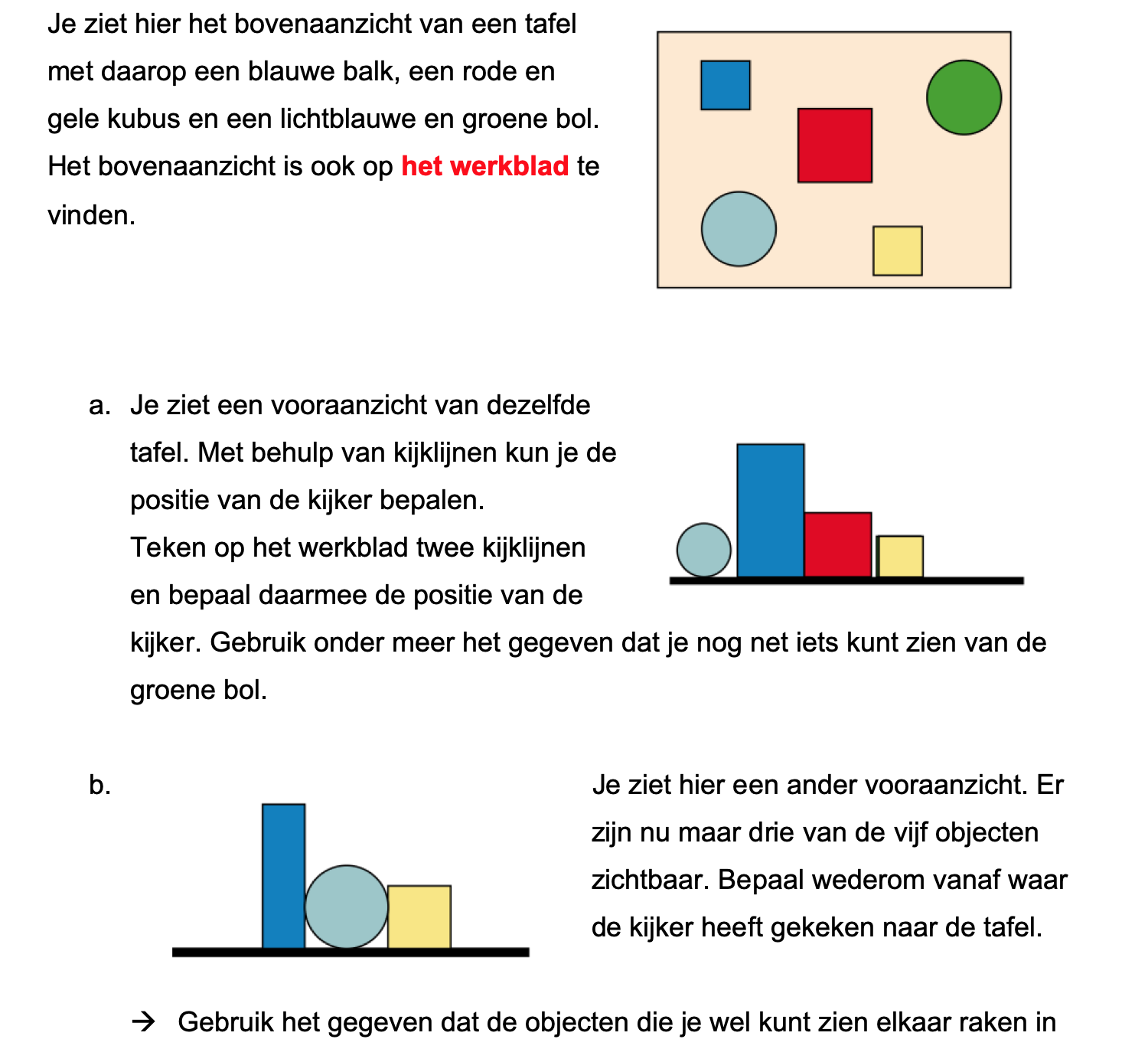
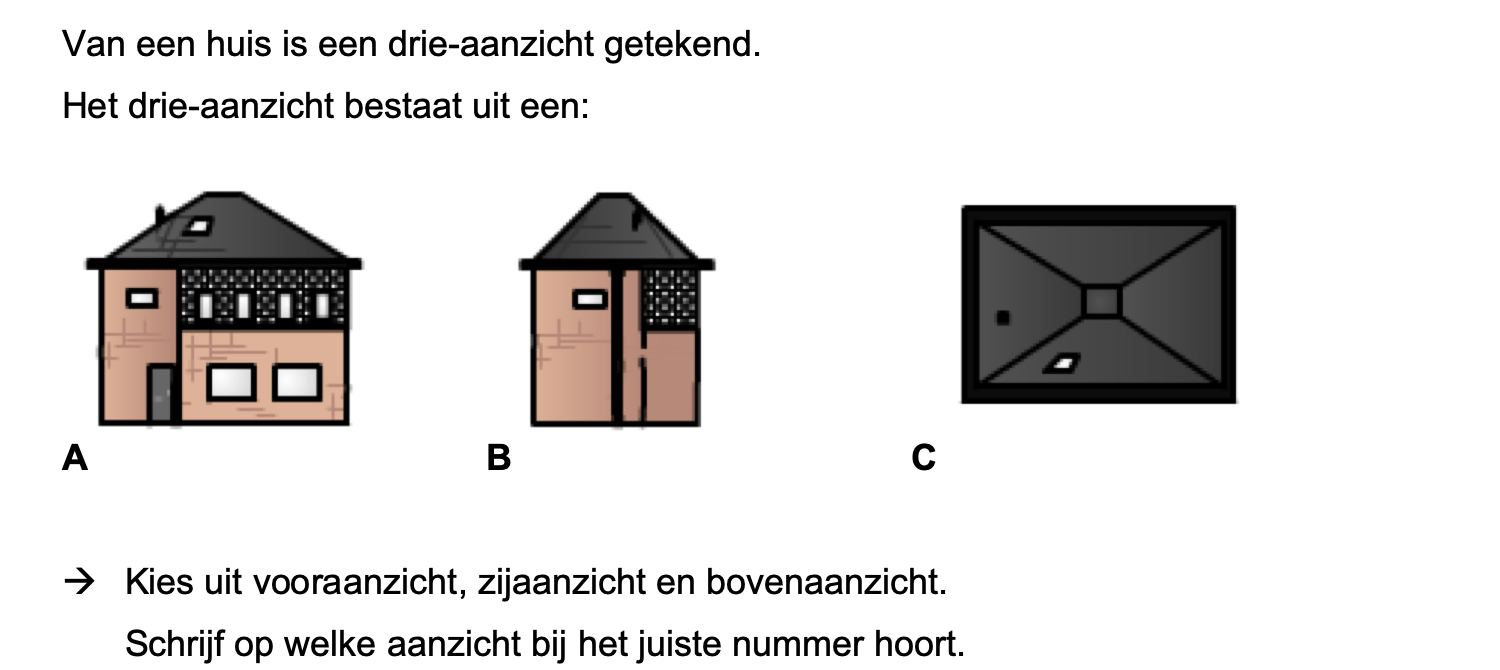
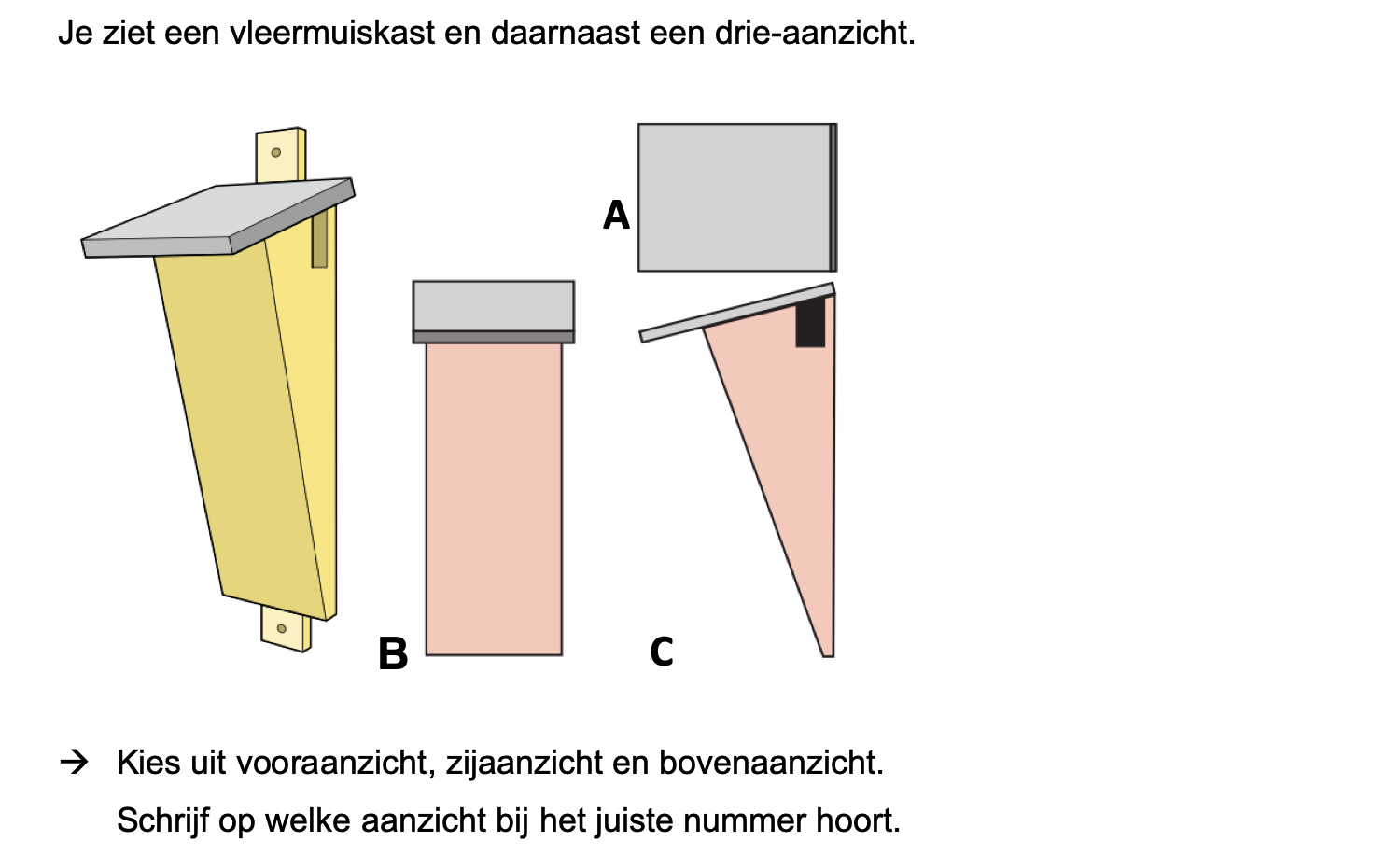
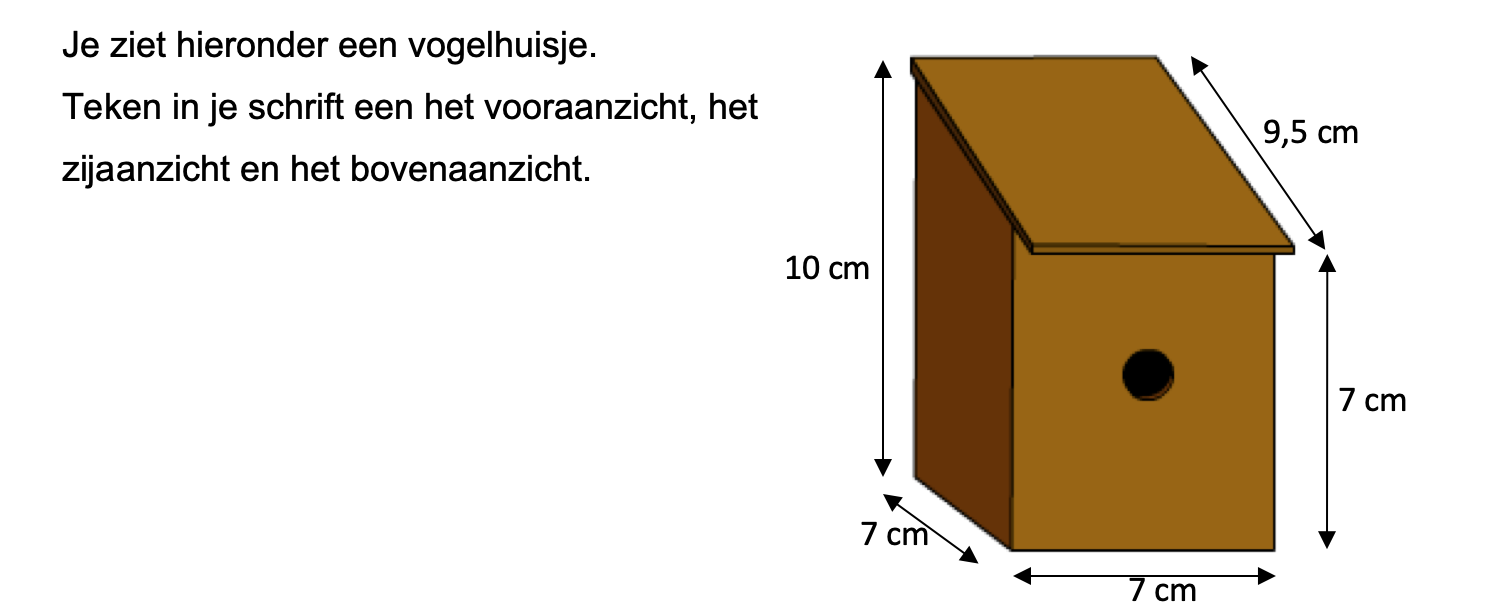
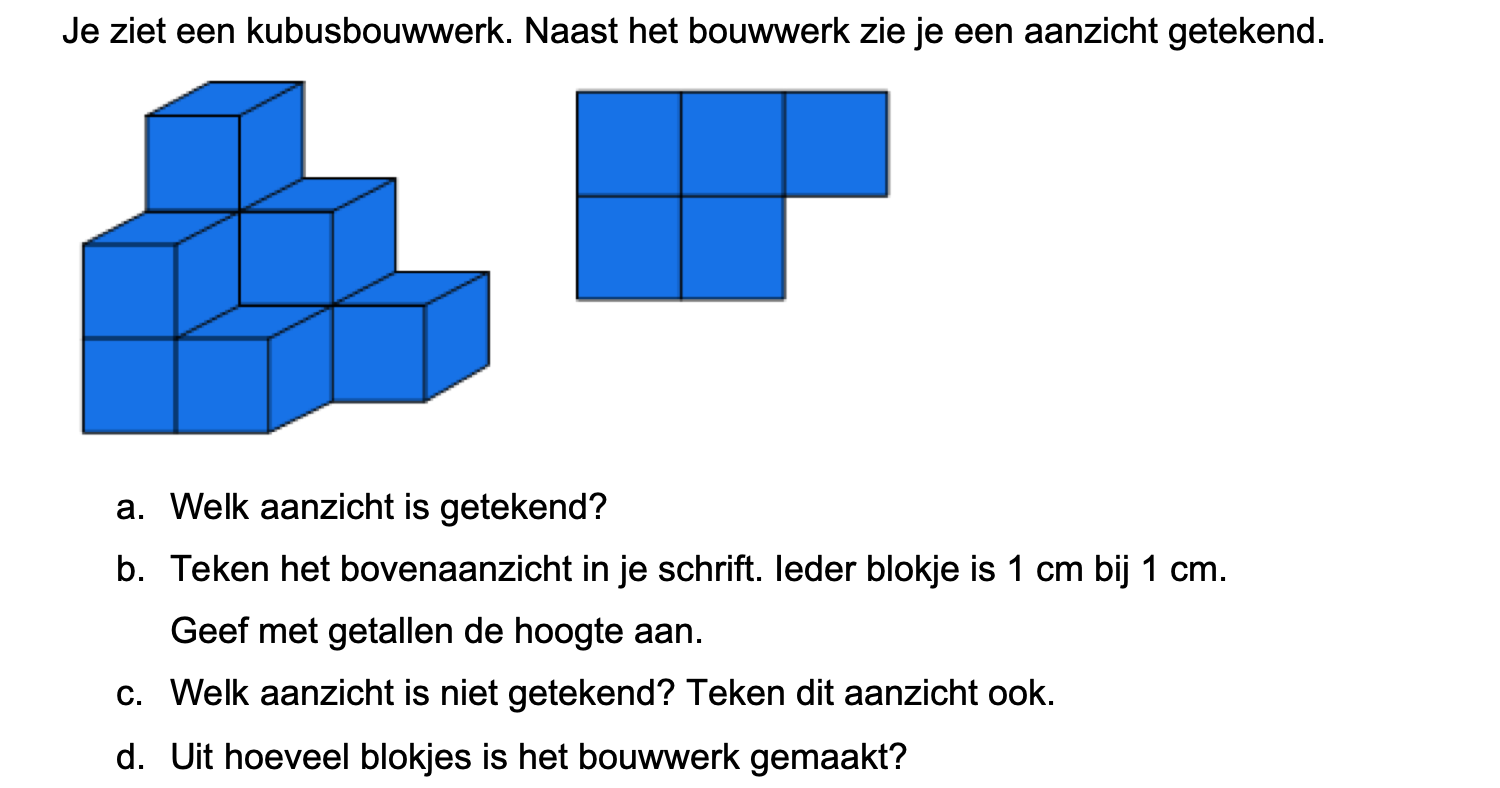
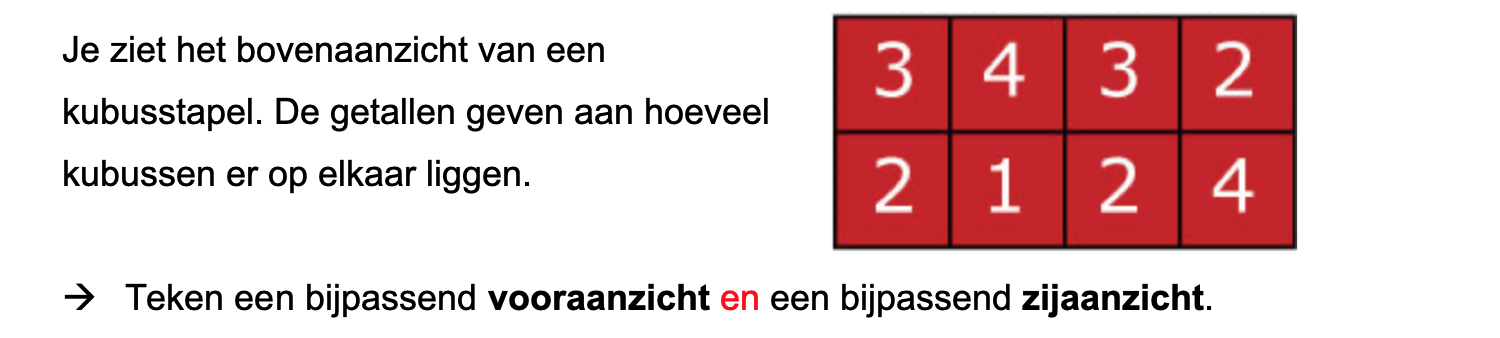
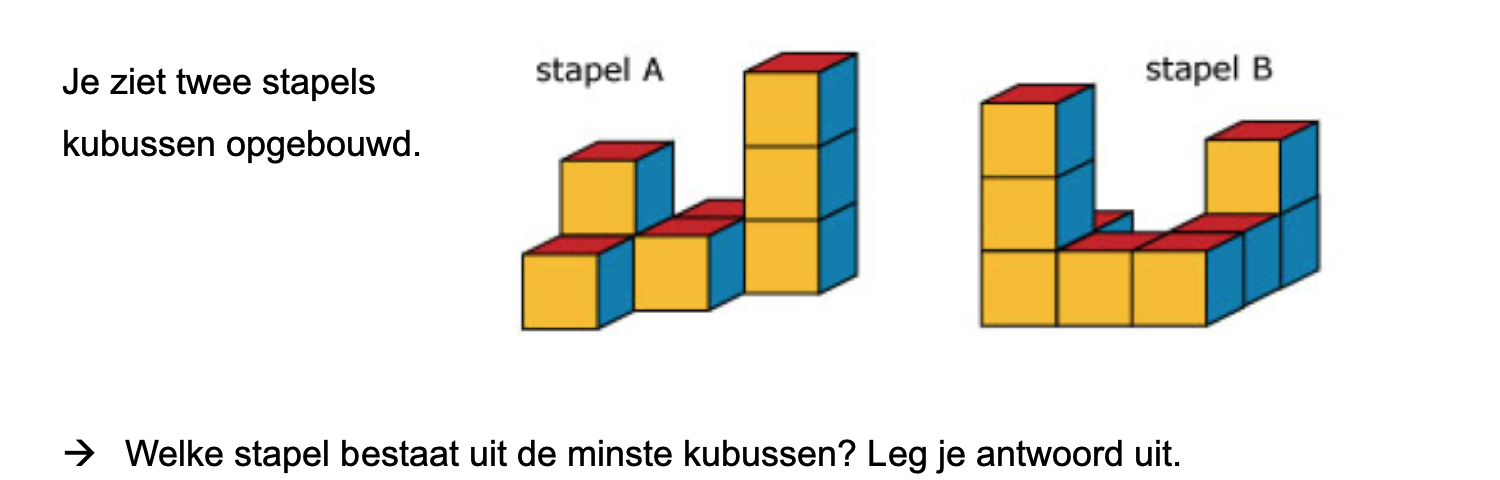
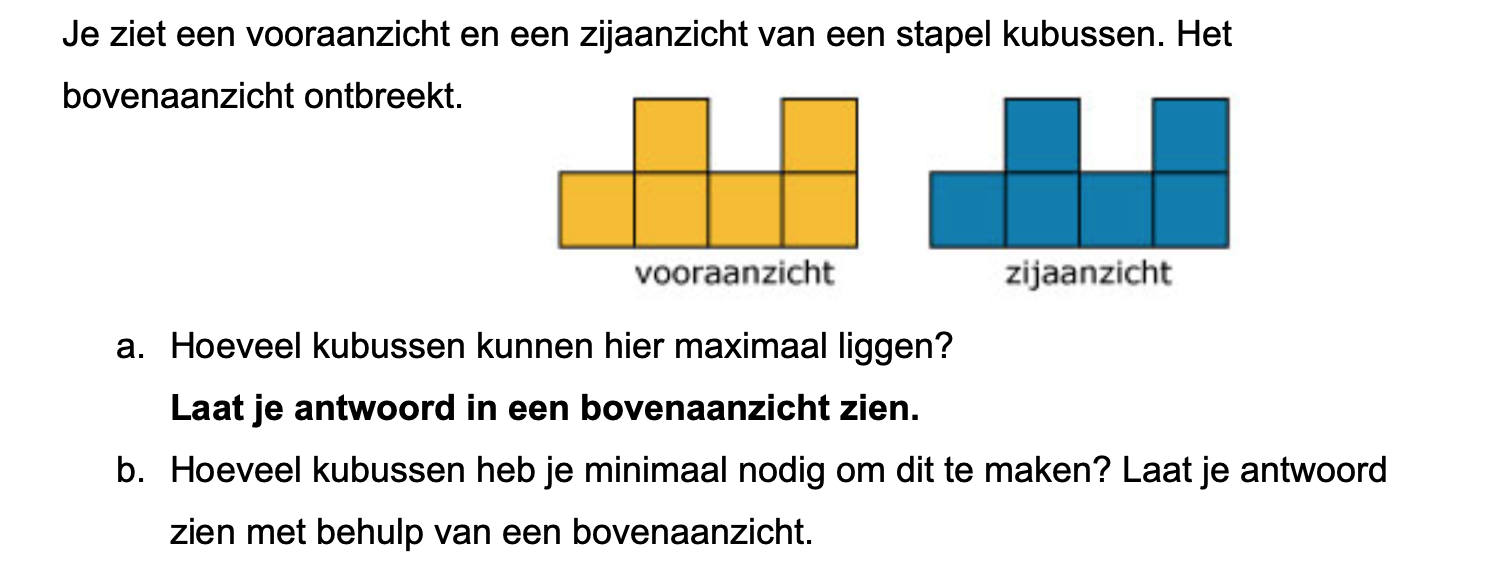
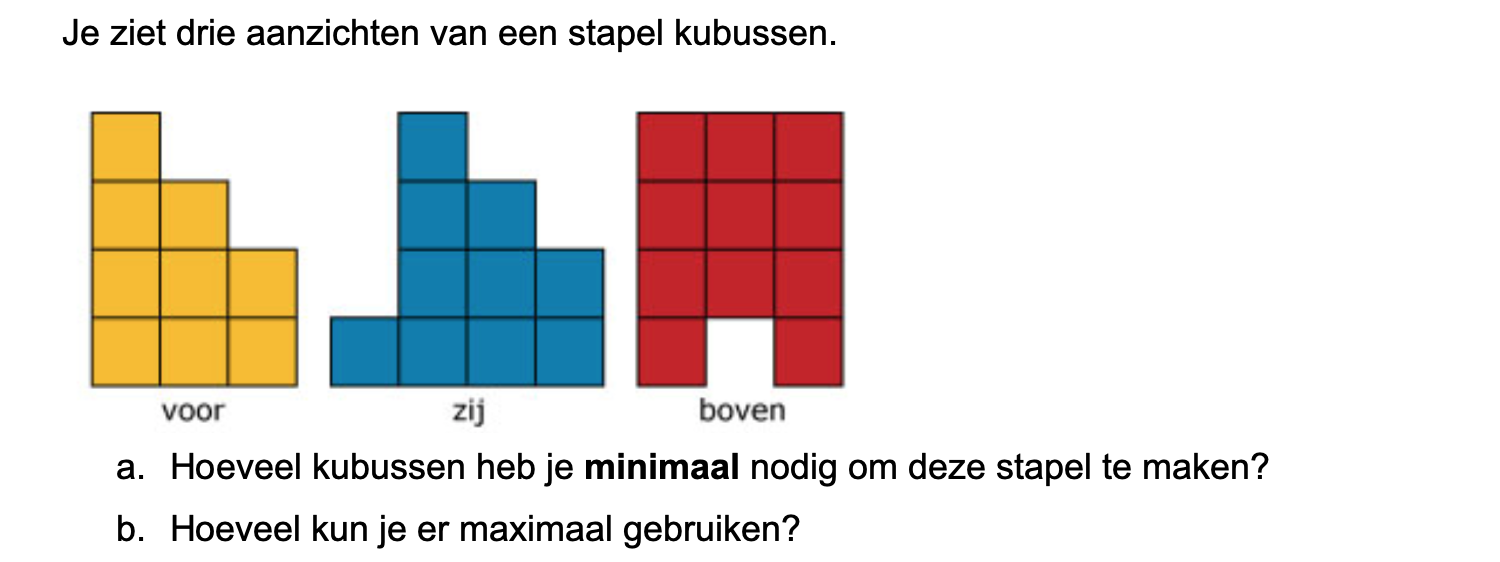
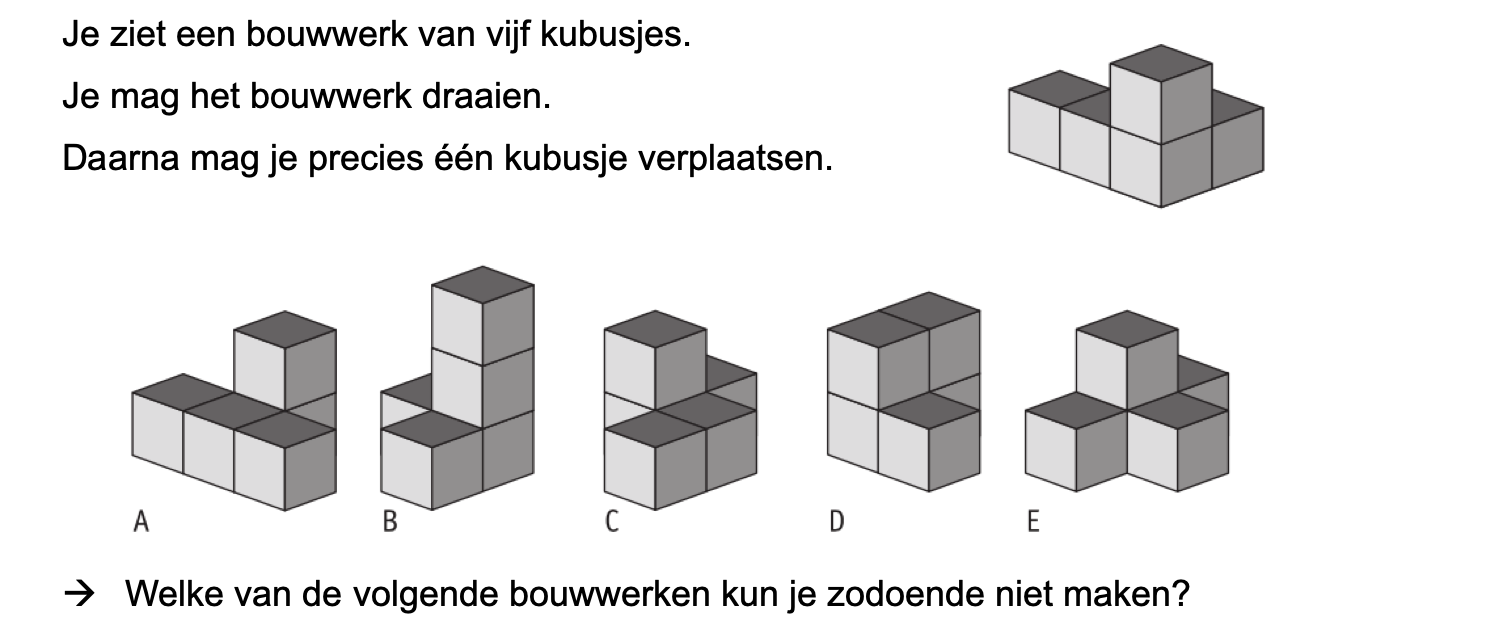
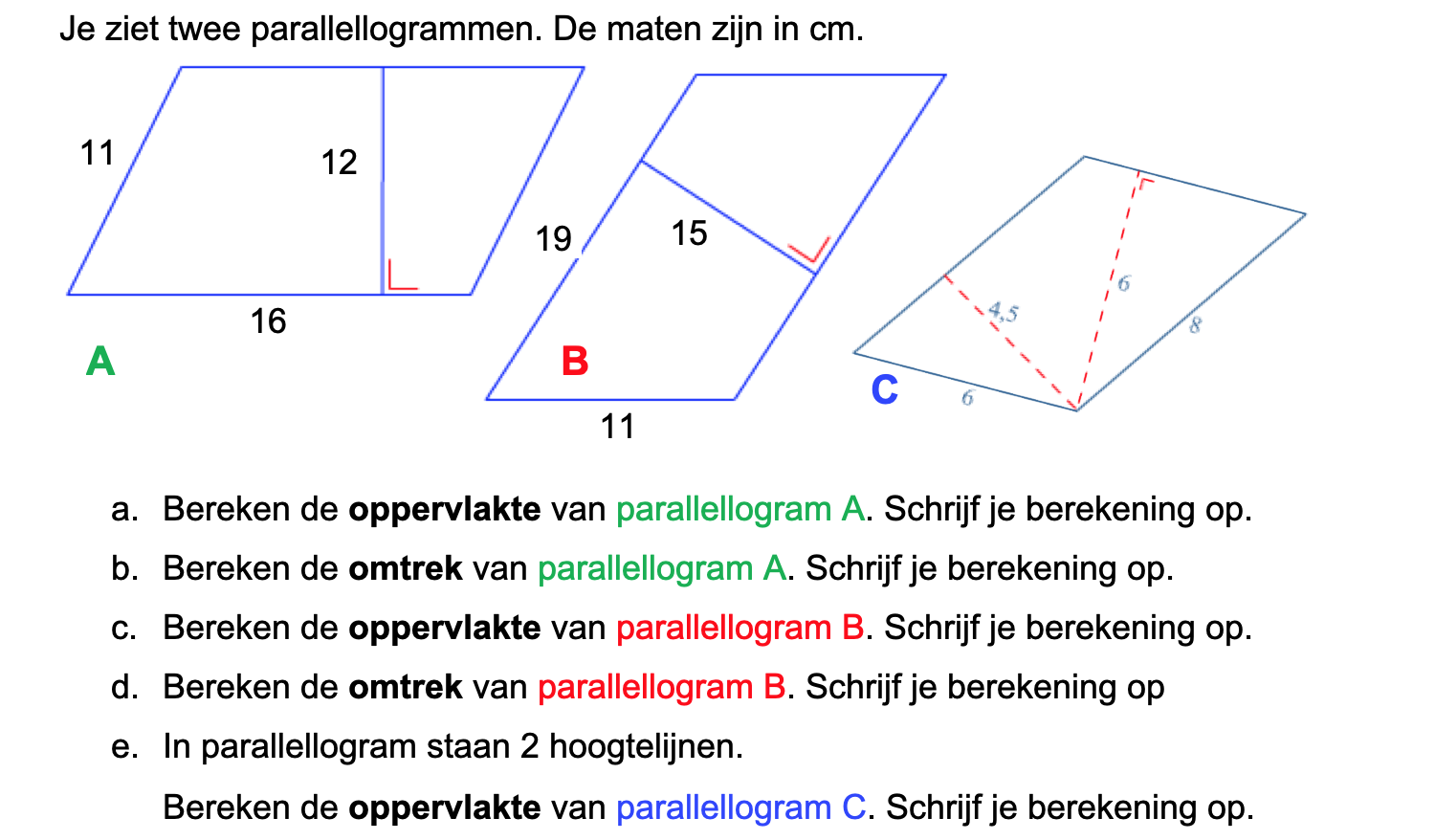
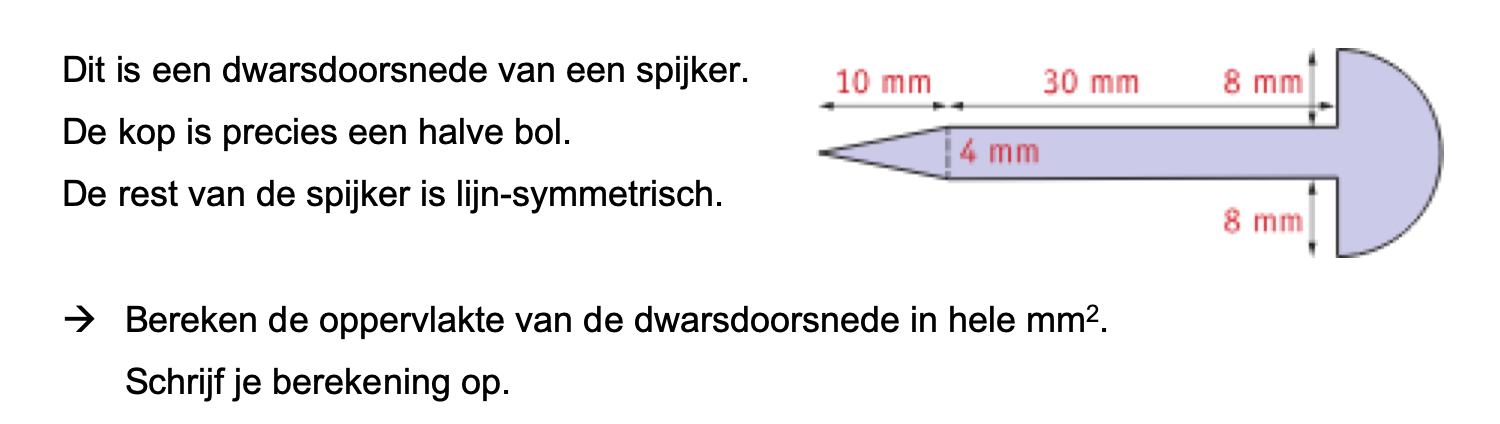
Nog enkele opgaven om te oefenen voor het proefwerk.
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Bestudeer uit de Kennisbank wiskunde het onderdeel:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
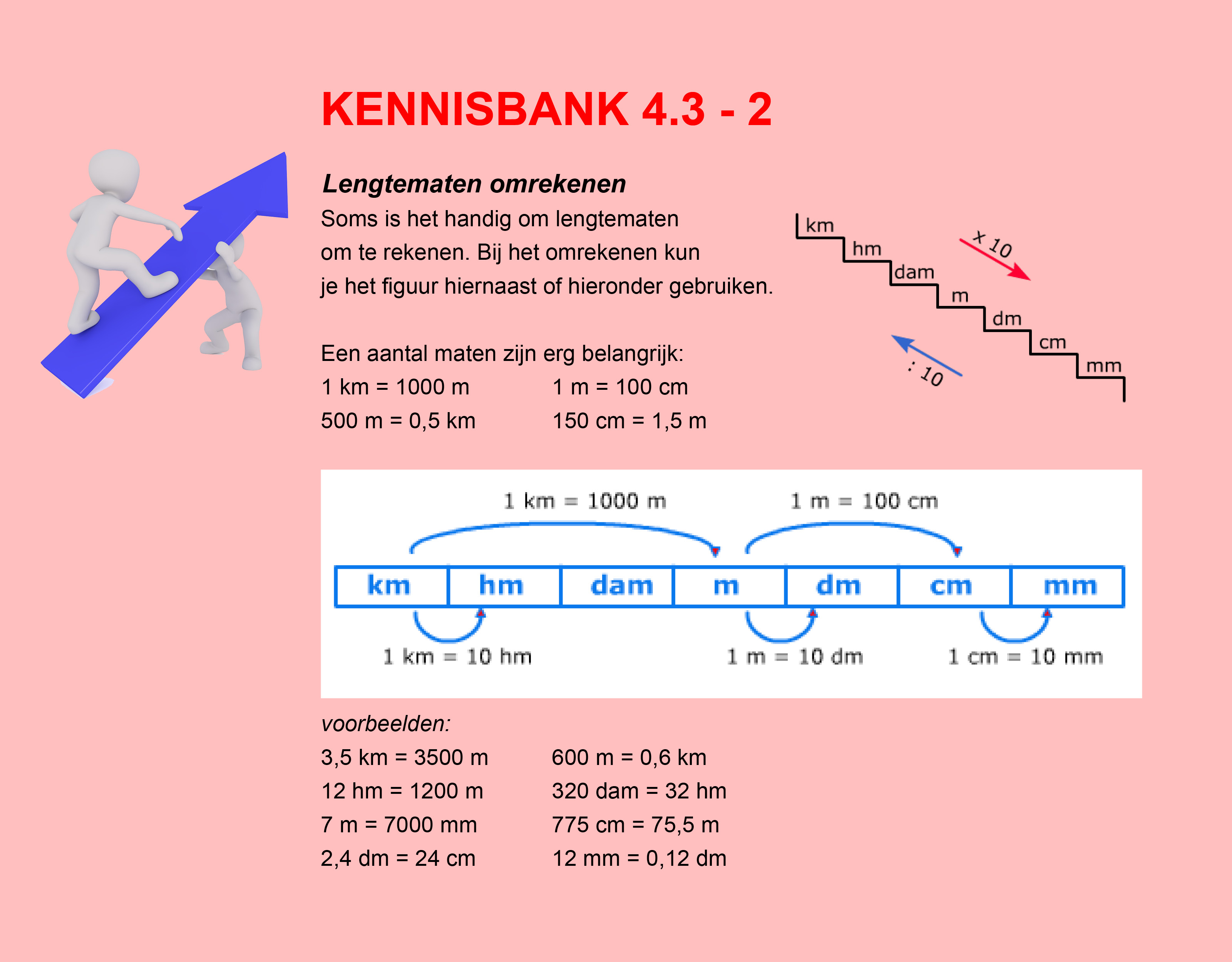
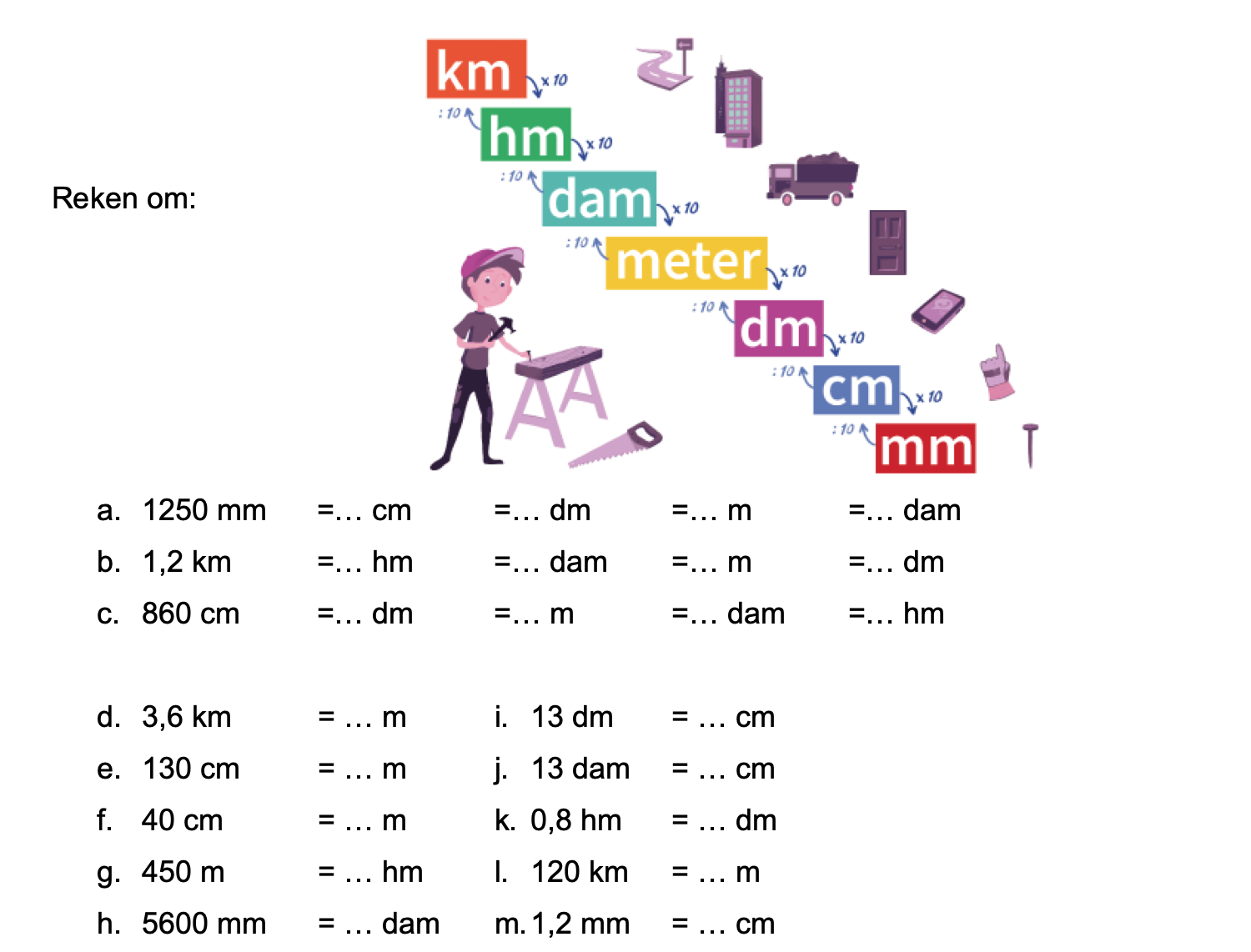
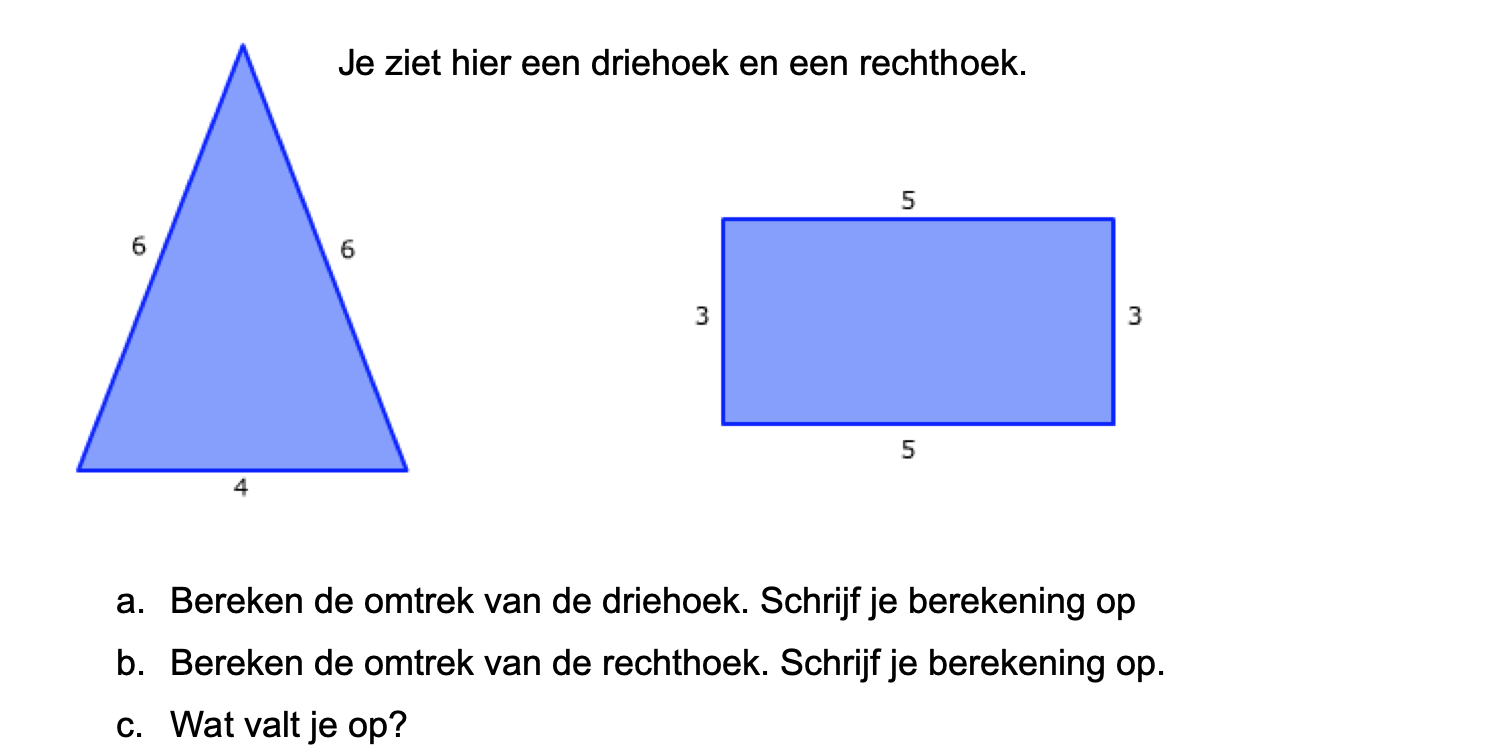
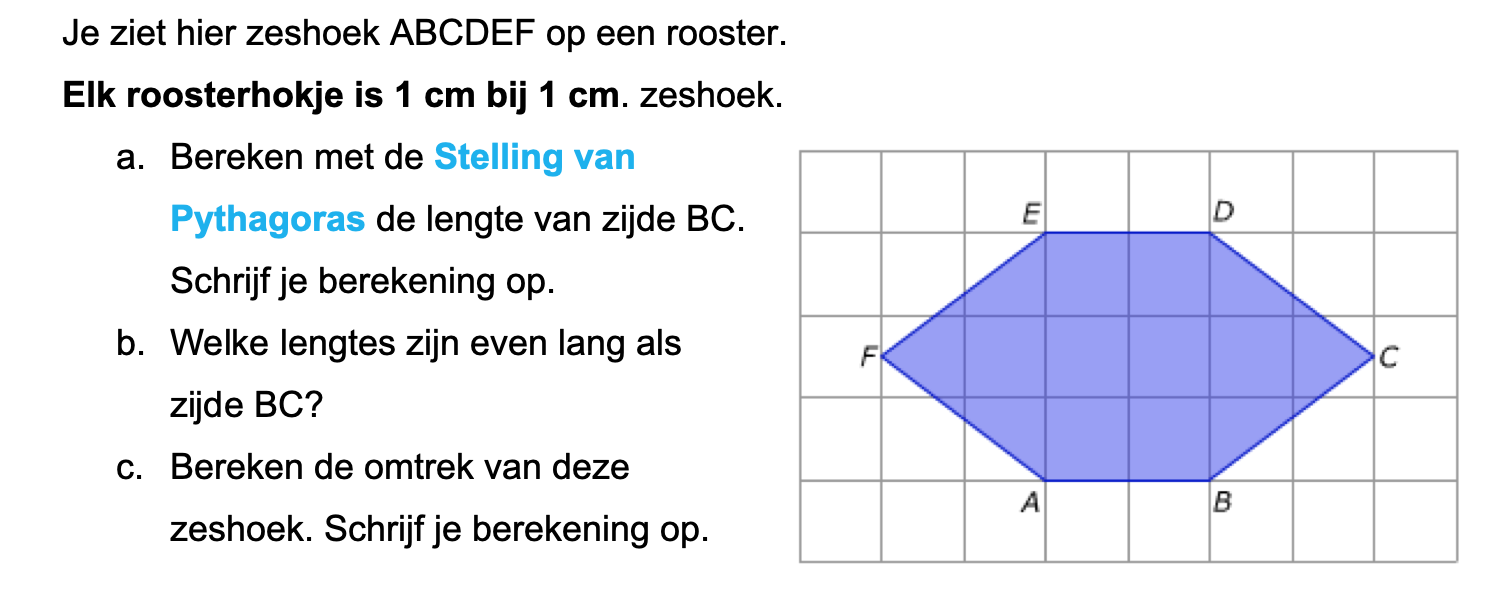
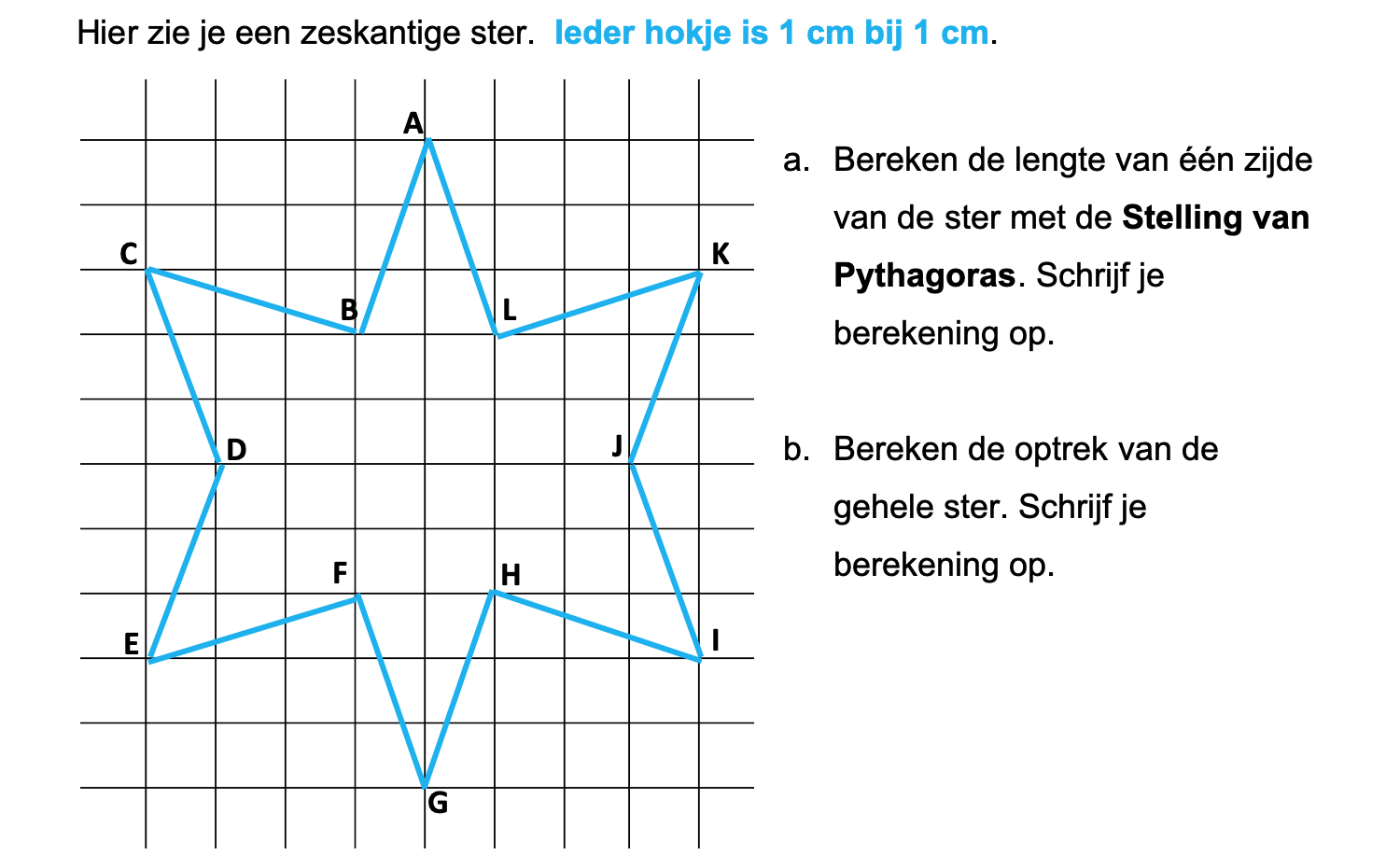
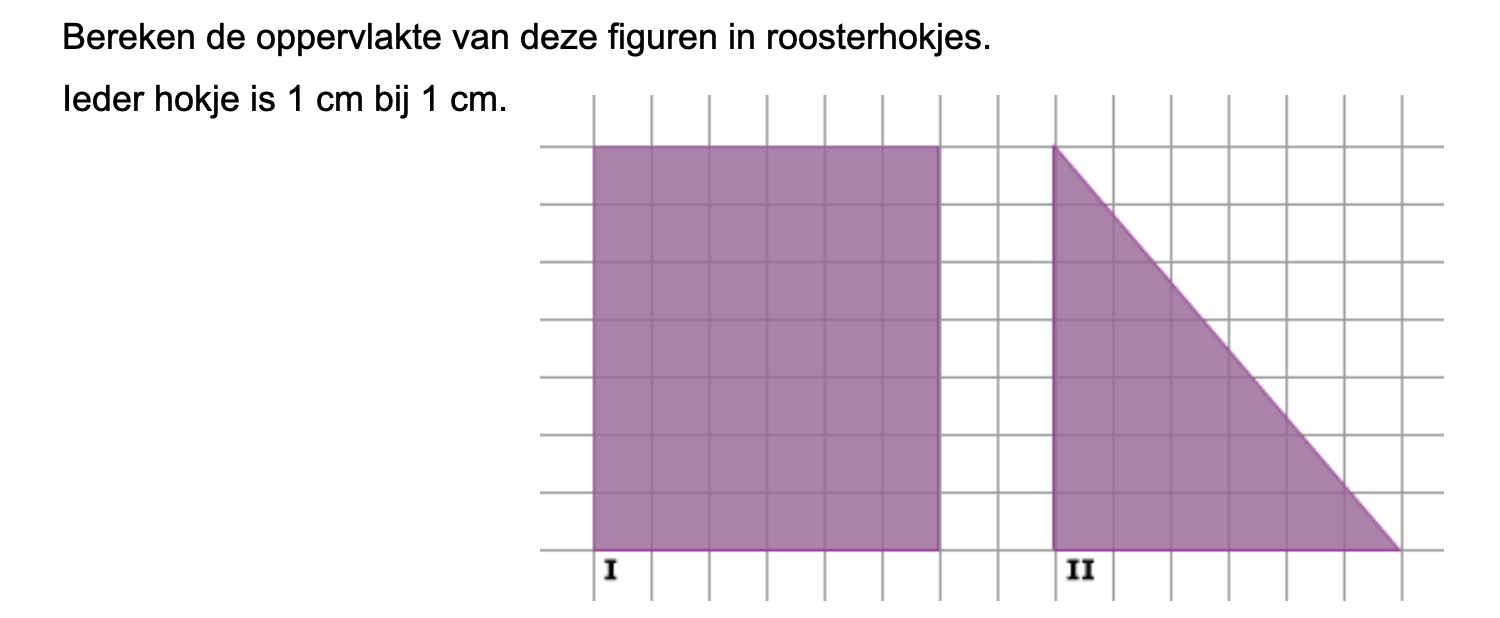
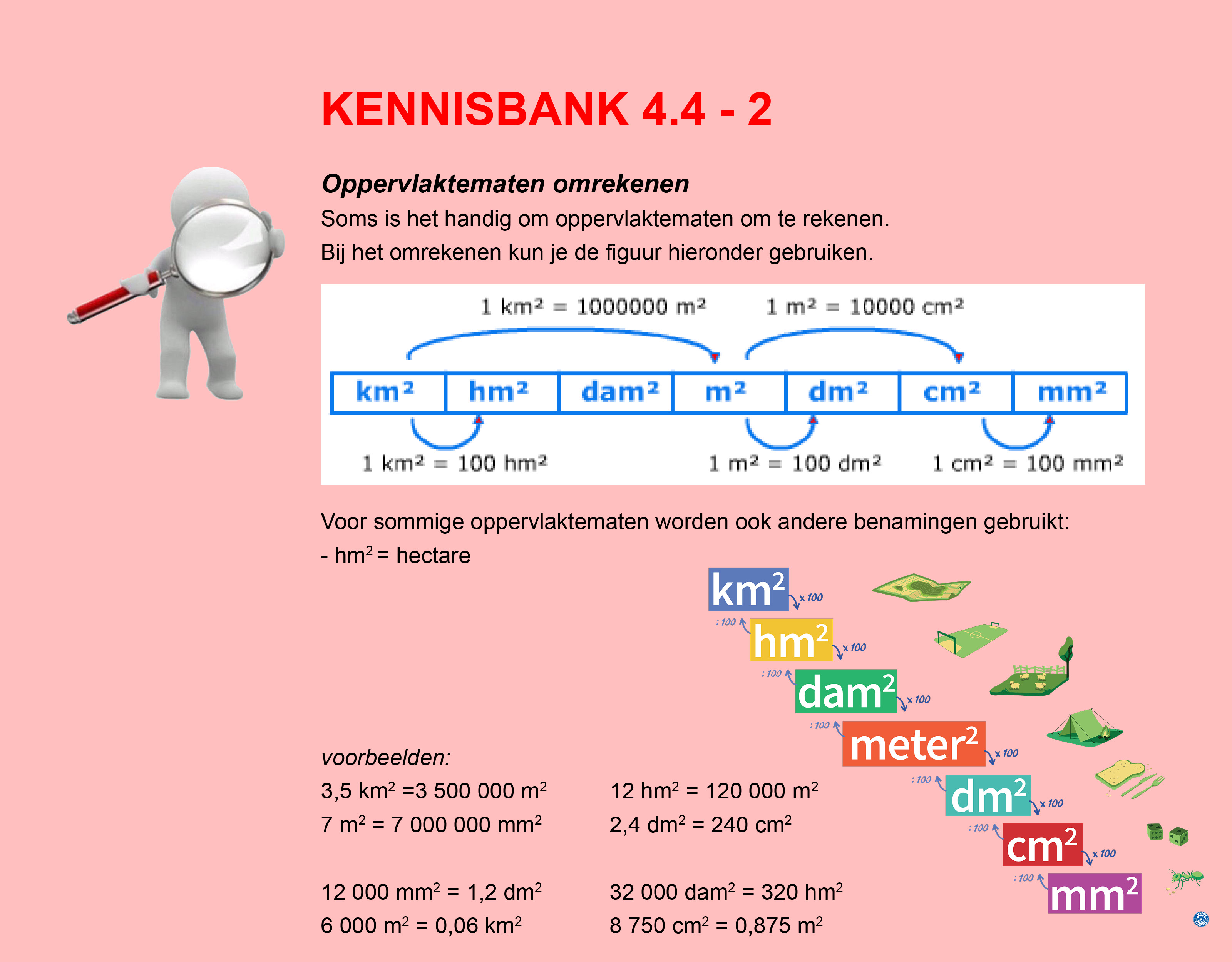
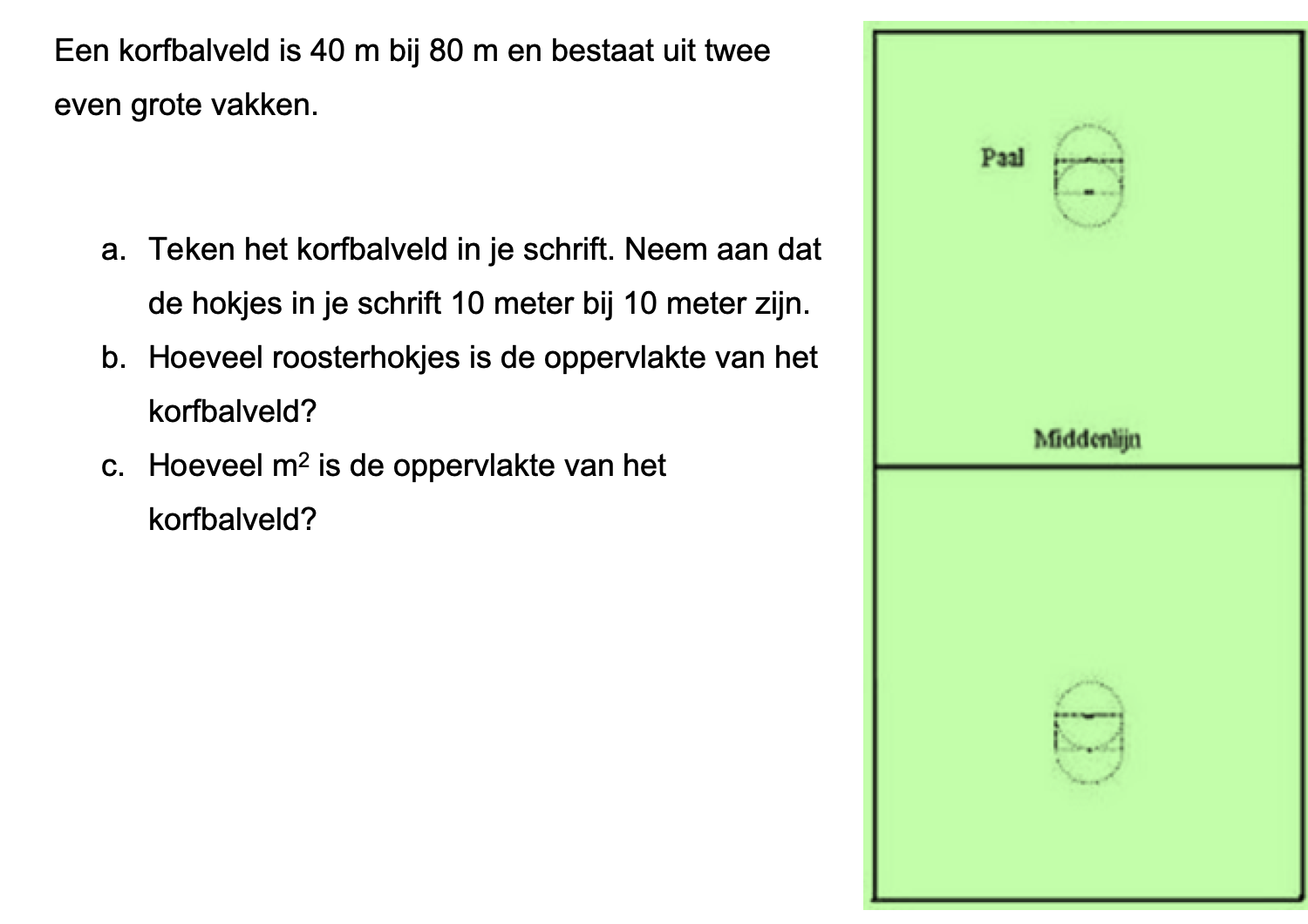
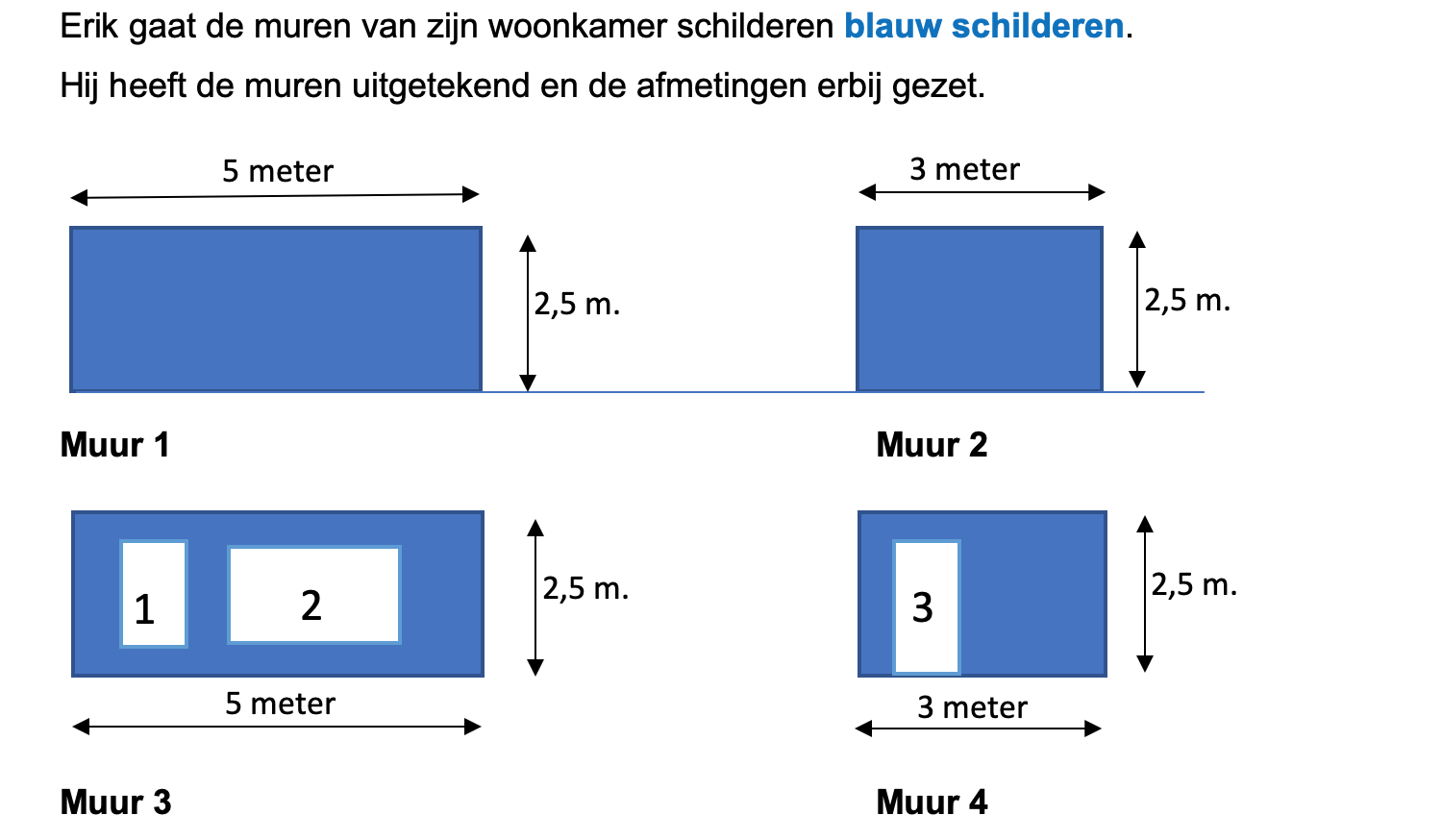
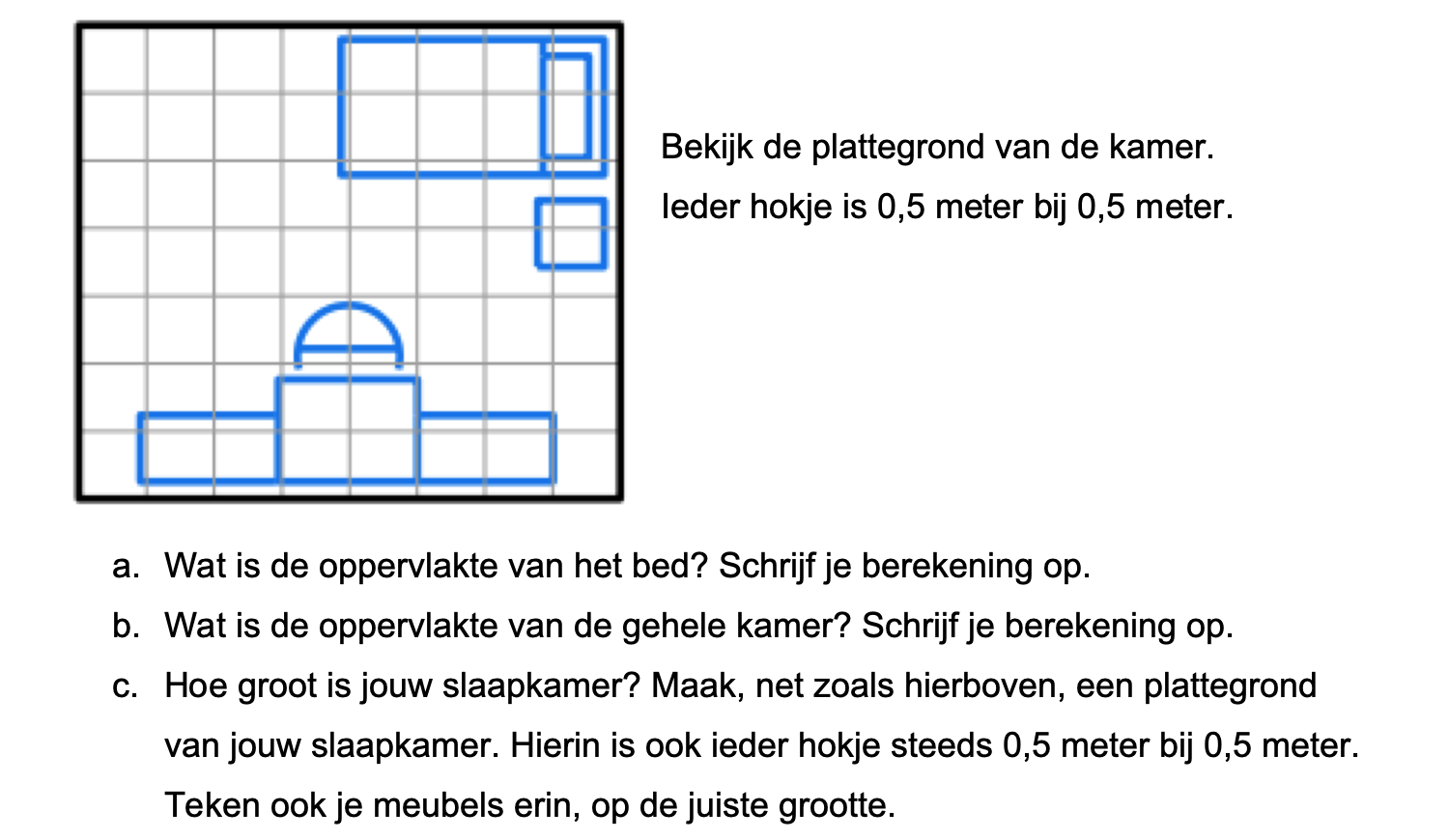
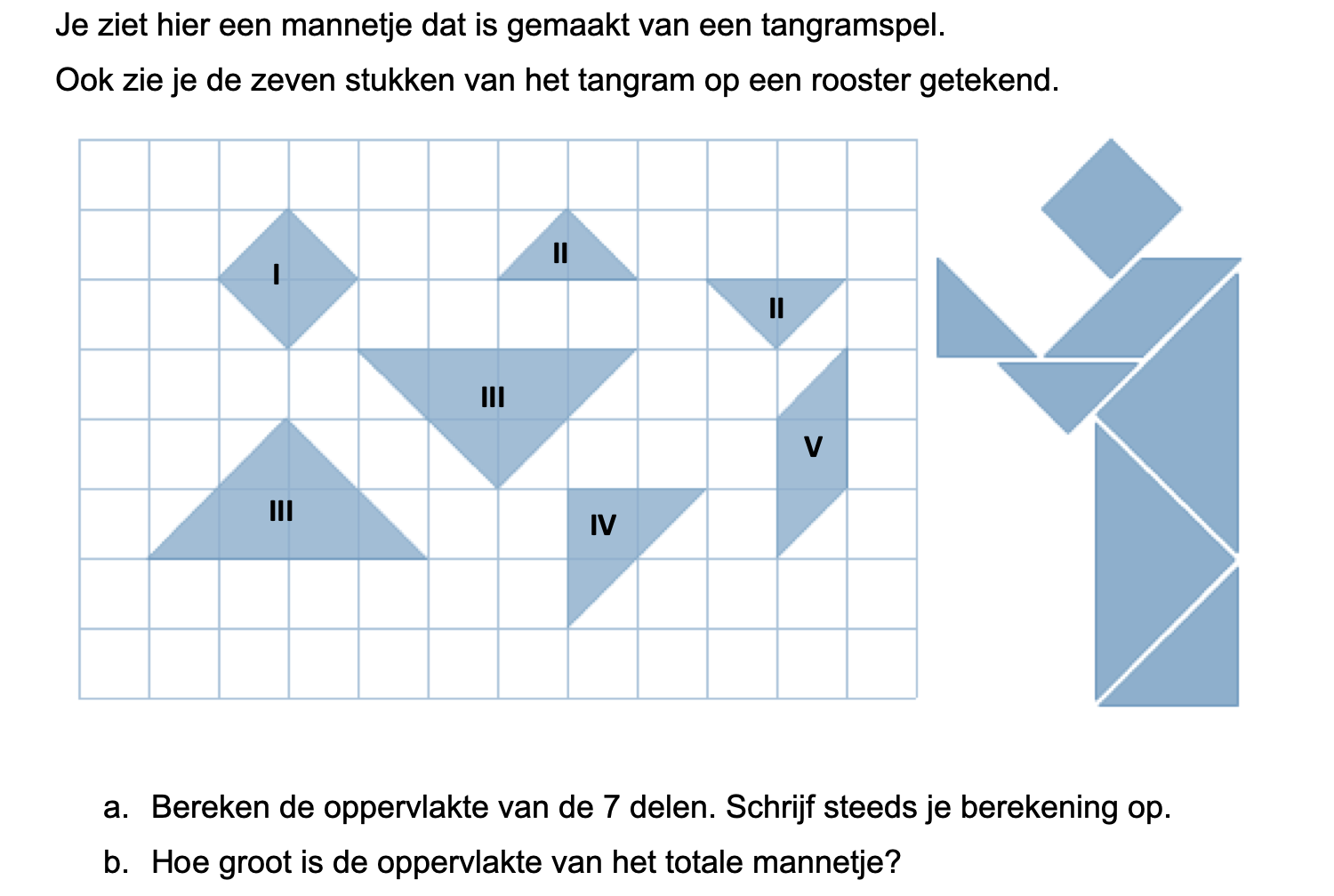
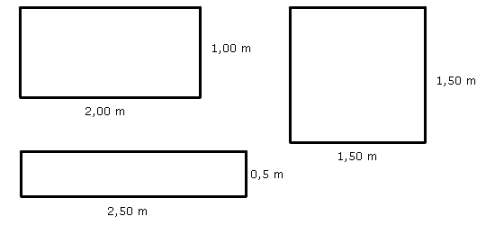
Bestudeer eerst uit de Kennisbank wiskunde het onderdeel: Oppervlakte
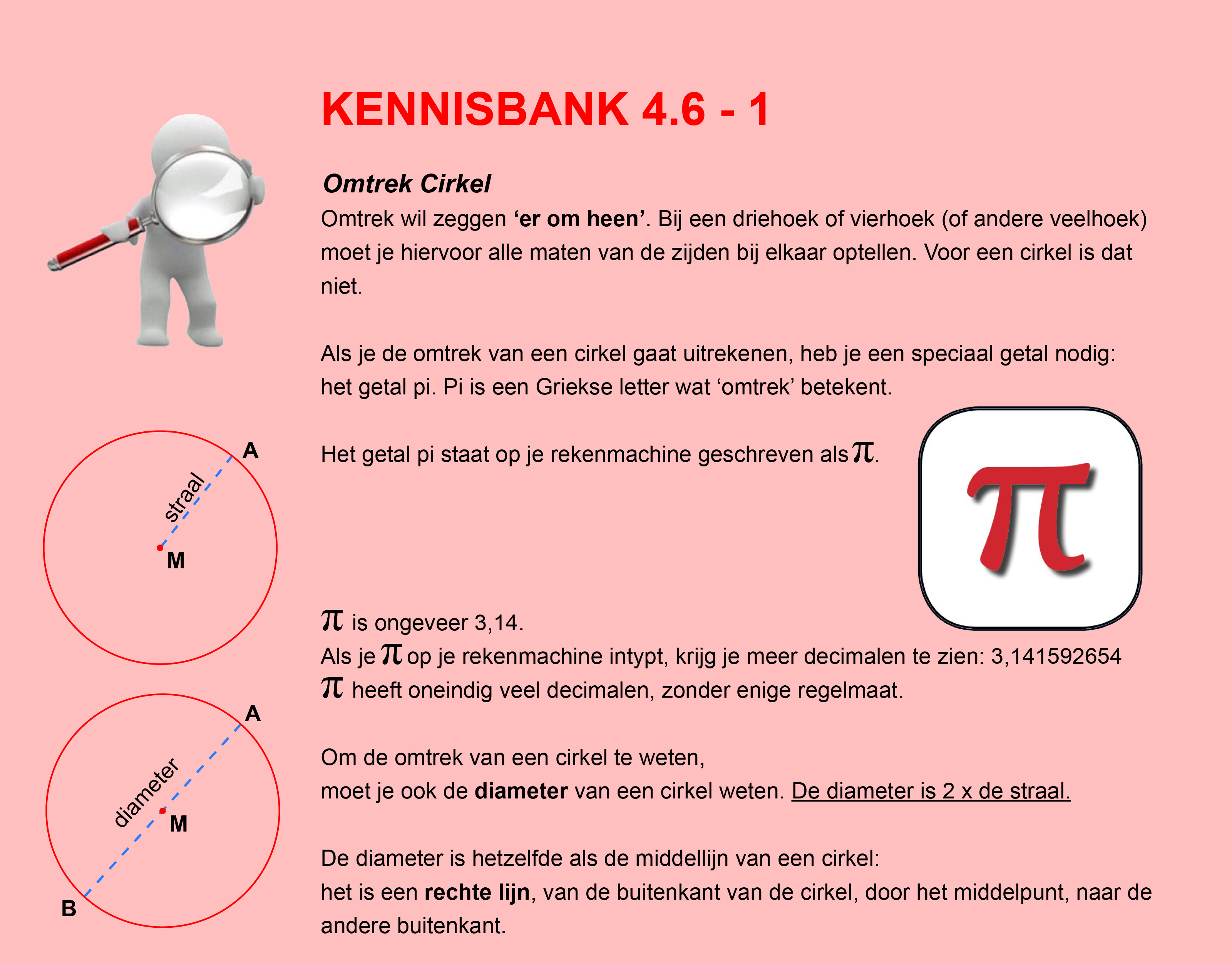
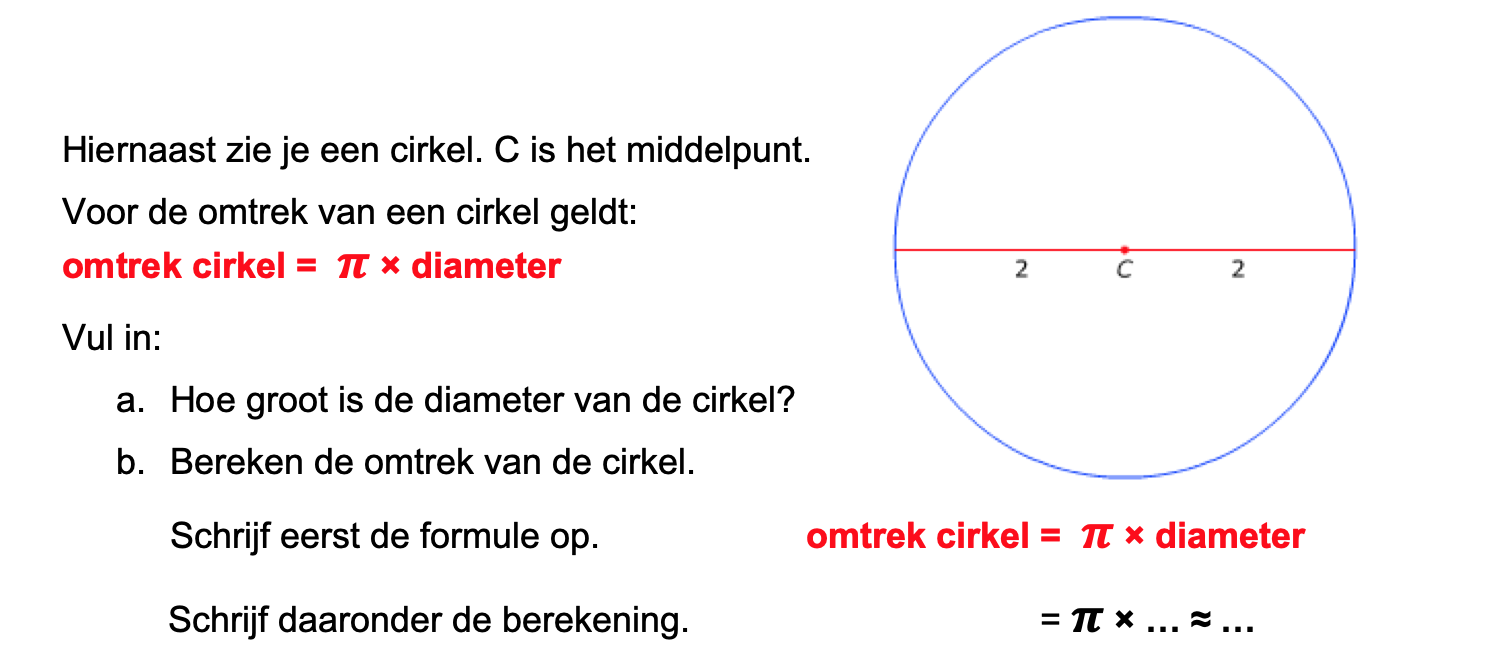
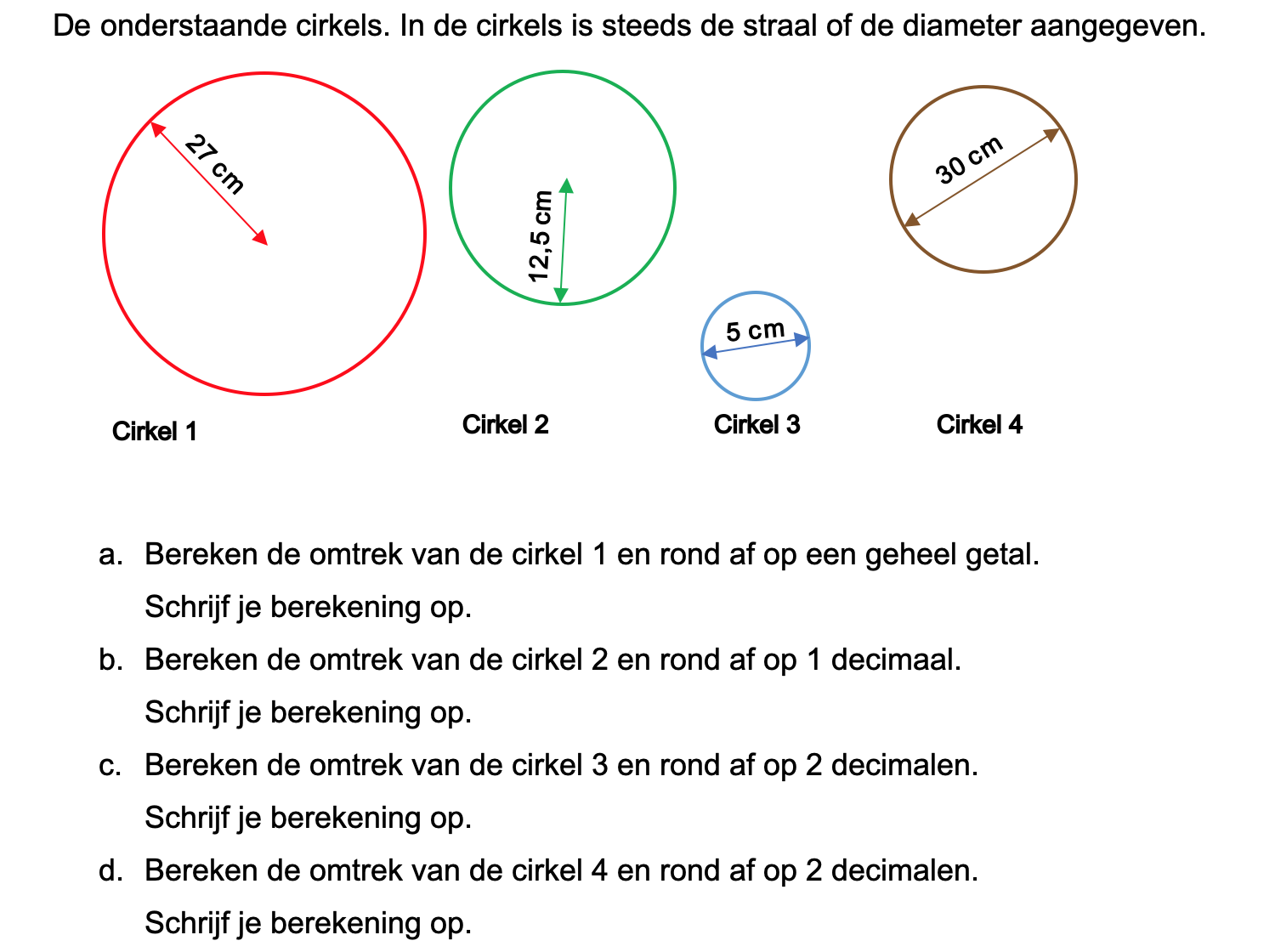
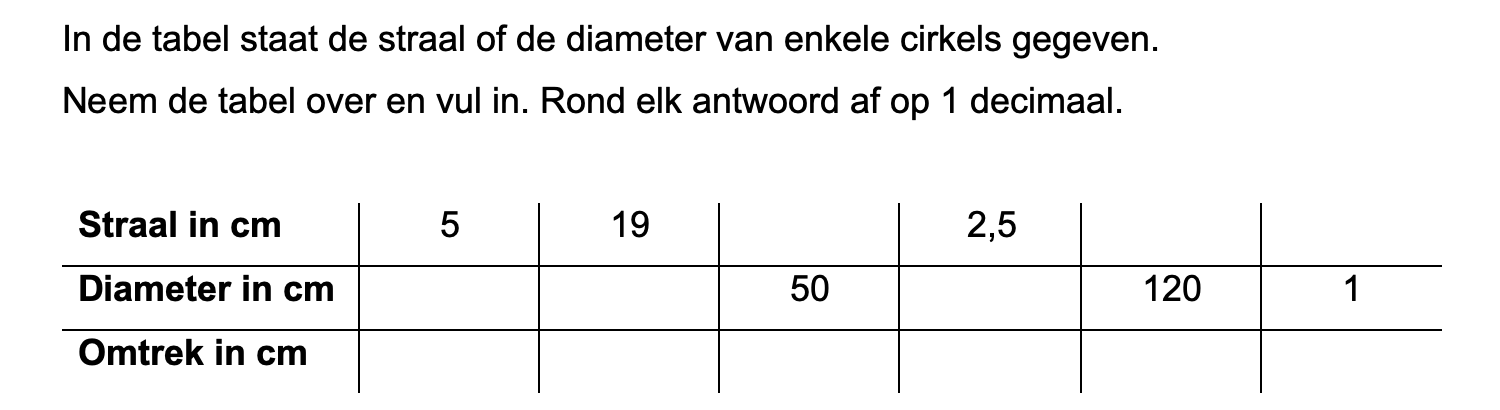
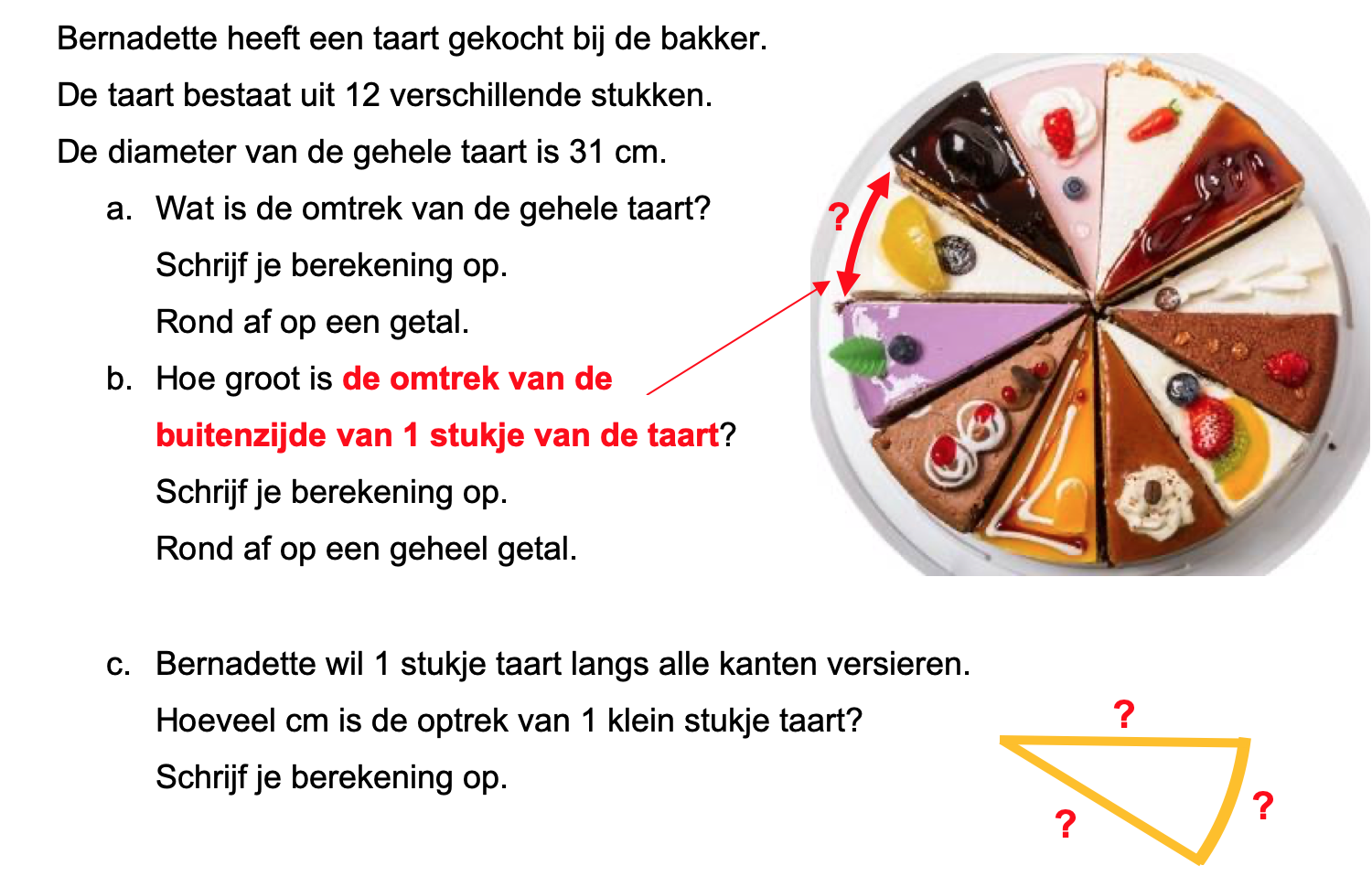
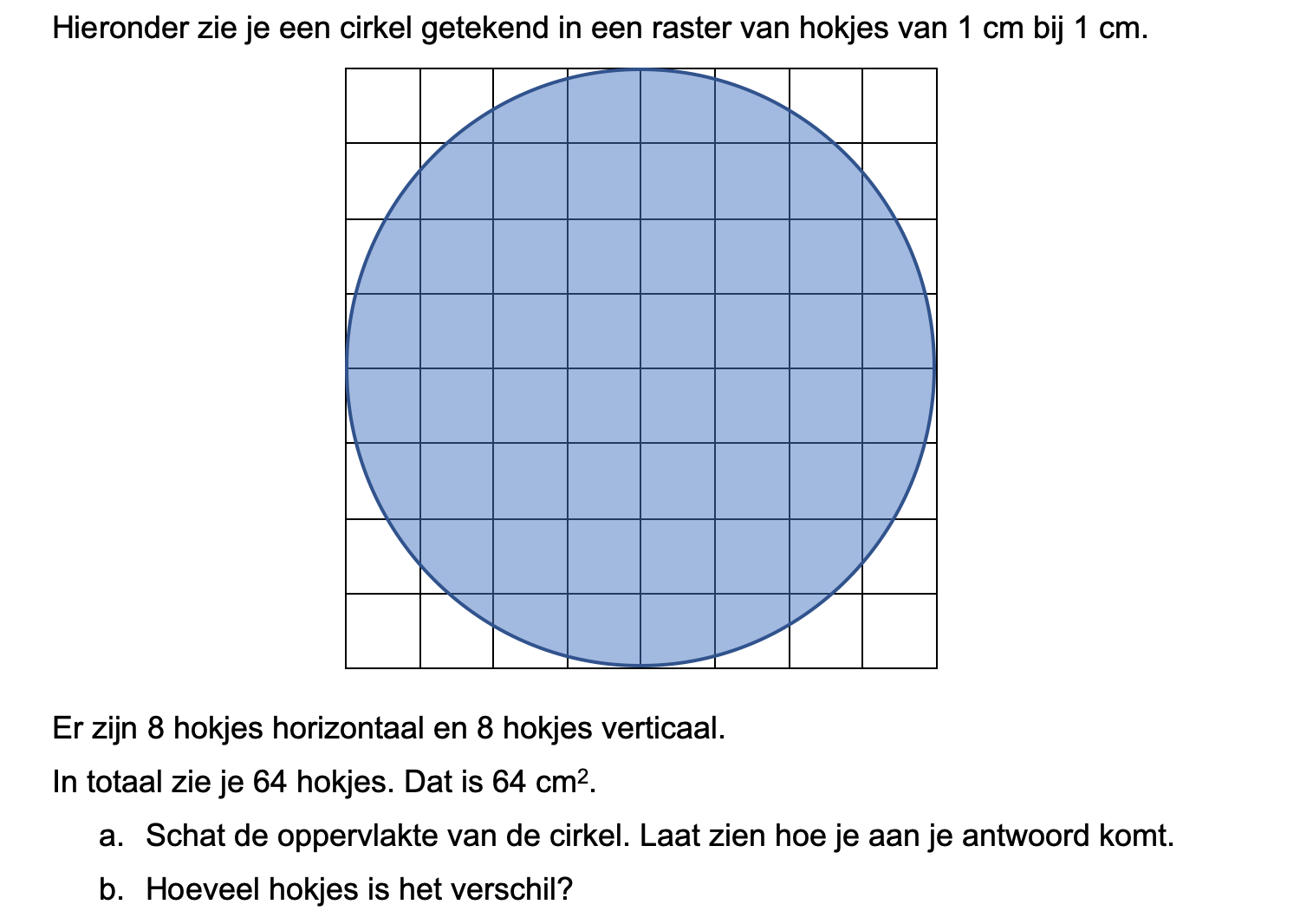
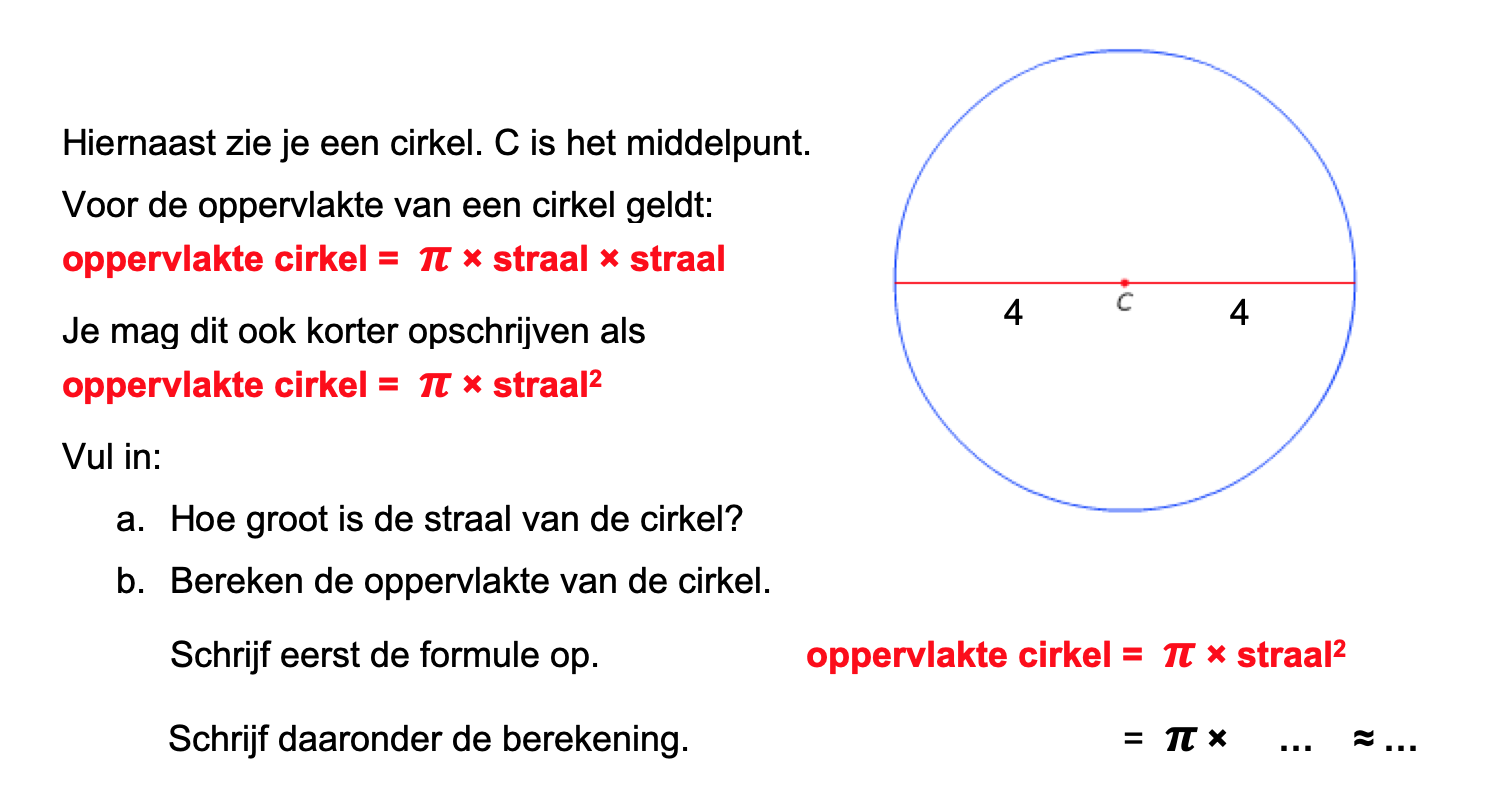
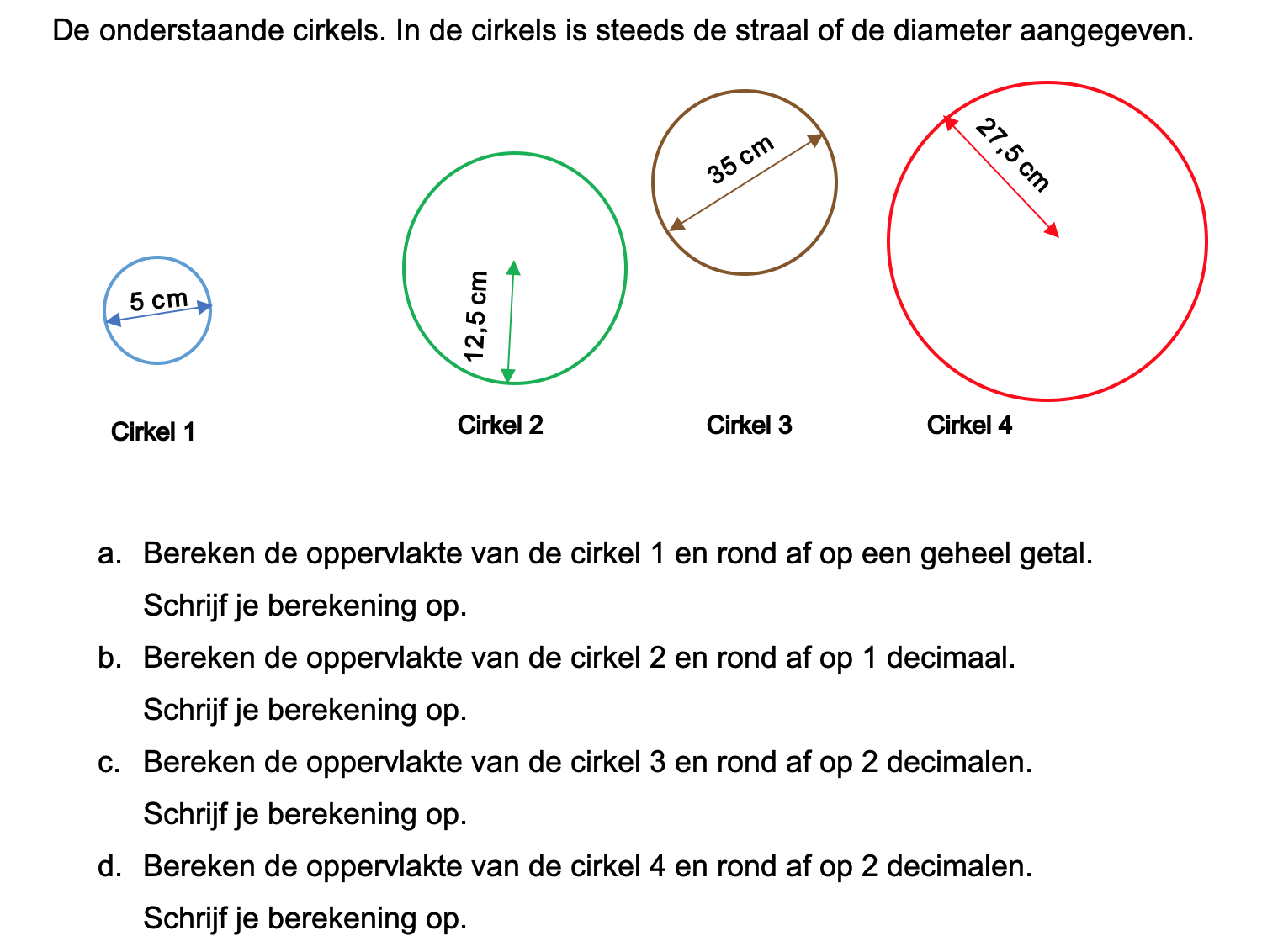
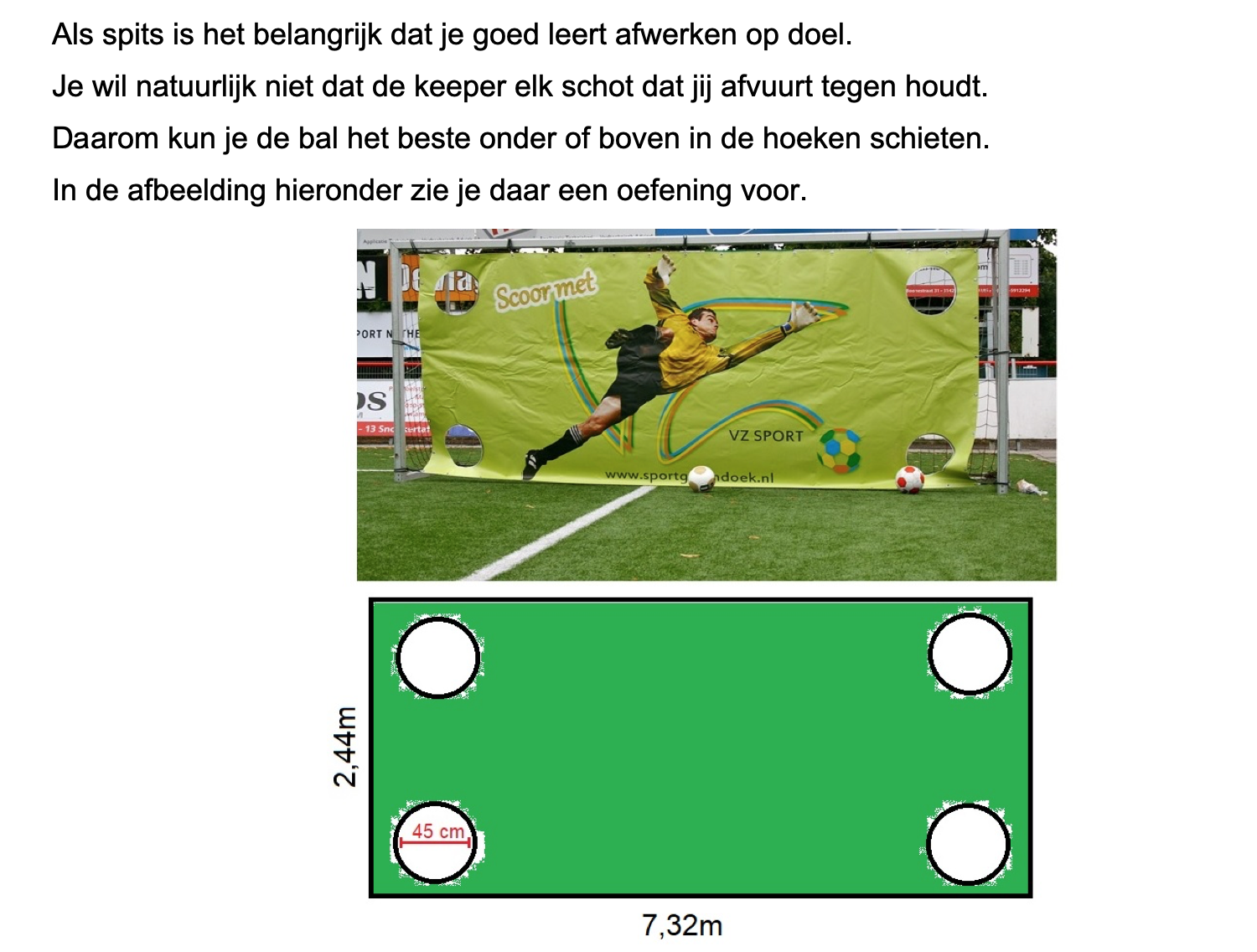
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
Ter voorbereiding op je proefwerk maak je de volgende opgaven:
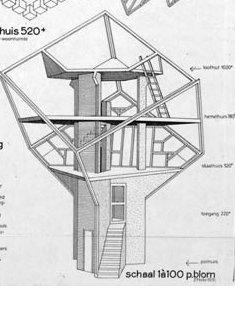
De prijs van de kavels is verschillend:
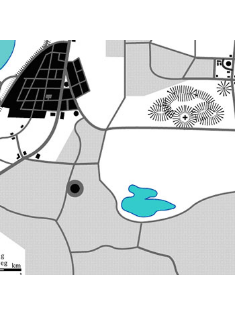
In de thema´s/opdrachten van de Stercollecties wiskunde wordt regelmatig verwezen naar de Kennisbank wiskunde. In de Kennisbank vind je de theorie die je nodig hebt voor het beantwoorden van de vragen en het maken van de opdrachten.
