Het arrangement Lesblok Afstanden is gemaakt met Wikiwijs van Kennisnet. Wikiwijs is hét onderwijsplatform waar je leermiddelen zoekt, maakt en deelt.
- Auteur
- Laatst gewijzigd
- 28-05-2018 14:30:46
- Licentie
-
Dit lesmateriaal is gepubliceerd onder de Creative Commons Naamsvermelding 4.0 Internationale licentie. Dit houdt in dat je onder de voorwaarde van naamsvermelding vrij bent om:
- het werk te delen - te kopiëren, te verspreiden en door te geven via elk medium of bestandsformaat
- het werk te bewerken - te remixen, te veranderen en afgeleide werken te maken
- voor alle doeleinden, inclusief commerciële doeleinden.
Meer informatie over de CC Naamsvermelding 4.0 Internationale licentie.
Aanvullende informatie over dit lesmateriaal
Van dit lesmateriaal is de volgende aanvullende informatie beschikbaar:
- Eindgebruiker
- leerling/student
- Moeilijkheidsgraad
- gemiddeld
Bronnen
| Bron | Type |
|---|---|
|
Tekenen van een loodlijn. https://www.youtube.com/watch?v=WnDFXhsxYQA&t=26s |
Video |
|
Construeren van een middelloodlijn https://www.youtube.com/watch?v=cXXt-yVO8-E |
Video |
|
Construeren van een bissectrice (deelllijn) https://www.youtube.com/watch?v=Ks6dy_9EshI |
Video |
|
Construeren van de omgeschreven cirkel. https://www.youtube.com/watch?v=76lBlyPqrIg |
Video |
|
Construeren van de ingeschreven cirkel. https://www.youtube.com/watch?v=1d4nGcmSmp8 |
Video |
Gebruikte Wikiwijs Arrangementen
Wiskunde Wageningse Methode OUD. (2017).
10. Afstanden

 Met afstand bedoelen we de lengte van de kortste verbinding. De afstand van twee punten
Met afstand bedoelen we de lengte van de kortste verbinding. De afstand van twee punten  Lijn
Lijn  Lijnstuk
Lijnstuk  Een halve lijn heeft één grenspunt, loopt dus aan één kant van het grenspunt onbeperkt door.
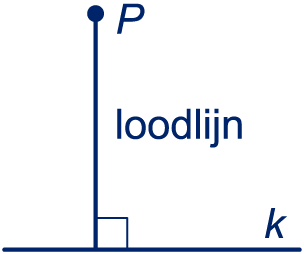
Een halve lijn heeft één grenspunt, loopt dus aan één kant van het grenspunt onbeperkt door. De middelloodlijn van lijnstuk
De middelloodlijn van lijnstuk  De deellijn van een hoek deelt een hoek in twee even grote hoeken. Alle punten, die op de deellijn liggen, liggen even ver van de benen van een hoek af.
De deellijn van een hoek deelt een hoek in twee even grote hoeken. Alle punten, die op de deellijn liggen, liggen even ver van de benen van een hoek af.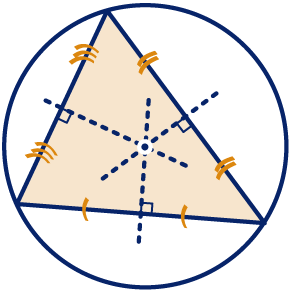 De drie middelloodlijnen van een driehoek gaan door één punt. Dit punt ligt even ver van de hoekpunten van de driehoek en is het middelpunt van de omgeschreven cirkel.
De drie middelloodlijnen van een driehoek gaan door één punt. Dit punt ligt even ver van de hoekpunten van de driehoek en is het middelpunt van de omgeschreven cirkel.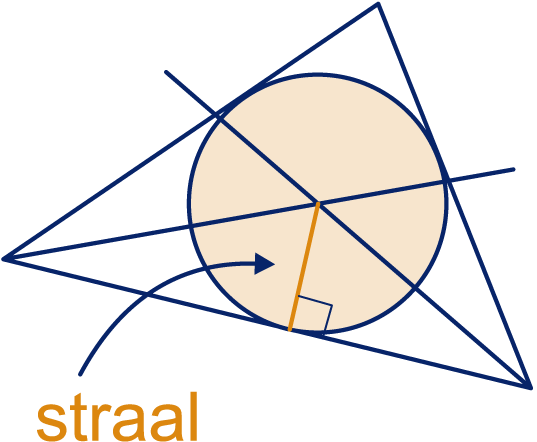 De drie deellijnen van de hoeken van een driehoek gaan door één punt. Dit punt ligt even ver van de drie zijden van de driehoek en is het middelpunt van de ingeschreven cirkel. Als je de cirkel wilt tekenen, moet je eerst de straal vinden. Laat vanuit het middelpunt een loodlijn neer op één van de zijden, dan is dat de straal.
De drie deellijnen van de hoeken van een driehoek gaan door één punt. Dit punt ligt even ver van de drie zijden van de driehoek en is het middelpunt van de ingeschreven cirkel. Als je de cirkel wilt tekenen, moet je eerst de straal vinden. Laat vanuit het middelpunt een loodlijn neer op één van de zijden, dan is dat de straal.